On the Origin of Order in the Genome Organization of ssRNA Viruses

Abstract

Single-stranded RNA (ssRNA) viruses form a major class that includes important human, animal, and plant pathogens. While the principles underlying the structures of their protein capsids are generally well understood, much less is known about the organization of their encapsulated genomic RNAs. Cryo-electron microscopy and x-ray crystallography have revealed striking evidence of order in the packaged genomes of a number of ssRNA viruses. The physical determinants of such order, however, are largely unknown. We study here the relative effect of different energetic contributions, as well as the role of confinement, on the genome packaging of a representative ssRNA virus, the bacteriophage MS2, via a series of biomolecular simulations in which different energy terms are systematically switched off. We show that the bimodal radial density profile of the packaged genome is a consequence of RNA self-repulsion in confinement, suggesting that it should be similar for all ssRNA viruses with a comparable ratio of capsid size/genome length. In contrast, the detailed structure of the outer shell of the RNA density depends crucially on steric contributions from the capsid inner surface topography, implying that the various different polyhedral RNA cages observed in experiment are largely due to differences in the inner surface topography of the capsid.

Introduction

Viruses package their genomes into protective protein containers called capsids (1). Their distinct packaging strategies are adapted to the physical properties of their genomic RNAs and DNAs. For example, double-stranded DNA viruses with genomes of a comparatively large persistence length of ∼45 nm (2), typically use a molecular motor to package their genomes into their preassembled capsid. As a consequence, they exhibit a spool-like structure (3). By contrast, viruses with single-stranded DNA or RNA (ssRNA) genomes are characterized by a much smaller persistence length of ∼1 nm (4), and therefore can employ a cooperative mechanism in which genome packaging and protein capsid assembly occur simultaneously. As a consequence, the genome may take on vital roles that enhance assembly efficiency of the protein container. For example, it has been shown, for bacteriophage MS2, that interactions between short stem loops (from within the genomic RNA sequence) and capsid proteins trigger allosteric conformational changes that convert protein dimers, that naturally occur in a symmetric form, into the asymmetric form needed to build the capsid (5). Moreover, it has been shown that RNA stem loop interactions with capsid proteins are responsible for directing virus assembly toward a relatively small number of the combinatorially possible pathways (6), thereby allowing assembly to be described by a small set of simple rules (7).

To better understand this intricate interaction between the viral genome and the capsid proteins, it is important to determine the physical principles underlying the structure of the packaged viral genome. For a number of RNA viruses, intriguing structural features have been observed: for example, a dodecahedral cage in Pariacoto virus; a double-shell organization in bacteriophage MS2; and a number of other polyhedral cage structures in a range of RNA viruses (7,8). Biomolecular simulation makes it possible to probe the physical determinants of these structures. In these studies, single-stranded RNA and single-stranded DNA interactions with the capsid are modeled using the basic principles of polyelectrolyte interactions with charged surfaces, based on a coarse-grained model of the genome as a string of beads, each representing a nucleotide (9–13).

In many of these studies (12,13), the virus capsid was represented as an isotropic spherical container with embedded positive charges; in others more detailed capsid models were used, e.g., based on the electrostatic potential of the capsid in the case of Cowpea Chlorotic Mottle Virus (9), or via incorporating details of the crystal structure of the capsid inner surface in the case of Pariacoto virus (10). For the Pariacoto virus, the simulations revealed that the charge distribution on the interior surface of the virus capsid acts as a template for the assembly of the genome into a dodecahedral cage, via protein-RNA interactions arising from the extension of the N-terminal peptide arms of the capsid proteins into the capsid interior (10). None of these studies, however, has probed, systematically, the individual contributions of different energetic and structural components, and the role of confinement, to the observed order in the packaged genome structure.

To address this, we performed a series of coarse-grained molecular dynamics (MD) simulations for our test system, the RNA Bacteriophage MS2 (Fig. 1). In particular, we assessed the individual contributions of RNA self-interaction due to spherical confinement, and the role of both electrostatic and steric effects of the capsid surface topography.

Figure 1.

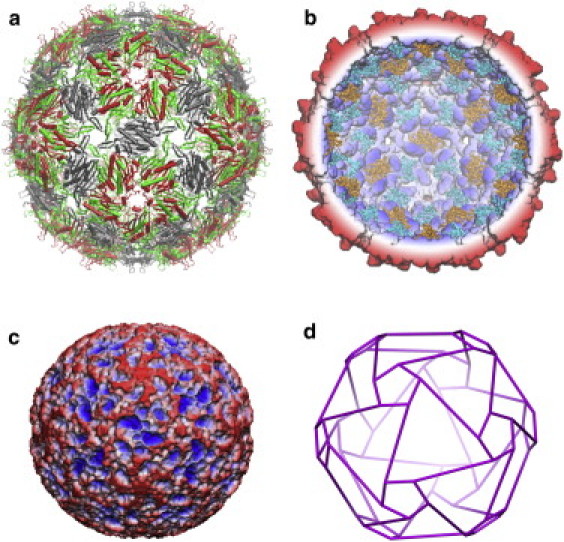
(a) X-ray crystal structure of the MS2 virus capsid (PDB ID:1ZDH) viewed along the particle twofold axis. The MS2 capsid is composed of 180 proteins that are organized as three quasiequivalent protein conformers (A–C, colored green, red, and gray, respectively). (b) A cross-section of the solvent-accessible surface perpendicular to the twofold symmetry axis, with the translational repressor stem loops underneath the AB dimers represented (turquoise) as well as those underneath the CC dimers (orange). (c) The solvent-accessible surface of the inner surface of the capsid. (d) Schematic representation of the RNA density distribution in the vicinity of this surface as revealed by cryo-EM (28). (Reprinted from Toropova et al. (28) with permission from Elsevier. License No.: 2695380729569.) In panels b and c, the surfaces are radially colored (from blue, r = 100 Å to red, r = 140 Å).

Our simulations revealed that the observed bimodal radial distribution of the ssRNA genome in the MS2 virus arises from the electrostatic self-repulsion of the RNA chain when confined within a spherical volume of a radius corresponding to that of the virus. We show that this provides an interpretation of results from experiments on capsid reassembly in the presence of subgenomic RNA fragments (14). Our analysis shows that for genome lengths corresponding to ∼30% of the ssRNA genome of MS2, the electrostatic repulsion within the genomic RNA results in it being fully accommodated in the outer shell. This suggests that the observed disappearance of the inner shell, for these shorter RNA fragments, is more likely to be due to a reorganization of the outer shell, rather than to artifacts of the icosahedral averaging procedures applied in the cryo-EM reconstructions. We moreover find that the detailed structure of the outer RNA shell arises largely from steric interactions with the capsid inner surface, implying an intricate interdependence of the capsid inner surface topography and the genome organization in ssRNA viruses. Insights from this work may potentially inform strategies in areas such as antiviral therapy or polymer packaging in viral capsids for applications in bionanotechnology (15).

Material and Methods

We performed four MD simulations for probing the influence of the virus capsid on the packaging of the RNA genome using different combinations of interaction potentials (see Table 1 for details) including explicit account of RNA self-interaction (E _RNA-RNA), implicit account of interactions with the solvent (E_RNA-solvent), and implicit account of interactions with the capsid proteins (E_RNA-capsid):

$$E_{total}=E_{RNA-RNA}+E_{RNA-solvent}+E_{RNA-capsid}.$$ (1)

The RNA was modeled as a self-avoiding flexible chain of connected beads with each bead representing a single nucleotide of the MS2 genome (3569 nucleotides): a homopolymeric model that does not account for the specific nucleotide sequence of the naturally occurring genome sequence. The coordinates of the crystal structure of the MS2 capsid proteins were obtained from the VIPER database (16) (PDB-ID:1ZDH).

Table 1.

Summary of the interaction potentials used in the MD simulations of the RNA genome

ID	Number of trajectories	Duration/trajectory (ns)	Etotal
			ERNA-RNA	ϕcapsid-steric	ϕcapsid-elect	Spherical boundary r = 110 Å
MD1	3	500	On	On	On	Off
MD2	3	500	On	On	Off	Off
MD3	3	500	On	Off	On	On
MD4	3	500	On	Off	Off	On

RNA self-interaction (E_RNA-RNA)

The interaction potential of the beads in the RNA chain was modeled using a molecular-mechanics force field. Bonded interactions were described by harmonic bond, angle, and dihedral potentials while the nonbonded potentials comprised a Coulombic term and a van der Waals term. For the Coulombic term, a charge of −0.25 was assigned to each bead and a dielectric constant of 4 was used where a distance cutoff of 70 Å with a switching function was employed. The charge of −0.25 has been extensively used in coarse-grained RNA simulations to mimic the effects of counterions and solvent (9). Moreover, a recent study on the electrostatic potential of a 70S ribosome showed that these charges result in a potential that is comparable to that generated from a full atomistic model using APBS (17). For the van der Waals term, a 12-6 Lennard-Jones potential was used with a radius of 5 Å and a well-depth of 1.0 kcal mol⁻¹. A van der Waals radius of 4–5 Å has been successfully used to reproduce internucleotide contact distances within ribosomal RNA (18). The equilibrium bond length, angles, and dihedrals parameters and the corresponding force constants of unpaired nucleotides were adopted from the NAST force field (19). Use of the parameters corresponding to unpaired nucleotides is justified in terms of the nature of the coarse-grained RNA model employed that does not take into account the secondary structure of RNA.

RNA interaction with the solvent

Frictional and fluctuating forces due to interaction with the solvent were implicitly included via a Langevin equation (20):

$$m\ddot{r}=\mathbf{F}-\gamma \mathbf{v}+\psi \left(t\right).$$ (2)

Here, m and r denote the mass and position of the bead, F is the force acting on the bead by other beads, γ is the damping coefficient, v is the bead velocity, and ψ(t) is a temperature-dependent random force due to collisions with the solvent. The mass m was set to 321.41 a.m.u. (corresponding to the mean nucleotide mass for the MS2 genome) while γ was set to 10 ps⁻¹. The value of γ was dictated by the characteristics of the system; smaller values of γ were found to result in unstable simulations. We note that the value of this parameter is more likely to affect the timescale of the simulation (i.e., reaching equilibrium) rather than the results, and thus, the conclusions we draw (which do not refer to the dynamics of the system).

RNA interaction with the capsid proteins

Interaction of the RNA beads with the capsid proteins was implicitly accounted for via two types of interactions—interaction of the beads with the capsid electrostatic potential, and steric interaction with the capsid inner surface:

$$E_{RNA-capsid}=E_{RNA-capsid-elect}+E_{RNA-capsid-steric}.$$ (3)

The electrostatic potential for the MS2 capsid proteins (ϕ_capsid-elect in Table 1) was calculated on a grid, with a spatial resolution of 0.5 Å, by numerically solving the nonlinear Poisson-Boltzmann equation (21,22) using the APBS package (23). Atomic charges were adopted from the CHARMM27 force field (24,25). The protonation states of ionizable residues for the capsid proteins were adjusted to pH 5 using the PROPKA program (26) and the salt concentration was set to 0.04 M to conform to experimental data on genomic organization within the MS2 capsid (5). The capsid-solvent boundary was defined as the solvent-accessible surface using a probe radius of 1.4 Å. The solvent dielectric constant was set to 78.5, and the capsid protein interior dielectric constant to 4.

The steric interaction of the RNA with the virus capsid was modeled by a grid potential (ϕ_{capsid-steric} in Table 1) that is repulsive when overlapping with the capsid protein solvent-accessible surface, and zero elsewhere. Thus, the interaction energy of an RNA bead with the capsid proteins at a given position in space is calculated by multiplying its charge by the value of the capsid electrostatic potential and the capsid steric potential using tricubic interpolation. NAMD (v2.71) (27) was used to derive forces from these potentials in the MD simulations.

MD simulation details

The MD program NAMD (v2.71) (27) was used to simulate the dynamics of the RNA genome inside the MS2 virus capsid using different combinations of RNA-capsid interactions (see Table 1). Each simulation comprises three MD trajectories, each started from a different initial conformation of the RNA chain that was generated using a self-avoiding random walk constrained within a sphere of radius 90 Å; the number of random steps used was equal to the length of the MS2 full genome. Initial structures were centered inside the capsid and were subjected to 1000 steps of conjugate gradient energy minimization under spherical boundary harmonic restraints at a distance of 90 Å from the capsid center with a force constant of 5.0 kcal mol⁻¹ Å⁻². The MD simulation was then conducted at 300 K for 500 ns using a time step of 5 fs. In the first 5 ns, the spherical boundary force constant was reduced by 0.5 kcal mol⁻¹ Å⁻² every 0.5 ns. After this, the spherical boundary restraint was removed and the system was equilibrated for 300 ns. Finally, a production phase was run for 200 ns and the RNA structures were collected every 0.5 ns (400 frames per trajectory) and stored for further analysis.

Results and Discussion

We carried out a series of coarse-grained molecular dynamics simulations to probe the impact of the capsid electrostatic potential, the steric interactions representing the topography of the capsid inner surface, and the effect of spherical confinement on genome organization. In the first simulation (MD1), both electrostatic and steric interactions were present, whereas in the second (MD2) and the third (MD3), steric or electrostatic interactions were considered in isolation. In the fourth simulation (MD4), neither steric nor electrostatic interactions with the capsid were present and a spherically symmetric boundary potential was used to confine the RNA genome within a sphere of a size comparable to the MS2 capsid.

Radial density profile of the packaged RNA genome

The radial profile of the RNA density within the capsid is similar in all four simulations and shows two peaks, at ∼53 Å and ∼110 Å from the capsid center (see Fig. 2). This is in good agreement with the experimentally determined cryo-EM mass-density map for the genomic RNA in MS2, that revealed a two-shell architecture with an inner shell between ∼42 and 65 Å, and an outer shell between ∼84 and 108 Å (28). The similarity of the RNA distribution across all simulations (MD1–4) suggests that the detailed electrostatic and steric interactions of the capsid with the RNA beads are not important for the global architecture of the packaged RNA genome. Instead, it is a consequence of RNA self-repulsion due to confinement within a restricted volume, with electrostatic interactions accounting for ∼95% of the total energy of the system at the end of the simulations. Repeating all simulations while setting the charges on the RNA beads to zero, results in the disappearance of this two-shell architecture (see Fig. S1 in the Supporting Material). This supports the conclusion that electrostatically driven self-repulsion of RNA in confinement is the main driving force underlying the bimodal radial distribution of the packaged ssRNA genome.

Figure 2.

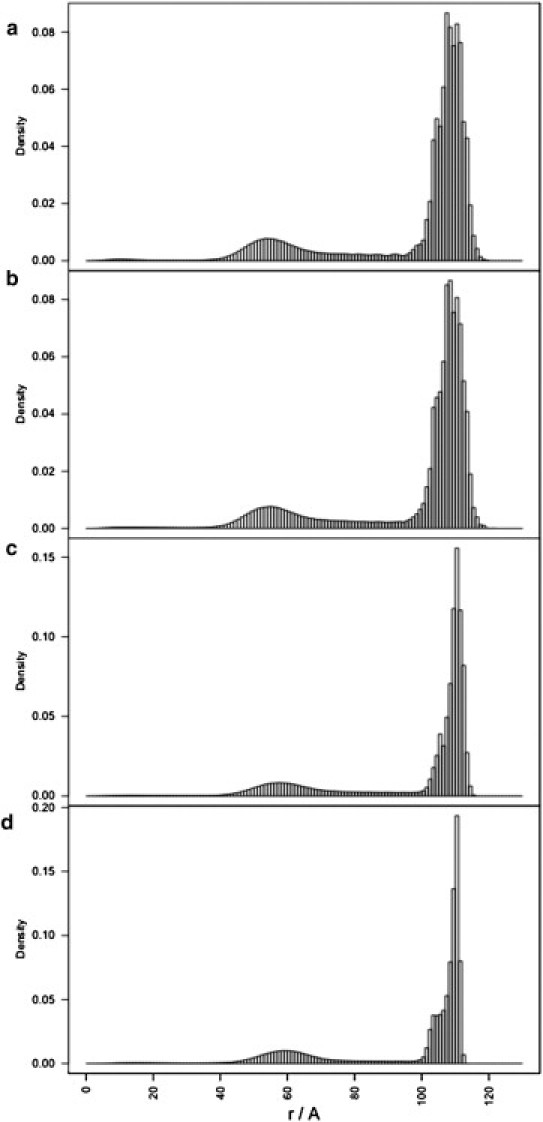
Radial density profiles of the RNA chain for the MD1 (a), MD2 (b), MD3 (c), and MD4 (d) simulations.

This also suggests that the number of RNA shells and their placement within the capsid depend on genome length. To test this, the MD1 simulation (Table 1) was repeated using three subgenomic fragments that correspond to 90%, 60%, and 30% of the full-length MS2 genome (see Fig. 3). The simulations show a decrease in density of the inner shell for successively shorter genome lengths, with the inner shell virtually disappearing at 30% of the full genome length (corresponding to ∼1190 nucleotides). This is consistent with reassembly experiments with subgenomic fragments of genomic RNA of comparable length (e.g., fragments of 928 nucleotides in Rolfsson et al. (14)), in which the inner RNA shell is not visible via cryo-EM. However, it was not possible to conclude from those data whether the disappearance of the inner shell is due to lower occupancy in the central region (e.g., due to enhanced flexibility) leading to a lack of visibility in cryo-EM reconstructions based on icosahedral averaging, or due to a reorganization of the outer RNA shell (14). Our results suggest that it is more likely to be the latter, and that the RNA redistributes in the outer shell to make maximal contact with the capsid inner surface as a consequence of RNA self-repulsion.

Figure 3.

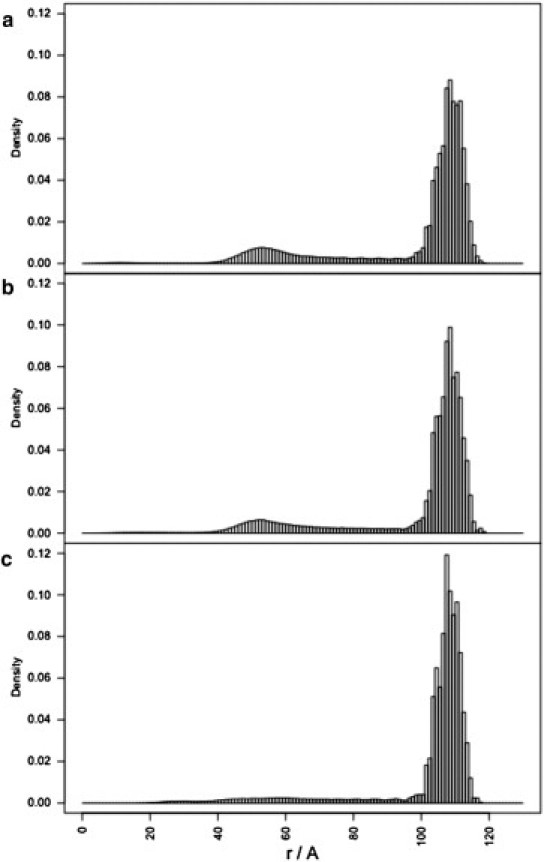
Radial density profiles of the RNA chain for the MD1 simulation using genome lengths that correspond to (a) 90%, (b) 60%, and (c) 30% of the full-length MS2 genome.

Although our analysis is carried out for the specific example of MS2, our results suggest that the profile of the bimodal radial density of the packaged genome should be similar for all ssRNA viruses with a comparable ratio of RNA genome length to capsid volume. Indeed, a similar distribution of the RNA density has also been reported in flock house virus (29) and in Pariacoto virus (10). This corroborates our conclusion that, rather than being determined by detailed structural features of the capsid proteins or RNA secondary structure, the general two-shell architecture of the packaged genome is a consequence of the physics of spherical confinement of a self-charged polyelectrolyte chain.

This has broader implications for our understanding of the basic principles that underlie the mechanism of genome packaging within ssRNA viruses. Factors dictating the optimal length of the packaged genome have been the focus of several studies (30–33). Based on direct adsorption of the genome to the capsid, the packaged genome length was found to be proportional to the capsid surface area (31) whereas it was found to be proportional to the net charge of the capsid based on electrostatic analysis of genome packaging in virus capsids with N-terminal arms (33). However, organization of ssRNA into distinct multiple shells could offer viruses a versatile means to efficiently package genomes of different lengths. Nonmonotonic genome packaging efficiency, with respect to genome length, has been observed in simulations of polymer encapsidation in the virus capsid (31); however, no explicit consideration of multiple shell organization was taken into account.

RNA genome organization in the outer RNA shell is determined by the capsid inner surface topography

We consider next the physical factors that give rise to the specific polyhedral structure of the RNA shells observed in experiment (28). In particular, we investigate the physical determinants of the polyhedral organization of the outer RNA shell (Fig. 1 d). For this purpose, the individual RNA chain conformations sampled from each simulation were icosahedrally averaged (34) and the resulting densities were mapped onto the surfaces of a series of concentric spheres of radii: 80, 90, 100, and 110 Å (see Fig. 4).

Figure 4.

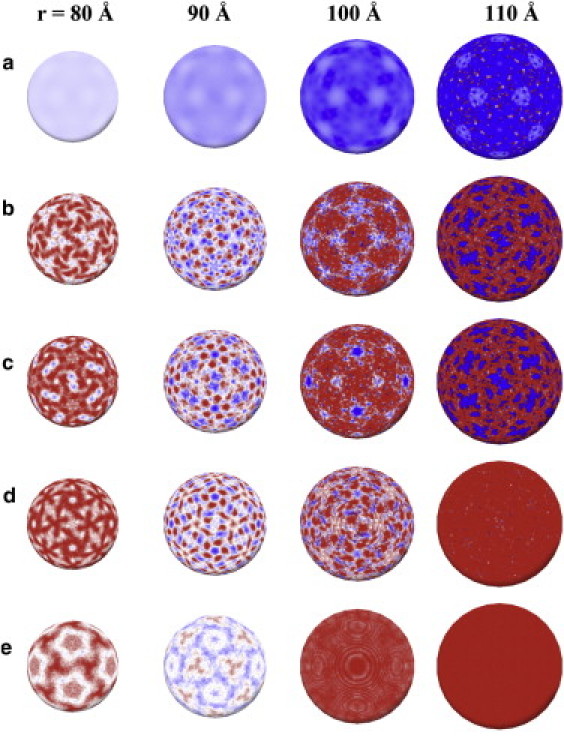
(Rows) (a) Electrostatic potential of the MS2 capsid; (b–e) the average RNA density of the icosahedrally averaged trajectories for the MD1, MD2, MD3, and MD4 simulations respectively. (Columns) a mapping of these properties onto the surfaces of concentric spheres at radii r = 80, 90, 100, and 110 Å, respectively. The electrostatic potential in panel a changes smoothly from −1 kT/e (red) to 1 kT/e (blue), whereas the RNA density (b–e) changes from highest (red) to lowest density (blue).

A comparison of the results at 110 Å (i.e., at a radius corresponding to the capsid inner-surface) reveals that the RNA densities in MD1 and MD2 are very similar (see Fig. 4, b and c) and resemble the polyhedral organization observed via cryo-EM. By contrast, there appears to be no discernible structure in MD3 and MD4 (see Fig. 4, d and e), i.e., in simulations that do not take the steric interactions with the capsid inner surface into account. This suggests that the detailed structure of the outer RNA shell is a result of steric interactions that force the RNA chain to align within the crevices of the capsid inner surface. This implies that the capsid inner surface acts as a mold for the RNA. Indeed, its structure is rugged, with inward protrusions (shown in blue in Fig. 1, b and c) extending to a radius of ∼105 Å at the twofold symmetry axes of the capsid.

The overall arrangement of the genomic RNA in the vicinity of this radius reflects the topography of the capsid inner surface exhibiting a bias toward occupation under the particle fivefold symmetry axes rather than the twofold symmetry axes where the protrusions are located. This correspondence between the topography of the capsid inner surface and genome organization in the outer RNA shell is reflected by the striking complementary of the RNA density pattern in MD1 and MD2 (see Fig. 4, b and c; rightmost column) and the topography of the capsid inner-surface (see Fig. 1 c). It is moreover consistent with x-ray crystallographic results (35), which reveal that RNA stem loops are located within the crevices of the capsid inner surface around the particle fivefold axes (see Fig. 1 b).

The RNA density pattern observed at 80 Å is in good agreement with the observed genome mass density from cryo-EM microscopy (28): a polyhedral shell arranged into pentagonal configurations under the fivefold symmetry axes that are connected by triangles (see Fig. 1 d). Despite not being in a direct contact with the capsid inner surface, this arrangement, especially under the fivefold axes, strikingly reflects the capsid inner-surface topography (see Fig. 1 c). None of the other simulations reproduced this characteristic pattern of organization.

The picture that emerges is of an intricate interplay of interactions: the alignment of the RNA chain into the crevices of the capsid inner-surface (r = 110 Å) leads to a nonuniform buildup of repulsive electrostatic RNA self-interactions in close proximity to the surface. Away from the capsid surface, the modulation of the genome density, in part by the capsid electrostatic potential (see Fig. 4 a), results in an alternating pattern of high to low RNA density at successively lower radii (see Fig. 4 b; r = 110–80 Å). Notably, this leads to a similarity in the pattern of RNA density at 110 Å and 80 Å that reflects the capsid inner-surface topography. The increased RNA density around the fivefold symmetry axes at 80 Å, a radius intermediate between the outer and inner shells, is in agreement with cryo-EM results that reveal the preferred location of the crossing of the RNA genome chain from the outer to the inner shell to be under the fivefold symmetry axis (28). This suggests that the influence of the rugged topography of the capsid inner-surface propagates throughout and beyond the outer radial shell of the RNA—thereby acting as a template for genomic organization.

Conclusion

We have investigated the physical principles underlying the observed order in the genome organization of ssRNA viruses based on a representative model system, the bacteriophage MS2. A series of coarse-grained molecular dynamics simulations was performed to examine the impact of individual contributions of the capsid inner-surface topography, RNA-self interaction due to spherical confinement, and electrostatic interactions with the capsid.

The simulations reveal that the overall organization of the packaged genome, i.e., the two-shell architecture, is due to self-repulsion of the polyelectrolyte RNA chain in confinement. However, the fine details of the RNA structure in the outer shell are determined by steric interactions with the rugged topography of the capsid inner surface. In particular, it results from an alignment of the RNA chain into the surface crevices, primarily driven by RNA self-repulsion. We therefore conclude that the charge distribution on the capsid does not affect the overall organization of the genome, in terms of its radial distribution; however, it could influence the fine details of RNA organization in the outer shell (along with its preferred mode of crossing between the two shells). Our analysis of RNA organization for subgenomic-length fragments confirms this: it provides further insights into the interpretation of cryo-EM data (14), suggesting that a rearrangement of the outer RNA shell is the most likely cause for the disappearance of the inner shell.

Our coarse-grained model of the genomic RNA does not allow for basepairing of nucleotides. Although this is entirely suitable for our analysis of the impact of different energetic components and confinement on the overall features of genome organization, it does not allow us to address other issues that relate to the role of RNA secondary structure. For example, cryo-EM reconstructions have shown that there are connections between the outer and inner RNA shell at the particle fivefold axes, given by density that is consistent with a basepaired portion of RNA (28). Such issues could be addressed by a model that takes into account information on the locations of RNA stem loops in the genome sequence that is the subject of an ongoing work.

Our analysis reveals an intricate relationship between capsid inner surface topography and genome organization. Building upon these insights has the potential to inform other fields of work. For example, perturbation of inner-capsid surface, e.g., via binding of small molecules, could lead to the disruption of genome packaging, and thereby of virus assembly, and may thus be a route for the development of novel antiviral drug therapies. Also, we note that viral capsids are able to package polymers other than their genomic RNAs. For example, monodisperse icosahedral viruslike particles were created via self-assembly of capsomeres of the Cowpea Chlorotic Mottle Virus in the presence of polystyrene sulfonate instead of ssRNA (36). Our results suggest that manipulation of the capsid inner surface, e.g., via protein engineering, could be a novel route to the creation of custom-made nanocontainers, supporting specific packaging arrangements, for applications in bionanotechnology (15).