The Growth of Sickle Hemoglobin Polymers

Abstract

The measurement of polymer growth is an essential element in characterization of assembly. We have developed a precise method of measuring the growth of sickle hemoglobin polymers by observing the time required for polymers to traverse a photolytically produced channel between a region in which polymers are created and a detection region. The presence of the polymer is functionally detected by observing its ability to create new polymers through the well-established process of heterogeneous nucleation. Using this method, we have determined the rate constants for monomer addition to and release from polymer ends, as well as their temperature dependences. At 25°C we find k₊ = 84 ± 2 mM⁻¹ s⁻¹ and k₋ = 790 ± 80 molecules/s from each end. These numbers are in accord with differential interference contrast measurements, and their ratio gives a solubility measured on individual fibers. The single-fiber solubility agrees with that measured in sedimentation experiments. The concentration dependence of the monomer addition rate is consistent with monomer addition, but not oligomer addition, to growing polymers. The concentration dependence suggests the presence of an activation enthalpy barrier, and the rate of monomer addition is not diffusion-limited. Analysis of the temperature dependence of the monomer addition rate reveals an apparent activation energy of 9.1 ± 0.6 kcal/mol.

Introduction

The measurement of polymer growth is an essential element in the characterization of assembly. From such measurements one can determine the critical concentration or solubility, for example, as well as determining the stoichiometry of the growth process, thereby establishing whether the polymer or fiber grows by adding monomers or oligomers.

Sickle hemoglobin polymerization was characterized some time ago, including an unusual double nucleation process in which nuclei may form directly from monomers (homogeneous nucleation) or by monomer coalescence into nuclei on polymer surfaces (heterogeneous nucleation) (1). These nucleation processes endow the reaction with very high concentration dependence, to which the nucleus size and the solution nonideality corrections contribute in almost equal amounts. Because of this high apparent reaction order (nearing the 100th power of concentration for nucleation at low concentrations (2)), studying the overall reaction does not reveal the details of the growth process as well as it reveals those of the nucleation process. This means that certain details of the process, such as the growth by addition of small aggregates versus addition of monomers, cannot be easily probed by the usual strategy of observing the polymerization process as conditions are varied.

Sedimentation studies of sickle hemoglobin (Hb) polymerization in the mid-1970s established that extensive centrifugation after polymerization yielded a supernatant concentration of Hb that was identified as a solubility for the reaction (3). We have recently found ways to measure the final concentrations without centrifugation and have determined that in solutions, polymerization ceases at concentrations greater than this putative solubility (4,5). This premature termination has been attributed to the occlusion of growing polymer ends, but it leaves open the question of whether the final concentration measured in centrifugation experiments is truly the relevant parameter for polymer growth, or whether the centrifugation process might itself have influenced the hemoglobin system. For example, it is known that the solubility of crystals is lower than that of polymers (6,7), and thus it is plausible that polymer-polymer interactions increase stability and cause the mass of sedimented polymers to represent a value below solubility. Thus, a measurement of the solubility (or critical concentration) executed on individual fibers would be of great interest.

Differential interference contrast (DIC) microscopy has been employed to attempt to follow fiber growth and dissolution since the classic studies of Briehl et al., which confirmed the double-nucleation model by direct observation (8–11). Because sickle Hb polymer diameters are only 20 nm, it is impossible to observe individual fibers directly. DIC microscopy uses the tracking of a diffraction shadow to infer polymer growth. However, the presence of polymer bundles, established both in studies designed to measure bending (12) and in electron microscopy studies (13), might raise questions as to whether observed DIC images would reflect the behavior of individual fibers. In addition, it has been difficult in DIC experiments to control the local concentration of monomers to allow determination of rate constants (11). The latter problem is typical of many techniques that would otherwise be natural candidates for performing such measurements. For example, to provide accurate measurements of the rate constant of growth, atomic force microscopy methods must assume that few monomers have been consumed in the process of fibrillization. Other methods have also been developed, such as delicate microbalance methods for observing monomer addition to growing fibrils (14). The latter, of course, does not distinguish between processes that might add monomers to the sides of fibers versus processes that grow the fibers linearly.

We present a novel approach to measuring polymer growth, based on function rather than observation of morphology. The function we probe is the ability of polymers to generate other polymers via heterogeneous nucleation. The experiment employs the creation of dynamic patterned regions of deoxyHbS in thin slides by laser photolysis of COHbS.

The experiment begins with illumination of an incubation circle (incubator) 12 μm in diameter, where a collection of fibers forms via homogeneous and heterogeneous nucleation in the laser-deoxygenated region. After a few seconds, when polymers have formed in the incubator, a thin channel 15–30 μm long is added to the illuminated pattern. Polymers from the incubator begin to grow along the channel and toward the detection region (detector). After a preset channel-on time, the last few micrometers of the channel get illuminated and the already-lit part of the channel is turned off. If illumination of the channel is not long enough, no polymers will have reached the detection region. The experiment is repeated with longer channel-on times. After some critical time, typically tens of seconds, the fastest fibers will reach the detector. The measurement of this critical time is the goal of these experiments. The signature that polymers have completely traversed the channel while it is illuminated is a drop in transmitted intensity in the detector, due to the additional polymers in that area generated by heterogeneous nucleation onto the polymer that has successfully traversed the channel.

With this approach we demonstrate that polymer growth obeys simple kinetics, corresponding to single monomer addition. Growth is zero when the monomer concentration is at the single-fiber solubility, which turns out to be equal to that measured in centrifugation. In addition, we have measured the temperature dependence of the growth rate and have determined an activation enthalpy for polymer growth and polymer dissolution.

Materials and Methods

Hemoglobin was purified by column chromatography as previously described (15) and prepared in 0.15 M phosphate buffer, pH 7.35. Samples also contained 0.50 M sodium dithionite that acted as an oxygen scavenger. The effect of the dithionite has been shown previously (11) to yield final pH values slightly above pH 7. Concentrations were determined by diluting 2 μl hemoglobin solution into 6 ml phosphate buffer and measuring spectra on an HP8452 diode array spectrophotometer. Samples were prepared in a glove box filled with humidified CO. HbAS 50:50 samples were prepared by mixing concentrated HbA and HbS at a volume ratio that was the inverse of their concentration ratio.

Measurements were performed on an optical apparatus with a probe beam that is set up as a horizontal microspectrophotometer (Fig. 1). The light source is a 150 W xenon arc lamp passed through an Acton monochromator. Condenser and objective were both Leitz 100× oil-immersion objectives. Detection was by a Photometrics Cool-Snap HQ CCD camera. Photolysis took place via the 488-nm beam from a Spectra Physics 164 argon ion laser. Data collection and signal timing were integrated through a PC running LabView.

Figure 1.

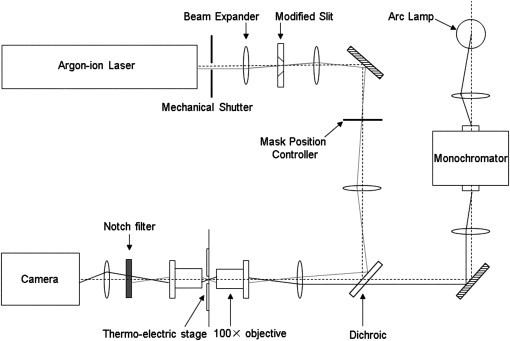
Schematic of the optical setup. A probe beam was set up as a horizontal microspectrophotometer with a 150-W xenon arc lamp, passed through an Acton monochromator. Condenser and objective were both Leitz 100× oil-immersion objectives. The detector was a Photometrics Cool-Snap HQ CCD camera. Photolysis was induced via the 488-nm beam from a Spectra Physics 164 argon ion laser. The laser beam was inserted into the beam path with a dichroic filter. The photolysis beam was imaged on a slit, with a hole in both blades. A physical mask was moved across the image of the slit by a mask position controller. The laser was blocked from reaching the detector by a notch filter.

The photolysis beam was imaged on a slit modified by drilling a hole in both blades with the slit closed. An aluminum mask with two rectangular parts (Fig. 2) 12 mm apart was moved along the slit. A motorized stage holding the mask had three consecutive settings, with first only the hole opened (incubation), then the slit added (elongation), and finally just the very end of the slit opened (detection) (Fig. 2). After ∼5 min of illumination forming patterns and taking images, a shutter blocked the laser for 30 s to allow all polymers to dissolve in the sample. The process was then restarted, with longer exposure of the channel. The diameter of the incubation circle was 12 μm. The channel connecting incubator and detector was typically 0.8 μm wide, and ∼25 μm long. The dimensions of the channel were varied, with no detectable effect on the rates measured. For example, when channel width was changed from 0.8 μm to 1.6 μm, the growth rate changed from 1.17± 0.11 μm/s to 1.18 ± 0.11 μm/s. In a similar way, changing channel length had no effect. A channel of length 18.8 μm had a growth rate of 1.18 ± 0.11 μm/s, and when the channel length was increased to 31.2 μm, the growth rate remained essentially the same, viz. 1.17 ± 0.11 μm/s. Note that these experiments in which channel lengths and widths are varied are also reported below as part of the overall data set.

Figure 2.

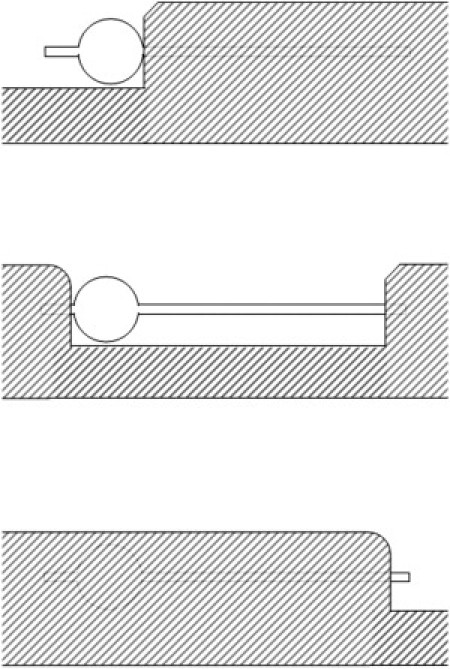
Sequence of photolysis in various areas. The shaded area represents a mask that is in a plane equivalent to the image of the mask, a slit with a hole. When the experiment begins, light can only reach the sample through the circle. Once polymers have formed in this incubation circle, the mask is moved to the right, unblocking the illumination of the channel. After some preset time, the mask is again moved to the right, extinguishing the channel, and leaving a tiny region. This detection area is observed for a period to determine whether polymers have propagated this far while the channel was on.

The degree of photolysis in the channel was determined by observing the change in optical density in the Soret band spectrum before polymerization. Polymerization was monitored by observing an increase in absorbance at 425 nm, near the isosbestic point between spectra for HbCO and Hb.

A series of growth measurements were made as a function of temperature using a thermoelectric stage for the sample and thermoelectric collars for the objectives. The collars are necessary because with oil-immersion objectives, there is significant thermal contact between the sample and the objectives. Three independent temperature controllers were built using a separate computer running a LabView program with standard proportional-integral-derivative (PID) control on stage as well as objective collars. Some data sets were collected before installation of the thermal controls. In those experiments, temperature near the photolyzed region of the sample was monitored by an Omega DP25B electronic thermometer with an Omega CO1-T thermocouple. Although temperature variation between experiments was small, it was enough to add considerable imprecision to the data unless corrected. To do so, we assumed a linear correction of the rate of growth by expanding the growth rate, J, according to the equation

$$\mathit{J}\left(\mathit{T},\mathit{c}\right)=\mathit{J}\left({\mathit{T}}_{\mathit{o}},\mathit{c}\right)+\left(\mathit{dJ}/\mathit{dT}\right)\Delta \mathit{T},$$ (1)

in which it was assumed that dJ/dT is a constant independent of c and T_o is a reference temperature, taken here as 25°C, approximately the ambient temperature of the measurements. This procedure was effective in reducing the dispersion of the data.

Results

The light going through the detection circle is shown as a function of time for a typical set of experiments (Fig. 3). The time is measured from the point at which the polymers are first permitted to emerge from the incubation circle. Because the wavelength of observation is not at an exact isosbestic of HbCO and Hb, there is a change in absorbance as soon as the detection circle is photolyzed. Note that the detection circle is not photolyzed at the same time in each of these exposures of the connecting channel, and thus, the small step of intensity decrease occurs at a slightly different time for each such exposure. If no polymers have reached the detection circle, the transmission remains flat. However, when polymers do reach the detection circle, there is a further, large drop in transmission. This arises from the diffusion of monomers into the detection region to replace solution monomers that are depleted by their incorporation into polymers. These polymers do not diffuse out of the region, yet new monomers diffuse in, and thus there is a net increase in local concentration, as we have reported previously (16,17). This can ultimately create regions of concentration in the vicinity of 55 g/dl, a value comparable to that found after extensive centrifugation. This process of diffusion causes the absorbance to grow and the transmission to drop. This drop only occurs when the channel between incubator and detector is illuminated long enough for a fiber to arrive at the detection region.

Figure 3.

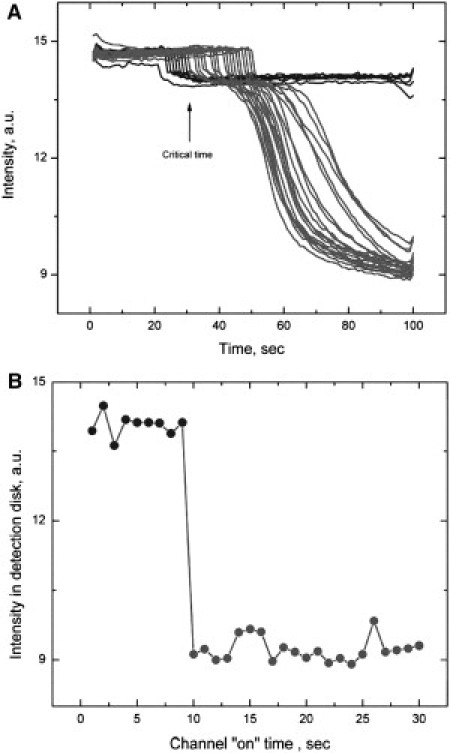
(A) Typical transmitted intensity in arbitrary units in the detection area as a function of time. The dips of the signal are due to photolysis. If the laser is allowed to photolyze COHbS and create deoxyHbS at this area, the deoxy HbS absorbs a little more than the COHbS at the transmitted light wavelength (425 nm). The detection signals with no polymer reaching the detection area are in blue. The detection signals with polymer reaching the detection area are in red. (B) Existence of a threshold. The intensity in the detection area (in arbitary units) at 100 s is observed for various times of exposure of the channel. At some threshold value, the intensity drops, signifying the growth of a large mass of polymers in that region.

In our apparatus, the detector is only turned on right before the channel is turned off. Thus, photolysis of the detection circle is seen to commence at later and later times, corresponding to longer and longer exposure of the channel. Once the detector is photolyzed (turned on), polymerization will be observable after an inherent delay that occurs because polymers grow exponentially and the parameters of that exponential give the appearance of a latency, even though polymerization actually commences at time zero. As can be seen, the delay is essentially the same for all curves, and its starting point progresses to the right, simply due to the later turn-on times. The most important feature of this application is a fixed, minimum exposure time for which the channel must be illuminated for polymerization to be induced in the detector (Fig. 3 B). This exposure time is thus the time required for a polymer to grow to the length of the channel, and dividing length by time yields the growth rate.

This experiment was repeated for different initial concentrations (Fig. 4). In addition, a 50:50 mixture of HbA and HbS was used (circle with cross). The experiment was also repeated with laser power reduced so as to give partial photolysis (half-solid circle). The extent of photolysis was determined by the absorbance spectrum.

Figure 4.

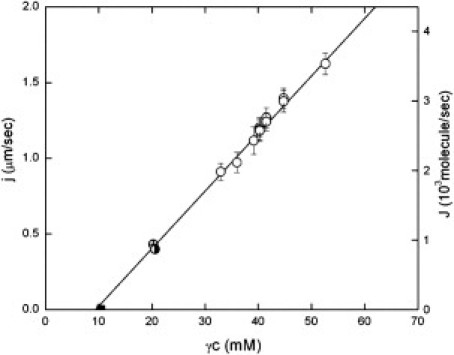
Polymer growth rate as a function of activity. Activity is the product of an activity coefficient, γ (Eq. 3), and c, the concentration of monomers that are competent to polymerize. As described in the text, the values of the activity coefficients are well known. Included are data for different length and width channels, as described in the text. Empty circles are full photolysis data for pure HbS. The crossed circle is the 50:50 HbA/HbS mixture data. The half-solid circle represents data obtained from partial photolysis. Error bars are determined by the spacing of the tested intervals (cf. Fig 3), which are discretely chosen. The error was thus ±1 s in exposure. The data shows excellent linearity. The intercept at J = 0 gives the solubility. The value of solubility determined in sedimentation experiments is shown as the solid square point on the abscissa, and it was not used in the best-fit straight line that is drawn through the data. The slope of the curve gives the monomer addition rate constant, k₊, which is found to be 84 ± 2 mM⁻¹ s⁻¹.

Data were plotted as a function of the activity of the monomers, which is the product of the concentration, c, and an activity coefficient, γ. Activity coefficients were calculated using the simple function

$$\gamma =\text{exp}\left(8\varphi /{\left(1-\varphi \right)}^2\right),$$ (2)

in which ϕ is the volume fraction, given by ϕ = vc where v is the specific volume of Hb, taken as 0.77 cc/g (18). These activity coefficients are based on treating the Hb molecule as a hard sphere, an approach that has been extraordinarily successful at describing the colligative properties of Hb (19). Sedimentation and osmotic pressure data are accurately reproduced with such hard-sphere activity coefficients, in which the only variable is the specific volume of Hb (20). The specific volume so determined agrees well with the volume determined from x-ray structures. The hard-sphere activitiy coefficients are often described by a seventh-order virial expansion (19). However, we have found that Eq. 2 is numerically equivalent over the ranges of volume fraction encountered and can be further justified theoretically as an expansion of the Carnahan-Starling expression (20).

For mixture and partial photolysis data, γ is calculated using ϕ determined from the total concentration (i.e., HbA + HbS, or COHbS + HbS). However, the value of c employed is based on the concentration of polymerization-competent species. For HbAS the copolymerization probability is 0.375 for hybrid molecules (17,21). Hybrids are distributed binomially, so that a 50:50 mixture contains 25% HbA, 25% HbS, and 50% HbAS hybrids (22). Thus, the concentration employed in the product γc is 0.375 times the HbAS concentration (0.375 × 0.5 × c), plus 0.25 × c to account for the pure HbS component. For partial photolysis, we used an allosteric model and computed the fraction of unligated T states of the sample for determination of c (23). For the mixture and partial-photolysis experiments, however, the total Hb concentration was used for computing activity coefficients in Eq. 2.

The growth rates are all plotted in Fig. 4 as a function of activity, γc. As can be seen, an excellent straight line results. These data include channels with different dimensions. Although the average channel length was 25.0 μm, it was as long as 33.5 μm for some experiments and as short as 14.9 μm for others.

The rate of growth of a fiber is the difference between addition of molecules to and loss of molecules from the growing end. When monomers are the only species that add or leave, the growth rate is given by

$$J=k_{+}\gamma c-k_{-}.$$ (3)

This expression comes from replacing the bimolecular rate constant k₊ with k₊γγ_p/γ^‡ where γ_p is the activity coefficient of the polymer to which the monomer adds, and γ^‡ is the activity coefficient of the activated complex (24). For a long polymer, γ_p ≈ γ^‡, so that these terms cancel.

The linearity of the growth rate as a function of γc is consistent with such a growth model, and the slope of that curve yields the monomer addition rate, k₊. At 25°C we find k₊ = 84 ± 2 mM⁻¹ s⁻¹ and k_- = 790 ± 80 molecules/s. In using DIC microscopy, Briehl and Guzman found k₊ = 73 mM⁻¹ s⁻¹ (10), whereas Agarwal et al. found k₋ = 850 molecules/s (9). These values are half the quoted values in the source, since they pertain to the fiber end rather than the entire fiber. The net rate of fiber growth would accordingly be twice the values above.

The intercept of the activity (x) axis is where J = 0 and must thus be the activity at solubility, c_s. At that point, γ_sc_s = k₋/k₊. The solubility as determined by sedimentation experiments (25) is shown as a point on the x axis, and was not used in the fit. As can be seen, the x-intercept (single-fiber solubility) and the sedimentation-determined value of solubility agree very well.

The variation of J with temperature can be used to find the temperature dependence of k_+. The experiment was repeated at several temperatures, and the values of k₊ were determined from the temperature dependence of c_s (Fig. 5).

Figure 5.

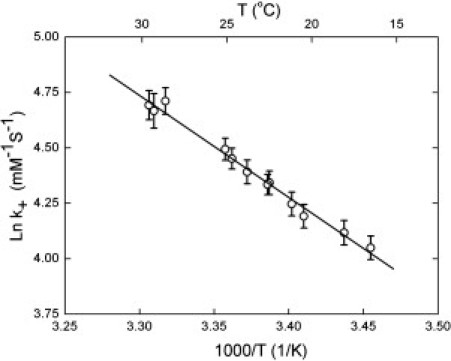
The ln of the monomer addition rate constant, k₊ (mM⁻¹ s⁻¹), as a function of reciprocal absolute temperature. Rate constants were determined as in Fig. 4. The slope of this curve gives an activation energy of 9.1 ± 0.6 kcal/mol.

Discussion

The method developed here clearly can measure growth rates under a variety of conditions. The systematic behavior of the growth rates determined using this method strongly supports the assumption that these are indeed individual fiber measurements. Because the method depends on function (i.e., the ability of fibers to promote heterogeneous nucleation), we can say that the measurement here is of the most rapid propagation along the channel. Since other fibers could grow parallel to the first fiber, it is possible for bundles, as well as individual fibers, to pass along the channel. However, the lead fiber is that which is likely to be detected even in the presence of additional fibers.

The presence of a 14-stranded cross section in the standard HbS fibers in principle allows for the possibility of adding more than a single molecule at a time. Such oligomer addition in the process of growth has been proposed in amyloid formation, for example (26). Polymer growth in such a mechanism would be proportional to the population of oligomers, which in turn would be related to activity raised to some power greater than unity. However, the linearity of the growth rate with monomer activity conclusively excludes such a mechanism. Although it has long been assumed that growth occurs by monomer addition, this is, to our knowledge, the first demonstration that the assumption is correct.

In a recent set of studies, we also found that sickle hemoglobin polymerization stops before the process depletes the monomer concentration to the values customarily described as the solubility, measured in sedimentation experiments (4,5). Those sedimentation studies that first led to labeling of a terminal concentration as a solubility were thorough in demonstrating that the values of concentration measured had all the properties of an equilibrium state (3). Nonetheless, such measurements involved packing polymers by extended periods of high-speed centrifugation, and it might be questioned whether centrifugation had any role in the process. For example, interfiber interactions might further stabilize fibers in the densely packed pellets and create a terminal concentration that does not represent the behavior of individual fibers. (For a theoretical treatment of such coalescence phenomena, the reader may wish to consult Duyndam and Odijk (27).) The close agreement between the extrapolated concentration at which growth ceases and the sedimentation solubilities strongly supports the assumption that the two methods have measured the same quantity, and that therefore interfiber interactions in the sedimentation measurements have no significant effect on the measured solubility. Although this assumption had been the working hypothesis, this experiment provides the first confirmation of its fundamental correctness of which we are aware.

Over a 10° interval, the elongation rate constant k₊ increases by ∼65% in a highly Arrhenius manner. This yields an enthalpy of 38.3 ± 2.4 kJ/mol (9.14 ± 0.56 kcal/mol).

The monomer addition process involves the translational diffusion of molecules from solution to the tip of the growing polymer, as well as rotational diffusion of molecules so they will orient correctly at the growing tip. Although the temperature dependence might be thought to exclude diffusion-limited reaction directly, the dependence of viscosity on temperature can readily endow a diffusion-limited reaction with significant temperature dependence. However, diffusion in concentrated media also depends on concentration and this allows us to discriminate between mechanisms. If the rate were diffusion-controlled, then normalization by the diffusion constant should remove that dependence, i.e., if k₊ = k₊^oD, where D is the diffusion constant, then plotting J versus γcD should produce a linear (or at least simple) relationship. The concentration dependence of D is empirically given by D = D_o(1 – ϕ)^6.5 (28), in which ϕ is the volume fraction occupied by monomers, as described above. Thus, Fig. 4 becomes modified as shown in Fig. 6, where J is plotted as a function of γcD/D_o. It is clear that the result is no longer a simple linear function as given by Eq. 3, and that the points no longer follow a simple curve. The critical differences come in the mixture points, viz. the HbA/S mixture, and the partial photolysis experiments. As seen in Fig. 4, these points are completely aligned with the linear plot when activity is used as the independent variable. We therefore conclude that the simplest overall explanation is that the polymer growth rate is not diffusion-controlled, involves monomer addition only, and thus follows the simple growth law of Eq. 3 with an activated barrier.

Figure 6.

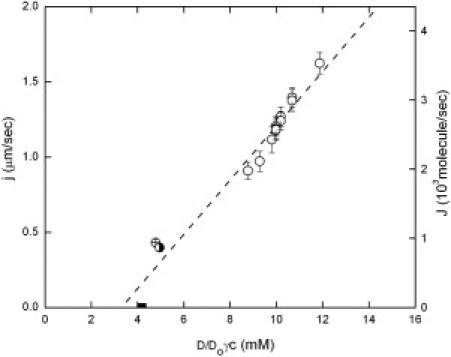
Adjustment of Fig. 4 to account for concentration-dependent diffusion. To examine the possible role of diffusion in the reaction, the data of Fig. 4 have been replotted as a function of γcD/D_o, where diffusion constant D is concentration-dependent. D_o is a constant. The data no longer follow a simple linear relationship, as in Fig. 4. The symbols are the same as in Fig. 4.

It is interesting to note that the monomer off-rate is almost temperature-independent, as shown in Fig. 7. This implies that there is no enthalpic barrier to monomers leaving the polymer. There will of course be some barrier to climb, since the molecules in the polymer cannot be unstable with respect to monomers in solution, and the temperature independence requires that this barrier be entropic. The existence of the enthalpic barrier to growth may be due to the cost of removing water at the hydrophobic contact sites (29). It has been contended that the removal of a small number of water molecules at the contact site might account for the similarity of activation enthalpies (∼7.2 kcal/mol) observed for a wide range of substances (30).

Figure 7.

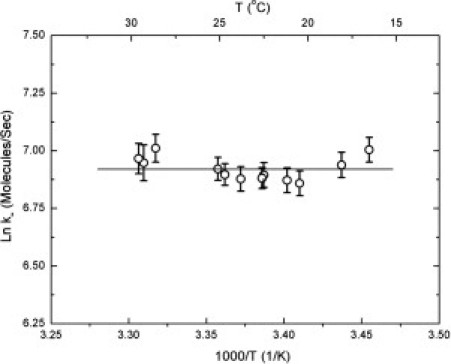
The ln of the monomer off-rate, k_–, as a function of temperature. The flatness of the data suggests that the barrier to monomer escape from the polymer is entirely entropic.

The values obtained above provide useful insight into the pathophysiology of the disease. Under physiological temperatures (37°C) and concentrations (5 mM), a fully deoxygenated red cell will grow fibers at a remarkable 21 μm/s. Given the resting cell's diameter of ∼6 μm, such polymer growth clearly spans the cell rapidly. Even given a more physiological state of 50% deoxygenation, from the results shown in Fig. 4 we can still estimate the growth rate, which is ∼10 μm/s. Since capillary transit times are only in the range of seconds, it is clear that fibers will quickly span the cell during its passage. This makes possible an outward Brownian ratchet pressure that comes from the obstruction of the polymer ends, which may contribute to capillary occlusion.