The impact of physiologic noise correction applied to functional MRI of pain at 1.5 & 3.0 Tesla

Abstract

This study quantified the impact of the well-known physiologic noise correction algorithm RETROICOR applied to a pain FMRI experiment at two field strengths: 1.5 and 3.0 Tesla (T). In the 1.5 T acquisition, there was an 8.2% decrease in timecourse variance (σ) and a 227% improvement in average model fit (increase in mean R² _a). In the 3.0 T acquisition, significantly greater improvements were seen: a 10.4% decrease in σ and 240% increase in mean R² _a. End-tidal carbon dioxide (ETCO₂) data was also collected during scanning and used to account for low-frequency changes in cerebral blood flow; however, the impact of this correction was trivial compared to applying RETROICOR. Comparison between two implementations of RETROICOR demonstrated that oversampled physiologic data can be applied either by down-sampling or modification of the timing in the RETROICOR algorithm with equivalent results. Further, there was no significant effect from manually aligning the physiologic data with corresponding image slices from an interleaved acquisition, indicating that RETROICOR accounts for timing differences between physiologic changes and MR signal changes. These findings suggest that RETROICOR correction, as it is commonly implemented, should be included as part of the data analysis for pain FMRI studies performed at 1.5 and 3.0 T.

Introduction

This paper focuses on reducing noise in blood oxygen-level dependent (BOLD) functional magnetic resonance imaging (FMRI) to improve the detection of brain activation in the acquired data. Much of the noise in FMRI data is from physiologic sources and the proportion of total signal noise due to physiologic fluctuations increases at 3.0 Tesla (T) compared to 1.5 T [1]. Thus, the increase in contrast to noise ratio seen in functional imaging at higher field strength is accompanied by increases in physiologic noise proportional to field strength [2], some of which may be removed with the use of a correction algorithm.

The physiologic noise correction algorithm most commonly implemented for FMRI is RETROICOR [3]. This technique generates Fourier series regressors based on the phases of the respiratory and cardiac cycles at each image acquisition using simultaneously acquired physiologic data from respiratory belt (RB) and pulse plethysmograph (PPG) sensors. The regressors from the RETROICOR algorithm can be applied to the FMRI data during pre-processing [3] or included in the general linear model (GLM) framework that is used to detect effects of interest along with other nuisance regressors such as motion parameters [4]. Additionally, low-frequency changes in the FMRI timecourse not explained by the cyclic RETROICOR regressors may be removed with additional processing of the respiratory [5] or cardiac [6] timeseries.

Another source of physiologic noise results from the slow changes in cerebral blood flow (CBF) during scanning that are correlated to changes in respiration. It has been previously demonstrated that changes in end-tidal carbon dioxide (ETCO₂) can affect the BOLD signal [7-8]. Correlation in time between ETCO₂ fluctuations and BOLD signal changes illustrates this effect [9], which under some experimental conditions can be estimated from the RB waveform [10]. Ultimately, more insight into the impact of noise correction techniques is needed to discover the optimal set of tools for physiologic noise correction for a given FMRI experiment.

In this study, physiologic noise correction for pain FMRI data acquired at 1.5 and 3.0 T was quantitatively assessed for effects on the variance in each voxel timecourse (σ), task model fit, and activation extent. The primary objective of this study was to compare the effects of RETROICOR on pain FMRI between acquisitions at two field strengths. It was hypothesized that a greater reduction in timecourse variance and a greater increase in model fit and activation would be seen at higher field strength. Three secondary analyses were also performed. First, ETCO₂ data was used as an additional noise regressor to explain low frequency respiration-induced cerebral blood flow changes. The addition of ETCO₂ correction was hypothesized to result in further decreases in timecourse variance and additional increases in model fit and increased activation compared to applying RETROICOR alone. Second, the RETROICOR algorithm was modified to account for the interleaved image slice acquisition order and also to accept higher sampling rate cardiac and respiratory data, which was expected to perform as well as or better than the native implementation.

Methods

Acute pain FMRI experiments were performed on healthy right-handed adult subjects using two different field strength scanners. Study protocols were approved by the Biomedical Institutional Review Board of The Ohio State University. Informed consent was obtained from all subjects and each was free to withdraw at any time.

Transcutaneous electrical nerve stimulation was used as the painful stimulus. Two electrodes were placed on the lateral aspect of the right index finger, straddling the proximal interphalangeal joint. This location was selected to stimulate the digital nerve in the finger and avoid the muscle contractions that accompany stimulation of more proximal nerves. An intra-operative nerve stimulator (MaxiStim Model ST6, Life Tech, Stafford, TX) was connected to the electrodes and the 100 Hz tetany setting was used for painful stimulation. To determine the appropriate intensity for each subject, stimulator current was gradually increased while the subjects continuously rated the intensity of the pain sensation verbally on a numerical scale, where 0 was no pain and 10 was the worst pain imaginable. The stimulator current was increased until the subject reported a pain rating of 5 out of 10, and this level was used during FMRI scanning. The experiment consisted of four 30-second periods of painful stimulation interleaved with 30-second rest periods, giving a total experiment time of 4.5 minutes.

Seven datasets were acquired at 1.5 T from subjects with the following gender and age distribution: 4 male, 3 female, mean age 31.1 ± 6.8 years (standard deviation), age range 26 – 46 years. A 1.5 T General Electric Medical (Milwaukee, WI) Signa scanner (Revision 8.4) was used. Functional MRI scans were collected with a BOLD sensitive single-shot gradient echo sequence using echo-planar-imaging readout, a transmit-receive head coil, and the EPIBOLD software (General Electric Medical) with the following parameters: TR = 3 s, TE = 50 ms, flip angle = 90°, 64 × 64 matrix, in-plane resolution = 3.75 × 3.75 mm, and slice thickness = 5 mm. The phase-encode direction was oriented along the anterior-posterior dimension. Twenty-eight (28) axial slices with no gap were acquired in an interleaved fashion giving whole brain coverage. The functional datasets for analysis consisted of 90 brain volumes.

Six subjects were scanned at 3.0 T, with two identical datasets acquired in each. The subjects had the following gender and age distribution: 4 male, 2 female, mean age 31.8 ± 11.3 years (standard deviation), age range 23 – 53 years. Only one volunteer was scanned at both field strengths, the subject pools were otherwise independent. Initial processing showed excessive motion in one of the datasets for two different subjects and these were excluded from further analysis, leaving 10 datasets from the 3.0 T acquisition. A Philips 3 T Intera scanner (Philips Medical Systems, The Netherlands) was utilized, using a gradient echo sequence with echo-planar-imaging readout. Whole brain coverage was achieved with 35 contiguous 4 mm thick axial slices acquired in an interleaved fashion. The echo time was TE = 30 ms, with other imaging parameters kept the same as in the 1.5 T acquisition. An 8-channel receive-only head coil was used with sensitivity encoding (reduction factor 2), in order to reduce the echo train length and minimize image distortion [11-12].

Before physiologic noise correction, image data were preprocessed offline with FSL [13] version 4.1.1. This included brain extraction [14], spatial smoothing using a Gaussian kernel of full-width at half-maximum of 7 mm, high pass temporal filtering with a period cutoff of 60 s, and motion correction using linear registration [15]. Slice-timing correction and pre-whitening were not used as part of the data analysis pipeline.

Physiologic monitoring data from each subject was recorded during FMRI data collection. The RB was placed around the subject near the inferior costal margin. The PPG sensor was placed on one of the subject’s fingers to measure the oxygenation changes in peripheral blood that occur with each heartbeat. Subjects scanned at 1.5 T wore a nasal cannula while those at 3.0 T wore a MAC-line (Oridion, Jerusalem, Israel), either of which allowed continuous sampling of expired air. These were connected by sampling tubing to a Datex Capnomac Ultima clinical gas monitor (GE Healthcare Bio-Sciences, Piscataway, NJ) located just outside the magnet room. The Datex monitor continuously sampled at 200 mL/min and gave an analog voltage output that was a scaled version of the expired CO₂ concentration waveform, allowing recording of the capnograph.

The analog outputs of these sensors along with a trigger signal from the scanner were connected to a BIOPAC MP-30 data acquisition unit (BIOPAC Systems, Sacramento, CA) and were sampled at 200 Hz for the 1.5 T data and at 500 Hz for the 3.0 T data. The time scales for all four acquisition channels were synchronized, so the amplitude of each physiologic parameter relative to the time of each image acquisition could be precisely determined. The RB and PPG data were both low-pass filtered in AcqKnowledge version 3.5.7 (BIOPAC Systems) using a digital infinite impulse response filter with a cutoff of 2 Hz to remove high frequency signal fluctuations caused by interference from the rapid switching of the gradient magnets.

The expired CO₂ sampling delay time was determined for each experimental setup to be 17.0 s for the 1.5 T data and 8.2 s for the 3.0 T data. The acquired capnograph was processed with custom code implemented in MATLAB (The Math Works, Natick, MA) to account for this delay for the expired air to traverse the sampling tubing and reach the gas monitor. The peak value at the end of each expiration, defined as the ETCO₂ value, was determined using a ±1 s window. In this way, one ETCO₂ value per breath was extracted from the expired CO₂ waveform. The resulting ETCO₂ timecourse was parsed for incomplete breaths in which the peak value did not reflect a full expiration and these values were replaced with the average value of the previous and subsequent ETCO₂ value. These ETCO₂ values with known timing relative to each TR acquisition window were interpolated to the beginning of each TR interval, giving one value per image volume with fixed timing relative to all slice acquisitions.

The RB and PPG timecourses were processed using MATLAB to format them for input to a version of RETROICOR that generated slice-specific regressors (provided by Jacco de Zwart of the National Institutes of Health, with permission from Gary Glover of Stanford University). The RETROICOR algorithm was implemented with individual RB and PPG corrections for this analysis, but included both corrections, as commonly implemented, unless otherwise noted. In implementing the RETROICOR script as received, the physiologic data was downsampled to 40 Hz and reformatted for input to RETROICOR. All peaks in the PPG data were found using a 0.5 s window, and the peak location replaced with a flag value of -1000. The RB timecourse values were rescaled to unsigned integers between 0 and 32,000. This native implementation reflects the manner in which RETROICOR is commonly applied by many FMRI researchers. A modified implementation of RETROICOR was also created that allowed for the physiologic data to be input at the higher sampling rate. As part of the modified implementation, the image slices were reordered according to the sequence in which they were acquired during the interleaved acquisition before applying RETROICOR, and then replaced in their anatomic order after correction. Since RETROICOR was expected to perform as well or better with these modifications, data from this modified implementation was used for comparisons.

FMRI data was analyzed for pain activation both without and with different combinations of physiologic noise correction applied after pre-processing: RB correction, PPG correction, standard RETROICOR correction, and RETROICOR + ETCO₂ correction. ETCO₂ correction was performed by convolving the interpolated ETCO₂ timecourse with an empirically optimized response function, regressing the result against each voxel timeseries, and subtracting the significantly correlated (p < 0.05) portion from the data.

Functional analysis was performed on each voxel timeseries with FEAT version 5.98, a part of FSL 4.1.1 [16]. The timing of the block-design pain stimulation paradigm was the primary model input, convolved with the default hemodynamic response function. The first derivative of the pain stimulation paradigm was also included as an effect of no interest, to account for variability in the shape of the hemodynamic response function or imperfections in stimulus delivery timing [17]. Individual subject images were registered to the Montreal Neurologic Institute standard space brain [15]. Group average maps were created with a fixed effects model using FLAME [18-19]. Group maps were thresholded using clusters determined by Z > 2.0 and a (corrected) cluster significance threshold of p < 0.05 [20].

Summary statistics were calculated at each voxel in the individual subject functional-space brain-extracted images before and after each correction or combination of corrections was applied. These were then averaged across each subject’s brain and then averaged across subjects. The timecourse variance, indicated by σ, was calculated as the standard deviation of the FMRI data in each voxel in the time dimension. The adjusted coefficient of multiple determination (R² _a) was calculated for each voxel, using the equation: R²_a = 1 - [SSE / (n-p)] / [SST / (n-1)], where SSE is the sum of the squared residuals from model fitting at each timepoint, n is the number of timepoints in the data, p is the number of parameters or explanatory variables in the model, and SST is the sum of the squared differences between the data value at each timepoint and the temporal average. The maximum and mean R² _a values were determined for each dataset, then averaged across subjects. Finally, the statistically thresholded individual subject activation maps were processed to determine the number of activated voxels for each combination of noise correction and the average across subjects was calculated. For statistical comparisons, a two-sample t-test assuming unequal variance was used, with p < 0.05 considered significant.

Results

Table 1 shows the summary statistics for the different combinations of noise correction applied at both field strengths. Comparing the average results across field strengths, the timecourse variance, model fit, and percent brain activation were all significantly greater in the 3.0 T compared to the 1.5 T acquisition. The variability between subjects, as indicated by the across-subject standard deviation, was generally greater at 3.0 T. Differences between each noise correction combination are listed in Table 2 as magnitude and percent change, and significant differences with correction applied are noted as described in the table legend.

Table 1.

Whole brain all subject averages ± across-subject standard deviation for measures of the impact of physiologic noise correction.

	Correction Applied	σ (%)	Max R2a	Mean R2a	Activation (%)
1.5 T	No correction	0.282 = 0.055	0.4067 ± 0.0765	0.0360 ± 0.0047	2.79 ± 1.60
	RB only	0.278 = 0.055	0.4183 ± 0.0912	0.0564 ± 0.0040	2.60 ± 1.55
	PPG only	0.278 = 0.055	0.4059 ± 0.0666	0.0568 ± 0.0048	2.78 ± 1.76
	RETROICOR	0.259 = 0.054	0.5860 ± 0.2103	0.1177 ± 0.0289	2.35 ± 1.40
	RETROICOR + ETCO2	0.254 = 0.053	0.5706 ± 0.2244	0.1175 ± 0.0326	2.14 ± 3.03
3.0 T	No correction	0.366 = 0.114	0.4481 ± 0.0980	0.0572 ± 0.0246	7.66 ± 5.71
	RB only	0.359 = 0.113	0.4610 ± 0.0888	0.0783 ± 0.0247	7.91 ± 5.72
	PPG only	0.360 = 0.113	0.4622 ± 0.0788	0.0765 ± 0.0255	7.63 ± 5.71
	RETROICOR	0.328 – 0.104	0.7459 + 0.0872	0.1945 + 0.0531	6.97 + 4.88
	RETROICOR + ETCO2	0.320 = 0.090	0.7522 ± 0.0718	0.2028 ± 0.0487	6.82 ± 5.00

Legend: σ (%) = temporal standard deviation of the preprocessed FMRI data timecourse as a percentage of the total MR signal amplitude. Max and mean R² _a are, respectively, the maximum and average adjusted coefficient of multiple determination. Activation (%) is the number of activated voxels expressed as a percentage of the total.

Table 2.

Comparisons of summary statistics between select combinations of noise correction.

Correction Comparison	%Δ σ		%Δ Max R2a
Field Strength:	1.5 T	3.0 T	1.5 T	3.0 T
RB vs. none	-1.63 #	-1.93	2.87	2.86
PPG vs. none	-1.59	-1.59	-0.19 #	3.12
RETROICOR vs. none	-8.17 #	-10.35	44.08 * #	66.44 *
[RETROICOR + ETCO2] vs. RETROICOR	-1.84	-2.44	-2.62 #	0.84
[RETROICOR + ETCO2] vs. none	-9.86 #	-12.54	40.32 * #	67.84 *
Correction Comparison	%Δ Mean R2 a		%Δ Activation
Field Strength:	1.5 T	3.0 T	1.5 T	3.0 T
RB vs. none	56.82 *	37.05 *	-7.04 #	3.24
PPG vs. none	57.98 * #	33.77 *	-0.36	-0.5
RETROICOR vs. none	227.32 * #	240.32 *	-15.79	-9.06
[RETROICOR + ETCO2] vs. RETROICOR	-0.23 #	4.24	-9.18	-2.2
[RETROICOR + ETCO2] vs. none	226.59 * #	254.76 *	-23.53	-11.06

Legend: Values listed are the percent difference in the parameter between the two analyses listed for comparison. RETROICOR includes both RB and PPG correction components. Statistical significance of the changes in summary statistics is indicated as follows:

^*significant change (p < 0.05) when implementing the correction (listed to left) for the data acquisition indicated (column headings);

^#significant difference between the 1.5 and 3.0 T acquisitions when comparing the impact of the same correction.

The application of each noise correction tended to reduce the average temporal variance, σ, but none of these changes reached statistical significance. Despite this, the reductions seen with RETROICOR were significantly larger in the 3.0 T acquisition. At both field strengths, RETROICOR including both RB and PPG regressors caused a greater reduction in σ than either the RB or PPG component applied individually. The reduction in σ with ETCO₂ correction, listed as “[RETROICOR + ETCO2] vs. RETROICOR” in Table 2, showed 5-fold less change compared to the standard RETROICOR algorithm, at both field strengths. To summarize the σ results from Table 1 and Table 2, timecourse variance is significantly greater in the higher field strength acquisition (p = 0.011), and there is a significantly greater reduction in σ with RETROICOR applied to data acquired at higher field (p = 0.013).

Implementation of RETROICOR resulted in significant increases in maximum and mean R² _a, as listed in Table 2. The R² _a data parallels the changes in σ, as improvements due to the individual RB or PPG components of RETROICOR are overshadowed by larger increases with full RETROICOR correction at both field strengths. The impact of ETCO₂ correction on model fit was markedly less than the other corrections and the changes were not statistically significant. On average, RETROICOR improved model fit by 240% at 3.0 T, which was significantly (p < 0.0001) greater than the 227% improvement at 1.5 T.

The activation extent was greater at 3.0 T than at 1.5 T (p < 0.001). The changes in the percentage of brain activation for each noise correction combination are listed in the lower right portion of Table 2. None of the noise corrections caused significant changes in activation, and the change in the overall amount of activation with RETROICOR correction was not significantly different between field strengths (p = 0.42). A similar trend was seen with RB and PPG corrections as with the other summary statistics; the decrease in the percent activation with full RETROICOR was greater than with either component applied individually.

Table 3 shows a comparison of the performance of the two implementations of the RETROICOR algorithm, which are described in the methods. The column headings indicate the sampling rate of the physiologic data used, with the modified implementations at higher sampling rate also including the described correction for the interleaved slice acquisition order. The change in the summary statistics with correction was similar using either technique, as no statistically significant differences were detected between implementations.

Table 3.

Comparisons of summary statistics with noise correction using different implementations of RETROICOR.

		%Δ σ		%Δ Max R2a		%Δ Mean R2a		%Δ Activation
	Sampling Rate (Hz):	40	200	40	200	40	200	40	200
1.5 T	RB vs. none	-1.60	-1.63	2.18	2.87	57.97	56.82	-10.86	-7.04
	PPG vs. none	-1.68	-1.59	-0.48	-0.19	56.39	57.98	-2.20	-0.36
	RETROICOR vs. none	-8.00	-8.17	41.28	44.08	224.72	227.32	-14.45	-15.79
	Sampling Rate (Hz):	40	500	40	500	40	500	40	500
3.0 T	RB vs. none	-1.97	-1.93	3.66	2.86	37.61	37.05	1.10	3.24
	PPG vs. none	-1.68	-1.59	1.95	3.12	33.73	33.77	-0.13	-0.50
	RETROICOR vs. none	-9.62	-10.35	64.90	66.44	230.63	240.32	-5.80	-9.06

Legend: The sampling rate at the top of each column denotes the native (40 Hz) or modified (200 or 500 Hz) implementation. Values listed are the percent difference in the parameter between the two analyses listed for comparison; no statistically significant differences were detected. RETROICOR includes both RB and PPG correction components.

Finally, Fig. 1 shows how the group average activation maps from the data collected at both field strengths were modulated by physiologic noise correction. In both datasets, bilateral activation was seen in the primary and secondary somatosensory cortices, insula, and prefrontal cortex. Additionally, the 1.5 T dataset showed activation in the left cerebellum, and bilateral thalamus. Each noise correction had some effect on the group activation maps. In the 1.5 T dataset, the predominant change was a decrease in activation caused by ETCO₂ correction, shown in yellow. This includes the removal of entire clusters of activation such as in the right prefrontal cortex and thalamus. The changes to the 3.0 T dataset were more subtle, with changes predominantly occurring on the periphery of activated clusters. At 3.0 T, voxels were also more commonly affected by both RETROICOR and ETCO₂ correction, which is shown as white.

Figure 1.

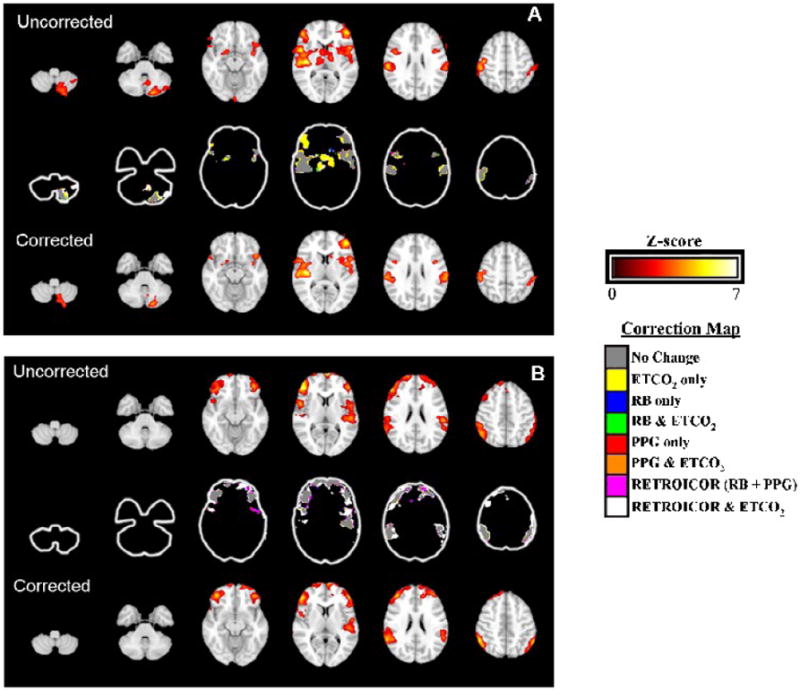
Selected slices of the group average activation maps for the 1.5 T (A) and 3.0 T (B) datasets. Images are displayed in radiologic orientation, with the right side of the brain on the left side of the image. The top row in each panel shows brain activation without noise correction applied, while the bottom row shows the activation with RETROICOR and ETCO₂ correction applied. The colorbar to the upper right shows the Z-score scale for the overlay in these images. The center row in each panel illustrates which type of noise correction was responsible for changes in the group activation maps. The color-key shown to the lower right provides the legend.

Discussion

In the initial description of RETROICOR [3], one slice of resting-state FMRI data from three subjects was analyzed, and a reduction was shown in the percent signal components in spectra associated with respiratory and cardiac frequencies. The timecourse variance was also shown to decrease in some regions of the brain, but these changes were not statistically significant [3]. Subsequent quantitative analyses of the impact of RETROICOR have also been performed on resting-state [5-6, 21] as well as task [5, 22] FMRI data. In this study, RETROICOR is implemented with ETCO₂ correction for pain task FMRI at 1.5 and 3.0 T and several metrics are calculated: timecourse variance, model fit, and extent of activation. Each of these measures has been used previously in the literature to quantify the effects of physiologic noise correction, and the impact of correction is expected to be accentuated with pain, which causes changes in breathing rate and depth [23], heart rate [24], and ETCO₂ [23].

The R² _a value indicates goodness of model fit [25] and is adjusted for the number of regressors used in the GLM, such that R² _a will decrease with the addition of an explanatory variable that does not explain its share of the variance in the data being modeled. The maximum R² _a calculated in this study refers to the voxel with the best model fit in each analysis, which is not necessarily the same voxel when performing model comparisons. The mean R² _a represents the average model fit over the entire brain of each subject, including areas that are not strongly activated by the pain stimulus. The significant increases in R² _a in this study with RETROICOR demonstrated an improvement in fit to the pain stimulus model, despite no significant changes in average activation.

Previous work has shown an increase in physiologic noise, signal to noise ratio, and contrast to noise ratio at 3.0 T compared to 1.5 T that is accompanied by increases in activation extent in the visual (44%) and motor (36%) cortices [2]. This is consistent with the results for no correction shown in Table 1. The significantly greater timecourse variance in the 3.0 T data in this study reproduced the known increase in temporal variance with increasing field strength. However, the use of SENSE encoding at 3.0 T was another important difference between the two acquisitions that contributes to the increased timecourse variance [11] and, with reduction factor 2, has been demonstrated to mildly reduce activation extent [12]. Despite this increased noise, the average uncorrected pain model fit, measured by mean R² _a, was 59% greater at 3.0 T compared to 1.5 T. The pain activation at 3.0 T covered 63% greater area than at 1.5 T, consistent with results for other cognitive tasks with increased field strength [26].

The impact of physiologic noise correction in the 1.5 T and 3.0 T acquisitions is summarized in Table 2. RETROICOR caused significant increases in R² _a in both datasets. In comparing the impact of RETROICOR across field strengths, the reduction in σ and the increases in R² _a were significantly greater when applied to the 3.0 T data. This suggests that the increased noise and increased activation seen in the uncorrected data at 3.0 T was accompanied by a greater effect of physiologic noise correction on FMRI results at higher field. Since the noise generated by SENSE is not directly correlated to physiologic fluctuations, the greater impact of physiologic noise correction in the 3.0 T analysis is unlikely to be a result of this difference between the two acquisitions.

The relative contribution of physiologic noise increases with field strength up to 7.0 T [27], however a large portion of this noise is not related to the cardiac and respiratory cycles, and thus not amenable to correction by RETROICOR [28]. Furthermore, a portion of this physiologic noise depends on signal strength, which is determined by acquisition parameters such as voxel dimension and flip angle [1, 27]. Analysis of RETROICOR at field strengths above 3.0 T were beyond the scope of this study, but previous work [27] suggests that the potential for increased impact at 7.0 T would not exceed 2.5-fold greater than that seen at 3.0 T and would depend greatly on the acquisition technique used.

To determine the individual impact of the RB and PPG components of RETROICOR, each was applied separately to the data. As shown in Table 2, the effects of RB and PPG correction on the summary statistics were generally similar in magnitude. The effect from the combined RETROICOR correction was always greater than either effect individually and usually greater than the sum of the individual effects. This synergistic effect on the summary statistics examined here is likely explained by the creation of different Fourier series terms for full RETROICOR compared to the series created for the individual RB and PPG corrections.

Changes in breathing during FMRI scanning occurring at frequencies much lower than respiration cause BOLD signal fluctuations that are not removed by RETROICOR correction [5]. It is possible to correct for these changes using a measure of respiratory tidal volume changes [10]. However, ETCO₂ changes are a more direct representation of the arterial CO₂ changes that drive the BOLD signal changes [9]. This led to the inclusion of ETCO₂ data as an additional noise regressor. The application of ETCO₂ correction to the pain data in this study had no statistically significant effect on the summary statistics calculated. This is inconsistent with prior data [9, 29] showing a strong correlation between ETCO₂ and BOLD changes and likely reflects a suboptimal technique for ETCO₂ correction. The latency between ETCO₂ fluctuations and BOLD signal changes has recently been shown to vary greatly across subjects with a heterogeneous spatial pattern [30], implying that the fixed response function applied uniformly throughout all subject’s data from both acquisitions of this study may inadequately model the effect of ETCO₂. Further optimization of ETCO₂ correction was beyond the scope of this study, but is expected to reveal a more significant relationship when a more robust transfer function is used.

RETROICOR was originally written for input physiologic data sampled at 40 Hz [3], and, in this study, two methods are compared for dealing with physiologic data sampled faster. It was shown, by the lack of statistical differences between the two techniques in Table 3, that there was no relative advantage to either downsampling the data to 40 Hz, or modifying the RETROICOR algorithm to process higher sampling rate data. Thus, RETROICOR implemented with physiologic data sampled at any rate ≥ 40 Hz should perform equivalently. The similar performance between the modified and native implementations of RETROICOR also confirms that the coefficients of the underlying Fourier series can change to account for timing differences between physiologic changes and MR signal changes, as manually aligning the image slices with the physiologic data did not significantly impact the results.

The discordances between the activation maps from the two acquisitions shown in Fig. 1, most notably in the cerebellum and thalamus, are likely not entirely explained by differences in field strength. Subtle differences in the activation maps for the same task performed at two field strengths are common [2, 26, 31-32], but there are several explanations for these larger differences as well. The first is inter-subject variability in pain FMRI studies, a review [33] of which found that only 37% showed thalamic activation and only 15% detected cerebellar activation, while a majority showed activation in the primary and secondary somatosensory cortices and the insula. This is consistent with Fig. 1; the primary and secondary somatosensory cortices and the insula are activated bilaterally in both maps, while the cerebellum and thalamus are only activated in the 1.5 T data. Additionally, the use of SENSE at 3.0 T also likely reduced activation extent and significance [12] and may have contributed to the differences in maps between the two acquisitions.

Most of the group activation map changes seen when physiologic noise correction was applied involved slight changes to the periphery of activated clusters. There was a trend towards reduced activation, as indicated by the decreases in average percent brain activated, though these were not statistically significant. However, with correction, local increases in both the significance and extent of activation were also seen in Fig. 1. For examples, see the changes in the left secondary somatosensory cortex in the 1.5 T map shown in panel A, fifth slice from left, lower cluster on right side of image and also the right secondary somatosensory cortex in the 3.0 T map shown in panel B, fifth slice from left, lower cluster on left side of image. These varying findings indicate that, depending on the signal and noise structure in a particular voxel, correction may act to increase either the sensitivity or specificity of activation.

Conclusions

When applied to pain FMRI at 1.5 and 3.0 T, RETROICOR significantly improved model fit. These results were unaffected by using physiologic data with a sampling rate higher than 40 Hz and were also unaffected by correcting for the interleaved slice acquisition order, validating the commonly used RETROICOR algorithm. Timecourse variance was greater in data acquired at higher field strength and physiologic noise reduction with RETROICOR correction was also greater at higher field. ETCO₂ correction for pain FMRI was also explored, but found to be of secondary importance compared to RETROICOR correction. These findings suggest that RETROICOR, as it is commonly implemented, should be included as part of the data analysis for pain FMRI studies performed at 1.5 and 3.0 T.