Resolution Control for Balancing Overview + Detail in Spatial, Multivariate Analysis

Abstract

Parallel coordinates, re-orderable matrices, and dendrograms are widely used for visual exploration of multivariate data. This research proposes an approach to systematically integrate the methods in a complementary manner for supporting multi-resolution visual data analysis with an enhanced overview+detail exploratory strategy. The paper focuses on three topics: (1) dynamic control across resolutions at which data are explored; (2) coordination and color mapping among the views; and (3) enhanced features of each view designed for the overview+detail exploratory tasks. We contend that systematically coordinating the views through user-controlled resolutions within a highly interactive analysis environment will boost productivity for exploration tasks. We offer a case study analysis to demonstrate this potential. The case study is focused on a complex, geographically referenced dataset including public health, demographic and environmental components.

1. INTRODUCTION

Data can be complex, containing heterogeneous themes to address complicated problems. For example, when analyzing public health data, domain experts usually consider demographic and environmental data as well. Meanwhile, data are often voluminous and high dimensional. The strategies to address the problems are (1) decomposition, abstraction and classification¹, which reduce data (both the number of items and dimensions) to manageable pieces (Simon, 1969, Siirtola, 2003) and (2) interactive exploration of the data following a process of “overview first, zoom and filter, then details-on-demand” (Shneiderman, 1996), which is usually abbreviated as overview+detail. Multi-resolution visualization can effectively support the strategies because it represents data at different levels of abstraction, displaying a large amount of data in an overview at a coarse resolution (high abstraction), and individual data at finer resolutions as analysts zoom in (Stolte et al., 2003). Visualizing data at an appropriate resolution is critical because some patterns are absent in an overview, and only exposed at a finer resolution; while a view at low abstraction could display an overwhelming amount of data, hiding general trends that could appear only at some intermediate resolution (see demonstrations in section 4.1, 4.2). An exploration can miss important patterns if it starts with an overview and zooms at predetermined resolutions and steps. We believe that an exploration would be more productive if an analyst can systematically adjust and interactively determine the most appropriate level of detail for a specific analysis task during the exploration process.

This research proposes a systematic “zoom” approach which we call resolution control. Generally in the cartographic community, the term data resolution indicates “the granularity of the data that is used in mapping… each level of resolution represents a different ‘grain’ of the data”(Terry A. Slocum et al., 2003, p 104). Applying this concept, we use the term resolution here to refer to the level-of-detail at which data is abstracted (e.g. aggregated, amalgamated or clustered) and visualized as a single entity (see detail in the section of 3.4). The concept of resolution control refers to interactively adjusting and determining an appropriate level-of-detail that satisfies an analysis task and facilitates identification of interesting patterns. The goal of resolution control is to display key characteristics of data, while hiding unnecessary details to avoid displaying an overwhelming amount of data. To support the mechanism, this research introduces a concept of dynamic-resolution-view (abbreviated as dr-view) that fits between the traditional overview and detail view. The dr-view complements the two views by dynamically displaying abstracted data at a user-specified resolution, thus relieves the analyst from facing overwhelming information at an inappropriate resolution, and provides more perspectives for investigation (see detail in section 3.5).

Following from the above, we propose an enhanced exploration strategy for analyzing geospatial, multivariate data in a multi-resolution environment: overview → dynamic-resolution-views, filer→ simultaneous details on demand. The strategy is abbreviated as overview → dr-views→ details. We employ and integrate four visualization views to support the proposed methods: a re-orderable matrix, an extended dynamic dendrogram (attached to the matrix), an extended parallel coordinate plot (PCP), and a geographic choropleth map (henceforth abbreviated as GeoMap). We will demonstrate the complementary roles played by the views and the ways they are integrated and coordinated to achieve our research goal. The research is implemented in a pure-Java, standalone software application called the Visual Inquiry Toolkit (VIT). Initiated by Jin Chen and Alan MacEachren, the VIT is built upon components of GeoVISTA Studio, but tailored for a narrow range of data analysis tasks. It provides an experimental environment for developing and testing advanced visualization and computational methods (e.g. the matrix tool and the resolution control mechanism described here), prior to their introduction into the GeoVISTA Studio library of tools.

The approach developed is illustrated through a case study analysis of a geographically-referenced, high-dimensional cancer-related dataset. Specifically, the case study investigates the covariate relationship between the target variable – breast cancer mortality – and its potential risk factor variables. While our research addressed geographic multivariate data analysis, we feel that many of the concepts and approaches described here are relevant to the visualization of general multivariate data as well.

The reminder of the paper is organized as follows. Section 2 reviews related literature. Section 3 discusses the core topics of the research, which include re-ordering and color encoding in a matrix view, the complementary roles of matrix and parallel coordinates views, and the mechanism of dynamic resolution control. Section 4 presents the case study. Section 5 summarizes the methods, discusses the limitations, and outlines planned future development.

2. RELATED WORK

We discuss briefly two research topics that are directly related to this research: multivariate visualization and multi-resolution visualization.

2.1 Multivariate visualization

The typical advanced visualization methods for multivariate data include scatterplot matrices (Andrews, 1972), multivariate glyphs (Pickett et al., 1995), parallel coordinate plots (Inselberg, 1985), and permutation matrices (Mäkinen and Siirtola, 2000, Bertin, 1981). A comprehensive review of the methods can be found in Keim et al.(2005). Although each of the methods has its limitations, the parallel coordinate plots and permutation matrices can complement each other to support exploration of multivariate data (Siirtola, 2003), especially for those adopting an overview + details strategy.

A parallel coordinate plot (PCP) is suited to investigating high dimensional data in detail. It depicts a data item via a polyline (henceforth also called a string), revealing subtle multivariate differences between data items. However, PCP suffers from overplotting problems when visualizing even a modest number of data items. The typical solution is to visualize a data abstraction (e.g. groups, clusters) rather than individual data items (Ward, 2004, Andrienko and Andrienko, 2005a), at the price of losing detail information. An enhanced solution is to allow parallel coordinates to switch between an overview and detail view mode (Chen et al., 2006), and that approach is adopted in this research. Another problem with PCP is that interpretation of multivariate patterns (represented by the shape of polylines) and comparison between variables are influenced by the order of the axes. To address the problem, our implementation of PCP supports reordering axes manually and sorting axes automatically (e.g. based on their correlation values against a specified variable).

The permutation matrix can provide an overview that exposes structural patterns and hot spots for the entire dataset, by sorting the rows and columns (Bertin, 1981, Siirtola, 1999, Siirtola and Makinen, 2005). Hierarchical clustering methods are typically integrated with a matrix to support sorting, and the clusters can be hierarchically visualized in a dendrogram. This approach is widely adopted for multivariate analysis (e.g. analyzing gene expression data) (Bar-Joseph et al., 2001, Eisen et al., 1998). Seo et al. (2002) introduced a rank-by-feature approach, and enhanced the method by employing a filtering bar in the dendrogram. The bar can dynamically filter and query clusters based on their similarity. Although effective in exposing major patterns, a permutation matrix is limited in visualizing subtle differences between clusters/data items, because it requires analysts to interpret and compare the multivariate characteristics of clusters solely based on colors of the matrix’s mosaic cells. This is perceptually a difficult task.

Hence, the matrix and PCP can potentially complement each other for visualizing multivariate patterns in overview and detail views. This research proposes integration of the two methods, leveraging on PCP for cluster validation and resolution control.

2.2 Multi-resolution visualization

Multi-resolution visualization and control has drawn attention from several researchers in recent years. Stolte et al. (2003) provide an interesting method for multiple resolution data visualization, but the method focuses on formalized multiscale visualization and on zooming along multiple dimensions, rather than on multivariate data analysis. Ham (2003) employed the matrix for visualizing information from large software projects at multiple levels of abstraction. Cui (2006) developed a method for measuring data abstraction quality in resolution control. Wang et al.(2005) proposed an error tolerances approach for interactive resolution control in scientific visualization. Fua et al. (2000) proposed a structure-based-brush mechanism that supports interactive control on resolution (measured as cluster size) with instant feedback from various multivariate visualization methods; for example, a parallel coordinate plot displays the mean value of clusters at a given resolution. Drawing upon the previous research, this research develops an alternative resolution control mechanism based on an integration of a dendrogram, re-orderable matrix, and parallel coordinate plot. Our method adds multi-resolution capacity to the effective multivariate visualization methods (i.e. matrix and PCP), as explained in the section 3.

3. Coordinating Multiple Views for Resolution Control

In this section, we present our method of dynamic resolution control that supports the proposed overview → dr-views→ details exploratory analysis process. We first briefly introduce the case study data that is used for demonstration of our methods in section 3 and for the case study in section 4. Section 3.2 discusses how to achieve an overview in a matrix; section 3.3 outlines integration of a matrix and a PCP in a complementary manner. Extended from our previous work(Chen et al., 2006), the methods explained in the two sections contain incremental improvements that are necessary for developing our resolution control method. Section 3.4 focuses on dynamical adjustment of resolution. Finally, section 3.5 explains dynamic resolution control in multiple linked views and the way the method balances the overview and detail views, thus supporting the proposed overview → dr-views→ details exploratory analysis process.

3.1. The Case Study Data

The data is a multivariate, geographically-aggregated dataset that contains thematically-heterogeneous components, including public health, demographic and environmental data. The dataset is for analysis of U.S. breast cancer mortality and potential risk factor variables. It contains the following variables: (1) age-adjusted breast cancer mortality rate from 1971 to 2000 for all women with 5-year averages (henceforth abbreviated as cancer rate); (2) demographic risk factors such as population density, per-capita income, percentage of individuals without health insurance, etc; (3) behavioral risk factors such as obesity, having smoked, etc.; (4) percentage of hazardous chemicals in the atmosphere. To be concise, we list only the variables that are related to our case study in section 4. The data is aggregated at the U.S. state level (future research will focus on scaling the methods for application of larger data sets, e.g. counties for the entire U.S.). Therefore, a data item is referenced by a U.S. state, and represented as a polygon in the GeoMap, a matrix row, a string in the PCP. Many thematic variables (either a cancer mortality rate or a covariate) have multiple time steps. A time step represents the variable value aggregated for a particular period. Either a time step or a variable is treated as a dimension and represented as a matrix column, and an axis in the PCP. For example, cancer rate data used here has six time spans (1971-1975, 1976-1980, 1981-1985, 1986-1990, 1991-1995, 1996-2000), represented by six axes in the PCP, so that temporal changes of cancer can be analyzed together with information about covariates. To describe things more generally, in this paper, the term variable also refers to a time step. Therefore, there are 60+ variables displayed in the matrix and PCP. Figure 1 shows how the data is visualized in a matrix.

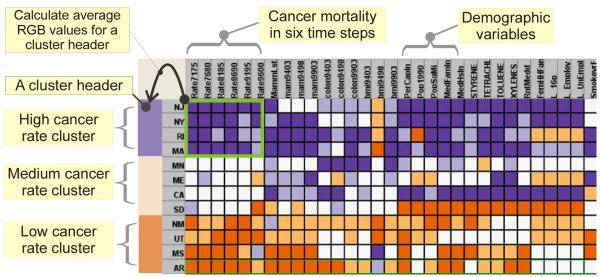
Figure 1.

The data, which is in a tabular form, is visualized in the matrix overview. A column represents a variable; and a row represents a U.S. state, with the row header displaying the state abbreviation (e.g. CA for California). Here only a subset of data is displayed for the illustration purposes. The matrix rows and columns are computationally re-ordered to expose patterns. The data is abstracted into three clusters as highlighted in the three cluster headers, characterized as low, medium and high cancer rates. A cluster header’s color is generated based on the mean RGB values of those matrix cells that represent the target variable – cancer rate – of the cluster, as highlighted in the green rectangle at the left-up corner.

3.2. Matrix Serves As an Overview – Re-ordering and Color Encoding

This section discusses how to achieve an overview in a matrix, which exposes overall patterns at a coarse resolution. Computationally reordering a permutation matrix is an effective method for exposing overall, structural patterns (Makinen and Siirtola, 2000, Siirtola and Makinen, 2005, Bertin, 2001). Agglomerative hierarchical clustering algorithms (Jain and Dubes, 1988) are widely employed to derive 1D ordering of the matrix rows and columns (Seo and Shneiderman, 2002, Bar-Joseph et al., 2001). This research applies our previous work (Chen et al., 2006, Chen, 2006), and extends the re-orderable matrix method to multi-covariate analysis (e.g. between a cancer and potential risk factor variables). In the matrix, a row represents a place (e.g. a U.S. state), and a column represents a variable (e.g. cancer mortality). The matrix rows are ordered to group the states with similar multivariate characteristics together. In addition, we apply a new variable-based ordering mechanism: when merging two clusters, always put the cluster containing the higher mean values of the target variable – breast cancer mortality – on one side (e.g. top), put the other cluster on the other side. Eventually, all the clusters are ordered from low-cancer-rate to high-cancer-rate clusters (Figure 1). We can also computationally re-order matrix columns to group the variables with similar characteristics together. Sometimes, manually adjusting column sequence is necessary to reflect thematic priority and relationships among variables. Take our case study as example: after computationally re-ordering on the columns, we manually place the cancer rate variables as the left-most six columns (each represents the mortality in a five-year time step), with medical screening variables and demographic variables on the next.

Graphically representing data in permutation matrices is important for visually exposing patterns. Applying an inappropriate representation method could cause biased interpretation and even hide patterns. Two approaches are widely employed (Bertin, 1981, Bertin, 2001): (1) size-encoding – fill matrix with shapes (rectangle and circle), the size of which are correlated with an attribute value (Siirtola and Makinen, 2005, Kincaid, 2004); (2) color-encoding – a heatmap, often colored by a divergent color scheme (e.g. green-black-red) or sequential color scheme (e.g. yellow-orange-red). The color values are mapped into data values or even some complex multivariate patterns such as in (Chen et al., 2006, Guo et al., 2006, Chen et al., in process). Both methods have advantages and limitations. A size-encoding matrix is usually preferred for visually comparing attributes (e.g. those amount-related attributes such as population, income); however, the matrix can display only a small amount of data because each matrix cell must be in a reasonably large size. In contrast, a color-encoding matrix allows displaying a large amount of data because each matrix cell can be in a size as small as one to two pixels. However, color-encoding matrix has difficulty in discriminating subtle numerical difference (Kincaid, 2004), thus usually serves only as an overview rather than a detail view. Moreover, when applied to multi-linked views (e.g. a matrix, a PCP and a choropleth map), color-encoding is often favored over size-encoding because colors can be shared across different visualization methods. On the other hand, size-encoding method is considerably limited when applied to the linked views. For example, it does not make sense to encode an attribute value with a polyline’s size in a PCP. This research adopts color-encoding because we use multi-linked views, and the matrix serves as an overview.

This research favors divergent color schemes over sequential ones, although the VIT supports both schemes. Traditionally when coloring a choropleth map, a sequential scheme is suited to representing ordered data that ranges from low to high, whereas a diverging scheme puts equal emphasis on mid-range critical values and extremes at both ends of the data range (Brewer and Harrower, 2002, Harrower and Brewer, 2003). However, when visualizing a relative large dataset, more colors are required for increased number of categories; resulting in less distinction among sequential colors. Consequentially, small graphic entities become hard to distinguish, especially in the case of slim PCP polylines and tiny matrix cells. Because diverging color scheme can provide more distinguishable colors than the sequential color scheme, researchers often choose the former over the later when visualizing a large dataset, especially in multi-linked views composed of matrix and/or PCP views, as in (Guo et al., 2006, Seo and Shneiderman, 2002, Bar-Joseph et al., 2001, Keim et al., 2004). This research adopts a divergent color scheme for two reasons: (1) our multi-resolution visualization could generate considerable amount of categories (clusters) at finer resolutions, thus requiring more distinct colors; (2) our cancer analysis is concerned with both low and high cancer mortality data items. Specifically, blue encodes a high value, white encodes a medium value, and orange encodes low value, with variations between blue-white and orange-white to represent specific data values (Figure 1).

To effectively characterize and summarize the clusters, we introduce an idea of cluster header, which is a color rectangle located on the left side of the matrix that highlights main characteristics of the corresponding cluster. In Figure 1, three cluster headers summarize cancer rate of the clusters into three qualitative categories: low, median, and high rates. The cluster header’s color can express either a multivariate pattern of a cluster (Guo et al., 2005, Chen et al., 2006) or mean values of a target variable for units in each cluster (e.g. the average cancer mortality of a cluster). The color that encodes an average value of a cluster can be generated via two approaches: (1) calculate average data value first and then encode them with the color; or (2) calculate average RGB values of the matrix cells that represent the target variable(s) of the cluster. While the first approach can quantitatively characterize clusters in term of variables with homogeneous meanings (e.g. several time steps of a variable), the second approach can qualitatively characterize the clusters in terms of the magnitude of the heterogeneous variables (e.g. breast cancer rates and population density). We adopt approach 2 for coloring the cluster headers since they only need to qualitatively depict the clusters at a coarse resolution (e.g. low, median, high rates). The matrix and PCP can display the clusters at a finer resolution. The cluster headers facilitate the coordination between the matrix and PCP, as discussed next.

3.3. Link Two Complimentary Views: Matrix and PCP

As discussed in the section 2, when linked each other, a matrix and a PCP complementarily provide an overview and a detail view for visualizing multivariate patterns. In addition, link-views between the matrix and PCP are essential for our resolution control mechanism in that the PCP provides instant feedbacks for determining resolution. A matrix and a PCP can be linked complementarily via two strategies (Chen et al., 2006): (1) dynamic link (Buja et al., 1991) (2) static link (Andrienko and Andrienko, 2005b). Readers are referred to (Chen et al., in process) for detail discussion on the two links. Simply put, a dynamic link can simultaneously highlight a matrix cell and corresponding string in the PCP so that various aspects of the data can be investigated concurrently. The dynamic link is usually achieved by the moving mouse over a single data item, or brushing a subset of data items operations. In contrast to the dynamic link, a static link emphasizes linkage across views in a static manner (without human interaction). A static link is achieved by applying same color to visual elements in multiple views so that they are known to visualize the same or related “things”. The Static link strategy is essential to achieve an overview of the entire dataset because it allows simultaneous linkage and visual distinction among multiple data subsets (e.g. clusters) without human interaction. While the concept of a dynamic link is widely used in modern linked-views visualization systems (e.g. GeoVISTA Studio), implementing a static link between a matrix and PCP has not exploited fully.

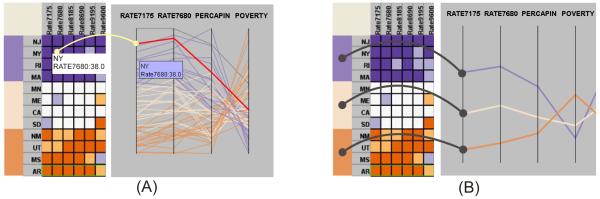
To achieve a static link between the matrix and PCP on a cluster level, both views need to provide summarized information in clusters. The matrix can summarize clusters via the cluster headers as explained previously. Our PCP implementation allows switching between an overview mode (to display data groups) and a detail view mode (to display individual data items), as described in (Chen et al., 2006). In the overview mode (Figure 2, (B)), a string represents a cluster (by displaying the median value of the cluster’s data items for each variable) and thus depicts a multivariate pattern for the cluster. The string’s size indicates the number of data items contained in the clusters. The larger the number, the larger the size. The string representing a cluster is mapped to a cluster of matrix rows. In the detail view mode (Figure 2 (A)), a single string represents an individual data item, each of which is assigned the cluster’s color. The string is mapped to a matrix row.

Figure 2.

(A) With the dynamic link, a matrix cell is mapped to a string in the PCP (detail view mode), which is highlighted in red. (B) With the static link, three clusters in the matrix are mapped to the three strings in the PCP (overview mode) via colors. The curves demonstrate the links. For illustration purposes, only four variables are displayed in the PCP.

The linking is established by assigning a PCP string with the same color as the corresponding cluster header. Through the color, an analyst can easily identify a PCP string (a cluster) that carries a particular value range of the target variable. For example, a blue string represents a high cancer rate cluster. This allows the analyst to identify qualitative covariate relationships between a target variable and other variables (e.g. cancer rate and risk factor variables), by simply looking at comparable ordering of colored strings on different axes. In Figure 2 (B), the PERCAPIN axis (per capita income) has colored strings in a blue-gray-orange order from top to bottom. The order of the colored strings suggests a positive correlation between per capita income and breast cancer mortality, by which the clusters are derived. Similarly, an orange-gray-blue order suggests a negatively correlation (e.g. between POVERTY and breast cancer mortality, see more examples in Figure 5). Traditionally, a PCP allows identification of covariate relationships by comparing shape of polylines between two neighboring axes. Comparing the order of colored strings allows identifying relationships between multiple non-neighboring axes. A GeoMap can be linked to the matrix in the same way; with spatial entities belonging to a cluster assigned the same color as the corresponding cluster header.

Figure 5.

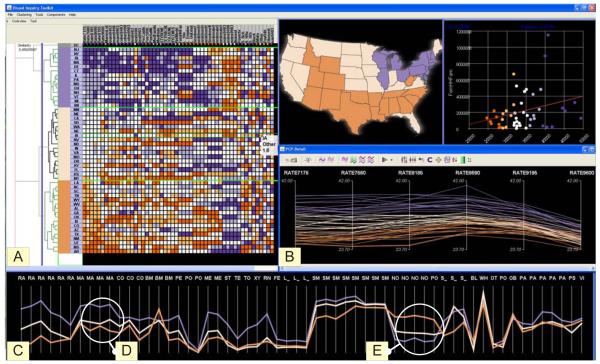
Overview of the VIT. With the current resolution, the entire dataset is abstracted as three clusters primarily based on the cancer rates. (A) The dendrogram-matrix overview of entire dataset. (B) The PCPd displays data items for the six time steps of breast cancer mortality. (C)The PCPo (a dr-view) abstracts the data into three clusters. The map shows breast cancer mortality for white women aggregated for the period of 1971-2000. (D) The variables that show positive relationship with the cancer mortality. (E) The variables that show negative relationship with the cancer mortality.

3.4. Dynamic Adjustment on Resolution

Evidence shows that adopting an appropriate scale is critical for analyzing geographically-aggregated data (Lam, 1990, Schneider et al., 1993). A related famous problem is the modifiable areal unit problem (MAUP) (Openshaw, 1984) – collecting data at different areal units or aggregating data in different ways will significantly influence analysis outcomes. Although abundant literature has addressed the MAUP problem, most of the research was conducted from perspectives of statistics and/or spatial analysis (Fotheringham and Wong, 1991, Anselin and Getis, 1992, Jelinski and Wu, 1996, Dungan et al., 2002, Nakaya, 2000, Cain et al., 1997). Visual analytics of spatial data in a multi-resolution environment remains an unexplored, but important issue, which has attracted attention of researchers (Dykes and Brunsdon, 2007, Morehart et al., 1999) in recent years. Drawing upon multi-resolution visualization methods for multivariate analysis (as outlined in section 2.2), we develop the resolution control mechanism for analysis of spatial, multivariate data.

As presented here, scale refers to data resolution that defines the level of detail at which data is abstracted. The nature of data abstraction can be characterized in two ways as proposed by Cui et al. (2006): (1) data abstraction level - the ratio between the size of the abstracted dataset and the original dataset; (2) data abstraction quality - the degree to which the abstracted dataset represents the original dataset. The goal of the resolution control methods introduced here is to balance the requirement for maximizing the data abstraction level (to reduce number of data elements to investigate at a time), and the requirement for minimizing the variance within each abstracted dataset so that they can represent the key characteristics of the original dataset. Data abstraction can be achieved by two approaches: data sampling and data clustering. This research adopts the clustering approach because clusters often form a hierarchy (i.e. a cluster usually contains several sub-clusters), which provides a natural way to organize and visualize data at various levels of detail. The hierarchy is also found in spatial entities (i.e. a larger region consists of some small regions), providing an easy way to control spatial resolution. Specifically, this research adopts agglomerative hierarchical clustering methods to generate a bottom-up hierarchical structure of resolutions.

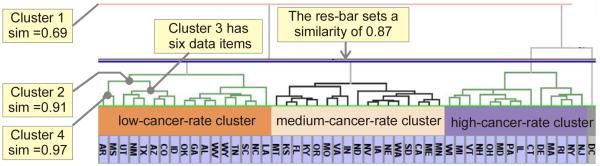
A hierarchical clustering method can group data items into clusters based on their similarities, which are usually expressed as Euclidean distance in multivariate space (Terry A. Slocum et al., 2003, p92, Jain and Dubes, 1988). The hierarchical clusters are usually visualized in a dendrogram. A dendrogram is a binary tree in which a branch (connecting two sub-branches or leaves) represents a cluster and a leaf represents an individual data item (Jain and Dubes, 1988). A cluster contains two sub-clusters, and the length of branches expresses a distance (dissimilarity) between the two sub-clusters. As illustrated in Figure 3, a bottom cluster (e.g. Cluster 4), which contains fewer data items of higher similarity, has smaller variance and a lower level of data abstraction; while a top cluster (e.g. Cluster 2), which contains more data items of lower similarity, has larger variance and a higher level of data abstraction. Therefore with hierarchical clusters, we can achieve a desired resolution by simply specifying similarity of data items within a cluster. Slocum (2003, p.97) describes the process as “determining an appropriate number of clusters”, the goal of which is to “create groups of observations, with each group being relatively homogeneous and different from another group”

Figure 3.

For illustration purposes, we rotate the dendrogram and display it in a horizontal orientation; therefore the matrix row headers (represent U.S. states) are illustrated as columns. Here, similarity is abbreviated as sim. Visualized as a branch, Cluster 4 contains two data items with similarity of 0.97. Cluster 3 contains six data items. Cluster 2 has Cluster 3 and Cluster 4 as the sub-clusters, which have similarity of 0.91; thus Cluster 2 has eight data items. Cluster 1 is the root cluster that includes all sub-clusters.

To achieve dynamic control of data resolution, this research integrates the dendrogram with the matrix, and adds a similarity-control bar on the dendrogram (as shown in Figure 3). As an analyst drags the bar up and down, the bar specifies the minimum value of pair-similarity within a cluster, divides the entire dataset into a specific number of clusters (e.g. three major clusters as shown in Figure 3), and thus achieves a data resolution of interest. The bar itself is not a new idea and adopted by several researchers (Bar-Joseph et al., 2001, Seo and Shneiderman, 2002) to interactively divide data into sub-clusters with a particular similarity. This research applies and extends the idea to dynamic resolution control in multi-linked views, thus achieving multi-resolution visualization on spatial and multivariate data. We label the bar as “resolution control bar” (abbreviated res-bar, subsequently). Specifically, the bar can control resolution in two approaches. With the first approach, the bar can adjust clusters’ similarity to achieve a coarse resolution on the dendrogram, which is integrated with the cluster headers. As shown Figure 3, we set the similarity of 0.87; and the entire dataset is abstracted and summarized as three qualitative categories (clusters) in terms of breast cancer mortality: low, median, and high mortality. The categories are visualized in three cluster headers in diverging colors: orange, white (with light orange), and blue. By interactively dividing data into sub-clusters, we achieve an overview of the data at a coarse resolution on the dendrogram. Integrated with the dendrogram, the matrix displays patterns at a finer, intermediate resolution (with a cell depicting an observation’s attribute). However, the overview alone is insufficient; analysts are also interested in identifying and interpreting patterns at a finer resolution from spatial and multivariate perspectives. This can be addressed by the second approach: the system broadcasts the resolution to the linked views, and achieves intermediate resolutions on the PCP for visualizing multivariate data, and spatial resolution on the GeoMap, as discussed next.

3.5. Dynamic Resolution Control with Multi-Linked Views

With the capacity of dynamically adjusting resolution on the overview, an analyst needs to determine an appropriate resolution for a specific analysis task. There is an array of numeric criteria for measuring quality of data abstraction as proposed by Cui et al. (2006). In contrast, this research aims to assist an analyst by providing instant, visual feedbacks on spatial, multivariate patterns exposed at a particular resolution. Specifically, as the resolution changes dynamically, we propose to visualize and monitor subtle changes of multivariate and spatial patterns, respectively in a PCP and a choropleth map that serves as the dynamic-resolution-view (abbreviated as dr-view). Whenever detecting an interesting multivariate or spatial pattern(s), the analyst can freeze the resolution and investigate the pattern in the detail views. The multiple-linked dr-views introduced here aims to enhance the traditional overview + zooming+ details visualizations (Shneiderman, 1996), including graphic zooming and semantic zooming (Bederson and Hollan, 1994, Woodruff et al., 2001). The dr-views fits between the overview and detail views, and balances the requirement for displaying entire dataset with a highly-abstracted resolution in the overview, and the requirement for displaying a subset of data with a finer resolution in the detail views. Traditional zooming methods, which filter and visualize a subset of data at a finer resolution in the overview, have some limitations for spatial, multivariate analysis. First, only a subset of data is displayed in the zoomed-in view, thus the analyst loses the context of entire dataset. Second, a visualization method serving as the overview may not be suitable for displaying detail information at a finer solution, Take the matrix overview as an example: the matrix is not suitable for detecting subtle different among multivariate patterns, as discussed previously. Moreover, an overview provides only single perspective, thus exposing only one type of pattern (i.e. either multivariate patterns in a matrix, or spatial patterns in a choropleth map). In contrast, our resolution control mechanism aggregates the entire dataset and visualizes it at a dynamic level of abstraction in multiple dr-views, which simultaneously expose spatial and multivariate patterns; but still preserves the overview that provides the context.

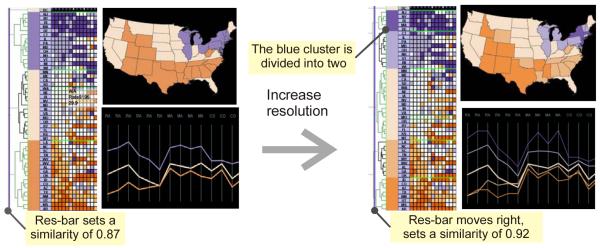
The resolution control mechanism is implemented in the VIT, and is composed of four primary visual components: a dendrogram integrated with a re-orderable matrix, a PCP, and a GeoMap. The PCP (in the overview mode) and the GeoMap serve as the dr-views. The four components are all linked, they monitor and respond the movement of the res-bar. As the analyst drags the res-bar back and forth on the dendrogram, the entire dataset is automatically “divided” into a decreasing or increasing number of sub-clusters (as represented by the cluster headers); each has a minimum similarity value specified by the res-bar (Figure 4). Accordingly, the sub-clusters are visualized as PCP strings, and as geographic regions in the GeoMap, all in the same color as the corresponding cluster header. Figure 4(left) shows that the data is initially abstracted into three clusters in the dendrogram overview, with multivariate profile of the three clusters displayed in the PCP, and with spatial patterns in the GeoMap. Then the analyst adjusts the res-bar to a finer resolution; and the data is abstracted into five clusters: the blue and orange clusters are “broken” into two clusters respectively as resolution increases (Figure 4, right). With dynamically-adjusted resolution, different and potentially-useful multivariate and spatial patterns will be exposed.

Figure 4.

Resolution control process: initially the entire dataset is abstracted into three clusters (left); as resolution is increased, the dataset is abstracted into five clusters (right). The matrix overview remains the same, exposing structural patterns; while the dr-views provide additional perspectives: the PCP displays multivariate characteristics of the clusters; the GeoMap displays the geographic distribution of the clusters. To save space, only a subset of variables is displayed.

Equipped with the resolution control mechanism, the VIT supports the overview → dr-views→ details exploratory analysis process while simultaneously displaying data at multiple levels of resolution. The dendrogram and matrix serves as the overview, displaying the entire dataset at a coarse resolution. The dr-views display data at a dynamic level of resolution, providing instant feedbacks for resolution control. A PCP (in the detail view mode) serves as the detail view for investigation of a small subset of data at a finer resolution. An overview of the VIT is shown in Figure 5. An exploration can follow two approaches starting from the matrix overview. With the first approach, an analyst can identify hot spots and structural patterns in the matrix, select a subset of data and investigate in the detail view. With the second approach, the analyst can gradually adjust the level of resolution in the dendrogram, exposing interesting multivariate and/or geospatial patterns respectively in the dr-views. Whenever some interesting patterns are identified, the analyst can freeze at the resolution, then select and compare a subset of data/variables/patterns in the detail views, as demonstrated in detail in the section 4. We illustrate the process through static figures below, but the ability of the approach to help analysts explore data and find relevant patterns is enhanced substantially through real-time dynamic responses to user control that propagates among the views.

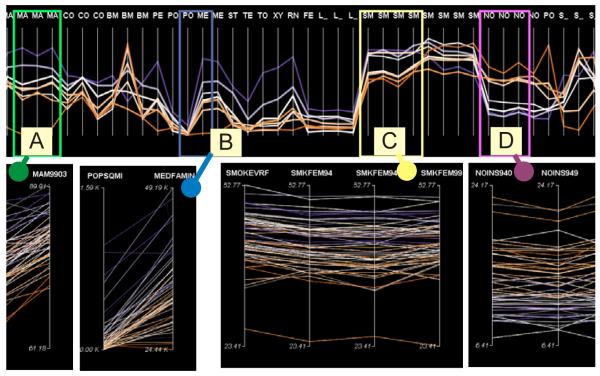
Our detail-view PCP is equipped with a function of multi-threads investigation that is designed for analysis of high dimensional data. When exploring high dimensional datasets, an analyst may find multiple interesting patterns within some subsets of variables. It is often desirable to initiate multiple threads of investigation on each subset of variables in detail and to compare them, all within the context of the overview. This research introduces a widget called a scanbox to our implementation of the PCP. A scanbox is instantiated here as a rectangle frame applied to an overview-mode PCP, which displays clusters and therefore is called PCPoverview (henceforth abbreviated as PCPo). The scanbox defines a particular focusing area (thus a subset of variables) on the PCPo. The scanbox is linked to another detail-view-mode PCP, which displays individual data items (called PCPdetailview, henceforth abbreviated as PCPd). The analyst can drag the scanbox horizontally along the PCPo and adjust the frame width to define the focusing area; the PCPd responds dynamically to display only the variables as defined within the scanbox. The analyst can instantiate multiple scanboxes, with each linked to a separate PCPd, thus concurrently comparing patterns involving several subsets of variables (as shown in Figure 7). With modern analysis environments equipped with dual monitors, multiple PCPd views can be instantiated and placed in the secondary monitor.

Figure 7.

Multi-thread investigations on multivariate patterns. Four scanboxes (A, B, C, D) are initiated in the PCPo and associated with four PCPd, each of which displays a subset data in detail. Scanbox A contains Mam with three time steps. B contains PopSqmi. C contains smoking rate with four time steps. D contains Noin with three time steps. The orders of the colored PCP strings suggest some positive relationship between cancer rate and the variables in A, B, C; and negative for the variables contained in D.

4. Case Study Analysis on Public Health Data

The case study focused on exploring the relationship of cancer mortality (specifically, age-adjusted breast cancer mortality for white women aggregated for the period of 1971-2000) with a range of potential covariates that include: (1) PopSqmi - population per square mile (i.e., population density); (2) Mam - percent of women ages 50-64 who had a mammogram in past 2 years; (3) Colon - percent of persons ages 40+ who had a colonoscopy, sigmoidoscopy or proctoscopy in past 5 years; (4) Xylenes - mixed isomers emissions (tons/year derived by the EPA in 1997); (5) Noin - percentage of population with no health insurance; (6) Poverty - percent in poverty all ages. The items (2), (3), (5) are collected and processed with multiple time periods: 1994-1998, 1999-2003; average values of 1994-2003, respectively.

4.1. Refine resolution to identify spatial-temporal patterns

As shown in the initial overview (Figure 5), the GeoMap displays the spatial patterns of the three clusters - the high-breast cancer-mortality region is located in the north-east (excluding Maine), while the low-cancer-mortality region is in the south (excluding Florida), southwest, and Rocky Mountain states (excluding Montana). The first six axes in the PCPo represent the cancer rate in the six time steps. We can see that the rate increased in the early years, reaching a peak during 1981-1985 (the third axis), then dropped after that. We also notice that while dropping nation wide, the rate seemed to drop more slowly in low-rate regions, as shown by the orange string. It prompts us to ask whether any region experienced an increase during the period, hence we need to view the data at a more refined resolution.

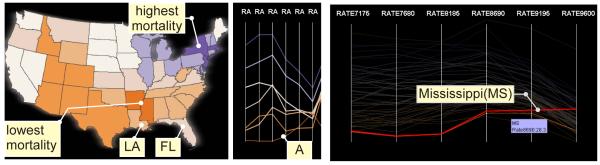
We drag the res-bar until some distinct clusters are found in dr-views (PCPo and GeoMap as shown in Figure 6). In the PCPo, a dark orange string describes a temporal trend different than other strings (Figure 6, A). We select the string (thus the cluster), and see that the cluster contains two data items, as displayed in the PCPd (Figure 6, right). We highlight one data item – Mississippi (MS), which is a temporal outlier that remained relatively constant after a rise in mortality rate, while all other states experienced a drop (shown as semi-transparent background).

Figure 6.

Breast cancer mortality across six time steps is displayed in the PCPo. Resolution is refined to expose a temporal outlier (A) in the PCPo and spatial patterns in the GeoMap. The temporal outlier in the PCPo is selected and displayed as two data items in the PCPd: breast cancer mortality in Mississippi increases after the years 1981-1985.

Meanwhile, the GeoMap displays spatial patterns in a more clear manner: (1) the states with darker blue, which are highlighted by string(s) in the PCPo as the highest mortality rate region, are: DC, NJ, NY, DE, MA, RI.; (2) Similarly the lowest mortality rate region is: MS, AR; (3) FL and LA are local spatial outliers that have relatively high mortality rates compared to their neighbors. LA and FL differ from their neighbors on a potential risk factor - high obesity (we do not demonstrate it here with limited paper space). There are some evidences that breast cancer mortality has some connection with obesity (Morimoto LM et al., 2002).

4.2. Refine resolution to identify multivariate patterns

Multivariate relationships can be easily identified via resolution control and multi-threads investigation: an appropriate resolution is set to expose salient patterns in dr-views; multiple investigations are carried concurrently in detail views. For example, an analyst can quickly identify potential multivariate relationships from the dr-view (PCPo) at a coarse resolution, where only three clusters are displayed (Figure 5). Positive relationships between the cancer rate and risk factor variables are suggested for those axes that have colored strings in a blue-gray-orange order from top to bottom (Figure 5, D), as explained in the section 3.3. Negative relationships are also suggested for those variables with an orange-gray-blue order (Figure 5, E). To investigate these variables in detail, we adjust dr-views to a finer resolution so that the entire dataset is abstracted into eight clusters, which are displayed in the PCPo as shown in Figure 7.

To investigate and compare these variables, we initiate four scanboxes (Figure 7 top A, B, C, D) in the PCPo, each of which is associated with a PCPd (Figure 7, bottom). The scanboxes allow the analyst to focus only on the variables contained in the scanboxes. We can see the orders of PCP strings across the selected variables – either orange-gray-blue or blue-gray-orange order – remains standing in both PCPo and PCPd. The strings’ order suggests some correlated relationships between the variables and cancer rate. Here we list some variables and their relationship with cancer rate: (1) positive correlation with Mam, PopSqmi, Smoking rate; (2) negative correlation with Noin (percentage of population with no health plan) and Poverty. Hypotheses can be generated based on these correlated relationships. For example, with correlation between breast cancer mortality and Mam, a hypothesis can be generated that more people living in a high mortality area had mammogram screen than those living in a low mortality area. The association of the cancer with smoking rate and population density (PopSqmi) will be discussed in the next section.

4.3. Refine resolution to analyze multivariate patterns

A controversial question about breast cancer risk factors is whether any link exists between smoking and breast cancer mortality; or put in another way, does smoking increase the risk of breast cancer mortality (NCI, 2006). The tools presented here are not designed to answer this (or similar) question(s) comprehensively. However, the overall approach, methods, and tools introduced can support efforts to explore the complex multivariate relationships that underlie this question. To illustrate, we analyze the covariate relationship between breast cancer mortality and female smoking rate (precisely, the percent of females over 18 who ever smoked cigarettes).

Following from the previous analysis that suggests a positive correlation between the cancer mortality and smoking rate, we adjust the dr-views to a finer resolution, abstracting the entire dataset into nine clusters. Consequentially, two “unusual” clusters, A and B in Figure 8 (II), are exposed. The other seven of the nine clusters are displayed a blue-gray-orange order along the four axes, suggesting the positive relationship (as shown in Figure 8 (I)). Clusters A and B are displayed in a manner that does not follow the blue-gray-orange order, suggesting a non-positive relationship between the two variables for the data items contained in the two clusters. Next we further investigate the association of the cancer mortality with smoking rate and other variable(s) by comparing an “unusual” cluster with the one of the seven “usual” clusters.

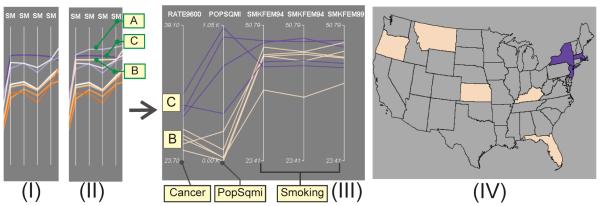
Figure 8.

Investigate association of breast cancer mortality with smoking rate and PopSqmi, from the dr-views (PCPo) to the detail view (PCPd). As shown in (II), the nine clusters are displayed in the PCPo (dr-view) as nine strings across the four axes; each axis represents a time step of the smoking rate. The plot (I) displays seven clusters, with A and B in (II) filtered out. The PCPd displays the states in cluster B and C, showing an obvious association of the cancer mortality with PopSqmi, but not with the smoking rates, as shown in (III). The states in cluster B and C are shown geographically in (IV), in light orange and blue respectively.

Because the cluster B (light orange) has similar smoking rates as in cluster C (blue), we compare the two by selecting them in the PCPo; the states that belong to the clusters are displayed in the PCPd (Figure 8 (III)). Although they vary slightly in the smoking rate values, the states in the blue cluster (cluster C) have higher values than those in the light-orange cluster on both cancer mortality variables as well on the population density (PopSqmi). This suggests that breast cancer mortality is as strongly associated with population density as with smoking rates in the selected regions (Figure 8 (IV)). A possible explanation for this association is that population density may be a surrogate for other covariates; e.g., population density may correlate with characteristics of the environment (e.g., pollutants or other toxins that are more prevalent in urban areas) or with biological factors such as psychological stress, either of which may correlate with breast cancer mortality. While investigating such relationships is well beyond the scope of our current research, some research have reported that women living in urban areas are more likely to develop breast cancer than those who live in rural areas (Millikan, 2004, Byrne, Fletcher).

5. Discussion

We have demonstrated the ways that multi-resolution visualization can facilitate spatial, multi-variate analysis. Although applicable for correlation and multi-variate analyses, fixed-resolution visualization methods and traditional statistics, including spatial statistics (e.g. geographic weighted regression (Fotheringham et al., 2000)), are limited in analyzing spatial data with multiple resolutions because of the modifiable area unit problem. The resolution control mechanism presented here provides a complementary way for analysis and interpretation of correlation and multivariate association in a multi-resolution environment. The proposed approach for analysis of geospatial, multivariate data with resolution control offers two major advantages. First, it guides analysts systematically to navigate through the data gradually at appropriate levels of resolution, increasing the chance of identifying useful patterns. Second, it allows multi-threaded investigation of data in detail views, within the context of overviews at various levels of resolution, enhancing interpretation and understanding of the found patterns. The current limitation of the research is that the tools do not yet scale to large datasets (i.e. U.S. county level data). However, we believe the approach introduced here offers a promising direction and we are currently addressing the scalability issue.

Our research is informed by the previous task analysis and testing research that we (and our colleagues) have done with expert users, as reported in (Robinson et al., 2005, Robinson, 2007, Bhowmick et al., in process). The case study analysis reported here provides an initial proof-of-concept for the ideas. In future research, we plan to make the VIT available through the GeoEXplication (G-EX) Portal now under development. The G-EX Portal is an environment that (among several other features) will allow distributed users to learn how to use geovisual analytics methods and tools, share experiences in using these tools, provide feedback on the tools, and collaborate on research that makes use of the tools. We will use this environment to collect user data as part of our overall human-centered design process that the covers a suite of tools that the VIT is part of.