A Mathematical and Computational Approach for Integrating the Major Sources of Cell Population Heterogeneity

Abstract

Several approaches have been used in the past to model heterogeneity in bacterial cell populations, with each approach focusing on different source(s) of heterogeneity. However, a holistic approach that integrates all the major sources into a comprehensive framework applicable to cell populations is still lacking.

In this work we present the mathematical formulation of a cell population master equation (CPME) that describes cell population dynamics and takes into account the major sources of heterogeneity, namely stochasticity in reaction, DNA-duplication, and division, as well as the random partitioning of species contents into the two daughter cells. The formulation also takes into account cell growth and respects the discrete nature of the molecular contents and cell numbers. We further develop a Monte Carlo algorithm for the simulation of the stochastic processes considered here. To benchmark our new framework, we first use it to quantify the effect of each source of heterogeneity on the intrinsic and the extrinsic phenotypic variability for the well-known two-promoter system used experimentally by Elowitz et al. (2002). We finally apply our framework to a more complicated system and demonstrate how the interplay between noisy gene expression and growth inhibition due to protein accumulation at the single cell level can result in complex behavior at the cell population level.

The generality of our framework makes it suitable for studying a vast array of artificial and natural genetic networks. Using our Monte Carlo algorithm, cell population distributions can be predicted for the genetic architecture of interest, thereby quantifying the effect of stochasticity in intracellular reactions or the variability in the rate of physiological processes such as growth and division. Such in silico experiments can give insight into the behavior of cell populations and reveal the major sources contributing to cell population heterogeneity.

INTRODUCTION

Virtually every population of living organisms exhibits heterogeneity, a characteristic that endows even the simplest forms of life, bacteria, with the ability to exhibit surprisingly complex behavior at the population level. Until the previous decade, however, the biological paradigms and modeling frameworks for the design and control of biochemical processes did not consider population heterogeneity (Chung & Stephanopoulos, 1995; Fedoroff & Fontana, 2002). Their key assumption was that all cells behave like the average cell and, thus, continuum models of ordinary differential equations can describe the behavior of the population (Avery, 2006; Davidson & Surette, 2008). Even when one is interested only in the average dynamics of a population, however, the use of such continuum models may result in incorrect predictions (McAdams & Arkin, 1998). Thus, one must explicitly account for the heterogeneous nature of cell populations if one wants to accurately predict their productivity and to optimally design and/or control the associated biochemical process (Mantzaris, 2005).

A second important reason for studying non-genetic heterogeneity is its physiological importance for the survival of cell populations. Several studies have suggested that the viability of a cell population and its ability to efficiently adapt to sudden changes in environmental conditions may be linked to its phenotypic heterogeneity (McAdams & Arkin, 1999; McAdams et al., 2004; Sumner & Avery, 2002; Veening et al., 2008a; Veening et al., 2008b). Thus, the resistance of certain infectious bacteria to antibiotics could be explained on the basis of the existence of a small subpopulation that survives the shock and resumes growing after the antibiotic has been removed (Booth, 2002). Even when environmental changes do not pose a threat for the viability of the cell population, it has been demonstrated theoretically that a heterogeneous cell population can achieve faster growth rates than those of a homogeneous one (Thattai & van Oudenaarden, 2004).

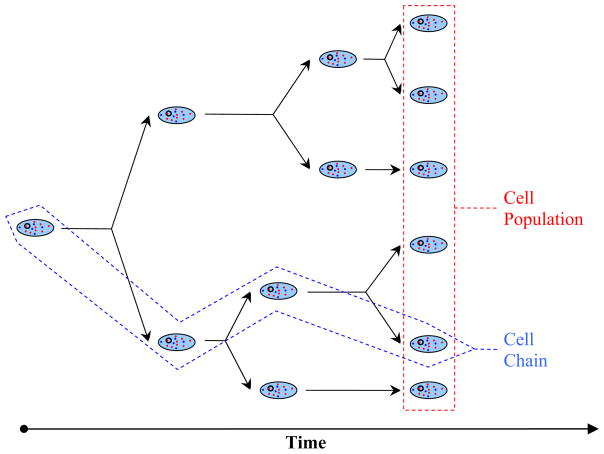
From the above discussion it emerges that a mathematical description of heterogeneous cell population dynamics is of great interest to several disciplines, ranging from chemical engineering to microbial ecology. Before we present an overview of the main frameworks developed for this purpose, we will define what we will refer to subsequently as “cell chain” and “cell population”. A cell chain is a collection defined by the following procedure: start from one mother cell; upon division choose one of its daughter cells; set this daughter to be the next mother cell; repeat (Figure 1). When tracking a cell chain in time, we essentially monitor the history of a single cell. On the other hand, a cell population consists of all the viable offspring observed at time t, which were generated by an arbitrary number of cells at t = 0. For simplicity, Figure 1 shows a population was generated from a single cell. However, our definition is more general.

Figure 1.

Cell chain versus cell population.

In order to predict the behavior of heterogeneous cell populations, Fredrickson and coworkers introduced the cell population balance (CPB) approach in the 1960’s (Eakman et al., 1966; Fredrickson et al., 1967; Tsuchiya et al., 1966). These models consist of partial integro-differential equations that describe the dynamics of the distribution of the physiological state of cells and are nonlinearly coupled with ordinary integro-differential equations describing substrate availability. The physiological state is generally a vector, whose components can include the intracellular contents of chemical species as well as morphometric characteristics of the cell (like size). CPB models require single cell information to predict the distribution of phenotypic characteristics at the population level. Specifically, they require knowledge of three intrinsic physiological functions that provide the growth rate, the division rate and the partition probability density function. For CPB models, therefore, heterogeneity is a consequence of the physiological functions that account for the different growth and division rates of the cells, as well as for unequal partitioning effects.

When the physiological state vector has two or more components, this approach leads to multidimensional CPB models that are very difficult to solve, even with the current computational power available. Therefore, Monte Carlo algorithms were developed to simulate realizations of the underlying processes and compute phenotypic distributions, numbers of cells or any other desirable characteristic of the cell population. Shah et al. (1976) developed such an algorithm to simulate mass distribution dynamics and Hatzis et al. (1995) extended it to simulate the multi-staged growth of phagotrophic protozoa. These algorithms are again computationally intensive because the number of cells in the population increases exponentially with time. Constant-number Monte Carlo algorithms (Mantzaris, 2006; Smith & Matsoukas, 1998) overcome this problem by simulating a constant number of cells that are assumed to be a representative sample of the overall population. These algorithms may start with a single cell and simulate the dynamics of the population until the number of offspring reaches the maximum number allowed.

All these CPB models, however, are deterministic since they assume that the underlying single cell dynamics are deterministic and provide the expected number density function of the cell population. Thus, CPB models cannot account for the inherent stochasticity of chemical reactions occurring in cellular control volumes or stochastic DNA-duplication. In addition, they neglect the fact that cell populations consist of discrete individual cells (Ramkrishna, 2000). Consequently, CPB models cannot account for stochastic effects originating from low cell numbers in the population. Such effects are significant during the initial times of population growth. Thus, one needs different approaches such as Monte Carlo algorithms (Mantzaris, 2006; Smith & Matsoukas, 1998) to successfully simulate them.

Shuler and coworkers used a conceptually different approach to describe the dynamics of cell populations (Ataai & Shuler, 1985; Domach & Shuler, 1984; Henson, 2003). They developed ensemble models that start with a number of individual cells, randomly perturb the intracellular parameters (or the initial conditions) of these cells to create an ensemble and use a single cell model to simulate the dynamical behavior of each cell in this ensemble. Thus, one can obtain distributions over the ensemble for any variable of the single cell model. Ensemble models have certain advantages. They are simpler than CPBs to formulate and do not require knowledge of the intrinsic physiological functions. Also, they can directly incorporate any single cell model and can solve problems involving many species. The disadvantages of the ensemble models include the prohibitively slow dynamic simulation for large ensembles, coupled with the fact that the accuracy with which we can determine the population distribution(s) depends on the ensemble size. Finally, ensemble models (like the CPB models) neglect the discrete nature of the intracellular content and do not take into account stochasticity of reaction phenomena.

The idea that intracellular reactions are stochastic processes was introduced in the early 20^th century with the advent of the chemical master equation (Gillespie, 1976; McQuarrie, 1967). Some of the early studies examined the effect of stochasticity in biochemical processes such as protein synthesis (Rigney & Schieve, 1977; Singh, 1969). Berg (1978) demonstrated the effect of stochasticity in partitioning events under the assumption of binomial partitioning (that is, each protein molecule has equal probability of being inherited by either daughter cell). Ko (1991; 1992) described stochasticity in gene induction using a model whose derivation is based on the random timings of bindings and dissociations of a transcription factor.

More recently, McAdams and Arkin employed an approach that takes into account stochastic effects in the entire biochemical pathway (gene induction and protein synthesis), but not in cell division events (McAdams & Arkin, 1997). Their approach was based on Gillespie’s Monte Carlo algorithm (Gillespie, 1976; 1977) which can be used to simulate exact sample paths of the chemical master equation. McAdams and Arkin (1997) used this algorithm to simulate the stochastic dynamics of intracellular processes, thereby showing that randomness can result in phenotypic variability within a cell population.

Gillespie’s algorithm was originally developed for constant control volumes. Gardiner (1983) generalized it by showing how to modify the propensity functions so that the algorithm can be used when the volume changes with time. Gibson and Bruck (2000) developed an exact efficient version of the algorithm that was further extended by Swain et al. (2002) to account for cell growth and division. This latter algorithm accounts for linear single cell growth, division after fixed time T into two cells of equal sizes, binomial partitioning of the contents to the two daughters and DNA-duplication at time arbitrarily set to 0.4·T. Only one daughter is followed after division, thereby simulating a cell chain (see Figure 1). Using this algorithm, Swain et al. (2002) demonstrated that the total noise of a genetic network can be decomposed into an intrinsic and an extrinsic component which have orthogonal contributions to the total noise. Extrinsic noise stems from noisy “inputs” to the genetic network such as a repressor concentration or the cell cycle state. Intrinsic noise stems from the randomness in the occurrence of the reactions that form the network. To test the orthogonality hypothesis experimentally, they suggested the two-reporter method used in a subsequent experimental work (Elowitz et al., 2002). Exponential cell growth and symmetric division was also incorporated to the Gillespie algorithm by Lu et al. (2004) who used the resulting algorithm in conjunction with hybrid simulation techniques to analyze the behavior of an unregulated gene system.

The algorithms proposed by Lu et al. (2004) and Swain et al. (2002) do not take into account variability in DNA-duplication or division times, but assume that the mother cell produces two daughters with the same volume. Furthermore, the hybrid simulation techniques used by the algorithm by Lu et al. (2004) are valid only for the limiting case of small and fast noise which requires high species copy numbers. Finally, both algorithms simulate single cells (cell chains) instead of cell populations.

Gillespie’s algorithm is computationally intensive when the species under consideration have high copy numbers. In this case, the algorithm spends most of the computational time sampling between fast events, whereas rare events are hardly ever simulated, a problem referred to as stiffness. A remedy for this problem is provided by the tau-leaping algorithms (Gillespie, 2001; Gillespie, 2003) that collectively sample fast events over a time interval by employing Poisson random variables. While these algorithms can result in huge savings in computational time, they fail if the number of reacting molecules is small. Since the Poisson distribution, is unbounded, a tau-leaping algorithm always runs the risk of predicting negative concentrations. More sophisticated tau-leaping algorithms have been developed to avoid this situation (Cao et al., 2005b), as well as algorithms that utilize the binomial distribution which is bounded (Chatterjee et al., 2005; Tian & Burrage, 2004). A different class of algorithms that accelerate stochastic simulation of reacting systems is based on the projection of fast dynamics onto slow ones, according to a procedure generally known as adiabatic approximation of fast modes (Cao et al., 2005a; Cao et al., 2005c; E et al., 2005; E et al., 2007). These algorithms employ a quasi-equilibrium approximation for the distribution of fast evolving variables, and subsequently simulate a master equation for the slow variables. In the latter equation, the propensities appear as averages over the distribution of the fast variables. For an excellent review of acceleration strategies in simulating the chemical master equation the reader is referred to Gillespie (2007).

In another approach to overcome the problem of stiffness, several studies modeled stochasticity in intracellular reactions, using stochastic differential equations (SDEs). We will refer to the use of SDEs as the Langevin approach following van Kampen (van Kampen, 1992). The resulting chemical Langevin equation treats the species concentrations as continuous random process of diffusive type (Gillespie, 2000; Kurtz, 1972; van Kampen, 1992). For, example, Kepler and Elston (2001) derived elegant approximations to exact stochastic models describing gene-regulatory networks. In these approximate models, noise captures the inherent stochasticity of the network in the limit of small noise amplitudes and fast fluctuations. Using these approximations, Kepler and Elston (2001) showed that qualitative changes in the probability density functions obtained by such networks can result solely from changes in the rate of operator fluctuations. Following a more phenomenological approach, other models impose noise as an ad hoc external noise source (Hasty et al., 2001; 2000) Such an approach has been used by Hasty et al. (2000) to build a model for the λ-bacteriophage genetic network showing how random fluctuations can be used to control the state of a biochemical switch. In this approach, however, stochasticity is somewhat artificial, since it does not stem from the randomness in reaction occurrences or cell division events.

Still, none of the aforementioned algorithms focuses on the cell population level. In an attempt to simulate cell populations exhibiting stochasticity in intracellular reactions and in cell division, Mantzaris (2007) proposed an algorithm that is based on the deterministic analogue (Mantzaris, 2006) but uses SDEs (Langevin approach) instead of deterministic reaction expressions. Using this algorithm, Mantzaris simulated a genetic network with positive feedback and showed that different sources of stochasticity can have a marked effect on the region of the parameter space where the system exhibits bistability (Mantzaris, 2007). However, the Langevin approach neglects the discrete nature of the molecular content of the cells and treats the copy numbers of species as continuous variables. In fact, the Langevin approach is valid for limiting cases of fast stochastic fluctuations with small amplitude since it is derived as an asymptotic approximation for large species copy numbers and fast operator fluctuations (Kepler & Elston, 2001). Thus, the predictive power of the algorithm developed by Mantzaris (2007) may be limited since significant intrinsic noise is brought about by low species copy numbers which result in slow and large stochastic fluctuations. Furthermore, the effects of cell growth, DNA-duplication and the partitioning of molecules as discrete entities are not taken into account by this algorithm.

Finally, Volfson et al. (2006) have developed an approach that combines ideas from the CPB and ensemble modeling frameworks and incorporates intrinsic noise effects in order to describe GFP production in yeast populations. This approach incorporates protein production under continuous cell growth, and asymmetric division effects, and can be used to simulate cell populations. However, several simplifying assumptions are made: the model distinguishes between only two generations of cells (mothers and daughter), assumes that all cells grow with the same rate, and upon division it treats the ratio between mother and daughter cell contents and volumes as fixed quantities, as opposed to random variables used in the CPB approach (see supplemetary text of Volfson et al., 2006). No DNA dynamics are modeled, but intrinsic stochasticity is taken into account using Gillespie’s approach.

The conclusion emerging from the previous discussion is that none of the current mathematical frameworks accounts for all the various sources of cell population heterogeneity, namely growth rate variability, stochasticity in DNA-duplication and cell division, and stochastic reaction occurrences for the genetic network under consideration. Thus, the scope of this work is to develop a general mathematical formulation that can incorporate the major sources of stochasticity at the cell population level (Table 1). Our study begins with some preliminary definitions regarding the state of a single cell and the state of the cell population. We subsequently build the cell population master equation (CPME) that governs the temporal dynamics of the probability of finding the cell population at a specific state and develop a Monte Carlo algorithm that enables us to simulate exact stochastic paths of this master equation. Finally, we apply these tools to analyze extrinsic and intrinsic noise sources on a two promoter system and investigate cell population behavior in an inducible system where protein accumulation slows down single cell growth.

Table 1.

(a): Summary of the sources of heterogeneity taken into account by the major theoretical frameworks pertaining to cell populations
	Intrinsic Noise	Intracellular Parameter Distributions	Growth	DNA Species	DNA Duplication	Stochastic Division	Population Level
Cell Population Balances			✓			✓	✓
Ensemble Methods		✓1	✓				✓
SVNMC Algorithm	✓2					✓	✓
Our Framework	✓	✓3	✓	✓	✓	✓	✓

(b) Comparison of the chemical master equation with the cell population master equation
	Intrinsic Noise	Cell-to-Cell Variability	Growth	DNA Species	DNA Duplication	Stochastic Division	Applicability
Chemical Master Equation	✓	No	✓4	✓	✓4	✓4	Cell Chain
Cell Population Master Equation	✓	Yes	✓	✓	✓	✓	Population

¹Cell-to-cell variability is introduced a-priori with distributions in initial values of intracellular parameters and kinetic constants.

²Intrinsic noise is realized through the Langevin formulation that does not account for the discrete nature of molecular contents.

³Variability of intracellular parameters (i.e. concentrations of regulatory species, such as activators, repressors, polymerases, or inducers) is a consequence of the stochastic nature of our algorithm.

⁴These sources were incorporated in the works of Swain et al. (Swain et al., 2002) and Lu et al. (Lu et al., 2004).

MODEL DEVELOPMENT

Framework

Adopting the formalism of the population balance framework (Ramkrishna, 2000), we assume that each cell can be completely described by a state vector that contains information about the chemical content of the cell and its morphometric characteristics such as length, membrane area or volume. This work will utilize only one morphometric characteristic, the volume. However, additional morphometric characteristics like membrane area or length can be incorporated. Thus, the state vector z of a cell is a vector of size n + 1 with n entries for species copy numbers and 1 entry for the volume. Clearly:

$$\mathbf{z}=(\mathbf{X},\text{V})\in \mathcal{Z}={({\mathbb{N}}_0)}^{\text{n}}\times {\mathbb{R}}_0^{+}$$ (1)

We also need to define a vector w for the state of the overall cell population. This vector will contain one entry for the number ν of individuals in the population and ν × (n + 1) entries that represent the states of each and every cell in that population. Therefore:

$$\mathbf{w}\in {\mathbb{N}}_0\times {\mathcal{Z}}^{{\mathbb{N}}_0}$$ (2)

In order to develop a cell population master equation (CPME) for the evolution of probability in our process we need to first define our ensemble. Since our focus is the cell population, our ensemble is a collection of cell populations. It is thus natural to consider the probability that we randomly sample the ensemble at time t picking a cell population that has ν individuals with individual states z_i, i = 1,…,ν. We denote this probability by J_ν(z₁,…,z_i,…,z_ν;t), the analog of the Janossy density used in the continuous population balances (Ramkrishna, 2000). It is important to note that this density is symmetric since the cells cannot be distinguished in any way other than their state. Thus, the value of J_ν(z₁,…,z_i,…,z_ν) remains unaltered by permutations of the z_i vectors and the normalization condition for J_ν will be (see Section 2 in the Supplemental Material for the derivation):

$$\sum _{\nu \ge 0}\left\{\sum _{{\mathbf{X}}_{\mathbf{1}}}\int \dots \sum _{{\mathbf{X}}_{\mathbf{\nu }}}\int \frac{1}{\nu !}·{\text{J}}_{\mathbf{\nu }}(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}){\text{dV}}_{\nu }\dots {\text{dV}}_1\right\}=1$$ (3)

The probability that the cell population will be extinct at time t is J₀(t). The probability that at time t the population will have ν cells is given as:

$$\text{P}\left[{\text{N}}_{\text{population}}=\nu \right]=\sum _{{\mathbf{X}}_{\mathbf{1}}}\int \dots \sum _{{\mathbf{X}}_{\mathbf{\nu }}}\int \frac{1}{\nu !}·{\text{J}}_{\mathbf{\nu }}(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}){\text{dV}}_{\nu }\dots {\text{dV}}_1$$ (4)

With the above observations in mind we are ready to write the cell population master equation that will describe the evolution of the probability distribution for a population of cells. In order to correctly derive each term, we need to keep in mind that J_ν((X₁,V₁),…,(X_i,V_i),…,(X_ν,V_ν);t) behaves as probability mass function in the species content coordinates but as probability density in the volume coordinates. Thus, the CPME (which is essentially a probability balance) will be written as:

$${\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{i}},{\text{V}}_{\text{i}}),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}+\mathrm{\Delta }\text{t})·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}-{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{i}},{\text{V}}_{\text{i}}),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}=+\sum _{\text{k}=1}^4{\text{ProbIn}}_{\text{k}}-\sum _{\text{k}=1}^4{\text{ProbOut}}_{\text{k}}$$ (5)

where the product:

$$\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}=\mathrm{\Delta }{\text{V}}_1·\mathrm{\Delta }{\text{V}}_2·\dots ·\mathrm{\Delta }{\text{V}}_{\nu }$$

denotes the volume of a small hypercube in the continuous component of the cell population state space, which pertains to the cell volumes. Therefore, the expression, J_n ((X₁,V₁),…, (X_i,V_i),…,(X_ν,V_ν);t) ·ΔV₁ ·ΔV₂ ·… · ΔV_ν gives the probability of having cell 1 with contents X₁ and volume between [V₁,V₁+ΔV₁), cell 2 with contents X₂ and volume between [V₂,V₂+ΔV₂), etc. Note that V₁, V₂, …, V_ν are continuous random variables pertaining to different cells in the population.

We will now derive term by term the probability inflows and outflows. In this process, we will only consider single events occurring at the time interval [t, t+Δt], since the probability of two events happening in this interval is (Δt²).

Chemical Reactions

Chemical reactions can result in the production or degradation of molecules, the synthesis of a new molecule from other molecules that serve as building blocks, or the fission of a molecule to its building blocks. Since our goal is to build a general framework we need to utilize a general formulation that will allow us to incorporate any chemical reaction network in the final CPME.

Let us now define the vector S with the chemical species of interest:

$$\mathbf{S}=\underset{\text{non}-\text{chrom}.\text{DNA}}{\underbrace{\{{\text{S}}_1,{\text{S}}_2,\dots {\text{S}}_{\text{n}}}},\underset{\begin{array}{c}\text{chrom}.\text{DNA}\text{species}1\\ \text{in}\text{its}\text{various}\text{states}\end{array}}{\underbrace{{\text{S}}_{\text{n}+1},{\text{S}}_{\text{n}+2},\dots ,{\text{S}}_{\text{n}+{\text{s}}_1}}},\dots ,\underset{\begin{array}{c}\text{chrom}.\text{DNA}\text{species}\text{d}\\ \text{in}\text{its}\text{various}\text{states}\end{array}}{\underbrace{{\text{S}}_{\text{N}-{\text{s}}_{\text{d}}+1},{\text{S}}_{\text{N}-{\text{s}}_{\text{d}}+2},\dots ,{\text{S}}_{\text{N}}\}}}$$ (6)

The total number of species is:

$$\text{N}=\text{n}+\sum _{\text{i}=1}^{\text{d}}{\text{s}}_{\text{i}}$$ (7)

where n is the number of non-chromosomal DNA species and d the number of chromosomal DNA species. The necessity for discriminating between chromosomal and non-chromosomal species comes from the fact that, upon division, chromosomal DNA species are partitioned equally in the two daughters. However, this is not generally true for the other species. Furthermore, each of the chromosomal DNA species i = 1,…,d may exist in s_i states. For example an operator may exist in three states: the free state O, the repressed state with one repressor molecule bound RO, or the repressed state with two repressor molecules bound R₂O. Thus for this case, s₁ = 3 and (S_n+1, S_n+2, S_n+3) = (O, RO, R₂O).

The chemical species of interest are assumed to interact according to a general chemical reaction network of m reactions with the N participating species S_i:

$${\left\{\sum _{\text{i}=1}^{\text{N}}{\alpha }_{\text{ij}}{\text{S}}_{\text{i}}\stackrel{{\text{k}}_{\text{j}}}{\to }\sum _{\text{i}=1}^{\text{N}}{\beta }_{\text{ij}}{\text{S}}_{\text{i}}\right\}}_{\text{j}=1}^{\text{m}}$$ (8)

where k_j is the deterministic reaction rate constant (intensive quantity). This is essentially the network of biochemical reactions that models the biological system or pathway of interest. In order to be able to assess the effect of reactions on the state of the cell we need to know how the species copy numbers change once a specific reaction event has occurred, and how frequently such reaction events occur.

If X_i denotes the copy number (number of molecules) of species S_i, we can define a vector v_j which expresses the change in the contents X of the cell as reaction j occurs in a cell. This vector is given as:

$${\mathbf{v}}_{\mathbf{j}}={\left\{{\beta }_{\text{ij}}-{\alpha }_{\text{ij}}\right\}}_{\text{i}=1}^{\text{N}}$$ (9)

That is, if the reaction is A + B → C and the species vector is [A B C], then v_j = [−1 −1 1].

To determine how frequently reactions occur, we consider the propensity function for reaction j, a_j(X,V), which is the stochastic analogue of a reaction rate. The propensity function gives the probability density that one event of reaction j will happen in the (t, t + Δt) time interval. Thus, the larger the propensity function of reaction j, the more likely it is that many reaction events of index j (j = 1,…, m) will happen during a time interval. Furthermore, the propensity that any reaction is going to happen is equal to the sum of the propensities (since the reaction occurrence events are mutually exclusive):

$${\text{a}}_{\text{r}}(\mathbf{X},\text{V})=\sum _{\text{j}=1}^{\text{m}}{\text{a}}_{\text{j}}(\mathbf{X},\text{V})$$ (10)

Particular expressions for the propensity functions will be given in a subsequent section since here we are primarily interested in deriving the general cell population master equation.

Now, the inflow of probability to state (ν,(X₁,V₁),…,(X_i,V_i),…,(X_ν, V_ν)) will be a sum of the contributions of each cell ς that exists in state (X_ς−v_j, V_ς) and undergoes one reaction event of index j in the next Δt. Therefore:

$${\text{ProbInfl}}_1=\sum _{\varsigma =1}^{\nu }\sum _{\text{j}=1}^{\text{m}}{\text{a}}_{\text{j}}({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\mathbf{j}},{\text{V}}_{\varsigma })·\mathrm{\Delta }\text{t}·{\text{J}}_{\nu }\left(({\mathbf{X}}_{\mathbf{1}},{\mathbf{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\mathbf{j}},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}\right)·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}$$ (11)

The outflow of probability due to reaction contains contributions from the cells that exist in state (ν, (X₁,V₁),…, (X_i,V_i),…, (X_ν,V_ν)) and undergo any reaction event:

$${\text{ProbOutfl}}_1=\sum _{\varsigma =1}^{\nu }\sum _{\text{j}=1}^{\text{m}}{\text{a}}_{\text{j}}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·\mathrm{\Delta }\text{t}·{\text{J}}_{\nu }\left(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}\right)·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}$$ (12)

DNA-duplication

The chromosomal DNA species are doubled during duplication. We assume that the newly produced chromosomal DNA species i exists in a basal state η_i. For example, in the aforementioned example of the operator existing in the free and the two bounded states, the basal state will be the free state. Then the production of new DNA can be expressed as:

$${\left\{{\left\{{\text{S}}_{{\eta }_{\text{i}}+\text{j}}\to {\text{S}}_{{\eta }_{\text{i}}+\text{j}}+{\text{S}}_{{\eta }_{\text{i}}}\right\}}_{\text{j}=1}^{{\text{s}}_{\text{i}}}\right\}}_{\text{i}=1}^{\text{d}}\text{where}:{\eta }_{\text{i}}=\text{n}+\sum _{\text{j}=1}^{\text{i}-1}{\text{s}}_{\text{j}}+1$$ (13)

Note that η_i, i = 1,…d, gives the index of the species in the S vector (equation 6) that corresponds to the basal state of the i^th DNA species.

To clarify the use of equation (13), we will consider a system involving three operators: O₁, O₂ and O₃. All three operators can be found in the free states just noted, but the first two can also be found in the repressed states O₁R, and O₂R respectively. From equation (6), the species vector becomes S = {S₁, …, S_n | O₁, O₁R, O₂, O₂R, O₃}. For illustration purposes we used a vertical bar to separate the non-DNA species from the DNA ones. In this example, d = 3, s = [2, 2, 1] and equation (13) translates to the following set of DNA duplication reactions:

$$\begin{array}{l}{\text{O}}_1\to {\text{O}}_1+{\text{O}}_1\\ {\text{O}}_1\text{R}\to {\text{O}}_1\text{R}+{\text{O}}_1\\ {\text{O}}_2\to {\text{O}}_2+{\text{O}}_1\\ {\text{O}}_2\text{R}\to {\text{O}}_2\text{R}+{\text{O}}_1\\ {\text{O}}_3\to {\text{O}}_3+{\text{O}}_1\end{array}$$

During a single duplication event, each of the previous reactions occurs as many times as the number of reactant molecules, during a single duplication event. For example, if O₁ = 2, O₂R = 1 and O₃ = 1, and all other contents are zero just before duplication, then the first DNA duplication reaction will occur twice, and the fourth and fifth reactions once. The resulting change in the species copy numbers is given by vector v_s, which has all its elements equal to zero except for those that correspond to each basal state η_i of DNA species i. The latter elements are equal to the number of available DNA species i = 1, …, d in all possible states:

$${\mathbf{v}}_{\mathbf{s}}={\left\{\sum _{\text{i}=1}^{\text{d}}\sum _{\text{j}=1}^{{\text{s}}_{\text{i}}}{\text{X}}_{{\eta }_{\text{i}}+\text{j}-1}·{\delta }_{{\eta }_{\text{i}},\text{k}}\right\}}_{\text{k}=1}^{\text{N}}$$ (14)

For the aforementioned example, equation (14) gives v_s = [0, …, 0 | 2, 0, 1, 0, 1].

Moreover, the DNA-duplication propensity function is a_s (X,V) and expresses the probability that duplication will happen in the next Δt as a function of the cell’s state.

Thus, similarly to the case of the reactions, the probability inflow to state (ν, (X₁,V₁),…, (X_i,V_i),…, (X_ν,V_ν)) will be a sum of the contributions of each cell ς that exists in state (X_ς−v_s,V_ς) and undergoes one duplication event in the next Δt. Therefore:

$${\text{ProbInfl}}_{\text{2}}=\sum _{\varsigma =1}^{\nu }{\text{a}}_{\text{s}}({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\mathbf{s}},{\text{V}}_{\varsigma })·\mathrm{\Delta }\text{t}·{\text{J}}_{\nu }\left(({\mathbf{X}}_{\mathbf{1}},{\mathbf{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\mathbf{s}},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}\right)·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}$$ (15)

The outflow of probability due to reaction contains contributions from the cells that exist in state (ν, (X₁,V₁),…, (X_i,V_i),…, (X_ν,V_ν)) and undergo DNA-duplication:

$${\text{ProbOutfl}}_{\text{2}}=\sum _{\varsigma =1}^{\nu }{\text{a}}_{\text{s}}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·\mathrm{\Delta }\text{t}·{\text{J}}_{\nu }\left(({\mathbf{X}}_{\mathbf{1}},{\mathbf{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}\right)·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}$$ (16)

Growth

The aforementioned reactions are assumed to be taking place in the volume of a cell, V(t), which is obtained by solving a differential equation governing cell growth like (Cooper, 1988):

$$\frac{\text{dV}}{\text{dt}}=\text{g}(\mathbf{X},\text{V})$$ (17)

This formulation assumes that growth is a deterministic process once X and V have been defined. Stochasticity comes from the randomness in the state of the cell. In reality the increase in cell mass and volume is random, due to stochasticity in the uptake and metabolism of nutrients from the extracellular environment. If the extracellular environment is homogeneous and since the overall cell consists of a large number of molecules, however, it is safe to assume that stochasticity in these processes will be neglegible.

For a single cell, equation (17) states that g(X,V)·Δt is the volume change that will occur during the infinitesimal time interval (t, t + Δt) and then the inflow of probability due to growth for any cell is:

$${\text{ProbIn}}_{\text{3}}=\sum _{\varsigma =1}^{\nu }\text{g}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·\mathrm{\Delta }\text{t}·{\text{J}}_{\nu }\left(({\mathbf{X}}_{\mathbf{1}},{\mathbf{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}\right)·\prod _{\begin{array}{l}\text{k}=1\\ \text{k}\ne \varsigma \end{array}}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}$$ (18)

The outflow of probability due to growth will be due to the growth of cells existing in states (X_ς,V_ς + ΔV_ς):

$${\text{ProbOut}}_{\text{3}}=\sum _{\varsigma =1}^{\nu }\text{g}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }+\mathrm{\Delta }{\text{V}}_{\varsigma })·\mathrm{\Delta }\text{t}·{\text{J}}_{\nu }\left(({\mathbf{X}}_{\mathbf{1}},{\mathbf{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }+\mathrm{\Delta }{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t}\right)·\prod _{\begin{array}{l}\text{k}=1\\ \text{k}\ne \varsigma \end{array}}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}$$ (19)

Essentially, the growth rate of each individual cell can be thought as the component of a vector field that is responsible for the transport of the Janossy density in the continuous component of the cell population state space. The probability inflow and outflow terms just noted will give rise to advective derivatives in the cell population master equation.

Division

We further assume that the cell divides with a propensity a_d(X,V) that is a function of the cell’s state. Since the partitioning of the content of the mother cell to the two daughters is random, we need to define the partitioning probability density function h(X_d,V_d | X_m,V_m) that gives the probability of a daughter cell having contents X_d and volume V_d, given that the mother had contents X_m and volume V_m. The contents and the volume of the other daughter will then be X_m − X_d and V_m − V_d respectively. Thus, for the mass and volume to be conserved the following must hold:

$$\text{h}({\mathbf{X}}_{\mathbf{d}},{\text{V}}_{\text{d}}\mid {\mathbf{X}}_{\mathbf{m}},{\text{V}}_{\text{m}})=\text{h}({\mathbf{X}}_{\mathbf{m}}-{\mathbf{X}}_{\mathbf{d}},{\text{V}}_{\text{m}}-{\text{V}}_{\text{d}}\mid {\mathbf{X}}_{\mathbf{m}},{\text{V}}_{\text{m}})$$ (20)

The partitioning probability density function has been introduced in the population balance framework (Ramkrishna, 2000). However, the state variables of that framework were continuous quantities. Clearly, the partitioning density function h can be constructed so that it expresses any partitioning law, such as binomial partitioning for non-chromosomal DNA species and equal partitioning with randomized state for the chromosomal DNA species.

We are now ready to derive the corresponding probability influx and outflux terms for the CPME. Whenever a cell divides it increases the number of cells in the population by one. Thus, the probability inflow to state (ν, (X₁,V₁),…, (X_ν,V_ν)) caused by division will come from cell populations that exist in some state (ν−1, (Y₁,U₁),…, (Y_ν−1,U_ν−1)) at time t. Since one cell divides into two daughters, the contents of two of the cells that exist in (ν, (X₁,V₁),…, (X_ν,V_ν)) at time t + Δt were previously (i.e. at time t) contained in a single cell within (ν−1, (Y₁,U₁),…, (Y_ν−1,U_ν−1)). Thus, consider an ensemble of cell populations that contain ν − 1 cells, exactly one of which exists in state (X_ς + X_θ,V_ς+ V_θ) and is dividing in the next Δt time interval. The fraction of populations that will end up in state (ν, (X₁,V₁),…, (X_ν,V_ν)) is equal to the fraction of those in which the dividing cell will produce daughter 1 in state (X_ς,V_ς) plus the fraction of those with daughter 1 in state (X_θ,V_θ). This can also be thought as the probability of the event that daughter 1 will be in state (X_ς,V_ς) or in state (X_θ, V_θ). Since the two latter events are disjoint, their probabilities are summed. Thus:

$${\text{ProbIn}}_4=\sum _{\varsigma =1}^{\nu -1}\sum _{\theta =\varsigma +1}^{\nu }{\text{a}}_{\text{d}}({\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })·\mathrm{\Delta }\text{t}·[\text{h}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }\mid {\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })·\mathrm{\Delta }{\text{V}}_{\varsigma }·\prod _{\begin{array}{l}\text{k}=1\\ \text{k}\ne \varsigma \end{array}}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}·{\text{J}}_{\nu -1}\left(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,\underset{\text{index}\varsigma }{\underbrace{({\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })}},\dots ,({\mathbf{X}}_{\mathbf{\theta }-\mathbf{1}},{\text{V}}_{\theta -1}),\underset{\text{index}\theta }{\underbrace{({\mathbf{X}}_{\mathbf{\theta }-\mathbf{1}},{\text{V}}_{\theta -1})}},\dots ,\underset{\text{index}\nu -1}{\underbrace{({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu })}};\text{t}\right)+\text{h}({\mathbf{X}}_{\mathbf{\theta }},V_{\theta }\mid {\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })·\mathrm{\Delta }{V}_{\theta }·\prod _{\begin{array}{l}\text{k}=1\\ \text{k}\ne \theta \end{array}}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}·{\text{J}}_{\nu -1}\left(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }-\mathbf{1}}+{\text{V}}_{\varsigma -1}),\underset{\text{index}\varsigma }{\underbrace{({\mathbf{X}}_{\mathbf{\varsigma }+\mathbf{1}}+{\text{V}}_{\varsigma +1})}},\dots ,\underset{\text{index}\theta }{\underbrace{({\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })}},\dots ,\underset{\text{index}\nu -1}{\underbrace{({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu })}};\text{t}\right)]$$ (21)

and due to the already discussed symmetry properties of h and J:

$${\text{ProbIn}}_4=2·\sum _{\varsigma =1}^{\nu -1}\sum _{\theta =\varsigma +1}^{\nu }[{\text{a}}_{\text{d}}({\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })·\mathrm{\Delta }\text{t}·\text{h}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }\mid {\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}·{\text{J}}_{\nu -1}(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta }),\dots ,({\mathbf{X}}_{\mathbf{\theta }-\mathbf{1}},{\text{V}}_{\theta -1}),({\mathbf{X}}_{\mathbf{\theta }+\mathbf{1}},{\text{V}}_{\theta +1}),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})]$$ (22)

The outflow of probability due to division is:

$${\text{ProbOut}}_4=\sum _{\varsigma =1}^{\nu }{\text{a}}_{\text{d}}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·\mathrm{\Delta }\text{t}·{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})·\prod _{\text{k}=1}^{\nu }\mathrm{\Delta }{\text{V}}_{\text{k}}$$ (23)

Overall Cell Population Master Equation

By substituting equations (11, 12, 15, 16, 18, 19, 21, 22) into equation (5), collecting terms, dividing by ${\displaystyle \prod _{\text{k}=1}^{\nu }}\mathrm{\Delta }{\text{V}}_{\text{k}}·\mathrm{\Delta }\text{t}$, and taking the limits as ΔV_k → 0, Δt → 0, we derive the following master equation:

$$\frac{\partial }{\partial \text{t}}{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{i}},{\text{V}}_{\text{i}}),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})=\sum _{\varsigma =1}^{\nu }\sum _{\text{j}=1}^{\text{m}}[{\text{a}}_{\text{j}}({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\mathbf{j}},{\text{V}}_{\varsigma })·{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\mathbf{j}},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})-{\text{a}}_{\text{j}}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})]+\sum _{\varsigma =1}^{\nu }[{\text{a}}_{\text{s}}({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\text{s}},{\text{V}}_{\varsigma })·{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }}-{\mathbf{v}}_{\text{s}},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})-{\text{a}}_{\text{s}}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})]-\sum _{\varsigma =1}^{\nu }\frac{\partial }{\partial {\text{V}}_{\varsigma }}\left[\text{g}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})\right]+2·\sum _{\varsigma =1}^{\nu -1}\sum _{\theta =\varsigma +1}^{\nu }{\text{a}}_{\text{d}}({\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })·\text{h}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }\mid {\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta })·{\text{J}}_{\nu -1}(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }}+{\mathbf{X}}_{\mathbf{\theta }},{\text{V}}_{\varsigma }+{\text{V}}_{\theta }),\dots ,({\mathbf{X}}_{\mathbf{\theta }-\mathbf{1}}{,\text{V}}_{\theta +1}),({\mathbf{X}}_{\mathbf{\theta }+\mathbf{1}}{,\text{V}}_{\theta +1}),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})-\sum _{\varsigma =1}^{\nu }{\text{a}}_{\text{d}}({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma })·{\text{J}}_{\nu }(({\mathbf{X}}_{\mathbf{1}},{\text{V}}_1),\dots ,({\mathbf{X}}_{\mathbf{\varsigma }},{\text{V}}_{\varsigma }),\dots ,({\mathbf{X}}_{\mathbf{\nu }},{\text{V}}_{\nu });\text{t})$$ (24)

Expressions for the Propensity Functions

In the previous section we derived the cell population master equation considering generic expressions for the propensity functions that pertain to transitional events such as reactions and divisions. Here we are going to discuss the specific forms of the propensity functions that will be used for the application of our model at the cell population level.

Chemical Reactions

Consider a reaction network of the form of equations (8) where chemical species interact inside a cellular volume V that is assumed to be well stirred. Following Gillespie (Gillespie, 1976), the propensity function a_j(X,V) of reaction j is a function of the number of molecules X_i of species i and the volume of the “container” that hosts the interacting molecules:

$${\text{a}}_{\text{j}}(\mathbf{X},\text{V})={\text{k}}_{\text{j}}·{\text{N}}_{\text{A}}·\text{V}·\prod _{\text{i}=1}^{\text{N}}\frac{{\alpha }_{\text{ij}}!}{{({\text{N}}_{\text{A}}·\text{V})}^{{\alpha }_{\text{ij}}}}·\left(\begin{array}{c}{\text{X}}_{\text{i}}\\ {\alpha }_{\text{ij}}\end{array}\right)$$ (25)

where N_A is Avogadro’s number.

Growth

Following Cooper (1988), this study will assume exponential cell growth. Other researchers have proposed linear, bilinear or other laws for cell growth during one cell cycle. Irrespectively of the particular growth law used, the model will always be able to reproduce Malthusian growth for the overall cell population. However, we choose the exponential law because it is biologically plausible (Cooper, 1988). Then:

$$\frac{\text{dV}}{\text{dt}}=\text{g}·\text{V}$$ (26)

Thus, given the state of the cell at time t and assuming that this state does not change, the cell volume at times t + τ can be found for every positive t.

$$\text{V}(\text{t}+\tau )=\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),\tau )=\text{V}(\text{t})·{\text{e}}^{\text{g}·\tau }$$ (27)

DNA-duplication

The DNA-duplication propensity function is a_s (X,V) and expresses the probability that duplication will happen in the next Δt depending on the cell’s state. We use a volume dependent expression for the duplication propensity:

$${\text{a}}_{\text{s}}(\mathbf{X},\text{V})={\left(\frac{\text{V}}{{\text{V}}_{\text{s},\text{crit}}}\right)}^{{\text{n}}_{\text{s}}}·{\delta }_{\sum _{\text{j}=\text{n}+1}^{\text{n}+{\text{s}}_1}{\text{X}}_{\text{j}},{\text{U}}_1}$$ (28)

where the Kronecker delta δ is unity when the copy numbers of chromosomal species 1 in any state sum to a nominal pre-duplication copy number U₁. This ensures that duplication is performed only once per cycle, when the chromosomal DNA species have copy number equal to U and the cell volume (size) is close to V_s,crit. Furthermore, n_s modulates the sharpness of the DNA-duplication mechanism: very high values result in duplication occurring precisely when the cell volume reaches the value V_s,crit. Lower values result in DNA duplication occurring randomly when the cell volume is around this critical value.

Division

For the division propensity we use an expression similar to that used for DNA-duplication:

$${\text{a}}_{\text{d}}(\mathbf{X},\text{V})={\left(\frac{\text{V}}{{\text{V}}_{\text{d},\text{crit}}}\right)}^{{\text{n}}_{\text{d}}}·{\delta }_{\sum _{\text{j}=\text{n}+1}^{\text{n}+{\text{s}}_1}{\text{X}}_{\text{j}},2·{\text{U}}_1}$$ (29)

where V_d,crit is a critical volume that need to be approached for the division to occur and n_d modulates the sharpness of the division mechanism. Here we require the copy numbers of chromosomal DNA species to be equal to 2·U. The partitioning of the content of the mother cell to the two daughters is governed by the partitioning probability density function (see equation 20). In order to construct a partitioning probability density function, we assume that volume partitioning is independent of content partitioning and, thus, can factorize the partitioning probability density function into a term for volume partitioning and a term for content partitioning. Following Ramkrishna (2000), the former term is assumed to have the form of a symmetric beta distribution:

$$\beta ({\text{V}}_{\text{d}}\mid {\text{V}}_{\text{m}})=\frac{1}{{\text{V}}_{\text{m}}}·\frac{\mathrm{\Gamma }(2·\text{q})}{{(\mathrm{\Gamma }(\text{q}))}^2}·{\left(\frac{{\text{V}}_{\text{d}}}{{\text{V}}_{\text{m}}}\right)}^{\text{q}-1}·{\left(1-\frac{{\text{V}}_{\text{d}}}{{\text{V}}_{\text{m}}}\right)}^{\text{q}-1}$$ (30)

where q is a parameter controlling the sharpness of the division mechanism. Higher values of q result in equal partitioning events being more probable.

We assume binomial partitioning for all non-chromosomal DNA species. The binomial partitioning of each species is performed independently and the “success probability” is equal to the daughter to mother volume ratio. This choice has the following physical meaning: during division, the mother cell “donates” each of the molecules it contains to one of the daughter cells. For each “donation event,” the probability that one molecule will result in the first daughter cell is V_d1/V_m (that is, the probability of success in each Bernoulli trial). Thus, the probability of the first daughter inheriting X_d,i molecules of species I, given that the mother has X_m,i molecules and the volumes of the daughter and mother are V_d and V_m respectively, is:

$${\text{b}}_{\text{i}}({\text{X}}_{\text{d},\text{i}}\mid {\text{X}}_{\text{m},\text{i}},{\text{V}}_{\text{m}},{\text{V}}_{\text{d}})=\left(\begin{array}{c}{\text{X}}_{\text{m},\text{i}}\\ {\text{X}}_{\text{d},\text{i}}\end{array}\right)·{\left(\frac{{\text{V}}_{\text{d}}}{{\text{V}}_{\text{m}}}\right)}^{{\text{X}}_{\text{d},\text{i}}}·{\left(1-\frac{{\text{V}}_{\text{d}}}{{\text{V}}_{\text{m}}}\right)}^{{\text{X}}_{\text{m},\text{i}}-{\text{X}}_{\text{d},\text{i}}}\text{for}\text{i}=1,\dots ,\text{n}$$ (31)

The chromosomal DNA species require symmetric partitioning (each daughter will inherit equal DNA content) but with randomized state. Let us focus, for example, on the chromosomal DNA species i which may be an operator that may exist in one of the following three states: free (O), bounded with one repressor (RO), bounded with two repressors (R₂O). The copy numbers of that species in the different states are given by vector ${\mathbf{X}}_{\mathbf{m}}^{\mathbf{DNA},\mathbf{i}}$ (subscript m stands for “mother”) defined as:

$${\mathbf{X}}_{\mathbf{m}}^{\mathbf{DNA},\mathbf{i}}={\left\{{\text{X}}_{\text{m},\text{k}}\right\}}_{\text{k}=\text{n}+\sum _{\text{j}=1}^{\text{i}-1}{\text{s}}_{\text{j}}+1}^{\text{n}+\sum _{\text{j}=1}^{\text{i}}{\text{s}}_{\text{j}}}$$ (32)

Also, let us set the copy number of DNA species i in any state for the mother and the daughter as:

$${\text{M}}_{\text{i}}=\sum _{\text{j}=1}^{{\text{s}}_{\text{i}}}{\text{X}}_{\text{m},\text{j}}^{\text{DNA},\text{i}}$$ (33)

$${\text{D}}_{\text{i}}=\sum _{\text{j}=1}^{{\text{s}}_{\text{i}}}{\text{X}}_{\text{d},\text{j}}^{\text{DNA},\text{i}}=\frac{{\text{M}}_{\text{i}}}{2}$$ (34)

Then, if the mother cell has one operator in the bounded state and the other in the free state, the daughter cell may inherit any one of the two operators. In general, let us focus on DNA species i that may exist in s_i states. The probability of the daughter cell inheriting ${\text{X}}_{\text{d},1}^{\text{DNA},\text{i}}$ molecules at state 1 out of the ${\text{X}}_{\text{m},1}^{\text{DNA},\text{i}}$ that the mother has and ${\text{X}}_{\text{d},2}^{\text{DNA},\text{i}}$ out of the ${\text{X}}_{\text{m},2}^{\text{DNA},\text{i}}$ etc., will be the product of the combinations of ${\text{X}}_{\text{m},\text{j}}^{\text{DNA},\text{i}}$ per ${\text{X}}_{\text{d},\text{j}}^{\text{DNA},\text{i}}$ for all states j, divided by the overall combinations of the total molecules of DNA species i in the mother per those in the daughter cell. This resembles the hypergeometric distribution but with a finite population containing more than two types of objects. For the simulation of a sequence of n draws without replacement from such a population see Section 3 of the Supplemental Material.

$${\text{c}}_{\text{i}}\left({\mathbf{X}}_{\mathbf{d}}^{\mathbf{DNA},\mathbf{i}}\mid {\mathbf{X}}_{\mathbf{m}},{\text{V}}_{\text{m}},{\text{V}}_{\text{d}}\right)=\prod _{\text{j}=1}^{{\text{s}}_{\text{i}}}\left(\begin{array}{l}{\text{X}}_{\text{m},\text{j}}^{\text{DNA},\text{i}}\hfill \\ {\text{X}}_{\text{d},\text{j}}^{\text{DNA},\text{i}}\hfill \end{array}\right)·{\left(\begin{array}{l}{\text{M}}_{\text{i}}\hfill \\ {\text{D}}_{\text{i}}\hfill \end{array}\right)}^{-1}\text{for}\text{i}=1,\dots ,\text{d}$$ (35)

Finally assuming that the partitioning occurs independently for every species (namely non-chromosomal DNA and chromosomal in any state), the overall partitioning probability density function h(X_d,V_d | X_m,V_m) will be:

$$\text{h}({\mathbf{X}}_{\mathbf{d}},{\text{V}}_{\text{d}}\mid {\mathbf{X}}_{\mathbf{m}},{\text{V}}_{\text{m}})=\beta ({\text{V}}_{\text{d}}\mid {\text{V}}_{\text{m}})·\prod _{\text{i}=1}^{\text{n}}{\text{b}}_{\text{i}}({\text{X}}_{\text{d},\text{i}}\mid {\mathbf{X}}_{\mathbf{m}},{\text{V}}_{\text{m}},{\text{V}}_{\text{d}})·\prod _{\text{i}=1}^{\text{d}}{\text{c}}_{\text{i}}({\mathbf{X}}_{\mathbf{d}}^{\mathbf{DNA},\mathbf{i}}\mid {\mathbf{X}}_{\mathbf{m}},{\text{V}}_{\text{m}},{\text{V}}_{\text{d}})$$ (36)

Monte Carlo Simulation

Inter-arrival times for reaction events

Our Monte Carlo algorithm must simulate continuous cell growth and the assumed instantaneous events of reaction, DNA-duplication or division. Thus, we need to know the distributions of the inter-arrival times between these instantaneous events. To calculate these distributions, we will use the concept of the interval of quiescence (Shah et al., 1977).

The probability at time t that the next reaction event will occur in the time interval [t+τ, t+τ+dτ] is equal to the following product of probabilities:

$$\text{P(reaction}\text{even}\text{occurs}\text{in}[\text{t}+\tau ,\text{t}+\tau +\text{d}\tau ]\mid \text{no}\text{reaction}\text{occurs}\text{in}[\text{t},\text{t}+\tau ]\text{)}·\text{P(no}\text{reaction}\text{occurs}\text{in}[\text{t},\text{t}+\tau ]\text{)}$$ (37)

Let us first consider the probability that no reaction event occurs, given that the cell exists in state (X,V) at time t. The following notation will be used:

$${\text{p}}_{\text{no}\text{rxn}}(\text{ending}\text{time}\mid \text{initial}\text{time},\{\text{initial}\text{number}\text{of}\text{molecules}\},\{\text{volume}\text{through}\text{time}\text{interval}\})$$ (38)

Note that the initial number of molecules stays constant throughout the time interval in which no reaction occurs. Evidently, the probability that no reaction will happen at time t = 0 is equal to 1 and this information will be used as an initial condition. Furthermore, since a_r(X,V) is the probability density that some reaction is going to happen at the next dτ_r time interval we can write the following probability balance:

$${\text{p}}_{\text{no}\text{rxn}}(\text{t}+{\tau }_{\text{r}}+\text{d}{\tau }_{\text{r}}\mid \text{t},\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}+\text{d}{\tau }_{\text{r}}))={\text{p}}_{\text{no}\text{rxn}}(\text{t}+{\tau }_{\text{r}}\mid \text{t},\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))·(1-{\text{a}}_{\text{r}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))·\text{d}{\tau }_{\text{r}})$$ (39)

subject to:

$${\text{p}}_{\text{no}\text{rxn}}(\text{t}\mid \text{t},\mathbf{X},\text{V}(\text{t}))=1$$

Therefore:

$$\frac{\text{d}}{\text{d}{\tau }_{\text{r}}}\left[ln({\text{p}}_{\text{no}\text{rxn}}(\text{t}+{\tau }_{\text{r}}\mid \text{t},\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}+\text{d}{\tau }_{\text{r}})))\right]=-{\text{a}}_{\text{r}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),\tau ))\Rightarrow {\text{p}}_{\text{no}\text{rxn}}(\text{t}+{\tau }_{\text{r}}\mid \text{t},\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))=exp\left[-\underset{0}{\overset{{\tau }_{\text{r}}}{\int }}{\text{a}}_{\text{r}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }^{\prime }))\text{d}{\tau }^{\prime }\right]$$ (40)

Now, the probability density that any reaction event will happen exactly at time t + τ_r is a_r(X,Φ(X,V(t),τ_r)). Therefore, the probability that the first reaction (of any kind) after time t will happen at time t + τ_r is:

$${\text{p}}_{\text{some}\text{rxn}}(\text{t}+{\tau }_{\text{r}}\mid \text{t},\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))={\text{a}}_{\text{r}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))·exp\left[-\underset{0}{\overset{{\tau }_{\text{r}}}{\int }}{\text{a}}_{\text{r}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }^{\prime }))\text{d}{\tau }^{\prime }\right]$$ (41)

Equation (41) defines the probability density of the inter-arrival times of reaction events. This equation needs the following information: the current state of the cell (X,V(t)), the cellular growth expression Φ that essentially gives the volume throughout the waiting-time interval, and the propensity functions of each reaction. The state of the cell is known at each step of the Monte Carlo algorithm and the cellular growth expression Φ is obtained from equation (27). Thus, one can generate random numbers following density (41) at any stage of the Monte Carlo run.

Note that the probability density (41) is not necessarily normalized to unity. In other words there may be cases where there is a finite probability that no reaction occurs in the future. This probability can be calculated as follows:

$$\underset{{\tau }_{\text{r}}\to \infty }{lim}{\text{p}}_{\text{no}\text{rxn}}(\text{t}+{\tau }_{\text{r}}\mid \text{t},\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))=exp\left[-\underset{{\text{I}}_{\infty }}{\underbrace{\underset{0}{\overset{\infty }{\int }}{\text{a}}_{\text{r}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }^{\prime }))\text{d}{\tau }^{\prime }}}\right]$$ (42)

Therefore, if the integral I_∞ diverges to infinity, it is almost sure that at least one reaction is going to occur in finite time. From the particular functional forms of the propensity functions, and assuming that Φ is monotonically increasing, one can easily deduce that in a network containing 0^th and 1^st order reactions I_∞ diverges to infinity.

Kind of reaction to be simulated

Once the Monte Carlo algorithm has determined that a reaction event is going to occur, a random number must be generated in order to determine which reaction is going to take place. This random number μ follows the probability mass function (Gillespie, 1977; Lu et al., 2004):

$${\text{p}}_{\text{reaction}\text{kind}=\mu }=\frac{{\text{a}}_{\mu }(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))}{{\displaystyle \sum _{\text{k}=1}^{\text{m}}}{\text{a}}_{\text{k}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))}$$ (43)

Thus, given the propensity functions at time t + τ_r the algorithm can generate a random number that represents which reaction event must be simulated.

Inter-arrival times for duplication events

One can repeat the derivation of the probability density of the reaction events’ inter-arrival times but now for the DNA-duplication events. The result is that the probability density of the inter-arrival times between division events is

$${\text{p}}_{\text{DNA}\text{dupl}}(\text{t}+{\tau }_{\text{s}}\mid \text{t},\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{s}}))={\text{a}}_{\text{s}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{s}}))·exp\left[-\underset{0}{\overset{{\tau }_{\text{s}}}{\int }}{\text{a}}_{\text{s}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }^{\prime }))\text{d}{\tau }^{\prime }\right]$$ (44)

The probability density a_s(X,V) has to be chosen carefully, so that the cell divides after some random time that is distributed around some fraction of the E. coli division time (the latter is 25–45 min for E. coli cells). To avoid infinite duplication times (equivalently: no future duplication events) the integral of a_s has to diverge to infinity:

$$\underset{0}{\overset{\infty }{\int }}{\text{a}}_{\text{s}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }^{\prime }))\text{d}{\tau }^{\prime }\to \infty$$ (45)

Inter-arrival time for division events

Similarly to the inter-arrival times for reaction or DNA-duplication events, the inter-arrival times for division events will be given as:

$${\text{p}}_{\text{no}\text{div}}(\text{t}+{\tau }_{\text{d}}\mid \mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{d}}))={\text{a}}_{\text{d}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }_{\text{r}}))·exp\left[\underset{0}{\overset{{\tau }_{\text{d}}}{\int }}{\text{a}}_{\text{d}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }^{\prime }))\text{d}{\tau }^{\prime }\right]$$ (46)

To avoid infinite division times the following must hold:

$$\underset{0}{\overset{\infty }{\int }}{\text{a}}_{\text{d}}(\mathbf{X},\mathrm{\Phi }(\mathbf{X},\text{V}(\text{t}),{\tau }^{\prime }))\text{d}{\tau }^{\prime }\to \infty$$ (47)

Volume ratio of the mother to the daughter cell

Once the Monte Carlo algorithm has determined that a division event is going to occur, a random number needs to be generated in order to determine the volume ratio of mother to daughter cell. This random number ρ ∈ [0,1] must follow a symmetric distribution in the sense that ρ and 1 − ρ must be identically distributed. In accordance to equation (30):

$$\rho \sim \beta (\text{q},\text{q})$$ (48)

Number of non-chromosomal molecules inherited by one daughter cell

For partitioning the non-chromosomal DNA species, the algorithm has to determine for each species how many molecules will be inherited by one daughter. Thus, n random numbers, one for each species, must be generated. In accordance to (31), these numbers will be chosen to follow binomial distributions with probability of success equal to ρ and number of trials equal to the molecular content of the mother cell.

$${\nu }_{\text{i}}\sim b(\rho ,{\omega }_{\text{i}})\text{for}\text{i}=1,\dots ,\text{n}$$ (49)

Number of chromosomal molecules inherited by one daughter cell

For partitioning the chromosomal DNA species, the algorithm will apply equal partitioning on the number of molecules but it will still have to determine the states of the inherited DNA molecules. As shown in Section 3 of the Supplemental Material, for the algorithm to determine how many molecules of chromosomal DNA species i will be inherited in state j, it suffices to generate a random number ${\nu }_{\text{n}+{\displaystyle \sum _{\text{k}=1}^{\text{i}-1}}{\text{s}}_{\text{i}}+\text{j}}$ that will follow a hypergeometric distribution denoted noted as hg (#Total, #Defective, #Draws):

$${\nu }_{\text{n}+\sum _{\gamma =1}^{\text{i}-1}{\text{s}}_{\gamma }+\text{j}}\sim hg\left(\sum _{\text{k}=\text{j}}^{{\text{s}}_{\text{i}}}{\text{X}}_{\text{m},\text{k}}^{\text{DNA},\text{i}},{\text{D}}_{\text{i}}-\sum _{\text{k}=1}^{\text{j}-1}{\nu }_{\text{n}+\sum _{\gamma =1}^{\text{i}-1}{\text{s}}_{\gamma }+\text{k}},{\text{X}}_{\text{m},\text{j}}^{\text{DNA},\text{i}}\right)\text{for}\text{j}=1,\dots ,{\text{s}}_{\text{i}}$$ (50)

Note that for the generation of each random number pertaining to state j the quantities that enter the calculation are always known: they are either mother cell contents or daughter cell contents of states 1,…, j − 1.

Outline of the algorithm

Consider a population that at time t has ν cells, each at state (X_i,V_i) for i = 1,…,ν. We assume that the cells do not interact with each other and, thus, we can compute a DNA-duplication, a division and a reaction inter-arrival time for each one of the cells. For each cell i (i = 1,…,ν), we can compute the inter-arrival times for the occurrence of a reaction, a DNA-duplication or a division event. The event that will take place first will be the one with the shortest inter-arrival time τ. Then, the first event will be simulated. If the event is a division, then both of the newborn cells will be taken into account by increasing the cell population number by one and storing the state of both newborn cells in the population state vector. Of course, one daughter will replace the mother cell. If the event is a reaction or a DNA-duplication, the state of the individual cell in which the reaction happened will be updated. Thus, the new state of the population will reflect the reaction duplication or division event and the inter-arrival times for the occurrences of the reaction or division events will be updated. For additional details on the algorithm (pseudo-code) please refer to Section 1 of the Supplemental Material.

The following important observations will help us optimize the algorithm:

1. The inter-arrival times of one cell are independent of those of all other cells. Thus, suppose that we have a population of ν cells at time t and the algorithm determines that a reaction or duplication event will happen in cell i at time t + τ. Then, the state of cell i will change and we will have to calculate new division and reaction inter-arrival times for cell i. For all the other cells, however, we can merely subtract τ from their inter-arrival times and the resulting inter-arrival times will follow the correct probability distributions for the respective event occurrences (see also Gibson & Bruck, 2000). We can use this strategy because there is no interaction between the cells in the population and, thus, if a reaction happens in cell i the other cells will not be affected. This would not be the case if the cells interacted with each other by an extracellular messenger and the event to be simulated was secretion of one messenger molecule to the extracellular space. In that case, all cells in the population would be affected by this event. Similarly, if a division event happens we will have to generate inter-arrival times for the reaction and division events of the two daughter cells. For all other cells, however, we can merely subtract τ from their inter-arrival times. Furthermore, we can eliminate the need for subtracting τ each time an event occurs by working with absolute rather than relative time since we can then always store the absolute time for the occurrence of the events of interest.

2. Since a duplication event always precedes a division event, we can set the duplication time to infinity immediately after a duplication event and recalculate it after a division event. Similarly, we can set the division times of the two daughters to infinity immediately after their birth and recalculate them after a duplication event.

3. Once we have taken care of the precedence of the duplication to division, the inter-arrival times for division and duplication are only volume dependent and volume evolves deterministically. Thus, we can calculate duplication or division inter-arrival times only once (after a division or a duplication event respectively). We do not have to update them every time a reaction event happens. This would not be the case, however, if the division or duplication propensities were also dependent on the copy numbers of other species in the cell.

4. The above observations enable us to make the minimum possible updates to the vectors containing the absolute times for the occurrences of the events to be simulated. Evidently, after each simulated event we will have to update at most 2· (m+2) absolute times (reaction, division and duplication times for two newborn cells) and to find the minimum between all times. Both tasks can be efficiently accomplished by using heap structures (binary trees). The absolute times for reaction, division and duplication are stored in three different heaps. Sorting in the heap occurs automatically upon update or addition of a new time after simulation of reaction/duplication or division events respectively.

Finally, we note that the number of cells in a population typically increases exponentially with time, thereby making the computational cost of long simulations prohibitive. To overcome this issue, we employed a constant number Monte Carlo scheme, in which a maximum number N_cellsmax of tracked cells (e.g. N_cellsmax = 10000) is retained in the population under consideration. If a division event results in a population size equal to N_cellsmax + 1, then the algorithm removes randomly a single cell from the population to restore the population size to N_cellsmax (Lee & Matsoukas, 2000; Smith & Matsoukas, 1998). Each cell in the population has equal probability of being discarded. This procedure results in a biased estimation of quantities, such as the cell population average. However, the bias becomes negligible as the maximum number of tracked cells (N_cellsmax) increases.

NUMERICAL RESULTS

Extrinsic and Intrinsic Noise in a Two Promoter System

For a first test of our algorithm, we will simulate the population dynamics resulting from a genetic network that consists of two genes under the influence of two identical repressible promoters. Elowitz and coworkers (Elowitz et al., 2002) used such a genetic network to decompose the extrinsic and intrinsic contributions of noise to the overall single cell noise. In particular, two GFP variants, a yellow (YFP) and a cyan (CFP), were cloned in opposite positions from the origin of replication into the E. coli chromosome. Expression of both proteins is driven from identical Lac repressible promoters and the fluorescence intensity of both variants is approximately the same. Thus, measurements of the fluorescence of the cells in the two different channels, yellow and cyan, can give indications of the intrinsic and the extrinsic noise. In particular, difference in the fluorescence of the two channels for the same cell originates from the intrinsic noise, and difference in the fluorescence between distinct cells is a result of the extrinsic noise.

Reaction Network, Growth, Duplication and Division Mechanisms

In order to model this system we consider a set of reactions with the participating species summarized in Table 2. Note that we have two chromosomal DNA species (the two operators) each of which can exist in two states namely O_Yfp, O_YfpLac and O_Cfp, O_CfpLac. Therefore the species vector is:

$$\mathbf{S}=\underset{\text{non}-\text{chrom}.\text{DNA}}{\underbrace{\{\text{RP},\text{RB},\text{Lac},{\text{R}}_{\text{Yfp}},\text{Yfp},{\text{R}}_{\text{Cfp}},\text{Cfp}}},\underset{\begin{array}{c}\text{chrom}.\text{DNA}\text{species}1\\ \text{in}\text{its}\text{various}\text{states}\end{array}}{\underbrace{{\text{O}}_{\text{Yfp}},{\text{O}}_{\text{Yfp}}\text{Lac}}},\underset{\begin{array}{c}\text{chrom}.\text{DNA}\text{species}2\\ \text{in}\text{its}\text{various}\text{states}\end{array}}{\underbrace{{\text{O}}_{\text{Cfp}},{\text{O}}_{\text{Cfp}}\text{Lac}\}}}$$ (51)

Table 2.

Symbols used for the species

Symbol	Species denoted
RP	RNA polymerase
RB	ribosome
Lac	Lac repressor
OYfp	free operator of yfp gene
OYfpLac	Lac repressed operator of yfp gene
RYfp	yfp mRNA
Yfp	Yfp protein molecule
OCfp	free operator of cfp gene
OCfpLac	Lac repressed operator of cfp gene
RCfp	cfp mRNA
Cfp	Cfp protein molecule
Ø	Generic source or sink

The reaction network is summarized in Table 3 together with the propensity functions of the reactions. The expression for the propensity functions are constructed using general formula (25) for each reaction. Equation (26) is used to simulate the cell growth process (exponential growth). The DNA-duplication propensity is taken as in expression (28). At every division event the total operator contents for yfp and cfp are doubled by introducing free operator contents equal to O_yfp,Total and O_cfp,Total. The division propensity is given by equation (29) and the partitioning mechanism is given by equations (30, 31, 35, 36). Table 4 gives the values for all parameters used in our simulations.

Table 3.

Propensity functions for the two promoter model

Reaction	Propensity1, 2, 3, 4	Description
(i) $Ø\stackrel{{\text{k}}_1}{\to }\text{RP}$	k1·VEcoli·NA	RNA polymerase production
(ii) $Ø\stackrel{{\text{k}}_2}{\to }\text{RB}$	k2·VEcoli·NA	Ribosome production
(iii) $Ø\stackrel{{\text{k}}_3}{\to }\text{Lac}$	k3·VEcoli·NA	Lac repressor production
(iv) ${\text{O}}_{\mathit{yfp}}+\text{Lac}\stackrel{{\text{k}}_4}{\to }{\text{O}}_{\mathit{yfp}}\text{Lac}$	$\frac{{\text{k}}_4}{{\text{V}}_{E.\mathit{coli}}·{\text{N}}_{\text{A}}}·{\text{O}}_{\mathit{yfp}}·\text{Lac}$	Repression of yfp gene
(v) ${\text{O}}_{\mathit{yfp}}\text{Lac}\stackrel{{\text{k}}_{-4}}{\to }{\text{O}}_{\mathit{yfp}}+\text{Lac}$	k−4·OYFPLac	Derepression of yfp gene
(vi) ${\text{O}}_{\mathit{yfp}}+\text{RP}\stackrel{{\text{k}}_{\text{5}}}{\to }{\text{O}}_{\mathit{yfp}}+\text{RP}+{\text{R}}_{\mathit{yfp}}$	$\frac{{\text{k}}_5}{{\text{V}}_{E.\mathit{coli}}·{\text{N}}_{\text{A}}}·{\text{O}}_{\mathit{yfp}}·\text{RP}$	yfp m-RNA production
(vii) ${\text{R}}_{\mathit{yfp}}+\text{RB}\stackrel{{\text{k}}_{\text{6}}}{\to }{\text{R}}_{\mathit{yfp}}+\text{RB}+\text{Yfp}$	$\frac{{\text{k}}_6}{{\text{V}}_{E.\mathit{coli}}·{\text{N}}_{\text{A}}}·{\text{R}}_{\mathit{yfp}}·\text{RB}$	Yfp protein production
(viii) ${\text{O}}_{\mathit{cfp}}+\text{Lac}\stackrel{{\text{k}}_7}{\to }{\text{O}}_{\mathit{cfp}}\text{Lac}$	$\frac{{\text{k}}_7}{{\text{V}}_{E.\mathit{coli}}·{\text{N}}_{\text{A}}}·{\text{O}}_{\mathit{cfp}}·\text{Lac}$	Repression of cfp gene
(xi) ${\text{O}}_{\mathit{cfp}}\text{Lac}\stackrel{{\text{k}}_{-7}}{\to }{\text{O}}_{\mathit{cfp}}+\text{Lac}$	k−7·OcfpLac	Derepression of cfp gene
(x) ${\text{O}}_{\mathit{cfp}}+\text{RP}\stackrel{{\text{k}}_{\text{8}}}{\to }{\text{O}}_{\mathit{cfp}}+\text{RP}+{\text{R}}_{\mathit{cfp}}$	$\frac{{\text{k}}_8}{{\text{V}}_{E.\mathit{coli}}·{\text{N}}_{\text{A}}}·{\text{O}}_{\mathit{cfp}}·\text{RP}$	cfp m-RNA production
(xi) ${\text{R}}_{\mathit{cfp}}+\text{RB}\stackrel{{\text{k}}_{\text{9}}}{\to }{\text{R}}_{\mathit{cfp}}+\text{RB}+\text{Cfp}$	$\frac{{\text{k}}_9}{{\text{V}}_{E.\mathit{coli}}·{\text{N}}_{\text{A}}}·{\text{R}}_{\mathit{cfp}}·\text{RB}$	Cfp protein production
(xii) $\text{RP}\stackrel{{\text{k}}_{10}}{\to }Ø$	k10·RB	RNA polymerase degradation
(xiii) $\text{RB}\stackrel{{\text{k}}_{11}}{\to }Ø$	k11·RP	Ribosome degradation
(xiv) $\text{Lac}\stackrel{{\text{k}}_{12}}{\to }Ø$	k12·Lac	Lac repressor degradation
(xv) ${\text{R}}_{\mathit{yfp}}\stackrel{{\text{k}}_{13}}{\to }Ø$	k13·Ryfp	yfp m-RNA degradation
(xvi) $\text{Yfp}\stackrel{{\text{k}}_{14}}{\to }Ø$	k14·Yfp	Yfp protein degradation
(xvii) ${\text{R}}_{\mathit{cfp}}\stackrel{{\text{k}}_{15}}{\to }Ø$	k15·Rcfp	cfp m-RNA degradation
(xviii) $\text{Cfp}\stackrel{{\text{k}}_{16}}{\to }Ø$	k16·Cfp	Cfp protein degradation

¹Variables without brackets denote number of molecules of the corresponding species.

²All propensity functions have units of min⁻¹

³Propensity functions contain a volume term V_E.coli are functions of time, since V_E.coli changes as the cell grows.

⁴Avogadro’s number: N_A = 6.0221367·10¹⁴ nmol⁻¹.

Table 4.

Parameter values for the two promoter system

Symbol	Units	Value
k1	(nM·min−1)	480
k2	(nM·min−1)	850
k3	(nM·min−1)	0
k4	(nM−1·min−1)	240
k−4	(min−1)	2.4
k5	(nM−1·min−1)	1.2·10−2
k6	(nM−1·min−1)	1.3·10−7
k7	(nM−1·min−1)	240
k−7	(min−1)	2.4
k8	(nM−1·min−1)	1.2·10−2
k9	(nM−1·min−1)	1.3·10−7
k10	(min−1)	0.01
k11	(min−1)	0.01
k12	(min−1)	0.01
k13	(min−1)	0.4
k14	(min−1)	0.01
k15	(min−1)	0.4
k16	(min−1)	0.01
Ocfp,Total	(molec.)	1
Oyfp,Total	(molec.)	1
g	(min−1)	0.02−1
nd	(dim/less)	20
Vd,crit	(L)	1.1·10−15
q	(dim/less)	80
ns	(dim/less)	20
Vs,crit	(L)	0.8·10−15

The system was simulated using several different parameter sets in order to elucidate the effect of each mechanism on the overall, as well as extrinsic and intrinsic noise (heterogeneity) in the cell population. The parameter values for the nominal set appear in Table 4 and when different parameter values are used, it is noted so in the particular Figure caption. For the nominal parameter set, the rate of repressor production k₃ is set equal to zero. Thus, even if repressor molecules exist initially, they will soon degrade leaving the operator eventually unrepressed.

The initial conditions for all simulations were constructed by solving the corresponding deterministic model and converting the concentrations to numbers of molecules. A population consisting of one cell (ν = 1) having those molecular contents is then used as the initial condition. Alternatively, one can also simulate a single cell chain prior to simulating the whole cell population. To obtain a cell chain, we start with a cell and track only one daughter after each successive division event. After sufficient time has passed so that the process has reached time invariance, the state of the cell is recorded. A population consisting of one cell having that recorded state can then be used as initial condition for the simulation of the population.

Nominal Parameter Set

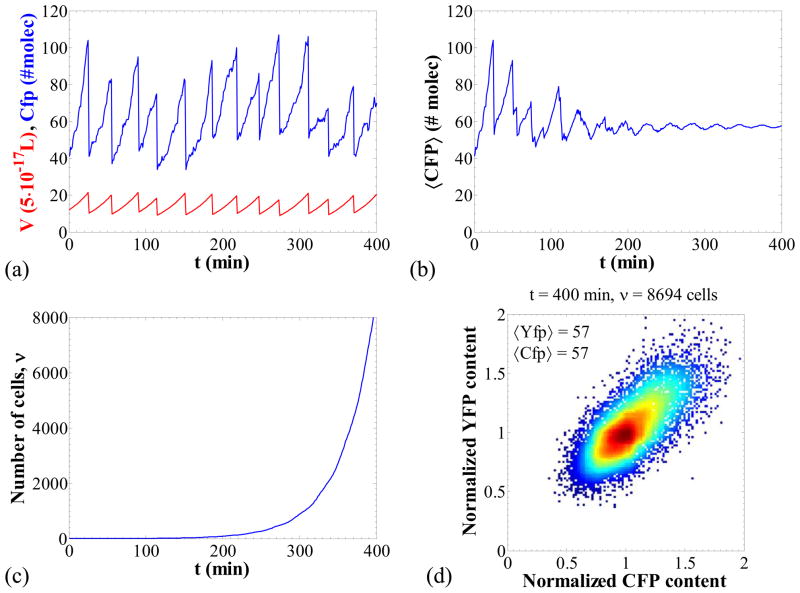
The parameter values for the nominal parameter set (Table 4) were chosen such that the simulation results agree qualitatively with the results in Elowitz et. al (Elowitz et al., 2002). Figure 2 shows a simulation for this parameter set for which all sources of noise that can be captured with our model are present. Panel (a) shows transients for the volume and CFP content. It is apparent that there is considerable stochasticity in both the content time course as well as the division times. Panel (b) portrays the population average CFP content with respect to time and panel (c) the number of individual cells in the population. For low numbers of cells the average content oscillates following the dynamics of the division. As more cells are born, however, their divisions occur in a much less synchronized fashion and the population average tends to a constant value.

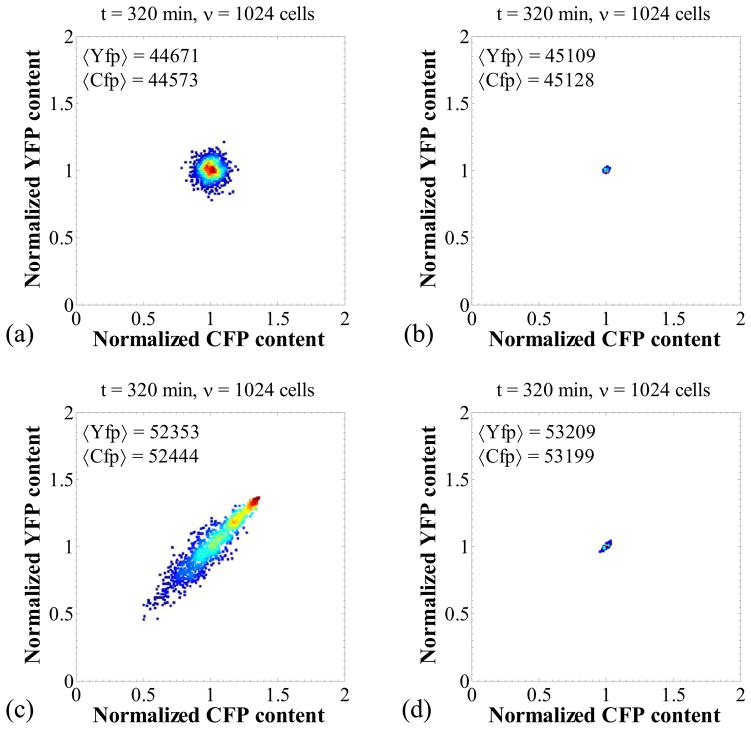
Figure 2.

Panel (a): Transient behavior of the CFP content and the volume for one cell chain out of the cell population. Panel (b): Transient behavior of the average CFP content of the cell population. Panel (c): Number of cells in the population as a function of time. Panel (c): Representative stochastic paths for the molecular content and the volume for the first 25 min (both computed by MC simulation). Panel (d): Normalized YFP content with respect to the normalized CFP content. Each point represents one cell. Color coding corresponds to density of points. Nominal parameter set (Table 4).

Finally, panel (d) shows the normalized YFP content versus the normalized CFP content in a plot similar to that used by Elowitz et al. (2002). Each point in this plot corresponds to one cell of the population. The observed scatter of points indicates the existence of noise which results in cell population heterogeneity. In our case, transcriptional and translational stochasticity is significant due to the low copy numbers of mRNA and protein. These are the intrinsic noise sources and contribute to the spread of points far from the diagonal CFP = YFP. Furthermore, the stochasticity in DNA-duplication and division, as well as the fluctuations in the contents of RNA polymerase and ribosomes, are the extrinsic noise sources and contribute to the elongation of the ellipsoid along the diagonal CFP = YFP.

Homogeneous Populations

In homogeneous populations, all cells have to behave identically which means that (i) the fluctuations of the species copy numbers due to reactions must be infinitesimally small, (ii) duplication and division events must occur in synchrony, (iii) the cells must divide in a way that the two daughter cells have equal volumes and contents. These three conditions will be met when the following are true.

First, the species copy numbers have to be as high as possible. It is known (Schrödinger, 1967) that the standard deviation of the species copy number in a reacting system is of the order of the inverse square root of the total number of interacting molecules. Thus, these fluctuations become negligible as the overall production rates of the interacting species become much larger than their respective degradation rates. Note that manipulating the copy number of the chromosomal operators has no physical significance. When no repression exists, however, the operator is always in the unbound state and thus does not contribute at all to the overall noise.

When reactions and divisions are synchronized, n_d and n_s must tend to infinity in equations (28) and (29). Also, parameter q in equation (30) must tend to infinity in order to have the cells partition into two daughters of the same volume,. Thus, the random number that expresses the ratio of volumes, ρ = V_d/V_m, will almost surely take the value of ½. In this case, and for large copy numbers of molecules in the cell, cell contents will then be partitioned equally between the two daughters. Equal partitioning of the contents is guaranteed by the limiting properties of the binomial distribution: as the number of molecules to be partitioned increases to infinity, the probability in the binomial distribution (31) tends to accumulate to the point ρ · X_m. Thus, each daughter will inherit approximately half of the molecules of the mother cell.

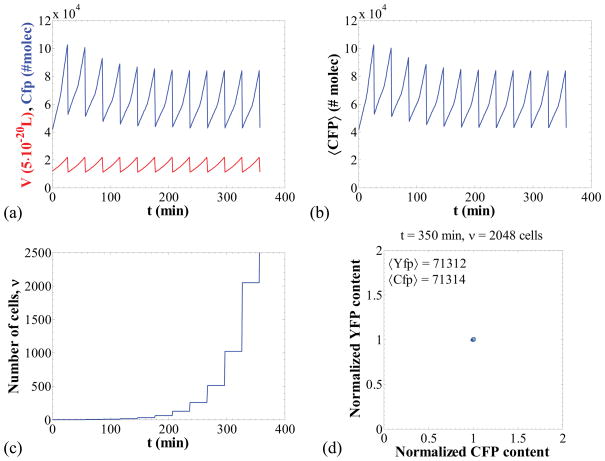
Figure 3 shows a simulation of the case where no heterogeneity is observed. For this case, the single cell time-courses for CFP content and volume appear periodic (Figure 3a), and so does the cell population average since the cells are synchronized (Figure 3b). As a result of this synchrony, the number of cells in the population increases in steps, in each of which the number of cells is doubled (Figure 3c). Finally, since no intrinsic or extrinsic noise is present, the CFP and YFP contents of all cells are identical at all times and, thus, the CFP versus YFP plot shows that all points representing cells are concentrated to a very narrow region of the CFP-YFP plane.

Figure 3.

Negligible intrinsic noise and synchronized DNA duplication and division. Panels (a–d) as in Figure 2 for the following parameter set: k₁ = 4800 nM/min, k₂ = 8500 nM/min, k₅ = 0.12 (nM·min)⁻¹, n_s = n_d = 10000. The requirement q → ∞ was numerically implemented by setting the daughter volumes equal to half the mother volume at every division. All other parameters as in Table 4.

Only Extrinsic or Only Intrinsic Noise

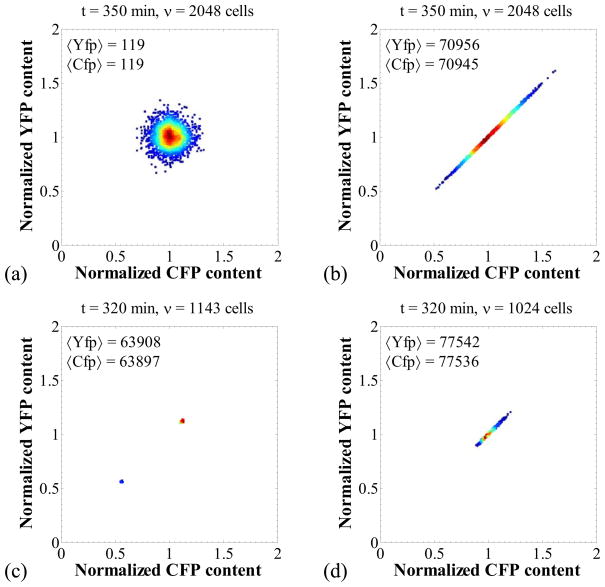
We have so far analyzed the limiting cases where the noise is negligible and where all sources of noise are significant. However, one can construct parameter sets where only extrinsic or only intrinsic noise is present. Thus, Figure 4a shows the CFP versus YFP graph in the case where only intrinsic noise is present. Stochasticity in the biomolecular reactions is significant, but DNA duplication and symmetric division events occur in synchrony. In this case, the points that represent cells form a circular pattern, showing that the variability in the Cfp and Yfp content of a single cell is equal to the variability of Cfp (or Yfp) content between different cells of the cell population.

Figure 4.

Isolation of intrinsic and extrinsic noise sources. Panels (a): intrinsic transcriptional noise only. Parameters as in Figure 3 but with k₅ = 2·10⁻⁴ (nM·min)⁻¹. Panel (b): extrinsic noise arising only from fluctuations in the RNA polymerase. Parameters as in Figure 3 but with k₁ = 1.2 nM/min, k₅ = 480 (nM·min)⁻¹. Panel (c): extrinsic noise arising from stochasticity in division as the only source. Parameters as in Figure 3 but with n_d = 20. Panel (d): extrinsic noise arising from stochasticity in division as the only source. Parameters as in Figure 3d but with n_s = 20.

On the other hand, Figure 4b pertains to a case where only extrinsic noise is present. The latter is brought about only by fluctuations in the RNA polymerase. Division is still symmetric in this case, and the duplication and division events are synchronized. Moreover, extrinsic noise is negligible because the transcriptional rates of cfp and yfp are high, thereby keeping mRNA and protein contents high. In this case, the points in the CFP and YFP graph are arranged along the line CFP = YFP. This indicates that the CFP and YFP contents are identical in any cell, but there exists variability between different cells of the cell population.

Furthermore, in order to isolate the effect of stochastic division we simulated a case that involves only this noise source (Figure 4c). In this case, the cell division events occur asynchronously, and thus, the cell population splits into two subpopulations, the mother cells and the daughter cells, that appear as two dots in the scatter plot because no other source of noise is present. Note that since division is still symmetric, the protein contents of the former are twice those of the latter (normalized contents of 1.12 and 0.56 respectively).

Similarly, the effect of stochastic DNA duplication was isolated as shown in Figure 4c. For this simulation, DNA duplication events are not synchronized between the cells, thereby creating heterogeneity in the rates of protein expression. This randomness manifests as an extrinsic noise source and results in a spread of the points along the line CFP = YFP.

Effect of Repression

In order to elucidate the effect of repression on the extrinsic and intrinsic noise, we first consider a parameter set that results in high numbers of molecules for all the species except the operators. Figure 5a shows that, for this parameter set, significant intrinsic noise is observed due to the uncorrelated fluctuations of the states of the cfp and yfp operators. If we consider a parameter set for which all species copy numbers are high, on the other hand, the noise becomes negligible as shown in Figure 5b. Note that the total copy number for each of the two operators is 1,000.

Figure 5.

Effect of repression in the apparent intrinsic and extrinsic noise. Panel (a): intrinsic apparent noise for single operators and high molecule numbers for other species. Parameter values as in Figure 3 but with k₃ = 2000 nM/min, k₄ = 2.4·10⁻⁵ (nM·min)⁻¹. Panel (b): negligible noise for multiple operators. Parameter values as in panel (a) with k₅ = 0.12·10⁻³ (nM·min)⁻¹, O_cfp,Total = O_cfp,Total = 1000. Panel (c): extrinsic and intrinsic apparent noise for low repressor copy numbers and single operator. Parameter values as in panel (a) with k₃ = 8.1·10⁻² nM/min, k₄ = 7.2·10⁻¹ (nM·min)⁻1. Panel (d): negligible noise for multiple operators even for low repressor numbers. Parameter values as in panel (b) with k₃ = 35 nM/min, k₅ = 0.12·10⁻³ (nM·min)⁻¹, O_cfp,Total = O_cfp,Total = 1000.

The two simulations just discussed pertain to cases where the repressor copy numbers are high. This is why no extrinsic noise was observed. If the repressor copy numbers are low, however, fluctuations in the state of the repressor create variability among the cells of the population (extrinsic noise), which is manifested as an ellipsoidal deformation of the cloud of points along the line CFP = YFP (Figure 5c). For the simulation of Figure 5c, only one operator for each protein exists. When the operator copy numbers are high (Figure 5d where O_yfp,Total = O_cfp,Total = 1000), then both intrinsic and extrinsic noise become negligible. One might have expected that only intrinsic noise would be eliminated. Since the repressor fluctuates in low copy numbers, however, the additional operators it can repress are a tiny fraction of the overall operators that exist in this case. Thus, the fluctuations of the number of free operators are low, thereby making extrinsic as well as intrinsic noise negligible.

Emergent complexity in population dynamics of protein expression

In the previous section, we assumed volume dependent growth rate and investigated the effect of extrinsic and intrinsic noise sources in the population behavior. In this section, we will consider a more complicated situation in which noisy protein expression slows down single cell growth. Cell population simulations will elucidate how this deceptively simple negative feedback can lead to emergent complexity in population level dynamics. The reaction network for this system appears in Table 5. The scheme incorporates constitutive repressor production, repression and induction of protein expression as well as leak expression (reaction viii). The inducer is assumed to exist in high concentrations that are also equal in the extracellular and intracellular space. Thus, the concentration of the inducer [I_ex] appears in the propensity of reaction (iii) rather than the number of inducer molecules.

Table 5.

Reaction network for the inducible expression system

Reaction	Propensity	Description
(i) $Ø\stackrel{{\text{k}}_{\text{MR}}}{\to }{\text{M}}_{\text{R}}$	kMR · VE.coli · NA	Repressor m-RNA production
(ii) ${\text{M}}_{\text{R}}\stackrel{{\text{k}}_{\text{R}}}{\to }{\text{M}}_{\text{R}}+\text{R}$	kR · MR	Repressor production
(iii) $\text{R}+2\text{I}\stackrel{{\text{k}}_{\text{i}}}{\to }{\text{I}}_2\text{R}$	ki · [Iex]2 · R	Repressor –inducer association
(iv) ${\text{I}}_2\text{R}\stackrel{{\text{k}}_{-\text{i}}}{\to }\text{R}+2\text{I}$	k−i · I2R	Repressor –inducer dissociation
(v) $\text{R}+\text{O}\stackrel{{\text{k}}_{\text{s}}}{\to }\text{RO}$	ks · R · O	Repressor –operator association
(vi) $\text{RO}\stackrel{{\text{k}}_{-\text{s}}}{\to }\text{R}+\text{O}$	k−s ·RO	Repressor –operator dissociation
(vii) $\text{O}\stackrel{{\text{k}}_{\text{1MP}}}{\to }\text{O}+{\text{M}}_{\text{P}}$	k1MP · O	Protein m-RNA production
(viii) $\text{RO}\stackrel{{\text{k}}_{0\text{MP}}}{\to }\text{RO}+{\text{M}}_{\text{P}}$	k0MP · RO	Leak m-RNA production
(xi) ${\text{M}}_{\text{P}}\stackrel{{\text{k}}_{\text{P}}}{\to }{\text{M}}_{\text{P}}+\text{P}$	kp · Mp	Protein translation
(x) ${\text{M}}_{\text{R}}\stackrel{{\lambda }_{\text{MR}}}{\to }Ø$	λMR · MR	Repressor m-RNA degradation
(xi) $\text{R}\stackrel{{\lambda }_{\text{R}}}{\to }Ø$	λR · R	Repressor degradation
(xii) ${\text{I}}_{\text{2}}\text{R}\stackrel{{\lambda }_{\text{12R}}}{\to }Ø$	λI2R· I2R	Repressor -inducer degradation
(xiii) ${\text{M}}_{\text{P}}\stackrel{{\lambda }_{\text{MP}}}{\to }Ø$	λMP·MP	Protein m-RNA degradation
(xiv) $\text{P}\stackrel{{\lambda }_{\text{P}}}{\to }Ø$	λP· P	Protein degradation

Constitutive protein expression and size dependent growth rate

Let us first simulate the system neglecting repression and assuming growth rate to be only size dependent. For these simulations, no repressor is produced (parameter k_MR is set to zero) and thus the protein is constitutively expressed. Single cell growth is exponential (equation 27) and at every division event the total operator content is doubled. The division propensity is given by equation (29) and the partitioning mechanism is given by equations (30, 31, 35, 36). Table 6 gives the values for all parameter used in our simulations. These values were loosely based on a previous work on the effect of intrinsic stochasticity on the lac operon system (Stamatakis & Mantzaris, 2009).

Table 6.

Parameter values for the inducible expression system

Symbol	Units	Value
kMR	(nM·min−1)	0.5
kR	(min−1)	8
ki	(min−1)	3·10−7
k−i	(min−1)	12
ks	(nM−1·min−1)	960
k−s	(min−1)	2.4
k1MP	(min−1)	0.5
k0MP	(min−1)	0.01
kP	(min−1)	30
λMR	(nM−1·min−1)	0.462
λR	(min−1)	0.2
λI2R	(min−1)	0.2
λMP	(min−1)	0.462
λP	(min−1)	0.2
OTotal	(molec.)	1
g0	(min−1)	0.0231
ng	(dim/less)	3
[P]crit	(nM)	∞
nd	(dim/less)	25
Vd,crit	(L)	1.4·10−15
q	(dim/less)	80
ns	(dim/less)	25
Vs,crit	(L)	10−15

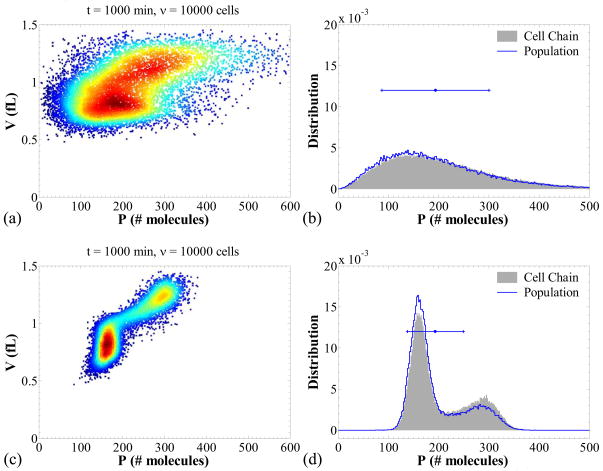
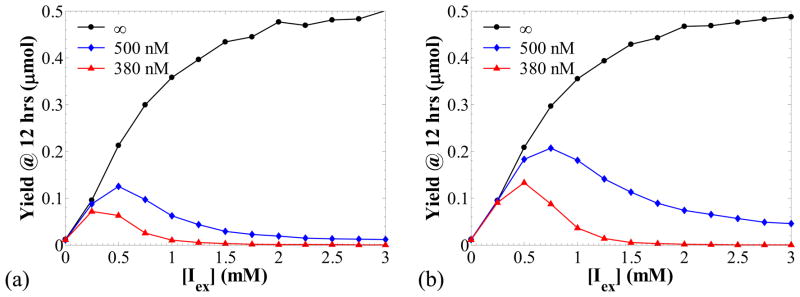
We investigate two scenarios: (i) slow transcription and fast translation and (ii) fast transcription and slow translation. These scenarios correspond to panels (a, b) and (c, d), respectively of Figure 6. Panels (a) and (c) show scatter plots for the protein contents versus cell volumes, in which each point represents one cell. High (low) numbers of points in the (P, V) plane are denoted with warm (cold) colors. Thus, this graph mimics a flow cytometry scatter plot in which the horizontal axis could be a fluorescence level (FL1) and the vertical axis the forward scatter (FSC). Panels (b) and (d) show the single cell probability distribution in comparison to the cell population number density for the protein content.

Figure 6.

Cell population scatter plots and comparison of the cell chain versus population distributions for the system, in the absence of repressor (k_MR = 0 nM/min). Panels (a, b): slow transcription, k_1MP = 0.5 min⁻¹, k_0MP = 0.01 min⁻¹, and fast translation, k_P = 30 min⁻¹. Panels (c, d): fast transcription, k_1MP = 50 min⁻¹, k_0MP = 1 min⁻¹, and slow translation, k_P = 0.3 min⁻¹. The error-bars in panels (b) and (d) show the mean and the two standard deviations for the population distributions (each line segment denotes one standard deviation). The values of parameters that are not mentioned appear in Table 6.

These graphs reveal that when transcription is slow, transcriptional noise dominates population heterogeneity (Figure 6, panel a) and the variability of the protein contents in the cell population is larger. Furthermore, the probability distribution for the protein content in a cell chain appears to be very close to the distribution of protein contents across the cell population (Figure 6, panel b).

When translation is slow and transcription is fast, several interesting phenomena are observed. In this case, the dominant source of noise is at the translational level and, since mRNA is abundant, the population variability is significantly lower than in the previous case. Such phenomena have been observed before (Thattai & van Oudenaarden, 2001). What is notable in this case, however, is that the subpopulations with different DNA contents can be identified in the scatter plot. The cells that have not undergone DNA duplication yet have lower volumes and protein contents, in contrast to those that have undergone this process. This generates bimodality in the distribution of protein contents (Figure 6, panel d).

Interestingly, Figure 6d shows that the distribution of protein contents in a cell chain (see Figure 1 for definition) is different than that across the cell population. Specifically, the model predicts lower protein contents for the cell population, since the lower mode of the population distribution is more prominent than the corresponding mode of the cell chain. The opposite holds for the upper mode. This phenomenon is a direct consequence of the fact that cell populations include all pairs of newborn daughter cells, whereas only one of the daughter cells is accounted for in a cell chain. More specifically, the division event produces two daughters with low contents which both become members of the overall cell population. Therefore, in the cell population, the lower contents of the newborn cells are weighted more heavily due to the fact that the newborn cells at time t + dt are twice as many as those which underwent division in the time interval [t, t + dt]. Such an effect is absent when one is simulating a cell chain, thereby generating a disparity between the cell chain and the cell population distributions observed in panel (d). Note that this disparity also exists in panel (b) but is much less prominent because of the dominance of the transcriptional noise in the overall heterogeneity.

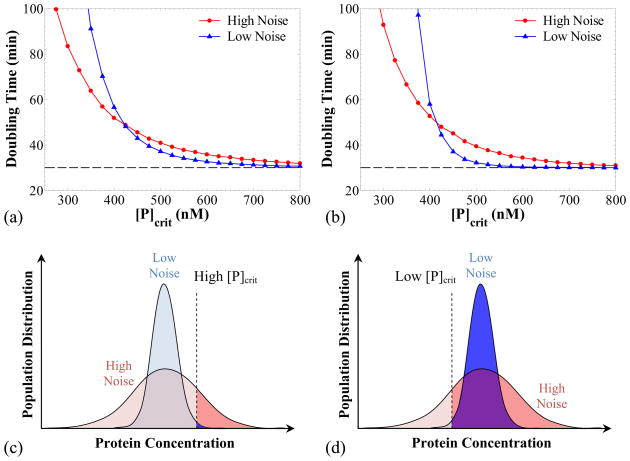
Interplay between growth rate variability and intrinsic noise

For the simulations just shown, the single cell growth rate was taken to be dependent on the volume (size) of the cell and independent of the protein concentration. Let us now assume that high protein concentrations result in growth retardation either due to toxicity or just by imposing a burden on the metabolic machinery of the cell. Consequently, the exponential single cell growth rate equation (26) no longer holds in this case. Instead, we can model this retardation effect by considering a growth rate that depends on volume and protein concentration:

$$\text{g}(\text{V},[\text{P}])=\frac{{\text{g}}_0·\text{V}}{{\left(\frac{[\text{P}]}{{[\text{P}]}_{\text{crit}}}\right)}^{{\text{n}}_{\text{g}}}+1}$$ (52)

[P]_crit is the protein concentration for half-maximal growth (the maximum growth is obtained for zero protein concentration), and n_g modulates the sharpness of the decrease of the growth rate. In this case, function Φ will be the solution of the differential equation:

$$\frac{\text{dV}}{\text{dt}}=\frac{{\text{g}}_0·\text{V}}{{\left(\frac{\text{P}}{{\text{V}·\text{N}}_{\text{A}}·{[\text{P}]}_{\text{crit}}}\right)}^{{\text{n}}_{\text{g}}}+1}$$ (53)

and is given in closed form as:

$$\mathrm{\Phi }(\text{V},\text{t}\mid {\text{V}}_0)=\frac{\alpha }{\text{W}{({\text{e}}^{-{\text{n}}_{\text{g}}·({\text{g}}_0·\text{t}+{\text{C}}_1-ln(\alpha ))})}^{\frac{1}{{\text{n}}_{\text{g}}}}}$$ (54)

where:

$$\begin{array}{l}\alpha =\frac{\text{P}}{{\text{N}}_{\text{A}}·{[\text{P}]}_{\text{crit}}}\\ {\text{C}}_1=ln({\text{V}}_0)-\frac{1}{{\text{n}}_{\text{g}}}·{\left(\frac{\alpha }{{\text{V}}_0}\right)}^{{\text{n}}_{\text{g}}}\end{array}$$ (55)

and W is the product-log or Lambert W function, namely the inverse of f(w) = w·exp(w). Note that in the argument of W in equation (54) evaluation of the exponential may result in overflow errors if large times are considered (such as the division times when growth is very slow). To circumvent this problem we used the de Bruijn and Comtet’s expansion for W(e^x) retaining terms up to ((ln(ln(x))/ln(x))⁶) (Corless et al., 1997).

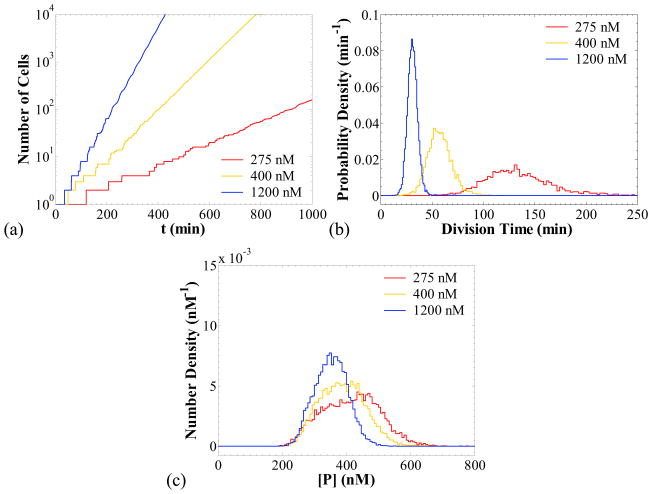
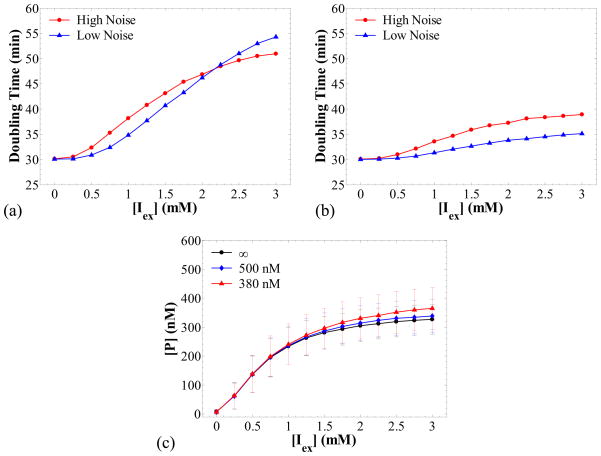
Figure 7a shows a logarithmic plot of the number of cells in the population as a function of time for three different values of [P]_crit: 275, 400 and 1,200 nM. The simulation predicts that the number of cells in the population increases exponentially in time, and the rate of increase (proliferation rate) is a strong function of [P]_crit. The lower the value of [P]_crit, the lower the average single cell growth rate is and, therefore, the higher the cell division time becomes as shown in panel (b). The division time probability densities shown in panel (b) were calculated from a cell chain. It is interesting to observe that the division times exhibit a higher variability as the proliferation rate decreases. As shown in Table 7, the coefficient of variation (CV) for the division time increases from 15 % for [P]_crit = 1200 nM, to 25 % for [P]_crit = 275 nM.

Figure 7.

Cell population simulations when protein production results in retardation of cell proliferation in the absence of repressor (k_MR = 0 nM/min) for different values of [P]_crit (noted in the legends). Panel (a): number of cells in the population versus time. Panel (b): probability density of the division times from a simulation of a cell chain. Panel (c): cell population distributions of the protein concentration. Fast transcription, k_1MP = 50 min⁻¹, k_0MP = 1 min⁻¹, and slow translation, k_P = 0.3 min⁻¹. Other parameters as in Table 6.

Table 7.

Means and CVs for division times and protein concentrations

[P]crit (nM)	Mean tdiv (min)	CV for tdiv	Mean [P] (nM)	CV for [P]
275	134	25 %	414	21 %
400	58	20 %	388	18 %
1200	31	15 %	352	14 %

Panel (c) of Figure 7 shows the effect of [P]_crit on the distribution of protein concentration. We observe that the distribution shifts to higher protein concentrations for lower values of [P]_crit, a phenomenon that could be explained as follows: since lower [P]_crit values result in slower growth rates; the dilution effect due to the expansion of the cell volume (Fredrickson, 1976) progressively diminishes. Consequently, more protein is accumulated into the cell, thereby shifting the cell population distribution for [P] to higher values. Additionally, the CV of the distribution increases (Table 7), an effect that could be attributed to the higher variability of division times for lower [P]_crit.

It is of great interest to investigate the effect of noise strength on the cell population proliferation rate, since for other systems it has been observed that noise promotes proliferation (Thattai & van Oudenaarden, 2004). To this end, we perform simulations with the parameter sets of Figure 6b and 6d for a range of critical concentrations [P]_crit for half-maximal growth. These two parameter sets result in different noise strengths, which we will refer to as high (Figure 6b, high CV in the distribution) and low (Figure 6d, low CV). In the absence of growth retardation effects (that is if [P]_crit → ∞), the mean protein content and concentration over the population are practically the same (P ≈ 193 molecules, [P] ≈348 nM), thereby allowing us to isolate the effect of noise magnitude on proliferation rate. The latter is quantified by the (average) doubling time, calculated as follows: for each simulation we fit a line to the base 2 logarithm of the number of cells versus time, and take the doubling time as the inverse of the slope.

The results are shown in Figure 8a and 8b. The retardation effect is apparently more prominent for lower values of [P]_crit, for which the cell grows more slowly, thereby taking more time to divide. Hence, for both noise strengths the doubling time is a decreasing function of [P]_crit. However, there is a striking difference between the doubling times computed for the two parameter sets. For low [P]_crit values (strong growth retardation), high noise appears to promote faster proliferation. This trend is reversed for high [P]_crit values for which high noise results in lower proliferation rates. Figure 8b shows that the difference between the doubling times in the two cases becomes more pronounced for higher values of the sharpness parameter n_g (see equation 53). For an intermediate [P]_crit the proliferation rates of the two cases become equal.

Figure 8.

Effect of noise strength on cell proliferation rates in the absence of repressor. Panel (a): k_MR = 0 nM/min; intermediate sharpness value, n_g = 5. Panel (b): as in panel (a) with higher sharpness value, n_g = 10. Parameter values: for the high noise simulations as in Figure 6a, b and for the low noise as in Figure 6c, d. Panels (c, d): explanation of the inversion effect shown in panel (a). See text for details.

Panels (c) and (d) of Figure 8 provide an explanation for this “inversion” effect. For high noise, the cell population distribution of the protein concentration is wider than that for low noise, as shown schematically in Figure 8, but they both have the same mean. The dashed vertical line indicates the critical protein concentration [P]_crit for which half-maximal growth rate is achieved. For protein concentrations [P] > [P]_crit, the retardation effect is rather strong, while the opposite holds for [P] < [P]_crit. Let us first consider the case where [P]_crit is high (Figure 8c). In this case, the proportion of the high noise distribution that lies to the right of the dashed line is much greater than the corresponding proportion for the low noise distribution. Consequently, the population following the high noise distribution is more susceptible to growth retardation, and therefore, the population with the low noise distribution will proliferate faster. This situation is reversed for low [P]_crit (Figure 8d). In the latter case, the low noise distribution lies almost entirely in the region where the retardation effect is strong, and thus the population exhibiting low noise will proliferate faster. The arguments just presented neglect the specifics of single cell growth shaping the cell population distribution (see discussion of Figure 7). They provide, however, a simple intuitive explanation of the behavior observed in Figure 8a and 8b. The same arguments are also valid for multimodal distributions, such as those of Figure 6d. In conclusion, noise can play a dual role. It can either promote or inhibit cell proliferation, depending on the specifics of the underlying single cell dynamics.

Inducible protein expression in the presence of noise and growth rate variability

Having investigated the dynamics of the systems in the absence of repressor, we now turn our attention to the case where repressor is being produced and protein expression is triggered by a non-metabolizable inducer (such as IPTG).

Figure 9a shows the average doubling time with respect to the extracellular inducer concentration for a low value of [P]_crit (the critical protein concentration for half maximal growth), and for the two different noise magnitudes investigated in Figure 8. Interestingly, the “inversion” effect is also observed in this case and can be explained in a similar way as before. For low induction levels, the low noise distribution remains localized to low protein concentrations [P] < [P]_crit whereas the high noise distribution spans across a wide concentration range, including values [P] < [P]_crit (refer to Figure 8c). Thus, low induction levels promote faster growth rates (shorter doubling times) for the population exhibiting low noise. The situation is reversed for high induction levels, for which the low noise distribution now lies entirely in a range of concentrations that result in slow growth. The high noise distribution on the other hand exhibits a tail at low protein concentrations for which cells proliferate faster (refer to Figure 8d). Hence, for high induction levels, the population with the high noise grows faster. This inversion effect is suppressed for higher values of [P]_crit, as shown in Figure 9b, since for such values both distributions span protein concentrations appreciably smaller than [P]_crit. In this case, low noise invariably results in faster growth.

Figure 9.

Panel (a): Average doubling time as a function of external inducer concentration [I_ex], for different noise magnitudes. High and low noise case parameter sets as in Figure 8a, b, respectively, and k_MR = 0.5 nM/min, k_R = 8 min⁻¹, [P_crit] = 380 nM. Panel (b): as in panel (a), with [P]_crit = 500 nM. Panel (c): protein concentration in the cell population at 360 min, as a function of [I_ex] for the low noise case and varying [P]_crit noted in the legend (∞ denotes absence of growth retardation). Each bar denotes one standard deviation of the cell population distribution.

It is also worth noting that due to the dilution effect previously discussed in Figure 7c, the average protein concentration of the cell population is affected by the value of [P]_crit. In particular, this average concentration is observed to shift to higher values for more pronounced growth retardation, as shown in Figure 9c.

From the preceding discussion it emerges that if one is interested in producing high amounts of a protein that slows down cell growth, high induction levels have two major competing effects. On the one hand, induction leads to the de-repression of the gene of interest and subsequently to high protein expression rates; this is a desirable effect. On the other hand, protein accumulation following induction impedes single cell growth and thus the number of cells in the population increases at a lower rate; this is an undesirable effect, since the protein yield is proportional to the number of cells harvested. Thus, for very high or very low induction levels, protein yields would be low. It is expected that an optimal induction level exists, for which the protein yield is maximized.

Using our framework, we can identify this optimal induction level. To this end, we assume that a batch reactor is inoculated with 10⁸ cells at time t_i = 0 hrs and the cells are harvested at time t_f = 12 hrs. The protein yield would then be equal to the number of cells at the final time multiplied by the average protein content over the population. Note that for the calculation of the latter we need to average over the cell population number density function and not the probability density of a cell chain (see Figure 6d and pertinent discussion). Thus:

$$\text{Y}={10}^8·\overline{\text{P}}·2^{\overline{\text{g}}·{\text{t}}_{\text{f}}}$$ (56)

where Y is the yield in mols, P̄ the population average protein content and ḡ the population average growth rate (obtained by linear fitting of the log₂ of the number of cells versus time). Figure 10 presents the resulting yields as a function of extracellular inducer concentration. Panel (a) corresponds to the high noise parameter set and panel (b) to the low noise case. As expected, the yield is a monotonic function of induction level when there is no growth retardation. If retardation occurs, the simulations predict that maximum yield is achieved for relatively low induction levels. Stronger retardation shifts the optimum induction levels to lower values for both noise magnitudes (high, panel a; and low, panel b). Notice also that low noise leads to higher yields, due to the fact that higher proliferation rates are achieved for induction levels in the vicinity of the optimum one (namely for I_ex around 500 μM to 1 mM).

Figure 10.

Protein yields as a function of extracellular inducer concentration for three different values of [P]_crit. Panel (a): high noise case (parameter set as in Figure 9a, b). Panel (b): low noise case (parameter set as in Figure 9c, d).

DISCUSSION

This study presented the development of a cell population master equation that models the dynamics of a heterogeneous cell population. The processes modeled are cell growth, intracellular reactions, DNA-duplication and cell division and the equation treats the reacting molecules and the cell numbers as discrete quantities. We also developed a Monte Carlo algorithm that allows for the simulation of exact paths of this cell population master equation We used this algorithm to demonstrate the effect of various extrinsic and intrinsic noise sources on a two-promoter system, as well as emergent complexity at the cell population level for an inducible expression system in which protein accumulation slows down growth.

The importance of developing these tools becomes apparent in view of the complex interplays of the different sources of heterogeneity observed in biological systems. Studying one source of heterogeneity in isolation can definitely give insight on the effect of this source. For example, a Gillespie simulation can show the effect of stochasticity in intracellular reactions. However, the sources of heterogeneity are in dynamical interaction. In the second system studied here, the effect of stochasticity in intracellular reactions depends on the cell size and the number of DNA molecules that exist in the cell. Thus, if we consider two cells, one of which has undergone DNA-duplication and is larger than the other, stochasticity in intracellular reactions will result in different phenotypic variations for these cells. This was demonstrated by the numerical results presented in the previous section, in which a cell population was observed to split into two subpopulations as a result of stochasticity in division (Figure 4c), or stochasticity in DNA duplication and low intrinsic noise (Figure 6d). Consequently, a mathematical framework that can accurately describe the interactions of the various sources of heterogeneity may reveal novel features that could not be discovered by studying each source in isolation from the others.

Furthermore, the necessity of focusing on populations rather than on single cells becomes evident when the number of cells in the population may change as a result of the function of the genetic network under consideration. Typical examples of such genetic networks are those that contribute to the survival of a cell population under environmental stress conditions like heat shock protein systems (heat shock protein systems, Genevaux et al., 2007) or antibiotic resistance (Jayaraman, 2008), post-segregational killing systems (Mongold, 1992), or the cell cycle (Murray, 2004). Moreover, it is important to take into account the dynamics of the whole cell population when phenotypic variability, results in differential fitness. This study investigated such a case, in which protein accumulation slows down single cell growth. Since protein expression is noisy, there is significant variability in the protein concentrations of the cell population, which results in growth rate variability. For this case, our simulations revealed that the magnitude of intrinsic noise affects the cell population proliferation rates: high noise may lead to faster or slower proliferation depending on the strength of the growth retardation effect. If protein expression is triggered by an extracellular inducer, we also showed that, in the presence of growth retardation, there is an optimum level of induction that maximizes protein yield for a batch process.

The mathematical and computational tools developed here are suitable for the analysis of more complicated cases as well. In a system, for example, where two phenotypes exist with one phenotype growing faster than the other, one expects that the faster growing phenotype will become dominant. Now, suppose that a drug is administered in the environment and only the slower growing phenotype exhibits drug resistance. In this case, it is not trivial to predict which phenotypes and at what fractions will be observed in the cell population. In silico viability studies with our framework could give tremendous insight in patient recovery and relapse during treatment of a disease with a drug.