False Discovery Rate Control With Groups

Abstract

In the context of large-scale multiple hypothesis testing, the hypotheses often possess certain group structures based on additional information such as Gene Ontology in gene expression data and phenotypes in genome-wide association studies. It is hence desirable to incorporate such information when dealing with multiplicity problems to increase statistical power. In this article, we demonstrate the benefit of considering group structure by presenting a p-value weighting procedure which utilizes the relative importance of each group while controlling the false discovery rate under weak conditions. The procedure is easy to implement and shown to be more powerful than the classical Benjamini–Hochberg procedure in both theoretical and simulation studies. By estimating the proportion of true null hypotheses, the data-driven procedure controls the false discovery rate asymptotically. Our analysis on one breast cancer dataset confirms that the procedure performs favorably compared with the classical method.

1. INTRODUCTION

Ever since the seminal work of Benjamini and Hochberg (1995), the concept of false discovery rate (FDR) and the FDR controlling Benjamini–Hochberg (BH) procedure have been widely adopted to replace traditional methods, like family-wise error rate (FWER), in fields such as bioinformatics where a large number of hypotheses are tested. For example, in gene expression microarray experiments or brain image studies, each gene or brain location is associated with one hypothesis. Usually there are tens of thousands of them. The more conservative family-wise error rate controlling procedures often have extremely low power as the number of hypotheses gets large. Under the FDR framework, the power can be increased.

In many cases, there is prior information that a natural group structure exists among the hypotheses, or the hypotheses can be divided into subgroups based on the characteristics of the problem. For example, for gene expression data, Gene Ontology (The Gene Ontology Consortium 2000) provides a natural stratification among genes based on three ontologies. In genome-wide association study, each marker might be tested for association with several phenotypes of interest; or tests might be conducted assuming different genetic models (Sun et al. 2006). In clinical trials, hypotheses are commonly divided into primary and secondary based on the relative importance of the features of the disease (Dmitrienko, Offen, and Westfall 2003). Ignorance of such group structures in data analysis can be dangerous. Efron (2008) pointed out that applying multiple comparison treatments such as FDR to the entire set of hypotheses may lead to overly conservative or overly liberal conclusions within any particular subgroup of the cases.

In multiple hypothesis testing, utilizing group structure can be achieved by assigning weights for the hypotheses (or p-values) in each group. Such an idea of using group information and weights has been adopted by several authors. Efron (2008) considered the Separate-Class model where the hypotheses are divided into distinct groups, and showed the legitimacy of such separate analysis for FDR methods. Benjamini and Hochberg (1997) analyzed both the p-value weighting and the error weighting methods and evaluated different procedures. Genovese, Roeder, and Wasserman (2006) investigated the merit of multiple testing procedures using weighted p-values and claimed that their weighted Benjamini–Hochberg procedure controls the FWER and FDR while improving power. Wasserman and Roeder (2006) further explored their p-value weighting procedure by introducing an optimal weighting scheme for FWER control. Roeder et al. (2006) considered linkage study to weight the p-values and showed their procedure improved power considerably when the linkage study is informative. Although in clinical trials, Finner and Roter (2001) pointed out that FDR control is hardly used, it is still potentially interesting to explore possible applications of FDR with group structures in clinical trials settings. Other notable publications include Storey, Taylor, and Siegmund (2004) and Rubin, van der Laan, and Dudoit (2005).

Very few results, however, have been published so far on proper p-value weighting schemes for procedures that control the FDR. In this paper, we will present the Group Benjamini–Hochberg (GBH) procedure, which offers a weighting scheme based on a simple Bayesian argument and utilizes the prior information within each group through the proportion of true nulls among the hypotheses. Our procedure controls the FDR not only for independent hypotheses but also for p-values with certain dependence structures. When the proportion of true null hypotheses is unknown, we show that by estimating it in each group, the data-driven GBH procedure offers asymptotic FDR control for p-values under weak dependence. This extends the results of both Genovese, Roeder, and Wasserman (2006) and Storey, Taylor, and Siegmund (2004).

When the information on group structure is less apparent, an alternative is to apply techniques such as clustering to assign groups. It can be a good strategy when we have spatially clustered hypotheses, that is, if one hypothesis is false, the nearby hypotheses are more likely to be false. For example, Quackenbush (2001) pointed out that in microarray studies, genes that are contained in a particular pathway or respond to a common environmental challenge, should show similar patterns of expression. Clustering methods are useful for identifying such gene expression patterns in time or space.

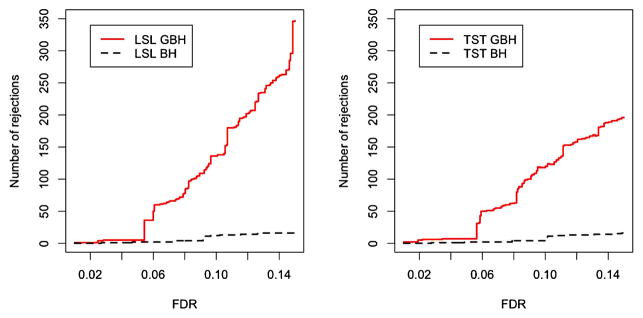
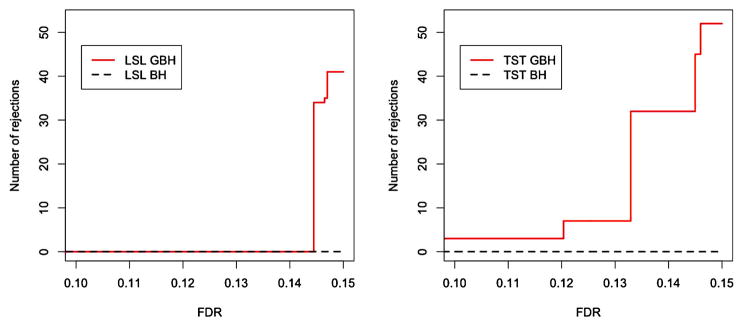
Our simulation results indicate that when the proportions of true nulls in each group are different, the GBH procedure is more powerful than the BH procedure while keeping the FDR controlled at the desired level. The GBH procedure also works well for situations where the number of signals is small among the hypotheses. Therefore, the procedure could be applied to microarray or genome-wide association studies where a large number of genes are monitored but only a few among them are actually differentially expressed or associated with disease. We apply our procedure to the analysis of a well-known breast cancer microarray dataset using two different grouping methods. The results indicate that the GBH procedure is able to identify more genes than the BH procedure by putting more focus on the potentially important groups. Figure 1 shows the advantage of the GBH procedure over the BH procedure under k-means clustering for two methods of estimating the true null hypotheses in each group.

Figure 1.

Breast cancer study, 24,184 genes. Plot shows the number of signals detected by GBH and BH procedures versus prespecified FDR level. Left panel: adaptive LSL GBH procedure. Right panel: adaptive TST GBH procedure. Details for LSL and TST approaches are in Section 2.3. Genes are assigned into six groups using k-means clustering. Data from van’t Veer et al. (2002). The online version of this figure is in color.

The rest of the paper is organized as follows. After a brief review of the FDR framework and the classical BH procedure, we present our GBH procedure in Section 2.2 and investigate our weighting scheme from both practical and Bayesian perspectives. Comparison of the classical BH and the GBH procedures in terms of expected number of rejections is discussed in Section 2.4. After discussing the data-driven GBH procedure in Section 2.3, we prove its asymptotic FDR control property in Section 3. Simulation studies of the BH and GBH procedures for normal random variables are reported in Section 4, including both independent and positive regression dependent cases. In Section 5, we show an application of the GBH procedure on a breast cancer dataset, using both the Gene Ontology grouping and k-means clustering strategies. The proofs for the main theorems are included in the Appendix.

2. THE GBH PROCEDURE

In this section, we introduce the Group Benjamini–Hochberg (GBH) procedure. It takes advantage of the proportion of true null hypotheses, which represents the relative importance of each group. We first examine the case where the proportions are known and then discuss data-driven procedures where the proportions are estimated based on the data.

2.1 Preliminaries

We first review the FDR framework and the classical BH procedure. Consider the problem of testing N hypotheses H_i vs H_Ai, i ∈ I_N = {1, …, N} among which n₀ are null hypotheses and n₁ = N − n₀ are alternatives (signals). Let V be the number of null hypotheses that are falsely rejected (false discoveries) and R be the total number of rejected hypotheses (discoveries). Benjamini and Hochberg (1995) introduced the FDR, which is defined as the expected ratio of V and R when R is positive, that is,

$$\text{FDR}=E\left[\frac{V}{R\vee 1}\right],$$ (2.1)

where R ∨ 1 ≡ max(R, 1). They also proposed the BH procedure which focuses on the ordered p-values P₍₁₎ ≤ ··· ≤ P_(N) from N hypothesis tests. Given a level α ∈ (0, 1), the BH procedure rejects all hypotheses of which P_(i) ≤ P_(k), where

$$k=max\left\{i\in \{1,\dots ,N\}:P_{(i)}\le \frac{i\alpha }{N}\right\}.$$ (2.2)

Benjamini and Hochberg (1995) proved that for independent hypotheses, the BH procedure controls the FDR at level π₀α where π₀ = n₀/N is the proportion of true null hypotheses. Hence, the BH procedure actually controls the FDR at a more stringent level. One can therefore increase the power by first estimating the unknown parameter π₀ using, say, π̂₀, and then applying the BH procedure on the weighted p-values π̂₀P_i, i = 1, …, N at level α. Such a data-driven method is referred to as an adaptive procedure.

2.2 The GBH Procedure for the Oracle Case

When group information is taken into consideration, we assume that the N hypotheses can be divided into K disjoint groups with group sizes n_g, g = 1, …, K. Let I_g be the index set of the gth group. The index set I_N of all hypotheses satisfies

$$I_N=\underset{g=1}{\overset{K}{\cup }}{I}_g=\underset{g=1}{\overset{K}{\cup }}(I_{g,0}\cup I_{g,1}),$$ (2.3)

where I_g,0 = {i ∈ I_g : H_i is true} consists of indices for null hypotheses and I_g,1 = {i ∈ I_g : H_i is false} is for the alternatives. Let n_g,0 = |I_g,0| and n_g,1 = n_g − n_g,0 be the number of null and alternative hypotheses in group g, respectively. Then π_g,0 = n_g,0/n_g and π_g,1 = n_g,1/n_g are the corresponding proportions of null and alternative hypotheses in group g. Let

$${\pi }_0=\frac{1}{N}\sum _{g=1}^K{n}_g{\pi }_{g,0}$$ (2.4)

be the overall proportion of null hypotheses. In this section, we consider the so-called “oracle case,” where π_g,0 ∈ [0, 1] is assumed to be given for each group. The case for unknown π_g,0 is discussed in Section 2.3.

Definition 1 (The GBH procedure for the oracle case)

1. For each p-value in group g, calculate the weighted p-values $P_{g,i}^w=\frac{{\pi }_{g,0}}{{\pi }_{g,1}}{P}_{g,i}$. Let $P_{g,i}^w=\infty$ if π_g,0 = 1. If π_g,0 = 1 for all g, accept all the hypotheses and stop. Otherwise go to the next step.

2. Pool all the weighted p-values together and let $P_{(1)}^w\le \cdots \le P_{(N)}^w$ be the corresponding order statistics.

3. Compute

   $$k=max\left\{i:P_{(i)}^w\le \frac{i{\alpha }^w}{N}\right\},\text{where}{\alpha }^w=\frac{\alpha }{1-{\pi }_0}.$$

   If such a k exists, reject the k hypotheses associated with $P_{(1)}^w,\dots ,P_{(k)}^w$; otherwise do not reject any of the hypotheses.

The GBH procedure weights the p-values for each group depending on the corresponding proportion of true null hypotheses in the group, that is, π_g,0. This idea is intuitively appealing because for any group with a small π_g,0, more rejections are expected and vice versa. The weight π_g,0/π_g,1 differentiates groups by (relatively) enlarging p-values in groups with larger π_g,0, therefore larger power is expected after applying the BH procedure on the pooled weighted p-values.

Benjamini and Yekutieli (2001) introduced the concept of positive regression dependence on subsets (PRDS) and proved that the BH procedure controls the FDR for p-values with such property. Finner, Dickhaus, and Rosters (2009, p. 603) argued that the PRDS property implies

$$Pr\{R\ge j\mid P_i\le t\}\text{is}\text{nonincreasing}\text{in}t$$ (2.5)

for any j ∈ I_N, i ∈ ∪_g I_g,0 and t ∈ (0, jα/N]. Examples of distribution satisfying the PRDS property include multivariate normal with nonnegative correlations and (absolute) multivariate t-distribution. It is worth pointing out that independence is a special case of PRDS; see Benjamini and Yekutieli (2001) and Finner, Dickhaus, and Rosters (2007 and Finner, Dickhaus, and Rosters (2009) for details.

For the oracle case, the following theorem guarantees that the GBH procedure controls the FDR rigorously for p-values with the PRDS property (hence provides FDR control for independent p-values as well).

Theorem 1

Assume the hypotheses satisfy (2.3) and the proportion of trull null hypotheses, π_g,0 ∈ [0, 1], is known for each group, then the GBH procedure controls the FDR at level α for p-values with the PRDS property.

Genovese, Roeder, and Wasserman (2006) analyzed the method of p-value weighting for independent p-values and proved FDR control of their procedure with a general set of weights. Some of the arguments in the proof of the above theorem can be implied by theorem 1 in Genovese, Roeder, and Wasserman (2006, p. 513). Nevertheless, we not only extend the result to p-values with the PRDS property, but also make up a small gap in their proof of FDR control (Genovese, Roeder, and Wasserman 2006, p. 514, first equation). Furthermore, the GBH procedure makes use of the information (i.e., π_g,0) embedded within each group, and provides a quasi-optimal way of assigning weights. Its advantage can be understood in two perspectives.

The GBH Procedure Works Well for Data With Sparse Signals

In many cases of multiple hypothesis testing, there tends to be a strong assumption that there are few signals, that is, most of the N hypotheses are true nulls. In microarray studies, for instance, majority of the genes are not related to certain disease, therefore we have the situation in which the π_g,0 of each group will be close to 1. Our weighting strategy performs well in such settings. For example, suppose we have two groups of p-values with π_1,0 = 0.9 and π_2,0 = 0.99. According to the GBH procedure, we are going to multiply 0.9/0.1 = 9 to the first group and 0.99/0.01 = 99 to the second group. Performing multiple comparison procedure on the combined weighted p-values means we put more attention on the p-values from the first group rather than the second one. As a result, more signals are expected. In the extreme case where one of the proportions is 1, say, π_1,0 = 1 and π_2,0 ∈ (0, 1), according to the GBH procedure, all the p-values in the first group are rescaled to ∞, therefore no rejection (signal) would be reported in that group and our full attention would be focused on the second group. This is consistent with the fact that the first group contains no signal.

The GBH Procedure Has a Bayesian Interpretation

From the Bayesian point of view, the weighting scheme, π_g,0/π_g,1, can be interpreted as follows. Let H_g,i be a hypothesis in group g such that H_g,i = 0 with probability π_g,0 and H_g,i = 1 with probability π_g,1 = 1 − π_g,0. Let P_g,i be the corresponding p-value and has a conditional distribution

$$P_{g,i}\mid H_{g,i}=0\sim U_g;P_{g,i}\mid H_{g,i}=1\sim F_g.$$

The “Bayesian FDR” (Efron and Tibshirani 2002) of H_g,i for P_g,i ≤ p is

$$Pr(H_{g,i}=0\mid P_i\le p)=\frac{{\pi }_{g,0}{U}_g(p)}{{\pi }_{g,0}{U}_g(p)+{\pi }_{g,1}{F}_g(p)}.$$ (2.6)

If U_g follows a uniform distribution, the above equation becomes

$$\begin{array}{l}Pr(H_{g,i}=0\mid P_{gi}\le p)=\frac{{\pi }_{g,0}p}{{\pi }_{g,0}p+{\pi }_{g,1}{F}_g(p)}\\ =\frac{({\pi }_{g,0}/{\pi }_{g,1})p}{({\pi }_{g,0}/{\pi }_{g,1})p+F_g(p)}\\ =\frac{{[F_g(p)]}^{-1}({\pi }_{g,0}/{\pi }_{g,1})p}{{[F_g(p)]}^{-1}({\pi }_{g,0}/{\pi }_{g,1})p+1}.\end{array}$$

Note that the above equation is an increasing function of [F_g(p)]⁻¹(π_g,0/π_g,1)p, therefore ranking the Bayesian FDR is equivalent to focusing on the quantity

$$P_g^{\ast }=\frac{1}{F_g(p)}\frac{{\pi }_{g,0}}{{\pi }_{g,1}}p.$$ (2.7)

Then the ideal weight for the p-values in group g should be [F_g(p)]⁻¹(π_g,0/π_g,1), which can be viewed as two sources of influence on the p-values. If F_g = F for all g, the first influence is through [F(p)]⁻¹, which can be regarded as the p-value effect. The other influence is the relative importance of the groups, that is, π_g,0/π_g,1. In practice, F_g is usually unknown and hard to estimate, especially when the number of alternatives is small. Hence, we just focus on the group effect in the ideal weight. Note that the weight we choose, that is, π_g,0/π_g,1 is not an aggressive one, since the cut-off point for the original p-values is big for important groups with small π_g,0/π_g,1, which implies that the ideal weight for groups with small π_g,0/π_g,1 is relatively smaller.

2.3 The Adaptive GBH Procedure

As mentioned in the previous sections, knowledge of the proportion of true null hypotheses, that is, π₀, can be useful in improving the power of FDR-controlling procedures. Such information, however, is not available in practice. Estimating the unknown quantity using observed data is then a natural idea, which brings us to the adaptive procedure.

Definition 2 (The adaptive GBH procedure)

1. For each group, estimate π_g,0 by π̂_g,0.

2. Apply the GBH procedure in Definition 1, with π_g,0 replaced by π̂_g,0.

Various estimators of π₀ were proposed by Schweder and Spjøtvoll (1982) and Storey (2002) and Storey, Taylor, and Siegmund (2004) based on the tail proportion of p-values, and by Efron et al. (2001) based on the mixture densities of null and alternative distribution of hypotheses. Jin and Cai (2007) estimated π₀ based on the empirical characteristic function and Fourier analysis. Meinshausen and Rice (2006) and Genovese and Wasserman (2004) provided consistent estimators of π₀ under certain conditions.

The adaptive GBH procedure does not require a specific estimator of π_g,0, therefore people may choose their favorite estimator in practice. We take the following two examples to illustrate the practical use of the adaptive GBH procedure.

Example 1 [Least-Slope (LSL) method]

The least-slope (LSL) estimator proposed by Benjamini and Hochberg (2000) performs well in situations where signals are sparse. Hsueh, Chen, and Kodell (2003) compared several methods including Schweder and Spjøtvoll (1982), Storey (2002), and the LSL estimator, and found that the LSL estimator gives the most satisfactory empirical results.

Definition 3 (Adaptive LSL GBH procedure)

1. For p-values in each group g, starting from i = 1, compute l_g,i = (n_g + 1 − i)/(1 − P_g,(i)), where P_g,(i) is the ith order statistics in group g. As i increases, stop when l_g,j > l_g,j−1 for the first time.

2. For each group, compute the LSL estimator of π_g,0

   $${\gamma }_g^{\text{LSL}}=min\left(\frac{\lfloor l_{g,j}\rfloor +1}{n_g},1\right).$$ (2.8)

3. Apply the GBH procedure at level α with π_g,0 replaced by ${\gamma }_g^{\text{LSL}}$.

The LSL estimator is asymptotically related to the estimator proposed by Schweder and Spjøtvoll (1982). It is also conservative in the sense that it overestimates π_g,0 in each group.

Example 2 [The Two-Stage (TST) method]

Benjamini, Krieger, and Yekutieli (2006) proposed the TST adaptive BH procedure and showed that it offers finite-sample FDR control for independent p-values.

Definition 4 (Adaptive TST GBH procedure)

1. For p-values in each group g, apply the BH procedure at level α′ = α/(1 + α). Let r_g,1 be the number of rejections.

2. For each group, compute the TST estimator of π_g,0

   $${\gamma }_g^{\text{TST}}=\frac{n_g-r_{g,1}}{n_g}.$$ (2.9)

3. Apply the GBH procedure at level α′ with π_g,0 replaced by ${\gamma }_g^{\text{TST}}$.

The TST method applies the BH procedure in the first step and uses the number of rejected hypotheses as an estimator of the number of alternatives.

Both the LSL and TST methods are straightforward to implement in practice and in the next section we show both of them have good asymptotic properties. Our simulation and real data analysis show that they outperform the adaptive BH procedure, in which the group structure of the data is not considered.

Remark 1

We should point out that in applications, the adaptive GBH procedure does not rely on which estimator people choose. The performance, however, does depend on the distribution of signal among groups. If there is no significant difference in the proportions of signals among hypotheses for different groups, the adaptive GBH procedure degenerates to uni-group case. As long as the groups are dissimilar in terms of true null proportion and the estimator of π_g,0 can detect (not necessarily fully detect) the proportion of true null hypotheses for each group, the adaptive GBH procedure is expected to outperform the adaptive BH procedure.

2.4 Comparison of the GBH and BH Procedures

In previous sections, we show that the GBH procedure controls the FDR for the finite sample case when the π_g,0’s are known. It is of interest to compare the performance of GBH with that of the BH procedure. In this section, we are going to compare the expected number of rejections for the two procedures.

Benjamini and Hochberg (1995) showed that the BH procedure controls the FDR at level π₀α. In order to compare the BH and GBH procedures at the same α level, we consider the following rescaled p-values:

$$\text{BH}:{\pi }_0\mathbf{P}\text{vs}\text{GBH}:\frac{{\pi }_{g,0}}{{\pi }_{g,1}}(1-{\pi }_0){\mathbf{P}}_g,$$ (2.10)

where π_g,0 ∈ (0, 1). Note that π₀ = π_g,0(1 − π₀)/π_g,1 when π_g,0 = π₀ for all g.

For group g, let D_g be the distribution of p-values such that

$$D_g(t)={\pi }_{g,0}{U}_g(t)+{\pi }_{g,1}{F}_g(t),$$ (2.11)

where U_g and F_g are the distribution functions for p-values under the null and alternative hypotheses. Let D̃_g(t) be the empirical cumulative distribution function of p-values in group g, that is,

$${\stackrel{\sim }{D}}_g(t)=\frac{1}{n_g}\left(\sum _{i\in I_{g,0}}\{P_i\le t\}+\sum _{i\in I_{g,1}}\{P_i\le t\}\right).$$ (2.12)

It is proved in Lemma 2 that under weak conditions D̃_g(t) converges uniformly to D_g(t).

For the uni-group case, in the framework of (2.10), it has been proved by several authors (Benjamini and Hochberg 1995; Storey 2002; Genovese and Wasserman 2002; Genovese, Roeder, and Wasserman 2006) that the threshold of the BH procedure can be written as

$$T_{\text{BH}}=\underset{t\in [0,{\pi }_0]}{sup}\left\{t:\frac{t}{C_N(t/{\pi }_0)}\le \alpha \right\},$$

where $C_N(t)=\frac{1}{N}{\sum }_{i\in I_N}\{P_i\le t\}$ is the empirical cumulative distribution function of the p-values, and the procedure rejects any hypothesis with a p-value less than or equal to T_BH. We can extend this result to the framework of GBH. For notation purpose define $\mathbf{a}={\{a_g\}}_{g=1}^K$ where ag = π_g,0(1 − π₀)/(1 − π_g,0). Let G_N (a, t) be the empirical distribution of the weighted p-values, that is,

$$\begin{array}{l}{G}_N(\mathbf{a},t)=\frac{1}{N}\sum _{g=1}^K{n}_g{\stackrel{\sim }{D}}_g\left(\frac{t}{a_g}\right)\\ =\frac{1}{N}\sum _{g=1}^K\left(\sum _{i\in I_{g,0}}\left\{P_i\le \frac{t}{a_g}\right\}+\sum _{i\in I_{g,1}}\left\{P_i\le \frac{t}{a_g}\right\}\right).\end{array}$$ (2.13)

Note that N · G_N (a, t) is the number of rejections for the (oracle) GBH procedure with respect to the threshold t on the weighted p-values. When π₀ < 1, where π₀ defined in (2.4) is the overall proportion of null hypotheses, it can be shown that the threshold of the GBH procedure is equivalent to

$$T_{\text{GBH}}=\underset{t\in c(\mathbf{a})}{sup}\left\{t:\frac{t}{G_N(\mathbf{a},t)}\le \alpha \right\},$$

where c(a) = {t : 0 ≤ t ≤ max_g a_g}.

For any fixed threshold t ∈ c(a), let [R_BH(t)] and [R_GBH(t)] be the expected number of rejections of the BH and GBH procedure, respectively. The following theorem provides a sufficient condition for 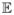[R_BH(t)] ≤ 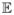[R_GBH(t)].

Lemma 1

Let U_g and F_g be the distributions of p-values under the null and alternative hypotheses in group g. Assume U_g = U and F_g = F for all g. If U ~ Unif[0, 1] and x ↦ F(t/x) is convex for x ≥ t̃, where $\stackrel{\sim }{t}=(1-{\pi }_0){min}_g\frac{{\pi }_{g,0}}{1-{\pi }_{g0}}$, then 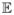[R_BH(t)] ≤ 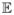[R_GBH(t)].

Take the classical normal mean model for an example. Suppose we observe X_i = θ + Z_i, where $Z_i\stackrel{\text{iid}}{\sim }\text{N}(0,1)$. Consider the multiple testing problem

$$H_i:\theta =0\text{vs}{H}_{Ai}:\theta ={\theta }_A>0,i=1,\dots ,N.$$

The distribution of p-values under alternative is F(u) = 1 − Φ[Φ⁻¹ (1 − u) − θ_A], where Φ is the standard Normal distribution function. It can be shown that x ↦ F(t/x) is convex if

$${\theta }_A\le \frac{2\phi ({\mathrm{\Phi }}^{-1}(1-t/\stackrel{\sim }{t}))}{t/\stackrel{\sim }{t}},$$ (2.14)

where φ is the standard Normal density function. Note that t/t̃ is the threshold of the unscaled p-values for rejecting the corresponding hypotheses in one group, therefore t/t̃ is small. Since the right-hand side of (2.14) is a decreasing function of t/t̃, (2.14) becomes θ_A ≤ 4.12 when t/t̃ ≤ 0.05 and θ_A ≤ 5.33 when t/t̃ ≤ 0.01. This suggests the convexity is true for most of the cases.

For adaptive procedures, π_g,0 is replaced by its estimator π̂_g,0. Let $\widehat{\mathbf{a}}={\{{\widehat{a}}_g\}}_{g=1}^K$ where â_g = π̂_g,0(1 − π̂₀)/(1 − π̂_g,0) and π̂₀ = Σ_g n_g π̂₀/N. To conduct the BH procedure adaptively, we first estimate π₀ by π̂₀ and then perform the BH procedure at level α/π̂₀. The corresponding threshold of the adaptive BH procedure is

$${\widehat{T}}_{\text{BH}}=\underset{t\in [0,{\widehat{\pi }}_0]}{sup}\left\{t:\frac{t{\pi }_0/{\widehat{\pi }}_0}{C_N(t/{\widehat{\pi }}_0)}\le \alpha \right\},$$ (2.15)

and the threshold of the adaptive GBH procedure is

$${\widehat{T}}_{\text{GBH}}=\underset{t\in c(\widehat{\mathbf{a}})}{sup}\left\{t:\frac{{\sum }_{g=1}^K{\pi }_g{\pi }_{g,0}t/{\widehat{a}}_g}{G_N(\widehat{\mathbf{a}},t)}\le \alpha \right\},$$ (2.16)

where

$$G_N(\widehat{\mathbf{a}},t)=\frac{1}{N}\sum _{g=1}^K\left(\sum _{i\in I_{g,0}}\{P_i\le t/{\widehat{a}}_g\}+\sum _{i\in I_{g,1}}\{P_i\le t/{\widehat{a}}_g\}\right).$$ (2.17)

Remark 2

Both (2.15) and (2.16) depend on the data, hence they are no longer fixed. In the next section we are going to prove that T̂_BH and T̂_GBH converges in probability to some fixed $t_{\text{BH}}^{\ast }$ and $t_{\text{GBH}}^{\ast }$, respectively. Theorem 4 in Section 3.1 demonstrates that $t_{\text{BH}}^{\ast }\le t_{\text{GBH}}^{\ast }$ and therefore the adaptive GBH procedure rejects more than the adaptive BH procedure asymptotically.

3. GBH ASYMPTOTICS

In many applications of multiple hypothesis testing, not only are the proportions of true null hypotheses unknown, but the number of hypotheses is also very large. It is hence applicable to analyze the behavior of the GBH procedure for large N. In this section, we focus on the asymptotic property of the adaptive GBH procedure.

Genovese, Roeder, and Wasserman (2006) and Storey, Taylor, and Siegmund (2004) proved some useful results for asymptotic FDR control using empirical process argument for the BH procedure. We extend them further in the setting of the GBH procedure. We first discuss the case where we have consistent estimator of the proportion of true null hypotheses, then move on to a more general case.

3.1 Adaptive GBH With Consistent Estimator of π_g,0

When N → ∞ and the number of groups K is finite, we assume the following condition is satisfied in every group

$$\begin{array}{l}\frac{n_g}{N}\to {\pi }_g,\frac{n_{g,0}}{n_g}\to {\pi }_{g,0},\frac{n_{g,1}}{n_g}\to {\pi }_{g,1},\\ \text{where}{\pi }_g,{\pi }_{g,0},{\pi }_{g,1}\in (0,1).\end{array}$$ (3.1)

By the construction, Σ_g π_g = 1 and π_g,0 + π_g,1 = 1. The following lemma shows that (2.12) converges uniformly to (2.11) under the above condition.

Lemma 2

Under (3.1), let U_g(t) and F_g(t) be continuous functions. For any t ≥ 0, if the p-values satisfy

$$\frac{1}{n_{g,0}}\sum _{i\in I_{g,0}}\{P_i\le t\}\stackrel{\text{a}.\text{s}.}{\to }{U}_g(t),$$ (3.2)

$$\frac{1}{n_{g,1}}\sum _{i\in I_{g,1}}\{P_i\le t\}\stackrel{\text{a}.\text{s}.}{\to }{F}_g(t).$$ (3.3)

Then ${sup}_t\mid {\stackrel{\sim }{D}}_g(t)-D_g(t)\mid \stackrel{\text{a}.\text{s}.}{\to }0$.

Storey, Taylor, and Siegmund (2004) described weak dependence as any type of dependence in which Conditions (3.2) and (3.3) are satisfied. Weak dependence contains the case of independent p-values, but for p-values with the PRDS property, these conditions are not necessarily true. An example is given in Section 4.

In this section, we focus on the case when we have consistent estimator of π_g,0 in every group, that is,

$${\widehat{\pi }}_{g,0}\stackrel{P}{\to }{\pi }_{g,0}\in (0,1)\text{for}\text{all}g.$$ (3.4)

Recall that $\widehat{\mathbf{a}}={\{{\widehat{a}}_g\}}_{g=1}^K$, where â_g = π̂_g,0 (1 − π̂₀)/(1 − π̂_g,0). Under the above condition, we have $\widehat{\mathbf{a}}\stackrel{P}{\to }\mathbf{a}$. Let $G(\mathbf{a},t)={\sum }_{g=1}^K{\pi }_g({\pi }_{g,0}{U}_g(t/a_g)+{\pi }_{g,1}{F}_g(t/a_g))$ be the limiting distribution of the weighted p-values for all groups and let B(a, t) = t/G(a, t). Then define

$$t_{\text{GBH}}^{\ast }=\underset{t\in c(\mathbf{a})}{sup}\{t:B(\mathbf{a},t)\le \alpha \}.$$

The following theorem establishes the asymptotic equivalence of (2.16) and $t_{\text{GBH}}^{\ast }$, and thus implies asymptotic FDR control of the adaptive GBH procedure.

Theorem 2

Suppose Conditions (3.1) through (3.4) are satisfied for all groups. Suppose further that U_g(t) = t for 0 ≤ t ≤ 1 in every group. If t ↦ B(a, t) has a nonzero derivative at $t_{\text{GBH}}^{\ast }$ and lim_t↓0 B(a, t) ≠ α, then ${\widehat{T}}_{\text{GBH}}\stackrel{P}{\to }{t}_{\text{GBH}}^{\ast }$ and FDR(T̂_GBH) ≤ α + o(1).

Note that the statement of the theorem has a similar flavor as theorem 2 in Genovese, Roeder, and Wasserman (2006, p. 515). But our assumption is weaker and more importantly, the π̂_g,0’s are estimated based on the data.

Similarly, for the adaptive BH procedure, we define the distribution of all p-values as C(t) = π₀U(t) + (1 − π₀)F(t), where U(t) and F(t) are continuous functions. Let $t_{\text{BH}}^{\ast }$ be such that

$$t_{\text{BH}}^{\ast }=\underset{t\in [0,{\pi }_0]}{sup}\left\{t:\frac{t}{C(t/{\pi }_0)}\le \alpha \right\}.$$

The following theorem illustrates that asymptotically the adaptive GBH procedure has more expected number of rejections than the adaptive BH procedure. Note that R_BH(·) and R_GBH(·) denote the number of rejections of the BH and GBH procedures, respectively.

Theorem 3

Under Conditions (3.1) through (3.4). Assume in each group U_g(t) = U(t) = t, 0 ≤ t ≤ 1 and F_g(t) = F(t), where x ↦ F(t/x) is convex for x ≥ min_g a_g. Assume further that both B(a, t) and t/C(t/π₀) are increasing in t. If π₀ ≥ α and lim_t↓0 t/C(t/π) ≤ α, then $t_{\text{BH}}^{\ast }\le t_{\text{GBH}}^{\ast }$, and therefore

$$\mathbb{E}[R_{\text{BH}}({\widehat{T}}_{\text{BH}})]/\mathbb{E}[R_{\text{GBH}}({\widehat{T}}_{\text{BH}})]\le 1+o(1).$$

Remark 3

Sometimes the assumption that all the alternative hypotheses across different groups follow the same distribution may not be appropriate. The condition F_g(t) = F(t) in the above theorem is necessary to establish Theorem 3. However, that assumption is not a necessity in establishing Theorem 2 and Theorem 4, where we show FDR control for the adaptive GBH procedure.

3.2 Discussion for Inconsistent Estimator of π_g,0

For a general estimator of π_g,0, let π̂_g,0 ∈ (0, 1] be an estimator of π_g,0 such that

$${\widehat{\pi }}_{g,0}\stackrel{P}{\to }{\zeta }_g\in (0,1]\text{and}\overline{\zeta }=\sum _g{\pi }_g{\zeta }_g<1,$$ (3.5)

where the latter condition means at least one ζ_g is less than 1 among all groups. Let $\mathit{\rho }={\{{\rho }_g\}}_{g=1}^K$ where ρ_g = ζ_g/(1 − ζ_g) and ρ_g = ∞ when ζ_g = 1. Then, we have $\widehat{\mathbf{a}}\stackrel{P}{\to }\mathit{\rho }$. Let $G(\mathit{\rho },t)={\sum }_{g=1}^K{\pi }_g({\pi }_{g,0}{U}_g(t/{\rho }_g)+{\pi }_{g,1}{F}_g(t/{\rho }_g))$ be the limiting distribution of the weighted p-values for all groups. Denote $B(\mathit{\rho },t)=\frac{{\sum }_{g=1}^K{\pi }_g{\pi }_{g,0}t/{\rho }_g}{G(\mathit{\rho },t)}$ and define

$$t_{\text{GBH}}^{\ast }=\underset{t\in c(\mathit{\rho })}{sup}\{t:B(\mathit{\rho },t)\le \alpha \}.$$ (3.6)

Theorem 4

Suppose Conditions (3.1) through (3.3) and (3.5) are satisfied for all groups. Suppose further that U_g(t) = t for 0 ≤ t ≤ 1 and ζ_g ≥ b_gπ_g,0 for some b_g > 0 in every group. If t ↦ B(ρ, t) has a nonzero derivative at $t_{\text{GBH}}^{\ast }$ and lim_t↓0 B(ρ, t) ≠ α, then ${\widehat{T}}_{\text{GBH}}\stackrel{P}{\to }{t}_{\text{GBH}}^{\ast }$ and FDR(T̂_GBH) ≤ α/min_g{b_g} + o(1). In particular, FDR(T̂_GBH) ≤ α + o(1) when b_g ≥ 1 for all groups.

The theorem generalizes the result in Theorem 2 and indicates that the adaptive GBH procedure controls the FDR at level α not only for consistent estimators of π_g,0’s, but also for asymptotically conservative estimators.

Remark 4

For the TST estimator ${\gamma }_g^{\text{TST}}$ in (2.9), note that

$${\gamma }_g^{\text{TST}}=1-\frac{1}{n_g}\sum _{i\in I_g}\{P_i\le {\widehat{T}}_0\},$$

where T̂₀ is the threshold for the BH procedure in the first step. Following from Theorem 4, ${\widehat{T}}_0\stackrel{P}{\to }{t}_0$, where t₀ satisfies t₀/(π_g,0t₀ + π_g,1F_g(t₀)) = α′. Since F_g(t₀) ≤ 1, it can be shown that t₀ ≤ (1 − π_g,0)α′/(1 − α′π_g,0). Then,

$${\gamma }_g^{\text{TST}}\stackrel{P}{\to }{\pi }_{g,0}(1-t_0)+{\pi }_{g,1}(1-F_g(t_0))=1-\frac{t_0}{\alpha }\ge (1-{\alpha }^{\prime }){\pi }_{g,0}.$$

Therefore, by Theorem 4 the adaptive TST GBH procedure controls FDR at level α′/(1 − α′) = α asymptotically.

Remark 5

As n_g → ∞, the LSL estimator ${\gamma }_g^{\text{LSL}}$ defined in (2.8) can be viewed as a special case of the estimator π̂_g,0(λ) proposed by Schweder and Spjøtvoll (1982). For fixed λ, π̂_g,0(λ) satisfies

$${\widehat{\pi }}_{g,0}(\lambda )=\frac{n_g-{\sum }_{i\in I_g}\{P_i\le \lambda \}}{n_g(1-\lambda )}\stackrel{\text{a}.\text{s}}{\to }{\pi }_{g,0}+{\pi }_{g,1}\frac{1-F_g(\lambda )}{1-\lambda }\ge {\pi }_{g,0},$$

under Conditions (3.2) and (3.3). Therefore, π̂_g,0(λ) is asymptotically conservative and by Theorem 4 the FDR is controlled asymptotically at α for π̂_g,0(λ).

4. SIMULATION STUDIES

For simplicity, assume the hypotheses are divided into two groups. Without loss of generality, assume there are n observations in each group. Consider the following model, let

$$S_{gi}={\theta }_i+\sqrt{1-{\xi }_g}·Z_{gi}-\sqrt{{\xi }_g}{Z}_0,i=1,\dots ,n;g=1,2$$ (4.1)

be the ith test statistic in group g, where Z_gi and Z₀ are independent standard Normal random variables. Note that Cov(T_gu, T_gv) = ξ_g, for u, v ∈ {1, …, n}, u ≠ v and the model satisfies the PRDS property discussed in Section 2.2 when 0 ≤ ξ_g ≤ 1. Similar dependence structures were considered in Finner, Dickhaus, and Roters (2007) and Benjamini, Krieger, and Yekutieli (2006). Note that when ξ_g > 0, Conditions (3.2) and (3.3) are not satisfied for large N due to the extra Z₀ term.

Consider the hypothesis testing problem with two groups H₀ : θ_j = 0 vs H_a : θ_j > 0, for j = 1, …, 2n. In this section, we compare the performances of the BH and GBH procedures for both oracle and adaptive cases. For the adaptive BH procedure, we compute the (either LSL or TST) estimator π̂₀ for all p-values and then apply the BH procedure at level α/π̂₀.

Four combinations of π_g,0’s are considered: (1) π_1,0 = 0.9 vs π_2,0 = 0.2; (2) π_1,0 = 0.8 vs π_2,0 = 0.4; (3) π_1,0 = 0.99 vs π_2,0 = 0.9; (4) π_1,0 = 0.999 vs π_2,0 = 0.9. In each case, we generate n_g = 10,000 test statistics for each of the two groups based on (4.1). In every group, n_gπ_g,0 of the hypotheses are null and the rest are alternatives with corresponding θ = 3 in one group and θ = 5 in the other group. Other combinations of n and θ’s are also considered and the results are similar. Since we have the information about which hypothesis is from the alternative, the power for the two procedures can be obtained, which is the proportion of true rejections among the false null hypotheses. The power of the BH and GBH procedures is evaluated in pairs based on 200 iterations for each of the 20 FDR levels between 0.01 and 0.2. The results for the oracle and adaptive cases are as follows.

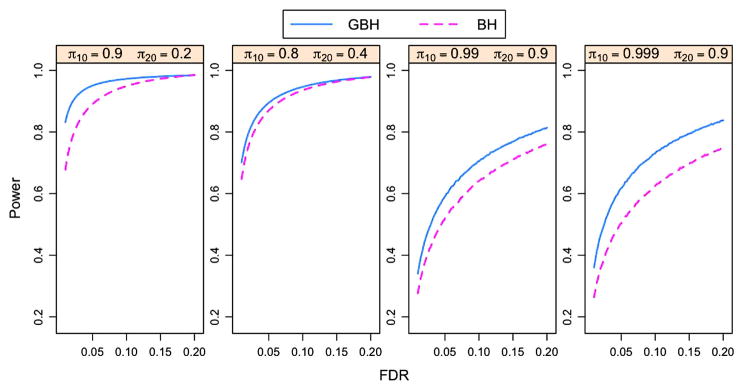
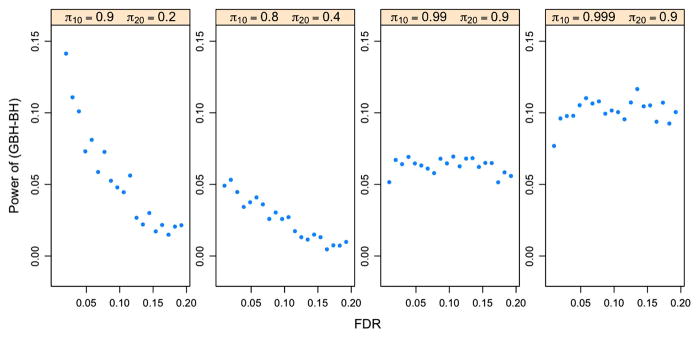
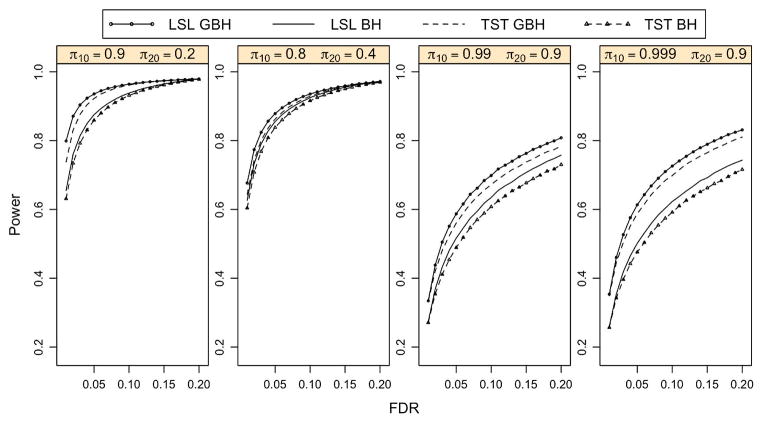
For the oracle case with independent p-values, Figure 2 indicates that the GBH procedure outperforms the BH procedure in all four cases, especially when π_g,0’s are close to 1 (the last two panels). The more the groups differ in π_g,0, the larger the difference is obtained in the power of the two procedures. This is also true for p-values with the PRDS property. Figure 3 shows the power difference between the GBH and BH procedures for p-values under model (4.1) with ξ₁ = ξ₂ = 0.5. All points being above zero indicates the GBH procedure outperforms the BH procedure for all four cases.

Figure 2.

Power curves of the oracle BH and GBH procedures for independent p-values. The p-values are generated based on model (4.1) with ξ₁ = ξ₂ = 0 and n = 10,000 for each group. Each panel corresponds to one combination of π_g,0’s for two groups. The online version of this figure is in color.

Figure 3.

Power differences of the oracle BH and GBH procedures for p-values with the PRDS property. The p-values are generated based on model (4.1) with ξ₁ = ξ₂ = 0.5 and n = 10,000 for each group. Each panel corresponds to one combination of π_g,0’s for two groups. The online version of this figure is in color.

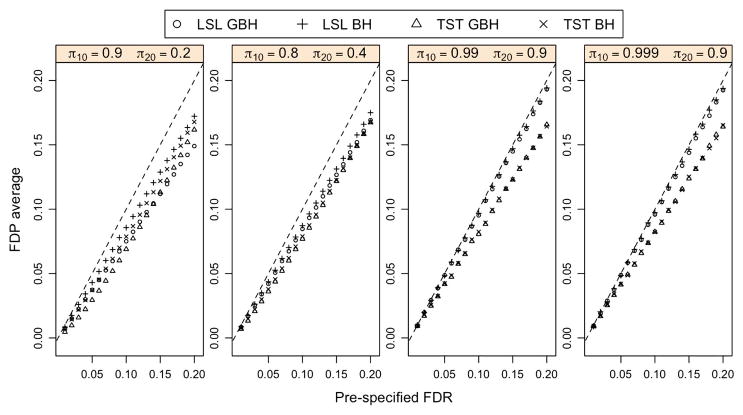
For the adaptive case with independent p-values, we estimate the unknown π_g,0’s using either the TST or LSL method introduced in Section 2.3. Figure 4 indicates that the average of the false discovery proportion (FDP) is controlled at a prespecified FDR level for both the BH and GBH procedures with either the TST or LSL method. The power improvement of the adaptive GBH over the adaptive BH procedure is shown in Figure 5. Both the TST GBH and the LSL GBH procedures are more powerful than the corresponding adaptive BH procedures.

Figure 4.

Comparison of the average FDP and the prespecified FDR for the adaptive BH and GBH procedures. The dash line is the 45-degree line. The p-values are generated based on model (4.1) with ξ₁ = ξ₂ = 0 and n = 10,000 for each group. Each point of the FDP is the average of 200 iterations. The online version of this figure is in color.

Figure 5.

Power curves of the adaptive BH and GBH procedures for independent p-values. The p-values are generated based on model (4.1) with ξ₁ = ξ₂ = 0 and n = 10,000 for each group. Each panel corresponds to one combination of π_g,0’s for two groups. The online version of this figure is in color.

We also analyze the performance of the adaptive GBH procedure for weighting scheme other than π_g,0/π_g,1. According to (2.6), when U_g is uniform, the Bayesian FDR is [π_g,0/D_g(p)]p, where D_g(p) is the distribution function of p-values in group g. It’s therefore natural to consider the weight π̂_g,0/D̃_g(p), where D̃_g is the empirical distribution, as pointed out by a referee. Although this weight takes into consideration of the distribution of p-values in each group, the power of the adaptive procedure using this weight is often low in the situation where we have sparse signals and estimating the alternative distribution is difficult.

5. APPLICATIONS

van’t Veer et al. (2002) used microarrays to study the primary breast tumors of 78 young patients, of which 44 developed cancer in less than 5 years and the other 34 were cancer free during that period. In total 24,184 genes were monitored and p-values were obtained for each gene by comparing the mean ratio of log₁₀ intensities. A fraction of the data is listed in Table 1.

Table 1.

Part of the breast cancer dataset in van’t Veer et al. (2002)

Gene ID	Developed cancer in 5 years				Cancer-free in 5 years				p-value
	patient 1	patient 2	…	patient 44	patient 45	patient 46	…	patient 78
AA000990	0.080	0.130	…	0.136	−0.513	−0.098	…	−0.015	0.7937
AA001113	−0.159	−0.087	…	−0.116	0.190	−0.204	…	0.082	0.4897
AA001360	−0.018	−0.024	…	−0.255	0.114	−0.042	…	0.200	0.1224
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮

NOTE: The entries are adjusted log₁₀(red/green) ratios from cDNA microarrays. The p-values were calculated based on a two-sample t-test for each gene.

In order to apply the GBH procedure which makes use of the group structure, we need to stratify the genes first. Here we consider two grouping strategies.

5.1 Grouping Using Gene Ontology (GO)

The GO project (The Gene Ontology Consortium 2000) provides detailed annotations for a gene product’s biology. It consists of three ontologies, namely Biological Process, Molecular Function, and Cellular Component, each representing a key concept in Molecular Biology. The GO terms are classified into one of the three ontologies. Based on the GO terms, one can construct a top-down tree diagram, in which the higher nodes represent more general biological concepts.

The tree structure provides the idea of GO grouping which can be summarized as follows. After choosing one of the three ontologies, say Biological Process, some higher nodes are selected as ancestors according to the generic GO slim file, which contains the broad overview of each ontology without the detail of each GO terms (available at http://www.geneontology.org/GO.slims.shtml). Next, for those genes with GO IDs, we trace them upward to the nodes we have chosen. Genes that share common ancestors are then grouped together. The biggest concern for GO grouping in our case is that the mapping rate is low. Even though the GO consortium updates their data base on a daily basis, not every gene in our data has a GO ID. For our case, 9492 of the 24,184 genes have the annotation information for Biological Process, therefore the mapping rate for our data is 9492/24,184 ≈ 39%.

However, we may still use the remaining 9492 genes to see the difference of using group information in multiple hypothesis testings. We first divide the genes into four groups with respect to Biological Process, that is, (1) Cell communication; (2) Cell growth and/or maintenance; (3) Development; and (4) Multifunction. The results for the adaptive BH and GBH procedures are listed in Table 2. For simplicity, we just report the results for the LSL method.

Table 2.

Comparison of the adaptive LSL GBH and the adaptive LSL BH procedures for GO grouping. FDR level = 0.15

Group	# of genes	${\widehat{\pi }}_{g,0}^{\text{LSL}}$	LSL BH	LSL GBH
(1) Cell communication	593	0.995	0	3
(2) Cell growth/maintenance	4142	0.987	0	13
(3) Development	434	0.989	0	0
(4) Multifunction	4323	0.983	0	25
Total	9492		0	41

At FDR level 0.15, Table 2 indicates that the adaptive GBH procedure focuses more on groups with smaller estimated π_g,0’s, that is, groups (2) and (4), and is able to discover genes that are not detectable using the adaptive BH procedure. In fact, as shown in Figure 6, using either the LSL or TST method, the adaptive BH procedure cannot detect any signals when the FDR level is less than 0.15.

Figure 6.

Breast cancer study, 9492 genes. The plots show the number of genes detected by the adaptive BH and GBH procedures using Gene Ontology grouping. Left panel: the LSL method. Right panel: the TST method. Data from van’t Veer et al. (2002). The online version of this figure is in color.

Even though the mapping rate for this dataset is low, the idea of GO grouping could be a good choice if the data were collected in terms of GO identities; or the mapping between the GO ID and other gene IDs (e.g., GenBank Accession Number) was more complete. Then each group may correspond to different biological processes or genetic functions within the tumor and the GBH method can help us to find more signals among desired groups.

5.2 Grouping Using k-Means Clustering

Another grouping idea is to apply clustering. Here we choose k-means clustering with initial points satisfying maximum separation rule based on all the 78 samples. Note that we are not just clustering the p-values. Unlike GO grouping, k-means clustering makes use of the whole dataset and we do not have to worry about the mapping rate. Although we do have the difficulties regarding cluster analysis, for example, the choice of initial points, number of clusters, and the interpretation of each cluster, we use it as an illustrative example to compare the performances of the adaptive BH and GBH procedures.

In order to have a reliable estimator for each group, six clusters are selected such that within each cluster there are at least 200 genes. Table 3 shows the results for the two procedures using the LSL method at FDR level 0.1. Most of the additional discoveries found by the adaptive GBH procedure come from the first cluster, which is expected to contain more signals because the estimated π_g,0 is relatively smaller than the others. Gene-annotation enrichment analysis confirms that those 109 genes selected by the GBH procedure in the first cluster are closely associated with cell cycle, mitosis, chromosome segregation, and phosphoprotein, which are common factors related to breast cancer. Similar analyses on the four and five-cluster cases indicate that the number of genes detected by the adaptive GBH procedure is 145 and 226, respectively. Out of those genes, 94 of them are overlapping with the six-cluster case. Comparing with an average of eight genes discovered by random grouping, which assigns groups randomly with the same group sizes as the above three cases, clustering and using the GBH procedure is advantageous in our case.

Table 3.

Comparison of the adaptive LSL GBH and the adaptive LSL BH procedures for k-means grouping. FDR level = 0.1

Cluster	# of genes	${\widehat{\pi }}_{g,0}^{\text{LSL}}$	LSL BH	LSL GBH
1	1904	0.871	4	109
2	214	0.991	0	0
3	1368	0.999	0	0
4	2458	0.969	1	19
5	7058	0.999	4	2
6	11,164	0.996	3	6
Total	24,184		12	136

For comparison of the two procedures over a range of FDR levels, Figure 1 shows the increment in the number of signals detected by the adaptive GBH over BH procedure for both the LSL and TST methods. This indeed shows that by applying the GBH procedure, more signals can be detected.

6. SUMMARY

We have presented a new approach of p-value weighting procedure GBH for controlling the FDR when the hypotheses are believed to have some group structure. We prove that it controls the FDR for hypotheses with the positive regression dependence property when the proportions of true null hypotheses π_g,0’s are known in each group. The weighting scheme (π_g,0/π_g,1) for the p-values in each group makes it possible to focus on groups that are expected to have more signals.

By estimating π_g,0 for each group, we propose the adaptive GBH procedure and show that it controls the FDR asymptotically under weak dependence. We demonstrate the benefit of the adaptive GBH over BH by two methods of estimating π_g,0, namely the LSL (Benjamini and Hochberg 2000) and the TST (Benjamini, Krieger, and Yekutieli 2006) estimators. As we have pointed out, the choice of the estimator for π_g,0 in general does not affect the performance of the adaptive GBH procedure. In practice, people may choose the estimator based on their own preference.

APPENDIX: PROOFS

Proof of Theorem 1

The proof is based on the proof of theorem 4.1 in Finner, Dickhaus, and Roters (2009). Let ϕ = (ϕ₁, …, ϕ_N) be the multiple testing procedure. ϕ_i = 0 means retaining H_i and ϕ_i = 1 means rejecting H_i. The FDR for oracle GBH is

$$\begin{array}{l}\text{FDR}({\varphi }_{\text{GBH}})=E\left[\frac{V}{R\vee 1}\right]=E\left[\frac{V}{R\vee 1}\sum _{j\in I_N}\{R=j\}\right]\\ =\sum _{g=1}^K\sum _{i\in I_{g,0}}\sum _{j\in I_N}\frac{1}{j}Pr(R=j,{\varphi }_{g,i}=1)\\ =\sum _{g=1}^K\sum _{i\in I_{g,0}}\sum _{j\in I_N}\frac{1}{j}Pr\left(R=j,\frac{{\pi }_{g,0}}{{\pi }_{g,1}}{P}_{g,i}\le \frac{j}{N}{\alpha }^w\right).\end{array}$$

Note that if π_g,0 = 0 or π_g,0 = 1 for some g, that group doesn’t contribute to the FDR because I_g,0 = ∅ if π_g,0 = 0 and $Pr(R=j,\frac{{\pi }_{g,0}}{{\pi }_{g,1}}{P}_{g,i}\le \frac{j}{N}{\alpha }^w)=0$ if π_g,0 = 1 (we treat π_g,0/π_g,1 as ∞). Let η = {g : π_g,0 ∈ (0, 1)}. Then

$$\text{FDR}({\varphi }_{\text{GBH}})=\sum _{g\in \eta }\sum _{i\in I_{g,0}}\sum _{j\in I_N}\frac{1}{j}Pr\left(R=j,\frac{{\pi }_{g,0}}{{\pi }_{g,1}}{P}_{g,i}\le \frac{j}{N}{\alpha }^w\right).$$

Using the proof of theorem 4.1 in Finner, Dickhaus, and Rosters (2009), we have

$$\begin{array}{l}\text{FDR}({\varphi }_{\text{GBH}})\le \sum _{g\in \eta }\frac{{\pi }_{g,1}{\alpha }^w}{{\pi }_{g,0}N}\sum _{i\in I_{g,0}}Pr\left(R\ge 1\mid P_{g,i}^w\le \frac{1}{N}{\alpha }^w\right)\\ =\sum _{g\in \eta }\frac{{\pi }_{g,1}{\alpha }^w}{{\pi }_{g,0}N}\sum _{i\in I_{g,0}}1=\sum _{g\in \eta }\frac{{\pi }_{g,1}{\alpha }^w}{{\pi }_{g,0}N}·n_g{\pi }_{g,0}\\ =\frac{{\sum }_{g\in \eta }{n}_g{\pi }_{g,1}}{{\sum }_{g=1}^K{n}_g{\pi }_{g,1}}\alpha \le \alpha .\end{array}$$

Proof of Lemma 1

For the unweighted case, the expected number of rejections of BH procedure for a given threshold t, where t ≤ t̃ = (1 − π₀) max_g π_g,0/π_g,1 is

$$\begin{array}{l}\mathbb{E}[R_{\text{BH}}(t)]=\mathbb{E}\sum _{g=1}^K\sum _{j\in I_g}\{{\pi }_0{P}_j\le t\}\\ =\mathbb{E}\sum _{g=1}^K\left(\sum _{j\in I_{g,0}}\left\{P_j\le \frac{t}{{\pi }_0}\right\}+\sum _{j\in I_{g,1}}\left\{P_j\le \frac{t}{{\pi }_0}\right\}\right)\\ \le Nt+\sum _{g=1}^K{n}_g{\pi }_{g,1}F\left(\frac{t}{{\pi }_0}\right).\end{array}$$

Similarly, the expected number of rejections of GBH procedure for t ≤ t̃ is

$$\begin{array}{l}\mathbb{E}[R_{\text{GBH}}(t)]=\mathbb{E}\sum _{g=1}^K\sum _{j\in I_g}\left\{\frac{{\pi }_{g,0}}{{\pi }_{g,1}}(1-{\pi }_0)P_j\le t\right\}\\ =Nt+\sum _{g=1}^K{n}_g{\pi }_{g,1}F\left(\frac{{\pi }_{g,1}t}{{\pi }_{g,0}(1-{\pi }_0)}\right).\end{array}$$

Let ε_g = n_gπ_g,1/Σ_g n_gπ_g,1 and x_g = π_g,0 (1 − π₀)/π_g,1. Now that x ↦ F(t/x) is convex for all x ≥ t̃. We have F(t/Σ_gε_gx_g) ≤ Σ_g ε_gF(t/x_g), that is,

$$F\left(\frac{t}{{\pi }_0}\right)\le \frac{1}{{\sum }_g{n}_g{\pi }_{g,1}}\sum _{g=1}^K{n}_g{\pi }_{g,1}F\left(\frac{{\pi }_{g,1}t}{{\pi }_{g,0}(1-{\pi }_0)}\right).$$

Therefore, 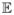[R_BH(t)] ≤ 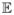[R_GBH(t)] for t ≤ t̃.

Proof of Lemma 2

Consider the estimator of D_g(t) defined in (2.12). Under (3.1), for any t ≥ 0,

$$\begin{array}{l}\underset{t}{sup}|{\stackrel{\sim }{D}}_g(t)-D_g(t)|\le \underset{t}{sup}\left|\frac{n_{g,0}}{n_g}\frac{1}{n_{g,0}}\sum _{i\in I_{g,0}}\{P_i\le t\}-{\pi }_{g,0}{U}_g(t)\right|+\underset{t}{sup}\left|\frac{n_{g,1}}{n_g}\frac{1}{n_{g,1}}\sum _{i\in I_{g,1}}\{P_i\le t\}-{\pi }_{g,1}{F}_g(t)\right|\\ \le \left|\frac{n_{g,0}}{n_g}-{\pi }_{g,0}\right|+{\pi }_{g,0}\underset{t}{sup}\left|\frac{1}{n_{g,0}}\sum _{i\in I_{g,0}}\{P_i\le t\}-U_g(t)\right|+\left|\frac{n_{g,1}}{n_g}-{\pi }_{g,1}\right|+{\pi }_{g,1}\underset{t}{sup}\left|\frac{1}{n_{g,1}}\sum _{i\in I_{g,1}}\{P_i\le t\}-F_g(t)\right|,\end{array}$$

where ${sup}_t\mid n_{g,0}^{-1}{\sum }_{i\in I_{g,0}}\{P_i\le t\}-U_g(t)\mid \stackrel{\text{a}.\text{s}.}{\to }0$ and ${sup}_t\mid \{n_{g,1}^{-1}\times {\sum }_{i\in I_{g,1}}\{P_i\le t\}-F_g(t)\mid \stackrel{\text{a}.\text{s}.}{\to }0$ by Glivenko–Cantelli Theorem. Therefore, ${sup}_t\mid {\stackrel{\sim }{D}}_g(t)-D_g(t)\mid \stackrel{\text{a}.\text{s}.}{\to }0$.

Proof of Theorem 2

Theorem 4 generalizes this theorem. See the proof of Theorem 4.

Proof of Theorem 3

Under the conditions that U_g(t) = U(t) = t and F_g(t) = F(t) for all g, in the proof of Lemma 2, we show that G(a, t) ≥ C(t/π₀) for all 0 ≤ t ≤ min_g a_g. Since G(a, π₀) ≤ π₀ = t/C(t/π₀)|_t=π0 and both G(a, t) and t/C(t/π₀) are increasing, we have G(a, t) ≥ C(t/π₀) for all 0 ≤ t ≤ max_g a_g. Deduce B(a, t) ≤ t/C(t/π₀) for t ∈ c(a). Therefore $t_{\text{BH}}^{\ast }\le t_{\text{GBH}}^{\ast }$. Conditions lim_t↓0 t/C(t/π) ≤ α and π₀ ≥ α guarantee that $t_{\text{BH}}^{\ast }>0$.

Note that both G(a, t) and t/C(t/π₀) are continuous, we have

$$\frac{t_{\text{BH}}^{\ast }}{C(t_{BH}^{\ast }/{\pi }_0)}=\frac{t_{\text{GBH}}^{\ast }}{G(\mathbf{a},t_{\text{GBH}}^{\ast })}.$$

Since $t_{\text{BH}}^{\ast }\le t_{\text{GBH}}^{\ast }$, deduce $C(t_{\text{BH}}^{\ast }/{\pi }_0)\le G(\mathbf{a},t_{\text{GBH}}^{\ast })$. For the adaptive BH procedure, the number of rejections R_BH(T̂_BH) = Σ_i∈IN{P_i ≤ T̂_BH/π̂₀} = N · C_N (T̂_BH/π̂₀), and

$$\mid C_N({\widehat{T}}_{\text{BH}}/{\widehat{\pi }}_0)-C(t_{\text{BH}}^{\ast }/{\pi }_0)\mid \le \underset{t\ge 0}{sup}\mid C_N(t/{\widehat{\pi }}_0)-C(t/{\widehat{\pi }}_0)\mid +\mid C({\widehat{T}}_{\text{BH}}/{\widehat{\pi }}_0)-C(t_{\text{BH}}^{\ast }/{\pi }_0)\mid ,$$

where ${sup}_{t\ge 0}\mid C_N(t/{\widehat{\pi }}_0)-C(t/{\widehat{\pi }}_0)\mid \stackrel{\text{a}.\text{s}.}{\to }0$ by Glivenko–Cantelli Theorem and $\mid C({\widehat{T}}_{\text{BH}}/{\widehat{\pi }}_0)-C(t_{\text{BH}}^{\ast }/{\pi }_0)\mid \stackrel{P}{\to }0$ by continuous mapping theorem. Therefore $C_N({\widehat{T}}_{\text{BH}}/{\widehat{\pi }}_0)\stackrel{P}{\to }C(t_{\text{BH}}^{\ast }/{\pi }_0)$. Analogously one can show that $G_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})\stackrel{P}{\to }G(\mathbf{a},t_{\text{GBH}}^{\ast })$. A more generalized argument is shown in the proof of Theorem 4. By dominant convergence theorem we have $N^{-1}\mathbb{E}[R_{\text{BH}}({\widehat{T}}_{\text{BH}})]\to C(t_{\text{BH}}^{\ast }/{\pi }_0)$ and $N^{-1}\mathbb{E}[R_{\text{GBH}}({\widehat{T}}_{\text{GBH}})]\to G(\mathbf{a},t_{\text{GBH}}^{\ast })$. Therefore 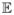[R_BH(T̂_BH)]/ 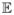[R_GBH(T̂_GBH)] ≤ 1 + o(1).

Proof of Theorem 4

The proof applies Glivenko–Cantelli Theorem as in Storey, Taylor, and Siegmund (2004) and Genovese, Roeder, and Wasserman (2006). Let S = c(â) ∪ c(ρ). For any t ∈ S, we have

$$\underset{t\in S}{sup}\mid G_N(\widehat{\mathbf{a}},t)-G(\mathit{\rho },t)\mid \le \underset{t\ge 0}{sup}\mid G_N(\widehat{\mathbf{a}},t)-G(\widehat{\mathbf{a}},t)\mid +\underset{t\ge 0}{sup}\mid G(\widehat{\mathbf{a}},t)-G(\mathit{\rho },t)\mid .$$

Note that for t ≥ 0,

$$\begin{array}{l}\underset{t}{sup}\mid G_N(\widehat{\mathbf{a}},t)-G(\widehat{\mathbf{a}},t)\mid =\frac{1}{N}\sum _{g=1}^K{n}_g\underset{t}{sup}\mid {\stackrel{\sim }{D}}_g(t/{\widehat{a}}_g)-D_g(t/{\widehat{a}}_g)\mid \\ \le \frac{1}{N}\sum _{g=1}^K{n}_g\underset{t}{sup}\mid {\stackrel{\sim }{D}}_g(t)-D_g(t)\mid \stackrel{\text{a}.\text{s}.}{\to }0,\end{array}$$ (A.1)

where the last step is implied by Lemma 2. On the other hand,

$$\underset{t\ge 0}{sup}\mid G(\widehat{\mathbf{a}},t)-G(\mathit{\rho },t)\mid =\frac{1}{N}\sum _{g=1}^K{n}_g\underset{t\ge 0}{sup}\mid D_g(t/{\widehat{a}}_g)-D_g(t/{\rho }_g)\mid .$$

Since D_g is continuous on [0, +∞) and lim_t→∞ D_g(t) = 1 is finite, D_g is uniform continuous. By continuous mapping theorem, $\mid t/{\widehat{a}}_g-t/{\rho }_g\mid \stackrel{P}{\to }0$. Therefore ${sup}_{t\in S}\mid D_g(t/{\widehat{a}}_g)-D_g(t/{\rho }_g)\mid \stackrel{P}{\to }0$. So we have ${sup}_{t\in S}\mid G_N(\widehat{\mathbf{a}},t)-G(\mathit{\rho },t)\mid \stackrel{P}{\to }0$.

Let $B_N(\widehat{\mathbf{a}},t)=\frac{{\sum }_g{n}_{g,0}t/{\widehat{a}}_g}{N·G_N(\widehat{\mathbf{a}},t)}$. According to (2.16) and (3.6), T̂_GBH = sup_t∈c(â){t : B_N (â, t) ≤ α} and $t_{\text{GBH}}^{\ast }={sup}_{t\in c(\mathit{\rho })}\{t:B(\mathit{\rho },t)\le \alpha \}$, where $B(\mathit{\rho },t)=\frac{{\sum }_g{\pi }_g{\pi }_{g,0}t/{\rho }_g}{G(\mathit{\rho },t)}$. Note that the assumption lim_t↓0 B(π, t) ≠ α implies $t_{\text{GBH}}^{\ast }>0$.

We first show ${\widehat{T}}_{\text{GBH}}\stackrel{P}{\to }{t}_{\text{GBH}}^{\ast }$. For any ξ > 0, note that B(ρ, t) is increasing for t ≥ max_g ρ_g, therefore $B(\mathit{\rho },t_{\text{GBH}}^{\ast }+\xi )>\alpha$, otherwise it contradicts with $t_{\text{GBH}}^{\ast }$ being the supremum. Fix δ > 0, for any δ′ ≥ δ, let $t^{\prime }=t_{\text{GBH}}^{\ast }+{\delta }^{\prime }$. Then

$$\begin{array}{l}\underset{{\delta }^{\prime }\ge \delta }{inf}{B}_N(\widehat{\mathbf{a}},t^{\prime })=\underset{{\delta }^{\prime }\ge \delta }{inf}\frac{(1/N){\sum }_g{n}_{g,0}{t}^{\prime }/{\widehat{a}}_g}{G_N(\widehat{\mathbf{a}},t^{\prime })}\\ \ge \underset{{\delta }^{\prime }\ge \delta }{inf}\frac{{\sum }_g{\pi }_g{\pi }_{g,0}{t}^{\prime }/{\rho }_g-{\sum }_g\mid n_{g,0}/N{\widehat{a}}_g-{\pi }_g{\pi }_{g,0}/{\rho }_g\mid t^{\prime }}{G(\mathit{\rho },t^{\prime })+{sup}_{t\in S}\mid G_N(\widehat{\mathbf{a}},t)-G(\mathit{\rho },t)\mid }\\ \ge \frac{1-{\epsilon }_1}{[1/{inf}_{{\delta }^{\prime }\ge \delta }B(\rho ,t^{\prime })]+{\epsilon }_2},\end{array}$$

where ε₁ = Σ_g |n_g,0/Nâ_g − π_gπ_g,0/ρ_g|/(Σ_g π_gπ_g,0/ρ_g), and ε₂ = sup_t∈S |G_N (â, t) − G(ρ, t)|/(Σ_g π_gπ_g,0t′/ρ_g). Since ${\epsilon }_2\stackrel{P}{\to }0$ and inf_δ′≥δ B(ρ, t′) > α, it can be derived that Pr(∩_δ′≥δ {B_N (â, t′) > α}) → 1 which implies $Pr({\widehat{T}}_{\text{GBH}}<t_{\text{GBH}}^{\ast }+\delta )\to 1$.

On the other hand, since B(ρ, t) has a nonzero derivative at $t_{\text{GBH}}^{\ast }$, it must be positive, otherwise $t_{\text{GBH}}^{\ast }$ cannot be the supremum of all t such that B(ρ, t) ≤ α. Thus, t ↦ B(ρ, t) is an increasing function and for any ξ > 0, $B(\mathit{\rho },t_{\text{GBH}}^{\ast }-\xi )<\alpha$. For any δ > 0, let $t°=t_{\text{GBH}}^{\ast }-\delta$,

$$\begin{array}{l}{B}_N(\widehat{\mathbf{a}},t°)=\frac{(1/N){\sum }_g{n}_{g,0}t°/{\widehat{a}}_g}{G_N(\widehat{\mathbf{a}},t°)}\\ \le \frac{{\sum }_g{\pi }_g{\pi }_{g,0}t°/{\rho }_g+{\sum }_g\mid n_{g,0}/N{\widehat{a}}_g-{\pi }_g{\pi }_{g,0}/{\rho }_g\mid t°}{G(\mathit{\rho },t°)-{sup}_{t\in S}\mid G_N(\widehat{\mathbf{a}},t)-G(\mathit{\rho },t)\mid }\\ \le \frac{1+{\epsilon }_1}{[1/B(\rho ,t°)]-{\epsilon }_2},\end{array}$$

where ${\epsilon }_2\stackrel{P}{\to }0$ and B(ρ, t°) < α. Then Pr(B_N (â, t°) < α) → 1. Deduce $Pr({\widehat{T}}_{\text{GBH}}>t_{\text{GBH}}^{\ast }-\delta )\to 1$. Combine this and previous result we get ${\widehat{T}}_{\text{GBH}}\stackrel{P}{\to }{t}_{\text{GBH}}^{\ast }$.

Next, we prove FDR(T̂_GBH) ≤ α/min_g{b_g} + o(1). Let

$$H_N(\widehat{\mathbf{a}},t)=\frac{1}{N}\sum _{g=1}^K\sum _{i\in I_{g,0}}\{P_i\le t/{\widehat{a}}_g\}$$

be the empirical distribution of p-values under null hypothesis for adaptive GBH procedure. Note that ${\widehat{T}}_{\text{GBH}}\stackrel{P}{\to }{t}_{\text{GBH}}^{\ast }$ implies $Pr({\widehat{T}}_{\text{GBH}}>t_{\text{GBH}}^{\ast }-\delta )\to 1$ for any δ > 0. Since $t_{\text{GBH}}^{\ast }>0$, deduce Pr(T̂_GBH > 0) → 1. On the other hand, the assumption ζ̂ < 1 rules out the situation where T̂_GBH/â_g → 0 for all groups. Therefore Pr(Σ_g Σ_i∈Ig {P_i ≤ T̂_GBH/â_g} ≥ 1) → 1. Then the false discovery proportion (FDP) is

$$\text{FDP}({\widehat{T}}_{\text{GBH}})=\frac{N^{-1}{\sum }_{g=1}^K{\sum }_{i\in I_{g0}}\{P_i\le {\widehat{T}}_{\text{GBH}}/{\widehat{a}}_g\}}{N^{-1}{\sum }_{g=1}^K{\sum }_{i\in I_g}\{P_i\le {\widehat{T}}_{\text{GBH}}/{\widehat{a}}_g\}}=\frac{H_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})}{G_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})},$$

where H_N (â, T̂_GBH) satisfies

$$\begin{array}{l}\left|H_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})-\frac{1}{N}\sum _{g=1}^K{n}_{g,0}{U}_g({\widehat{T}}_{\text{GBH}}/{\widehat{a}}_g)\right|\\ \le \frac{1}{N}\sum _{g=1}^K{n}_{g,0}\underset{t\in c(\widehat{\mathbf{a}})}{sup}\left|\frac{1}{n_{g,0}}\sum _{i\in I_{g,0}}\{P_i\le t/{\widehat{a}}_g\}-U_g(t/{\widehat{a}}_g)\right|\\ \le \frac{1}{N}\sum _{g=1}^K{n}_{g,0}\underset{t\ge 0}{sup}\left|\frac{1}{n_{g,0}}\sum _{i\in I_{g,0}}\{P_i\le t\}-U_g(t)\right|.\end{array}$$

By Condition (3.2), Glivenko–Cantelli Theorem implies ${sup}_{t\ge 0}\mid \frac{1}{n_{g,0}}\times {\sum }_{i\in I_{g,0}}\{P_i\le t\}-U_g(t)\mid \stackrel{\text{a}.\text{s}.}{\to }0$. Therefore,

$$\left|H_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})-\frac{1}{N}\sum _{g=1}^K{n}_{g,0}{U}_g({\widehat{T}}_{\text{GBH}}/{\widehat{a}}_g)\right|\stackrel{\text{a}.\text{s}.}{\to }0.$$ (A.2)

Now that ${\widehat{T}}_{\text{GBH}}\stackrel{P}{\to }{t}_{\text{GBH}}^{\ast }$ and by (3.1),

$$\frac{1}{N}\sum _{g=1}^K{n}_{g,0}{U}_g({\widehat{T}}_{\text{GBH}}/{\widehat{a}}_g)\stackrel{P}{\to }\sum _{g=1}^K{\pi }_g{\pi }_{g,0}{U}_g(t_{\text{GBH}}^{\ast }/{\rho }_g).$$ (A.3)

Combine (A.2) and (A.3) we have

$$H_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})\stackrel{P}{\to }\sum _{g=1}^K{\pi }_g{\pi }_{g,0}{U}_g(t_{\text{GBH}}^{\ast }/{\rho }_g).$$ (A.4)

On the other hand,

$$\begin{array}{l}\mid G_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})-G(\mathit{\rho },t_{\text{GBH}}^{\ast })\mid \\ \le \mid G_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})-G(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})\mid +\mid G(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})-G(\mathit{\rho },t_{\text{GBH}}^{\ast })\mid \\ \le \underset{t\ge 0}{sup}\mid G_N(\widehat{\mathbf{a}},t)-G(\widehat{\mathbf{a}},t)\mid +\mid G(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})-G(\mathit{\rho },t_{\text{GBH}}^{\ast })\mid ,\end{array}$$

where ${sup}_{t\ge 0}\mid G_N(\widehat{\mathbf{a}},t)-G(\widehat{\mathbf{a}},t)\mid \stackrel{\text{a}.\text{s}.}{\to }0$ by (A.1) and $\mid G(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})-G(\mathit{\rho },t_{\text{GBH}}^{\ast })\mid \stackrel{P}{\to }0$ by continuous mapping theorem. Therefore,

$$G_N(\widehat{\mathbf{a}},{\widehat{T}}_{\text{GBH}})\stackrel{P}{\to }G(\mathit{\rho },t_{\text{GBH}}^{\ast }).$$ (A.5)

Since $t_{\text{GBH}}^{\ast }>0$ and ζ̄ < 1, we have $G(\mathit{\rho },t_{\text{GBH}}^{\ast })>0$. By (A.4) and (A.5),

$$\text{FDP}({\widehat{T}}_{\text{GBH}})\stackrel{P}{\to }\frac{{\sum }_{g=1}^K{\pi }_g{\pi }_{g,0}{U}_g(t_{\text{GBH}}^{\ast }/{\rho }_g)}{G(\mathit{\rho },t_{\text{GBH}}^{\ast })}.$$

By dominated convergence theorem,

$$\text{FDR}({\widehat{T}}_{\text{GBH}})=E[\text{FDP}({\widehat{T}}_{\text{GBH}})]\to \frac{{\sum }_{g=1}^K{\pi }_g{\pi }_{g,0}{U}_g(t_{\text{GBH}}^{\ast }/{\rho }_g)}{G(\mathit{\rho },t_{\text{GBH}}^{\ast })}.$$ (A.6)

Note that ζ_g ≥ b_gπ_g,0 for some b_g > 0. Deduce ρ_g ≥ b_gπ_g,0/(1 − ζ_g). Since U_g(t) ≤ t for all t ≥ 0, we have

$$\frac{{\sum }_{g=1}^K{\pi }_g{\pi }_{g,0}U(t_{\text{GBH}}^{\ast }/{\rho }_g)}{G(\mathit{\rho },t_{\text{GBH}}^{\ast })}\le \frac{1}{{min}_g\{b_g\}}\frac{(1-\overline{\zeta })t_{\text{GBH}}^{\ast }}{G(\mathit{\rho },t_{\text{GBH}}^{\ast })}\le \frac{\alpha }{{min}_g\{b_g\}}.$$

Hence, FDR(T̂_GBH) ≤ α/min_g{b_g} + o(1).