Abstract
Clinical imaging with structural MRI routinely relies on multiple acquisitions of the same region of interest under several different contrast preparations. This work presents a reconstruction algorithm based on Bayesian compressed sensing to jointly reconstruct a set of images from undersampled k-space data with higher fidelity than when the images are reconstructed either individually or jointly by a previously proposed algorithm, M-FOCUSS. The joint inference problem is formulated in a hierarchical Bayesian setting, wherein solving each of the inverse problems corresponds to finding the parameters (here, image gradient coefficients) associated with each of the images. The variance of image gradients across contrasts for a single volumetric spatial position is a single hyperparameter. All of the images from the same anatomical region, but with different contrast properties, contribute to the estimation of the hyperparameters, and once they are found, the k-space data belonging to each image are used independently to infer the image gradients. Thus, commonality of image spatial structure across contrasts is exploited without the problematic assumption of correlation across contrasts. Examples demonstrate improved reconstruction quality (up to a factor of 4 in root-mean-square error) compared to previous compressed sensing algorithms and show the benefit of joint inversion under a hierarchical Bayesian model.
Keywords: Simultaneous sparse approximation, clinical MRI, sparse Bayesian learning
Introduction
In clinical applications of structural magnetic resonance imaging (MRI), it is routine to image the same region of interest under multiple contrast settings to enhance the diagnostic power of T1, T2, and proton-density weighted images. In this article, we present a Bayesian framework that makes use of the similarities between the images with different contrasts in jointly reconstructing MRI images from undersampled data obtained in k-space. To the best of our knowledge, ours is the first attempt towards joint reconstruction of such multi-contrast scans. Our method applies the joint Bayesian compressive sensing (CS) technique of Ji et al. (1) to the multi-contrast MRI setting with modifications for computational efficiency and k-space acquisition efficiency. Compared to conventional CS algorithms that work on each of the images independently (e.g. (2)), this joint inversion technique is seen to improve the reconstruction quality at a fixed undersampling ratio and to produce similar reconstruction results at higher undersampling ratios (i.e., with less data).
Conventional CS produces images using sparse approximation with respect to an appropriate basis; with gradient sparsity or wavelet-domain sparsity, the positions of nonzero coefficients correspond directly to spatial locations in the image. A natural extension to exploit structural similarities in multi-contrast MRI is to produce an image for each contrast setting while keeping the transform-domain sparsity pattern for each image the same. This is called joint or simultaneous sparse approximation. One of the earliest applications of simultaneous sparse approximation was in localization and used an algorithm based on convex relaxation (3). An early greedy algorithm was provided by Tropp et al. (4). Most methods for simultaneous sparse approximation extend existing algorithms such as Orthogonal Matching Pursuit (OMP), FOCal Underdetermined System Solver (FOCUSS) (5), or Basis Pursuit (BP) (6) with a variety of ways for fusing multiple measurements to recover the nonzero transform coefficients. Popular joint reconstruction approaches include Simultaneous OMP (SOMP) (4), M-FOCUSS (7), and the convex relaxation algorithm in (8). All of these algorithms provide significant improvement in approximation quality, however they suffer from two important shortcomings for our problem statement. First, they assume that the signals share a common sparsity support, which does not apply to the multi-contrast MRI scans. Even though these images have nonzero coefficients in similar locations in the transform domain, assuming perfect overlap in the sparsity support is too restrictive. Second, with the exception of (9), most methods formulate their solutions under the assumption that all of the measurements are made via the same observation matrix, which in our context would correspond to sampling the same k-space points for all of the multi-contrast scans. As we demonstrate, observing different frequency sets for each image increases our overall k-space coverage and improves reconstruction quality.
The general joint Bayesian CS algorithm recently presented by Ji et al. (1) addresses these shortcomings and fits perfectly to the multi-contrast MRI context. Given the observation matrices Φi ∈ ℂ Ki×M with Ki representing the number of k-space points sampled for the ith image and M being the number of voxels, the linear relationship between the k-space data and the unknown images can be expressed as yi = Φi xi where i = 1,…,L indexes the L multi-contrast scans and yi is the vector of k-space samples belonging to the ith image xi. Let us further denote the vertical and the horizontal image gradients as and , which are approximately sparse since the MRI images are approximately piecewise constant in the spatial domain. In the Bayesian setting, our task is to provide a posterior belief for the values of the gradients and , with the prior assumption that these gradients should be sparse and the reconstructed images should be consistent with the acquired k-space data. Each image formation problem (for a single contrast) constitutes an inverse problem of the form yi → xi and the joint Bayesian algorithm aims to share information among these tasks by placing a common hierarchical prior over the problems. Such hierarchical Bayesian models can capture the dependencies between the signals without imposing correlation, for example by positing correlation of variances between zero-mean quantities that are conditionally independent given the hyperparameters. Data from all signals contribute to learning the common prior (i.e., estimating the hyperparameters) in a maximum likelihood framework, thus making information sharing among the images possible. Given the hierarchical prior, the individual gradient coefficients are estimated independently. Hence, the solution of each inverse problem is affected by both its own measured data and by data from the other tasks via the common prior. The dependency through the estimated hyperparameters is essentially a spatially-varying regularization, so it preserves the integrity of each individual reconstruction problem.
Apart from making use of the joint Bayesian CS machinery to improve the image reconstruction quality, the proposed method presents several novelties. First, we reduce the Bayesian algorithm to practice on MRI data sampled in k-space with both simulated and in vivo acquisitions. In the elegant work by Ji et al. (1), their method was demonstrated on CS measurements made directly in the sparse transform domain as opposed to the k-space domain that is the natural source of raw MRI data. The observations yi were obtained via yi = Φiθi where θi are the wavelet coefficients belonging to the ith test image. But in all practical settings of MRI data acquisition, the observations are carried out in the k-space corresponding to the reconstructed images themselves, i.e. we do not acquire the k-space data belonging to the wavelet transform of the image. In our method as presented here, we obtain measurements of the image gradients by a simple modification of the k-space data and thus overcome this problem. After solving for the gradient coefficients with the Bayesian algorithm, we recover images that are consistent with these gradients in a least-squares setting. Secondly, our version accelerates the computationally-demanding joint reconstruction algorithm by making use of the Fast Fourier Transform (FFT) to replace some of the demanding matrix operations in the original implementation by Ji et al. This makes it possible to use the algorithm with higher resolution data than with the original implementation, which has large memory requirements. Also, we exploit partially-overlapping undersampling patterns to increase our collective k-space coverage when all images are considered; we report that this flexibility in the sampling pattern design improves the joint CS inversion quality. Additionally, we generalize the algorithm to allow inputs that correspond to complex-valued images. Finally, we compare our findings with the popular method in (2) and with the M-FOCUSS joint reconstruction scheme. In addition to yielding smaller reconstruction errors relative to either method, the proposed Bayesian algorithm contains no parameters that need tuning. To our knowledge, this is the first presentation of joint reconstruction of multi-contrast MRI data with either M-FOCUSS or joint Bayesian reconstruction.
Theory
Compressed Sensing in MRI
Compressed sensing has received abundant recent attention in the MRI community because of its demonstrated ability to speed up data acquisition. Making use of CS theory to this end was first proposed by Lustig et al. (2), who formulated the inversion problem as
| (1) |
where Ψ is the wavelet basis, TV (.) is the ℓ1 norm of discrete gradients as a proxy for total variation, β trades off wavelet sparsity and gradient sparsity, FΩ is the undersampled Fourier transform operator containing only the frequencies ω ∈ Ω and ε is a threshold parameter that needs to be tuned for each reconstruction task. This constrained inverse problem can be posed as an unconstrained optimization program (2)
| (2) |
where λwavelet and λTV are wavelet and total variation regularization parameters that again call for tuning.
Conventional Compressed Sensing from a Bayesian Standpoint
Before we present the mathematical formulation that is the basis for our method, this section briefly demonstrates that it is possible to recover the conventional CS formulation in Eq. 2 with a Bayesian treatment. For the moment, consider abstractly that we are working with a sparse signal x ∈ RM that is observed by compressive measurements via the matrix Φ ∈ RK×M, where K < M. The general approach of Bayesian CS is to find the most likely signal coefficients with the assumptions that the signal is approximately sparse and that the data are corrupted by noise with a known distribution. The sparsity assumption is reflected by the prior defined on the signal coefficients, whereas the noise model is expressed via the likelihood term.
As a means to justify Eq. 2, we present a commonly-used signal prior and noise distribution. We model the data as being corrupted by additive white Gaussian noise with variance σ2 via y = Φx + n. In this case, the probability of observing the data y given the signal x is a Gaussian probability density function (pdf) with mean Φ x and variance σ2,
| (3) |
which constitutes the likelihood term. To formalize our belief that the signal x is sparse, we place a sparsity-promoting prior on it. A common prior is the separable Laplacian density function (10)
| (4) |
Invoking Bayes' theorem, the posterior for the signal coefficients can be related to the likelihood and the prior as
| (5) |
We seek the signal that maximizes this posterior probability via maximum a posteriori (MAP) estimation. Since the denominator is independent of x, the MAP estimate can be found by minimizing the negative of the logarithm of the numerator:
| (6) |
This expression is very similar to the unconstrained convex optimization formulation in Eq. (2); we could obtain Eq. (2) with a slightly more complicated prior that the wavelet coefficients and gradient of the signal of interest follow Laplacian distributions. Therefore, it is possible to view the convex relaxation CS algorithms as MAP estimates with a Laplacian prior on the signal coefficients. It is possible to view many algorithms used in CS as MAP estimators with respect to some prior (11).
Extending Bayesian Compressed Sensing to Multi-Contrast MRI
The Bayesian analysis in the previous section has two significant shortcomings. First, it is assumed that the signal of interest is sparse with respect to the base coordinate system. To get the maximum benefit from estimation with respect to a separable signal prior, it is critical to change to coordinates in which the marginal distributions of signal components are highly peaked at zero (12). For MR image formation, we aim to take advantage of the highly peaked distributions of image-domain gradients, and we show how to modify k-space data to obtain measurements of these gradients. Second, the optimal MAP estimation through Eq. (6) requires knowledge of parameters λ and σ. Our method eliminates the tuning of such parameters by imposing a hierarchical Bayesian model in which λ and σ are modeled as realizations of random variables; this introduces the need for “hyperpriors” at a higher level of the model, but as we detail below, it suffices to eliminate tuning of the hyperpriors using a principle of least informativeness. Along with addressing these shortcomings, we also discuss modifications for joint reconstruction across contrast preparations.
In the multi-contrast setting, the signals represent MRI scans with different image weightings, e.g. we might have obtained T1, T2 and proton density weighted images for the same region of interest. These are not sparse directly in the image domain. Therefore, it is beneficial to cast the MRI images into a sparse representation to make use of the Bayesian formalism. The fact that the observation matrices FΩi ∈ ℂKi×M in MRI are undersampled Fourier operators makes it very convenient to use spatial image gradients as a sparsifying transform (13,14). To obtain the k-space data corresponding to vertical and horizontal image gradients, it is sufficient to modify the data yi according to
| (7) |
| (8) |
where ; and are the ith image gradients; and are the modified observations; and ω and υ index the frequency space of the n by m pixel images, with n · m = M. To solve Eq. (2), Lustig et al. (2) proposes to use the conjugate gradient descent algorithm, for which it is relatively straightforward to incorporate the TV norm. But algorithms that do not explicitly try to minimize an objective function (e.g. OMP and Bayesian CS) will need to modify the k-space data according to Eqs. (7) and (8) to make use of the Total Variation penalty in the form of spatial derivatives.
Secondly, we need to express the likelihood term in such a way that both real and imaginary parts of the noise ni ∈ ℂKi in k-space are taken into account. We rearrange the linear observations as
| (9) |
for i = 1,…, L, where Re (.) and Jm (.) indicate real and imaginary parts with the understanding that we also have an analogous set of linear equations for the horizontal gradients . For simplicity, we adopt the notation
| (10) |
where , Ni ∈ R2Ki, and Φi ∈ R2Ki×M correspond to the respective concatenated variables in Eq. (9). With the assumption that both real and imaginary parts of the k-space noise are white Gaussian with some variance σ2, the data likelihood becomes
| (11) |
With these modifications, it is now possible to compute the MAP estimates for the image gradients by invoking Laplacian priors over them. Unfortunately, obtaining the MAP estimates for each signal separately contradicts with our ultimate goal to perform joint reconstruction. In addition, it is beneficial to have a full posterior distribution for the sparse coefficients rather than point estimates, since having a measure of uncertainty in the estimated signals leads to an elegant experimental design method. As argued in (10), it is possible to determine an optimal k-space sampling pattern that reduces the uncertainty in the signal estimates. But since the Laplacian prior is not a conjugate distribution to the Gaussian likelihood, the resulting posterior will not be in the same family as the prior, hence it will not be possible to perform the inference in closed form to get a full posterior. The work by Ji et al. (1) presents an elegant way of estimating the image gradients within a hierarchical Bayesian model. This approach allows information sharing between the multi-contrast scans, at the same yields a full posterior estimate for the sparse coefficients. In the following section, we attempt to summarize the algorithm used for finding this distribution and depict our complete image reconstruction scheme in Fig. 1.
Figure 1.
Joint image reconstruction begins with modifying the undersampled k-space data to obtain undersampled k-space representations of vertical and horizontal image gradients. After finding the hyperparameters via Maximum Likelihood (ML) estimation, the means of the posterior distributions are assigned to be the gradient estimates. Finally, images are integrated from gradient estimates via solving a Least Squares (LS) problem.
Bayesian Framework to Estimate the Image Gradient Coefficients
Hierarchical Bayesian representation provides the ability to capture both the idiosyncrasy of the inversion tasks and the relations between them, while allowing closed form inference for the image gradients. According to this model, the sparse coefficients are assumed to be drawn from a product of zero mean normal distributions with variances determined by the hyperparameters
| (12) |
where is a zero mean Gaussian density function with variance . In order to promote sparsity in the gradient domain, Gamma priors are defined over the hyperparameters α
| (13) |
where Γ(.) is the Gamma function, and a and b are hyper-priors that parametrize the Gamma prior. To see why the combination of Gaussian and Gamma priors will promote a sparse representation, we can consider marginalizing over the hyperparameters α to obtain the marginal priors acting on the signal coefficients (1,10,15)
| (14) |
which turn out to yield improper priors of the form in the particular case of uniform hyper-priors a = b = 0. Similar to our analysis for the Laplacian prior, this formulation would introduce an ℓ1 regularizer of the form if we were interested in a non-joint MAP solution. Here, we should also note that the hyperparameters α are shared across the multi-contrast images, each αj controlling the variance of all L gradient coefficients through Eq. (12). In this case, αj 's diverging to infinity implies that the pixels in the jth location of all images are zero, due to the zero-mean, zero-variance Gaussian prior at this location. On the other hand, a finite αj does not constrain all L pixels in the jth location to be non-zero, which allows the reconstruction algorithm to capture the diversity of sparsity patterns across the multi-contrast scans.
In practice, we would also need to estimate the noise variance σ2 as it propagates via the data likelihood term to the posterior distribution of gradient coefficients (Eq. 5). Even though it is not difficult to obtain such an estimate in image domain if we had the full k-space data, this would not be straightforward with undersampled measurements. Therefore, we follow Ji et al. (1) and slightly modify our formulation so that we can integrate out the noise variance analytically while computing the posterior. This is made possible by including the noise precision α0 = σ−2 in the signal prior,
| (15) |
We further define a Gamma prior over the noise precision parameter α0
| (16) |
In all of our experiments, we set the hyper-priors c = d = 0 to express that we favor no a priori noise precision as they lead to the “least informative” improper prior p(α0 ∣ c = 0,d = 0) ∝ 1/α0. The choice of priors in Eqs. (15-16) lets us analytically compute the posterior for the image gradients , which turns out to be a multivariate Student-t distribution with mean and covariance with A = diag(α1,…,α M). This formulation is seen to allow robust coefficient shrinkage and information sharing thanks to inducing a heavy-tail in the posterior (1). It is worth noting that placing a Gamma prior on the noise precision does not change the additive nature of observation noise, however a heavier-tailed t-distribution replaces the normal density function in explaining this residual noise. This has been seen to be more resilient in allowing outlying measurements (1).
Now that we have an expression for the posterior , all we need to do is to find a point estimate for the hyperparameters α ∈ RM in a maximum likelihood (ML) framework. This is achieved by searching for the hyperparameter setting that makes the observation of the k-space data most likely, and such an optimization process is called evidence maximization or type-II maximum likelihood method (1,10,15). Therefore, we seek the hyperparameters that maximize
| (17) |
We stress that data from all L tasks contribute to the evidence maximization procedure via the summation over conditional distributions. Hence, the information sharing across the images occurs through this collaboration in the maximum likelihood estimation of the hyperparameters. Once the point estimates are constituted using all of the observations, the posterior for the signal coefficients is estimated based only on its related k-space data due to . Thus, all of the measurements are used in the estimation of the hyperparameters, but only the associated data are utilized to constitute an approximation to the gradient coefficients.
Ji et al. show that it is possible to maximize Eq. (17) with a sequential greedy algorithm, in which we begin with a single basis vector for each signal, then keep adding the basis function that yields the largest increase in the log likelihood at each iteration. Alternatively, a hyperparameter corresponding to a basis vector that is already in the dictionary of current bases can be updated or deleted, if this gives rise to the largest increase in the likelihood at that iteration. We added a final refinement to Ji et al.'s Bayesian CS algorithm by replacing the observation matrices that we need to store with the Fast Fourier Transform (FFT). This enables us to work with MRI images of practical sizes; otherwise each of the observation matrices would occupy 32GB of memory for a 256×256 image. We refer the reader to Appendix B in (1) for the update equations of this algorithm. Our FFT refinement for the sequential algorithm is detailed in the Appendix.
Reconstructing the Images from Horizontal and Vertical Gradient Estimates
Once the image gradients and are estimated with the joint Bayesian algorithm, we seek to find the images consistent with these gradients and the undersampled measurements . Influenced by (13), we formulate this as a least squares (LS) optimization problem
| (18) |
for i = 1,…, L where ∂x xi and ∂y xi represent vertical and horizontal image gradients. Using Eqs. (7) and (8) and invoking Parseval's Theorem, the optimization problem can be cast into k-space
| (19) |
where Xi, and are the Fourier transforms of xi, and , respectively and XΩi is the transform of xi restricted to the frequency set Ωi. Based on this, we arrive at the following solution by representing Eq. (19) as a quadratic polynomial and finding the root with λ → ∞
| (20) |
Finally, taking the inverse Fourier transform gives the reconstructed images .
Extension to Complex-Valued Images
In the general case where the underlying multi-contrast images are complex-valued, the linear observation model of Eq. 9 is no longer valid. Under the assumption that the support of the frequency set Ωi is symmetric, it is possible to decouple the undersampled k-space observations belonging to the real and imaginary parts of the signals,
| (21) |
| (22) |
| (23) |
Here, [kx, ky] index the frequency space and yi* [−kx,(−)ky ] is the complex conjugate of index-reversed k-space observations. In the case of one dimensional undersampling, the constraint on Ωi would simply correspond to an undersampling pattern that is mirror-symmetric with respect to the line passing through the center of k-space. After obtaining the k-space data and belonging to the real and imaginary parts of the ith image xi, we solve for Re(xi) and Jm(xi) jointly in the gradient domain, in addition to the joint inversion of multi-contrast data, hence exposing a second level of simultaneous sparsity in the image reconstruction problem. Final reconstructions are then obtained by combining the real and imaginary channels into complex-valued images.
Methods
To demonstrate the inversion performance of the joint Bayesian CS algorithm, three data sets that include a numerical phantom, the SRI24 brain atlas, and in vivo acquisitions, were reconstructed from undersampled k-space measurements belonging to the magnitude images. In addition, two datasets including a numerical phantom and in vivo multi-contrast slices, both consisting of complex-valued images, were also reconstructed from undersampled measurements to test the performance of the method with complex-valued image-domain signals. The results were quantitatively compared against the popular implementation by Lustig et al. (2), which does not make use of joint information across the images, as well as our realization of the M-FOCUSS algorithm, which is an alternative joint CS reconstruction algorithm.
CS Reconstruction with Extended Shepp-Logan Phantoms
To generalize the Shepp-Logan phantom to the multi-contrast setting, we generated two additional phantoms by randomly permuting the intensity levels in the original 128×128 image. Further, by placing 5 more circles with radii chosen randomly from an interval of [7, 13] pixels and intensities selected randomly from [0.1, 1] to the new phantoms, we also aimed to represent the idiosyncratic portions of the scans with different weightings. A variable-density undersampling scheme in k-space was applied by drawing three fresh samples from a power law density function, so that the three masks' frequency coverage was only partially overlapping. Power law sampling indicates that the probability of sampling a point in k-space is inversely proportional to the distance of that point to the center of k-space, which makes the vicinity of the center of k-space more densely sampled. To realize this pattern, again Lustig et al.'s software package (2) was used, which randomly generates many sampling patterns and retains the one that has the smallest sidelobe-to-peak ratio in the point spread function. This approach aims to create a sampling pattern that induces optimally incoherent aliasing artifacts (2). A high acceleration factor of R = 14.8 was tested using the joint Bayesian CS, Lustig et al.'s gradient descent and the M-FOCUSS algorithm. For the gradient descent method, using wavelet and TV norm penalties were seen to yield better results than using only one of them. In all experiments, we tested all combinations of regularization parameters λTV and λwavelet from the set {10−4,10−3,10−2,0}and retained the setting that gave the smallest reconstruction error as the optimal one. In the Shepp-Logan experiment, the parameter setting λTV = λwavelet = 10−3 was seen to yield optimal results for the gradient descent method. The number of iterations was taken to be 50 in all of the examples. The Bayesian algorithm continues the iterations until convergence, which is determined by
| (24) |
where Δℓk is the change in log likelihood at iteration k and Δℓmax is the maximum change in likelihood that has been encountered in all k iterations. The convergence parameter η was taken to be 10−8 in this example. For the M-FOCUSS method, each image was undersampled with the same mask as phantom 1 in the joint Bayesian CS since M-FOCUSS does not admit different observation matrices.
SRI24 Multi-Channel Brain Atlas Data
This experiment makes use of the multi-contrast data extracted from the SRI24 atlas (16). The atlas features structural scans obtained with three different contrast settings at 3T,
Proton density weighted images: obtained with a 2D axial dual-echo fast spin echo (FSE) sequence (TR = 10000 ms, TE = 14 ms)
T2 weighted images: acquired with the same sequence as the proton density weighted scan, except with TE = 98 ms.
T1 weighted images: acquired with a 3D axial IR-prep Spoiled Gradient Recalled (SPGR) sequence (TR = 6.5 ms, TE = 1.54 ms)
The atlas images have a resolution of 256×256 pixels and cover a 24-cm field-of-view (FOV). Since all three data sets are already registered spatially, we applied no post-processing except for selecting a single axial slice from the atlas. Prior to reconstruction, retrospective undersampling1 was applied along the phase encoding direction with acceleration R = 4 using a different undersampling mask for each image. Again a power law density function was utilized in selecting the sampled k-space lines. In this case, a 1-dimensional pdf was employed, so that it was more likely to acquire phase encoding lines close to the center of k-space. Reconstructions were performed using Lustig et al.'s conjugate gradient descent algorithm (with λTV λwavelet = 10−3), joint Bayesian method (with η = 10−9) and the M-FOCUSS joint reconstruction algorithm.
3T Turbo Spin Echo (TSE) Slices with Early and Late TE's
T2-weighted axial multi-slice images of the brain of a young healthy male volunteer were obtained with two different TE settings using a TSE sequence (256×256 pixel resolution with 38 slices, 1×1 mm in-plane spatial resolution with 3 mm thick contiguous slices, TR = 6000 ms, TE1 = 27 ms, TE2 = 94 ms). Out of these, a single image slice was selected and its magnitude was retrospectively undersampled in k-space along the phase encoding direction with acceleration R = 2.5 using a different mask for each image, again by sampling lines due to a 1-dimensional power law distribution. The images were reconstructed using Lustig et al.'s algorithm with an optimal parameter setting (λTV = λwavelet = 10−3), joint Bayesian CS algorithm (with η = 10−9) and the M-FOCUSS method.
Complex-Valued Shepp-Logan Phantoms
Using four numerical phantoms derived from the original Shepp-Logan phantom, two complex valued numerical phantoms were generated by combining the four images in real and imaginary pairs. Retrospective undersampling was applied along the phase encoding direction with acceleration R = 3.5 using a different undersampling mask for each image. A 1-dimensional power law density function was utilized in selecting the sampled k-space lines, making it more likely to acquire phase encoding lines close to the center of k-space. We again randomly generated many sampling patterns and retained the one that has the smallest sidelobe-to-peak ratio in the point spread function, but also constrained the sampling masks to be mirror-symmetric with respect to the center of k-space. This way, it was possible to obtain the undersampled k-space data belonging to the real and imaginary channels of the phantoms separately. The images were reconstructed using Lustig et al.'s algorithm (λTV = λwavelet = 10−3), joint Bayesian CS algorithm (reconstructing real & imaginary parts together, in addition to joint multi-contrast reconstruction) and the M-FOCUSS method. Further, non-joint reconstructions with the Bayesian CS method (doing a separate reconstruction for each image, but reconstructing real & imaginary channels of each image jointly) and the FOCUSS algorithm (non-joint version of M-FOCUSS) were conducted for comparison with Lustig et al.'s approach.
Complex-Valued Turbo Spin Echo Slices with Early and Late TE's
To test the performance of the algorithms on complex-valued in vivo images, axial multi-slice images of the brain of a young healthy female subject were obtained with two different TE settings using a TSE sequence (128×128 pixel resolution with 38 slices, 2×2 mm in-plane spatial resolution with 3 mm thick contiguous slices, TR = 6000 ms, TE1 = 17 ms, TE2 = 68 ms). Data were acquired with a body coil and both the magnitude and the phase of the images were recorded. To enhance SNR, 5 averages and a relatively large 2-mm in-plane voxel size were used. A single slice was selected from the dataset and its raw k-space data were retrospectively undersampled along the phase encoding direction with acceleration R = 2 using a different mask for each image, again by sampling lines due to a 1-dimensional power law distribution. For the complex-valued image-domain case, the masks were constrained to be symmetric with respect to the line passing through the center of k-space. The images were reconstructed using Lustig et al.'s algorithm (λTV = λwavelet = 10−3), our joint Bayesian CS algorithm (reconstructing real & imaginary parts and multi-contrasts together) and the M-FOCUSS method. In addition, non-joint reconstructions with the Bayesian CS method (using a separate reconstruction for each image, but reconstructing real & imaginary parts of each image together) and the FOCUSS algorithm were performed.
Results
CS Reconstruction with Extended Shepp-Logan Phantoms
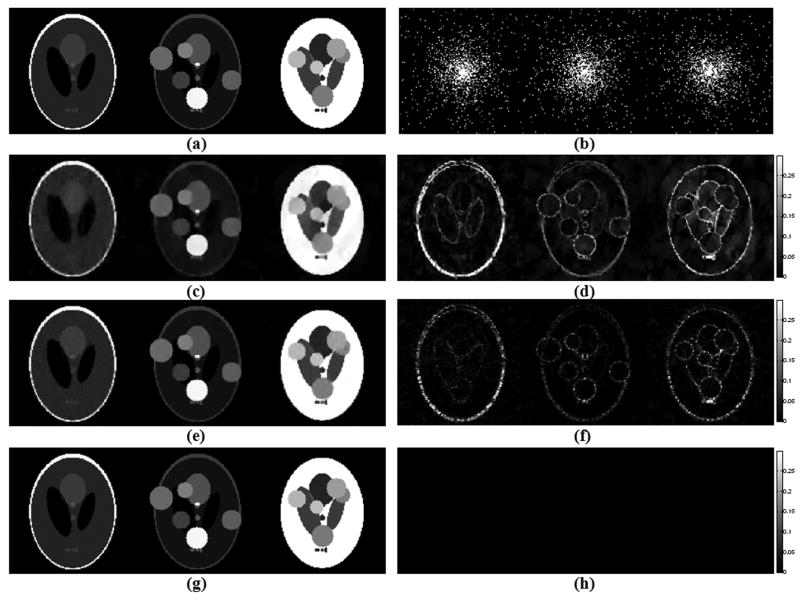
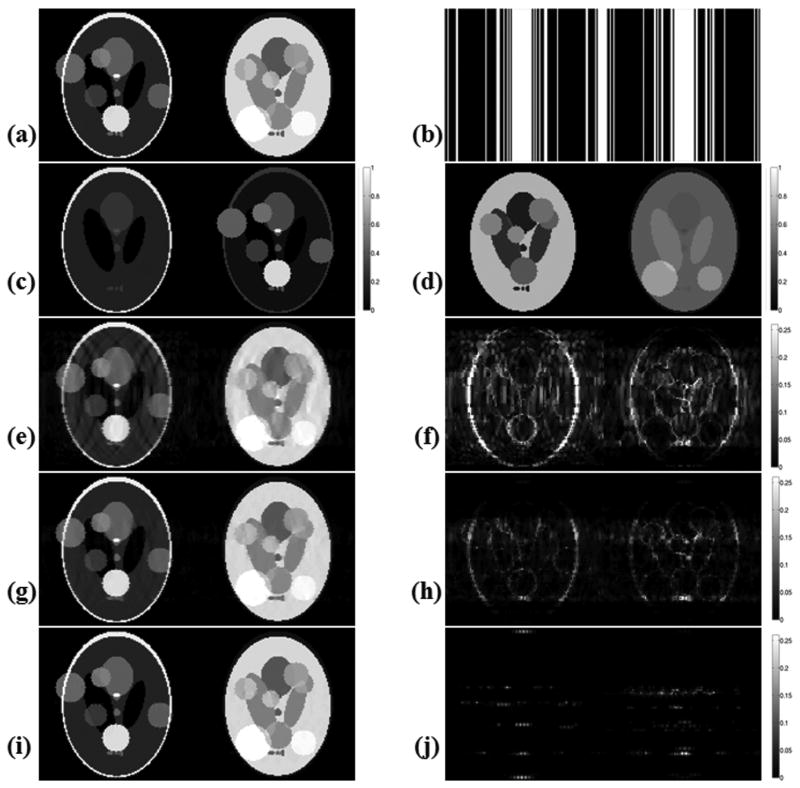
Fig. 2 presents the reconstruction results for the three algorithms for the extended phantoms, along with the k-space masks used in retrospective undersampling. At acceleration R = 14.8, the Bayesian algorithm obtained perfect recovery of the noise-free numerical phantom, whereas the gradient descent algorithm by Lustig et al. returned 15.9 % root mean squared error (RMSE), which we define as
Figure 2.
Reconstruction results with the extended Shepp-Logan phantoms after undersampling with acceleration R = 14.8, at 128×128 resolution. (a) Phantoms at Nyquist rate sampling. (b) Undersampling patterns in k-space corresponding to each image. (c) CS reconstructions with Lustig et al.'s algorithm yielded 15.9 % RMSE (root-mean-square error). (d) Absolute error plots for Lustig et al.'s method. (e) Reconstructions obtained with the M-FOCUSS joint reconstruction algorithm have 8.8 % RMSE. (f) Absolute difference between the Nyquist sampled phantoms and the M-FOCUSS reconstruction results. (g) Joint Bayesian CS reconstruction resulted in 0 % RMSE. (h) Absolute error plots for the Bayesian CS reconstructions.
Original images are scaled between [0,1]. All absolute error plots are scaled by clipping at half of the maximum error incurred by Lustig et al.'s algorithm in order to emphasize the results, so that the errors larger than this get saturated in the images.
| (25) |
where x is the vector obtained by concatenating all L images together, and similarly x̂ is the concatenated vector of all L reconstructions produced by an inversion algorithm. The M-FOCUSS joint reconstruction algorithm yielded an error of 8.8 %. The reconstruction times were measured to be 5 minutes for gradient descent, 4 minutes for M-FOCUSS and 25 minutes for the joint Bayesian CS algorithm.
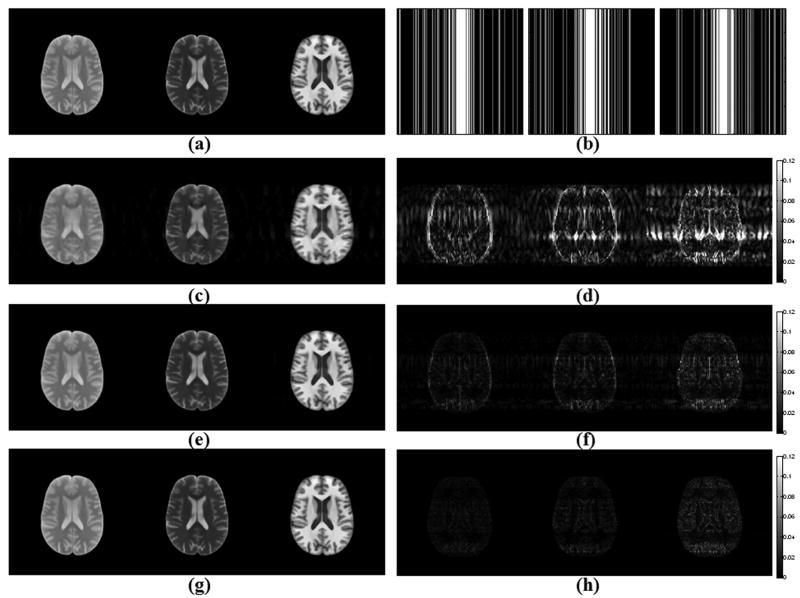
SRI24 Multi-Channel Brain Atlas Data
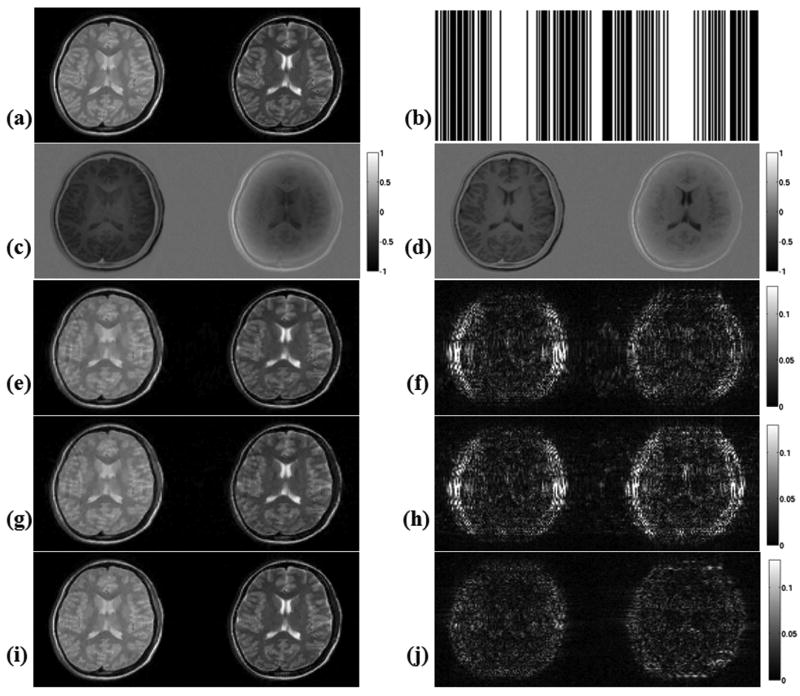
The results for reconstruction upon phase encoding undersampling with acceleration R = 4 are given in Fig. 3. In this case, Lustig et al.'s algorithm returned 9.4 % RMSE, while the error was 3.2 % and 2.3 % for M-FOCUSS and joint Bayesian CS methods, respectively. The reconstructions took 43 minutes for gradient descent, 5 minutes for M-FOCUSS and 26.4 hours for the Bayesian CS algorithm.
Figure 3.
Reconstruction results with SRI24 atlas after undersampling along the phase encoding direction with R = 4, at 256×256 resolution. (a) Atlas images at Nyquist rate sampling. (b) Undersampling patterns in k-space corresponding to each image. (c) Applying the gradient descent algorithm proposed by Lustig et al. resulted in reconstructions with 9.4 % RMSE. (d) Absolute difference between the gradient descent reconstructions and the Nyquist rate images. (e) M-FOCUSS reconstructions have 3.2 % RMSE. (f) Absolute error plots for the M-FOCUSS algorithm. (g) Joint Bayesian reconstruction yielded images with 2.3 % RMSE. (h) Error plots for the joint Bayesian reconstructions.
Original images are scaled between [0,1]. All absolute error plots are scaled by clipping at half of the maximum error incurred by Lustig et al.'s algorithm in order to emphasize the results, so that the errors larger than this get saturated in the images.
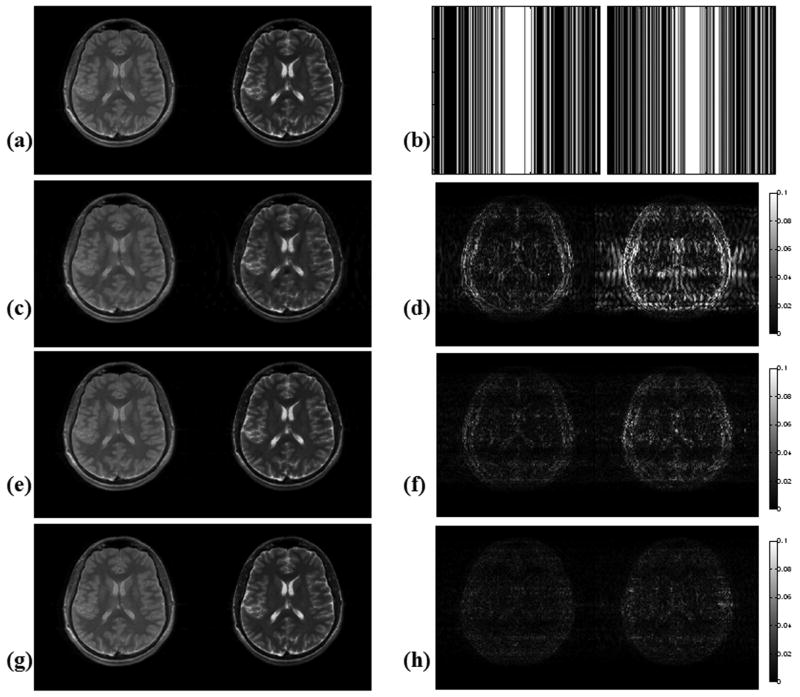
Turbo Spin Echo (TSE) Slices with Early and Late TE's
Fig. 4 depicts the TSE reconstruction results obtained with the three algorithms after undersampling along phase encoding with acceleration R = 2.5. In this setting, Lustig et al.'s code returned a result with 9.4 % RMSE, whereas M-FOCUSS and joint Bayesian reconstruction had 5.1 % and 3.6 % errors, respectively. The total reconstruction times were 26 minutes for gradient descent, 4 minutes for M-FOCUSS and 29.9 hours for the Bayesian CS algorithm.
Figure 4.
Reconstruction results with TSE after undersampling along the phase encoding direction with R = 2.5, at 256×256 resolution. (a) TSE scans at Nyquist rate sampling. (b) Undersampling patterns used in this experiment. (c) Reconstructions obtained with Lustig et al.'s gradient descent algorithm have 9.4 % RMSE. (d) Plots of absolute error for the gradient descent reconstructions. (e) M-FOCUSS joint reconstruction yielded images with 5.1 % RMSE. (f) Error plots for the M-FOCUSS results. (g) Images obtained with the joint Bayesian CS reconstruction returned 3.6 % RMSE. (h) Error plots for the Bayesian CS reconstructions.
These results are also included in Table 1 as “PE, (Fig. 4)” for comparison with reconstruction using the same undersampling pattern.
Original images are scaled between [0,1]. All absolute error plots are scaled by clipping at half of the maximum error incurred by Lustig et al.'s algorithm in order to emphasize the results, so that the errors larger than this get saturated in the images.
For brevity, we present additional results in Table 1 from more extensive tests in which we experimented with various undersampling patterns and accelerations. To test the algorithms' performance at a different resolution, we also downsampled the TSE and atlas images to size 128×128 prior to undersampling, and noted similar RMSE results as the high resolution experiments. The table also includes an experiment with 256×256 TSE scans accelerated along the phase encoding with R = 2.5, but using the same undersampling pattern for both images.
Table 1.
Summary of additional reconstruction results on the TSE and SRI 24 datasets using the three algorithms after retrospective undersampling with various patterns and acceleration factors.
| Dataset | Resolution | Undersampling method | Acceleration factor R | RMSE % | ||
|---|---|---|---|---|---|---|
| Lustig et al. | M-Focuss | Bayesian CS | ||||
| TSE | 256×256 | Phase encoding (PE) | 3 | 9.7 | 6.8 | 5.8 |
| 256×256 | Power law | 6 | 8.1 | 7.8 | 6.3 | |
| 256×256 | PE (Fig. 4) | 2.5 | 9.4 | 5.1 | 3.6 | |
| 256×256 | PE, same pattern | 2.5 | 4.7 | |||
| 128×128 | PE | 2 | 8.1 | 3.8 | 2.1 | |
| SRI 24 | 256×256 | Radial | 9.2 | 6.0 | 4.5 | 3.0 |
| 128×128 | PE | 3 | 7.2 | 4.2 | 3.1 | |
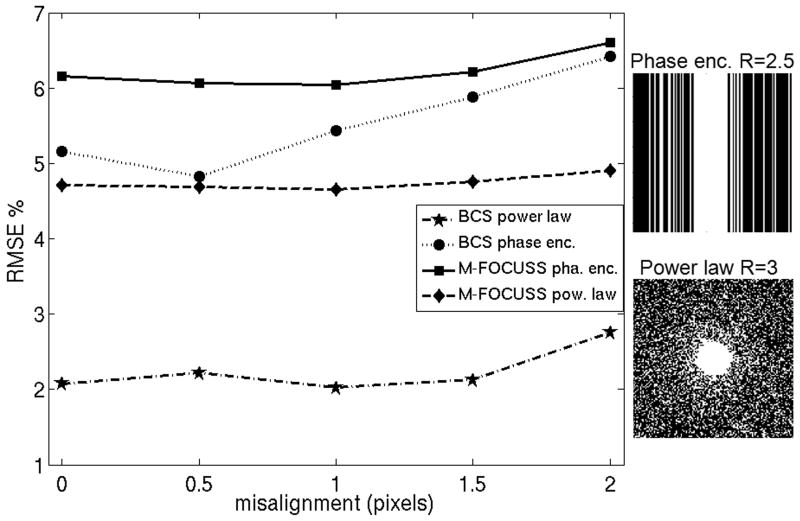
Impact of Spatial Misregistration on Joint Reconstruction
Due to aliasing artifacts caused by undersampling, image registration prior to CS reconstruction across multi-contrast images is likely to perform poorly. We investigated the effect of spatial misalignments by shifting one of the images in the TSE dataset relative to the other by 0 to 2 pixels with step sizes of ½ pixels using two different undersampling patterns. The first pattern incurs R = 3 acceleration by 2D undersampling with k-space locations drawn from a power law probability distribution. In this case, we tested the effect of vertical misalignments. The second pattern undersamples k-space at R = 2.5 in the phase encoding direction, for which we tested horizontal dislocations. For speed, we used low resolution images at size 128×128. We tested M-FOCUSS and joint Bayesian CS methods for robustness against misregistration and observed that the effect of spatial misalignment was mild for both (Fig. 5). Even though Bayesian CS consistently had less reconstruction errors relative to M-FOCUSS on both undersampling patterns at all dislocations, the performance of M-FOCUSS was seen to change less relative to Bayesian CS with respect to the incurred translations. For joint Bayesian CS, reconstruction error increased from 2.1 % to 2.8 % at 2 pixels of vertical shift for power law sampling, and from 5.2 % to 6.4 % at 2 pixels of horizontal shift for phase encoding sampling; for the M-FOCUSS method error increased from 4.7 % to 4.9 % for power law sampling, and from 6.2 % to 6.6 % for phase encoding sampling.
Figure 5.
To investigate the impact of spatial misalignments on joint reconstruction with Bayesian CS and M-FOCUSS, one of the TSE images was shifted relative to the other by 0 to 2 pixels with step sizes of ½ pixels using power law and phase encoding undersampling patterns. For speed, low resolution images with size 128×128 were used. For joint Bayesian CS, reconstruction error increased from 2.1 % to 2.8 % at 2 pixels of vertical shift for power law sampling, and from 5.2 % to 6.4 % at 2 pixels of horizontal shift for phase encoding sampling; for the M-FOCUSS method error increased from 4.7 % to 4.9 % for power law sampling, and from 6.2 % to 6.6 % for phase encoding sampling.
Complex-Valued Shepp-Logan Phantoms
Absolute values of the reconstruction results after undersampling with a symmetric mask with R = 3.5 for the complex-valued phantoms are depicted in Fig. 6. For complex signals, we use the error metric RMSE = 100 · ‖X̂ − X‖2 / ‖X‖2. In this case, Lustig et al.'s algorithm returned a result with 13.1 % RMSE, whereas joint reconstructions with M-FOCUSS and joint Bayesian methods had 5.4 % and 2.4 % errors, respectively. The total reconstruction times were 21 minutes for gradient descent, 0.5 minutes for M-FOCUSS and 18 minutes for the Bayesian CS algorithm. On the other hand, reconstructing each complex-valued image separately with FOCUSS and Bayesian CS yielded 6.7 % and 4.6 % RMSE.
Figure 6.
Reconstruction results with the complex-valued Shepp-Logan phantoms after undersampling with acceleration R = 3.5, at 128×128 resolution. (a) Magnitudes of phantoms at Nyquist rate sampling. (b) Symmetric undersampling patterns in k-space corresponding to each image. (c) Real and imaginary parts of the first phantom (on the left in (a)). (d) Real and imaginary parts of the second phantom (on the right in (a)). (e) CS reconstructions with Lustig et al.'s algorithm yielded 13.1 % RMSE. (f) Absolute error plots for Lustig et al.'s method. (g) Reconstructions obtained with the M-FOCUSS joint reconstruction algorithm have 5.4 % RMSE. (h) Absolute difference between the Nyquist sampled phantoms and the M-FOCUSS reconstruction results. (i) Joint Bayesian CS reconstruction resulted in 2.4 % RMSE. (h) Absolute error plots for the Bayesian CS reconstructions.
Original magnitude images are scaled between [0,1]. All absolute error plots are scaled by clipping at half of the maximum error incurred by Lustig et al.'s algorithm in order to emphasize the results, so that the errors larger than this get saturated in the images.
Complex-Valued Turbo Spin Echo Slices with Early and Late TE's
Reconstruction results are compared in Fig. 7 for the discussed algorithms. Lustig et al.'s method had 8.8 % error upon acceleration by R = 2 with a symmetric pattern, whereas the joint reconstruction algorithms M-FOCUSS and joint Bayesian CS yielded 9.7 % and 6.1 % RMSE. The processing times were 20 minutes for gradient descent, 2 minutes for M-FOCUSS and 5.2 hours for the Bayesian CS algorithm. Non-joint reconstructions with FOCUSS and Bayesian CS returned 10.0 % and 8.6 % errors.
Figure 7.
Reconstruction results for complex-valued TSE images after undersampling along the phase encoding direction with R = 2, at 128×128 resolution. (a) Magnitudes of the TSE scans at Nyquist rate sampling. (b) Symmetric undersampling patterns used in this experiment. (c) Real and imaginary parts of the early echo image (on the left in (a)). (d) Real and imaginary parts of the late echo image (on the right in (a)). (e) Reconstructions obtained with Lustig et al.'s gradient descent algorithm have 8.8 % RMSE. (d) Plots of absolute error for the gradient descent reconstructions. (e) M-FOCUSS joint reconstruction yielded images with 9.7 % RMSE. (f) Error plots for the M-FOCUSS results. (g) Images obtained with the joint Bayesian CS reconstruction returned 6.1 % RMSE. (h) Error plots for the Bayesian CS reconstructions.
Original magnitude images are scaled between [0,1]. All absolute error plots are scaled by clipping at half of the maximum error incurred by Lustig et al.'s algorithm in order to emphasize the results, so that the errors larger than this get saturated in the images.
With the same dataset, additional reconstructions were performed to quantify the effect of the symmetry constraint on the sampling masks. Both of the late and early TE images were reconstructed 5 times with freshly generated, random masks with R = 2 (no symmetry constraints) and also 5 times with freshly generated symmetric masks again at R = 2. Using Lustig et al.'s method (λTV = 10−3) with the random masks yielded an average error of 10.5 %, whereas using symmetric masks incurred an average error of 11.5 %.
Discussion
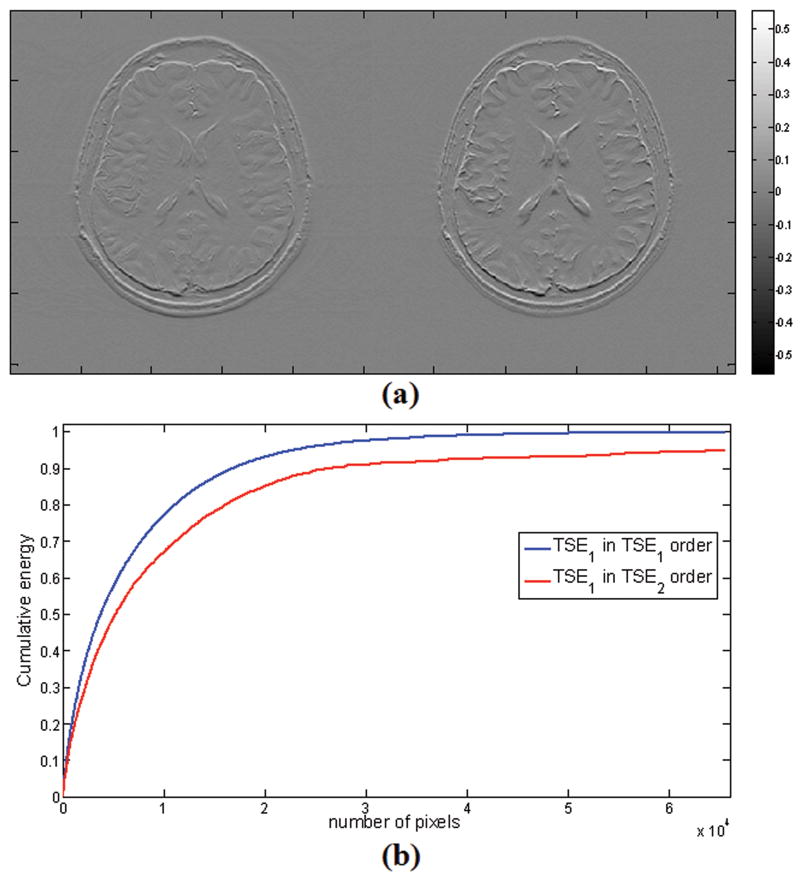
The application of joint Bayesian CS MRI reconstruction to images of the same object acquired under different contrast settings was demonstrated to yield substantially higher reconstruction fidelity than either Lustig et al.'s (non-joint) algorithm or joint M-FOCUSS, but at the cost of substantially increased reconstruction times in this initial implementation. In contrast to M-FOCUSS, the proposed algorithm allows for different sampling matrices being applied to each contrast setting and unlike the gradient descent method, it has no parameters that need adjustments. The success of this algorithm is based on the premise that the multi-contrast scans of interest share a set of similar image gradients while each image may also present additional unique features with its own image gradients. In Fig. 8 we present the vertical image gradients belonging to the TSE scans, and conduct a simple experiment to quantify the similarity between them. After sorting the image gradient magnitudes of the early TSE scan in descending order, we computed the cumulative energy in them. Next, we sorted the late TSE gradient magnitude in descending order and calculated the cumulative energy in the early TSE gradient by using the pixel index order belonging to the late TSE scan. This cumulative sum reached 95 % of the original energy, thus confirming the visual similarity of the two gradients.
Figure 8.
(a) Image gradients for the multi-contrast TSE scans demonstrate the similarity under the gradient transform. (b) To quantify this similarity, we computed the cumulative energy of the image gradient of early TSE scan (TSE1 in TSE1 order). Then we sorted the late TSE scan (TSE2) in descending order, and computed the cumulative energy in TSE1 corresponding to the sorted indices in TSE2 which gave the curve TSE1 in TSE2 order. The similarity of the curves indicates similar sparsity supports across images.
It is important to note that in the influential work by Ji et al. (1), the authors also consider joint reconstruction of MRI images. However their dataset consists of five different slices taken from the same scan, so the motivation for their MRI work is different from what we present here. Even though the multislice images have considerable similarity from one slice to the next, one would expect multi-contrast scans to demonstrate a yet higher correlation of image features and a correspondingly larger benefit in reconstruction fidelity.
Two aspects of the proposed Bayesian reconstruction algorithm demand further attention. First, relative to the other two algorithms we investigated, the Bayesian method is dramatically more time consuming. The reconstruction times can be on the order of hours, which is prohibitive for clinical use as currently implemented. As detailed in the Results section, the proposed algorithm is about 40 times slower than gradient descent, and about 300 times slower than M-FOCUSS for the in vivo data. We expect future implementations and optimizations that utilize specialized scientific computation hardware to overcome this current drawback. Particularly, it is common to observe an order of magnitude speed-up with CUDA (Compute Unified Device Architecture) enabled Graphics Processing Units when the problem under consideration can be adapted to the GPU architecture (17). In a recent work, using CUDA architecture in compressed sensing was reported to yield accelerations up to a factor of 40 (18). We expect that parallelizing matrix operations and FFTs can yield significant performance boost. On the other hand, an algorithmic reformulation can be another source of performance increase. Solving the inference problem via variational Bayesian analysis (19) was seen to yield an order of magnitude speed-up relative to the greedy Bayesian CS method for non-joint image reconstruction.
A second aspect of this reconstruction method that requires further analysis is the potentially detrimental impact of source data that are not perfectly spatially aligned. To maximize the information sharing among the inversion tasks, it is crucial to register the multi-contrast scans before applying the joint reconstruction. To minimize the adverse consequences of such misalignment, future implementations might deploy either real-time navigators (e.g. (20)) or retrospective spatial registration among datasets based on preliminary CS reconstructions without the joint constraint. For some acquisitions, subtle, non-rigid spatial misregistration may occur due to eddy-current or B0 inhomogeneity induced distortions. To correct for such higher-order translation effects, several fast and accurate correction methods have been proposed (e.g. (21,22)) and could be applied for correction of undersampled images in joint Bayesian reconstruction. As our preliminary investigation in the Results section demonstrates, joint Bayesian CS algorithm is robust against misregistration effects up to shifts of 2 pixels, and we believe that existing registration techniques can bring us within this modest range. Alternatively, future work aimed at the simultaneous joint reconstruction and spatial alignment might pose an interesting and challenging research project in this area, which might be accomplished by introducing additional hidden variables.
Regarding real-valued image-domain datasets, the presented CS reconstructions obtained with Lustig et al.'s conjugate gradient descent method yielded 2 to 4 times of the RMSE returned by the joint Bayesian algorithm. Even though this error metric cannot be considered the sole criterion for “good” image reconstruction (23), we believe that making use of similarities between multi-contrast scans can be a first step in this direction. In the more general case where we tested the methods with complex-valued images, the improvement in RMSE reduced to about 1.5 times on the in vivo data with the joint Bayesian algorithm. When we reconstructed the individual images separately, but using their real & imaginary parts jointly, we also noted that this non-joint version of the Bayesian algorithm outperformed both Lustig et al.'s method and M-FOCUSS on the complex-valued numerical data and the TSE scans. This might suggest that exploiting the similarity between real and imaginary channels of the images can also be source of performance increase. It is important to note that the current Bayesian algorithm requires the sampling patterns to be symmetric in order to handle complex-valued images, and this constraint might be reducing the incoherence of the aliasing artifacts. As reported in the Result section, using symmetric patterns instead of unconstrained ones increased the error incurred by Lustig et al.'s algorithm from 10.5 % to 11.5 %, which seems to be a mild effect. Even though the proposed joint reconstruction algorithm increases the collective coverage of k-space by sampling non-overlapping data points across the multi-contrast images, this benefit might be dampened by the symmetry constraint.
For comparison, we implemented the M-FOCUSS joint reconstruction algorithm and noted that it also attained smaller RMSE figures compared to the gradient descent technique. Even though M-FOCUSS is seen to outperform other competing matching pursuit based joint algorithms (7), the Bayesian method proved to exploit the signal similarities more effectively in our experiments. This is made possible by the fact that the Bayesian framework is flexible enough to allow idiosyncratic signal parts, and strict enough to provide information sharing. Importantly, the Bayesian approach also permits the use of different observation matrices for each signal. This allows us to increase the total k-space coverage across the multi-contrast scans, and its benefit can be seen from the two experiments conducted on the TSE scans with acceleration R = 2.5 along the phase encoding direction. The Bayesian reconstruction results displayed in Fig. 4 are obtained by using a different undersampling pattern for k-space corresponding to each image, and this yielded 2.6 times less RMSE compared to Lustig et al.'s algorithm, demonstrating the benefits of variations in the sampling pattern for different contrast weightings. On the other hand, the experiment in Table 1 that uses the same pattern for both images returned 2 times smaller RMSE compared to the gradient descent method. However, M-FOCUSS has the advantage of being a much faster algorithm with only modest memory requirements. Interestingly, the performance of the M-FOCUSS algorithm deteriorated significantly when tested on the complex-valued signals, yielding poorer results relative to Lustig et al.'s method for the complex-valued TSE dataset. Even though the joint Bayesian algorithm also suffered a performance decrease, it still yielded significantly lower errors with the complex-valued signals.
In the current implementation of the joint CS reconstruction algorithm, datasets with different contrast were undersampled to the same degree. Future work will explore asymmetric undersampling among the component images where, for instance, one fully sampled acquisition could be used as a prior in a joint CS reconstruction of the remaining undersampled contrast sources. The relative tradeoffs of this approach compared to the equally-undersampled regime remain unexplored, but it may yield improvements in robustness or acceleration of the overall image acquisition for multi-contrast data. Another direction for future work is the application of the covariance estimates for the posterior distribution produced by the Bayesian algorithm, which could be used to design optimal undersampling patterns in k-space so as to reduce the uncertainty in the estimated signal (10,24). Also, it is possible to obtain SNR priors, which might be utilized in the Gamma prior p(α0 ∣ c,d) = Ga(α0 ∣ c,d) defined over the noise precision α0 in the Bayesian algorithm. We used the setting c = d = 0 to incur a non-informative noise prior which would not bias the reconstructions towards a particular noise power. In our informal experiments, we also obtained smaller RMSE scores with this setting. Yet the optimal selection of c and d needs further investigation.
Results in this work do not cover parallel imaging considerations, yet combining compressive measurements with multichannel acquisitions has received considerable attention, e.g. (25,26). Even though exposing the Bayesian formalism to parallel imaging is beyond our current scope, treating the receiver channels as a similarity axis in addition to the contrast dimension might be a natural and useful extension of the work presented here.
In addition to the demonstration of the joint CS reconstruction of multiple different image contrasts, other applications lend themselves to the same formalism for joint Bayesian image reconstruction. These include, for instance,
Quantitative Susceptibility Mapping (QSM): In this setting, we again aim to solve an inverse problem of estimating a susceptibility map χ related to the phase of a complex image image |M| ejϕ via an ill-posed inverse kernel. Since the magnitude part |M| is expected to share common image boundaries with χ, it might be possible to use it as a prior to guide the inversion task.
Magnetic Resonance Spectroscopic Imaging (MRSI): Combining spectroscopic data with high resolution structural scans might help reducing the lipid contamination due to the subcutaneous fat or enhance resolution of brain metabolite maps.
Multi-modal imaging techniques: Simultaneous acquisitions with different modalities (e.g. PET-MRI) may benefit from joint reconstruction with this Bayesian formulation.
Conclusions
We presented the theory and the implementation details of a Bayesian framework for joint reconstruction of multi-contrast MRI scans. By efficient information sharing among these similar signals, the Bayesian algorithm was seen to obtain reconstructions with smaller errors (up to a factor of 4 in RMSE) relative to two popular methods, Lustig et al.'s conjugate gradient descent algorithm (2) and the M-FOCUSS joint reconstruction approach (7).
Acknowledgments
The authors would like to thank Borjan Gagoski, Eva-Maria Ratai, Audrey Fan and Trina Kok for their help in collecting the experimental data.
National Institutes of Health NIH R01 EB007942. Contract grant sponsor: National Science Foundation (NSF); Contract grant number: 0643836. Siemens Healthcare. The Siemens-MIT Alliance.
Appendix
Using the Fast Fourier Transform (FFT) in the update equations: Normally, we would need to store and use the matrices Φi which would be a large burden on the memory. Luckily, it possible to implement the operations Φix and by using the FFT. These expressions are ubiquitous in the update equations for the sequential Bayesian CS algorithm, and replacing them with their FFT equivalent makes the storage of these observation matrices no longer necessary:
Computing Φi x
Starting with an empty 2D image t, we populate its entries that correspond to the set of chosen basis function indices B with the vector x: t(B) ← x
We take the 2D FFT and concatenate the vectorized versions of the real and the imaginary parts, Φi x ≡ [Re(fft2(t)), Jm(fft2(t)) ]T
Computing
Given the vector y ∈ R2K, we form the complex vector z ∈ ℂK : z ≡ y1:K + jyK+1:2K, Where y1:K is the vector formed by using only the first half of y and yK+12K contains the second half.
Again starting with an empty 2D image t, we populate its entries that correspond to the set of chosen basis function indices B with the vector z: t(B) ← z
Then the vectorized version of the real part of the 2D IFFT operation yields the desired result,
Footnotes
We use the retrospective undersampling phrase to indicate that k-space samples are discarded synthetically from data obtained at Nyquist rate in software environment, rather than skipping samples during the actual scan.
References
- 1.Ji SH, Dunson D, Carin L. Multitask Compressive Sensing. IEEE T Signal Proces. 2009;57(1):92–106. [Google Scholar]
- 2.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 3.Malioutov D, Cetin M, Willsky AS. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE T Signal Proces. 2005;53(8):3010–3022. [Google Scholar]
- 4.Tropp JA, Gilbert AC, Strauss MJ. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Process. 2006;86(3):572–588. [Google Scholar]
- 5.Gorodnitsky IF, Rao BD. Sparse signal reconstruction from limited data using FOCUSS: A reweighted minimum norm algorithm. IEEE T Signal Proces. 1997;45(3):600–616. [Google Scholar]
- 6.Chen SSB, Donoho DL, Saunders MA. Atomic decomposition by basis pursuit. Siam Rev. 2001;43(1):129–159. [Google Scholar]
- 7.Cotter SF, Rao BD, Engan K, Kreutz-Delgado K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE T Signal Proces. 2005;53(7):2477–2488. [Google Scholar]
- 8.Duarte MF, Sarvotham S, Baron D, Wakin MB, Baraniuk RG. Distributed compressed sensing of jointly sparse signals. 2005 39th Asilomar Conference on Signals, Systems and Computers; 2005. pp. 1537–1541. Vols 1 and 2. [Google Scholar]
- 9.Zelinski AC, Goyal VK, Adalsteinsson E. Simultaneously Sparse Solutions to Linear Inverse Problems with Multiple System Matrices and a Single Observation Vector. Siam J Sci Comput. 2010;31(6):4553–4579. doi: 10.1137/080730822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ji SH, Xue Y, Carin L. Bayesian compressive sensing. IEEE T Signal Proces. 2008;56(6):2346–2356. [Google Scholar]
- 11.Rangan S, Fletcher AK, Goyal VK. arXiv. 2009. Asymptotic analysis of MAP estimation via the replica method and applications to compressed sensing. 09063234v1. [Google Scholar]
- 12.Mallat SG. A wavelet tour of signal processing : the Sparse way. Amsterdam; Boston: Elsevier/Academic Press; 2009. p. xx.p. 805. [Google Scholar]
- 13.Maleh R. PhD Thesis. 2009. Efficient sparse approximation methods for medical imaging. [Google Scholar]
- 14.Candes EJ, Romberg JK, Tao T. Stable signal recovery from incomplete and inaccurate measurements. Commun Pur Appl Math. 2006;59(8):1207–1223. [Google Scholar]
- 15.Tipping ME. Sparse Bayesian learning and the relevance vector machine. J Mach Learn Res. 2001;1(3):211–244. [Google Scholar]
- 16.Rohlfing T, Zahr NM, Sullivan EV, Pfefferbaum A. The SRI24 Multichannel Atlas of Normal Adult Human Brain Structure. Hum Brain Mapp. 2010;31(5):798–819. doi: 10.1002/hbm.20906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Murphy M, Keutzer K, Vasanawala S, Lustig M. Clinically Feasible Reconstruction Time for L1-SPIRiT Parallel Imaging and Compressed Sensing MRI. 8th Annual ISMRM Scientific Meeting and Exhibition, 2010; 2010. [Google Scholar]
- 18.AGILE: An open source library for image reconstruction using graphics card hardware acceleration. submitted to 19th Annual ISMRM Scientific Meeting and Exhibition; 2011. [Google Scholar]
- 19.He LH, Chen HJ, Carin L. Tree-Structured Compressive Sensing With Variational Bayesian Analysis. IEEE Signal Proc Let. 2010;17(3):233–236. [Google Scholar]
- 20.van der Kouwe AJW, Benner T, Dale AM. Real-time rigid body motion correction and shimming using cloverleaf navigators. Magn Reson Med. 2006;56(5):1019–1032. doi: 10.1002/mrm.21038. [DOI] [PubMed] [Google Scholar]
- 21.Duyn JH, Yang YH, Frank JA, van der Veen JW. Simple correction method for k-space trajectory deviations in MRI. J Magn Reson. 1998;132(1):150–153. doi: 10.1006/jmre.1998.1396. [DOI] [PubMed] [Google Scholar]
- 22.Jezzard P, Balaban RS. Correction for Geometric Distortion in Echo-Planar Images from B-0 Field Variations. Magn Reson Med. 1995;34(1):65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 23.Sharma SD, Fong C, Tzung B, Nayak KS, Law M. Clinical Image Quality Assessment of CS-Reconstructed Brain Images; 18th Annual ISMRM Scientific Meeting and Exhibition. 2010. [Google Scholar]
- 24.Seeger M, Nickisch H, Pohmann R, Scholkopf B. Optimization of k-space trajectories for compressed sensing by Bayesian experimental design. Magn Reson Med. 2010;63(1):116–126. doi: 10.1002/mrm.22180. [DOI] [PubMed] [Google Scholar]
- 25.Liang D, Liu B, Wang JJ, Ying L. Accelerating SENSE Using Compressed Sensing. Magn Reson Med. 2009;62(6):1574–1584. doi: 10.1002/mrm.22161. [DOI] [PubMed] [Google Scholar]
- 26.Weller DS, Polimeni JR, Grady LJ, Wald LL, Adalsteinsson E, Goyal VK. Combining nonconvex compressed sensing and GRAPPA using the nullspace method. 18th Annual ISMRM Scientific Meeting and Exhibition 2010; 2010. [Google Scholar]