Which, if any, hydrates will crystallise? Predicting hydrate formation of two dihydroxybenzoic acids

Abstract

A study of two dihydroxybenzoic acid isomers shows that computational methods can be used to predict hydrate formation, the compound : water ratio and hydrate crystal structures. The calculations also help identify a novel hydrate found in the solid form screening that validates this study.

Changes in hydration states of crystalline compounds throughout the manufacturing process often cannot be avoided. The identification of hydrates (crystals that incorporate water into the structure) and their hydration/dehydration conditions is essential in the development of pharmaceutical compounds. The presence of water in the crystal lattice may lead to very different physicochemical properties, and so influence the bioavailability of a drug compound.¹ Hydrate formation is a widespread phenomenon; it is believed that it might occur for up to three quarters of pharmaceutical compounds² and is observed for a third of organic molecules.^3–5 The probability of water inclusion is particularly high when charged groups (salts) or polar groups, such as carbonyl (), ether (C–O–C), hydroxyl (O–H) and primary amine (N–H) groups are present,² which is usually the case in pharmaceuticals.

Even for the types of molecules prone to hydrate formation, it is not certain that any hydrates will be formed, let alone the stoichiometry (the compound : water ratio). For example, 2,4-dihydroxybenzoic acid (2,4-DHB) forms two hydrates, a stable hemihydrate (QIVTUK)⁶ and a metastable monohydrate whose structure could not be determined experimentally.⁷ In contrast, the 2,5 isomer of dihydroxybenzoic acid (2,5-DHB) forms no hydrates, as shown by the accompanying solid form screen (ESI^†) which found four novel solvates.

Multiple analytical techniques have to be used to characterise the solid state of any compound. Over the last decade methodologies for computationally generating crystal structures have progressed considerably,⁸ becoming a useful complement to experimental solid form screening.^9,10 crystal structure prediction calculations are now being successfully performed on multi-component systems, such as co-crystals,^8,11 solvates^12–16 and salts.^17,18 Evaluating whether the co-crystal or solvate will crystallise and its stoichiometry is an additional challenge. There have been successes in rationalising the experimentally observed stoichiometries for co-crystals¹⁹ and acetic acid solvates.^13,14 Only four attempts to predict stoichiometric hydrates^‡ have been undertaken,^15,16,20 including the hydrate set as a target in the last blind test of crystal structure prediction.²¹ In order to complete and understand the differing hydration behaviour seen in our screens for solid state forms of the pharmaceutically relevant molecules 2,4- and 2,5-DHB (ESI^†), we perform the first computational organic hydrate study which considers different stoichiometries.

Hypothetical hemi-, mono- and dihydrate crystal structures were generated in an extensive search²² and the lattice energies evaluated accurately,²³ allowing for minor conformational change²⁴ and molecular polarisation²⁵ within the crystal, as detailed in the ESI.^† The stability of the different hydrate stoichiometries for both isomers relative to the anhydrate and ice was assessed from the stabilisation energy per water molecule (E_stab, Fig. 1). Assuming that hydrate formation is thermodynamically driven and that this can be estimated by relative lattice energies, we can predict which of the hydrates are more stable than the anhydrate by comparing E_stab with the lattice energy of ice. Using the same computational model, E_latt (ice) varies from −66.61 to −70.11 kJ mol⁻¹ for the ordered polymorphs II, VIII, XI and XV (ESI^†).^26–29 This leads to a comparison with a range of lattice energies rather than a single value.

Fig. 1.

Definition of the molecules and the starting conformations used in the searches for possible hydrate structures, and the definition of the stabilisation energy E_stab from the lattice energy^§ of each predicted hydrate structure and the given lattice energy of the experimentally most stable DHB anhydrous polymorph (AH) as determined by thermal and slurrying measurements (ESI^†). Hydrate formation is thermodynamically expected if E_stab < E_latt (ice).

Fig. 2 shows that 2,5-DHB is expected not to form a hydrate, but that 2,4-DHB can form both mono- and hemihydrates, but not a dihydrate, in agreement with the extensive experimental screen.

Fig. 2.

Crystal energy landscape of dihydroxybenzoic acid hydrates plotted by stabilisation energy per water molecule in the lattice, E_stab (Fig. 1). Each symbol denotes a crystal structure (Tables S9 and S10, ESI^†) which is a lattice energy minimum. The range of ice polymorph energies is in yellow. Only the most stable structures are shown, so the upper region of the hemihydrate landscape omits many 2,4-DHB structures.

The structure of the known 2,4-DHB hemihydrate (Fig. 3) was found as second in energy (Fig. 2), although the difference between E_stab (Fig. 1) and E_latt for the most stable ice polymorph, VIII, is small. The global minimum of the hemihydrate search is closely related to the most stable anhydrate structure (Fig. S7, ESI^†).

Fig. 3.

Overlay of the predicted (green) and experimentally determined 2,4-DHB hemihydrate (red), with a rmsd₁₅^¶ of 0.218 Å.

Several 2,4-DHB monohydrates were predicted to be thermodynamically feasible, and could be used to propose a structure for the unsolved, metastable monohydrate (Fig. 4). The experimental powder X-ray diffraction pattern of the monohydrate matches that simulated from the most stable structure as well as the experimental hemihydrate powder pattern matches that simulated from the corresponding calculated hemihydrate (Fig. 5). Further spectroscopic and X-ray diffractometric^|| evidence (ESI^†) confirms that the dimerised carboxylic acid group and acid⋯water interactions (Fig. 4), lattice parameters and space group of the most stable computed structure correspond to the monohydrate. However, since the searches with different p-OH proton conformations (Fig. 1) also generated low energy structures with very similar diffraction patterns (Fig. 5), differing only in the positions of the p-OH and adjacent water protons but not in the packing (Fig. S11, ESI^†), we cannot eliminate the possibility of variations in the proton positions or proton disorder. Characterising the proton positions in the experimental structure is not currently possible, because the metastability prevents the growth of crystals suitable for single crystal diffraction studies.

Fig. 4.

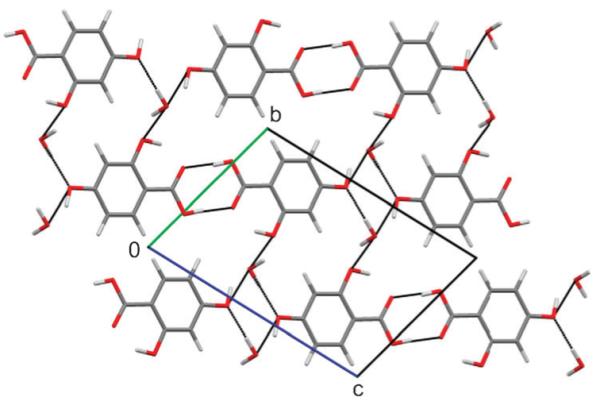
The most stable computed structure of 2,4-DHB monohydrate. Black lines indicate the hydrogen bond interactions.

Fig. 5.

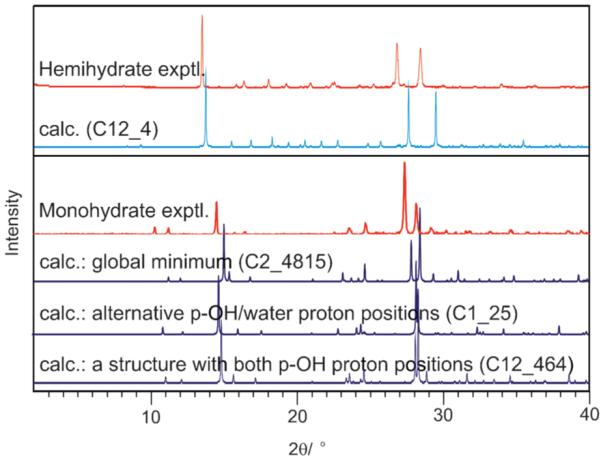
Experimental powder X-ray diffraction patterns (hemi- and monohydrate) obtained at room temperature compared with simulated patterns (λ = 1.5418 Å) for the calculated structures (Table S10, ESI^†). For the monohydrate, the diffractogram of the proposed structure (Fig. 4) is contrasted with other structures that differ only in the p-OH and adjacent water proton positions (ESI^†, 6.3).

The two isomers differ in the hydrogen bonding motifs of the computed hydrate structures. The carboxylic acid dimer is found in nearly all 2,4-DHB low-energy hydrate structures, whereas two thirds of the 2,5-DHB low-energy hydrates have water molecules hydrogen bonded to the acid group. This is significant because both isomers form the expected carboxylic acid dimer in their anhydrous forms. Despite the structural differences, the hydrates of the two isomers are comparable in lattice energy (Tables S9 and S10, ESI^†). The dominant reason for the different hydrate formation propensity (Fig. 2) is that the hydrate forming isomer, 2,4-DHB, is less stable and less dense in the anhydrous state than the 2,5-DHB isomer.

We have reported the first successful crystal structure prediction of the compound : water ratio of stoichiometric hydrates. Moreover, a structure for the 2,4-DHB monohydrate could be proposed which is consistent with extensive experimental data. The experimentally observed stability order of the two 2,4-DHB hydrate stoichiometries is not reproduced. Improving the calculations to give more accurate free energies, including possible proton disorder,²⁶ would help increase confidence in thermodynamic versus possible kinetic arguments for which hydrates are observed. However, the calculation of the crystal energy landscapes of the potential hydrate structures of these isomers provide considerable support and rationalisation of the extensive experimental hydrate screening.