Genome-Wide Heterogeneity of Nucleotide Substitution Model Fit

Abstract

At a genomic scale, the patterns that have shaped molecular evolution are believed to be largely heterogeneous. Consequently, comparative analyses should use appropriate probabilistic substitution models that capture the main features under which different genomic regions have evolved. While efforts have concentrated in the development and understanding of model selection techniques, no descriptions of overall relative substitution model fit at the genome level have been reported. Here, we provide a characterization of best-fit substitution models across three genomic data sets including coding regions from mammals, vertebrates, and Drosophila (24,000 alignments). According to the Akaike Information Criterion (AIC), 82 of 88 models considered were selected as best-fit models at least in one occasion, although with very different frequencies. Most parameter estimates also varied broadly among genes. Patterns found for vertebrates and Drosophila were quite similar and often more complex than those found in mammals. Phylogenetic trees derived from models in the 95% confidence interval set showed much less variance and were significantly closer to the tree estimated under the best-fit model than trees derived from models outside this interval. Although alternative criteria selected simpler models than the AIC, they suggested similar patterns. All together our results show that at a genomic scale, different gene alignments for the same set of taxa are best explained by a large variety of different substitution models and that model choice has implications on different parameter estimates including the inferred phylogenetic trees. After taking into account the differences related to sample size, our results suggest a noticeable diversity in the underlying evolutionary process. All together, we conclude that the use of model selection techniques is important to obtain consistent phylogenetic estimates from real data at a genomic scale.

Introduction

At large or genomic scales, the patterns that have shaped molecular evolution are largely heterogeneous. Variations in nucleotide composition and types of substitution rates are evident ranging from the large, that is, chromosomes or chromosomal regions (Lercher et al. 2004), to the small scale, where variations occur among and within the different domains and sites that constitute genomic loci (Yang 1996; Nachman and Crowell 2000).

Initial approaches to the understanding of molecular evolution considered that the variation in rates within genomes resulted from the interplay of genetic drift and natural selection on an underlying mutational process that may have been uniform across the genome. Today, several studies have provided growing amounts of evidence that the process of mutation is in itself complex, responding to composition, context dependent, and mechanistic effects which yield regionally variable rates of substitution. These effects hold both for coding and noncoding regions (Subramanian and Kumar 2003; Lercher et al. 2004) and the variation in sequence composition together with the chemical properties of nucleotides (Galtier et al. 2001), the processes of replication (Prioleau 2009) and transcription (Mugal et al. 2009), the mutagenic nature of recombination in mammals (Galtier et al. 2001), differential rates of sex-biased germ line mutation (Nachman and Crowell 2000), and even cryptic context dependent effects (Hodgkinson et al. 2009), among others, come together to produce the underlying mosaic pattern of changes upon which evolutionary forces may operate.

Indeed, genome analyses need to consider this large amount of heterogeneity. In particular, modern phylogenetic approaches should use appropriately simple or complex probabilistic substitution models that take into account those parameters that capture the features under which different genomic regions may have evolved (Sullivan and Joyce 2005). In general, it has been shown that substitution models that are unnecessarily complex can increase the variance of the estimates, which is likely to make the estimation of evolutionary history more difficult (Kelchner and Thomas 2007). Also, when the model of evolution assumed is oversimplified, phylogenetic methods may lose accuracy and consistency leading to incorrect trees more often or converging to an incorrect tree with increased amounts of data (Felsenstein 1978; Huelsenbeck and Hillis 1993; Penny et al. 1994; Bruno and Halpern 1999). At the same time, it is important to remember that the biological processes underlying evolution will be more complex than any of the available models. All models are wrong, but some are useful (Box 1976). Models themselves are tools, and an adequate model, rather than capturing the full complexity of underlying biological process, can tell us what inferences the data support (Burnham and Anderson 2003). While several efforts have concentrated on the development and understanding of techniques for model selection (for a review, see Sullivan and Joyce 2005; Kelchner and Thomas 2007), up until now no extensive descriptions of overall model fit at a complete genomic scale have been reported in the literature. Notably, next-generation sequencing technologies are providing vast arrays of biological data, and phylogenetics will have to deal with very large multigene or genomic data sets making the understanding of model-fit heterogeneity fundamental.

Here, three separate genomic data sets consisting of 5 mammals, 15 vertebrate, and 12 Drosophila species were analyzed in order to characterize substitution model fit and parameter estimation at a genomic scale. The results of different model selection strategies, taking model selection uncertainty into account, and exploring the effect of variations in the amount of data and divergence present across the genome, are presented together with an analysis of the effect of model-fit heterogeneity on phylogenetic inference.

Materials and Methods

The longest transcripts of orthologous coding genes from the complete genomes of 5 mammals (human, chimpanzee, rat, mouse, and dog) and 15 vertebrates (human, chimp, orangutan, mouse, rat, dog, cow, horse, chicken, guinea pig, opossum, platypus, stickleback, zebra fish, and fugu) were obtained from Ensembl version 54 (www.ensembl.org). Sequences were aligned using Muscle (Edgar 2004), with a maximum running time of 5 h or 9,999 iterations, and filtered with Gblocks (Castresana 2000) where the minimum number of sequences for a conserved position and flank position, the maximum contiguous nonconserved positions, the minimum block length, and percentage of allowed gaps were set to 3, 4, 8, 10, 0 and 11, 13, 8, 10, 50 for mammals and vertebrates, respectively (alignments are available from the authors by request). Filtering parameters for vertebrates were scaled relative to the number of sequences while choosing a slightly more stringent value for the minimum number of sequences for a conserved position and allowing for a higher percentage of gaps per column otherwise. Filtered alignments for the longest transcripts of genes with orthologs in each of the 12 Drosophila genomes were obtained from the Drosophila 12 Genomes Consortium (2007). After eliminating alignments with less than 50 nucleotides, the mammal, vertebrate, and Drosophila genomic sets consisted of 12726, 4482, and 6664 genes, respectively.

The jModelTest program (Posada 2008) was used on individual alignments of orthologs to estimate the best-fit models of nucleotide substitution and obtain Phyml's (Guindon and Gascuel 2003) maximum likelihood trees and estimates of model parameters for 88 reversible models of nucleotide substitution (table 1). Both point estimates and model averaged estimates of base frequencies, relative substitution rates, transition/transversion rate ratio (ti/tv), the alpha shape of the gamma distribution for rate variation among sites (a), the proportion of invariable sites (pinv), and parameter importance were considered (see Posada and Buckley 2004). To make them more comparable across models and data sets, we scaled the relative substitution rates so they refer the same unit of time, that in which we expect to see exactly one change per site. To do this, we divided the estimates reported by jModelTest by 2 × fA × fC × rAC′ + 2 × fA × fC × rAG′ + 2 × fA × fT × rAT′ + 2 × fC × fG × rCG′ + 2 × fC × fT × rCT′ + 2 × fG × fT × rGT′, where the unscaled relative substitution rate between nucleotide X and Y is rXY′, and fX is the stationary frequency of nucleotide X. Descriptive statistics on parameter distributions were obtained excluding outliers (those beyond a cutoff value of three times the interquartile distance for each parameter distribution). Three different model selection criteria were employed: the Akaike Information Criterion (AIC) (Akaike 1974), the Bayesian Information Criterion (BIC) (Schwarz 1978), and hierarchical likelihood ratio tests (hLRTs) (Posada and Crandall 1998).

Table 1.

Model Families and Parameters

Model EF		Rate Partitions	Model UF
K	Name		Name	K
S + 1	JC	rAC = rAG = rAT = rCG = rCT = rGT	F81	S + 4
S + 2	K80	rAC = rAT = rCG = rGT, rAG = rCT	HKY	S + 5
S + 3	TrNef	rAC = rAT = rCG = rGT, rAG, rCT	TrN	S + 6
S + 3	TPM3	rAC = rCG, rAT = rGT, rAG = rCT	TPM3uf	S + 6
S + 3	TPM2	rAC = rAT, rCG = rGT, rAG = rCT	TPM2uf	S + 6
S + 3	TPM1	rAC = rGT, rAT = rCG, rAG = rCT	TPM1uf	S + 6
S + 4	TIM3ef	rAC = rCG, rAT = rGT, rAG, rCT	TIM3	S + 7
S + 4	TIM2ef	rAC = rAT, rCG = rGT, rAG, rCT	TIM2	S + 7
S + 4	TIM1ef	rAC = rGT, rAT = rCG, rAG, rCT	TIM1	S + 7
S + 5	TVMef	rAC, rAT, rCG, rGT, rAG = rCT	TVM	S + 8
S + 6	SYM	rAC, rAT, rCG, rGT, rAG, rCT	GTR	S + 9

NOTE.—Twenty-two nucleotide substitution model families with equal (EF) or unequal (UF) base frequencies and different number of parameters (K) are considered. A total of 88 individual models can be obtained by specifying a proportion of invariant sites (+I), gamma-distributed site rates (+G), both (+I+G), or neither for each of the 22 families. K = M + B, where M = 1 (+I), 1 (+G), 2 (+I+G), or 0 (no rate variation), and B is the number of branches (B = 2S − 3, where S is the number of sequences in the alignment).

The AIC measures the expected distance between the true model and the estimated model:

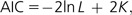where L is the maximized likelihood score for a model and K is the number of parameters in the model. It can be interpreted as the amount of information lost when we use a given model to approximate the actual process of molecular evolution. Therefore, the model with the smallest AIC is preferred. The BIC provides an approximate solution to the natural log of the Bayes factor:

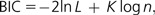where n is the sample size, approximated here by the total number of characters in the alignment. As with the AIC, the smaller the BIC, the better the fit of the model to the data. A nice feature of AIC and BIC is that they offer an instantaneous ranking of the models. In this way, we can easily compute the difference for model i:

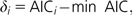In turn, these differences can be used to obtain the relative weight of any model of R models:

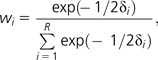Given that the sum of weights for all models add to 1, it is easy to establish an approximate confidence set of models by summing the weights from largest to smallest until the sum reaches the desired threshold. Furthermore, given the model weights, it is possible to obtain model-averaged estimates (also known as multimodel estimates) for any parameter (Burnham and Anderson 2003). For example, a model-averaged estimate of the relative substitution rate between adenine and cytosine (φA–C) using the model weights (w) for R candidate models would be:

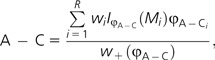where 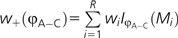and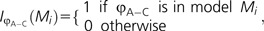

A quite different strategy is the use of hLRTs, where models are compared in a pairwise fashion using a series of predefined likelihood ratio tests:

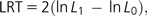where L₁ is the maximum likelihood under the more parameter-rich complex model and L₀ is the maximum likelihood under the less parameter-rich simple model (null model). When the two models compared are nested (i.e., the null model is a special case of the alternative model), and the null hypothesis is correct, this statistic is asymptotically distributed as a χ² distribution with a number of degrees of freedom equal to the difference in number of free parameters between the two models. Conveniently AIC and the BIC can be easily used to compare nested and nonnested models.

For AIC and BIC, both the best model and the 95% confidence set of models best fitting each alignment in the data set were considered in the analysis. AIC or BIC model weights were estimated to examine model selection uncertainty and parameter contribution to the averaged estimates (see Posada and Buckley 2004). In order to examine the possible effects of sampling and divergence on the fit of different models, we also subdivided the data into sections according to alignment length and pairwise nucleotide diversity (Nei and Li 1979) by selecting genes found in the same quartile of both parameter distributions (LP hereafter): “low LP” (722 genes; first quartiles), “mid LP” (722 randomly sampled genes from the second and third quartiles), and “high LP” (554 genes; fourth quartiles). As such, long genes with low variation and short genes with high variation were excluded from the analysis. Graphics and statistics were obtained using the R package (R Development Core Team 2008).

In order to understand whether the observed model-fit heterogeneity along the genome could have substantial effects in phylogenetic inference, comparisons among the maximum likelihood trees obtained for the best-fit model and those of 1) all other models, 2) those contained within the 95% confidence interval (95% CI), and 3) those outside of the 95% CI, were evaluated using four different tree distance metrics: the symmetric difference (RF), which considers clade differences among trees (Robinson and Foulds 1981), the branch score (BS) (Kuhner and Felsenstein 1994) which measures the square difference between branch lengths among trees, and the K-tree score (KS) together with its associated scaling factor (SF) (Soria-Carrasco et al. 2007) which considers differences in branch length after minimizing the difference in divergence between trees. In order to compare data sets with different numbers of species (S), the tree distances were rescaled dividing by the number of clade comparisons in the case of the RF score, RF′ = RF/(2 × (S − 3)), and by the number of branches in for the BS and KS, D′ = D/(2 × S − 3), where D is BS or KS. Statistical differences among trees were evaluated using pairwise Kishino–Hasegawa (KH) (Kishino and Hasegawa 1989), Shimodaira–Hasegawa (SH) (Shimodaira and Hasegawa 1999), and Approximately Unbiased (AU) tests (Shimodaira 2002).

Results

Heterogeneity of the Best-Fit Model

Figure 1 shows the results obtained using AIC as the selection criterion for all three genomic sets. Of the 88 reversible nucleotide substitution models considered, 82 were selected as best-fit models among all genomic sets (JC+I, F81+I, JC+G, F81+G, JC+I+G, and F81+I+G where never identified as best-fit models; JC and F81 had a negligible representation with 1 and 3 genes, respectively). Considering only the relative substitution parameters and the base frequencies forming the instantaneous rate matrix of a model (henceforth the “model family”; i.e., the JC family includes the JC, JC+I, JC+G, and JC+I+G models), 21 of 22 possible families were represented in the best-fit set.

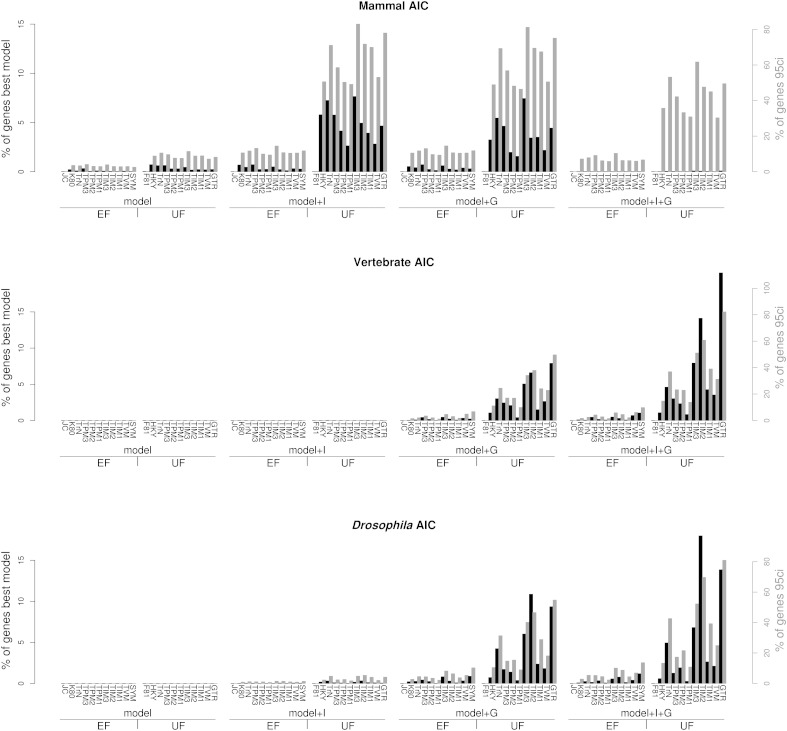
Fig. 1.—

Genome-wide model diversity. Bars represent the percentage of times a given substitution model (x axis) is the best model (black bars, left y axis) or is included in the 95% CI (95ci: gray bars, right y axis) using AIC. Models are shown grouped according to their base frequency and rate variation among sites parameterization and ordered by increasing number of parameters within each group (see table 1).

The frequency with which each model was found to be the best-fit model across the genome varied considerably among the different genomic sets (table 2). The patterns found for vertebrates and Drosophila were quite similar yet different from those found in mammals. In the vertebrate and Drosophila sets, there was a tendency toward more complex models (i.e., more parameters) leading to larger differences among the frequencies of each successive model when ranked from the most highly represented to the least represented. In general and considering all three species sets, more than a few families (a minimum of 6–10 of 22) or models (a minimum of 11–17 of 88) were required to explain at least 80% of the genes.

Table 2.

Genome-Wide Model Family Ranking

	Data/Count	Rank
		1	2	3	4	5	6	7	8	9	10
AIC best model	Mammal	TIM3	TrN	TPM3uf	GTR	HKY	TIM2	TIM1	TPM2uf	TVM	TPM1uf
	10	15.09	12.69	10.39	9.08	9.03	8.37	7.43	4.14	2.81	2.63
	Vertebrate	GTR	TIM2	TIM3	TrN	TIM1	TVM	TPM3uf
	7	28.29	20.73	12.96	7.61	4.26	3.53	3.01
	Drosophila	TIM2	GTR	TIM3	TrN	TIM1	TVM
	6	28.84	23.2	12.83	9.17	4.98	2.1
AIC 95% CI	Mammal	TIM3	GTR	TrN	TIM2	TIM1	TPM3uf	HKY	TVM	TPM2uf	TPM1uf
		59.34	52.69	51.02	49.43	47.84	41.81	36.01	35.27	34.86	33.48
	Vertebrate	GTR	TIM2	TIM3	TIM1	TrN	TVM	TPM3uf	TPM2uf	HKY	TPM1uf
		32.98	24.7	21.31	15.81	15.37	13.5	10.07	9.95	6.43	5.92
	Drosophila	GTR	TIM2	TIM3	TrN	TIM1	TVM	TPM2uf	TPM3uf	HKY	SYM
		34.95	30.39	24.29	19.68	18.04	11.26	9.89	8.59	6.49	6.31
AIC best model LP mammal	Low LP	TrN	HKY	TIM3	TIM1	TPM3uf	TPM1uf	TIM2	TPM2uf	TrNef	TIM2ef
	12	22.44	14.82	9.56	7.48	5.54	5.12	5.12	4.02	2.35	1.39
	Mid LP	TIM3	TrN	TPM3uf	TIM2	HKY	GTR	TPM2uf	TPM1uf	TIM1	TVM
	10	17.31	14.13	11.08	9.83	9.14	7.34	4.02	3.46	3.19	2.77
	High LP	GTR	TVM	TIM3	TPM3uf	TPM2uf	TIM2	TrN
	7	25.09	15.7	14.98	12.27	5.05	4.15	3.79

Note.—The set of model families with 1) the highest representation under the best model, 2) the 95% CI, or 3) the best model for different subsets of the mammal set varying in both alignment length and pairwise nucleotide diversity (“Best Model LP Mammal”) are shown ranked by their frequency (as a percentage) in each of the three sets of species (labels under the “Data” column, first and second main rows) or low, median, and high values of LP (labels under the “Data” column, third main row). Only the first ten ranks shown, and where the best model is considered (first and third main rows), only the minimum number of families required to explain at least 80% of all genes were considered (numbers under the “Count” column).

Differences in Parameterization

Best-fit models with particular parameterizations were much more common than others. This is especially evident in figure 2, where different base frequency, relative substitution rate, and rate heterogeneity parameterizations are compared within each of the three species sets analyzed. Best-fit models usually included unequal base frequencies (UF) and rate variation among sites (either considering a proportion of invariable sites (+I), gamma distributed rates (+G) or both (+I+G)). Within these, models only considering +I were much more frequent than those with +G in the mammal set, whereas those considering both +I and +G were much more frequent in both vertebrate and Drosophila sets.

FIG. 2.—

Genome-wide representation of model parameterizations. Bars indicate the percentage of best-fit models in each category. EF and UF indicate equal or unequal base frequencies, respectively. IG, G, I, and N indicate models +I+G, models +G, models +I, and models without rate variation, respectively. ti = tv and ti,tv correspond to equal or unequal transition and transversion rates. 2 ti and 1 ti indicate 1 or 2 different transition rates. 1 tv, 2 tv, and 4 tv indicate 1, 2, or 4 different transversion rates. r1, r2, and r3 indicate the index of the TIM and TVM models (see table 1). For ti1–2, tv1, 2, 4, and r1–3, JC and F81, found to have negligible genome-wide representations, were excluded. Black lines show the expected percentage of models under each parameterization of the 88 considered. Significantly different proportions among pairwise comparisons (binomial test, P < 0.05) are labeled with an asterisk.

Across the genomic sets, the most striking variation in the relative rate matrices of the best-fit models occurred between the F81 model (labeled as ti = tv in fig. 2) and the rest of the UF variants (ti,tv), indicating that transition and transversions occur at different rates for the vast majority of genes. Within the latter, best-fit models specifying two types of transitions (2 ti) were significantly more common than those with only one transition rate (1 ti). For transversions, best-fit models specifying only one type of transversion were significantly less common than those with two or four different transversion rates, whereas the representation of best-fit models with four transversion rates grew with the number of species. Also, considering the three possible combinations of the four distinct types of transversions under two transversion rate models (r1, r2, or r3 corresponding to: rAC = rGT, rAT = rCG; rAC = rAT, rCG = rGT; or rAC = rCG, rAT = rGT, respectively), r3 was always found at a significantly lower proportion. Finally, it was clear that where partitions among parameters differed most among sets (site rate heterogeneity, number of transversion rates, and among possible combinations of two transversion rates), parameter partitions were more similar between the vertebrate and Drosophila sets than either of them was with the mammal set (fig. 2).

Taking Model Selection Uncertainty into Account

When considering the set of models that fell within the 95% CI (fig 1, gray bars), results were similar to those observed for the best-fit models. The only marked difference occurred in the mammal set, where +I+G models were found highly represented under the 95% CI, but seldom identified as best-fit models (only 0.34% of all best-fit models contained +I+G under this data set).

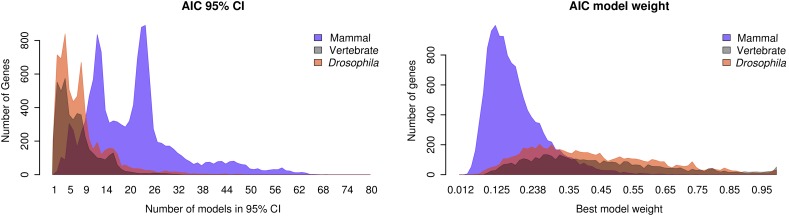
It is also of interest to consider how model uncertainty itself varied across the data sets. The distribution of the number of models in the 95% CI and best model weight for each species set under the AIC is shown in figure 3. For the mammal, vertebrate, and Drosophila sets, the maximum number of models in the CI was 69, 33, and 48, respectively, with medians of 21, 6, and 6. The bimodal distribution for the mammal set is further characterized in supplementary figure S1 (Supplementary Material online), where a decomposition of model frequencies by number of models under the CI shows that the valley between both peaks is due to a lack of power for differentiating among models other than GTR, TrN, and TIM variants with comparable certainty. Similarly, model weights were highest in the vertebrate set and smallest in the mammal set.

Fig. 3.—

Distribution of model selection uncertainty. The histograms, depicted as shaded areas, show the number of models in the AIC 95% CI set (left) and the best AIC weight (right) per gene for all genes in each of the three species sets analyzed.

The Effect of Alignment Length and Pairwise Nucleotide Diversity

Both parameters considered jointly, hereafter LP, were evaluated using the mammal set (table 2, bottom). As LP increased, the minimum number of best-fit AIC models required to explain at least 80% of the genes decreased from 12 to 10 and 7 as subsets of low, medium, and high LP were considered (see Materials and Methods). Accordingly, the most frequently represented best-fit AIC models shifted toward more complex relative rate parameterizations. Under high LP, GTR accounted for approximately a fourth of all genes (25.09%), followed by TVM (15.7%), and TIM3 (14.98%). In general, the TVM, TPM3uf (12.27%), and TMP2uf (5.05%) families were more frequently selected under high LP, decreasing, albeit maintaining, the bias where two instead of one of transition rates were found with higher frequencies. Also, an increased LP resulted in a decrease in the size of the 95% CI (number of models) and an increase in the weight of the AIC model (data not shown).

Heterogeneity in Parameter Estimates

At a genomic scale, heterogeneity was observed not only in the best-fit models selected and most frequent parameterizations but also in that under any given best-fit model, most parameter estimates also varied broadly among genes. A complete table with summarizing statistics of genomic parameter values is provided in supplementary table S1 (Supplementary Material online). Histograms for most parameter distributions are shown in figure 4.

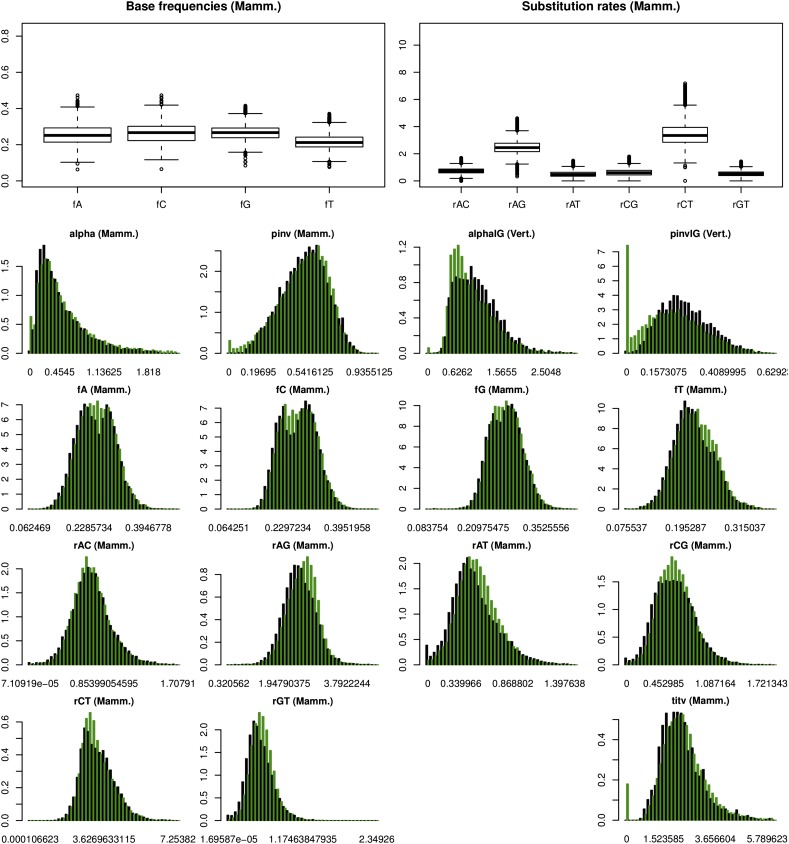
Fig. 4.—

Genome-wide parameter estimate distributions. Examples are shown for estimates derived from the AIC best-fit model (black) and the weighted average of all models in the 95% AIC CI (green). All parameters shown, except alphaIG and pinvIG derived from the 15 species set, are from the five species set. pinv, pinvIG and alpha, and alphaIG are the proportion of invariant sites and shape parameter of the gamma distribution used to model rate variation among sites from the +I (with a considerable representation in the mammal set only) or +I+G models (with considerable representation in the 12 and 15 species sets only), respectively. ti/tv is the transition/transversion rate ratio—considerably represented only in the five species set. Relative substitution rate estimates were “scaled” to facilitate comparisons (see Materials and Methods).

The frequencies of the four nucleotide bases (A, C, G, and T) were similar across species sets and ranged from a minimum value of 0.06 to a maximum of 0.47. While median values were close to the equal frequency value of 0.25, that of T showed a general bias toward lower frequencies with a mean of approximately 0.21. In the mammal set, and when considering the estimates derived from the best-fit model only, the distributions of the frequency of A and C, slightly less that of G, and even less so that of T, were bimodal around 0.25.

The variation in the transition/transversion rate ratio was large ranging, from 0.69 to well over 6, with a median of 2.24 in the mammal set, the latter being consistent with the commonly accepted ratio of transitions being twice as frequent as transversions on average. On the other hand, the median for the Drosophila and vertebrate species sets were 1.35 and 1.78 where only 116–100 genes contained models with the parameter.

The relative rate parameters (rAC, rAG, rAT, rCG, rCT) among all three species sets showed wide ranges and different median estimates, (fig. 4, supplementary table S1, Supplementary Material online). The two transition rates, rAG and rCT, were consistently higher than the transversion rates. They also showed the highest variation among species sets where both showed higher estimates in the mammal set, followed by the Drosophila, and vertebrate sets (supplementary table S1, Supplementary Material online). Interestingly, the distributions of the point and model-averaged estimates were very similar (black and green bars, respectively) in all cases.

The proportion of invariant sites also showed considerable variation ranging from 2% to 98% with a median of approximately 50% and a left skew in the distribution. The variation in the alpha parameter of the gamma distribution ranged from values of 0.01 to well over 2 with a median of 0.41 to 0.53 and a right skew (supplementary table S1, Supplementary Material online. In general, model-averaged parameter estimates (blue rows, supplementary table S1, Supplementary Material online; green bars, fig. 4), obtained as weighted means of all models within the 95% CI, were in agreement with best model estimates.

Parameter heterogeneity from the perspective of a CI can also be looked at through the representation of parameter importances (supplementary fig.S2, Supplementary Material online). Their distributions support the parameter partitions described thus far.

Considering Alternative Selection Criteria

The results presented so far were obtained using AIC as the selection criterion. Under BIC, the results (supplementary fig. S3, Supplementary Material online) were different in terms of the most frequent model families and parameter complexity—BIC selected simpler models but suggested similar model patterns and overall model-fit heterogeneity when compared with AIC.

Overall, 82/88 models or 22/22 model families were observed for the best-fit BIC model among all three genomic species sets. The TVMef, TVMef+I, SYM, SYM+I, F81+G, JC+I+G, F81+I+G models were absent throughout. In this case, both extremes of model complexity (JC, F81, and GTR) showed considerably low representations (supplementary fig. S4, Supplementary Material online) when compared with the results obtained with AIC. Again, the frequencies of individual models among species sets and parameterizations varied, showing patterns that agreed more between the Drosophila and vertebrate sets and differed in mammals. However, unlike under AIC, the mammal set showed a tendency toward models with the lowest complexity in rate parameterization.

In terms of variation among the different types of parameterization, the use of BIC (supplementary fig. S4, Supplementary Material online) led to the same general patterns among parameter partitions than AIC, albeit with small differences. The 95% CI set showed very similar frequencies agreeing with those obtained from the best model (gray vs. black bars, supplementary fig. S3, Supplementary Material online). Considering a subset of the mammal set with high values for length and nucleotide diversity (LP), rate parameterizations still showed a preference for less parameter rich models but agreed notably with AIC in terms of rate heterogeneity and base frequency partitions: +I (56.86%) and +G (37.00%) were the most frequent and UF models (90.43%) were much more frequent than their EF analogs. Also, as LP increased, the minimum number of models required to explain at least 80% of the genes grew from 4 to 6 in the mammal set. HKY (24.91%) was again the most represented best-fit model, but K80, which was previously observed as the second most represented model, dropped from 20.54% to 2.53%. Also, more parameter rich models, such as TPM3uf (23.83%) and TIM3 (9.39%), were found among the set of most highly represented models.

Finally, the hLRT showed markedly reduced levels of heterogeneity in model fit and in general a preference for much simpler models (supplementary fig. S5, Supplementary Material online). For example, HKY was by far the most frequent best-fit model, followed by TrN, JC, and the TIMuf variants, notably, without I or G parameterizations (together covering >80% of all genes) in the mammal set.

The Effect of Model Selection on the Estimation of Phylogenetic Trees

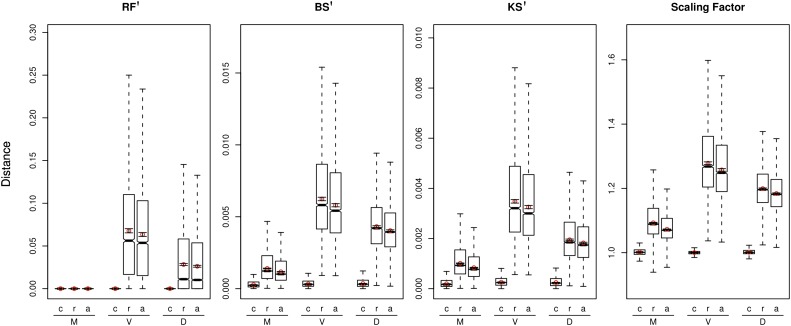
The effect of different models on phylogenetic reconstruction were evaluated by comparing the tree obtained from the best fit AIC model with all the rest (a) and either those contained (c) or excluded (r) from the AIC 95% CI set. With respect to tree topology (RF′) and or branch length (BS′ and KS′), the trees derived from models in the 95% CI set showed much less variance and significantly smaller distances to the tree estimated under the best-fit model than trees derived from models outside this interval (fig. 5). On the other hand, when only those models falling outside of the CI were considered, or when no distinction was made, the differences in tree distances observed were highly significant. Similar results were obtained when considering differences in the amount of global divergence in trees using only the scaling factor SF. In this case, the 95% CI set average was equally and proportionally distributed around 1, whereas the other two groups were generally scaled by a factor > 1. Overall, the differences in variance and mean phylogenetic distance grew (r and a groups) with tree size (mammals < Drosophila < vertebrates) but remained notably low for the 95% CI set (c) among the various distance metrics.

FIG. 5.—

Model selection and tree distances. Boxplots show rescaled mean tree distances to the best-fit model tree from trees estimated under models within the ci95 set (c), models outside of the ci95 set (r), and all models (a = c + r). Four different metrics are shown: RF′ = symmetric difference distance per clade, BS′ = branch score distance per branch, KS′ = K-score distance per branch, and SF = scaling factor. 99% CIs are shown as whiskers extending from the red points. CIs were inferred excluding outliers—estimates falling beyond 1.5 times the interquartile distance.

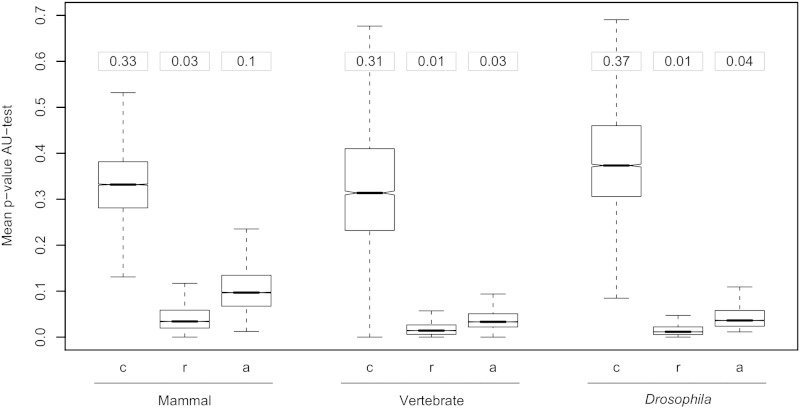
Moreover, to evaluate if trees produced by different models were on average significantly different between these groups, the analysis was repeated considering the distribution of P values obtained from the AU test. Figure 6 shows the mean P value per gene for the trees estimated under models in groups a, c, or r. Across all three genomic sets, models within the 95% CI (c) showed a nonsignificant P value (mean P  values = 0.3–0.4), whereas for the other sets, P values tended to decrease and become significant (a) especially for the set of models (r) outside the 95% CI (mean P values = 0.01–0.03).

Fig. 6.—

Model selection and phylogenetic inference. Boxplots show the distributions of the P values for the AU test estimated under models within the ci95 set (c), models outside of the ci95 set (r), and all models (a = c + r). Whiskers depict the largest value within 1.5 times the interquartile distance of each distribution. Values in boxes above plots show the overall mean for each distribution.

Finally, because the use of the most complex model (GTR+I+G) by default is sometimes common practice, we computed the number of times the tree topologies inferred under the GTR+I+G and AIC models were identical (i.e., RF = 0). They were 99.5%, 96.0%, and 90.7% for the mammal, Drosophila and vertebrate sets, respectively, showing an increasing amount of disagreement as the number of species increased. Similarly, the mean distance (variance in parenthesis) between GTR+I+G and the AIC model increased with the number of species. RF distances between both models in the mammal, Drosophila, and vertebrate sets, respectively, were 0.01 (0.03), 0.57 (1.46), and 1.67 (21.89), BS distances were 0.15 (8.33), 0.17 (13.26), and 0.51 (21.89), and the corresponding KS distances were 0.02 (0.17), 0.09 (9.42), and 0.20 (4.66). In most cases, the AIC and GTR+I+G trees were not statistically different (P ≥ 0.05) according to the pairwise KH and SH tests. The KH test was significant in 0.27%, 0.04%, and 0.07% of the alignments for the mammal, Drosophila, and vertebrate sets, respectively. The corresponding values for the SH test were 0.35%, 0.16%, and 0.16%. In addition, the AU tests rejected the AIC trees 0.3%, 0.2%, and 11% of the time and the GTR+I+G trees 1.2%, 1.7%, and 8.2% of the time, respectively. In addition, because we know the putative species phylogeny for these sets of species (Drosophila 12 Genomes Consortium 2007; Santini et al. 2009; Hallstrom and Janke 2010), we computed the number of times the estimated gene trees and the known species tree showed the exact same topology. When the gene trees were estimated under the AIC model the percentages were 98.7%, 32.2%, and 3.48% for mammals, Drosophila, and vertebrates, respectively. When we assumed a GTR+I+G model, the percentages were 98.6%, 32.2%, and 3.39%, respectively. Considering a 50% majority-rule consensus tree with all genes trees for a given species set, the resulting topology was identical to that of the species tree in both cases.

Discussion

Up until now, no extensive descriptions of relative model fit at the genomic scale had been reported in the literature. Here, results from three different genomic sets clearly show that different genes are best explained by different models of nucleotide substitution, suggesting that selecting among the variety of substitution models available is justified.

When considering the results from best-fit models or from the 95% CI set of models, several patterns were discerned. Most of the 88 models considered were selected as the best fit for at least one gene, whereas some models, although present, showed a clearly low frequency of representation. The effect was mainly due to a marked preference for different parameterizations where, independent of whether AIC or BIC were considered, the most frequent best-fit models assumed unequal based frequencies, different transition and transversion rates, and some form of rate variation among sites (either +I or +G).

The patterns of genomic heterogeneity inferred considering models under the approximate 95% CIs were markedly similar to those obtained using the best-fit model. However, an exception was observed in the mammal set, where the representation of +I+G models grew considerably under the AIC 95% CI in relation to the best model. Conceivably, and given the difference among the mammal and both the vertebrate and the Drosophila sets, the low divergence and number of species in the mammal set favor a scenario where the inclusion of either parameter that is able to account for some variation in rates among sites (+I or +G), almost systematically outweighs the cost of including both parameters in the AIC score. Albeit, given the difference in results between the best model and 95% CI set, this does not occur without a given degree of uncertainty. In terms of both selection criteria, and considering LP as a proxy for the effect of sampling, rate parameterizations at a genomic scale are most accurately described as generally heterogeneous over all possibilities with the exception of two: no partition (one rate for all transitions and transversions), which is largely absent, and partitions among transversions not separating rAC from rGT and rAT from rCG which are noticeably less frequent (r3, fig. 2). In terms of other parameterizations, irrespective of the selection criterion used, and taking into account LP and model selection uncertainty, UF are preferred of EF models, and the inclusion of at least +I or +G is preferred over models without parameterization of rate heterogeneity among sites. The scenario described is that while certain parts of model space are clearly less frequent, overall model fit at a genomic scale is largely heterogeneous, where many models are required to explain sequence evolution, particularly when taking into account sampling variance and divergence across a genome.

At the same time, it is important to note that the complexity of the best-fit models was larger for the genomic sets with higher number of species. For example, the number of different transversion rates, the proportions of UF to EF and that of +I+G to +G to +I to the bare model, all increased with the number of sequences (fig. 2). This is expected given that model selection procedures aim to minimize parameterization that does not significantly account for variation observed in the data. However, it is also interesting to note that while the Drosophila and vertebrates are the closest in the number of sequences analyzed (12 and 15 species, respectively), Drosophila and mammals are the closest in the evolutionary time covered (roughly 100 and 40 Ma, respectively. Hedges 2002; Springer et al. 2003), as vertebrates cover >400 Ma (Blair and Hedges 2005). Thus, the result that the overall genomic evolutionary patterns described by nucleotide substitution model fit, either obey common parameterization patterns among all species sets or vary mostly according to the number of species analyzed, suggests that the number of species and characters analyzed across the alignment had a stronger contribution to the variation in the statistical patterns observed than possible evolutionary characteristics particular to the species considered in each set. This observation is also supported by the fact that increased alignment length and diversity as a proxy for the effect of sampling (LP) also increased model complexity, decreased model selection uncertainty—as seen from the distribution of model weights or the size of the 95% CI, and affected overall model heterogeneity as portrayed through AIC and BIC. In the last case, it is interesting to notice that increasing LP had similar effects as increasing the number of species and affected the minimum number of models required to explain at least 80% of the data. Again as the number of characters or sequences in the alignment increased, both criteria moved toward more complex models, but as where AIC grew away from a more heterogeneous representation of rate parameterizations to include mostly the more complex models, BIC grew into a heterogeneous representation of rate parameterizations and away from the inclusion of mostly simple models. Considering that AIC_c provided results that were virtually the same as those from AIC (data not shown), this can be explained by the stronger penalization term for the number of parameters in BIC when compared with AIC.

In this line, it is also important to highlight the strong difference in the level of portrayed heterogeneity observed when considering the hLRT selection strategy. As noted previously (Kelchner and Thomas 2007), the number of models observed, and those required to explain at least 80% of the genomic data sets, was considerably reduced according to the hLRTs. Yet unlike in Kelchner and Thomas (2007), a slight skew toward more simple instead of relatively complex models is found. Moreover, considering that for 86.0%, 100%, and 99.9% of genes under the mammal, vertebrate, and Drosophila sets, respectively, the best-fit hLRT model was not included within the AIC 95% CI, the notion that hLRT can fall short of portraying the extent of heterogeneity present at a genomic scale gains importance.

In addition, one can also consider if different parameterizations are independent of each other or interact producing different patterns. Interestingly, especially when comparing patterns among +I and +G models, the distribution of model frequencies among rate and frequency parameterizations between these groups was most notably proportional, suggesting little or no interaction between I and G parameterizations and other model parameters. In the case of frequency parameterization partitions—equal (EF) or unequal (UF) base frequencies, some slight differences are observed among the representation of other parameters, suggesting a possible interaction among nucleotide frequencies and rate parameters. For example, under all three genomic sets, TrN was selected more often than TPM3uf, whereas the opposite was true for their EF versions—TrNef and TPM3 (supplementary fig. S3, Supplementary Material online). This suggests that under an EF scenario, considering different types of transversions tended to be more successful, whereas under UF, different rates among transitions became more common among best-fit models.

The considerable amount of variation observed among genes under any given model particularly supports the notion that evolutionary patterns are largely heterogeneous, highlighting the importance of model selection to study genomic data sets. For example, while the median of the transition/transversion rate estimate in the mammal set was consistent with the commonly accepted ratio of transitions being twice as frequent as transversions on average, it ranged from 0.685 to well over 6. Relative substitution rates between nucleotides and base frequency estimates also showed considerable levels of variation among all species sets. Estimates of the alpha parameter of the gamma distribution used to model rate variation among sites indicated that there are genes ranging from, those with highly conserved sites and little rate heterogeneity, to others with highly heterogeneous rate distributions, whereas most fell generally under a moderate form of the former pattern. Point ML and model-averaged estimates were very similar, which suggests that parameter estimation is quite consistent across different models, especially across those with a better fit to the data.

The relevance of taking model selection uncertainty into account in phylogenetic analyses is clear from our results. Trees derived from models under the 95% CI produced estimates in strong agreement with those obtained under the best-fit model. At the same time, models falling outside this interval resulted in significantly different trees. On one hand, these results show that while there may still be theoretical issues when choosing how to weigh candidate phylogenies resulting from different models, previous doubts on the possible lack of a relationship between AIC scores and resulting trees (Ripplinger and Sullivan 2008) are put aside. Additionally, taking into account that previous studies have shown that best-fit models tend to give better trees than less fit models—or at least equally good trees (Sullivan and Joyce 2005), we conclude that the use of model selection techniques is beneficial to obtain accurate phylogenetic estimates from real data at a genomic scale. In part because the real substitution process is more complex than any of the models we consider, some have advocated the use of the most complex model by default, without reference to model fit (Yang 2006). Here, the use of the most complex model (GTR+I+G) instead of the AIC model did not lead to important changes in the resulting phylogenetic estimates. The corresponding trees had the same topology in most cases, and only in very few instances were they statistically different. Logically, the differences grew with the number of sequences but were always scarce, something expected given that our data consist of “easy” trees, with relatively long branches and few taxa. In summary, the topological tests and the comparison with the known trees suggest that both strategies performed equally well with our data. In general, using the AIC model should imply less computational time than the most complex model but depending among other things on the number of candidate models, sequence divergence, and number of sequences. In theory, the AIC should reduce the variance of the phyogenetic estimate, although here the observed variances were similar. In order to clarify their relative behavior in more complex cases, specific simulation studies are needed.

Most genes recovered the “known” mammalian species tree, but this was not true for the Drosophila and vertebrate sets. In the former case, only a third of the genes recovered the known species topology, whereas the rest showed alternatives in which the position of Drosophila erecta and Drosophila yakuba changed with respect to the Drosophila melanogaster species. This can be explained in terms of extensive lineage sorting (Pollard et al. 2006) and also regarding the relationships of Drosophila grimshawi, Drosophila virilis, and Drosophila mojavenis, which are known to be problematic. For the vertebrates, only a little more than 3% of the genes showed the “expected” topology. Here, the changes affected mostly the relationships within the human, chimp, and orangutan clade and the dog, cow, and horse clade. Lineage sorting is not an important force at least in the former clade (Hobolth et al. 2011) and most of the disagreement probably arises from sampling error. Many of these genes are small and will be unable to provide information to resolve the shorter branches. Also the Phyml search implemented in jModelTest is not the most thorough. The relationships within the latter clade are controversial (Hou et al. 2009). Reassuringly, in all three genomic data sets the consensus trees constructed with all gene trees were largely compatible with the expected topologies.

In summary, our results have shown that it takes more than only a few models to explain genomic evolution and that model choice can affect parameter inference including phylogenetic trees. This is particularly relevant given that many studies which rely specifically on these models for testing hypothesis, reconstructing phylogenies, or obtaining parameter estimates are still found based on single models (i.e., JC, K80, HKY or GTR), sometimes chosen arbitrarily, on large sets of concatenated data without consideration of the possible effects of model choice and model-fit heterogeneity. The large heterogeneous nature of genomes and both current and future availability of increasing amounts of sequences merit the consideration of methodologies that can appropriately handle the amount of diversity present in large scale biological data. While model selection and multimodel inference will likely not be a broad spectrum strategy for all challenges, our results suggest that they provide a valid means to address what is a considerable amount of diversity across the genome, by selecting a group of best-fitting models that maximize phylogenetic accuracy.

Supplementary Material

Supplementary figures S1–S5 and table S1 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).