Skip to main content
NCBI home page
European Spine Journal logoLink to European Spine Journal
. 2011 Jul 28;20(Suppl 5):578–585. doi: 10.1007/s00586-011-1924-1

Sagittal parameters of the spine: biomechanical approach

Pierre Roussouly 1,✉, João Luiz Pinheiro-Franco 2
PMCID: PMC3175922  PMID: 21796394

Abstract

According to the anatomical segmentation, spine curves are the sacral kyphosis (sacrum), lumbar lordosis (L1 to L5), thoracic kyphosis (T1 to T12) and cervical lordosis (C1 to C7). From the morphological point of view the vertebrae of a curve are not identical: from cranial to caudal and vice versa there is a progressive anatomical modification. Both curves of the thoraco-lumbar spine may be divided at the Inflexion Point where lordosis turns into kyphosis. A geometrical construct of each curve by two tangent arcs of circle allows understanding the reciprocal changes between both curves. Lumbar Lordosis is mainly dependent on SS orientation, and the top of thoracic curve on C7 is very stable over the sacrum. Thoracic curve is dependent on lumbar lordosis orientation and C7 positioning. On a reverse effect, structural changing of thoracic kyphosis may affect the shape of the lumbar lordosis and the orientation of the pelvis.

Keywords: Sagittal balance, Spine curves, Lordosis, Thoracic kyphosis, Geometrical analysis

Introduction

Hippocrates the Koan (460–370 B.C.), the most prominent physician of antiquity and recognized as the founder of scientific medicine [1] was the first to describe curvatures in the human body spine. In his book “On Joints”, he described the anatomy and the diseases of the spine and suggested treatments for patients with spinal deformities [1, 2]. Hippocrates described the normal curves of the spine and, to render the curved course of the vertebral column, he used the term “ithiscolios” [2], which indicates that the spine is straight in the coronal, but curved in the sagittal plane [1, 3].

This organization of the spine in successive curvatures in the sagittal plane is crucial for maintaining an erect, totally vertical, bipedal position. This is a specificity of the mankind. All primates are able to displace themselves in a bipedal manner. The Homo sapiens, however, is the only one capable of performing it for long distances and long time in a stable manner [4, 5]. This is because human is the only vertebrate to have a lordotic lumbar curvature. Spinal sagittal curves appear progressively with growth and are well established when the standing position and walking are possible. It is just at the end of the skeleton growth that the morphology of the spino-pelvic setting is fixed. Stagnara et al. [6] demonstrated the strong relation of the lumbar curve with the tilt of the sacral slope. They defined a “static spine” when the lumbar lordosis was flat and a “dynamic spine” when the curvature was more pronounced. The anatomical segmentation nomenclature of the spine, based on the curves of the sagittal plane, has been the main way of description for a long time. In Hippocrates’ treatise “On Nature of Bones” [1, 7], vertebrae were classified into three groups: cervical, thoracic and lumbar. Sacral vertebrae and the coccyx were not included as parts of the spine; however, Hippocrates referred to both when he described the normal curves of the spine in “On Joints” [2]. Today, with the anatomy of vertebrae divided into sacral, lumbar, thoracic and cervical, the main curvatures logically follow this division. The curvatures with an anterior concavity in the sagittal plane are called kyphosis whilst curves with a posterior concavity are named lordosis. By then, according to the anatomical segmentation, spine curves are the sacral kyphosis (sacrum), lumbar lordosis (L1 to L5), thoracic kyphosis (T1 to T12) and cervical lordosis (C1 to C7). Recently, this division has been contested [8]. From the morphological point of view, it is well known that vertebrae of a curve are not identical: from cranial to caudal and vice versa there is a progressive anatomical modification, that is, L1 is morphologically different from L5. From the functional point of view, new evidence has been demonstrated [8, 9]. Roussouly proposed a functional segmentation of the spine curves in the sagittal plane, where the limits of the curves were defined by the point where the orientation of the curves was changes [8]. By this way, considering the final end of the lumbar curve as S1 plate, the proximal limit of the lordotic curve may be sometimes higher than L1 (extending to the lower thoracic area) and sometimes lower. Thus, it is important to understand that both could exist: short lumbar lordosis and long lumbar lordosis.

The arc of a circle design

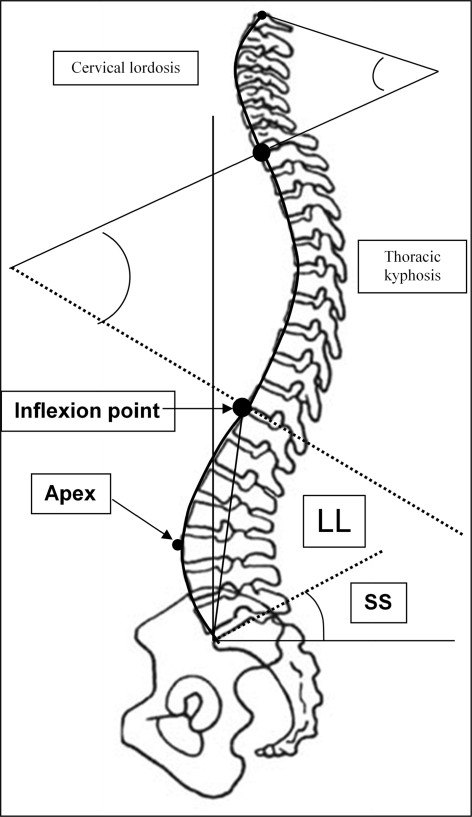
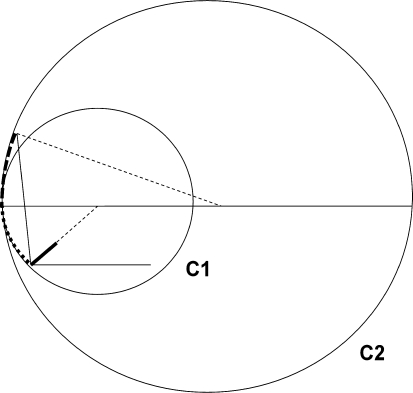
The lumbar lordosis is not evenly distributed from the proximal limit to the sacrum. The contribution of each lumbar vertebra to the lordosis increases progressively from L1 to the sacrum. The 2/3 of the total lordosis are shown in the lower lumbar spine L4–S1 [9]. Different geometrical constructions of the spine have been proposed: arch of circle [10], quadrant of an ellipse [11]. The ellipsoid design is very realistic, but difficult to use in everyday clinical practice [9]. Berthonnaud et al. [10] described a construction where lumbar lordosis is represented as two arcs of circle tangent at the apex of the curve and then, the total lordosis is the sum of the lordosis value above and the lordosis value below the apex (Fig. 1). The clinical utility is explained later on; however, this construct allows the analysis of the two arcs, their respective function in the curve organization, especially in the lumbar area. Quantification of the curves may be obtained using either the Cobb method or tangent method.

Fig. 1.

Fig. 1

Open in a new tab

Subdivision of the sagittal spinal curvatures. Cervical spine goes from C1 to C7. Thoraco-lumbar spine is limited by C7/T1 and the sacral plateau. Inflexion Point is the place where the lordosis curve turns in kyphosis. This is a variable limit between lordosis and kyphosis

Global spine balance

To the analysis of the global balance of the spine, several points have been proposed. One of them, the external ear conducts, is useful to indicate the head positioning. The T9 tilt was described by Duval-Beaupère et al. as an indicator of the spine balance at the body mass centre level [12, 13]. It comprehends the vertical projection of the centre of weight behind the coxo–femoral joints. The T9 tilt is the angle between the line linking the midpoint of the femoral heads axis with the centre of the T9 vertebra body and the vertical line crossing the midpoint of the femoral heads axis. The tilt is positive when the centre of the T9 vertebral body is projected posterior to the midpoint of the femoral heads axis and negative when anterior [14]. Easier to be read on sagittal X-rays, C7 plumb line is the most commonly used index of the global balance. This parameter has been historically quantified by measuring the position of a vertical line originating in the centre of the C7 vertebral body with respect to the posterior superior corner of S1 [15–17].

Kuntz et al. [18] noted in a review of the literature that global parameter as C7 plumb line was a stable, reliable index of the sagittal balance, being maintained in narrow ranges for alignment of the spine over the pelvis and femoral heads. Initially, the position of C7 plumb line was referred by the horizontal distance from a vertical plumb line centred in the middle of the C-7 VB to an anatomical landmark (centre of femoral heads for instance); afterwards, several angles referring C7 to a vertical or a horizontal line were used. We defined the spino-sacral angle (SSA), an intrinsic angle to quantify the global kyphosis of the whole spine. The SSA was defined as the angle between the line from the centre of C7 to the centre of the sacral plate and the sacral plate line itself. We found a strong correlation between the SSA and the sacral slope and the lumbar lordosis [19–21]. In this paper, we focused on thoracic, lumbar and sacral spine. For this description of spinal parameters we excluded the cervical spine, which needs to have a specific study.

Spine segmentation

Classically, as aforementioned, the limits of the thoracic and lumbar curves were based on anatomical segmentation with a transition between thoracic kyphosis and lumbar lordosis at the level of T12–L1. The distal limit of lumbar lordosis was frequently assumed to be the inferior plate of L5. However, recently some authors have extended this limit to the S1 plate [8, 22, 23], as this line corresponds to the line of the sacral slope, which, in turn, influences strongly the lumbar lordosis angle [6, 8, 23]. Accordingly, it became evident that there was a great variability of lumbar lordosis length, with proximal limit higher or lower than the classical anatomical limit T12–L1. Using computerized reconstruction of the spine curvatures with the software Optispine® (SMAIO, Lyon, France) it became possible by providing anatomical landmarks, to obtain the curves, to calculate automatically the pelvic and spinal parameters, to estimate the spinal sagittal balance and visualize the exact point where the orientation of the curves changes, where lordosis turns in kyphosis. Berthonnaud et al. [10] defined this turning point as the Inflexion Point. Having this in mind, lumbar lordosis was defined as the segment of the spine between the sacral plate and the Inflexion Point, without any reference to a specific anatomical landmark. By then, a thoracic vertebra, T12, may be part of the lumbar lordosis, as we have already demonstrated in previous studies. On the other hand, the thoracic kyphosis was defined as the segment of the spine between the distal Inflexion Point (inferiorly) and the proximal Inflexion Point (superiorly). The fact that the proximal Inflexion Point between thoracic and cervical spine could be lower or higher than C7 is of poor utility for the compensatory mechanisms of the thoraco-lumbar spine in case of global spine sagittal imbalance. Therefore, we deem the midpoint of the inferior plate of C7 as the superior limit of thoracic kyphosis. It would be different in case of analysis of the cervical spine orientation. The main interest of C7 is its relative stable position over the pelvis.

Geometry of the curves

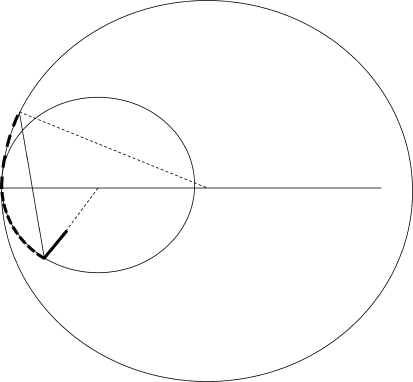
Another critical landmark to define during the analysis of the curvature (kyphosis or lordosis) construction is the apex of the curve in the sagittal plane, where the most anterior (in case of lordosis) point of the lumbar spine touches a vertical line. At this point, the curvature, e.g., the lumbar lordosis, can be divided into two segments according to its position above or below the horizontal line crossing this point (the apex). Berthonnaud et al. [10] defined two tangent arcs of a circle and placed the centre of each arc on a horizontal line drawn from the apex. Consequently, even if the radius of each arc has different lengths, both arcs remain, respectively, on two tangent circles on the apex.

Lumbar lordosis construction

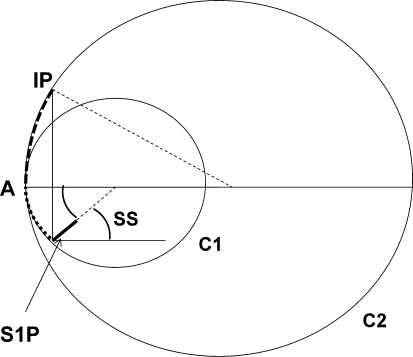
The lumbar curvature is therefore, divided into two tangent arcs of circle with the purpose of studying sagittal balance implications of each arc. The inferior arc extends from S1 to the apex, the upper arc from the apex to the inflexion point. The centre of the inferior arc is located at the intersection of the horizontal line running from the apex and the line following the sacral plate; the radius of the upper arc is set by the line perpendicular to the tangent to the spinal curve at the level of the inflexion point (Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

Geometrical construct of Lumbar Lordosis (LL) by two tangent arcs of circle. LL is limited proximally by the Inflexion Point (IP) and distally by the sacral plateau (S1P). C1 and C2 are two tangent circles on the apex (A) of LL. LL is divided in two arcs; the upper one from IP to A is located on C2, the lower between A and S1P is on C1. As complementary angles, lower arc equals SS

This geometrical construct demonstrates that the angle of the inferior arc of lumbar lordosis is equal to the sacral slope angle. Thus, as there is a strong correlation between the Sacral Slope and the Lumbar Lordosis (R = 0.86; p < 0.001), we inferred that the inferior arc has a significant influence on lumbar lordosis [8, 9]. We found a constant value of 20° for the upper arc whatever the shape of the spine [8]. Theoretically, we may assume that the global angle of lumbar lordosis has to be equal to SS + 20° (inferior arc angle + superior arc angle). As SS is variable according to the Pelvic Tilt, one clinical application of these findings may be in the strategy of correction of hypolordosis with osteotomy: the surgeon may first determine the expected post-operative PT and the corresponding expected post-operative SS and then add 20° to obtain the final wished value of lordosis after surgical correction.

The variability of SS according to the great range of Pelvic Incidence may explain the different morphologies of lordosis that we have previously classified in four main types [8]. When SS is higher, the values of lordosis increase, mainly on distal segments L4–L5, L5–S1, at the expense of higher values of the inferior arc. Thus, it is mandatory to restore lordosis on this area, which is generally compromised by degenerative discopathies. Conversely, if SS is small, the angle of the inferior arc is small, with less need of lordosis restoration. There are two extremes to express these situations by geometry: either the inferior arc is very small, or it is close to a straight line and the radius of the arc of circle is very long (lordosis type 2). These variations of the inferior arc (SS) lead to the description of four main types of lordosis:

  • Type 1: SS < 35°, short and small lordosis, long kyphosis exceeding the thoraco-lumbar transition zone, reaching lower thoracic spine (Fig. 3).

  • Type 2: SS < 35°, long and flat lordosis (Fig. 4).

  • Type 3: 35° < SS < 45°, mean length and mean angle of lordosis (Fig. 5).

  • Type 4: SS > 45°, very curved lordosis, higher extension and angle (Fig. 6).

Fig. 3.

Fig. 3

Open in a new tab

Type 1: Regarding a low grade Sacral Slope, length of the inferior arch C1 is very small. Lordosis is mainly represented by the superior arch. Globally a short lordosis is associated with a long thoraco-lumbar kyphosis

Fig. 4.

Fig. 4

Open in a new tab

Type 2: Both arcs of circle (C1 and C2) have long radius and they approximate a straight line resulting in a flat lordosis

Fig. 5.

Fig. 5

Open in a new tab

Type 3: Sacral Slope is between 35° and 45°, increasing by the way, length and angle of the lower arch. Upper arch remains stable around 20°

Fig. 6.

Fig. 6

Open in a new tab

Type 4: Sacral Slope is over 45°, increasing dramatically length and angle of the inferior arch. There is an important risk of forward tilt of lumbar lordosis. The inflexion point may over pass the anatomical limit of L1T12

Anatomical changes of the lumbar spine

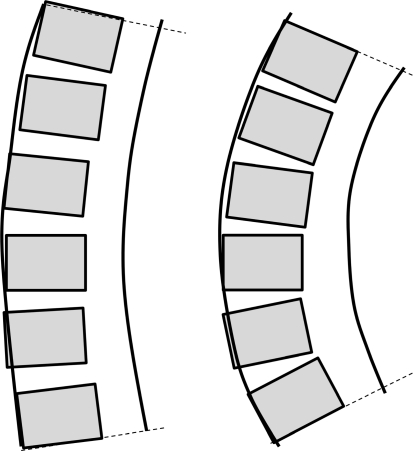
The type of lordosis may be related to the anatomical morphology/size of posterior elements (facet joints/interspinous processes). We may compare virtually two spines, one Type 2 and one Type 4 lordosis, with the same extension of functional spinal units (FSU) (disc + vertebral body) and the same length of the anterior body line; the facet joints and spinous processes are positioned behind, on lines parallel to vertebral body line (Fig. 7). In a Type 2 lordosis, as the lordosis is flat, the anterior bodyline exhibits a huge radius for the circle of the inferior arc and almost the same for the facet line. This is different from Type 4 lordosis where the radiuses of the arcs are smaller, with in consequence a smaller length of the posterior facet line. Consequently, we may expect larger spaces for facets and spinous processes in Type 2 than in Type 4 lordosis. Facet joints and spinous processes are probably bigger in Type 2 than in Type 4. Anatomical or radiological studies relating the size of the facet joints to the type of lordosis are required to confirm this hypothesis. This hypothesis may explain a lower capacity of extensibility of Type 2 spine when compared with Type 4. Otherwise, in small people, mainly women, the size of the facets is proportionally reduced in Type 4 and may explain the mechanical fragility of facet joints and the higher risk of arthritis and degenerative spondylolisthesis.

Fig. 7.

Fig. 7

Open in a new tab

In a Type 2 Lordosis (left) the area occupied by posterior elements is longer for a same number of vertebrae, than in a Type 4 lordosis (right). By this way posterior elements (facets and spinous processes) are smaller in Type 4 than in Type 2. This geometrical effect may be emphasized in small person

Thoracic kyphosis construction

Likewise, the thoracic kiphosis may be constructed between the inflexion point and C7 body centre, using tangent arcs of circles. The inferior arc of the thoracic spine has the same radius drawing as the superior arc of the lumbar curve. Thus, there is a direct relationship between lordosis and kyphosis. In case of flat lordosis (Type 2) the upper arc of lordosis is poorly tilted and it is followed by the inferior arc of kyphosis, which is flat. When lordosis is very curved (Type 4), by the same construct, thoracic kyphosis is pronounced (Fig. 8).

Fig. 8.

Fig. 8

Open in a new tab

On the left a backward Tilt of lordosis allows a bigger amount of kyphosis above with the risk of a local hyperextension. In the middle, Lordosis is well balanced there is no Tilt. On the right, forward Tilt, lordosis orientation is unbalanced

Orientation of the curves

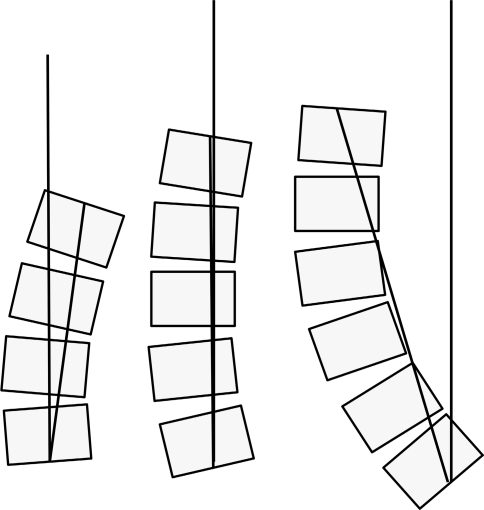
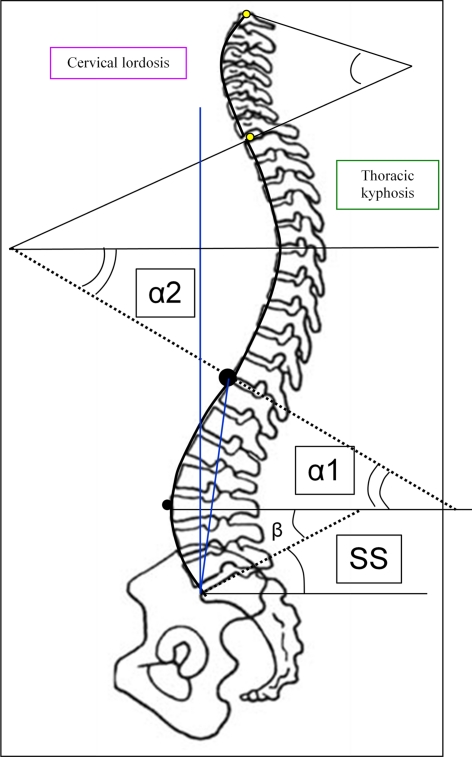
On examining a lordosis or a kyphosis, there is a line drawn between both extremities of the curve, these lines defining angle. The orientation of this line relative to the vertical line is called lordosis tilt or kyphosis tilt [10]. Normally the lumbar lordosis tilts backward in a well-balanced spine. A slight forward tilt may be acceptable. A big amount of anterior tilt may bring to an imbalanced situation (Fig. 9). This is the case in pathology in imbalanced high-grade lumbar spondylolisthesis. In severe thoracic kyphosis, an anterior tilt may bring C7 plumb line also in imbalanced position.

Fig. 9.

Fig. 9

Open in a new tab

Kyphosis sub division: when the lower lumbar lordosis angle (β) equals SS, the lower thoracic kyphosis angle (α2) equals the upper lumbar lordosis angle (α1). The orientation of the upper thoracic kyphosis angle is determined by C7 positioning

C7 positioning and spine orientation

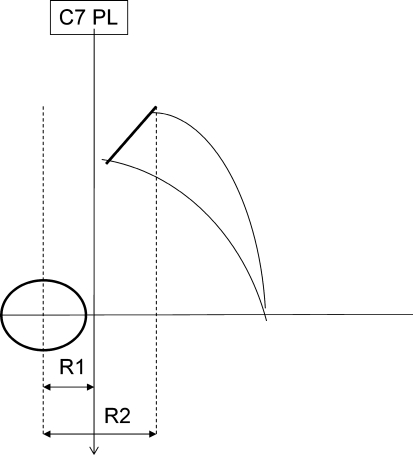
Numerous authors have considered the centre of C7 as the crucial point of the global sagittal balance [8, 9, 15–17]. Instead of upper thoracic vertebrae, C7 has been chosen as it can be easily seen on long sagittal X-rays. Plumb line passing through C7 (C7 PL) was the first way of positioning. It was related to an anatomical pelvic landmark as the centre of the Hip Axis (HA), or the posterior point of the sacral plate (post S1). Usually the horizontal distance between C7 PL and an anatomical landmark is calculated. It is well established that it is better not to use distance to characterize this position and especially to compare situations on different X-rays. Most of X-rays are made without calibration, and errors are possible when comparing two distances on different radiographs. To avoid this problem, Barrey [9] proposed a ratio between the horizontal distances from C7 PL to HA and between HA and post S1 (Fig. 10). This ratio provides an adimensional value concerning the position of C7 PL in relation to the vertical lines passing through HA and through post S1. When it is superior to 1, C7 PL is passing behind the posterior point of the sacral plate (ideal, balanced situation); when it is between 0 and 1, C7 PL is located between HA and post S1; and when it is negative, C7 PL is forward HA. The spine is considered as well balanced when the C7 plumb line is located behind post S1. When C7 PL moves forward but locates still behind HA, balance is compromised. Finally, when C7 PL is displaced forward to HA there is a proof of severe imbalance.

Fig. 10.

Fig. 10

Open in a new tab

In order to avoid errors with distance magnification C. Barrey proposed a ratio between horizontal distance from the centre of the femoral heads (FH) and C7PL (R1) and the distance from FH and the posterior edge of the sacral plate (R2). R1/R2 is negative when C7 PL is forward FH. 0 < R1/R2 < 1 when C7PL is between FH and the sacrum, and R1/R2 > 1 when C7PL is behind the sacrum

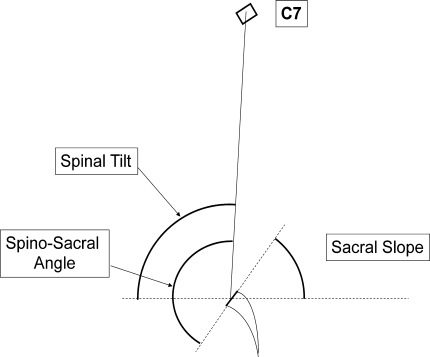
Another method, other than with the plumb line, to position C7 and analyse the global spinal balance is using angles. The tilt of C7 or Spinal Tilt (ST) is the angle formed by the horizontal line and the line running from the centre of C7 to the centre of the sacral plate. A value greater than 90° indicates that the centre of C7 vertebral body is behind the centre of upper sacral plate, whereas for values less than 90°, the centre of C7 vertebral body is in front of the centre of upper sacral plate [24]. The Spino Sacral Angle (SSA) corresponds to the angle between the sacral plate and the line described above, between the midpoint of C7 and the centre of the sacral plate (Fig. 11). ST is a functional parameter and reflects the global orientation of the spine. SSA is a morphological parameter and reflects the global kyphosis of the spine. Both parameters ST and SSA are linked by the relation: SSA = ST + SS. We demonstrated that the mean values of ST remain relatively stable and that there is a strong correlation between SSA and SS [19]. In a recent study of 709 asymptomatic volunteers, Mac-Thiong et al. obtained mean values of ST of 90.8° ± 3.4 and 130.4° ± 8.1 for SSA [24]. These authors confirmed the strong correlation between SSA and SS. The relation between both parameters SSA and SS is almost linear. In other words, in balanced spine, when SS increases, SSA decreases in the same proportion in order to maintain C7 over the sacrum. Debarge et al. [25] used SSA to analyse severe kyphosis in ankylosing spondylitis. They demonstrated a substantial decrease of SSA in this pathology and the effect of lumbar osteotomy on improving this angle. As the Pelvic Incidence (PI) well correlates with SS, a good correlation is expected between SSA and PI, as confirmed by Mac-Thiong et al. [24]. Roughly, an individual with low PI will need less SSA than one with high PI, as, for example, in a case of severe imbalance of a person with a small PI, he/she will need less correction (less lordosis, smaller osteotomy) than a person with high PI (more lordosis, bigger osteotomy), [25].

Fig. 11.

Fig. 11

Open in a new tab

ST determines extrinsically the position of C7 regarding the horizontal line. SSA represents the value of the global kyphosis of the spine. They are linked by the relation: SSA = SS + ST

Global shape of the spine: curves’ correlation

To characterize the spine, the first segment is the lumbar lordosis from S1 plate to the Inflexion Point and the second one is the thoracic kyphosis whose top is C7 position. In a well-balanced spine, lumbar lordosis is organized according to SS, which, in turn, depends on the shape of the pelvis quantified by the PI. At the level of the Inflexion Point, the lordotic spine in extension turns into the kyphotic spine in flexion. In a well-balanced spine, C7 PL is behind the sacral posterior endpoint; the kyphosis runs from the Inflexion Point to C7. Its length and angulation depends on length and angulation of the lumbar lordosis and vice versa. According to these relations, spinal parameters are interdependent. One change in one segment induces a change in the reciprocal segment according to the flexibility of the spine. If the thoracic kyphosis increases, lumbar lordosis increases in order to maintain C7 in right position. Reversely, when lumbar lordosis decreases, thoracic kyphosis decreases, flattening the back. Obviously, compensatory intrinsic spinal curves changes in the sagittal plane are not acute, but a result of progressive changes. In pathology, these mechanisms are dramatically magnified; a local increased kyphosis induces always a painful compensation by stressing the adjacent spine in extension. When the adjacent extension mechanism is surpassed, the only way to compensate the kyphotic evolution (loss of SSA) is the retroversion of the pelvis. At that time the progressive impairment of balance is obvious by both increased PT and anterior displaced C7 PL.

Conclusion

Both curves of the thoraco-lumbar spine may be divided at the Inflexion Point where lordosis turns into kyphosis. A geometrical construct of each curve by two tangent arcs of circle allows understanding the reciprocal changes between both curves. Lumbar Lordosis is mainly dependent on SS orientation, and the top of thoracic curve on C7 is very stable over the sacrum. Thoracic curve is dependent on lumbar lordosis orientation and C7 positioning. On a reverse effect, structural changing of thoracic kyphosis may affect the shape of the lumbar lordosis and the orientation of the pelvis.

Conflict of interest

None of the authors has any potential conflict of interest.

References

  • 1.Marketos SG, Skiadas P (1999) Hippocrates. The father of spine surgery. Spine (Phila Pa 1976) 24(13):1381–1387 [DOI] [PubMed]
  • 2.(1927) Hippocrates. On Joints. In: Capps E, Page TE, Rouse WHD, (eds) Withington ET, trans. Hippocrates: The Loeb Classical Library, vol III. W. Heinemann, London, pp 200–397
  • 3.(1965) Galen. Hippocrates de articulis liber et Galeni in eum commentarii quatuor. In: Kuhn CG (ed) Claudii Galeni Opera Omnia, vol XVIII. Part I. Hildesheim, G. Olms Verlag, Germany, pp 300–767
  • 4.Senut B, Devillers M (2008) Et le singe se mit debout. Editions Albin Michel: 157–165 (in French)
  • 5.Pinheiro-Franco JL, Roussouly P, Vaccaro AR (2010) Importância do Equilíbrio Sagital no Tratamento Cirúrgico da Doença Degenerativa Discal Lombar. In: Conceitos Avançados em Doença Degenerativa Discal Lombar. Pinheiro-Franco JL, Vaccaro AR, Benzel EC, Mayer H-M (eds), DiLivros Publisher (Rio de Janeiro): 277–286 (in Portuguese)
  • 6.Stagnara P, De Mauroy JC, Dran G, Gonon G, Costanzo G, Dimnet J, Pasquet A (1982) Reciprocal angulation of vertebral bodies in a sagittal plane: approach to references for the evaluation of kyphosis and lordosis. Spine (Phila Pa 1976) 7(4):335–342 [DOI] [PubMed]
  • 7.(1982) Hippocrates. On nature of bones. In: Littre PE (ed) Oeuvres Completes d’ Hippocrate, vol 9. A. M. Hakkert, Amsterdam. pp 162–197
  • 8.Roussouly P, Berthonnaud E, Dimnet J. Geometrical and mechanical analysis of lumbar lordosis in an asymptomatic population: proposed classification. Rev Chir Orthop Reparatrice Appar Mot. 2003;89(7):632–639. [PubMed] [Google Scholar]
  • 9.Barrey C (2004) Equilibre sagittal pelvi-rachidien et pathologies lombaires dégénératives. Etude comparative à propos de 100 cas. Thèse Doctorat—Université Claude-Bernard, Lyon 1 (in French)
  • 10.Berthonnaud E, Dimnet J, Roussouly P, Labelle H. Analysis of the sagittal balance of the spine and pelvis using shape and orientation parameters. J Spinal Disord Tech. 2005;18(1):40–47. doi: 10.1097/01.bsd.0000117542.88865.77. [DOI] [PubMed] [Google Scholar]
  • 11.Janik TJ, Harrison DD, Cailliet R, Troyanovich SJ, Harrison DE. Can the sagittal lumbar curvature be closely approximated by an ellipse? J Orthop Res. 1998;16:766–770. doi: 10.1002/jor.1100160620. [DOI] [PubMed] [Google Scholar]
  • 12.Duval-Beaupere G, Schmidt C, Cosson P. A Barycentremetric study of the sagittal shape of spine and pelvis: the conditions required for an economic standing position. Ann Biomed Eng. 1992;20:451–462. doi: 10.1007/BF02368136. [DOI] [PubMed] [Google Scholar]
  • 13.Duval-Beaupère G, Legaye J. Composante sagittale de la statique rachidienne. Rev Rhum. 2004;71:105–119. doi: 10.1016/j.rhum.2003.09.018. [DOI] [Google Scholar]
  • 14.Boulay C, Tardieu C, Hecquet J, Benaim C, Mouilleseaux B, Marty C, Prat-Pradal D, Legaye J, Duval-Beaupère G, Pélissier J. Sagittal alignment of spine and pelvis regulated by pelvic incidence: standard values and prediction of lordosis. Eur Spine J. 2006;15(4):415–422. doi: 10.1007/s00586-005-0984-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Gelb DE, Lenke LG, Bridwell KH, et al. (1995) An analysis of sagittal spinal alignment in 100 asymptomatic middle and older aged volunteers. Spine (Phila Pa 1976) 20:1351–1358 [PubMed]
  • 16.Royen BJ, Toussaint HM, Kingma I, et al. Accuracy of the sagittal vertical axis in a standing lateral radiograph as a measurement of balance in spinal deformities. Eur Spine J. 1998;7:408–412. doi: 10.1007/s005860050098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Vedantam R, Lenke LG, Bridwell KH et al (2000) The effect of variation in arm position on sagittal spinal alignment. Spine (Phila Pa 1976) 25:2204–2209 [DOI] [PubMed]
  • 18.Kuntz C, 4th, Levin LS, Ondra SL, Shaffrey CI, Morgan CJ. Neutral upright sagittal spinal alignment from the occiput to the pelvis in asymptomatic adults: a review and resynthesis of the literature. J Neurosurg Spine. 2007;6(2):104–112. doi: 10.3171/spi.2007.6.2.104. [DOI] [PubMed] [Google Scholar]
  • 19.Roussouly P, Gollogly S, Noseda O, Berthonnaud E, Dimnet J (2006) The vertical projection of the sum of the ground reactive forces of a standing patient is not the same as the C7 plumb line: a radiographic study of the sagittal alignment of 153 asymptomatic volunteers. Spine (Phila Pa 1976) 31(11):E320–E325 [DOI] [PubMed]
  • 20.Jackson RP, MacManus AC (1994) Radiographic analysis of sagittal plane alignment and balance in standing volunteers and patients with low back pain matched for age, sex and size. Spine (Phila Pa 1976) 19:1611–1618 [DOI] [PubMed]
  • 21.Jackson RP, Peterson MD, MacManus AC, Hales C (1998) Compensatory spinopelvic balance over the hip axis and better reliability in measuring lordosis to the pelvic radius on standing lateral radiographs of adult volunteers and patients. Spine (Phila Pa 1976) 23:1750–1767 [DOI] [PubMed]
  • 22.Legaye J, Hecquet J, Marty C, Duval-Beaupère G. Equilibre sagittal du rachis. Relations entre bassin et courbures rachidiennes sagittales en position debout. Rachis. 1993;5:215–226. [Google Scholar]
  • 23.Legaye J, Duval-Beaupère G, Hecquet J, Marty C. Pelvic incidence: a fundamental pelvic parameter for three-dimensional regulation of spinal sagittal curves. Eur Spine J. 1998;7:99–103. doi: 10.1007/s005860050038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Mac-Thiong JM, Roussouly P, Berthonnaud E, Guigui P (2010) Sagittal parameters of global spinal balance: normative values from a prospective cohort of seven hundred nine Caucasian asymptomatic adults. Spine (Phila Pa 1976) 35(22):E1193–1198 [DOI] [PubMed]
  • 25.Debarge R, Demey G, Roussouly P. Radiological analysis of ankylosing spondylitis patients with severe kyphosis before and after pedicle subtraction osteotomy. Eur Spine J. 2010;19(1):65–70. doi: 10.1007/s00586-009-1158-7. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from European Spine Journal are provided here courtesy of Springer-Verlag

RESOURCES