Sex-Specific Incompatibility Generates Locus-Specific Rates of Introgression Between Species

Abstract

Disruption of interactions among ensembles of epistatic loci has been shown to contribute to reproductive isolation among various animal and plant species. Under the Bateson–Dobzhansky–Muller model, such interspecific incompatibility arises as a by-product of genetic divergence in each species, and the Orr–Turelli model indicates that the number of loci involved in incompatible interactions may “snowball” over time. We address the combined effect of multiple incompatibility loci on the rate of introgression at neutral marker loci across the genome. Our analysis extends previous work by accommodating sex specificity: differences between the sexes in the expression of incompatibility, in rates of crossing over between neutral markers and incompatibility loci, and in transmission of markers or incompatibility factors. We show that the evolutionary process at neutral markers in a genome subject to incompatibility selection is well approximated by a purely neutral process with migration rates appropriately scaled to reflect the influence of selection targeted to incompatibility factors. We confirm that in the absence of sex specificity and functional epistasis among incompatibility factors, the barrier to introgression induced by multiple incompatibility factors corresponds to the product of the barriers induced by the factors individually. A new finding is that barriers to introgression due to sex-specific incompatibility depart in general from multiplicativity. Our partitioning of variation in relative reproductive rate suggests that such departures derive from associations between sex and incompatibility and between sex and neutral markers. Concordant sex-specific incompatibility (for example, greater impairment of male hybrids or longer map lengths in females) induces lower barriers (higher rates of introgression) than expected under multiplicativity, and discordant sex-specific incompatibility induces higher barriers.

GENE flow may persist between incipient species for extended periods, even in the face of severe disruptions in the fertility, viability, or behavior of hybrids or their descendants. For example, introgression appears to persist between Drosophila pseudoobscura and D. persimilis, in spite of the rise, ∼850,000 years ago (Leman et al. 2005), of a second-chromosome inversion associated with multiple mechanisms of reproductive isolation. In these species, at least three inverted chromosomal regions appear to contribute to hybrid incompatibility (Noor et al. 2001), and in general, the number of incompatible interactions among loci is expected to “snowball” as divergence time increases (Orr 1995; Orr and Turelli 2001). Here we address the effects of multiple incompatibility loci on the rate of introgression at neutral marker loci throughout the genome. This study departs from previous work (e.g., Barton and Bengtsson 1986) by addressing sex specificity in expression of disruptions associated with hybridization, in rates of crossing over between incompatibility factors and marker loci, and in linkage to sex chromosomes or other regions transmitted in a sex-specific manner.

Nonuniform divergence among genomic regions

Among the most robust patterns that have emerged from genome-scale surveys is the nonuniformity across genomic regions of divergence among populations. Geography constitutes a major explanatory variable for global patterns of variation in human genomes (Rosenberg et al. 2002; Coop et al. 2009). Humans show striking locus-specific F_ST, the classical index of population structure (Akey et al. 2002; Holsinger and Weir 2009), with many regions showing extreme values beyond three empirical standard deviations from the mean for a chromosome; (Weir et al. 2005). This pattern is observed in a wide variety of nonhuman species as well (e.g., Rieseberg et al. 1999; Machado and Hey 2003; Teeter et al. 2009).

The widely used IM program (isolation with migration, Hey and Nielsen 2004, 2007) uses observations of nucleotide variation at multiple, independent loci to infer introgression rates and other demographic parameters assumed to be common to all genomic regions. Hey and Nielsen (2004) applied their method separately to each of 14 markers in D. pseudoobscura and D. persimilis, obtaining estimates of introgression rates that varied over orders of magnitude: for example, a scaled rate of flow from D. persimilis to D. pseudoobscura of M₂ = 0.09 for per (X-linked) and M₂ = 4.25 for Adh (autosomal). Earlier work (Wang et al. 1997) also indicated substantial differences between loci in rates of gene exchange.

Genetic analyses across interspecific hybridization zones provided the first demonstrations of the differential permeability of reproductive barriers across the genome (Barton and Hewitt 1985). Incompatibility is expected to impede introgression throughout the genome, but more intensely in regions harboring incompatibility factors (Bengtsson 1985; Barton and Bengtsson 1986; Navarro and Barton 2003). A number of studies have reported lower rates of introgression in regions shown to contain factors contributing to interspecific incompatibility. Using markers located on all 17 chromosomes of sunflowers Helianthus annuus and H. petiolaris, Rieseberg et al. (1999) found significantly higher divergence between the species in 26 regions, of which 16 were associated with reduced pollen fertility in hybrids. A more recent study of these species found numerous amino acid differences fixed between the species near breakpoints of inverted regions, where quantitative trait loci for hybrid pollen sterility tend to cluster (Strasburg et al. 2009). Lower introgression rates in the vicinity of known incompatibility factors have been detected between house mice Mus musculus musculus and M. m. domesticus (Payseur et al. 2004; Payseur and Nachman 2005), among host races of pea aphids (Via 2009), and between D. pseudoobscura and D. persimilis (Kulathinal et al. 2009).

One interpretation of nonuniform divergence is that genomic regions that show extreme variation among demes have experienced recent selective sweeps restricted to certain geographical localities (reviewed by Schlötterer 2003; Beaumont and Balding 2004; Storz 2005). This view holds that demographic structure should affect the pattern of variation in a uniform manner, with locus specificity indicative of selection (e.g., Akey et al. 2002). Beyond sweeps, distinct species or local subpopulations of the same species may undergo genetic divergence through various processes, including adaptation to local ecological conditions (e.g., Charlesworth et al. 1997).

Here, we use “incompatibility selection” to describe selective regimes characterized by neutrality within a specific demographic unit and negative selection elsewhere. Under this process, an incompatibility locus is generally monomorphic within populations for selectively equivalent forms of the wild-type allele, except for occasional introductions of deleterious foreign alleles, which are fully functional in their home deme. While incompatibility selection may derive from disruption of deme-specific ensembles of interacting loci formed during past episodes of selective sweeps, the present genomic state is nontransient, maintained by a balance between negative selection and introgression.

Barriers to neutral gene flow

Bengtsson (1985) addressed the effect of interspecific incompatibility on introgression of regions linked to incompatibility loci, characterizing the “gene flow factor” as the probability that a newly arrived gene at a neutral marker locus will become incorporated into the local gene pool. Barton and Bengtsson (1986) characterized reproductive barriers due to multiple, epistatic incompatibility factors. Navarro and Barton (2003) used this framework to study the rate of accumulation of incompatibility factors between species. In the absence of sex specificity of any kind, loci unlinked to incompatibility factors face identical barriers to introgression and the joint barrier induced by multiple incompatibility factors corresponds to the product of the barriers generated by the factors individually.

Here, we address the implications for neutral introgression of sex specificity. Sex specificity may include differences between the sexes in fertility or viability of hybrids and their descendants, in rates of crossing over between a neutral marker locus and incompatibility factors, or in transmission of the marker or incompatibility loci (including sex linkage or sex-limited transmission). For clarity, we restrict consideration to a pair of hybridizing species.

Our results depart markedly from expectations in the absence of sex specificity. Reproductive barriers generally show epistasis, even in the absence of functional interactions among incompatibility factors. This form of epistasis in introgression rate reflects associations between sex and incompatibility factors and between sex and neutral markers. Such associations tend to generate locus-specific introgression rates, even in the absence of physical linkage of marker loci to incompatibility factors. In general, concordance among incompatibility factors in their relative expression between the sexes (for example, more severe effects in hybrid males than in females or greater crossover rates in females) generates lower reproductive barriers (greater introgression) than the multiplicative expectation and discordance generates higher barriers. Submultiplicativity of barriers arising under concordance appears to reflect the greater efficiency of selection (Haldane 1957; Hill and Robertson 1966; Barton 1995) in eliminating incompatibility factors that more severely impair the same sex.

Theoretical Framework

Our major results fall into two classes. First, we describe the derivation of relative reproductive rate, the expected contribution to future generations of a foreign marker gene introduced by a migrant relative to a marker gene in a resident. Related to the gene flow factor of Bengtsson (1985), relative reproductive rate is the central quantity in a coalescent-based approximation to the evolutionary process at neutral sites in a genome subject to incompatibility selection. Second, we address the barrier to introgression generated by multiple incompatibility factors that show no functional epistasis. This analysis presents a partitioning of variation in relative reproductive rate of neutral marker genes on all possible backgrounds.

For simplicity, we use terminology applicable to species with chromosomal sex determination in which males are heterogametic. In the context of Table 1, we indicate the modifications required to address cases with heterogametic females.

Table 1 . One-factor reproductive values.

Positiona		Relative contributionb			Relative reproductive rated
Factor	Marker	ηf	ηm	Factor–sex associationc	Female migrant	Male migrant
A	A	${\frac{{\sigma }_{\text{f}}[r_{\text{f}}-{\sigma }_{\text{m}}(r_{\text{f}}-r_{\text{m}})/2]}{1\hspace{0.17em}-\hspace{0.17em}\overline{\sigma }(1\hspace{0.17em}-\hspace{0.17em}\overline{r}}}^d$	$\frac{{\sigma }_{\text{m}}[r_{\text{m}}+{\sigma }_{\text{f}}(r_{\text{f}}-r_{\text{m}})/2]}{1\hspace{0.17em}-\hspace{0.17em}\overline{\sigma }(1\hspace{0.17em}-\hspace{0.17em}\overline{r}}$	$\frac{{\sigma }_{\text{f}}{r}_{\text{f}}-{\sigma }_{\text{m}}{r}_{\text{m}}-{\sigma }_{\text{f}}{\sigma }_{\text{m}}(r_{\text{f}}-r_{\text{m}})}{1\hspace{0.17em}-\hspace{0.17em}\overline{\sigma }(1\hspace{0.17em}-\hspace{0.17em}\overline{r}}$	$\frac{\overline{\sigma }\overline{r}}{1\hspace{0.17em}-\hspace{0.17em}\overline{\sigma }(1\hspace{0.17em}-\hspace{0.17em}\overline{r})}$	$\frac{\overline{\sigma }\overline{r}}{1\hspace{0.17em}-\hspace{0.17em}\overline{\sigma }(1\hspace{0.17em}-\hspace{0.17em}\overline{r})}$
A	X	$\frac{{\sigma }_{\text{f}}(4+{\sigma }_{\text{m}})}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{{\sigma }_{\text{m}}(4+{\sigma }_{\text{f}})}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{4({\sigma }_{\text{f}}-{\sigma }_{\text{m}})}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{2({\sigma }_{\text{f}}+{\sigma }_{\text{m}})+{\sigma }_{\text{f}}{\sigma }_{\text{m}}}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{{\sigma }_{\text{f}}(4+{\sigma }_{\text{m}})}{8-{\sigma }_{\text{f}}(2+{\sigma }_{\text{m}})}$
A	Y	—	$\frac{{\sigma }_{\text{m}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{m}}}$	—	—	$\frac{{\sigma }_{\text{m}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{m}}}$
A	mt	$\frac{{\sigma }_{\text{f}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}}$	—	—	$\frac{{\sigma }_{\text{f}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}}$	—
X	A	$\frac{{\sigma }_{\text{f}}(4+{\sigma }_{\text{m}})}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{{\sigma }_{\text{m}}(4+{\sigma }_{\text{f}})}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{4({\sigma }_{\text{f}}-{\sigma }_{\text{m}})}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{2({\sigma }_{\text{f}}+{\sigma }_{\text{m}})+{\sigma }_{\text{f}}{\sigma }_{\text{m}}}{8\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(2\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})}$	$\frac{4+{\sigma }_{\text{f}}}{8-{\sigma }_{\text{f}}(2+{\sigma }_{\text{m}})}$
X	X	$\frac{2{\sigma }_{\text{f}}{r}_{\text{f}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}(1\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})(1\hspace{0.17em}-\hspace{0.17em}{r}_{\text{f}})}$	$\frac{2{\sigma }_{\text{f}}{\sigma }_{\text{m}}{r}_{\text{f}}}{2-{\sigma }_{\text{f}}(1\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})(1-r_{\text{f}})}$	$\frac{2{\sigma }_{\text{f}}(1-{\sigma }_{\text{m}})r_{\text{f}}}{2-{\sigma }_{\text{f}}(1\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})(1\hspace{0.17em}-\hspace{0.17em}{r}_{\text{f}})}$	$\frac{{\sigma }_{\text{f}}(1+{\sigma }_{\text{m}})r_{\text{f}}}{2-{\sigma }_{\text{f}}(1\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})(1\hspace{0.17em}-\hspace{0.17em}{r}_{\text{f}})}$	$\frac{2{\sigma }_{\text{f}}{r}_{\text{f}}}{2-{\sigma }_{\text{f}}(1\hspace{0.17em}+\hspace{0.17em}{\sigma }_{\text{m}})(1\hspace{0.17em}-\hspace{0.17em}{r}_{\text{f}})}$
X	Y	—	σm	—	—	1
X	mt	$\frac{{\sigma }_{\text{f}}}{2-{\sigma }_{\text{f}}}$	—	—	$\frac{{\sigma }_{\text{f}}}{2-{\sigma }_{\text{f}}}$	—
mt	A	$\frac{{\sigma }_{\text{f}}{\sigma }_{\text{m}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}}$	σm	$-\frac{2{\sigma }_{\text{m}}(1-{\sigma }_{\text{f}})}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}}$	$\frac{{\sigma }_{\text{m}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}}$	1
mt	X	$\frac{{\sigma }_{\text{f}}{\sigma }_{\text{m}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}}$	σm	$-\frac{2{\sigma }_m(1-{\sigma }_f)}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_f}$	$\frac{{\sigma }_{\text{m}}}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{f}}}$	1
mt	Y	—	—	−	—	1
Y	A	—	$\frac{{\sigma }_{\text{m}}}{2-{\sigma }_{\text{m}}}$	$\frac{2(1-{\sigma }_{\text{m}})}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{m}}}$	1	$\frac{1}{2\hspace{0.17em}-\hspace{0.17em}{\sigma }_{\text{m}}}$
Y	X	—	—	—	1	1
Y	mt	—	—	—	1	—

^aGenomic location: autosomal (A), X-linked (X), Y-linked (Y), mitochondrial (mt).

^bRelative contribution to future generations of the marker held by a female (η_f) or a male (η_m) carrier of the factor.

^cη_f − η_m; compare Equation 8.

^d$\overline{r}$ and $\overline{\sigma }$ are defined in Equation B8.

Genealogical migration rate

Effects of selection on gene flow:

In the population genetics literature, the backward migration rate generally refers to the proportion of the local gene pool that derives from the gene pool of a different deme in the immediately preceding generation; the forward migration rate denotes the rate at which genes contribute in the immediately succeeding generation to a gene pool different from the one in which they presently reside. In the presence of selection, the forward and backward rates differ, even under a time-reversible migration process. Further, contribution of introgressed genes to future generations depends not only on the rate of mixing of gene pools but also on the reproductive success of their carriers (Karlin 1982).

Selection can change the fundamental structure of the coalescent process at a target of selection (Krone and Neuhauser 1997; Neuhauser and Krone 1997) and influences the coalescent process at neutral sites linked to targets of selection. Of central importance to the latter process is the waiting time between migration events traced backward along the line of descent of a randomly sampled gene. Modeling the distribution of waiting time as exponential, we refer to the parameter of that distribution as the genealogical migration rate. Neutral substitution proceeds at rates expected in the absence of selection (Birky and Walsh 1988), with neutral divergence between demes dependent on the genealogical migration rate. Our index of introgression differs from earlier definitions that refer to the frequencies of species-specific marker alleles (e.g., Barton 1979; Gavrilets 1997; Kobayashi et al. 2008).

Relative reproductive rate:

We model the waiting time between migration events traced backward along the line of descent of a neutral marker gene as exponential, assigning its parameter as

$$g=m\omega ,$$ (1)

for g the genealogical migration rate in the deme from which the gene currently resides, m the backward migration rate, and ω the relative reproductive rate, representing the expected contribution to future generations of the marker gene. Relative reproductive rate reflects the number and expression of foreign incompatibility alleles in the background of the focal marker gene over many generations into the future.

At each of n incompatibility loci, let 1 denote the foreign incompatibility allele and 0 the local wild-type allele (the form that functions well in the local genome). A gene at the neutral marker locus may reside on 2ⁿ⁺¹ possible backgrounds, defined by sex (female or male) and the states of the alleles at the n incompatibility loci (1 or 0).

Females bearing the 1 incompatibility allele in heterozygous form at locus i and no other locus have fitness σ_f,i relative to females bearing only 0 alleles; σ_m,i denotes the relative fitness of a male carrying the 1 allele only at locus i. We assume no functional epistasis among the incompatibility factors with respect to fitness: the fitness of carriers of multiple foreign incompatibility alleles at the same or different loci corresponds to the product of the σ-values of those alleles.

As in earlier work (e.g., Bengtsson 1985), we assume a monotonic decrease in the number of foreign incompatibility alleles in the line of descent of a neutral marker gene traced forward in time. This assumption reflects the virtual absence within the local population of those deleterious genes; we address the implications of within-population polymorphism at incompatibility loci in a separate work (Fusco and Uyenoyama 2011).

At the point of zygote formation, v represents the vector of number of descendants of the focal marker gene on the 2ⁿ⁺¹ backgrounds. After a single generation, the expected distribution of descendants becomes vC, for C a product of matrices representing selection (S) on zygotes followed by genetic transmission of the marker across the possible backgrounds (T):

$$\mathbf{C}=\mathbf{ST}.$$ (2)

To establish a common basis for transmission of the focal marker gene through male and female carriers, we scale the contributions of males by the reproductive value of males (Fisher 1930). Because males transmit gametes to the next generation only to the extent that they succeed in fertilizing eggs, males have reproductive value f/(1 − f), for f the proportion of females among reproductives, relative to unity for females.

In a generation in the remote future, the expected total number of descendant genes is ${\lim }_{t\to \infty }\mathbf{v}{\mathbf{C}}^t\mathbf{e}$, for e the vector with all elements equal to 1. Relative to a marker gene on a pure local background, the contribution of a marker gene introduced by a migrant corresponds to

$$\omega =\underset{t\to \mathrm{\infty }}{\lim }\frac{{\mathit{v}}_{\mathit{m}}{\mathit{C}}^t\mathit{e}}{{\mathit{v}}_{\mathit{r}}{\mathit{C}}^t\mathit{e}},$$ (3)

for v_m denoting the distribution of backgrounds of the marker gene in the hybrid offspring of the migrant and v_r the analogous vector for a marker gene in offspring of a resident in the same generation as the hybrid. Kobayashi et al. (2008) proposed a similar measure, which they called the “neutral effective migration rate.” Although they formulated their definition in terms of the frequency of an allele introduced by migrants, they noted its relationship to the history of a randomly sampled lineage.

As the number of generations into the future (t) grows large, the spectral radius λ of C comes to dominate (Equation 3). For diagonalizable C, λ corresponds to a simple, positive root of the characteristic equation and the set of eigenvectors that span the space (Appendix A addresses more general cases). Transmission of the focal marker genes through t generations is determined from

$${\mathit{C}}^t=\mathit{Q}{\mathit{D}}^t{\mathit{Q}}^{-1},$$

for D a diagonal matrix with the eigenvalues of C along the diagonal, Q a matrix of right eigenvectors written as columns, and Q⁻¹ a matrix of left eigenvectors written as rows. For sufficiently large t, λ^t comes to dominate the nonzero entries of D^t, which implies

$$\mathit{\omega }=\frac{{\mathit{v}}_{\mathit{m}}\mathit{q}}{{\mathit{v}}_{\mathit{r}}\mathit{q}},$$ (4)

for q the right eigenvector associated with the dominant eigenvalue λ of C. In keeping with the Fisherian notion, we term q (Equation 4) the reproductive value vector, the ith element of which represents the expected ultimate contribution to future generations of a marker gene on the ith background.

In the Mathematica notebook (matrix builder.nb) provided in Supporting Information, File S1 and File S2, the matrices reflect an ordering first of females bearing backgrounds containing the maximum number of foreign (Equation 1) incompatibility alleles through successively fewer down to zero foreign alleles (resident background) and then of males bearing these backgrounds. In the case of introgression at an autosomal marker induced by incompatibility factor 1 alone, for example, the reproductive value vector (Equation 4) corresponds to

$$\mathit{q}\mathrm{=}{\left({\eta }_{f,1},{\eta }_{f,0},{\eta }_{m,1}f/\left(1-f\right),{\eta }_{m,0}f/\left(1-f\right)\right)}^{\prime },$$

in which η_f,1 denotes the relative contribution to future generations of the marker gene borne by a female carrier of the foreign incompatibility allele relative to that of a noncarrier female or male (η_f,0 = η_m,0 = 1), η_m,1 is the analogous quantity for a male carrier, and the prime is the transpose. Relative reproductive rate (Equation 4) corresponds to

$$\omega =\frac{(f,0,1-f,0)\mathbf{q}}{(0,f,0,1-f)\mathbf{q}}=\frac{{\eta }_{\text{f,1}}+{\eta }_{\text{m,1}}}{2}$$

in which v_m = (f, 0, 1 − f, 0) and v_r = (0, f, 0, 1 − f) reflect that the focal migrant and the focal resident each produce daughters and sons in proportions f and (1 − f). Appendix B explicitly presents the matrices and the reproductive value vector q (Equation 4) for the case of an autosomal marker gene linked to a single autosomal incompatibility locus.

We use ω (Equation 4), defined in terms of contribution to future generations, to approximate the backward-perspectived genealogical migration rate g (Equation 1). Results of simulation studies indicate excellent agreement between the expected and observed distributions of number of migration events traced backward along a randomly sampled lineage (Figure 2 and Appendix C). The Mathematica notebook matrix builder.nb (File S1 and File S2) constructs transmission matrix C and produces the reproductive value vector q (Equation 4) under user-specified values for the number of incompatibility loci, genomic locations of the marker and incompatibility loci, and sex-specific selection coefficients and recombination parameters.

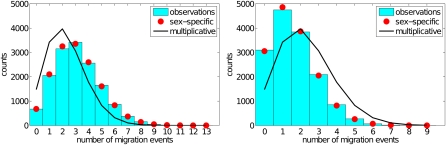
Figure 2 .

Simulated distribution of the number of migration events traced back along the line of descent of a randomly selected gene at the autosomal neutral marker locus in a genome containing two autosomal incompatibility loci, under multiplicative fitnesses and no linkage among any of the loci. For each of 15,000 independent replicates using a modified version of SFS CODE (Hernandez 2008), we simulated 100,000 generations forward in time and then counted the number of migration events in a randomly sampled line of descent traced backward in time. Each of the two populations comprised 1000 genes (500 diploid individuals), with the proportion of migrant genes each generation set to m₁₂ = m₂₁ = 1 × 10⁻⁴. Left, the foreign allele at the incompatibility loci reduced the fitness of their heterozygous male carriers (σ_m,1 = σ_m,2 = 0.3), with no effect on female carriers (σ_f,1 = σ_f,2 = 1). The observed counts (histogram) showed an excellent match (χ² = 12.1, 11 d.f.) to the Poisson distribution determined from our approximation (Equation 1) of the parameter of the exponential waiting time between migration events (g = 3.096, red circles). In contrast, the distribution predicted by assuming multiplicative barriers (black line) showed a poor fit (χ² = 4924, 9 d.f.), predicting too few migration events (g = 2.318). Right, the histogram shows the counts under incompatibility due to loci with discordant relative effects on the sexes: the foreign allele at one locus caused greater detriment to males than to females (σ_m,1 = 0.3, σ_f,1 = 1), with opposite effects at the other locus (σ_m,2 = 1, σ_f,2 = 0.3). Our approximation (g = 1.5916, red circles) again fitted the observations well (χ² = 6.3, 7 d.f.), contrary to the multiplicative prediction (g = 2.318, χ² = 3758, 7 d.f.). Discordance between the incompatibility loci on the relative impairment of males and females induces a greater barrier (fewer migration events) than expected under multiplicativity.

Partitioning of variation in long-term contribution

We assume the absence of functional epistasis among incompatibility loci in expression of the deleterious effects of incompatibility: the fitness of individuals bearing multiple foreign incompatibility alleles is equal to the product of the fitnesses induced by the alleles separately. Even so, our results indicate pervasive departures of the overall reproductive barrier from the product of the barriers induced by incompatibility factors individually. Here, we introduce a decomposition of variation in relative reproductive rate (Equation 4) in terms of interactions among incompatibility factors and sex.

Epistasis:

Expression (4) defines relative reproductive rate as a linear combination of elements of the reproductive value vector q, which gives the contributions to future generations of a marker gene on all possible backgrounds.

We explore the basis of departures from multiplicativity of the overall relative reproductive rate ω (Equation 3) at a neutral marker locus induced by multiple incompatibility factors.

We view reproductive value vector q (Equation 4) as a multiway table of a Fisherian factorial design experiment. Binary factors representing sex and the allelic state of the incompatibility loci affect the response variable of contribution to future generations of the focal marker gene.

Our index of epistasis corresponds to an analog of multilocus disequilibrium as proposed by Bennett (1954), in which, for example, the two-way association corresponds to a covariance:

$$E\left[(A_i-\overline{A_i})(A_j-\overline{A_j})\right].$$

In the case at hand, we interpret E[A_i] as the expected relative contribution to future generations of the focal marker gene held by an individual bearing the foreign incompatibility allele at locus i and no other locus,

$$E[A_i]=\overline{A_i}={\omega }_i,$$

with

$$E[{\displaystyle \prod _{i\in \Omega }}{A}_i]={\omega }_{\Omega }$$

the expected long-term contribution in the presence of foreign incompatibility alleles at all loci having an index in the set Ω and no other loci. Superscripts specify the context: for example, ${\omega }_{\Omega }^{\text{X,f}}$ denotes the relative reproductive rate at an X-linked marker gene introduced by a female migrant and ${\omega }_{\Omega }^{\text{X,m}}$ the rate in the case of a male migrant.

Two-way epistasis reflects the departure from multiplicativity of barriers to introgression:

$$e_{ij}=E\left[(A_i-\overline{A_i})(A_j-\overline{A_j})\right]={\omega }_{ij}-{\omega }_i{\omega }_j.$$

Appendix E shows that for an autosomal marker (superscript A), k-way epistasis among k autosomal incompatibility loci corresponds to

$$e_{{\Omega }_{[k]}}^{\text{A,f}}=e_{{\Omega }_{[k]}}^{\text{A,m}}={\displaystyle \sum _{j=2}^k{(-1)}^{k-j}}{\displaystyle \sum _{{\Omega }_{[j]}\subseteq {\Omega }_{[k]}}{\delta }_{{\Omega }_{[j]}}}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b},$$ (5)

for Ω_[k] a set of k indexes representing incompatibility loci, Ω_[j] a subset of Ω_[k] comprising j indexes, Ω_[k]\Ω_[j] the set of indexes in Ω_[k] but not in Ω_[j], and

$${\delta }_{{\Omega }_{[j]}}={\omega }_{{\Omega }_{[j]}}-{\displaystyle \prod _{i\in {\Omega }_{[j]}}{\omega }_i}$$ (6)

the departure of relative reproductive rate from multiplicativity. This partitioning of k-way epistasis includes components for all subsets of $2,\dots ,\hspace{0.17em}k$ loci, giving a total of ${\displaystyle {\sum }_{j=2}^k\left(\begin{array}{c}k\\ j\end{array}\right)}=2^k-(k+1)$ terms. It has the intuitively appealing property of zero epistasis for sets that include any neutral locus j (E[A_j] = ω_j = 1), reflecting cancellation between terms of the form E[… A_j …] and $E[\dots \overline{A_j}\dots ]$.

We apply this partitioning of epistasis to relative reproductive rate (Equation 4) for an arbitrary number of incompatibility factors, assuming no linkage among the factors or the marker. Relative reproductive rate at an autosomal marker corresponds to

$${\omega }_{{\Omega }_{[k]}}^{\text{A,f}}={\omega }_{{\Omega }_{[k]}}^{\text{A,m}}=\frac{{\eta }_{\text{f},{\Omega }_{[k]}}+{\eta }_{\text{m},{\Omega }_{[k]}}}{2},$$ (7)

reflecting the equal transmission of the marker through the female and male hybrid offspring of migrants of either sex. Expression (7) also applies to an X-linked marker introduced by a female migrant (${\omega }_{{\Omega }_{[k]}}^{\text{X,f}}$); for a male migrant, ${\omega }_{{\Omega }_{[k]}}^{\text{X,m}}={\eta }_{\text{f},{\Omega }_{[k]}}$, reflecting that only female offspring carry the marker.

For cases in which relative reproductive rate corresponds to Equation 7, Appendix E shows that the overall departure from multiplicativity (Equation 6) decomposes into indexes of interaction between the foreign allele at incompatibility locus i and sex:

$${\Delta }_i=\frac{{\eta }_{\text{f},i}-{\eta }_{\text{m},i}}{2}.$$ (8)

Positive Δ_i signifies a positive effect of femaleness: neutral marker genes borne by females contribute to future generations at higher rates than those borne by males. Negative Δ_i signifies that a marker gene on background i carried by a male contributes to future generations at a higher rate than a gene on the same background in a female. Sex-specific departures from multiplicativity correspond to

$${\delta }_{\text{f},{\Omega }_{[j]}}={\eta }_{\text{f},{\Omega }_{[j]}}-{\displaystyle \prod _{i\in {\Omega }_{[j]}}{\eta }_{\text{f},i}}$$ (9a)

$${\delta }_{\text{m},{\Omega }_{[j]}}={\eta }_{\text{m},{\Omega }_{[j]}}-{\displaystyle \prod _{i\in {\Omega }_{[j]}}{\eta }_{\text{m},i}}.$$ (9b)

Appendix E shows that

$$e_{{\Omega }_{[k]}}=\{\begin{array}{ll}\frac{1}{2}{\displaystyle \sum _{j=2}^k{(-1)}^{k-j}}{\displaystyle \sum _{{\Omega }_{[j]}}\left({\delta }_{\text{f},{\Omega }_{[j]}}+{\delta }_{\text{m},{\Omega }_{[j]}}\right)}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}\hfill & k\text{ odd}\hfill \\ \frac{1}{2}{\displaystyle \sum _{j=2}^k{(-1)}^{k-j}}{\displaystyle \sum _{{\Omega }_{[j]}}\left({\delta }_{\text{f},{\Omega }_{[j]}}+{\delta }_{\text{m},{\Omega }_{[j]}}\right)}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}+{\displaystyle \prod _{i=1}^k{\Delta }_i}\hfill & k\text{ even}.\hfill \end{array}$$ (10)

Results

Barriers due to single sex-specific incompatibility factors

A major objective is to explore the effects of sex specificity on barriers to neutral introgression. Appendix D presents in detail the case of X-linkage of both the marker locus and an incompatibility locus, illustrating the modifications to transmission matrix T (Equation 2) to accommodate sex specificity. Here, we address the effect on the relative reproductive rate ω (Equation 4) of the genomic locations of the marker locus and of a single incompatibility locus.

Table 1 presents reproductive values at a marker locus in a genome together with a single incompatibility locus, with the loci at various locations in the genome, including autosomal (A), X-linked (X), Y-linked (Y), and mitochondrial (mt). The reproductive value columns list the relative long-term contribution to future generations of female (η_f) and male (η_m) carriers of the foreign incompatibility factor, and the factor–sex association column gives the difference between them (η_f,1 − η_m,1; compare Equation 8). The final columns show the overall relative reproductive rates (Equation 4) of marker alleles introduced by female (ω^f) and male migrants (ω^m). For cases in which offspring of both sexes can transmit the marker and carry the incompatibility factor (A or X), the relative reproductive rate (Equation 4) of a female migrant corresponds to the average of the reproductive values of its female and male offspring:

$$\frac{{\eta }_{\text{f,1}}+{\eta }_{\text{m,1}}}{2}$$

(compare Equation 7). In the case of an autosomal marker and an X-linked incompatibility factor, a marker allele introduced by a male migrant has higher relative reproductive rate,

$$\frac{{\eta }_{\text{f,1}}+1}{2},$$

reflecting that sons of male migrants are free of the incompatibility factor. In the case of either an autosomal or an X-linked incompatibility factor, the relative reproductive rate at an X-linked marker allele introduced by a male migrant corresponds to η_f alone, reflecting that only daughters of male migrants carry the marker.

We assume that males do not transmit mitochondria, with the implication that incompatibility due to foreign mitochondria (mt) presents no barrier to autosomal or X-linked markers borne by a male migrant $({\omega }_{\text{mt}}^{\text{A,m}}={\omega }_{\text{mt}}^{\text{X,m}}=1)$. Similarly, incompatibility factors on the X chromosome or mitochondria present no barrier to Y-linked markers $({\omega }_{\text{X}}^{\text{Y}}={\omega }_{\text{mt}}^{\text{Y}}=1)$ because the marker and the factor are never transmitted to the same offspring.

Birds and various other organisms exhibit ZW sex determination, with male homogamety (ZZ) and female heterogamety (ZW). Reproductive values under this system correspond to those given in Table 1, with Z substituted for X and W for Y. Because complete cosegregation of mitochondria and the W chromosome constitutes in essence complete linkage between these regions, the reproductive values for cases involving a marker or a factor on mitochondria can be obtained from Table 1 by substituting mt for W.

Barriers due to multiple incompatibility factors

We describe conditions under which the relative reproductive rate ω (Equation 4) induced by multiple incompatibility factors corresponds to the product of the relative reproductive rates induced by the factors individually. Beyond this case (absence of sex specificity in expression of incompatibility, crossover rates, or genetic transmission), the joint barrier to introgression engendered by multiple incompatibility loci departs in general from the product of the barriers induced by the factors in isolation. Epistasis in relative reproductive rate as defined in this section and in Appendix E reflects such departures from multiplicativity.

Multiplicative barriers to introgression:

In the absence of sex specificity, the Kronecker structure of the transition matrix C (Equation B5) for an autosomal marker extends to multiple incompatibility loci with multiplicative effects on the survival or reproduction of carriers. Here, we show that the total barrier to introgression at a neutral autosomal marker locus corresponds to the product of the barriers generated by the incompatibility loci individually under (1) sex-independent incompatibility selection and recombination, (2) independent transmission of the factors conditional on transmission of the marker, and (3) sex-independent genetic transmission.

We consider l incompatibility loci, for which the foreign allele at locus i reduces the viability and fertility of its carriers by a factor of σ_i relative to noncarriers. Crossing over occurs between the focal marker gene and incompatibility locus i at rate r_i, independently of crossing over in other regions. This assumption implies that at most two incompatibility loci (flanking the marker locus) can reside on the chromosome bearing the marker locus, with all other incompatibility loci unlinked (r_f,j = r_m,j = $\frac{1}{2}$).

The selection matrix (Equation B1) generalizes to

$$\left(\begin{array}{cc}1& 0\\ 0& \frac{f}{1-f}\end{array}\right)\otimes \tilde{\mathbf{S}},$$

for $\tilde{\mathbf{S}}={\mathbf{S}}_{\mathbf{1}}\otimes \dots {\mathbf{S}}_{\mathbf{l}}$ with

$${\mathbf{S}}_{\mathbf{i}}=\left(\begin{array}{cc}{\sigma }_i& 0\\ 0& 1\end{array}\right).$$

Transmission of the autosomal marker and sex retains the form (Equation B2). Independent transmission of the factors conditional on transmission of the marker implies

$$\mathbf{F}=\left(\begin{array}{c}1\\ 1\end{array}\right)\otimes \tilde{\mathbf{R}},$$

for $\tilde{\mathbf{R}}={\mathbf{R}}_{\mathbf{1}}\otimes \dots {\mathbf{R}}_{\mathbf{l}}$ with

$${\mathbf{R}}_{\mathbf{i}}=\left(\begin{array}{cc}1-r_i& r_i\\ 0& 1\end{array}\right)$$

(compare Equation B3). The full transition matrix corresponds to

$$\begin{array}{c}\mathbf{C}=\left[\left(\begin{array}{cc}1& 0\\ 0& \frac{f}{1-f}\end{array}\right)\otimes \tilde{\mathbf{S}}\right]\left[\frac{1}{2}(f,1-f)\otimes \left(\begin{array}{c}1\\ 1\end{array}\right)\otimes \tilde{\mathbf{R}}\right]\\ =\left(\begin{array}{cc}1& 0\\ 0& \frac{f}{1-f}\end{array}\right)\left[\frac{1}{2}(f,1-f)\otimes \left(\begin{array}{c}1\\ 1\end{array}\right)\right]\otimes \tilde{\mathbf{S}}\tilde{\mathbf{R}}\end{array}$$

(compare Equation B5). The eigenvalues of $\tilde{\mathbf{S}}\tilde{\mathbf{R}}={\mathbf{S}}_{\mathbf{1}}{\mathbf{R}}_{\mathbf{1}}\otimes \dots {\mathbf{S}}_{\mathbf{l}}{\mathbf{R}}_{\mathbf{l}}$ correspond to products of the eigenvalues of the component matrices and its eigenvectors to Kronecker products of the eigenvectors of those matrices. In particular, elements of the reproductive value q (Equation 4) have the form

$${\eta }_{\text{f},\Omega }={\displaystyle \prod _{i\in \Omega }{\eta }_{\text{f},i}}{\eta }_{\text{m},\Omega }={\displaystyle \prod _{i\in \Omega }{\eta }_{\text{m},i}},$$ (11)

for Ω any subset of indexes in {1, … , l} and η_f,i = η_m,i the reproductive value of female and males carriers of the foreign incompatibility allele at locus i. Consequently, the overall relative reproductive rate (Equation 4) corresponds to the product of the reproductive rates across the loci individually (Equation B6):

$${\omega }_{1\dots l}^{\text{A,f}}={\omega }_{1\dots l}^{\text{A,m}}={\displaystyle \prod _{i=1}^l\frac{{\sigma }_i{r}_i}{1-{\sigma }_i(1-r_i)}}.$$ (12)

Multiplicative barriers also arise in the case of markers that are transmitted without recombination through only one sex: those on mitochondria or in the nonrecombining male- (female-)specific region of the Y (W) chromosome, for example. For markers transmitted only through females, the selection matrix (Equation B1) reduces to $\tilde{\mathbf{S}}={\mathbf{S}}_{\mathbf{1}}\otimes \dots {\mathbf{S}}_{\mathbf{l}}$, with S_i containing only the female selection parameter σ_f,i, and the recombination matrix $\tilde{\mathbf{R}}={\mathbf{R}}_{\mathbf{1}}\otimes \dots {\mathbf{R}}_{\mathbf{l}}$ contains the crossover rates for females alone. As the transition matrix reduces to $\mathbf{C}=\tilde{\mathbf{S}}\tilde{\mathbf{R}}$, the reproductive rate vector q has elements ${\eta }_{\text{f},\Omega }={\displaystyle {\prod }_{i\in \Omega }{\eta }_{\text{f},i}}$ and the overall relative reproductive rate (Equation 4) is given by Equation 13, with the selection and recombination parameters corresponding to the values for females. In the absence of linkage between the marker and the ith factor (r_f,i = $\frac{1}{2}$), the ith multiplicand of Equation 12 reduces to

$$\frac{{\sigma }_{\text{f},i}}{2-{\sigma }_{\text{f},i}}$$

(compare Equation B6). Complete linkage (r_f,i = 0) implies a zero overall relative reproductive rate (no introgression at the marker).

In this section, we have assumed the complete absence of sex specificity. The absence of interaction between any incompatibility locus and sex (Δ_i = 0 ∀i) and of all sex-specific departures from multiplicativity (${\delta }_{\text{f},{\Omega }_{[j]}}={\delta }_{\text{m},{\Omega }_{[j]}}=0\hspace{0.17em}\hspace{0.17em}\forall j$) (Equation 11) as well as of the overall departure (Equation 12) implies the absence of epistasis of all orders.

Nonmultiplicative barriers to introgression:

Violation of any of the postulates enumerated in the preceding section induces a departure from multiplicativity of the barriers to introgression generated by more than one incompatibility locus. In this sense, the postulates represent minimal conditions for multiplicativity. To explore the nature and implications of nonmultiplicative barriers, we address the relative reproductive rate at a marker locus (autosomal or X-linked) subject to incompatibility generated by two loci: both autosomal or one autosomal and one X-linked.

Epistasis between autosomal factors with sex-specific expression or recombination:

We explore the effects of sex specificity in expression of incompatibility or in crossover rates on the rate of introgression at an autosomal marker flanked by autosomal incompatibility loci 1 and 2.

Conditional on transmission of the marker, transmission from female parents of the two factors occurs independently of each other,

$$\left(\begin{array}{cc}1-r_{\text{f,1}}& r_{\text{f,1}}\\ 0& 1\end{array}\right)\otimes \left(\begin{array}{cc}1-r_{\text{f,2}}& r_{\text{f,2}}\\ 0& 1\end{array}\right),$$ (13)

for r_f,i the rate of crossing over in females between the marker and incompatibility locus i. A similar transmission matrix holds for male parents, with r_m,i, the crossover rate in males, substituted for r_f,i. In the absence of physical linkage, r_f,i = r_m,i = $\frac{1}{2}$. The foreign incompatibility allele at locus i reduces the viability of its female (male) carriers by a factor of σ_f,i (σ_m,i), with multiplicative effects in carriers bearing foreign alleles at both loci (e.g., σ_f,12 = σ_f,1σ_f,2).

Migrants of either sex produce female and male hybrid offspring in frequencies f and 1 − f. The relative reproductive rate at the marker locus (Equation 4) corresponds to

$${\omega }_{12}^{\text{A,f}}={\omega }_{12}^{\text{A,m}}=\frac{(f,0,0,0,1-f,0,0,0)\mathbf{q}}{(0,0,0,f,0,0,0,1-f)\mathbf{q}}=\frac{{\eta }_{\text{f,12}}+{\eta }_{\text{m,12}}}{2},$$ (14)

for η_f,12 and η_m,12 the contribution to future generations of the marker gene in females and males that bear the foreign factor at both incompatibility loci.

Our index of epistasis (Equation 10) among incompatibility loci reduces in this case to

$$e_{12}^{\text{A}}=\frac{{\delta }_{\text{f},12}+{\delta }_{\text{m},12}}{2}+{\Delta }_1{\Delta }_2=\frac{2{\Delta }_1{\Delta }_2}{\Gamma },$$ (15)

in which

$${\Delta }_i=\frac{{\eta }_{\text{f},i}-{\eta }_{\text{m},i}}{2}=\frac{{\sigma }_{\text{f},i}{r}_{\text{f},i}-{\sigma }_{\text{m},i}{r}_{\text{m},i}-{\sigma }_{\text{f},i}{\sigma }_{\text{m},i}(r_{\text{f},i}-r_{\text{m},i})}{2-{\sigma }_{\text{f},i}{r}_{\text{f},i}-{\sigma }_{\text{m},i}{r}_{\text{m},i}}$$ (16)

(compare Equation B9) and

$$\Gamma =2-{\sigma }_{\text{f},1}{\sigma }_{\text{f},2}\left(1-r_{\text{f},1}\right)\left(1-r_{\text{f},2}\right)-{\sigma }_{\text{m},1}{\sigma }_{\text{m},2}\left(1-r_{\text{m},1}\right)\left(1-r_{\text{m},2}\right).$$

In this case, the sex-specific measures of epistasis are proportional to each other:

$$\begin{array}{c}{\delta }_{\text{f},12}={\eta }_{\text{f},12}-{\eta }_{\text{f},1}{\eta }_{\text{f},2}=\frac{2{\sigma }_{\text{f},1}{\sigma }_{\text{f},2}\left(1-r_{\text{f},1}\right)\left(1-r_{\text{f},2}\right){\Delta }_1{\Delta }_2}{\Gamma }\\ {\delta }_{\text{m},12}={\eta }_{\text{m},12}-{\eta }_{\text{m},1}{\eta }_{\text{m},2}=\frac{2{\sigma }_{\text{m},1}{\sigma }_{\text{m},2}\left(1-r_{\text{m},1}\right)\left(1-r_{\text{m},2}\right){\Delta }_1{\Delta }_2}{\Gamma }.\end{array}$$ (17)

These autosomal factors undergo independent transmission (Equation 13) and cause no functional epistasis with respect to fitness of carriers. Furthermore, each in isolation induces the relative reproductive rate given by Bengtsson (1985), with the average crossover and viability rates substituted for the non-sex-specific parameters (Equation B7). Even so, the joint barrier to introgression departs in general from the product of the barriers induced by each locus separately (Equation 15).

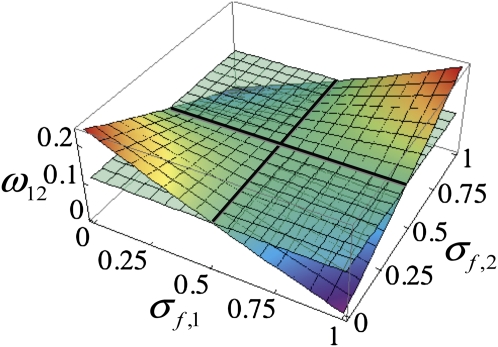
To explore the nature of epistasis due to sex specificity in the impairment of carriers of foreign incompatibility loci, we determined the relative reproductive rate (Equation 4) at an autosomal marker induced by two autosomal incompatibility factors in the absence of physical linkage (r_f,i = r_m,i = $\frac{1}{2}$ for i = 1, 2 in Equation 16). In Figure 1, the relatively flat plane corresponds to the expectation under multiplicative reproductive barriers, while the saddle-shaped surface shows the actual joint barrier, with heavy lines marking the only points of agreement between the actual and expected barriers. This example illustrates the general finding that incompatibility factors with concordant relative effects on the sexes (for example, both afflicting male carriers to a greater extent than female carriers) induce lower barriers to neutral introgression than the multiplicative expectation, and factors with discordant effects induce higher barriers.

Figure 1 .

Joint relative reproductive rate at a neutral autosomal marker locus induced by two autosomal factors in the absence of physical linkage. Each of the horizontal axes represents the fitness (relative viability or fertility) of female carriers of an autosomal factor (σ_f,i, i = 1, 2), with the fitness of a male carrier given by σ_m,i = 1 − σ_f,i. The saddle-shaped surface represents the relative reproductive rate at the marker locus induced by the two factors jointly and the relatively flat surface the rate under the multiplicative expectation. Thick lines indicate the intersection between the actual and expected barriers.

To verify the accuracy of our expression for the genealogical migration rate g (Equation 1), we conducted a numerical simulation study using SFS CODE (Hernandez 2008), modified to identify the lineage involved in each migration event. We specified an autosomal marker gene and two autosomal incompatibility loci under multiplicative fitnesses and no linkage among any of the loci. We simulated 100,000 generations forward in time and then counted the number of migration events in a randomly sampled line of descent traced backward in time. We compared the counts observed in 15,000 independent replicate runs to a Poisson distribution with the parameter determined by Equation 1 under the population parameters specified in the simulation (Figure 2 legend). Figure 2 indicates an excellent fit of the simulated data to our prediction. It also provides another illustration that incompatibility factors with concordant effects on the sexes induce lower barriers than expected under multiplicativity (Figure 2, left) and factors with discordant effects induce higher barriers (Figure 2, right).

Sex-specific recombination rates can generate epistasis even in the absence of sex specificity in carrier fitness (σ_f,i = σ_m,i = σ < 1). In this case, Equation 16 reduces to

$${\Delta }_i=\frac{\sigma (1-\sigma )(r_{\text{f},i}-r_{\text{m},i})}{2-\sigma (r_{\text{f},i}+r_{\text{m},i})}.$$

Rates of introgression at the marker exceed those expected under multiplicative barriers $(e_{12}^{\text{A}}>0)$ if crossing over between the marker and each of the flanking incompatibility factors occurs at higher rates in females than in males (Δ₁, Δ₂ > 0) or if both rates are higher in males (Δ₁, Δ₂ < 0).

X-linked marker with autosomal and X-linked incompatibility factors:

We address barriers generated by one A and one X incompatibility locus to introgression at an X-linked marker introduced by a female migrant (Appendix F gives the expressions for a male migrant). We assume no crossing over between the X-linked factor and the marker in (hemizygous) males (r_m,X = 0).

Epistasis in relative reproductive rate (Equation 10) between the X-linked and autosomal incompatibility loci corresponds to

$$e_{\text{AX}}^{\text{X}}={\omega }_{\text{AX}}^{\text{X}}-{\omega }_{\text{AX}}^{\text{X}}{\omega }_{\text{X}}^{\text{X}}=\frac{{\delta }_{\text{f,AX}}^{\text{X}}+{\delta }_{\text{m,AX}}^{\text{X}}}{2}+{\Delta }_{\text{A}}^{\text{X}}{\Delta }_{\text{X}}^{\text{X}}.$$ (18)

Table 1 gives the index of association between the autosomal factor and sex,

$${\Delta }_{\text{A}}^{\text{X}}=\frac{{\eta }_{\text{f,A}}^{\text{X}}-{\eta }_{\text{m,A}}^{\text{X}}}{2}=\frac{2({\sigma }_{\text{f,A}}-{\sigma }_{\text{m,A}})}{8-{\sigma }_{\text{f,A}}(2+{\sigma }_{\text{m,A}})},$$ (19)

and between the X-linked factor and sex,

$${\Delta }_{\text{X}}^{\text{X}}=\frac{{\eta }_{\text{f,X}}^{\text{X}}-{\eta }_{\text{m,X}}^{\text{X}}}{2}=\frac{{\sigma }_{\text{f,X}}{r}_{\text{f,X}}(1-{\sigma }_{\text{m,X}})}{2-{\sigma }_{\text{f,X}}(1+{\sigma }_{\text{m,X}})(1-r_{\text{f,X}})}.$$ (20)

Within-sex interactions correspond to

$${\delta }_{\text{f,AX}}^{\text{X}}={\eta }_{\text{f,AX}}^{\text{X}}-{\eta }_{\text{f,A}}^{\text{X}}{\eta }_{\text{f,AX}}^{\text{X}}=\frac{4{\sigma }_{\text{f,A}}{\sigma }_{\text{f,X}}\left(1-r_{\text{f,X}}\right){\Delta }_{\text{A}}^{\text{X}}{\Delta }_{\text{X}}^{\text{X}}}{\Gamma }$$ (21a)

$${\delta }_{\text{m,AX}}^{\text{X}}={\eta }_{\text{m,AX}}^{\text{X}}-{\eta }_{\text{m,A}}^{\text{X}}{\eta }_{\text{m,X}}^{\text{X}}=\frac{8{\sigma }_{\text{f,A}}{\sigma }_{\text{f,X}}\left(1-r_{\text{f,X}}\right){\sigma }_{\text{m,A}}{\sigma }_{\text{m,X}}{\Delta }_{\text{A}}^{\text{X}}{\Delta }_{\text{X}}^{\text{X}}}{\Gamma },$$ (21b)

giving an overall two-way epistasis between the incompatibility factors of

$$e_{\text{AX}}^{\text{X}}=\frac{8{\Delta }_{\text{A}}^{\text{X}}{\Delta }_{\text{X}}^{\text{X}}}{\Gamma },$$ (22)

in which

$$\Gamma =8-{\sigma }_{\text{f,A}}{\sigma }_{\text{f,X}}\left(1-r_{\text{f,X}}\right)\left(2+{\sigma }_{\text{m,A}}{\sigma }_{\text{m,X}}\right).$$

Because a male transmits its entire X chromosome (the marker together with any foreign incompatibility allele) to all daughters and no sons,

$${\eta }_{\text{m,X}}^{\text{X}}={\eta }_{\text{f,X}}^{\text{X}}{\sigma }_{\text{m,X}}$$

(Table 1). Accordingly, Equation 20 indicates that the X-linked factor obstructs transmission of the X-linked marker through males more than through females $({\Delta }_{\text{X}}^{\text{X}}>0)$ unless the X-linked factor causes complete sterility or inviability in females (σ_f,X = 0), has no deleterious effects in males (σ_m,X = 1), or shows absolute linkage to the marker (r_f,X = 0). The nature of epistasis, sex specific (Equation 21) as well as overall (Equation 22), depends on the effect of the autosomal factor $({\Delta }_{\text{X}}^{\text{X}})$. Expression (19) indicates positive epistasis (greater introgression than expected under multiplicativity) if the autosomal factor impairs male carriers to a greater extent (σ_f,A > σ_m,A).

Autosomal marker with autosomal and X-linked incompatibility factors:

We now consider introgression at an autosomal marker in a genome containing one A incompatibility locus, possibly linked to the marker, and one X locus. We assume a female migrant (Appendix F provides the expressions for a male migrant).

The overall two-way epistasis (Equation 10) between the incompatibility factors corresponds to

$$e_{\text{AX}}^{\text{A}}=\frac{4{\Delta }_{\text{A}}^{\text{A}}{D}_{\text{f}}}{[8-{\sigma }_{\text{f,X}}(2+{\sigma }_{\text{m,X}})]\Gamma },$$ (23)

for

$${\Delta }_{\text{A}}^{\text{A}}=\frac{{\eta }_{\text{f,A}}^{\text{A}}-{\eta }_{\text{m,A}}^{\text{A}}}{2}=\frac{{\sigma }_{\text{f,A}}{r}_{\text{f}}-{\sigma }_{\text{m,A}}{r}_{\text{m}}-{\sigma }_{\text{f,A}}{\sigma }_{\text{m,A}}(r_{\text{f}}-r_{\text{m}})}{2-{\sigma }_{\text{f,A}}{r}_{\text{f}}-{\sigma }_{\text{m,A}}{r}_{\text{m}}}$$ (24)

(compare to Equations 16 and 19), for D_f an index of association between sex and the X-linked factor (Equation F4) and Γ a positive quantity (Appendix F). The joint barrier to introgression departs from multiplicativity only if the autosomal factor shows an interaction with sex $({\Delta }_{\text{A}}^{\text{A}}\ne 0)$, reflecting sex-specific expression of incompatibility (σ_f,A ≠ σ_m,A) or sex-specific rates of crossing over with the marker (r_f,A ≠ r_m,A). Whether the overall epistasis $e_{\text{AX}}^{\text{A}}$ is positive or negative depends on the nature of the female-specific epistasis between the incompatibility factors (${\delta }_{\text{f,AX}}^{\text{A}}$ ∝ D_f (Equation F4), which in turn depends on parameters of both the autosomal and X-linked factors.

Indexes D_f and D_m (Equation F4) function as indicators of the effect of sex on the barrier to transmission of the autosomal marker locus induced by the X-linked incompatibility factor: positive values indicate higher transmission of the marker through female than through male carriers of the incompatibility factor. In general, D_m ≤ 0, signifying that femaleness reduces transmission by carriers of the X-linked incompatibility factor, with no effect (D_m = 0) only if the factor does not in fact contribute to incompatibility (σ_f,X = σ_m,X = 1). This property may reflect that while female carriers pass the X-linked incompatibility factor to offspring of both sexes, male carriers pass it only to daughters.

Another indication of the intrinsic association of an X-linked incompatibility factor with sex is that it can affect the sign of the overall epistasis $e_{\text{AX}}^{\text{A}}$ even if it exhibits no sex specificity in expression of incompatibility or crossing over (σ_f,X = σ_m,X and r_f,X = r_m,X). In this case, the autosomal marker has lower reproductive rates in female carriers of the X-linked incompatibility factor than in male carriers (D_f, D_m < 0).

Discussion

We have explored the implications of sex-specific interspecific incompatibility for neutral introgression across the genome. We proposed a scaling of the backward migration rate (Equation 3) that accounts for sex-specific incompatibility selection and linkage and showed that the distribution of waiting times along a random lineage traced backward conforms well to the distribution determined by this scaling (Figure 2). Among the key qualitative findings are that (1) neutral introgression generally occurs at locus-specific rates, even in the absence of linkage of marker loci to incompatibility factors and (2) the joint barrier generated by multiple incompatibility factors is generally nonmultiplicative, even in the absence of functional epistasis among the incompatibility factors.

Here, we provide a qualitative discussion of these results, illustrate some implications for the interpretation of patterns of genetic variation in closely related Drosophila species, and suggest that sex specificity is a pervasive feature of interspecific hybridization in plants and animals.

Locus specificity in reproductive barriers reflects associations with sex

Factors contributing to interspecific incompatibility impede introgression of neutral markers at a rate that depends on the level of linkage, selection intensity, and functional epistasis among incompatibility factors (Bengtsson 1985; Barton and Bengtsson 1986; Navarro and Barton 2003). In the absence of sex specificity, the locus-specific nature of barriers to introgression extends only to regions immediately adjacent to targets of selection. For example, Table 1 indicates that in the absence of linkage with a neutral marker (r_f = r_m = $\frac{1}{2}$), a single factor transmitted through both sexes that induces non-sex-specific incompatibility (σ_f = σ_m = σ ≤ 1) either imposes no barrier to introgression at the marker or reduces it by a factor of σ/(2 − σ) [compare the “gene flow factor” (Equation F6) of Bengtsson 1985]. Factors borne on the mitochondria also have this effect, while Y-linked factors impede introgression on autosomes by a factor of 1/(2 − σ). In contrast, sex-specific incompatibility induces locus-specific barriers even at unlinked marker loci.

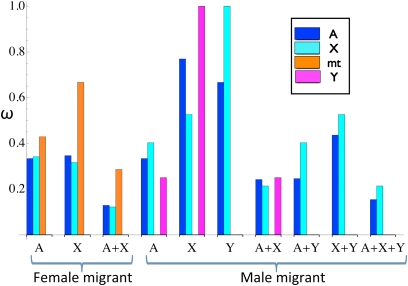
Sex specificity in expression of incompatibility, transmission, or level of linkage to incompatibility factors impedes introgression at neutral markers to unequal extents across genomic regions, even in the absence of functional epistasis. Figure 3 illustrates, for a female or male migrant, relative reproductive rates (Equation 4) at neutral marker loci at various locations in the genome (color-coded bars) with one or multiple incompatibility loci at locations indicated on the abscissa, assuming free crossing over (r = $\frac{1}{2}$) between the marker and any incompatibility factor. Because a male migrant never transmits both its X and Y chromosomes to the same offspring, an incompatibility factor on one chromosome poses no barrier to introgression of the other chromosome. Accordingly, Figure 3 shows relative reproductive rates of 1 for ${\text{ω}}_{\text{X}}^{\text{Y,m}}$ (magenta bar for an incompatibility factor only on the X) and ${\text{ω}}_{\text{Y}}^{\text{X,m}}$ (cyan bar for an incompatibility factor only on the Y), regardless of sex specificity. In all other cases, the differences in heights of the bars for a given set of locations for incompatibility factors arise as a consequence of sex specificity in intensity of incompatibility selection or transmission of the marker or incompatibility loci.

Figure 3 .

Relative reproductive rates at a neutral marker locus induced by incompatibility factors at various genomic locations for female or male migrants. Bars indicate the relative reproductive rate (Equation 4) of a neutral marker located on an autosome (A, blue) unlinked to any incompatibility locus (r_f,A = r_m,A = $\frac{1}{2}$), on the X chromosome (X, cyan), on the mitochondria (mt, orange), or on the Y chromosome (Y, magenta). Locations of one or more incompatibility factors are indicated on the abscissa [autosome only (A), autosome and X chromosome (A + X), etc.]. For X-linkage of both factor and marker, we assume free crossing over in females (r_f,X = $\frac{1}{2}$) and none in the hemizygous males (r_m,X = 0). To provide a basis for comparison, we assumed that the factors induce a common total intensity of incompatibility selection, constraining σ_f,⋅ + σ_m,⋅ = 1. Female carriers of the autosomal factor have viability σ_f,A = 0.6 and male carriers σ_m,A = 0.4, and for the X-linked factor, σ_f,X = 0.8 and σ_m,X = 0.2. For the Y-linked incompatibility locus, σ_m,Y = 0.5.

Locus-specific reproductive barriers of this kind reflect associations between sex and incompatibility factors and between sex and marker loci (last section of Results and Appendix E). Because neutral markers borne on X chromosomes or on mitochondria, for example, descend preferentially or exclusively through females, they experience incompatibility primarily in a female context. If male hybrids experience greater impairment, female-associated markers face lower barriers to introgression than male-associated markers. A Y-linked incompatibility factor introduced by a male migrant imposes no barrier to introgression at an X-linked marker because only its daughters carry the marker, but it does impede introgression at an autosomal marker, which accompanies the Y-linked factor in half of the sons of a male carrier. In Table 1, the factor–sex association column shows a measure of interaction (Equation 8) between a single incompatibility factor and sex in determining relative reproductive rate ω (Equation 4).

Differences between the sexes in levels of recombination have consequences similar to those of sex-specific expression of incompatibility. Greater rates of crossing over in females than in males, for example, permit greater introgression of female-associated markers linked to incompatibility factors.

Epistasis in relative reproductive rate

Our analysis of the joint barrier to neutral introgression induced by multiple incompatibility factors assumes the absence of functional epistasis: the fitness of individuals bearing multiple factors corresponds to the product of the fitnesses induced by the factors individually. Under equal impairment of male and female carriers of foreign incompatibility factors, transmission of incompatibility factors on autosomes, and equal rates of crossing over between the sexes, we confirm the multiplicativity of the barriers (Equation 12), as commonly assumed. These conditions appear to be minimal, as violation of any one causes departures from multiplicativity (Nonmultiplicative barriers to introgression section).

In general, discordance among incompatibility factors in the nature of association with sex tends to increase barriers to introgression. For example, Figure 1 depicts the relative reproductive rate of an autosomal marker in a genome containing two incompatibility loci with sex-specific expression (σ_f,i ≠ σ_m,i) in the absence of linkage between any pair of loci. It illustrates that the highest barriers (lowest ω-values, bluer regions) derive from a positive interaction (Equation 8) with femaleness in one factor (Δ_i > 0) and a negative interaction in another factor (Δ_j < 0). Positive epistasis arises under concordant associations (Δ_iΔ_j > 0), implying higher rates of gene flow (redder regions). For extreme manifestations of Haldane’s rule (σ_f = 1, σ_m = 0 or σ_m = 1, σ_f = 0), the actual rate of introgression is nearly twofold greater than expected under multiplicative reproductive barriers (red corners in Figure 1).

Rapid elimination of the deleterious foreign incompatibility factors permits greater neutral introgression. The selection process is more efficient if the factors tend to occur together (Hill and Robertson 1966; Barton 1995): in the same sex, in the present context. Concordance of the sex-specific effects of multiple incompatibility factors (greater impairment of male carriers than of female carriers, for example) implies their association with the same sex.

Interspecific incompatibility in Drosophila

Llopart et al. (2005) studied patterns of nucleotide divergence and polymorphism in sister species D. yakuba and D. santomea in 29 genomic regions, including sites on the X chromosome, the Y chromosome, autosomes, and mitochondria. Regions on the X and Y contribute to severe reductions in hybrid male fertility (Coyne et al. 2004) and quantitative trait loci contributing to both prezygotic and postzygotic isolation occur on the X chromosome and the autosomes (Moehring et al. 2006a,b). Llopart et al. (2005) found significantly lower ratios of shared to fixed polymorphisms between the species on the X chromosome than on autosomes, which they considered consistent with reduced introgression of X-linked sites due to the disproportionate contribution of the X to hybrid male sterility. To account for the difference in effective number of genes under X and autosomal linkage and its effects on levels of polymorphism, they also conducted coalescent simulations under IM-based (Hey and Nielsen 2004) estimates of demographic parameters. However, this approach indicated no significant reduction in introgression rate at X-linked relative to autosomal sites.

In confirmation of the expectations of Llopart et al. (2005), our model indicates that incompatibility due to a single X-linked factor permits greater introgression in autosomal than in X-linked regions,

$${\text{ω}}_{\text{X}}^{\text{A,f}}>{\text{ω}}_{\text{X}}^{\text{X,f}}\mathrm{and}{\text{ω}}_{\text{X}}^{\text{A,m}}>{\text{ω}}_{\text{X}}^{\text{X,m}},$$

regardless of the intensity of incompatibility selection (σ_f,X, σ_m,X), the rate of crossing over on the X (r_f,X), or the sex of the initial migrant (Table 1). The blue (autosomal marker) and cyan (X-linked marker) bars in Figure 3 for the case of a single X-linked factor (X on the abscissa) illustrate this effect.

In contrast, incompatibility due to a single autosomal factor introduced by a male migrant permits greater introgression in X-linked regions than in autosomal regions unlinked to the factor (r_f = r_m = $\frac{1}{2}$):

$${\text{ω}}_{\text{A}}^{\text{X,m}}>{\text{ω}}_{\text{A}}^{\text{A,m}}$$

[for example, blue (A) and cyan (X) bars in Figure 3 over A for a male migrant]. For autosomal factors introduced by a female migrant, higher introgression in X-linked regions

$${\text{ω}}_{\text{A}}^{\text{X,f}}>{\text{ω}}_{\text{A}}^{\text{A,f}}$$

holds for factors that impair male carriers more than female carriers (σ_f > σ_m).

Many aspects of incompatibility between D. yakuba and D. santomea show sex specificity, with multiple factors on the X chromosome, the Y chromosome, and autosomes contributing to hybrid male sterility (Coyne et al. 2004; Moehring et al. 2006a). Accordingly, we expect the overall barrier to introgression to show sex-related epistasis. To illustrate the implications, we compare the relative reproductive rates at X-linked and autosomal markers induced by incompatibility factors both on the X chromosome and on an autosome unlinked to the autosomal factor (r_f,A = r_m,A = $\frac{1}{2}$). For the case in which the X-linked factor causes complete sterility in hemizygous form (σ_m,X = 0), with maximal crossing over in females (r_f,X = $\frac{1}{2}$; r_m,X = 0 in hemizygous males), our model indicates uniformly higher introgression rates in X-linked than in autosomal regions for the case of a male migrant $({\text{ω}}_{\text{A,X}}^{\text{X,m}}>{\text{ω}}_{\text{A,X}}^{\text{A,m}}\text{)}$. For female migrants, with σ_m,X = 0,

$${\text{ω}}_{\text{A,X}}^{\text{X,f}}-{\text{ω}}_{\text{A,X}}^{\text{A,f}}\propto {\text{σ}}_{\text{f,A}}{\text{σ}}_{\text{f,X}}{\text{σ}}_{\text{m,A}}\left({\text{σ}}_{\text{f,A}}-{\text{σ}}_{\text{m,A}}\right).$$

This expression implies equal barriers to introgression on the autosome and the X chromosome $({\text{ω}}_{\text{A,X}}^{\text{X,f}}={\text{ω}}_{\text{A,X}}^{\text{A,f}})$ if either factor expresses dominant lethality or sterility (σ_f,Aσ_f,Xσ_m,A = 0). Otherwise, greater introgression is expected at X-linked than at autosomal sites $({\text{ω}}_{\text{A,X}}^{\text{X,f}}>{\text{ω}}_{\text{A,X}}^{\text{A,f}})$ if the effects of the autosomal factor conform to Haldane’s rule (σ_f,A > σ_m,A).

Contrary to the expectation of Llopart et al. (2005), these results indicate that sex specificity in crossing over and in postzygotic incompatibility can induce a greater barrier to introgression in autosomal regions unlinked to any incompatibility factor than in regions on the X that are loosely linked (r_f = $\frac{1}{2}$) to an incompatibility factor. The presence of an incompatibility factor on the Y, as reported by Coyne et al. (2004), would reinforce this trend by inhibiting introgression of autosomes but not the X chromosome because foreign X-linked markers and the foreign Y never occur in the same genome.

Even under parameter values for which ${\text{ω}}_{\text{A,X}}^{\text{X,f}}<{\text{ω}}_{\text{A,X}}^{\text{A,f}}$ (e.g., Figure 3), positive epistasis due to concordant sex-specific effects among factors (for example, greater impairment of male hybrids or higher rates of crossing over in females) may cause the joint barrier to exceed the multiplicative expectation considerably (Figure 1). In such cases, the introgression rate in unlinked autosomal regions may only slightly exceed the rate on the X, consistent with the nonsignificant differences reported by Llopart et al. (2005).

Unlike the expectation in the absence of sex specificity, Figure 3 illustrates marked differences in introgression rates among markers freely recombining with incompatibility loci. Our analysis of locus-specific introgression rates may contribute toward a basis for inferring the existence and location of incompatibility factors from the pattern of neutral variation throughout the genome. In particular, the ensemble response of marker loci in the four genomic regions shown in Figure 3 differs among models for the location of incompatibility loci and also between the sexes of the migrants within a given model.

Sex-specific transmission or expression of incompatibility factors

As sex specificity in expression of interspecific incompatibility or in crossover rates has been widely observed, our findings raise the possibility of pervasive locus-specific neutral divergence among species.

Lenormand and Dutheil (2005) have reviewed studies documenting differences in map length between males and females in both plants and animals, including humans (Li et al. 1998). In Drosophila, the premiere model organism for the experimental investigation of interspecific incompatibility, crossing over is suppressed altogether in males (Morgan 1914).

Assessment of factors contributing to postzygotic interspecific incompatibility that have been identified to the level of operons confirms the traditional view that speciation arises as a by-product of divergence of all manner of genes (reviewed in Orr et al. 2006; Araripe et al. 2010). While the homeobox gene Ods induces sterility in male hybrids between D. simulans and D. mauritiana (Ting et al. 1998), the oncogene Xmrk contributes to tumor formation in backcross Xiphophorus hybrids of both sexes (Schartl 2008), suggesting that sex-specific incompatibility is common but not universal.

Many of the iconic traits associated with intrinsic postzygotic isolation (Coyne and Orr 2004) affect reproduction, often showing sex-limited expression or different expression in male and female hybrids. Haldane’s (1922) rule holds in a number of animals, including Drosophila, in which hybrid males tend to suffer much more severe postzygotic incompatibility than do hybrid females (Coyne and Orr 2004, Chap. 8). Direct experiments have demonstrated that introgression of chromosomal segments from D. mauritiana into a D. simulans background (True et al. 1996; Tao et al. 2003) or into a D. sechellia background (Masly and Presgraves 2007) induces male sterility at rates severalfold higher than those of female sterility or inviability in both sexes.

Numerous studies have described pervasive sex specificity in gene regulation and expression (Michalak and Noor 2003; Ranz et al. 2003; Civetta and Singh 2006). Table 1 of Ranz et al. (2003) indicates that of the 4776 coding sequences surveyed, >61% showed sex-biased expression in D. melanogaster. Further, they found that genes expressed at higher levels in males showed significantly greater divergence in expression levels between D. melanogaster and D. simulans.

Together with Haldane’s (1922) rule, the disproportionately large effect of the X chromosome constitutes a major rule of speciation (Coyne and Orr 1989). Experiments introgressing small segments between Drosophila genomes indicate that a higher proportion of (hemizygous) introgressions on the X chromosome induce hybrid male sterility than do homozygous autosomal introgressions (True et al. 1996; Tao et al. 2003; Masly and Presgraves 2007). A number of workers have provided discriminating assessments of leading proposals for evolutionary mechanisms that could contribute to the large-X effect (True et al. 1996; Tao et al. 2003; Coyne and Orr 2004; Presgraves 2008). Whether this major trend reflects faster fixation of advantageous variants on hemizygous X chromosomes than on autosomes (Charlesworth et al. 1987; Kirkpatrick and Hall 2004), accelerated divergence of genes affecting sex or reproduction (Civetta and Singh 1998), segregation distortion of sex chromosomes (Tao et al. 2001), or other processes, the large-X effect itself suggests that a substantial proportion of factors contributing to interspecific incompatibility may generate locus-specific barriers to neutral introgression of the kind studied here.

Local adaptation within structured populations of conspecifics

Incompatibility selection may arise not only as a consequence of interspecific hybridization, but also through divergence due to local adaptation of subpopulations of the same species. Table 1 indicates that autosomal incompatibility factors reduce introgression of mitochondrial markers by a factor of σ_f/(2 − σ_f) and of Y-linked markers by a factor of σ_m/(2 − σ_m). This finding suggests that sex-specific differences in expression of locally adapted alleles might contribute to differences in divergence at mitochondrial and Y-linked markers (e.g., Seielstad et al. 1998; Oota et al. 2001; Ségurel et al. 2008), even if the propensity to migrate and mating success of migrants are independent of sex.

Polymorphisms for incompatibility factors within demes might be expected under incompatibility derived from local adaptation within species. In a separate work, we explore the effects of such characteristics on rates of introgression of neutral markers throughout the genome (Fusco and Uyenoyama 2011).

Appendix

Appendix A: Relative Reproductive Rate

Because C, describing genetic transmission and selection (Equation 2), is nonnegative, its spectral radius λ corresponds to a nonnegative characteristic value with modulus exceeded by no other eigenvalue and the eigenvector associated with λ is nonnegative (Gantmacher 1959, Chap. XIII, section 3). It has a Schur decomposition of the form

$$\mathbf{C}=\mathbf{QU}{\mathbf{Q}}^{-1},$$

for U a triangular matrix with the eigenvalues of the transformation along the diagonal (see, for example, Golub and Van Loan 1996). For convenience, we choose Q such that the eigenvalues appear along the diagonal in order of their moduli, with λ the first element. For t sufficiently large, λ^t dominates

$${\mathbf{C}}^t=\mathbf{Q}{\mathbf{U}}^t{\mathbf{Q}}^{-1},$$

implying

$$\omega =\frac{{\mathbf{v}}_{\mathbf{m}}{\mathbf{q}}_0}{{\mathbf{v}}_{\mathbf{r}}{\mathbf{q}}_0}$$

(compare Equation 4), for q₀ the column or the sum of the columns of Q that correspond to λ.

Appendix B: Single Autosomal Incompatibility Factor With an Autosomal Marker

To clarify the connection to earlier work, we address the case of an autosomal marker gene linked to a single autosomal incompatibility locus, for which a marker allele can reside on 4 = 2² possible backgrounds.

Beginning with the distribution of backgrounds at the point of formation of the hybrid or resident offspring (v_m or v_r in Equation 4), selection first reduces the frequency of carriers of the foreign incompatibility factor, with female carriers surviving and reproducing at rate σ_f and males at rate σ_m relative to individuals bearing no foreign incompatibility allele. Further, we scale the contributions of males by the Fisherian male reproductive value f/(1 − f). The selection matrix corresponds to

$$\mathbf{S}=\left(\begin{array}{cccc}{\sigma }_{\text{f}}& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& {\sigma }_{\text{m}}\frac{f}{1-f}& 0\\ 0& 0& 0& \frac{f}{1-f}\end{array}\right),$$ (B1)

in which the ordering of the elements corresponds to females bearing background 1 and 0 at the incompatibility locus and males bearing these backgrounds. Carriers of the focal marker gene of either sex transmit it to female and male offspring at rate $\frac{1}{2}$,

$$\frac{1}{2}(f,1-f),$$ (B2)

and transmission at the incompatibility locus given transmission of the marker gene is represented by

$$\mathbf{F}=\left(\begin{array}{cc}1-r_{\text{f}}& r_{\text{f}}\\ 0& 1\\ 1-r_{\text{m}}& r_{\text{m}}\\ 0& 1\end{array}\right),$$ (B3)

in which (1 − r_f) represents the probability that a female bearing the foreign incompatibility factor transmits it together with the focal marker gene and (1 − r_m) the analogous quantity for male carriers. Joint transmission at the marker and incompatibility loci follows

$$\mathbf{T}=\frac{1}{2}(f,1-f)\otimes \mathbf{F},$$ (B4) (B4)

for ⊗ the Kronecker product.

In the absence of sex specificity in rates of crossing over (r_f = r_m = r) and in expression of incompatibility (σ_f = σ_m = σ), the transition matrix corresponds to

$$\begin{array}{l}\mathbf{C}=\mathbf{S}\mathbf{T}=\left[\left(\begin{array}{cc}1& 0\\ 0& \frac{f}{1-f}\end{array}\right)\otimes \left(\begin{array}{cc}\sigma & 0\\ 0& 1\end{array}\right)\right]\left[\frac{1}{2}(f,1-f)\otimes \left(\begin{array}{c}1\\ 1\end{array}\right)\otimes \left(\begin{array}{cc}1-r& r\\ 0& 1\end{array}\right)\right]\\ =\left(\begin{array}{cc}1& 0\\ 0& \frac{f}{1-f}\end{array}\right)\left[\frac{1}{2}(f,1-f)\otimes \left(\begin{array}{c}1\\ 1\end{array}\right)\right]\otimes \left(\begin{array}{cc}\sigma (1-r)& \sigma r\\ 0& 1\end{array}\right).\end{array}$$ (B5)

The rightmost matrix, representing incompatibility selection and the conditional transmission of the incompatibility factor, has a dominant eigenvalue of unity, the right eigenvector corresponding to which is

$${\left(\frac{\sigma r}{1-\sigma (1-r)},\hspace{0.17em}1\right)}^{\prime }.$$

The remaining matrix product, representing scaling of male contributions and transmission of the focal marker gene, has dominant eigenvalue f, with right eigenvector

$${\left(1,\hspace{0.17em}\frac{f}{1-f}\right)}^{\prime }.$$

As the Kronecker product of these matrices, C has dominant eigenvalue f (the product of the eigenvalues of the matrices) with right eigenvector

$$\mathbf{q}={\left(1,\hspace{0.17em}\frac{f}{1-f}\right)}^{\prime }\otimes {\left(\frac{\sigma r}{1-\sigma (1-r)},\hspace{0.17em}1\right)}^{\prime }.$$

Relative reproductive rate (Equation 4) corresponds to

$$\omega =\frac{(f,\hspace{0.17em}0,\hspace{0.17em}1-f,\hspace{0.17em}0)\mathbf{q}}{(0,\hspace{0.17em}f,\hspace{0.17em}0,\hspace{0.17em}1-f)\mathbf{q}}=\frac{\sigma r}{1-\sigma (1-r)}.$$ (B6) (B6)

This expression, which has been derived numerous times (e.g., Equation A3 in Navarro and Barton 2003), corresponds to the “gene flow factor” of Bengtsson (1985) and “barrier strength” of Barton and Bengtsson (1986).

Under sex specificity in selection (Equation B1) or transmission (Equation B3), the relative reproductive rates of female and male carriers correspond to

$$\begin{array}{c}{\eta }_{\text{f}}=\frac{{\sigma }_{\text{f}}[2r_{\text{f}}-{\sigma }_{\text{m}}(r_{\text{f}}-r_{\text{m}})]}{2-{\sigma }_{\text{f}}(1-r_{\text{f}})-{\sigma }_{\text{m}}(1-r_{\text{m}})}\\ {\eta }_{\text{m}}=\frac{{\sigma }_{\text{m}}[2r_{\text{m}}+{\sigma }_{\text{f}}(r_{\text{f}}-r_{\text{m}})]}{2-{\sigma }_{\text{f}}(1-r_{\text{f}})-{\sigma }_{\text{m}}(1-r_{\text{m}})},\end{array}$$

implying a relative reproductive rate at the marker locus of

$$\omega =\frac{{\eta }_{\text{f}}+{\eta }_{\text{m}}}{2}=\frac{\overline{\sigma }\hspace{0.17em}\overline{r}}{1-\overline{\sigma }(1-\overline{r})},$$ (B7) (B7)

for

$$\begin{array}{c}\overline{\sigma }=\frac{{\sigma }_{\text{f}}+{\sigma }_{\text{m}}}{2}\\ \overline{r}=\frac{{\sigma }_{\text{f}}{r}_{\text{f}}+{\sigma }_{\text{m}}{r}_{\text{m}}}{{\sigma }_{\text{f}}+{\sigma }_{\text{m}}}\end{array}$$ (B8)

(compare Equation B6).

In general, sex of the initial migrant and the incompatibility factor show epistasis with respect to the long-term contribution of the focal marker gene to future generations (compare Equation 8):

$${\eta }_{\text{f}}-{\eta }_{\text{m}}=\frac{2[{\sigma }_{\text{f}}{r}_{\text{f}}(1-{\sigma }_{\text{m}})-{\sigma }_{\text{m}}{r}_{\text{m}}(1-{\sigma }_{\text{f}})]}{2-{\sigma }_{\text{f}}(1-r_{\text{f}})-{\sigma }_{\text{m}}(1-r_{\text{m}})}.$$ (B9) (B9)

No epistasis (η_f = η_m) arises in the absence of sex specificity either in expression of incompatibility (σ_f = σ_m) or in recombination (r_f = r_m). For a given total magnitude of selection (σ_f + σ_m), (η_f − η_m) increases with the excess viability or fertility of female over male carriers (σ_f – σ_m). Similarly, for a given total magnitude of recombination (r_f + r_m), (η_f – η_m) increases with the excess crossing over in female over male carriers (r_f – r_m).

Appendix C: Validation of the Neutral Approximation

Among our main theses is that the evolutionary process at neutral marker loci in a genome containing incompatibility factors is well approximated by a purely neutral process with a forward migration rate equal to our backward migration rate (Equation 1). This section presents confirmation of this proposal, on the basis of results of numerical simulations generated by SFS CODE (Hernandez 2008), modified to track migration events along lineages at a neutral marker locus.

Our neutral approximation holds that the number of migration events along a lineage follows a Poisson distribution with the parameter equal to the product of the number of generations observed and the per-generation backward migration rate (Equation 1). This construction implies that the waiting time between migration events along a lineage has an exponential distribution with the parameter equal to the backward migration rate. We assumed multiplicative effects of foreign incompatibility alleles, whether segregating at the same locus or at different loci.

We conducted forward simulations over t = 50,000 generations, specifying a two-deme model with equal population sizes (N₁ = N₂ = 1000 genes or 500 diploid individuals) and symmetric forward migration rates (N₁m₁₂ = N₂m₂₁ = 0.1). We assumed that the foreign incompatibility allele at each of two autosomal incompatibility loci reduces the viability of its carrier by a factor of σ = 0.65 and that migrants compete for mates on an equal basis with residents. In the absence of linkage among any of the two incompatibility loci and an autosomal marker locus, these assumptions imply a relative reproductive rate (Equation 4) of ω = 0.4815 and a genealogical migration rate (Equation 1) of g = 4.8148 × 10⁻⁵ at the neutral marker. A total of 36,233 migration events over 15,000 independent replicates showed an excellent fit (χ² = 3.946, 9 d.f.) to expectations under a Poisson distribution with parameter gt = 2.4074.

Because relative reproductive rate (Equation 3) represents a limit for large numbers of generations and negligible frequencies of foreign incompatibility alleles, one might expect discrepancies to arise in cases with forward migration rates sufficiently high to permit the migration of an individual carrying a foreign incompatibility allele back into the other species. To explore the limits of our model, we repeated the simulation experiment under forward migration rates an order of magnitude higher (N₁m₁₂ = N₂m₂₁ = 1.0). We found that 7.5% of migration events traced backward along a lineage involved backgrounds that differed from the pure resident background, compared to 0.087% for the lower forward migration rate. The distribution of the number of migration events along a random lineage departs significantly from a Poisson distribution (χ² = 90.4898, 32 d.f.): the observed mean (24.451) exceeds the expectation (b_it = 24.074) and the kurtosis value indicates excess mass in the tails. To provide a quantitative summary, we fit the observations to a Neyman’s type A distribution, a compound distribution that assumes that the Poisson parameter is itself a Poisson-distributed random variable,

$$\frac{\lambda }{\varphi }\sim \mathrm{Poisson}(\mu ),$$

for ϕ an index of clumping (see Johnson and Kotz 1969, Chap. 9). The observations show an excellent fit (χ² = 19.898, 24 d.f.) to a Neyman’s type A distribution with mean set equal to the observed mean and a least-squares estimate of the clumping parameter ϕ of 0.0141, obtained by minimizing the squared deviation between the observed variance up to the ninth moment and their expectations, using the probability generating function given in Johnson and Kotz (1969).

Appendix D: X-Linkage

We address the case of X-linkage of both the marker locus and a single incompatibility locus in an organism exhibiting X–Y sex determination with no crossing over on the X chromosome in hemizygous males.

As in the autosomal case, female carriers transmit the focal marker gene symmetrically to female and male offspring:

$$\frac{1}{2}(f,1-f)\otimes \left(\begin{array}{cc}1-r_{\text{f}}& r_{\text{f}}\\ 0& 1\end{array}\right).$$

In contrast, male carriers transmit the marker gene to all daughters, without recombination, and to no sons, with the last two rows of T corresponding to

$$\left(\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\end{array}\right)$$

(compare Equation B4).

For a female migrant, the relative reproductive rate (Equation 4) becomes

$${\text{ω}}_{\text{X}}^{\text{X,f}}=\frac{(f,0,1-f,0)\mathbf{q}}{(0,f,0,1-f)\mathbf{q}}=\frac{{\text{η}}_{\text{f}}+{\text{η}}_{\text{m}}}{2}=\frac{2{\sigma }_{\text{f}}{r}_{\text{f}}(1+{\sigma }_{\text{m}})}{2-{\sigma }_{\text{f}}(1+{\sigma }_{\text{m}})(1-r_{\text{f}})},$$

in which

$$\begin{array}{c}{\text{η}}_{\text{f}}=\frac{2{\sigma }_{\text{f}}{r}_{\text{f}}}{2-{\sigma }_{\text{f}}(1+{\sigma }_{\text{m}})(1-r_{\text{f}})}\\ {\text{η}}_{\text{m}}=\frac{2{\sigma }_{\text{f}}{\sigma }_{\text{m}}{r}_{\text{f}}}{2-{\sigma }_{\text{f}}(1+{\sigma }_{\text{m}})(1-r_{\text{f}})}.\end{array}$$

These expressions imply epistasis (Equation 8) between sex and the X-linked incompatibility locus proportional to

$${\text{η}}_{\text{f}}-{\text{η}}_{\text{m}}=\frac{2{\sigma }_{\text{f}}{r}_{\text{f}}(1-{\sigma }_{\text{m}})}{2-{\sigma }_{\text{f}}(1+{\sigma }_{\text{m}})(1-r_{\text{f}})}$$

(compare Equation B9). This expression indicates a positive interaction between femaleness and the foreign incompatibility factor under incomplete linkage (r_f > 0), regardless of whether male or female carriers suffer greater effects of incompatibility [sign of (σ_f − σ_m)]. This association may reflect higher recombination rates in females (r_f > r_m = 0).

For a male migrant, only female descendants receive the focal marker allele, implying a relative reproductive rate of

$${\text{ω}}_{\text{X}}^{\text{X,m}}=\frac{(f,0,0,0)\mathbf{q}}{(0,f,0,0)\mathbf{q}}=\frac{2{\sigma }_{\text{f}}{r}_{\text{f}}}{2-{\sigma }_{\text{f}}(1+{\sigma }_{\text{m}})(1-r_{\text{f}})}.$$

Appendix E: Epistasis Among Incompatibility Factors

Here we describe a measure of epistasis among incompatibility factors (compare Bennett 1954), applied to the relative reproductive rate (Equation 4) for an arbitrary number of incompatibility factors.

To establish Equation 5, we expand

$$\begin{array}{l}{e}_{{\Omega }_{[k]}}=E[{\displaystyle \prod _{i\in {\Omega }_{[k]}}(A_i-{\omega }_i)}]\\ ={\displaystyle \sum _{j=0}^k{(-1)}^{k-j}}{\displaystyle \sum _{{\Omega }_{[j]}}E}[{\displaystyle \prod _{i\in {\Omega }_{[j]}}{A}_i}]{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}\\ ={\displaystyle \sum _{j=1}^k{(-1)}^{k-j}}{\displaystyle \sum _{{\Omega }_{[j]}}\left(E[{\displaystyle \prod _{i\in {\Omega }_{[j]}}{A}_i}]-{\displaystyle \prod _{i\in {\Omega }_{[j]}}{\omega }_i}\right)}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}+{\displaystyle \prod _{b\in {\Omega }_{[k]}}{\omega }_b}{\displaystyle \sum _{j=0}^k\left(\begin{array}{c}k\\ j\end{array}\right)}{(-1)}^{k-j}\\ ={\displaystyle \sum _{j=2}^k{(-1)}^{k-j}}{\displaystyle \sum _{{\Omega }_{[j]}}{\delta }_{{\Omega }_{[j]}}}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b},\end{array}$$ (E1)

for Ω_[k] (k ≥ 2) a set of k indexes representing k incompatibility loci, Ω_[j] a set of j indexes in Ω_[k] (j ≤ k), Ω_[k]\Ω_[j] denoting the set of indexes in Ω_[k] but not in Ω_[j], and ${\delta }_{{\Omega }_{[j]}}$ representing the departure of relative reproductive rate from multiplicativity (Equation 6).

For relative reproductive rate corresponding to Equation 7, we address the relationship between the overall departure from multiplicativity (Equation 6) and the sex-specific measures (Equation 9). Using that η_f,i = ω_i + Δ_i and η_m,i = ω_i − Δ_i for Δ_i = (η_f,i − η_m,i)/2 (Equation 8), we have

$$\begin{array}{c}\frac{1}{2}({\displaystyle \prod _{i\in {\Omega }_{[j]}}{\eta }_{f,i}}+{\displaystyle \prod _{i\in {\Omega }_{[j]}}{\eta }_{m,i}})=\frac{1}{2}[{\displaystyle \prod _{i\in {\Omega }_{[j]}}(}{\omega }_i+{\Delta }_i)+{\displaystyle \prod _{i\in {\Omega }_{[j]}}(}{\omega }_i-{\Delta }_i)]\\ ={\displaystyle \prod _{i\in {\Omega }_{[j]}}{\omega }_i}+{\xi }_{{\Omega }_{[j]}},\end{array}$$ (E2)

for ${\xi }_{{\Omega }_{[j]}}$ representing terms of the form Δ_i. Note that

$${\xi }_{{\Omega }_{[j]}}={\delta }_{{\Omega }_{[j]}}-\frac{{\delta }_{\text{f},{\Omega }_{[j]}}+{\delta }_{\text{m},{\Omega }_{[j]}}}{2}.$$

In the expansion of Equation E2, terms involving an odd number of the Δ_i’s cancel out, while all the terms with an even number appear twice, implying

$${\xi }_{{\Omega }_{[k]}}={\displaystyle \sum _{i=1}^{\lfloor k/2\rfloor }{\displaystyle \sum _{{\Omega }_{[2i]}\subset {\Omega }_{[k]}}\left({\displaystyle \prod _{a\in {\Omega }_{[2i]}}{\Delta }_a}{\displaystyle \prod _{c\in {\Omega }_{[k]}\backslash {\Omega }_{[2i]}}{\omega }_c}\right)}},$$

for Ω_[2i] representing all subsets of Ω_[j] that contain 2i elements. We rewrite Equation E1 as

$$e_{{\Omega }_{[k]}}={\displaystyle \sum _{j=2}^k}{(-1)}^{k-j}{\displaystyle \sum _{{\Omega }_{[j]}}\left(\frac{{\delta }_{\text{f},{\Omega }_{[j]}}+{\delta }_{\text{m},{\Omega }_{[j]}}}{2}+{\xi }_{{\Omega }_{[j]}}\right)}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}.$$ (E3)

We find that

$${\displaystyle \sum _{j=2}^k{(-1)}^{k-j}}{\displaystyle \sum _{{\Omega }_{[j]}}{\xi }_{{\Omega }_{[j]}}}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}=\{\begin{array}{ll}0\hfill & \text{for }k\text{ odd}\hfill \\ {\displaystyle {\prod }_{i=1}^k{\Delta }_i}\hfill & \text{for }k\text{ even}.\hfill \end{array}$$

For k odd, this sum corresponds to

$$\begin{array}{c}{\displaystyle \sum _{j=2}^k}{(-1)}^{k-j}{\displaystyle \sum _{\Omega [j]}{\displaystyle \sum _{i=1}^{\lfloor j/2\rfloor }{\displaystyle \sum _{{\Omega }_{[2i]}\subset {\Omega }_{[j]}}\left({\displaystyle \prod _{a\in {\Omega }_{[2i]}}{\Delta }_a}{\displaystyle \prod _{c\in {\Omega }_{[j]}\backslash {\Omega }_{[2i]}}{\omega }_c}\right)}}}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}\\ ={\displaystyle \sum _{j=2}^k}{(-1)}^{k-j}{\displaystyle \sum _{i=1}^{\lfloor j/2\rfloor }\left(\begin{array}{c}k-2i\\ j-2i\end{array}\right)}{\displaystyle \sum _{{\Omega }_{[2i]}}{\displaystyle \prod _{a\in {\Omega }_{[2i]}}{\Delta }_a}}{\displaystyle \prod _{b\in {\Omega }_{[k]}\backslash {\Omega }_{[2i]}}{\omega }_b}\\ ={\displaystyle \sum _{i=1}^{\lfloor k/2\rfloor }{\displaystyle \sum _{{\Omega }_{[2i]}}{\displaystyle \prod _{a\in {\Omega }_{[2i]}}{\Delta }_a}}}{\displaystyle \prod _{b\in {\Omega }_{[k]}\backslash {\Omega }_{[2i]}}{\omega }_b}{\displaystyle \sum _{j=2i}^k\left(\begin{array}{c}k-2i\\ j-2i\end{array}\right)}{(-1)}^{k-j}\\ =0,\end{array}$$

and for k even,

$${\displaystyle \prod _{i=1}^k{\Delta }_i}+{\displaystyle \sum _{j=2}^{k-1}}{(-1)}^{k-j}{\displaystyle \sum _{{\Omega }_{[j]}\subset {\Omega }_{[k]}}{\xi }_{{\Omega }_{[j]}}}{\displaystyle \prod _{b\in ({\Omega }_{[k]}\backslash {\Omega }_{[j]})}{\omega }_b}={\displaystyle \prod _{i=1}^k{\Delta }_i}.$$

Substitution of these expressions into Equation E3 produces Equation 10.

Appendix F: Epistasis Between an X-Linked and an Autosomal Factor

X-linked marker (male migrant)

Because only female offspring of a male migrant receive the X-linked marker,

$${\text{ω}}_{\text{AX}}^{\text{X,m}}={\text{η}}_{\text{f,AX}}^{\text{X}},$$

with overall epistasis equal to the female-specific epistasis,

$$e_{\text{AX}}^{\text{X,m}}={\text{η}}_{\text{f,AX}}^{\text{X}}-{\text{η}}_{\text{f,A}}^{\text{X}}{\text{η}}_{\text{f,X}}^{\text{X}}={\text{δ}}_{\text{f,AX}}^{\text{X}},$$

for ${\text{δ}}_{\text{f,AX}}^{\text{X}}$ given in Equation 21a. As in the case of the female migrant, the sign of epistasis depends on ${\Delta }_{\text{A}}^{\text{X}}$ (Equation 19).

Autosomal marker

For a female migrant, epistasis (Equation 10) between the incompatibility loci corresponds to

$$e_{\text{A,X}}^{\text{A}}={\text{ω}}_{\text{AX}}^{\text{A}}-{\text{ω}}_{\text{A}}^{\text{A}}{\text{ω}}_{\text{X}}^{\text{A}}=\frac{{\text{δ}}_{\text{f,AX}}^{\text{X}}+{\text{δ}}_{\text{m,AX}}^{\text{X}}}{2}+{\Delta }_{\text{A}}^{\text{A}}{\Delta }_{\text{X}}^{\text{A}},$$ (F)

for ${\Delta }_{\text{A}}^{\text{A}}$ given by Equation 26 and

$${\Delta }_{\text{X}}^{\text{A}}=\frac{{\text{η}}_{\text{f,X}}^{\text{A}}-{\text{η}}_{\text{m,X}}^{\text{A}}}{2}=\frac{2({\text{σ}}_{\text{f,X}}-{\text{σ}}_{\text{m,X}})}{8-{\text{σ}}_{\text{f,X}}(2+{\text{σ}}_{\text{m,X}})}$$ (F2)

(Table 1). Within-sex interactions correspond to

$${\text{δ}}_{\text{f,AX}}^{\text{A}}={\text{η}}_{\text{f,AX}}^{\text{A}}-{\text{η}}_{\text{f,A}}^{\text{A}}{\text{η}}_{\text{f,X}}^{\text{A}}=\frac{2{\sigma }_{\text{f,A}}{\sigma }_{\text{f,X}}(1-r_{\text{f,A}})D_{\text{f}}{\Delta }_{\text{A}}^{\text{A}}}{[8-{\sigma }_{\text{f,X}}(2+{\sigma }_{\text{m,X}})]\Gamma }$$ (F3a)

$${\text{δ}}_{\text{m,AX}}^{\text{A}}={\text{η}}_{\text{m,AX}}^{\text{A}}-{\text{η}}_{\text{m,A}}^{\text{A}}{\text{η}}_{\text{m,X}}^{\text{A}}=\frac{2{\sigma }_{\text{m,A}}{\sigma }_{\text{m,X}}(1-r_{\text{m,A}})D_{\text{m}}{\Delta }_{\text{A}}^{\text{A}}}{[8-{\sigma }_{\text{f,X}}(2+{\sigma }_{\text{m,X}})]\Gamma },$$ (F3b) (F3b)

in which

$$\begin{array}{c}{D}_{\text{f}}\text{\hspace{0.17em}=\hspace{0.17em}4(}{\sigma }_{\text{f,X}}-{\sigma }_{\text{m,X}}\text{) }-{\sigma }_{\text{m,A}}{\sigma }_{\text{m,X}}\text{(1 }-r_{\text{m,A}}\text{)[4 }-{\sigma }_{\text{f,X}}\text{(3 + }{\sigma }_{\text{m,X}}\text{)]}\\ D_{\text{m}}\text{\hspace{0.17em}=\hspace{0.17em}2}{\sigma }_{\text{f,A}}{\sigma }_{\text{f,X}}\left(\text{1}-r_{\text{f,A}}\right)\left({\sigma }_{\text{f,A}}-{\sigma }_{\text{m,X}}\right)-\left[\text{4 }-{\sigma }_{\text{f,X}}\left(\text{3 + }{\sigma }_{\text{m,X}}\right)\right]\left[\text{4 }-{\sigma }_{\text{f,X}}{\sigma }_{\text{f,A}}\left(\text{1 }-r_{\text{f,A}}\right)\right]\\ \Gamma =8-{\sigma }_{\text{f,A}}{\sigma }_{\text{f,X}}\left(\text{1}-r_{\text{f,A}}\right)\left[2+{\sigma }_{\text{m,A}}{\sigma }_{\text{m,X}}\left(\text{1}-r_{\text{m,A}}\right)\right],\end{array}$$ (F4) (F4)

giving an overall two-way epistasis between the incompatibility factors of Equation 23. Comparison of Equations 17 and F3 suggests that D_f and D_m assume the role of Δ_X, an indicator of the nature of the interaction between sex and the X-linked incompatibility factor.

As indicated in the text following Equation 24, D_m is always nonpositive and zero only if the X-linked factor does not contribute to incompatibility selection (σ_f,X = σ_m,X = 1). In contrast, D_f is positive for

$${\text{σ}}_{\text{f,X}}>{\text{σ}}_{\text{m,X}}\left\{\text{1}\hspace{0.17em}\text{+}\hspace{0.17em}{\text{σ}}_{\text{m,A}}\left(1-r_{\text{m,A}}\right)\left[1-\frac{{\text{σ}}_{\text{f,X}}\left(3+{\text{σ}}_{\text{m,X}}\right)}{4}\right]\right\}\ge {\text{σ}}_{\text{m,X}}.$$ (F5) (F5)

Sufficient conditions for positive epistasis $e_{\text{AX}}^{\text{X}}$ (higher introgression) include that both factors cause greater impairment to female carriers (σ_f,A < σ_m,A and σ_f,X < σ_m,X) or that both cause sufficiently greater impairment to males, with positive Δ_A and Equation F5 satisfied. In the absence of sex specificity in expression of incompatibility due to the X-linked factor (σ_f,X = σ_m,X), D_f is nonpositive, implying either no epistasis $(e_{\text{AX}}^{\text{A}}=0)$ or

$$e_{\text{AX}}^{\text{A}}\propto -{\Delta }_{\text{A}}=-\left(r_{\text{f,A}}-r_{\text{m,A}}\right),$$

indicating negative epistasis (less introgression) if the map distance between the autosomal marker and the autosomal factor is greater in females.

For a male migrant, all female offspring and none of the male offspring of the migrant carry the X-linked factor, while offspring of both sexes carry the autosomal factor:

$${\text{ω}}_{\text{AX}}^{\text{A,m}}=\frac{(f,0,0,0,0,1-f,0,0)\mathbf{q}}{(0,0,0,f,0,0,0,1-f)\mathbf{q}}=\frac{{\text{η}}_{\text{f,AX}}^{\text{A}}+{\text{η}}_{\text{m,A}}^{\text{A}}}{2}.$$

Epistasis between the loci with respect to relative reproductive rate is given by

$$e_{\text{AX}}^{\text{A,m}}=\frac{{\text{δ}}_{\text{AX}}^{\text{A}}}{2}+\frac{{\Delta }_{\text{A}}^{\text{A}}\left({\text{η}}_{\text{f,X}}^{\text{A}}-1\right)}{2},$$

with ${\Delta }_{\text{A}}^{\text{A}}$ given by Equation 24, the within-female departure from multiplicativity ${\text{δ}}_{\text{f,AX}}^{\text{A}}$ by Equation F3a, and

$${\text{η}}_{\text{f,X}}^{\text{A}}-1=\frac{-2[4-{\sigma }_{\text{f,X}}(3+{\sigma }_{\text{m,X}})]}{8-{\sigma }_{\text{f,X}}(2+{\sigma }_{\text{m,X}})}.$$

As in the case of a female migrant (Equation 23), epistasis arises only if the autosomal factor is sex specific $({\Delta }_{\text{A}}^{\text{A}}\ne 0)$. Nonzero (η_f,X − 1) implies that the X-linked factor contributes to incompatibility (σ_f,X < 1 or σ_m,X < 1). For a male migrant, the overall value for epistasis between the autosomal and X-linked incompatibility factors is

$$e_{\text{AX}}^{\text{A,m}}=\frac{2D_{\text{m}}{\Delta }_{\text{A}}^{\text{A}}}{[8-{\sigma }_{\text{f,X}}(2+{\sigma }_{\text{m,X}})]\Gamma },$$

for D_m and Γ given in Equation F4. As D_m is negative if the X-linked factor contributes to incompatibility (σ_f,X < 1 or σ_m,X < 1), this expression indicates that the autosomal and X-linked factors show positive epistasis (higher introgression rates than expected under multiplicativity) if the autosomal factor permits greater reproductive rates through male than through female carriers $({\Delta }_{\text{A}}^{\text{A}}<0)$ and negative epistasis if female carriers show higher reproductive rates.