Entropy Based Genetic Association Tests and Gene-Gene Interaction Tests

Abstract

In the past few years, several entropy-based tests have been proposed for testing either single SNP association or gene-gene interaction. These tests are mainly based on Shannon entropy and have higher statistical power when compared to standard χ² tests. In this paper, we extend some of these tests using a more generalized entropy definition, Rényi entropy, where Shannon entropy is a special case of order 1. The order λ (>0) of Rényi entropy weights the events (genotype/haplotype) according to their probabilities (frequencies). Higher λ places more emphasis on higher probability events while smaller λ (close to 0) tends to assign weights more equally. Thus, by properly choosing the λ, one can potentially increase the power of the tests or the p-value level of significance. We conducted simulation as well as real data analyses to assess the impact of the order λ and the performance of these generalized tests. The results showed that for dominant model the order 2 test was more powerful and for multiplicative model the order 1 or 2 had similar power. The analyses indicate that the choice of λ depends on the underlying genetic model and Shannon entropy is not necessarily the most powerful entropy measure for constructing genetic association or interaction tests.

1. Introduction

The strategy of using a single locus to test for association with a particular phenotype has not been as successful as one would expect [Manolio et al. (2009)]. This may be due to different reasons such as the predominance of common variants in the genome-wide platforms, and the synergy between environment and genetic risk factors as well as between different genetic risk factors [Kraft et al. (2007), Thomas (2010)]. However, complex human genetic diseases are typically caused not only by marginal effects of genes or gene-environment interactions, but also by the interactions of multiple genes [Cordell (2009)]. Recently, gene-gene interaction, or epistasis, has been a hot topic in molecular and quantitative genetics.

If the effect at one genetic locus is altered or masked by the effects at another locus, single-locus tests or marginal tests may not be able to detect the association. By allowing for epistatic interactions among potential disease loci, we may succeed in identifying genetic variants that might otherwise remain undetected.

Several statistical techniques have been applied or developed in detecting statistical epistasis or gene-gene interaction [Cordell (2009)]. Among those techniques the most applied ones are logistic regression models and χ²-tests of independence due to easy access in well known statistical packages. However, little attention has been given to the entropy methods. Entropy methods are best known for their application in information theory with the seminal work byKullback and Leibler [Kullback and Leibler (1951)]. Shannon’s entropy is one of the most well known entropy measures, and it is the one that has been applied in single locus and gene-gene interaction analyses [Zhao et al. (2005), Dong et al. (2008), Kang et al. (2008)]. However, Shannon’s entropy is a particular case of a more generalized type of entropy, the Rényi entropy [Rényi (1960)].

The goal of this study is to extend the application of Shannon entropy to Rényi entropy in a single locus association as well as gene-gene interaction. Since entropy measures are nonlinear transformations of the variable distribution, an entropy measure of allele frequencies can amplify the allele difference between groups of interest (e.g. case/control). Furthermore, the extension to Rényi entropy introduces more flexibility in such transformations.

Thus, in this paper, we have proposed several Rényi entropy based tests and compared the performance of the novel tests to some traditional methods. We first introduced a single locus association test under two-group design, then a one-group gene-gene interaction test under linkage equilibrium (LE) assumption. The power of these tests was compared through simulations. We demonstrated that by properly choosing the Rényi entropy order λ, we could increase the power of the association test. We also discussed possible ways to construct a two-group interaction test and how to check whether an interaction effect is due to disease or not under case-control design. All the methods introduced in this paper were applied in analyzing real venous thromboembolism (VTE) case-control data.

Throughout this paper, we use the terminology “statistical gene-gene interaction test” or “statistical epistasis test” for interaction test. The word “entropy” refers to Rényi entropy unless otherwise specified. The simulation data sets were generated by GWAsimulator [Li et al. (2007)] and the analyses were performed by using R functions written by the authors.

2. Methods

2.1. Rényi Entropy

In information theory, entropy is a measure of the uncertainty associated with a random variable. One of the most common entropies is the Shannon entropy introduced by Shannon (1948), which is a special case of a more generalized type of entropy introduced by Rényi (1960).

The so called Rényi entropy is a family of functionals for quantifying the diversity, uncertainty, or randomness of a system. The Rényi entropy of order λ, λ ≥ 0, is defined as

$$H_{\lambda }(X)=\frac{1}{1-\lambda }\text{log}\left(\sum _{i=1}^n{p}_i^{\lambda }\right),$$

where X is a discrete random variable with n values of positive probabilities and ${\sum }_{i=1}^n{p}_i=1.$ Rényi entropy with higher values of λ is more dependent on higher probability events, while lower values of λ weight all possible events more equally.

Some Rényi entropy measures have quite natural interpretations, such as H₀(·) is defined as the logarithm of the number of values that have non-zero probabilities; H₂(·) is often called collision entropy and is the negative logarithm of the likelihood of two independent random variables with the same probability distribution to have the same value; and H_∞(·) is called min-entropy and is a function of the highest probability only.

The most well known Rényi entropy is the one with λ = 1. By applying L’Hopital’s rule, one can show that the formula of Rényi entropy reduces to the form of Shannon entropy:

$$H_1(X)=-\sum _{i=1}^n{p}_i\text{log}{p}_i.$$

2.2. Association Tests

In this section, we derive a model free association test based on Rényi entropy. Under a two-group design, such as a case-control design, one may test whether a set of SNPs or a single SNP is associated with the disease of interest by comparing the entropy of the first group (case group) to the second group (control group).

Let us assume a locus with k genotypes G₁, G₂, . . ., G_k. For the disease population, let $P_D=[p_1^D,\dots ,p_k^D]$ be the distribution of the genotypes, where $p_i^D$ is the probability of a case having genotype G_i at a locus of interest. Similarly let us denote the genotype distribution of normal population by $P_N=[p_1^N,\dots ,p_k^N],$ where $p_i^N$ is the probability of a control having genotype G_i at a locus of interest. Under null hypothesis of no association, P_D and P_N are identical.

For a given observed case-control data, let P̂_D and P̂_N be the estimated distribution of genotypes of cases and controls, respectively. The Rényi entropy of order λ is calculated as

$$H_{\lambda }({\widehat{P}}_D)=\frac{1}{1-\lambda }\text{log}\left(\sum _{i=1}^k{({\widehat{p}}_i^D)}^{\lambda }\right).$$ (1)

Similarly, one calculates H_λ (P̂_N). The difference between the two entropy statistics

$$S_{\lambda }^A=H_{\lambda }({\widehat{P}}_D)-H_{\lambda }({\widehat{P}}_N)$$ (2)

is then considered the association test statistic with superscript A standing for ”association”.

In the appendix, we show that the entropy statistic (2) follows asymptotically a normal distribution. Therefore, a test of difference between the two groups can be constructed, where a significant difference indicates a possible association between the SNP and the disease.

For multiple loci, it is worth noting that this test may include or exclude the effect of interaction depending on the way P_D and P_N are estimated. To allow for interaction, the genotype distributions should be jointly estimated. To test for marginal effects only, one could estimate P̂_D and P̂_N as the product of the marginal probability estimates.

When λ = 1, the Rényi entropy reduces to the Shannon entropy, i.e.,

$$\underset{\lambda \to 1}{\text{lim}}{H}_{\lambda }({\widehat{P}}_D)=-\sum _{i=1}^k({\widehat{p}}_i^D)\text{log}\hspace{0.17em}({\widehat{p}}_i^D).$$ (3)

Thus the statistic of the association test $S_1^A$ is a summation of terms of the form p_i log(p_i) − q_i log(q_i), where i is the index over all genotypes with p and q representing the corresponding distributions of the case group and the control group. By studying each component of the statistics, one can tell which genotype has the most impact on the statistics, and consequently, it can help us choose the appropriate λ for the association test. For the purpose of achieving more power to observe a difference between genotype frequency in cases and controls, the choice of λ depends on where the main difference lies, whether on the higher or the lower genotype frequencies. One should favor a larger λ value for the former and a smaller λ value for the latter.

The R codes of the entropy test are available upon request. We tested the computing time of the association test using a PC processor Intel(R) Core(TM) 2 Duo CPU P7750 @2.26GHz. The test data set contains 1000 cases and 1000 controls. It took about 0.4 sec to get the association test results of one SNP with 20 different λ values. Since most of the computational time is contributed to the calculation of frequency of genotypes, we recommend to apply the association test using multiple values of lambda simultaneously.

2.3. Interaction Test

2.3.1. One-group analysis (case-only or control-only)

In this section we describe the Rényi entropy based interaction test of two loci, L₁ and L₂, in detail. A generalization of the test for three or more loci is straight forward. Assume the two loci are in linkage equilibrium with the first locus having two alleles, A and a, and the second locus two alleles, B and b. Let $p_0^{L_1},p_1^{L_1},p_2^{L_1}$ denote the probabilities of three genotypes aa, aA and AA, respectively, at the first locus. Similarly, at the second locus, let $p_0^{L_2},p_1^{L_2},p_2^{L_2}$ denote the corresponding probabilities of three genotypes bb, bB and BB. Then the joint probability of the nine genotype combinations is represented by p_ij, i, j = 0, 1, 2, with i and j being the index of the genotypes at the first and second locus, respectively.

Define $q_{ij}=p_i^{L_1}{p}_j^{L_2}$ as the product of the two marginal probabilities. Under the null hypothesis of no interaction effect, the two loci are independent and the entropy calculated based on the true joint probability p_ij and on the induced q_ij should be identical.

We first estimate the joint and the marginal probabilities as the observed frequencies p̂_ij, ${\widehat{p}}_i^{L_1}$ and ${\widehat{p}}_j^{L_2}$. The induced joint probability is then the product of the observed marginal frequencies ${\widehat{q}}_{ij}={\widehat{p}}_i^{L_1}{\widehat{p}}_j^{L_2}$. The entropy (1) can be estimated using either the observed frequencies P̂ = p̂_ij or the induced frequencies Q̂ = q̂_ij. The proposed interaction (epistasis) test statistic, denoted as $S_{\lambda }^E$, is calculated as the entropy difference between the two entropy estimates,

$$S_{\lambda }^E=H_{\lambda }\left(\widehat{Q}\right)-H_{\lambda }\left(\widehat{P}\right)=H_{\lambda }\left({\widehat{P}}_1\right)=H_{\lambda }\left({\widehat{P}}_2\right)-H_{\lambda }\left(\widehat{P}\right),$$ (4)

where ${\widehat{P}}_1={\widehat{p}}_i^{L_1}$ and ${\widehat{P}}_2={\widehat{p}}_j^{L_2}$ are the observed marginal genotype distributions of the first and second locus, respectively. A statistically significant difference means an interaction between the two loci.

For case-only study, in the case where λ = 1 and n is the case-only sample size, the statistic $2n{S}_1^E$ is the interaction test statistic proposed by Kang et al. (2008). The statistics is asymptotically distributed as a χ² with 4 degrees of freedom. For a more general λ, the asymptotic distribution of (4) under null is unknown. Thus simulation methods such as Monte Carlo simulations are needed to determine its distribution and p-values. For a given pair of SNPs, permute the genotypes of one SNP among subjects to break the possible joint structure of the pair. Follow with a calculation of the test statistic $S_{\lambda }^E$ using the permuted data. Generate N permutation samples and for each permuted sample calculate the test to estimate the null distribution of (4).

We tested the computing time of the interaction test using a PC processor Intel(R) Core(TM) 2 Duo CPU P7750 @2.26GHz. The data set contains 1000 samples. The calculation of interaction tests is based on 1000 shuffles and it took about 10.5 sec to get the one-group test results of one pair of SNPs. Note that most of the computational time is attributed to the calculation of frequency of genotypes, thus it makes almost no difference if we test using only one value of lambda or multiple values of λ. The R code is available upon request.

2.3.2. Two-group analysis

A question one may ask is, for a given significant p-value of an interaction test, how does one know if the interaction is truly due to either the disease or to some unknown cause. Under a case-control design, we can apply the one group interaction test to both case and control groups separately. If the interaction effect is not due to the disease, we would expect the case group and control group to behave similarly. The question then becomes how to compare the test results between the two groups.

First, we compared the test statistics of two groups using the ratio of test statistics. Let $S_{\lambda }^E$ (Case) and $S_{\lambda }^E$ (Ctrl) be the corresponding test statistics of the two groups, then $S_{\lambda }^E$ (Case)/ $S_{\lambda }^E$ (Ctrl) should be close to 1 under null. If the ratio of the statistics is significantly different from 1, the case group and control group are not equivalent in terms of interaction, therefore, the difference may be associated with the disease. The null distribution of the ratio statistics can be estimated using the already generated permutation samples of each one-group analysis, thus, the computing time is just the summation of the computing time of two one-group analysis. Our simulation results (data not shown) showed that the power to detect the true difference is weak, especially when the marginal effect is strong. Larger sample size is needed to get reliable test results, however, the exact sample size is not easily determined. It depends on the disease model, the strength of the interaction and the marginal effects.

In the case where a significant p-value for the case group and an insignificant p-value for the control group are observed, a further permutation test can be performed to investigate whether these two groups are truly different in terms of p-value significance. Notice that here we compare the p-values of interaction tests, thus only interaction effect difference is studied. The comparison can be done using a 2-step procedure. In the first step the case-control indicator is shuffled to create new case and control groups and to recalculate the interaction test for these two groups. The second step is to compare the group p-value difference (defined as the p-value of the control group minus the p-value of the case group) of the observed data to the group p-value difference of the shuffled sample. Repeat these two steps n times (n to be determined by the investigators) to obtain the proportion of the shuffled sample group p-value difference exceeding the observed sample group p-value difference, which is the empirical p-value of the permutation test. A significant result of the permutation test indicates the case group has more significant interaction than the control group, which means the interaction is associated with the disease. Since this procedure requires a lot of permutation, this method is computational intensive and may be only feasible to apply to a small set of genes or SNPs. Using a PC processor Intel(R) Core(TM) 2 Duo CPU P7750 @2.26GHz, it takes n × 21 sec to compare the p-values of one pair of SNPs for a date set of 1000 cases and 1000 controls, where n is the number of permutations.

3. Simulation

In this study we performed Monte Carlo simulations to investigate the performance of the entropy-based tests for several λ values. We also compared our results with two other methods, χ²-test for contingency tables and likelihood ratio (LR) test for logistic regression. Data were simulated using GWA simulator Version 2.0 [Li et al. (2007)].

3.1. Simulation 1: Comparison between association tests

We studied the performance of the entropy-based association tests with parameter λ = 0.9,1,2 and compared it to the logistic regression method. LR tests were used to test for the significance of the allele effect in the regression model.

Data were simulated using logistic models [Li et al. (2007)]. Four different marginal effect models were considered: weak dominant, strong dominant, weak multiplicative and strong multiplicative. The dominant marginal effect (threshold marginal) is not affected by the number of copies of risk allele as long as at least one copy is present. The multiplicative marginal assumes the relative risk (compared to the risk with zero copy of risk allele) increases multiplicatively as the number of copies of the risk allele increases. Given a disease locus, let R₁ be the relative risk with 1 copy of risk allele and R₂ be the relative risk with two copies, then dominant marginal satisfies R₁ = R₂ and multiplicative marginal satisfies $R_2=R_1^2$.

Let g_i = 0,1,2 be the number of copies of the the risk allele at SNP i, and define f (g_i) = Pr(affected|g_i) as the penetrance for genotype g_i. Then, the disease models can be described by the following formula:

$$\text{logit}\left[f\left(g_i\right)\right]={\beta }_0+{\beta }_1{I}_{gi=1}+{\beta }_2{I}_{gi=2},$$ (5)

where β_j is the marginal effect coefficient of the disease locus with j copies of risk allele. These parameters are calculated approximately as the natural log of the corresponding relative risk.

For our simulation we fixed the risk allele frequency as 0.15. Relative risk R₁ was chosen to be 1.25 as weak and 1.5 as strong. For each disease model, 1000 data sets were simulated. The coefficients in (5) for each model are shown in the following Table 1:

Table 1:

Parameters for the four disease models: Weak Dominant (WD), Strong Dominant (SD), Weak Multiplicative (WM), Strong Multiplicative (SM)

Model	ß0	ß1	ß2
1: WD	−1.844	0.265	0.265
2: SD	−1.968	0.484	0.484
3: WM	−1.864	0.265	0.542
4: SM	−1.990	0.483	1.017

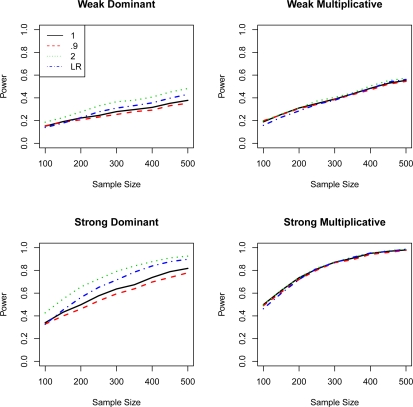
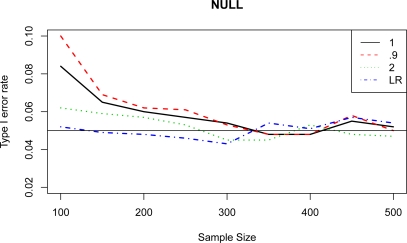
Each simulated data set was analyzed by Rényi entropy association tests with λ values of 0.9, 1, and 2. A logistic regression model assuming additive genetic effect was fitted to each data set. The likelihood ratio test was used to test the association of a single SNP to the disease. For each test, power was calculated as the percentage of having p value less than 0.05 over the 1,000 simulations. The power of the four tests under four disease models was summarized in Figure 1. We also evaluated the false positive (type I error) rates for the LR and entropy-based tests under different sample sizes. We observed that for a sample size less than or equal to 300, the LR test had the lowest type I error rate (below 0.05) followed by the entropy test with λ =2. For a sample size greater than 300, the entropy test with λ = 2.0 had the lowest type I error (Figure 2). Both LR test and entropy test with λ = 2 had good control of type I error with small sample size. All the tests had type I error close to the target 0.05 as sample size increased.

Figure 1:

Power and sample size for the likelihood ratio (LR) test and entropy-based test for λ values of 0.9, 1.0, and 2.0 under different marginal effects.

Figure 2:

Type I error rate of likelihood ratio (LR) test and entropy-based test with λ values of 0.9, 1.0 and 2.0

As shown in Figure 1, for dominant marginal effect models, the entropy-based test with λ = 2 was the most powerful among the four tests, and the power of entropy-based test with λ values of 0.9 and 1 were similar to the power of the LR test. For multiplicative marginal effect models, all four methods look similar. We applied two-tail matched pair t-test (matched by sample size) to compare the curves of each method. There was significant (p < 0.05) difference between entropy tests with different λ. Entropy tests with λ = 2 were significantly different from the LR test for all the models; entropy tests with λ = 1 and 0.9 were significantly different from the LR test for the dominant models.

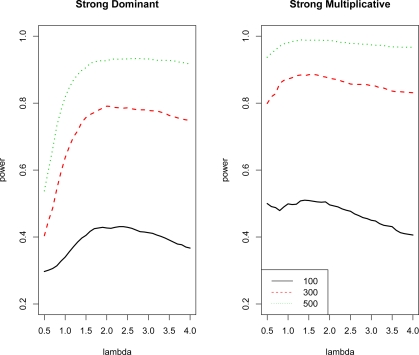
Figure 3 depicts the power of entropy-based test with different λ values for sample sizes 100, 300 and 500 under strong dominant and strong multiplicative marginal effects. The power of the test with λ between 1 and 2 was about the same for multiplicative model, while for dominant model, the power of λ = 1 test had much lower power compared to the λ = 2 test. The curves under multiplicative marginal effect were relatively flat compared to those under dominant marginal effect. The figure illustrates that the multiplicative model was not very sensitive to the choice of λ, while properly chosen λ greatly improved the power to detect the dominant marginal effect.

Figure 3:

Power of the entropy-based test with sample size 100, 300 and 500 for different λ values under strong dominant and multiplicative marginal effects

3.2. Simulation 2: Comparison between Interaction Tests

We studied the performance of the one-group and two group entropy-based interaction tests with parameter λ = 0.9,1,2 and compared the one-group test to the standard χ²-test of association between genotypes at the two loci for a case-only analysis. We considered two disease loci models with three types of marginal effects (no marginal, dominant marginal and multiplicative marginal) and two types of interaction effects (threshold interaction and multiplicative interaction).

The dominant interaction, also called threshold interaction, assumes the same interaction effect for all genotypes with at least one copy of risk allele at both disease loci. The multiplicative interaction increases multiplicatively as the number of copies of disease allele increases. Let r_ij be the relative risk with i copies of risk allele at disease locus 1 and j copies at disease locus 2 (compared to the case with i copies at locus 1 and j copies at locus 2 but without interaction effect). For threshold interaction, r₁₁ = r₁₂ = r₂₁ = r₂₂ holds. For multiplicative interaction, $r_{12}=r_{21}=r_{11}^2$ and $r_{22}=r_{11}^4$.

Let g_i =0,1,2 be the number of copies of the risk allele at a locus/gene/SNP i, (i = 1,2), and f (g₁,g₂) = Pr(affected|g₁,g₂) the penetrance for the genotypes (g₁,g₂). The disease models can then be described by the following formula:

$$\begin{array}{lll}\text{logit}[f(g_1,g_2)]\hfill & =\hfill & {\beta }_0+{\beta }_{11}{I}_{g_1=1}+{\beta }_{12}{I}_{g_1=2}+{\beta }_{21}{I}_{g_2=1}+{\beta }_{22}{I}_{g_2=2}\hfill \\ \hfill & \hfill & +{\gamma }_{11}{I}_{g_1=1,g_2=1}+{\gamma }_{12}{I}_{g_1=1,g_2=2}\hfill \\ \hfill & \hfill & +{\gamma }_{21}{I}_{g_1=2,g_2=1}+{\gamma }_{22}{I}_{g_1=2,g_2=2,}\hfill \end{array}$$ (6)

where the β_ij is the marginal effect coefficient of disease locus i with j copies of risk allele, ∀ i,j, and the γ_ij the interaction effect coefficient with i copies of risk allele at disease locus 1 and j copies of risk allele at disease locus 2. These parameters are calculated approximately as the natural log of the corresponding relative risk.

We simulated 1,000 data sets from each of the disease models specified above. We set the risk allele frequencies of 0.15 for locus 1 and 0.075 for locus 2 respectively, with a relative risk of r₁ = 4. The coefficients in (6) are specified in Table 2.

Table 2:

Coefficients of the six models (-/-): first letter labels the marginal effect and second letter labels the interaction effect. “N” for null, “D” for dominant, “M” for multiplicative.

Model	ß0	ß11	ß12	ß21	ß22	γ11	γ12	γ21	γ22
1: N/D	−1.816	0	0	0	0	1.386	1.386	1.386	1.386
2: D/D	−2.074	0.484	0.484	0.490	0.490	1.386	1.386	1.386	1.386
3: M/D	−2.096	0.483	1.017	0.490	1.037	1.386	1.386	1.386	1.386
4: N/M	−1.775	0	0	0	0	0.693	1.386	1.386	2.773
5: D/M	−2.023	0.484	0.484	0.490	0.490	0.693	1.386	1.386	2.773
6: M/M	−2.045	0.483	1.017	0.490	1.037	0.693	1.386	1.386	2.773

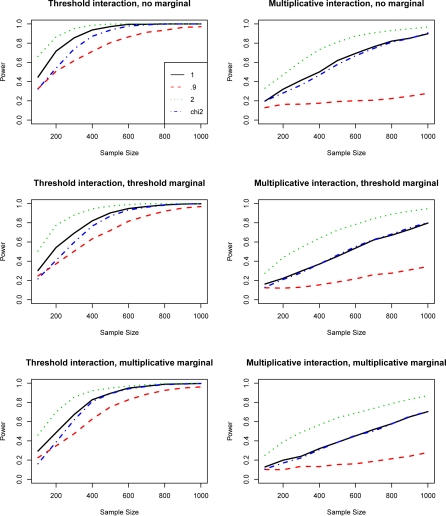
Under one group design (for instance, case-only), we evaluated the performance of the entropy-based test of three λ values, 0.9, 1.0, and 2.0 with the χ² test by comparing their powers. The simulation results (refer to Figure 4) showed that for all six models, the entropy tests $S_{\lambda }^E$ with λ ≥ 1 had higher power than the χ² test. On the other hand, the tests with λ < 1 had lower power. As shown in the figure, λ = 2 has the highest power especially for the models with multiplicative interaction. We applied two-tail matched pair t-test (matched by sample size) to compare the curves of each methods. There was significant (p < 0.05) difference between entropy tests with different λ. Entropy tests with λ = 2 and 0.9 were significantly different from the χ²-tests for all the models; entropy tests with λ = 1 were significantly different from the χ²-test for the models without marginal effect and for the model with dominant (threshold) marginal and interaction effects. By properly choosing parameter λ, one can potentially increase the power.

Figure 4:

Six models with different marginal and interaction effects under case-only design. Power of χ²-test and entropy-based tests with λ = 0.9, 1 and 2 are plotted against the sample size

Under two group design, we have also evaluated the performance of the ratio statistics to detect interaction for the case-control design. Our simulation showed that λ = 1 usually had better performance. We compared the test with the LR test under certain scenarios. The power of the ratio test was low, specially when the marginal effect was strong (data not shown). As stated in section 2.3.2, this test is only recommended for large sample size.

4. Real Data Application

4.1. Venous Thromboembolism (VTE) Data Set Description

The data set consists of 1270 VTE subjects and 1302 unrelated controls collected to participate in a candidate-gene study. 12,296 SNPs located in 764 genes were genotyped. More details about this study can be found in Heit et al. (2011). Because there is a genomic region on chromosome 1q24.2 that contains a cluster of 5 genes highly associated with VTE, we decided to investigate this region for potential association and SNP-SNP interactions using our proposed entropy-based tests. A total of 102 SNPs were analyzed.

4.2. Association

We applied entropy-based test with λ = 0.9, 1.0 and 2.0 to test the association of each single SNP. The LR test was performed using a logistic regression model with additive genetic effect. Twenty-one SNPs were identified as significant (p < 0.05) by each of the three entropy-based tests. The p-values of those 21 SNPs are listed in Table 3.

Table 3:

The p-values (from likelihood ratio test and entropy-based test with λ = 0.9,1 and 2) of the most significant 21 SNPs sorted by entropy-based association test with λ = 1.

SNP	Gene	LR	λ = 0.9	λ = 1	λ = 2
rs2420371	F5	2.22E-16	4.22E-15	1.33E-15	6.66E-16
rs16861990	NME7	2.11E-13	3.03E-12	1.14E-12	2.65E-13
rs1208134	SLC19A2	4.81E-13	9.34E-12	3.10E-12	3.43E-13
rs2038024	SLC19A2	1.09E-10	2.62E-09	1.27E-09	1.97E-10
rs3766031	ATP1B1	2.55E-05	1.73E-05	1.59E-05	5.55E-05
rs6656822	SLC19A2	2.35E-05	0.000259	0.000234	7.47E-05
rs4524	F5	0.001123	0.000403	0.000386	0.000558
rs10158595	F5	0.001018	0.000403	0.000392	0.000911
rs9332627	F5	0.001181	0.000415	0.000399	0.000604
rs2239851	F5	0.001189	0.000419	0.000403	0.000592
rs4525	F5	0.001262	0.000426	0.00041	0.000614
rs970741	F5	0.002286	0.001043	0.000997	0.001292
rs723751	SLC19A2/F5	0.00203	0.003416	0.003036	0.001767
rs6030	F5	0.000572	0.004033	0.003842	0.002098
rs3820059	C1orf114	6.92E-05	0.004635	0.004988	0.011502
rs2176473	NME7	0.000528	0.006444	0.007138	0.021481
rs4656687	F5	0.001071	0.007846	0.007588	0.004945
rs1040503	ATP1B1	0.001453	0.011241	0.012167	0.029942
rs10800456	F5	0.004685	0.01346	0.012734	0.007133
rs3766077	NME7	0.026623	0.034665	0.035445	0.045988
rs16828170	NME7	0.070794	0.03606	0.035897	0.035187

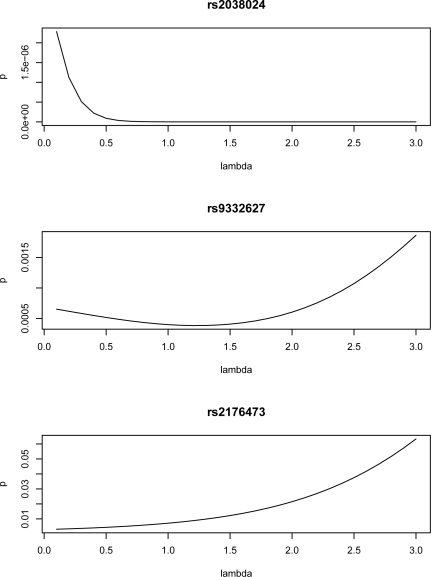
As previously stated, the Rényi entropy reduces to the Shannon entropy when λ = 1, therefore the entropy-based association test statistics is a summation of terms of the form p_i log(p_i) − q_i log(q_i), where i is the index over all genotypes of the SNPs in the test and p and q refer to the two different distributions of case group and control group, respectively. Each component of the statistics follows a normal distribution and the standard deviation can then be estimated by delta method (see Appendix). Thus, to illustrate the effect of Rényi Entropy parameter λ, we decomposed the test statistics at λ = 1. Three typical SNPs’ analysis results were displayed. One was very significantly associated with VTE (rs2038024) in all three tests, and the other two demonstrated a moderate significant association with VTE (rs9332627 and rs2176473). SNP names, genotypes, genotype frequencies within case group, genotype frequencies within control group, the component statistics, and the standard deviation estimate of each component and p-value are listed in Table 4. The analysis showed that the most significant component of SNP rs2038024 was genotype 0, followed by genotype 1 and genotype 2. It is worth noting that genotype 0 had the highest frequency, followed by genotype 1, with genotype 2 having the lowest frequency. For this SNP, the main difference between case and control groups came from the high frequency genotypes. To emphasize the difference on high frequency genotypes, one may increase the λ value. As shown in Figure 5 top panel, the p-value declined as λ increased. For SNP rs2176473, the genotype with lower frequency was more significant. In this case, the p-value decreased as the λ value moved toward 0 (Figure 5, bottom panel). For SNP rs9332627, there was no monotonicity between the genotype frequency and the significance of the components, and the minimum p-value was not achieved at the limits, but rather around λ = 1.2.

Table 4:

Decomposition of the Shannon entropy statistics of three SNPs

	Case freq	Ctrl freq	Stat comp	SD	p-value
rs2038024
0	0.6144	0.7281	0.0683	0.0112	9.36E-10
1	0.3368	0.2488	0.0204	0.0041	7.85E-07
2	0.0489	0.0230	0.0607	0.0171	3.78E-04
rs9332627
0	0.5923	0.5438	−0.0211	0.0085	0.0130
1	0.3644	0.3840	0.0003	0.0003	0.3158
2	0.0434	0.0722	−0.0537	0.0170	0.0016
rs2176473
0	0.3462	0.3940	0.0003	0.0001	0.0516
1	0.4740	0.4731	−0.0002	0.0050	0.9653
2	0.1798	0.1329	0.0403	0.0123	0.0010

Figure 5:

The changing pattern of entropy-based association test p-values of SNPs rs2038024, rs9332627 and rs2176473

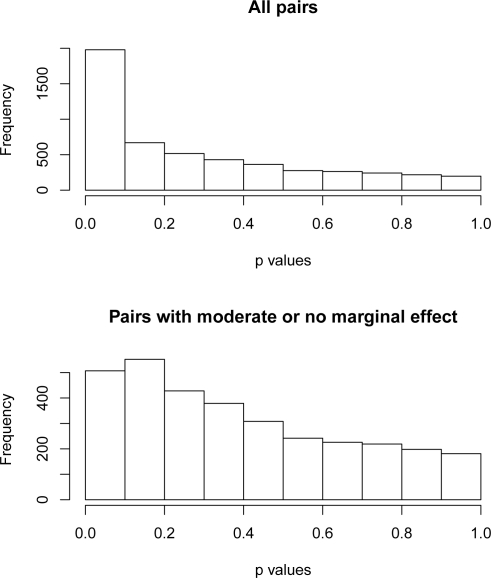
To investigate whether two or more SNPs are jointly associated with a phenotype, one can apply the entropy test to the joint frequency of the SNPs of interest. We checked the pairwise joint association for the VTE data set. As one would expect, pairs with one or both SNPs of strong marginal effect were strongly associated with the disease. Figure 6, upper panel, depicts the histogram of p-values (entropy-based association test with λ = 2) for all possible pairs. Thirty percent (1571 out of 5151) pairs had p-values less than 0.05. We also investigated the joint effect of SNPs without strong marginal effect. SNPs other than those 21 (identified by the previous association test based on the frequency of a single SNP) were considered SNPs with moderate or no marginal effect. The histogram in the lower panel of Figure 6 is based on the pairs with both SNPs moderate or of no marginal effect. Six percent (204 out of 3240) pairs had p-values less than 0.05. The shape of the histogram is a little skewed to the left. The joint association test seems to have lower power when the marginal effect is weak or absent.

Figure 6:

Distribution of p-values of entropy-based association tests for SNP pairs. Upper panel: SNP pairs of strong, moderate or no marginal effect. Lower panel: SNP pairs of moderate or no marginal effect.

4.3. Interaction

Entropy-based interaction tests were applied to the VTE data set. We first applied the tests to case group and control group separately. For an interaction associated with the disease, one would expect the test result of the case group to be significant while that of the control group insignificant. To check if the case group and the control group differ in terms of interaction effect, we applied further permutation to compare p-values between case and control groups. The case-control indicator was shuffled to create new case and control groups and tests were performed using the shuffled data. The details of the two-step procedure is described in the last paragraph of subsection 2.3.2.

Due to heavy computational burden, we only considered λ = 1 as an example, and we set up the threshold of significance and insignificance as 0.05 and 0.2, respectively, and only considered the SNP pairs with case group p-value less than 0.05 and control group p-value greater than 0.2. There were 182 pairs of SNPs that met the criteria. We applied the p-values comparison procedure to those 182 SNP pairs and calculated the p-values of the comparison (for a given SNP pair, it tests if the interaction effect of case group is more significant than the control group interaction effect). Among those p-values of comparison, 82 were less than 0.05. Accordingly, those 82 pairs, with a case group p-value smaller than the control group p-value, may have interaction associated with the disease and deserve further analysis. These pairs are listed in Table 5.

Table 5:

Significance of control case p-value difference.

SNP1	SNP2	P	SNP1	SNP2	P
rs16828170	rs12120904	0.000	rs1200082	rs2420371	0.016
rs16828170	rs9332618	0.000	rs10800456	rs6678795	0.017
rs1208134	rs6427202	0.000	rs1208134	rs4525	0.017
rs3766031	rs6703463	0.000	rs9332618	rs6663533	0.017*
rs16861990	rs6427202	0.000	rs16861990	rs9332627	0.017
rs3766031	rs2285211	0.000	rs6027	rs12755775	0.017*
rs16861990	rs4656687	0.000	rs1894691	rs1894702	0.018*
rs3766031	rs16828170	0.000	rs3766031	rs3766117	0.019
rs16861990	rs6678795	0.000	rs3766031	rs7545236	0.019
rs2213865	rs2420371	0.000	rs1208134	rs4524	0.020
rs16861990	rs6030	0.000	rs16828170	rs12120605	0.021
rs1892094	rs2420371	0.000	rs17516734	rs9332684	0.022*
rs12728466	rs2420371	0.000	rs9783117	rs2420371	0.022
rs3766031	rs1208370	0.000	rs16861990	rs4525	0.023
rs1208134	rs9332627	0.001	rs10158595	rs6678795	0.024
rs1208134	rs10800456	0.001	rs10158595	rs2239854	0.024
rs16861990	rs10800456	0.001	rs17518769	rs6027	0.027*
rs3753292	rs2420371	0.001	rs3766031	rs1894701	0.028
rs3766031	rs10753786	0.001	rs6018	rs9332684	0.028*
rs1200160	rs2420371	0.001	rs9783117	rs6022	0.030
rs1208134	rs970741	0.002	rs16862153	rs2420371	0.031
rs1208134	rs4656687	0.003	rs4524	rs2239854	0.032
rs723751	rs2420371	0.003	rs1894691	rs2239854	0.034*
rs2420371	rs6035	0.003	rs4525	rs2239854	0.034
rs16861990	rs12120605	0.003	rs9783117	rs1894701	0.034*
rs3766031	rs9287095	0.004	rs9783117	rs9332653	0.035*
rs1208134	rs2239851	0.005	rs9332624	rs6663533	0.035*
rs16861990	rs970741	0.005	rs3766031	rs12758208	0.036
rs1208134	rs6030	0.006	rs4524	rs3766119	0.039
rs1208134	rs6678795	0.006	rs2239851	rs3766119	0.039
rs12753710	rs2038024	0.006	rs1200138	rs3766077	0.040
rs1200131	rs1208134	0.006	rs2420371	rs9332628	0.040
rs6027	rs9332684	0.008*	rs6663533	rs12755775	0.040*
rs1208134	rs2213865	0.008	rs1200131	rs12758208	0.041*
rs2420371	rs12755775	0.008	rs1320964	rs2420371	0.042
rs3766031	rs6022	0.012	rs4525	rs3766119	0.045
rs1894691	rs3766119	0.012*	rs2239851	rs2239854	0.045
rs12120904	rs6663533	0.013*	rs9332653	rs6663533	0.046*
rs16861990	rs2239851	0.013	rs12074013	rs3766117	0.046*
rs1200131	rs16861990	0.013	rs9783117	rs7545236	0.047*
rs16861990	rs4524	0.015	rs9783117	rs3766117	0.049*

^*:Both SNPs have no significant main effect

5. Discussion

5.1. Choice of Rényi Parameter λ

We observed in our study that higher power can be achieved by properly choosing the entropy parameter λ. The optimal λ should be the one that amplifies the true difference between two populations, thus the choice of λ depends upon the true population allele frequencies and the source of difference. Although such information is usually not available, the family of entropy-based tests allow us to test the association and/or interaction with a different emphasis.

Since most of the computational time is devoted to estimate the allele frequencies of the permuted samples, once the frequencies become available, we recommend performing a series of Rényi entropy tests with multiple λs. A p-value vs. λ plot or a summary of multiple tests is usually recommended.

If one wants to make an interpretation based on tests of a fixed λ without prior knowledge of the optimal λ, we would suggest using 1 ≤ λ ≤ 3. According to our experience, the power of the entropy test is usually higher with λ in that range. Also, the interaction test λ < 1 may sometimes be misleading due to poor estimation of the distribution of the test statistics. A large number of permutation is usually required to achieve reliable p-value of the test.

5.2. Deviation from Uniform

In probability theory and information theory, the Rényi divergence measures the difference between two probability distributions. For probability distribution P and Q of discrete random variables, the Rényi divergence of order λ of the two distributions is defined as

$$D_{\lambda }\left(P\parallel Q\right)=\frac{1}{\lambda -1}\text{log}\sum _i\frac{p_i^{\lambda }}{q_i^{\lambda -1}}.$$

The Rényi entropy and Rényi divergence are related by H_λ (P) = H_λ (U) − D_λ (P‖U), where U represents the finite discrete uniform distribution which takes equal probability at any possible value. The uniform distribution is special as it is the one of maximum entropy, thus most unpredictable. We can rewrite the association test statistic as:

$$S_{\lambda }^A=H_{\lambda }\left({\widehat{P}}_D\right)-H_{\lambda }\left({\widehat{P}}_N\right)=D_{\lambda }\left({\widehat{P}}_N\parallel U\right)-D_{\lambda }\left({\widehat{P}}_D\parallel U\right).$$

The statistic can then be interpreted as the difference between the two distributions’ deviation from uniform. The interaction test can be represented as

$$S_{\lambda }^E=H_{\lambda }\left(\widehat{Q}\right)-H_{\lambda }\left(\widehat{P}\right)=D_{\lambda }\left({\widehat{P}}_1\parallel U\right)+D_{\lambda }\left({\widehat{P}}_2\parallel U\right)-D_{\lambda }\left(\widehat{P}\parallel U\times U\right).$$

The U × U is uniform distribution over the nine genotypic combinations of the two loci. The interaction test statistic compares the deviations from uniform of the sum of marginal distributions and that of the joint distribution.

It is easy to show that D₁(P‖Q) = H₁(Q) − H₁(P). However, this equation does not hold for general λ. If we replace the reference distribution U in the test statistics by some other distribution V, the equivalence between the entropy difference and the divergence difference does not hold except for λ = 1.0. Thus the extension from Shannon’s case where λ = 1.0 to Rényi’s case with general λ allows us to introduce other more reasonable reference distributions under various genetics settings. For example, V can be the population allele frequencies or the theoretical allele frequencies under certain model. The tests based on Rényi divergence with different reference distributions require further study and can be an interesting future research direction.

6. Appendix

Assume the loci of interest have k genotypes G₁,G₂, . . .,G_k, let p = [p₁, p₂, . . ., p_k], and ${\sum }_{i=1}^k{p}_i=1$ be the distribution of those genotypes in population. Let X = [X₁,X₂, . . .,X_k] be the number of observations of each genotype in the sample and n the sample size, then X has a multinomial distribution Mn(n, p). Note that for sufficiently large n, the multinomial distribution is approximately a multinormal distribution with mean E(X_i) = np_i and variance-covariance matrix given by Var(X_i) = np_i(1 − p_i) and Cov(X_i,X_j) = −np_ip_j (i ≠ j).

For P̂ = X/n = [X₁,X₂, . . .,X_k]/n = [p̂₁, p̂₂, . . ., p̂_k] we define E(P̂) = [p₁, p₂, . . ., p_k] = p and the variance-covariance matrix of P̂ as

$$\mathit{Var}(\widehat{P})={\mathrm{\Sigma }}_P=\frac{1}{n}\left(\begin{array}{cccc}{p}_1\left(1-p_1\right)& -p_1{p}_2& \cdots & -p_1{p}_k\\ -p_2{p}_1& p_2\left(1-p_2\right)& \cdots & -p_2{p}_k\\ ⋮& ⋮& \ddots & ⋮\\ -p_k{p}_1& -p_k{p}_2& \cdots & p_k\left(1-p_k\right)\end{array}\right)$$

First consider the Shannon’s entropy, $H_1(\widehat{P})=-{\sum }_{i=1}^k{\widehat{p}}_i\text{log}{\widehat{p}}_i$, and define the function

$$h\left(\widehat{P}\right)=\left[h\left({\widehat{p}}_1\right),h\left({\widehat{p}}_2\right),\dots ,h\left({\widehat{p}}_k\right)\right]=\left[{\widehat{p}}_1\text{log}{\widehat{p}}_1,{\widehat{p}}_2\text{log}{\widehat{p}}_2,\dots ,{\widehat{p}}_k\text{log}{\widehat{p}}_k\right].$$

The variance of h(P̂) can be approximated by the delta method as

$$\begin{array}{ll}V(n,p)& \approx {\left[\nabla h(p)\right]}^T{\sum }_P\nabla h(p)\\ & =\hspace{0.17em}\hspace{0.17em}\text{diag}\left(1+\text{log}{p}_1,\dots ,1+\text{log}{p}_k\right){\sum }_P\text{diag}\left(1+\text{log}{p}_1,\dots ,1+\text{log}{p}_k\right).\end{array}$$

Thus Var(H₁(P̂)) is the sum over all V(n, p)’s elements.

For the general Rényi’s entropy, $H_{\lambda }(\widehat{P})=\frac{1}{1-\lambda }\text{log}\left({\sum }_{i=1}^k{\widehat{p}}_i^{\lambda }\right)$, define the function $h(\widehat{P})=[h({\widehat{p}}_1),h({\widehat{p}}_2),\dots h({\widehat{p}}_k)]=[{\widehat{p}}_1^{\lambda },{\widehat{p}}_2^{\lambda },\dots {\widehat{p}}_k^{\lambda }]$, have $Z={\sum }_{i=1}^k{\widehat{p}}_i^{\lambda }$ and the function $g(Z)=\frac{1}{1-\lambda }\text{log}Z$. After applying the delta-method multiple times, we obtain

$$\text{Var}\left(H_{\lambda }\left(\widehat{P}\right)\right)=\frac{{\sum }_Z}{{\left(1-\lambda \right)}^{2_{z}2}},$$

where $z={\sum }_{i=1}^k{p}_i^{\lambda }$ and Σ_Z is the sum over all elements of the following matrix V(n, p), given by

$$V(n,p)=\text{diag}[\lambda p_1^{\lambda -1},\dots \lambda p_k^{\lambda -1}]{\sum }_P\text{diag}[\lambda p_1^{\lambda -1},\dots \lambda p_k^{\lambda -1}].$$

Let n₁ and n₂ be the sample size of case group and the sample size of control group, respectively. Under the null hypothesis of no association, the genotypic distributions of the disease population and the normal population are identical. Let the overall genotype population distribution be p = [p₁, p₂, . . ., p_k], and X_1i be the number of cases with genotype G_i, then X₁ = [X₁₁,X₁₂, . . .,X_1k] follows a multinomial distribution Mn(n₁, p). Similarly, let X₂ = [X₂₁,X₂₂, . . .,X_2k] be the distribution of controls over all genotypes, and X₂ follows a multinomial distribution Mn(n₂, p). When the case group and the control group are independent samples, the variance of the test statistics is simply the sum of the variance of the two entropies given by

$$\text{Var}(S_{\lambda }^A)=\text{Var}\left(H_{\lambda }\left({\widehat{P}}_D\right)\right)+\text{Var}\left(H_{\lambda }\left({\widehat{P}}_N\right)\right).$$

If there is no additional information about the distribution of genotypes in the overall population, p is usually estimated by (X₁+X₂)/(n₁+n₂).