Community-level spatial heterogeneity of chemical constituent levels of fine particulates and implications for epidemiological research

Abstract

Studies of the health impacts of airborne particulates’ chemical constituents typically assume spatial homogeneity and estimate exposure from ambient monitors. However, factors such as local sources may cause spatially heterogeneous pollution levels. This work examines the degree to which constituent levels vary within communities and whether exposure misclassification is introduced by spatial homogeneity assumptions. Analysis considered PM_2.5 elemental carbon (EC), organic carbon matter, ammonium, sulfate, nitrate, silicon, and sodium ion (Na⁺) for the United States, 1999–2007. Pearson correlations and coefficients of divergence were calculated and compared to distances among monitors. Linear modeling related correlations to distance between monitors, long-term constituent levels, and population density. Spatial heterogeneity was present for all constituents, yet lower for ammonium, sulfate, and nitrate. Lower correlations were associated with higher distance between monitors, especially for nitrate and sulfate, and with lower long-term levels, especially for sulfate and Na⁺. Analysis of colocated monitors revealed measurement error for all constituents, especially EC and Na⁺. Exposure misclassification may be introduced into epidemiological studies of PM_2.5 constituents due to spatial variability, and is affected by constituent type and level. When assessing health effects of PM constituents, new methods are needed for estimating exposure and accounting for exposure error induced by spatial variability.

Introduction

Ambient measurements of air pollution are commonly used as surrogates for exposure to investigate the relationship between air pollution and human health end points. However there exists spatial misalignment between the availability of pollutant data, typically at points for monitor locations, and the spatial scale used to measure health, often aggregated over a given area such as the county (Gryparis et al., 2009; Peng and Bell, in press). Community-wide concentration estimates are typically estimated through averaging monitor measurements over a given spatial area (e.g., zip code, metropolitan area, county). This can involve interpolation techniques such as kriging or inverse distance weighting, or applying the levels measured by a single representative monitor to a broad area.

For individual-level health data where a study subject’s residence or other location, such as school or work, is known, pollution exposure values are often estimated through measurements from the nearest monitor or some interpolation of nearby monitors. Although a smaller number of studies have used personal monitoring (Magari et al., 2002; Vallejo et al., 2006) or individual indoor and/or outdoor monitors at the study subject’s location (Belanger et al., 2006), such approaches are often cost prohibitive, and the vast majority of epidemiological research continues to rely on ambient monitors to generate exposure estimates. In ecologic studies, where aggregated pollutant levels are compared with aggregated health data, the exposure estimate for a given community is typically estimated as the spatially averaged ambient pollutant level (Zeger et al., 2000).

These approaches assume that pollution concentrations are spatially homogenous within the spatial unit used for analysis (e.g., county) or for a given distance range (e.g., the distance between the monitor(s) and the subjects). The assumption of spatial homogeneity of the pollutant is important for allowing the ambient average to be estimated using just a small number of monitors. However, a violation of the spatial homogeneity assumption in this case could lead to poor estimates of the ambient average and potentially biased estimates of risk parameters from regression models. Studies have shown that the choice of particulate matter sites used in epidemiological analysis can affect results (Ito et al., 1995).

The spatial properties of air pollution concentrations can be affected by several factors such as the relative contribution of local versus regional sources, atmospheric conditions (e.g., mixing height, atmospheric stability), and topography. The type of pollution can affect atmospheric dispersion and deposition; hence, different spatial heterogeneity can be expected for gaseous pollutants compared to particles, and among different particulates based on particle size, density, and shape, as well as source patterns. Monitors in a given region are more likely to have similar concentrations if the area’s pollution has larger contributions from secondary pollution compared to primary pollution. Communities with pollution from regional sources will have less spatial heterogeneity of pollution levels than communities with a higher relative contribution of local pollution sources.

Uniformity among air pollution measurements from different locations in a community can be considered in several ways, including temporal correlation and spatial similarity of absolute values. The temporal correlation of measurements across multiple monitors reflects whether levels rise and fall in similar patterns across time. However, two monitors could have perfectly correlated measurements but different absolute values of concentrations.

Research on particulates uses many different size distributions, such as particles with an aerodynamic diameter ≤10 or ≤2.5 µm (PM₁₀ and PM_2.5, respectively). Regional and spatial patterns in PM_2.5 and PM₁₀ health effects estimates, as well as a limited number of studies using PM_2.5 chemical constituents and sources, suggest that the chemical composition of the particle mixture has a role in toxicity (Laden et al., 2000; Dominici et al., 2006; Ostro et al., 2007; Bell et al., 2009; de Hartog et al., 2009; Peng et al., 2009). Here we use the term “constituent” to refer to one of the chemical components of PM_2.5, which is a mixture of many pollutants. Several previous studies have explored spatial variation among pollution levels, including many studies that examined particles; however, most focused on the total mass of particles of a given size distribution (Kim et al., 2008). A limited number of studies investigated this issue for chemical composition. Spatial variation of 14 PM_2.5 constituent levels from 1988 to 1998 was assessed for 18 monitors in the northeastern United States (Athanassiadis and Rao, 2003). Other studies examining this issue focused on a single city (Röösli et al., 2001; Ito et al., 2004; Martuzevicius et al., 2004; Venkatachari et al., 2006; So et al., 2007; Moreno et al., 2008) or small number of cities (Nerriere et al., 2007).

We investigated the spatial relationship of PM_2.5 chemical constituent concentrations for the period 1999 to 2007 for 480 monitors in the United States for seven chemical constituents of PM_2.5. This work builds on previous research that used a version of this data set for fewer years (2000– 2005) to investigate the chemical composition of PM_2.5 on a national and regional scale based on daily county-wide averages, but did not investigate spatial heterogeneity at the community scale (Bell et al., 2007). The database contains information for over 50 chemical constituents. We examined the daily levels of the various constituents and examined how relationships by monitor pairs (i.e., levels of pollutants at two different locations) are affected by the distance between location of monitor pairs, pollutant levels, and population density.

Methods

We used daily measurements of PM_2.5 chemical constituents for the continental United States based on ambient monitoring data collected by the US Environmental Protection Agency (US EPA) from January 1999 to December 2007. Data were obtained from the US EPA’s Office of Air Quality Planning and Standards and include information from the PM_2.5 Chemical Speciation Network, State and Local Air Monitoring Stations, Integrated Monitoring of Protected Visual Environments, and other monitoring networks. The analytical methods used are gravimetry for total mass; ion chromatography for nitrate $({\text{NO}}_3^{-})$, sulfate $({\text{SO}}_4^{2-})$, ammonium $({\text{NH}}_4^{+})$, and sodium ion (Na⁺); thermal optical analysis for elemental carbon (EC) and organic carbon; and X-ray fluorescence for silicon (Si) (US Environmental Protection Agency, 2001). More information on the sampling approaches, analytical methods, and quality assurance procedures is available in US EPA reports (US Environmental Protection Agency 2001, 2000). Although data are daily (i.e., 24-h averages), they are not available every day for all sites. The median frequency of data measurement was once every 3.7 days, and the average frequency was once every 4.6 days. We limited analysis to the constituents that were identified in earlier work to either vary with PM_2.5 total mass or contribute ≥1% to PM_2.5 total mass (Bell et al., 2007). These constituents are ${\text{NH}}_4^{+}$, EC, organic carbon matter (OCM), ${\text{NO}}_3^{-}$, Si, Na⁺, and ${\text{SO}}_4^{2-}$.

We excluded data that were suspect (e.g., US EPA-coded “lab issues”) and monitors that were not located in the continental United States. Organic carbon mass was estimated based on field correction values with a k value of 1.4. Monitors were included in analysis if they had data for at least 365 days in the study period and at least five observations in each season. Of these monitors, data from monitor pairs were analyzed if they were < 100 km apart and data were available for the constituent of interest for >90 observations days for both monitors (i.e., ≥90 same-day observation days).

The final data set included data from 354 monitors, although not all monitors satisfied our inclusion criteria for all constituents. The number of monitors was 324 for ${\text{NO}}_3^{-}$, 238 for ${\text{NH}}_4^{+}$, 327 for EC, 224 for OCM, 346 for Si, 218 for Na⁺, and 345 for ${\text{SO}}_4^{2-}$. The total number of observation days (i.e., monitor days), summed across all monitors, was 159,107 in total: 144,772 for ${\text{NO}}_3^{-}$; 92,851 for ${\text{NH}}_4^{+}$; 84,522 for EC; 152,340 for OCM; 153,392 for Si; 83,033 for Na⁺; and 152,340 for ${\text{SO}}_4^{2-}$.

The data include measurements that could be used to generate exposure estimates in epidemiological studies. However, this incorporates a variety of areas and land-use types. The location type varied with 23% of observations in urban locations, 55% in rural areas, and 21% in suburban locations, based on US EPA coding of the monitoring locations. The observations also covered several land-use types, including commercial areas (16%), industry (3%), vegetation areas (e.g., forests) (42%), residential communities (26%), agriculture (7%), and desert (4%).

The spatial variability among monitor measurements was estimated in several ways. For each monitor pair and constituent, we calculated the distance between monitors, the Pearson correlation across time, the coefficient of divergence (COD), and the long-term average of constituent levels calculated as an average across both monitors based on days in the study period with data available for both monitors for a given constituent. The COD for monitor pairs for each constituent were calculated as:

$${\text{COD}}_j^{i,k}=\sqrt{\frac{1}{p_j^{i,k}}{\displaystyle \sum _{t(j\in i,k)}^{p_j^{i,k}}{\left(\frac{x_{t,j}^i-x_{t,j}^k}{x_{t,j}^i+x_{t,j}^k}\right)}^2}}$$

where $x_{t,j}^i$ and $x_{t,j}^k$ are the concentration of constituent j on day t at monitors i and k, respectively, and $p_j^{i,k}$ the number of days with data for constituent j for both monitors i and k.

The COD reflects the variability of concentrations among monitor measurements, and is self-normalizing, so that if the coefficient approaches 0, the measurements have high similarity, whereas if the coefficient approaches 1, the measurements have low similarity. If measurements were identical, the COD would equal 0.

Although correlation results are useful to determine if concentrations covary across time, the COD provides insight into whether the overall concentrations across monitors are similar. The measures of correlations and CODs provide information that may be more relevant for some epidemiological study designs than others. For example, a time-series study that explores how day-to-day variation in pollutant levels is associated with day-to-day variation in health response could be affected by spatial heterogeneity that affects the temporal variation in exposure levels. However, an ecological study that compares health responses and exposure levels across communities could be affected by spatial heterogeneity related to the absolute levels.

A second-stage analysis was conducted with linear modeling to evaluate whether correlations were associated with the distance between monitors, the long-term averages of the constituents over the study period for each monitor pair, and the average population density for each monitor pair. Long-term averages were constructed based on the average across both monitors’ values for the subset of days for which data were available for the constituent of interest for both monitors in the monitor pair. Population density was calculated as the average of the number of persons/mile² for the counties in which the monitors were located based on the 2000 US Census (US Census Bureau, 2000). The linear models included centered variables for distance, long-term average, and population density, simultaneously. The linear model was repeated for each constituent.

The majority of sites had a single monitor; however, some sites had colocated monitors. These function as duplicate samples, under which observations would be identical without measurement error. Here we use the term “site” or “location” to refer to the specific place where measurement occurs, and “monitor” to refer to a single instrument producing a series of measurements. Thus, a single site may have more than one monitor. We investigated in a separate analysis the data at colocated monitors (distance = 0 km). Colocated monitors existed for all constituents. For ${\text{NO}}_3^{-}$, ${\text{SO}}_4^{2-}$, and Si, there were sites with three colocated monitors. Investigation of differences in constituent levels at colocated monitors explores measurement error, rather than spatial variability. For colocated monitors, we calculated the correlation, COD, and root mean squared error (RMSE). The RMSE represents the standard error of colocated measurements. Lower values indicate more similarity among measurements, and RMSE would equal 0 with perfect agreement. RMSE is calculated as follows:

$${\text{RMSE}}_j^{i,k}=\sqrt{\frac{1}{p_j^{i,k}}{\displaystyle \sum _{t(j\in i,k)}^{p_j^{i,k}}{\left(x_{t,j}^i-x_{t,j}^k\right)}^2}}$$

where $x_{t,j}^i$ and $x_{t,j}^k$ are the concentration of constituent j on day t at monitors i and k, respectively, and $p_j^{i,k}$ the number of days with data for constituent j for both monitors i and k.

Results

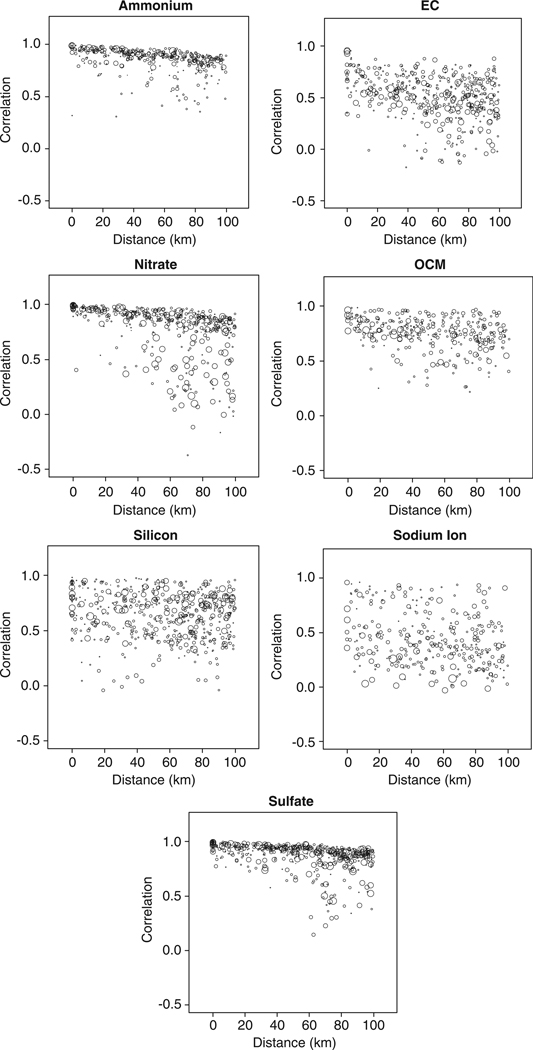
Table 1 shows the correlation of daily data for monitor pairs for each chemical constituent, categorized by the distance between monitors. These results indicate that levels of some constituents are more localized than others. The correlations of constituent levels at monitor pairs were generally higher for ${\text{NH}}_4^{+}$, ${\text{NO}}_3^{-}$, OCM, and ${\text{SO}}_4^{2-}$ than the other constituents. For all constituents, correlations were lowest at the highest distance category (50–100 km) and highest at close distances (< 10 km), and followed a general decline in correlations with increasing distance. Figure 1 shows correlation versus distance for each monitor pair for each constituent. Each circle represents a monitor pair, and the circle’s diameter is proportional to the number of observation days for a given monitor pair and constituent. Table 2 provides the CODs for monitor pairs by distance categories. Constituent levels were similar (COD closer to 0) for ${\text{NO}}_3^{-}$ and ${\text{SO}}_4^{2-}$ at smaller distances. The absolute levels generally became more divergent (larger COD) as distance increased.

Table 1.

Correlation of PM_2.5 chemical constituent concentrations for monitor pairs, by distance.

	Ammonium	EC	Nitrate	OCM	Sulfate	Na+	Silicon
0–5 km
Number of monitor pairs	14	18	17	14	18	14	18
Correlation: average	0.93	0.75	0.91	0.88	0.92	0.60	0.70
25th–75th percentile	0.91–0.95	0.61–0.87	0.92–0.97	0.84–0.93	0.85–0.96	0.42–0.85	0.51–0.80
5–10 km
Number of monitor pairs	19	19	18	19	21	17	20
Correlation: average	0.94	0.67	0.95	0.85	0.95	0.59	0.62
25th–75th percentile	0.94–0.97	0.64–0.76	0.94–0.97	0.82–0.91	0.94–0.99	0.36–0.88	0.46–0.92
10–20km
Number of monitor pairs	33	33	30	32	37	32	37
Correlation: average	0.89	0.60	0.93	0.78	0.93	0.48	0.64
25th–75th percentile	0.83–0.95	0.54–0.70	0.93–0.96	0.73–0.87	0.89–0.96	0.30–0.68	0.51–0.82
20–50km
Number of monitor pairs	112	123	114	107	134	105	135
Correlation: average	0.88	0.56	0.86	0.76	0.91	0.46	0.64
25th–75th percentile	0.88–0.94	0.49–0.71	0.85–0.93	0.73–0.85	0.90–0.96	0.26–0.68	0.48–0.82
50–100km
Number of monitor pairs	208	314	307	189	336	190	342
Correlation: average	0.82	0.46	0.69	0.73	0.83	0.38	0.62
25th–75th percentile	0.79–0.89	0.36–0.62	0.56–0.88	0.66–0.83	0.81–0.92	0.22–0.53	0.45–0.77
0–100km
Number of monitor pairs	386	507	486	361	546	358	552
Correlation: average	0.85	0.51	0.76	0.75	0.86	0.43	0.63
25th–75th percentile	0.83–0.93	0.40–0.68	0.75–0.92	0.70–0.86	0.85–0.94	0.26–0.56	0.47–0.79

Abbreviations: EC, elemental carbon; OCM, organic carbon matter.

Figure 1.

Correlation of monitor pairs versus distance for PM_2.5 chemical constituents. Note: Each circle represents a monitor pair. The size of the circle represents the number of observation days in each monitor pair; larger circles have larger sample sizes. EC, elemental carbon; OCM, organic carbon matter.

Table 2.

Coefficients of divergence of PM_2.5 chemical constituent concentrations for monitor pairs, by distance.

	Ammonium	EC	Nitrate	OCM	Sulfate	Na+	Silicon
0–5 km
Number of monitor pairs	14	18	17	14	18	14	18
COD: average	0.21	0.31	0.17	0.20	0.16	0.37	0.42
25th–75th percentile	0.12–0.28	0.25–0.32	0.10–0.19	0.17–0.23	0.11–0.22	0.32–0.41	0.32–0.51
5–10 km
Number of monitor pairs	19	19	18	19	21	17	20
COD: average	0.18	0.28	0.17	0.23	0.12	0.39	0.38
25th–75th percentile	0.11–0.19	0.19–0.33	0.12–0.20	0.19–0.27	0.07–0.16	0.33–0.45	0.31–0.44
10–20km
Number of monitor pairs	33	33	30	32	37	32	37
COD: average	0.20	0.31	0.20	0.27	0.15	0.42	0.43
25th–75th percentile	0.17–0.22	0.26–0.37	0.16–0.21	0.24–0.31	0.12–0.18	0.38–0.47	0.36–0.52
20–50km
Number of monitor pairs	112	123	114	107	134	105	135
COD: average	0.22	0.35	0.26	0.29	0.15	0.44	0.43
25th–75th percentile	0.16–0.25	0.27–0.40	0.19–0.30	0.23–0.35	0.11–0.18	0.40–0.50	0.36–0.51
50–100km
Number of monitor pairs	208	314	307	189	336	190	342
COD: average	0.25	0.39	0.37	0.31	0.23	0.47	0.46
25th–75th percentile	0.19–0.27	0.28–0.44	0.24–0.47	0.25–0.35	0.16–0.24	0.45–0.51	0.41–0.52
0–100km
Number of monitor pairs	386	507	486	361	546	358	552
COD: average	0.23	0.36	0.32	0.29	0.20	0.45	0.45
25th–75th percentile	0.17–0.26	0.27–0.42	0.21–0.38	0.23–0.34	0.13–0.22	0.42–0.51	0.38–0.52

Abbreviations: COD, coefficient of divergence; EC, elemental carbon; OCM, organic carbon matter.

Table 3 provides information on the correlation coefficients and CODs by region. The number of monitors varied greatly by region with the most monitors (235–296 depending on constituent) in the northeast region. Spatial heterogeneity varied little by region, although ${\text{NO}}_3^{-}$ was more heterogeneous in the northeast and southwest than other regions. ${\text{SO}}_4^{2-}$ was most homogenous in the northeast, whereas Na⁺ was the least homogenous in this region, compared to other regions.

Table 3.

Correlation and coefficients of divergence by region.

	Ammonium	EC	Nitrate	OCM	Sulfate	Na+	Silicon
Correlation
Northeast
Number of monitor pairs	244	275	295	235	296	237	293
Correlation: average	0.87	0.57	0.87	0.76	0.92	0.32	0.57
25th–75th percentile	0.85–0.93	0.48–0.69	0.83–0.93	0.70–0.86	0.89–0.96	0.19–0.43	0.43–0.72
Southeast
Number of monitor pairs	99	103	54	83	110	78	107
Correlation: average	0.79	0.48	0.79	0.72	0.87	0.66	0.78
25th–75th percentile	0.79–0.88	0.39–0.59	0.76–0.91	0.66–0.83	0.83–0.93	0.51–0.84	0.72–0.90
Northwest
Number of monitor pairs	19	52	55	19	56	19	67
Correlation: average	0.93	0.53	0.51	0.87	0.69	0.85	0.63
25th–75th percentile	0.89–0.95	0.37–0.72	0.21–0.92	0.84–0.92	0.53–0.88	0.78–0.88	0.51–0.79
Southwest
Number of monitor pairs	22	74	79	22	81	22	82
Correlation: average	0.83	0.34	0.53	0.72	0.77	0.50	0.63
25th–75th percentile	0.79–0.91	0.04–0.63	0.28–0.76	0.70–0.80	0.74–0.89	0.42–0.63	0.49–0.77
Coefficient of divergence (COD)
Northeast
Number of monitor pairs	244	275	295	235	296	237	293
COD: average	0.21	0.32	0.27	0.30	0.16	0.48	0.48
25th–75th percentile	0.17–0.24	0.26–0.38	0.20–0.33	0.24–0.34	0.13–0.18	0.45–0.52	0.43–0.53
Southeast
Number of monitor pairs	99	103	54	83	110	78	107
COD: average	0.27	0.35	0.29	0.27	0.18	0.40	0.41
25th–75th percentile	0.17–0.31	0.28–0.40	0.20–0.33	0.22–0.32	0.13–0.22	0.33–0.47	0.34–0.47
Northwest
Number of monitor pairs	19	52	55	19	56	19	67
COD: average	0.27	0.49	0.43	0.22	0.33	0.32	0.48
25th–75th percentile	0.23–0.33	0.33–0.63	0.19–0.65	0.20–0.27	0.17–0.46	0.29–0.35	0.39–0.56
Southwest
Number of monitor pairs	22	74	79	22	81	22	82
COD: average	0.25	0.45	0.45	0.31	0.26	0.42	0.37
25th–75th percentile	0.20–0.30	0.33–0.57	0.28–0.61	0.24–0.36	0.17–0.34	0.36–0.48	0.30–0.43

Abbreviations: EC, elemental carbon; OCM, organic carbon matter.

We also examined constituent levels at the subset of monitors that were colocated (distance = 0 km). Correlations, CODs, and the RMSE for colocated monitor pairs and the number of colocated monitors for each constituent are provided in Table 4. All constituents exhibited reasonably similar values (e.g., high correlations, low CODs) for colocated monitors; however, there were differences among same-day colocated measurements, and these differences varied by constituent. The highest correlations among colocated measurements were for ${\text{NO}}_3^{-}$ and ${\text{SO}}_4^{2-}$ (average correlations of 0.98 and 0.97, respectively). CODs were lowest for ${\text{NH}}_4^{+}$, ${\text{NO}}_3^{-}$, and ${\text{SO}}_4^{2-}$. For EC, colocated monitors had related but differing measurements (correlation of 0.75, COD of 0.22), indicating measurement error. Na⁺ and Si show somewhat higher COD values than other constituents (COD 0.31 and 0.41, respectively). No constituent exhibited the lack of measurement error (correlation = 1.0; COD and RMSE = 0.0), indicating that exposure error is introduced by measurement error, unrelated to spatial heterogeneity.

Table 4.

Correlation and coefficients of divergence of PM_2.5 chemical constituent concentrations for colocated monitor pairs.

	Ammonium	EC	Nitrate	OCM	Sulfate	Na+	Silicon
Number of monitor pairs	9	13	24	7	28	7	26
Correlation
Average	0.90	0.75	0.98	0.89	0.97	0.65	0.81
25th–75th percentile	0.92–0.99	0.68–0.82	0.97–0.99	0.87–0.92	0.95–1.0	0.43–0.96	0.76–0.93
Coefficient of divergence
Average	0.18	0.22	0.12	0.19	0.09	0.31	0.41
25th–75th percentile	0.09–0.14	0.18–0.24	0.09–0.17	0.13–0.22	0.05–0.13	0.17–0.40	0.31–0.50
RMSE (µg/m3)
Average	0.40	0.26	0.42	1.47	0.52	0.15	0.12
25th–75th percentile	0.27–0.44	0.17–0.36	0.11–0.53	1.06–1.71	0.24–0.72	0.08–0.19	0.06–0.15

Abbreviations: EC, elemental carbon; OCM, organic carbon matter.

As evidenced by Tables 1 and 2 and Figure 1, the relationship between constituent levels at monitor pairs generally decreases with distance; however, there also exists variability for correlation of constituent levels at monitor pairs at a given distance. For example, note that the correlation of monitor pairs at any specific distance exhibits a wide range of values (Figure 1), indicating that factors other than constituent type and distance have a role in spatial variability of constituent levels. We examined the relationship between correlation of monitor pair constituent levels and distance, long-term averages of the constituent levels, and population density, which might partially explain differing correlations for multiple monitor pairs at a specific distance. Across all included monitor pairs, the correlations among these variables (distance between monitor pairs, long-term constituent levels, and population density) were low (−0.28 to 0.22).

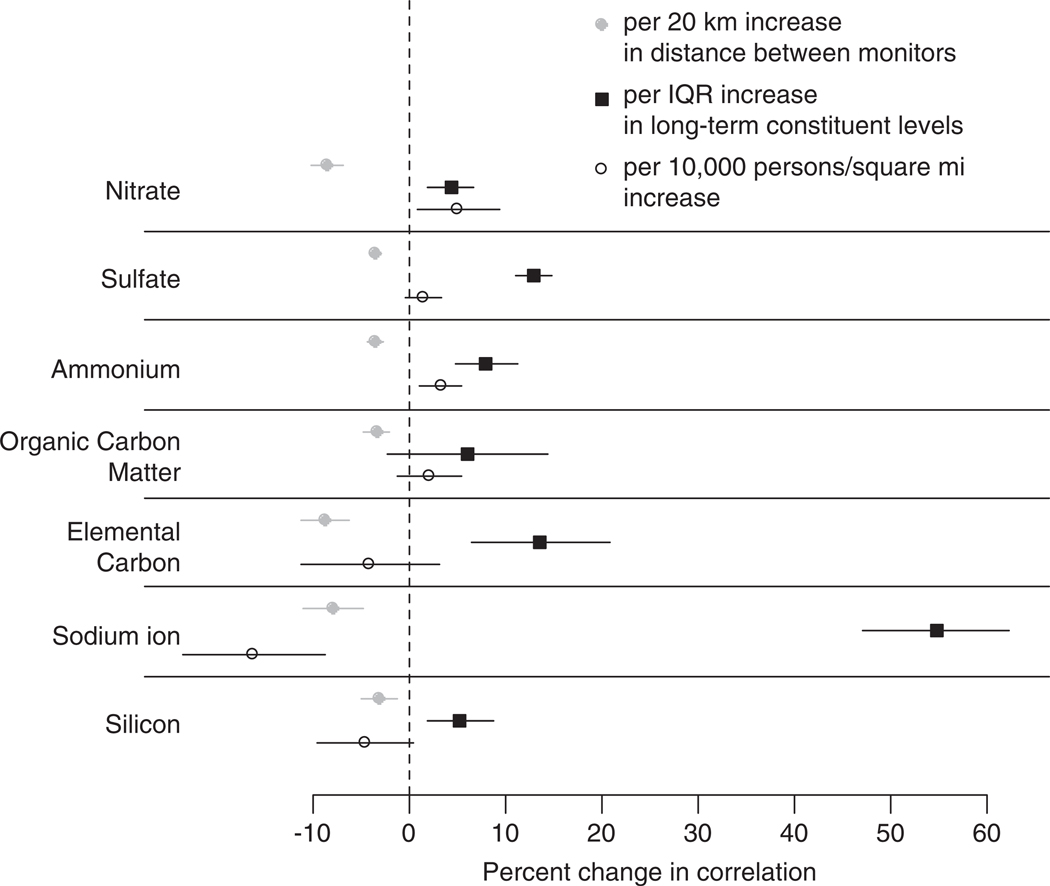
Higher distance between monitors was associated with lower correlations for all constituents, and higher long-term constituent levels were associated with higher correlations for all constituents, although results were not statistically significant for OCM. Population density did not exhibit clear patterns with correlations, as higher population density was associated with higher correlations for some constituents and lower correlations for others. Figure 2 shows the percent change in correlation of constituent levels at monitor pairs per interquartile range (IQR) increase in long-term constituent levels, an additional 20 km distance, or an additional 10,000 persons/mile² for population density. These results are for a model including variables for long-term constituent levels, distance between monitors, and population density. This model was conducted separately for each constituent. Correlations decreased with distance between monitors for all constituents, most dramatically for ${\text{NO}}_3^{-}$, EC, and Na⁺. An additional 20 km distance between monitor locations lowered correlations by 8.5% (95% interval 6.8, 10.2%) for ${\text{NO}}_3^{-}$, 8.8% (6.4, 11.3%) for EC, and 8.0% (4.9, 11.1%) for Na⁺. Correlations also were modified by long-term constituent levels with higher correlations corresponding to higher constituent levels. Results were statistically significant for all constituents other than OCM. An IQR increase in long-term Na⁺ levels (0.1 µg/m³ ) increased correlations by 55% (47, 62%). For ${\text{SO}}_4^{2-}$, an IQR increase in long-term levels (2.8 µg/m³) increased correlations by 12.9% (11.0, 14.8%).

Figure 2.

Percent change in correlation of constituent levels at monitor pairs as a function of distance between monitor pairs, long-term constituent levels, and population density. Note: The circles represent central estimates and the horizontal lines the 95% intervals. Interquartile range (IQR) values are 1.1, 2.8, 1.4, 3.5, 0.5, 0.1, and 0.1 µg/m³ for nitrate, sulfate, ammonium, organic carbon matter, elemental carbon, sodium ion, and silicon, respectively.

To examine the variation of monitor coverage and its potential impact on exposure estimates for health studies, we calculated the average population-weighted distance between zip code centroids and US EPA Speciation Trends Network (STN) PM_2.5 monitors for US continental counties with an STN monitor in 2006. Populations were based on the US 2000 census (US Census Bureau, 2000). Across the counties, the median population-weighted distance from a monitor was 14 km, with a maximum of approximately 54 km.

Discussion

Our findings indicate strong spatial heterogeneity among PM_2.5 chemical constituent concentrations at the community level and that this variation is a function of the constituent type, distance between locations, and long-term constituent levels. In particular, ${\text{SO}}_4^{2-}$ and ${\text{NH}}_4^{+}$ were the more spatially homogeneous pollutants, with correlations of 0.86 and 0.85, respectively. Monitor-level measurement error also introduces uncertainty in exposure estimates (e.g., correlation of 0.75 for colocated measurements of EC). All components exhibited higher correlations with higher pollutant levels, with statistically significant associations for all components other than OCM. These findings indicate that the misclassification of exposure for constituents in epidemiological studies will differ by the constituent, creating challenges for comparisons of results from different constituents.

In epidemiological settings, exposure misclassification will be impacted by the spatial area and monitor coverage, which will affect the distance between each study subject and the point location (i.e., monitor site) used to generate exposure estimates. The distance between study subjects and monitors will depend on the number of monitors, their location (e.g., center versus edge of the community), and the size and shape of the spatial area to be covered with respect to the monitoring locations. The variation in population-weighted distance between zip code centroids and monitor locations within counties shows that even if a uniform spatial unit is applied (e.g., a county), exposure misclassification can be greatly influenced by monitor coverage and size of the spatial unit. In other words, because spatial units (e.g., counties) have varying area, shape, population distribution, and monitoring networks, these differences introduce another source of variation in exposure misclassification for PM_2.5 chemical constituents.

Our results indicate that misclassification of exposure is also a function of long-term pollution levels. This implies that even if two studies focus on the same constituent and the distance between study subjects and monitors is identical across the two studies, the exposure misclassification could still differ by study and is anticipated to be larger for communities with lower constituent levels.

Other factors that may affect exposure misclassification include indoor/outdoor activity patterns, mobility as a study subject moves throughout the community, wind velocity, and topography. Buildings’ ventilation rates affect the infiltration of outdoor pollutants to the indoor environment. These factors may in fact vary by community and may affect subpopulations differently. For example, air conditioning use lowers penetration of outdoor air and varies by region. As another example, if one population has lower mobility within a city (e.g., infants, the elderly) their exposure is more accurately assessed by a fixed-point monitor than a population with higher mobility (e.g., persons traveling between home, work, and school). An understanding of the spatial heterogeneity of a given pollutant can help provide information on whether exposure misclassification is introduced not only through the use of a monitor or set of monitors, but also for those study subjects that have high mobility and are thereby exposed at multiple locations.

Measurement error in the form of different values for concentration levels measured at the same time period and location was observed in the analysis of colocated monitors (Table 4). Both positive and negative artifacts can exist, meaning the actual concentration may be higher or lower than the measurement. Such discrepancies can occur for many reasons, such as inadequate handling or storage of field blanks, which can especially affect the measurements of OCM, which are adjusted by filter blank values (Pun et al., 2004). The artifacts caused by organic carbon adsorption onto filters can vary by monitor type and season (Noll and Birch, 2008; Vecchi et al., 2009). Measurements from X-ray fluorescence methods can be affected by analytical uncertainties and interference (Graney et al., 2004; Flanagan et al., 2006). Other possible reasons for different measurements at colocated monitors include the loss of water or semi-volatiles, which can change from particle and gas forms. The impacts of these artifacts can be influenced by monitor and analysis methods, which may differ with respect to detection limits and measurement error (Pun et al., 2004; Chow et al., 2008; Hyslop and White, 2008). In most cases, colocated monitors are not present, so researchers must use estimates based on a single monitor without the benefit of duplicate sampling.

The potential misclassification of exposure resulting from spatial heterogeneity has implications for epidemiological studies, and these implications may vary depending on the study design. As an example, consider two monitors measuring the same pollutant daily with different absolute levels although those levels covary day to day. Such monitor values would work well in a study design relying on variation in exposure, but not in a study relying on variation in long-term levels. The reverse would apply to a situation in which two monitors have similar absolute levels with low day-today covariance. Analysis that compares day-to-day variation in pollution levels with day-to-day variation in health response rates, such as time-series analyses and case-crossover approaches, will be affected by spatial heterogeneity of pollution levels, but not by inaccuracies in the relationship between absolute levels at different monitors. In such cases, the variation in exposure across time is of key interest. Cross-sectional studies that compare effects across different communities would be affected by differences in the absolute concentrations across monitors (Wilson et al., 2005). Researchers should consider the spatial and temporal variation of PM_2.5 chemical component levels in relation to the study design used in health effects estimates. Our finding that spatial heterogeneity varies by constituent has implications for studies that examine the health effects of multiple pollutants simultaneously in regression models because measurement error in some pollutants can affect risk estimates for pollutants measured with little error (Carroll et al., 2006).

Spatial heterogeneity of PM chemical constituents is an important factor in studies of both short- and long-term effects. In cohort studies that estimate long-term effects, typical situations involve either predicting long-term exposure to a pollutant at a specific location (i.e., a home or residence) or predicting the average community-wide exposure to the pollutant. In the former case, spatial heterogeneity can introduce uncertainty to predictions of constituent levels at a specific location; in the latter case, spatial heterogeneity can result in exposure estimates taken from individual monitors that are unrepresentative of the community-wide exposure. In both cases, spatial heterogeneity can increase the uncertainty in prediction which, if ignored, can introduce bias in the risk estimation, as has been shown elsewhere (Gryparis et al., 2009; Peng and Bell, in press).

Typically, time-series studies assume that the pollutant of interest is homogeneous in space and that individual monitors are generally representative of community-wide ambient average concentrations. If a pollutant is spatially heterogeneous, then using a single monitor as a surrogate for a community-wide average concentration can induce classical measurement error. In the classical error model, the surrogate is noisier than the true concentration: w_t = x_t + u_t, where w_t is the surrogate (monitor value) on day t, x_t true value (community-wide ambient average), and u_t a random measurement error uncorrelated with the true concentration. Such a measurement error can occur when examining PM_2.5 constituents, many of which we have shown to be highly spatially heterogeneous. The effect of this classical measurement error, at least for simple linear models, can be to attenuate the estimate of the pollutant’s regression coefficient so that model results systematically underestimate the true risk. If s² is the variance of the measurement error u_t and υ² is the variance of the surrogate measure w_t, then in a simple linear regression, the estimate of the regression coefficient is attenuated by a factor of (υ² − s²)/υ², which is sometimes referred to as the reliability ratio (Zeger et al., 2000). In multiple regression models, similar effects can be observed, but the magnitude of attenuation will depend on correlations between the multiple variables in the model.

Spatial variability in pollutant levels can induce measurement error in time-series models that has not been thoroughly examined in detail in previous work, with a few exceptions. A recent study examined how time-series health effect estimates for emergency department visits in Atlanta, Georgia, the United States were affected by the spatial heterogeneity of pollution levels for PM_2.5 total mass and several gaseous pollutants (Sarnat et al., 2010). PM_2.5 effect estimates were not largely affected by the location of the monitoring site used to estimate exposure or the distance between the monitor and study population.

Table 5 summarizes studies that have examined spatial heterogeneity of PM total mass or PM chemical constituent concentrations. Several studies found lower spatial heterogeneity for secondary pollutants than primary pollutants. Results of the studies differed with respect to whether levels of EC were spatially heterogeneous across the community. In general, the single-community studies in Table 5 indicate less spatial variation for constituents that are likely to be regional in nature, such as ${\text{SO}}_4^{2-}$, which matches our results.

Table 5.

Summary of studies examining spatial heterogeneity of particulate matter and PM chemical constituents.

Study	Study location (time frame)	Form of PM	Selected findings
PM total mass studies.
(Ito et al., 1995)	Cook County, IL Los Angeles, CA (1985–1990)	PM10	Correlations for monitor pairs decreased with distance for both sites, but were lower at all distances for Chicago. Choice of monitoring sites used to estimate exposure impacted relative risks for PM10 and mortality.
(Burton et al., 1996)	Eight sites in Philadelphia, PA (summers 1992 and 1993)	PM10, PM25, PM coarse (PM10–2.5)	Fairly uniform levels of PM10 and PM2.5 across the study area based on ANOVA. Correlations of levels between sites were higher for PM2.5 than for the other PM forms. Levels more spatial heterogeneous for PM coarse.
(Ito et al., 2001)	Monitors in seven contiguous central and eastern US states (1988–1990)	PM10	Strong trend of decreasing correlation between monitor pair PM10 levels with increasing distance between monitors. Different correlations depending on location and land use.
(DeGaetano and Doherty, 2004)	20 sites in New York, NY (2000–2002, sampling period differs by monitor)	PM2.5	Relatively homogenous levels across the community, but lowest correlation in winter, which was the season with lowest levels. Wind direction did not greatly affect correlations of levels at monitor pairs.
(Grivas et al., 2004)	Four sites in Athens, Greece (June 2001–May 2002)	PM10	Significant spatial variation in PM10 levels. Correlation between monitor pairs ranged from 0.57 to 0.82.
(Pinto et al., 2004)	27 US urban areas (1999–2000)	PM2.5	Correlations and COD of PM2.5 within communities varied. For example, the range of between-monitor correlations was −0.07 to 0.99.
(Ito et al., 2005)	48 contiguous US states (1988–1997)	PM10	Distance between locations and regions affected correlation of PM10 at different locations. Higher correlations among PM10 in the eastern US than western US.
(Wilson et al., 2006)	One central site and 10 additional monitoring sites in Christchurch, New Zealand (July 2003 and June 2004)	PM10	High correlation of PM10 levels between central site and other sites, but large differences in absolute differences of levels.
(Grivas et al., 2008)	Eight sites in Athens, Greece (2001–2004)	PM10	Correlations between sites for PM10 levels ranged from 0.55 to 0.85. The correlations were affected by site type and were higher for urban areas. Site type had a larger role than the distance between monitors.
PM chemical constituent studies.
(Wongphatarakul et al., 1998)	Six monitors in Los Angeles, CA (January 1986–January 1987)	39 PM2.5 chemical constituents, converted to sources through cluster analysis	Correlation analysis for source factors (crustal, secondary, automobile, and residual oil PM2.5) used to investigate spatial variation within Southern CA air basin. Higher correlation for secondary PM2.5 than other sources (correlation coefficient range: 0.74–0.96). One monitor excluded due to levels very different from other sites.
(Blanchard et al., 1999)	San Joaquin Valley, CA (one area for 1–14 November 1995; three areas for 9 December 1995–6 January 1996)	>10 PM10 chemical constituents divided into categories (carbon, secondary, crustal species). Not all sites had information for all categories	Spatial representativeness of monitors generally higher for secondary PM10 particle category and lowest for crustal category.
(Suh et al., 1997)	Six sites in Washington, DC (June–August 1994)	Sulfate, nitrate, ammonium, and H+ PM2.5	Uniform concentrations across space for sulfate and H+. More variation in nitrate.
(Kim et al., 2000)	Five sites in Southern CA (January 1995–February 1996)	>40 constituents, a subset of which were analyzed for spatial variation	PM10 sulfate and EC levels exhibited low spatial heterogeneity. PM2.5 nitrate and ammonium showed higher spatial variation, whereas PM2.5 sulfate and EC did not.
(Röösli et al., 2001)	Basel area, Switzerland (4–80 sampling days in January 1997–May 1999, sampling days varied by constituent)	>10 PM10 constituents	Lower spatial heterogeneity for sulfate, sulfur, cadmium, chlorine, titanium, and potassium, with higher heterogeneity for nitrate, organic matter, bromine, chromium, iron, and lead.
(Athanassiadis and Rao, 2003)	18 Sites in Northeastern US (1998–1998)	14 PM2.5 constituents	Identified spatial scales for the constituent levels, with scales of 200–400 km for most constituents. Higher correlation coefficients for industrial and urban pollutants (aluminum, bromine, iron, selenium, zinc) for distances up to approximately 350 km.
(Martuzevicius et al., 2004)	11 sites in Cincinnati, OH (15–94 days in December 2001–November 2002, sampling days varied by site)	>40 PM2.5 constituents	Constituent levels showed high spatial heterogeneity, especially for metals. Sulfur exhibited less spatial variation.
(Ito et al., 2004)	Three sites in New York, NY (April 2001–December 2002)	>50 PM2.5 chemical constituents	Highest correlations across monitoring sites for sulfur, nitrate, sulfate, and ammonium. Of the seven constituents used in our study, the correlations for related constituents were ranked from highest to lowest correlations as nitrate, sulfate, ammonium, organic carbon, silicon, sodium, and EC.
(Martuzevicius et al., 2005)	13 sites in the greater Cincinnati and northern Kentucky area (2000–2003), 3 with chemical constituent data	12 PM2.5 constituents	Lower spatial heterogeneity for sulfur, organic carbon, and ammonium. High spatial heterogeneity for trace elements (iron, lead, manganese, nickel, vanadium, zinc).
(Venkatachari et al., 2006)	Two monitoring sites in New York, NY (12 January–5 February 2004)	Black carbon	Spatial heterogeneity, based on COD and correlations, evident and larger for black carbon than for PM2.5 total mass.
(Wade et al., 2006)	Five monitors in Atlanta MSA, GA (March 1999–August 2002)	Sulfate, nitrate, ammonium, EC, and organic carbon PM2.5	Semivariogram analysis for constituents indicate higher nugget values (reflecting measurement errors at distance = 0) for EC and organic carbon than other constituents. Lower sills (reflecting less spatial heterogeneity) for the predominantly secondary constituents (sulfate, nitrate, ammonium) than the predominantly secondary constituents (EC).
(Vega et al., 2007)	Six sites in central Mexico (February–March 2003). One urban, three suburban, two rural	23 constituents. Spatial variability examined for some constituents	Large spatial heterogeneity for PM2.5 sulfate. Less heterogeneity for PM2.5 nitrate, PM coarse nitrate, or PM coarse trace elements.
This study	354 US sites (1999–2007)	Ammonium, EC, nitrate, OCM, sulfate, Na+, and silicon PM2.5	Lower spatial heterogeneity for ammonium, sulfate, and nitrate. Lower correlation associated with higher distance between monitors and lower long-term constituent levels.

Abbreviations: ANOVA, analysis of variance; EC, elemental carbon; MSA, Metropolitan Statistical Area.

Note: For studies that examined PM total mass and constituents, results for constituents are presented here. Studies are ordered by date of publication.

A few studies directly examined the association between PM constituents and health outcomes. In a time-series study of six California counties, daily cardiovascular mortality had statistically significant associations with EC, OCM, potassium, and zinc (Ostro et al., 2007). In a study of 119 US counties, cardiovascular and respiratory hospital admissions were associated with EC and OCM (Peng et al., 2009). Similarly, an association was identified between PM mortality and morbidity with EC and OCM, as well as nickel and vanadium (Bell et al., 2009). Higher PM_2.5 total mass mortality effect estimates were observed when the PM composition had higher fractions of aluminum, arsenic, ${\text{SO}}_4^{2-}$, and nickel (Franklin et al., 2008). Consistent associations have been found thus far for PM constituents that we find to have higher levels of spatial heterogeneity and measurement error. This suggests that although significant associations have been estimated, the magnitude of the effects may be underestimated.

A key limitation of generating more accurate exposure estimates in epidemiological studies is the lack of available data, given the expense and feasibility issues associated with personal exposure monitoring. As many researchers wish to study health impacts in locations or time periods without measurement data, several approaches to improve exposure estimates are gaining use. Some approaches, including data imputation (Caffo et al., in press), primarily are applied to estimate air pollution levels on days, or other time units, without measurements and thereby improve estimation of exposure but do not contribute to information on spatial variability. Other approaches can be used to estimate concentrations at locations without monitors, thereby addressing spatial misalignment problems introduced by use of ambient monitors. These methods include the use of air quality modeling (Bell, 2006; Touma et al., 2006; Pun and Seigneur, 2008; Hogrefe et al., 2009); land-use regression and traffic modeling (Brauer et al., 2008; Karr et al., 2009; Von Klot et al., 2009; Holford et al., 2010); and other approaches including biomarkers, proximity to sources, and hybrid approaches (Zou et al., 2009; Baxter et al., 2010). Yet reliance on ambient monitoring networks to generate exposure estimates is likely to continue given the substantial resources already invested in developing these networks, the relative ease of their use, and the benefit of using actual measurements as opposed to estimated values.

Better understanding of spatial heterogeneity of PM_2.5 chemical constituents is needed to best interpret results from epidemiological studies. Our findings indicate that the pollutant, distance from monitors, and long-term pollutant levels affect exposure misclassification, which could hinder comparison of results across studies, even if they appear to use the same study design (e.g., same PM_2.5 constituent analyzed at the county level). Although a denser monitoring network would be ideal, cost considerations may prohibit extensive additional monitoring and even a network with very high coverage would not completely alleviate issues of spatial heterogeneity. To date most studies of PM constituents, and in fact most studies of air pollution more broadly, have not incorporated spatial modeling. Further research is needed to develop statistical methods that account for the different spatial variation across the PM_2.5 constituents in a location. Such methods could adjust risk estimates obtained from regression models, making them comparable across locations and across constituents.