Skip to main content
PMC home page
Springer logoLink to Springer
. 2011 Jul 9;197(10):987–997. doi: 10.1007/s00359-011-0661-6

Spatial reflection patterns of iridescent wings of male pierid butterflies: curved scales reflect at a wider angle than flat scales

Primož Pirih 1,✉, Bodo D Wilts 1,2, Doekele G Stavenga 1,2
PMCID: PMC3176396  PMID: 21744009

Abstract

The males of many pierid butterflies have iridescent wings, which presumably function in intraspecific communication. The iridescence is due to nanostructured ridges of the cover scales. We have studied the iridescence in the males of a few members of Coliadinae, Gonepteryx aspasia, G. cleopatra, G. rhamni, and Colias croceus, and in two members of the Colotis group, Hebomoia glaucippe and Colotis regina. Imaging scatterometry demonstrated that the pigmentary colouration is diffuse whereas the structural colouration creates a directional, line-shaped far-field radiation pattern. Angle-dependent reflectance measurements demonstrated that the directional iridescence distinctly varies among closely related species. The species-dependent scale curvature determines the spatial properties of the wing iridescence. Narrow beam illumination of flat scales results in a narrow far-field iridescence pattern, but curved scales produce broadened patterns. The restricted spatial visibility of iridescence presumably plays a role in intraspecific signalling.

Electronic supplementary material

The online version of this article (doi:10.1007/s00359-011-0661-6) contains supplementary material, which is available to authorized users.

Keywords: Pieridae, Multilayers, Scatterometry, Reflectance, Pterins

Introduction

Butterfly wings are patterned by differently coloured wing scales. The colour is due to the combined reflections of the cover scales and the underlying ground scales (Ghiradella 1989; Nijhout 1991; Stavenga et al. 2006). The scale colours are due to structural elements and/or due to pigments. A butterfly wing scale consists of a flat lower lamina and a structured upper lamina. The upper lamina is marked by longitudinal ridges, connected by cross-ribs. The components of the butterfly wing scales are commonly arranged irregularly, resulting in incident light being scattered more or less diffusely. When the nanostructures in the scales are regularly arranged, light interference results in structural (or physical) colours, as is the case in the famous iridescent Morpho butterflies (Vukusic and Sambles 2003; Kinoshita 2008; Kinoshita et al. 2008). Melanin, a pigment that absorbs throughout the visible wavelength range, is frequently employed to enhance the structural colours (Mason 1926, 1927; Yoshioka and Kinoshita 2006). When the wing scales contain pigments that absorb in only a restricted wavelength range, a pigmentary (or chemical) colour results.

Pierid butterflies package their short-wavelength absorbing wing pigments, the pterins, into small granules, which increase the scattering efficiency in the wavelength range where pterin absorption is low. Thus, the granules enhance the pigmentary colouration (Stavenga et al. 2004; Rutowski et al. 2005; Morehouse et al. 2007). In addition to the colouration with yellow, orange and/or red pigments, many pierid butterflies have wings with structural colours. Usually only males exhibit iridescence, presumably for impressing females, but in some cases both sexes are iridescent (Kemp 2006, 2007; Kemp and Rutowski 2007). In several species of the subfamily Coliadinae both the forewing and the hindwing are iridescent, e.g. Colias eurytheme, Colias electo, Eurema hecabe, Phoebis argante (Scott 1986; Rutowski et al. 2007a, b; Wijnen et al. 2007), but in most members of the Colotis group, belonging to the subfamily Pierinae (Braby et al. 2006), iridescence is restricted to the tips of the forewings (Stavenga et al. 2006; Wijnen et al. 2007). The iridescence originates in the cover scales, specifically in the ridges, which consist of a stack of elaborate lamellae, thus forming a multilayer reflector. Electron microscopic analysis demonstrated that the multilayered structures in pierids are very similar to those found in Morpho butterflies: the cross-section of the longitudinal ridges resembles the shape of a Christmas tree (Ghiradella et al. 1972; Ghiradella 1989; Vukusic et al. 1999; Giraldo et al. 2008; Wilts et al. 2011).

While the absorption spectra of the pterin pigments as well as the reflectance spectra and patterns of the iridescent wing areas of pierid butterflies have been described in considerable detail (Rutowski et al. 2005; Stavenga et al. 2006; Rutowski et al. 2007a; Wijnen et al. 2007; Wilts et al. 2011), only a few pioneering studies on the spatial distribution of the reflected light have been made so far (Rutowski et al. 2007b; Giraldo et al. 2008). In this study, we study six pierid species, i.e. the members of the Coliadinae Gonepteryx aspasia, G. cleopatra, G. rhamni, and Colias croceus, and the Colotis group members Hebomoia glaucippe and Colotis regina. We focus on the spatial radiation patterns of the structural and pigmentary wing colouration, using imaging scatterometry (ISM) and angle-dependent reflectance measurements (ARM). We have found that the iridescence spectra and far-field radiation patterns differed for each studied species. The scale curvature plays a crucial role in the angular distribution of iridescence, which is presumably important for intraspecific signalling, both in a static display and during flight.

Materials and methods

Animals

We have studied the iridescent males of six pierid species. Specimens of the Clouded Yellow, Colias croceus, were caught in the littoral part of Slovenia; the Cleopatra Brimstone, Gonepteryx cleopatra, near Argelliers (Hérault, France); the Common Brimstone, Gonepteryx rhamni, in Groningen (the Netherlands) and in Ljubljana (Slovenia); the Great Orange Tip, Hebomoia glaucippe, in Taiwan; the Queen Purple Tip, Colotis regina, was obtained from U. Dall’Asta (RMCA, Tervuren, Belgium); and the Lesser Brimstone, Gonepteryx aspasia, from K. Arikawa (Sokendai, Hayama, Japan).

Photography

The upper sides of the wings of the butterfly specimens were photographed with a Nikon D70 Mk I camera equipped with a Nikkor 70 mm f1.4 macro objective. The red channel of the CCD chip of this camera has sufficient UV sensitivity to allow UV photographs when using a blacklight lamp and a UV-passing filter combination (Schott glasses UG3 and BG17). The peak sensitivity in the UV was at about 370 nm.

Imaging scatterometry

The (far-field) spatial distribution of the light scattered from single scales was visualized with an imaging scatterometer. This instrument is built around an ellipsoidal mirror, collecting light from a full hemisphere around the first focal point containing the sample (Stavenga et al. 2009; Wilts et al. 2009). Because of its limited wavelength range (above 380 nm), we have used it to study the far-field scattering patterns of the blue-iridescent C. regina and the violet-iridescent H. glaucippe.

Single scales were glued to the tip of a glass micro-pipette (Giraldo 2008). A small piece of magnesium oxide served as a white diffuse reference object. RGB images were taken with an Olympus DP-70 camera. The scales were locally illuminated with sufficiently small spots (diameter 35 or 100 μm) to measure the effect of scale curvature. The intensity profile of each far-field scattering pattern was obtained from the blue channel of the images by averaging the values of each line of pixels.

Angle-dependent reflectance measurement

The angular distribution of the light scattered by the intact wings was measured with a set-up consisting of two optical fibres (Fig. 1), one for illumination (angle α) and the other for light detection (angle β), attached to two goniometers with the same rotation axis. The wings were placed on a black cardboard and positioned at the rotation axis of the two goniometers. The coordinate system was defined with the illumination and measurement meridians running from the wing base (α, β = −90°) to the wing apex (α, β = +90°). The two fibres were tilted equally to about 10° to the opposite sides of the central meridian, thus avoiding occultation.

Fig. 1.

Fig. 1

Open in a new tab

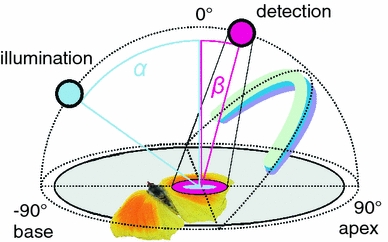
Diagram of the angle-dependent reflectance measurement (ARM) setup. The butterfly wing is positioned in the origin of a coordinate system determined by the two fibres, which rotate in the same vertical plane. The plane of the wing determines the horizontal plane of the coordinate system. The angles between the wing normal and the illumination and detection fibres are α and β, respectively. The wing is positioned so that its base corresponds to α = β = −90° and its apex to α = β = +90°

Reflectance spectra from iridescent wing areas were recorded with a diode-array spectrometer (UV–vis range 180–1,100 nm, AvaSpec 2048-2; Avantes, Eerbeek, the Netherlands), coupled to a 600 μm quartz fibre (FC-UV-600, Avantes) equipped with a quartz collimator (Col-UV/vis, Avantes). The same type of optics was used for the illumination. A diffusely scattering reference tile (Avantes WS-2) served as the white standard. The light source was an ozone-free XBO lamp.

The sampling angle (full width at half maximum, FWHM) of the detector, 3.9° at 600 nm and 4.6° at 300 nm, remained virtually constant at all angles (see also Stavenga et al. 2011). The diameter of the illuminated area was about 3 mm and that of the measurement circle about 9 mm, respectively, in the normal (vertical) position (α, β = 0°; Fig. 1). The sensor field of view was larger than the illuminated spot at all combinations of illumination and detection angles. Consequently, at a fixed detection angle (e.g. β = 0°), an ideal diffuse scatterer would yield the same reflectance R at all illumination angles α (see also Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

The Lesser Brimstone, Gonepteryx aspasia. a RGB photograph (bar 1 cm). b UV photograph with wide aperture illumination. c UV photograph with illumination from the left side. Only the right wing reflects towards the camera. d Reflectance spectra with variable illumination angle α, observed normal to the wing (β = 0°). The reflectance in the UV is highly directional

In the first series of ARM measurements on G. aspasia (Fig. 2), we measured reflectance spectra, R(λ), for light scattered in the normal direction (β = 0º) while varying the illumination angle α. In the main ARM dataset (Figs. 6, 8), reflectance spectra were measured at a number of fixed illumination angles α, i.e. α = [0°, ±30°, ±45°, ±60°], while the measurement angle β was varied between −75° and +75° in 5° or 10° steps (for an example of the measurement grid, see Suppl. Fig. 1). Additionally, we measured the reflectance when iridescence was optimal by stepping the illumination angle, α, from −75° to +75°, and adjusting the measurement angle β until the peak reflectance in the iridescence wavelength range was maximal. In the main dataset, in order to simulate a distant point source illuminating a unit area (as in the case of the sun), the measured reflectance, R, was transformed to reflectance per unit area (projected reflectance, R*) by a cosine projection of the illumination angle, i.e. R* = R cosα.

Fig. 6.

Fig. 6

Open in a new tab

Reflectance spectra measured with the ARM setup. a C. croceus. b G. rhamni. c G. aspasia. d G. cleopatra HW. e G. cleopatra FW. f H. glaucippe. g C. regina. The left column shows the spectra for the optimal iridescence line (angles β can be read from Fig. 5). The right column shows the spectra measured at the fixed angle of incidence α = 0°

Fig. 8.

Fig. 8

Open in a new tab

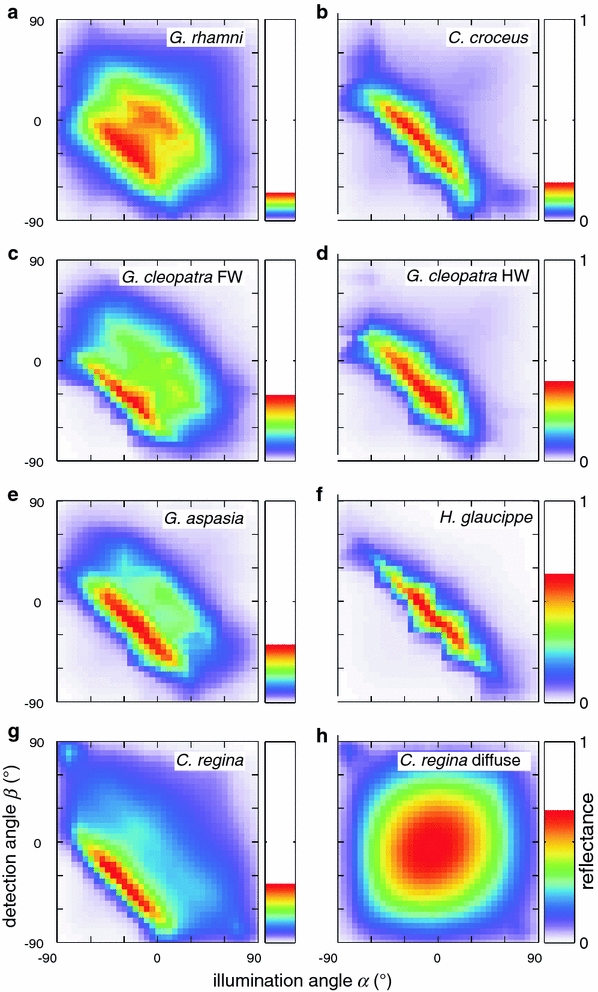
Spatial maps for the integrated short-wavelength reflectance of the iridescent wing parts of the investigated pierid butterflies. a G. rhamni, b C. croceus, c G. cleopatra FW, d G. cleopatra HW, e G. aspasia, f H. glaucippe, g C. regina. The scales of the species in the left column are curved, while the scales of the species in the right column are flat, resulting in differences of the angular width of the iridescence. h Diffusive (long-wavelength) reflectance of C. regina

Data were analysed with Matlab (Mathworks, USA). Band reflectance was measured in three ranges (340 ± 10, 420 ± 10, and 700 ± 10 nm). The first two bands were chosen to roughly approximate the UV (360 nm) and violet (420 nm) receptor of C. erate (Pirih et al. 2010), while the third band was designed to measure the diffuse reflectance of the wings at long wavelengths. The overall iridescence of each wing was measured as the average reflectance in the wavelength range starting at 300 nm and ending at 430 nm (G. rhamni forewing), 450 nm (G. cleopatra hindwing and G. aspasia forewing), 460 nm (H. glaucippe wing tip), 470 nm (G. cleopatra forewing), 480 nm (C. croceus) or 560 nm (C. regina wing tip), respectively. The upper boundaries of the iridescence bands were chosen close to the reflectance minima of each species. At each angle pair (α, β) the projected reflectance R* was interpolated into a mesh with 5° angular resolution using the Matlab internal routine griddata and the contributed routine gridfit (D’Erico 2005). Before the interpolation, zero values were added to the dataset R*(α, β) at the boundaries of both dimensions (α, β = ±90°). With this constraint, the obtained spatial map R*(α, β) of an ideal diffuser was close to a two-dimensional cosine function, and the obtained spatial map of an ideal mirror was close to a cosine-modulated line (β = −α), R*(α) ~ cos α.

Results

The upper sides of the wings of the investigated male pierids have different spatial reflection characteristics in the short wavelength range compared to those in the long wavelength range (Ghiradella et al. 1972; Ghiradella 1989; Rutowski et al. 2007a, b; Wilts et al. 2011). The wing reflection in the long wavelength range is diffuse and the reflection in the short-wavelength range is directional, as demonstrated by the Lesser Brimstone, Gonepteryx aspasia (Fig. 2). The forewing (FW) upper side is distinctly yellow; the hindwing (HW) upper side is somewhat paler (Fig. 2a), presumably due to a lower density of pterin pigment, most likely xanthopterin (Wijnen et al. 2007). Both the forewing and hindwing have orange spots, probably due to the presence of erythropterin. The forewings (except their edges) and the orange spots on the hindwings reflect UV light (Fig. 2b). When the specimen is illuminated from the left side, the UV reflection of only the right wing is seen (Fig. 2c).

We measured the directionality of the UV reflection on the forewings with the ARM setup, by changing the illumination direction while keeping the measurement fibre normal to the wing (β = 0°). The UV reflectance in the normal direction was maximal when the illumination was from the basal side (α = −45°, R = 0.8; Fig. 2d). The normal reflectance remained almost constant in the long-wavelength range, confirming that the pierid wings approximate perfect diffusers in the long wavelength range and that the field of view of the detector captured the full illumination spot (see “Materials and methods”).

The directional reflection at short wavelengths is due to the multilayered ridges of the cover scales (Wilts et al. 2011). Preliminary investigations on a variety of pierid butterflies showed that the directionality strongly depended on the species. To gain a quantitative understanding of the directional reflections, we first investigated the shape of isolated short-wavelength-reflecting cover scales using light microscopy. The cover scales in the wing tips of the Great Orange Tip, Hebomoia glaucippe, and the Queen Purple Tip, Colotis regina, appeared to have very different shapes. The scales of H. glaucippe are orange and strongly reflect UV–violet light (Wilts et al. 2011); the latter can be seen in RGB photographs as a faint violet reflection (Fig. 3a). The scales are virtually flat and only near the tip slightly curved (Fig. 3b). The scales of C. regina are red and additionally reflect blue light (Fig. 3d). When observing a scale of C. regina with an epi-illumination microscope, the position of the blue reflection strip changes when either the scale is rotated or the angle of light incidence is altered. This is due to the curved shape of the scale (Fig. 3e).

Fig. 3.

Fig. 3

Open in a new tab

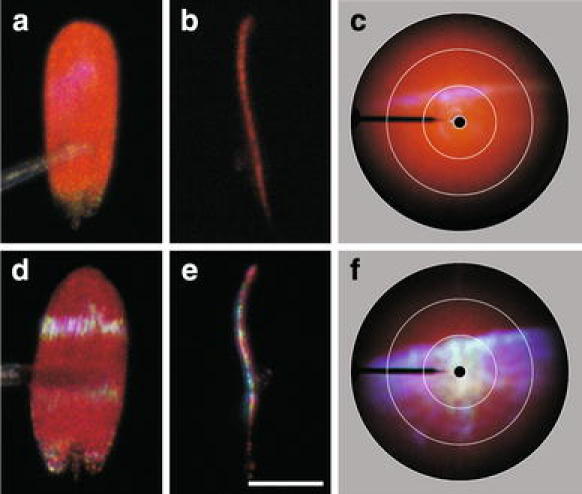
Shapes and scatterograms of single cover scales from the forewing tips of H. glaucippe (a–c) and C. regina (d–f). a, d Top-view of the scales. A distinct iridescence line is seen on top of the orange and red coloured scale, respectively. b, e Side-view of the scales; upper side to the left. The cover scale of H. glaucippe (b) is flat, except at the tip, and the cover scale of C. regina (e) is strongly curved. Bar a, b, d, e 50 μm. c, f Full hemisphere scatterograms from single scales, illuminated with white light. The white circles in the polar plots indicate angles of 5o, 30°, 60° and 90° with respect to the normal to the wing plane. The orange and red reflections are diffuse and fill the whole hemisphere. The short-wavelength iridescent reflections are spatially limited, for H. glaucippe (c) to a narrow angular space and for C. regina to a wider space (f)

We studied the far-field scattering patterns of the cover scales of H. glaucippe and C. regina with an imaging scatterometer, applying a narrow aperture white illumination focussed on the scale (diameter ~100 μm). The spatial scattering properties in the long and the short wavelength range clearly differ (Fig. 3c, f). The scales of both species reflected a diffuse orange (Fig. 3c) or red (Fig. 3f) scattering pattern, respectively, when illuminated in a small, central area of the scale. The scattering pattern filled virtually the full hemisphere. In the scatterogram of H. glaucippe a narrow violet–blue line emerged (Fig. 3c), while in the scatterogram of C. regina a broad, blue band overlapped the diffuse pattern (Fig. 3f).

The results of Fig. 3 suggest that in the case of C. regina, scale curvature is the cause for broadened scattering of blue light. This assumption was tested in the experiment of Fig. 4, where the scales of H. glaucippe and C. regina were illuminated at two different locations with a smaller spot size of 35 μm (insets Fig. 4c, f). In the case of H. glaucippe, the scattering pattern showed thin violet–blue strips that were almost constant for different spot locations, meaning that the direction of the reflected light was virtually independent of the illuminated spot (Fig. 4a, b). The scale of C. regina produced a broader blue scattering pattern, the extent of which depended on the location of illumination (Fig. 4d, e). We have quantified the angular spread of the scattering by measuring the scattering profiles (see rectangle in Fig. 4d) in the polar plots of Fig. 4a, b and Fig. 4d, e. The far-field scattering profiles are shown in Fig. 4c, f. The cover scales in the wing tips of H. glaucippe (Fig. 4c) reflect short-wavelength light into a narrow spatial angle, with a sharp, almost symmetric bell-shaped profile, while the scales of C. regina (Fig. 4f) reflect light into a broader angle, with an additional asymmetric tail. The FWHM is about 16° for H. glaucippe and about 40° for C. regina.

Fig. 4.

Fig. 4

Open in a new tab

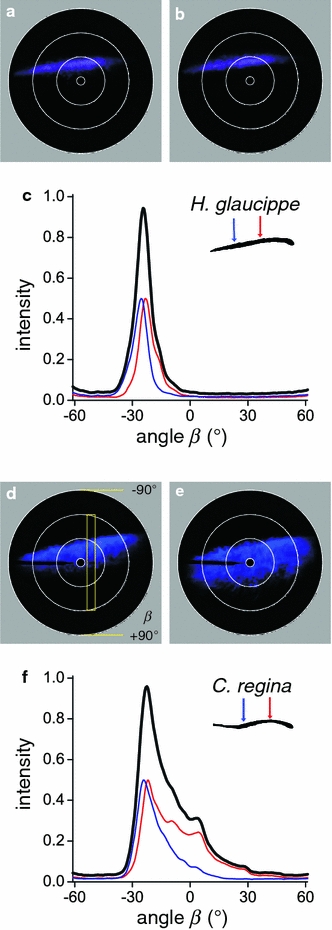
Local illumination for the differently curved scales of H. glaucippe and C. regina yielding different scattering patterns. a, b Scatterogram of a H. glaucippe scale illuminated near the root (a) and at the middle (b) of the scale. c Angular profiles of the scatterograms from a and b. d, e Scatterogram of a C. regina scale illuminated near the root (d) and at the middle (e) of the scale. The blue and red curves (c, f) represent the angular profiles vertically across the scatterograms (yellow rectangle in d). The black curves in c and f, representing the sum of the red and blue curves, show the limited spatial scattering by the scale of H. glaucippe and the wider spatial scattering of the C. regina scale

In our previous study on the morphology and spectral behaviour of pierid wing scales (Wilts et al. 2011), we noticed that the angle between the wing plane and the multilayer reflectors in the scale ridges varied among the investigated species. We have therefore studied the reflection and scattering patterns of the wing scales of a number of pierids in more detail with the ARM setup: C. croceus, G. rhamni, G. aspasia, G. cleopatra (both forewing and hindwing), H. glaucippe, and C. regina (Fig. 5, right column). All studied species had short-wavelength peaks in the UV, except for C. regina, where the peak was in the blue wavelength range (Fig. 5a).

Fig. 5.

Fig. 5

Open in a new tab

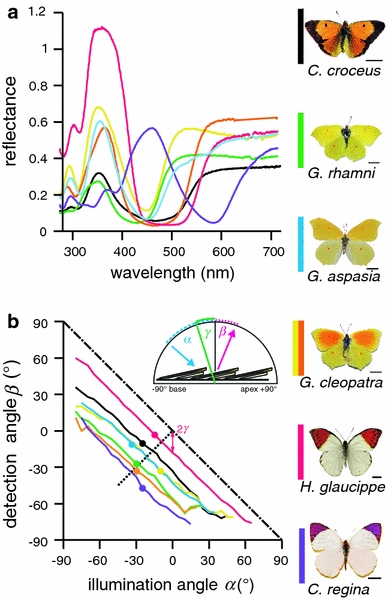
Reflectance spectra and angular dependence of the optimal iridescence path of the investigated pierid butterflies. a Reflectance spectra with the maximal short-wavelength reflectance measured with the ARM setup (at α ≈ β; for exact illumination and detection angles, see points in b). The line colours of the spectra are the same as those at the left of the photographs of the butterflies (right column, bars 1 cm). b Angular position of the detector (β) where the structural colouration is maximal as a function of the angular position of the illumination (α). The tilt angle γ can be read from the graph as half of the vertical (or horizontal) distance between the graph origin (α = β = 0°) and the optimal iridescence line, as is indicated with the arrowed line for H. glaucippe. The line of an ideal mirror is shown as a dash-dotted line. The experimentally measured positions of maximal iridescence are shown with thick dots and the expected positions for a tilted multilayer with a dotted line. The inset shows the arrangement of the scales on the wing, indicating the angles α, β and the multilayer tilt angle γ

The spectral and spatial reflection characteristics of the short-wavelength iridescence depend on the angle of illumination and detection. To visualise the spatial dependence of the iridescence peak, we changed the illumination angle, α, in steps of 5° and then determined the detection angle, β, where the amplitude of the short-wavelength band was maximal. In other words, we measured for each species the reflectance spectra along the path of optimal iridescence β(α) (Fig. 5b) and found its maximum, max(R*(α, β)) (Fig. 5a). If the iridescence had been due to a continuous flat multilayer, the optimal iridescence line given by β = −α would have been obtained. Although for all investigated species the optimal iridescence path was approximately linear, it deviated from the mirror line, indicating that the reflectors were tilted with respect to the wing plane. The total tilt angle, γ, follows from β = −α + 2γ, or γ = (α + β)/2. The tilt angle γ can thus be read as half the vertical distance between the measured optimal iridescence line and the flat-mirror line (Fig. 5b). The tilt angle is the largest in C. regina (γ ≈ −33°) and almost as large in G. cleopatra forewing (γ ≈ −30°) and G. rhamni forewing (γ ≈ −28°). It is smaller in G. aspasia forewing, C. croceus hindwing (both γ ≈ −22°) and G. cleopatra hindwing (γ ≈ −19°). The tilt is the smallest in H. glaucippe (γ ≈ −9°). The tilt angle derived for H. glaucippe should correspond to the angle between the wing and the scale, because in this species the ridge lamellae are parallel to the scale plane (Wilts et al. 2011). The larger tilt angle of C. regina is due to the pronounced scale curvature. In the other species, the lamellar multilayers of the scale ridges are tilted with respect to the scale surface, and the measured tilt angle should be a combination of the lamellar tilt angle (4°–6°), the scale curvature and the scale tilt angle with respect to the wing base (Wilts et al. 2011).

In our measurements of the optimal iridescence path (Fig. 5b), the peak wavelength of the short-wavelength reflectance changed with the angle of illumination. We have further analysed these spectral changes in Fig. 6. The waterfall plots (Fig. 6, left column) show the reflectance spectra measured along the optimal iridescence paths, that is, for each angle of illumination, α, the cosine-projected reflectance spectrum at the optimal detection angle, β, is shown (see Fig. 5b). For all species, the short-wavelength peak wavelength was approximately maximal (Fig. 5a) when α, β ~ γ, i.e. when the light was supposedly reflected normally from the (tilted) multilayer (Fig. 5b). The peak wavelength shifted hypsochromically (towards shorter wavelengths) when going away from the optimal point, as expected for iridescence due to a multilayer reflector (Wilts et al. 2011). The long-wavelength part of the reflectance spectra changed only in amplitude but not in shape, as expected for non-iridescent, diffusive materials.

Measurements along the path of optimal iridescence (Fig. 6, left column) are convenient for understanding the properties of colouration, but they do not represent a naturally occurring condition. A natural condition with static illumination, static observer and a rotating wing has been studied for C. eurytheme (Rutowski et al. 2007b). Another naturally occurring condition is that with a moving observer and a static, i.e. non-moving, wing. We therefore measured the reflectance spectra at various detection angles while keeping the illumination fixed normal to the wing, α = 0° (Fig. 6, right column). The short-wavelength reflectance bands were then limited to a small angular range in three cases (Fig. 6a, d, f, right column). In the other four cases the angular range was more spread out (Fig. 6b, c, e, g, right column). This can be directly understood from the curvature of the cover scales: the cover scales of C. croceus (Fig. 6a), G. cleopatra hindwing (Fig. 6d) and H. glaucippe (Fig. 6f) are flat, while those of G. rhamni, G. aspasia, G. cleopatra forewing, and C. regina are curved. The scale curvature in the two extreme cases (H. glaucippe and C. regina) is shown in Fig 3b, e.

Figure 7 gives an alternative representation of the far-field scattering profiles of the different pierid scales. The reflectances measured at various detection angles, β, with normal illumination, α = 0° (see Fig. 6, right column), were averaged over three wavelength ranges, 340 ± 10, 420±10, and 700±10 nm. The graphs show narrow angular reflectance distributions at 340 nm (Fig. 7a) and 420 nm (Fig. 7b), and a much broader distribution at 700 nm (Fig. 7c). The angular spread of the reflectance depends on the species. The two brightest and sharpest reflectance profiles in the UV are from the flat scales of H. glaucippe (FWHM ≈ 19°) and G. cleopatra hindwing (FWHM ≈ 35°; Fig. 7a). The curved scales of the forewings of the two studied Gonepteryx species have a double-peaked angular reflectance profile. The broadest profile, covering almost the whole hemisphere, was measured at 420 nm from the scales of C. regina (Fig. 7b). The asymmetric tail of C. regina is also visible in the scatterometer measurement (Fig. 4f). The short-wavelength angular reflectance profiles of H. glaucippe and C. regina measured from the wing patches with the goniometer (Fig. 7a, b) are, however, broader than the corresponding profiles obtained from single scales with the scatterometer (Fig. 4c, f). The additional spread is most likely due to varying orientations of the multilayered ridges and the scales on the wing.

Fig. 7.

Fig. 7

Open in a new tab

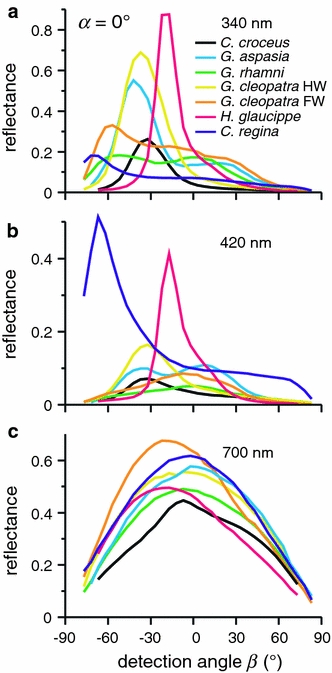
Reflectance profiles for normally incident illumination (α = 0°) for three different wavelengths. a 340 nm. b 420 nm. c 700 nm

The long-wavelength reflectance is for all species similar and has a cosine-like angular relationship (Fig. 7c). The departures from the symmetric, central position and the cosine shape towards negative values of the detection angle, β, i.e. towards the wing base, are presumably caused by differences in the tilt of the scales with respect to the wings and also by the scale curvature. Furthermore, shading due to scale stacking could occur. The reflectance maxima of the diffuse reflections, at long wavelengths, differ between the species, ranging between 0.4 in C. croceus and 0.7 in G. cleopatra forewing, roughly in accordance with the measurements performed with an integrating sphere (Wilts et al. 2011). The amplitude differences presumably result from different concentrations of the pigments and differences in scale stacking (Stavenga et al. 2006).

The angular spread of the iridescent wing colouration should have important consequences for the visibility of the wing pattern. We therefore investigated this aspect in more detail. To provide a general and comparative visualisation of the far-field iridescence patterns, we have averaged the reflectance over the iridescence bands (for wavelength ranges, see “Materials and methods”), at all measurement combinations of (α, β). The measurement grid was interpolated, resulting in a spatial map of the short-wavelength reflectance (Fig. 8). The resulting spatial maps show that the angular width of the iridescence signal strongly varies among the different pierid species. While some species, like H. glaucippe and C. croceus, reflect incident light into a limited spatial angle, others, like G. rhamni and C. regina, produce a considerably broadened far-field scattering pattern. A comparison of the scattering patterns with the scale shapes for all species clearly shows that the curved scales produce scattering patterns with an extended angular spread (Fig. 8a, c, e, g); the flatter scales produce a narrow scattering pattern (Fig. 8b, d, f). Figure 8h presents the scattering pattern in the long-wavelength range, at 700 nm, for C. regina, where the pigmentary colouration causes diffuse scattering. The pattern closely approximates that of a Lambertian diffuser. The waterfalls for spectral bands at 340, 380, 420 and 460 nm are shown in Suppl. Fig. 2.

Discussion

The colouration of the investigated male pierids is quite diverse and characteristic for each species. The diversity is threefold: first, the wing colouration patterns vary (Wijnen et al. 2007; Wilts et al. 2011); second, the reflectance spectra are different in terms of the long-wavelength cut-off and iridescence peak amplitude and position (Fig. 5a); third, the width of the far-field pattern of iridescence varies (Figs. 7, 8). Some general principles can nevertheless be recognized. The pigmentary colours, created by pterin pigments residing in the beads inside the scale lumen, are restricted to a few classes. These are white (with a low UV component), yellow, orange and red, depending on the expressed pterins (Wijnen et al. 2007). The concentration of pigment presumably varies among the studied species, as indicated by the differences in the diffuse reflectance in the long wavelength range (Fig. 7c).

The UV- or blue-iridescence reflectance peak of the studied pierids is separated from the long-wavelength diffuse reflectance by a minimum, due to pigmentary absorption. The structural and pigmentary colouration together create a highly chromatic signal. With a point-source like illumination, the iridescence pattern remains restricted to a limited spatial angle. The directionality of the structural colouration is thus best preserved in direct sunlight. An iridescent butterfly in flight under the sun will radiate flashes of short-wavelength light while the diffuse long-wavelength light will be less modulated (Rutowski et al. 2007b). The visibility of the wing-flap may be read from spatial maps (Fig. 8) by following the diagonal line from bottom-left to top-right. Flapping H. glaucippe wings, with flat scales, will radiate brief UV–violet flashes, whilst the wings of C. regina, with curved scales, will show longer-lasting blue flashes, assuming the same flapping frequency (Figs. 7, 8; Suppl. Fig. 2).

The narrow violet line in the scatterogram of H. glaucippe scales is reminiscent of a similar narrow blue line observed in scatterograms of Morpho scales (Stavenga et al. 2009), which was explained by diffraction of light by the slender, multilayered ridges (Vukusic et al. 1999; Kinoshita et al. 2002). Indeed, the iridescent structures of pierid and Morpho butterflies are similar (Rutowski et al. 2007b; Giraldo et al. 2008; Wilts et al. 2011). The difference in colour is due to the difference in spacing of the ridge lamellae (Wilts et al. 2011).

In the studied species, the optimal iridescence line is directed away from the mirror line (Fig. 5b). A minor angular shift is due to scale stacking (e.g. γ ≈ −9° in H. glaucippe). An additional angular shift (for instance, γ ≈ −30° in the case of G. cleopatra forewing) must be due to the combined effect of the lamellar multilayer tilt with respect to the scale plane and the scale curvature. Possibly, the tilt serves a purpose: it may be there to optimize the signal’s visibility under a certain constellation of the sun, the wing and the observer.

The wing reflectance spectra are probably tuned to the spectral sensitivities of the photoreceptors in the compound eyes (Stavenga and Arikawa 2006). The set of photoreceptors are known in considerable detail for two pierids, namely the Small White, Pieris rapae (Qiu et al. 2002; Stavenga and Arikawa 2006), and the Eastern Pale Clouded Yellow, Colias erate (Pirih et al. 2010). The two species both employ UV receptors (peaking at ~360 nm), violet/blue receptors (420–480 nm), green receptors (560 nm) and red receptors (620–660 nm). Very likely other pierids have photoreceptors with very similar spectral sensitivities: we may assume that a generic pierid eye contains one UV receptor class, at least one blue/violet class, a green class and at least one red class. The short-wavelength flashes of flying males could be detected as a distinct, short-lived UV signal against the longer-lasting green signal created by the non-iridescent wing reflections, for instance via a two or three receptor opponency mechanism (e.g. UV+/violet−/green+). In the case of C. regina, however, a combination of blue/red (purple) wing colours would require a different set of photoreceptor types for the opponency mechanism (e.g. blue+/green−/red+).

The visibility of a butterfly in flight depends on the contrasts that the wing reflections provide against the background. The reflections depend on several environmental factors (e.g. clearness of the sky, time of the day). Under clear sky conditions, a large part of short-wavelength radiation does not come directly from the sun beam, but from the diffuse sky, due to Rayleigh scattering. The structure-based wing reflection in the short-wavelength range (Fig. 3) therefore has two components, a directional component due to the sun and a wide-angle component due to sky light irradiation. During a wing flap, both components are swept through space. An observer thus sees a brief sun reflection component and a longer sky reflection component. In the evening, when the sun reddens, the sun component is reduced; this is also the case under overcast skies. Against a clear sky background, only the long-wavelength reflection provides a bright contrast. We note that all investigated butterflies, except C. regina, may appear darker than the sky in the blue–green wavelength range. In the case of a background of green vegetation, both the short- and the long-wavelength reflections stand out. In all cases, the contrast during the wing flap is further modulated by the projection angle of the wing, and by the distance to the observer.

We conclude that there are several realisations of combined structural and pigmentary colouration, having different spectral and spatial signatures, which are determined by the pigmentation, the nanostructured multilayer and the shape of the scale. It will be interesting to study how the resulting colouration is detected through the eyes of the conspecifics and the predators, both in terms of the wing pattern (near-field) and in terms of the signalling during flight (far-field). An especially intriguing aspect is the relative importance of the two signals in terms of mate choice. The data presented here and previously (Wilts et al. 2011) may provide a quantitative basis for studying these interesting questions.

Electronic supplementary material

Below is the link to the electronic supplementary material.

359_2011_661_MOESM1_ESM.pdf (21.9KB, pdf)

Suppl. Fig. 1 Spatial map of G. rhamni indicating the measurement positions with black dots (PDF 22 kb)

359_2011_661_MOESM2_ESM.pdf (63.8KB, pdf)

Suppl. Fig. 2 Spatial maps integrated over wavelength bands of 340 ± 10 nm, 380 ± 10 nm, 420 ± 10 nm, 460 ± 10 nm and 700 ± 10 nm. a C. croceus. b G. rhamni. c G. aspasia. d G. cleopatra HW. e G. cleopatra FW. f H. glaucippe. and g C. regina. The colour coding is a map of the absolute projected reflectance in the range R* = [0 .. 1] (PDF 64 kb)

Acknowledgments

We thank H.L. Leertouwer for expert technical assistance with photography, M. F. Wehling and two anonymous reviewers for constructive comments on the manuscript. Financial support was given by EOARD/AFOSR Grant FA8655-08-1-3012.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

References

  1. Braby MF, Vila R, Pierce NE. Molecular phylogeny and systematics of the Pieridae (Lepidoptera: Papilionoidea): higher classification and biogeography. Zool J Linn Soc. 2006;147:239–275. doi: 10.1111/j.1096-3642.2006.00218.x. [DOI] [Google Scholar]
  2. D’Erico J (2005) Surface Fitting using gridfit. Matlab File Exchange repository ID #8998. http://www.mathworks.com/matlabcentral/fileexchange/8998
  3. Ghiradella H. Structure and development of iridescent butterfly scales: lattices and laminae. J Morphol. 1989;202:69–88. doi: 10.1002/jmor.1052020106. [DOI] [PubMed] [Google Scholar]
  4. Ghiradella H, Aneshansley D, Eisner T, Silberglied R, Hinton HE. Ultraviolet reflection of a male butterfly: Interference color caused by thin-layer elaboration of wing scales. Science. 1972;178:1214–1217. doi: 10.1126/science.178.4066.1214. [DOI] [PubMed] [Google Scholar]
  5. Giraldo MA (2008) Butterfly wing scales: pigmentation and structural properties. PhD Thesis, University of Groningen. http://irs.ub.rug.nl/ppn/304871559
  6. Giraldo MA, Yoshioka S, Stavenga DG. Far field scattering pattern of differently structured butterfly scales. J Comp Physiol A. 2008;194:201–207. doi: 10.1007/s00359-007-0297-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Kemp DJ. Ultraviolet ornamentation and male mating success in a high-density assemblage of the butterfly Colias eurytheme. J Insect Behav. 2006;19:669–684. doi: 10.1007/s10905-006-9060-1. [DOI] [Google Scholar]
  8. Kemp DJ. Female butterflies prefer males bearing bright iridescent ornamentation. Proc Roy Soc B. 2007;274:1043–1047. doi: 10.1098/rspb.2006.0043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kemp DJ, Rutowski RL. Condition dependence, quantitative genetics, and the potential signal content of iridescent ultraviolet butterfly coloration. Evolution. 2007;61:168–183. doi: 10.1111/j.1558-5646.2007.00014.x. [DOI] [PubMed] [Google Scholar]
  10. Kinoshita S. Structural colors in the realm of nature. Singapore: World Scientific; 2008. [Google Scholar]
  11. Kinoshita S, Yoshioka S, Kawagoe K. Mechanisms of structural colour in the Morpho butterfly: cooperation of regularity and irregularity in an iridescent scale. Proc R Soc Lond B. 2002;269:1417–1421. doi: 10.1098/rspb.2002.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kinoshita S, Yoshioka S, Miyazaki J. Physics of structural colors. Rep Prog Phys. 2008;71:076401. doi: 10.1088/0034-4885/71/7/076401. [DOI] [Google Scholar]
  13. Mason CW. Structural colors in insects. 1. J Phys Chem. 1926;30:383–395. doi: 10.1021/j150261a009. [DOI] [Google Scholar]
  14. Mason CW. Structural colors in insects. 2. J Phys Chem. 1927;31:321–354. doi: 10.1021/j150273a001. [DOI] [Google Scholar]
  15. Morehouse NI, Vukusic P, Rutowski RL. Pterin pigment granules are responsible for both broadband light scattering and wavelength selective absorption in the wing scales of pierid butterflies. Proc R Soc B. 2007;274:359–366. doi: 10.1098/rspb.2006.3730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Nijhout HF. The development and evolution of butterfly wing patterns. Washington: Smithsonian Institution Press; 1991. [Google Scholar]
  17. Pirih P, Arikawa K, Stavenga DG. An expanded set of photoreceptors in the Eastern Pale Clouded Yellow butterfly, Colias erate. J Comp Physiol A. 2010;197:501–517. doi: 10.1007/s00359-010-0538-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Qiu X, Vanhoutte KJA, Stavenga DG, Arikawa K. Ommatidial heterogeneity in the compound eye of the male small white, Pieris rapae crucivora. Cell Tissue Res. 2002;307:371–379. doi: 10.1007/s00441-002-0517-z. [DOI] [PubMed] [Google Scholar]
  19. Rutowski RL, Macedonia JM, Morehouse N, Taylor-Taft L. Pterin pigments amplify iridescent ultraviolet signal in males of the orange sulphur butterfly, Colias eurytheme. Proc R Soc B. 2005;272:2329–2335. doi: 10.1098/rspb.2005.3216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Rutowski RL, Macedonia JM, Kemp DJ, Taylor-Taft L. Diversity in structural ultraviolet coloration among female sulphur butterflies (Coliadinae, Pieridae) Arthropod Struct Dev. 2007;36:280–290. doi: 10.1016/j.asd.2006.11.005. [DOI] [PubMed] [Google Scholar]
  21. Rutowski RL, Macedonia JM, Merry JW, Morehouse N, Yturralde K, Taylor-Taft L, Gaalema D, Kemp DJ, Papke RS. Iridescent ultraviolet signal in the orange sulphur butterfly (Colias eurytheme): spatial, temporal and spectral properties. Biol J Linn Soc. 2007;90:349–364. doi: 10.1111/j.1095-8312.2007.00749.x. [DOI] [Google Scholar]
  22. Scott JA. The butterflies of North America. Stanford: Stanford University Press; 1986. [Google Scholar]
  23. Stavenga DG, Arikawa K. Evolution of color and vision of butterflies. Arthropod Struct Dev. 2006;35:307–318. doi: 10.1016/j.asd.2006.08.011. [DOI] [PubMed] [Google Scholar]
  24. Stavenga DG, Stowe S, Siebke K, Zeil J, Arikawa K. Butterfly wing colours: scale beads make white pierid wings brighter. Proc R Soc Lond B. 2004;271:1577–1584. doi: 10.1098/rspb.2004.2781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Stavenga DG, Giraldo MA, Hoenders BJ. Reflectance and transmittance of light scattering scales stacked on the wings of pierid butterflies. Opt Express. 2006;14:4880–4890. doi: 10.1364/OE.14.004880. [DOI] [PubMed] [Google Scholar]
  26. Stavenga DG, Leertouwer HL, Pirih P, Wehling MF. Imaging scatterometry of butterfly wing scales. Opt Express. 2009;17:193–202. doi: 10.1364/OE.17.000193. [DOI] [PubMed] [Google Scholar]
  27. Stavenga DG, Wilts BD, Leertouwer HL, Hariyama T. Polarized iridescence of the multilayered elytra of the Japanese jewel beetle, Chrysochroa fulgidissima. Phil Trans R Soc B. 2011;366:709–723. doi: 10.1098/rstb.2010.0197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Vukusic P, Sambles JR. Photonic structures in biology. Nature. 2003;424:852–855. doi: 10.1038/nature01941. [DOI] [PubMed] [Google Scholar]
  29. Vukusic P, Sambles JR, Lawrence CR, Wootton RJ. Quantified interference and diffraction in single Morpho butterfly scales. Proc R Soc Lond B. 1999;266:1403–1411. doi: 10.1098/rspb.1999.0794. [DOI] [Google Scholar]
  30. Wijnen B, Leertouwer HL, Stavenga DG. Colors and pterin pigmentation of pierid butterfly wings. J Insect Physiol. 2007;53:1206–1217. doi: 10.1016/j.jinsphys.2007.06.016. [DOI] [PubMed] [Google Scholar]
  31. Wilts BD, Leertouwer HL, Stavenga DG. Imaging scatterometry and microspectrophotometry of lycaenid butterfly wing scales with perforated multilayers. J R Soc Interface. 2009;6 Suppl 2:S193–S202. doi: 10.1098/rsif.2008.0299.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wilts BD, Pirih P, Stavenga DG (2011) Iridescence and spectral properties of wing reflectance in pierid butterflies. J Comp Physiol A 197:693–702 [DOI] [PMC free article] [PubMed]
  33. Yoshioka S, Kinoshita S. Structural or pigmentary? Origin of the distinctive white stripe on the blue wing of a Morpho butterfly. Proc R Soc B. 2006;273:129–134. doi: 10.1098/rspb.2005.3314. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

359_2011_661_MOESM1_ESM.pdf (21.9KB, pdf)

Suppl. Fig. 1 Spatial map of G. rhamni indicating the measurement positions with black dots (PDF 22 kb)

359_2011_661_MOESM2_ESM.pdf (63.8KB, pdf)

Suppl. Fig. 2 Spatial maps integrated over wavelength bands of 340 ± 10 nm, 380 ± 10 nm, 420 ± 10 nm, 460 ± 10 nm and 700 ± 10 nm. a C. croceus. b G. rhamni. c G. aspasia. d G. cleopatra HW. e G. cleopatra FW. f H. glaucippe. and g C. regina. The colour coding is a map of the absolute projected reflectance in the range R* = [0 .. 1] (PDF 64 kb)

Articles from Journal of Comparative Physiology. A, Neuroethology, Sensory, Neural, and Behavioral Physiology are provided here courtesy of Springer

RESOURCES