Abstract
The tremendous evolutionary potential of RNA viruses allows them to thrive despite host defense mechanisms and endows them with properties such as emergence, host switching, and virulence. The frequency of mutant viruses after an infectious process results from the interplay between the error rate of the viral replicase, from purifying mechanisms acting after transcription on aberrant RNAs, and from the amplification dynamics of virus RNA positive (+) and negative (–) strands. Two extreme scenarios describing viral RNA amplification are the geometric growth, in which each RNA strand serves as template for the synthesis of complementary strands with the same efficiency, and the stamping machine, where a strand is reiteratively used as template to synthesize multiple copies of the complementary. The resulting mutation frequencies are completely different, being geometric growth largely more mutagenic than stamping machine. In this work we evaluate the contribution of geometric growth and stamping machine to the overall genome amplification of the plant (+)-strand RNA virus turnip mosaic virus (TuMV). By means of transfection experiments of Nicotiana benthamiana protoplasts with a TuMV cDNA infectious clone and by using strand-specific quantitative real-time PCR, we determined the amplification dynamics of viral (+) and (–) RNA during a single-cell infectious process. A mathematical model describing the amplification of each viral strand was fitted to the data. Analyses of the model parameters showed that TuMV (+) and (–) RNA amplification occurs through a mixed strategy with ∼93% of genomes produced via stamping machine and only ∼7% resulting from geometric growth.
RNA viruses are among the organisms displaying the fastest rates of evolution (Duffy et al. 2008), due to the combination of large population sizes and high mutation rates. Rapid evolution likely allows RNA viruses to thrive in the hostile environment of host cells where they replicate. In the case of positive (+)-strand RNA viruses, amplification of the viral genome is the result of an RNA-to-RNA transcription process that includes the synthesis of an antigenomic RNA intermediate of complementary polarity (–) that serves as the template for transcription of genomic (+) RNA progeny. This process occurs in the cytoplasm of infected cells in virus-induced membranous structures. There, the different components of the replication machinery, some encoded by the virus and others recruited from the host, act (Den Boon et al. 2010; Laliberté and Sanfaçon 2010). A central element in this machinery is the RNA-dependent RNA polymerase, the enzyme that ultimately catalyzes the synthesis of viral RNA. Positive-strand RNA viruses encode their own RNA polymerase, which always lacks proofreading exonuclease activity (Ferrer-Orta et al. 2006), a key property resulting in the high mutation rate of these pathogens (Sanjuán et al. 2010).
In addition to the error rate of the viral replicase, other factors also contribute to the mutation frequency resulting from the viral amplification process. One of them is the dynamics of within-cell viral (+) and (–) strands production. Two opposed theoretical scenarios describing the mode of the viral RNA amplification process are geometric growth and the so-called stamping machine (Sardanyés et al. 2009; Thébaud et al. 2010). When there is geometric growth, each RNA strand serves as a template for the synthesis of complementary strands with the same efficiency. In this replication mode, transcription errors are geometrically amplified, resulting in a relatively high mutation frequency, exceeding the error rate of the viral replicase. In the stamping machine, a few copies of the viral (–) replication intermediates produced from the genomic (+) RNA initially infecting the cell act as templates for the asymmetric synthesis of genomic (+) RNAs. In this case, the mutation frequency is approximately the error rate of the viral replicase, if purifying selection is disregarded. In other words, geometric replication within a cell results in a linear increase in the frequency of mutations per genomic (+) RNA molecules with the number of replication events, whereas for the stamping machine this frequency is independent of the number of replication cycles (Drake 1993; Drake and Holland 1999). In addition to this effect, geometric replication combined with the production of an excess of deleterious mutations has two other consequences for viral fitness (Sardanyés et al. 2009): (1) as templates that already carry de novo mutations will be used for replication during geometric growth, the average number of mutations per genome in a population is always larger than for the stamping machine, and (2) the average population fitness will be lower since the mutational load is higher. Due to all these properties, selection for increased mutational robustness may have favored the stamping machine replication strategy (Sardanyés et al. 2009). Given all these potential disadvantages, it is not obvious whether geometric replication may provide any clear advantage for RNA viruses. An advantage may be a more efficient evasion from immune pressures by quickly finding the right combination of escape mutations. However, this benefit should be balanced by the excessive production of deleterious mutations (Elena and Sanjuán 2005).
In practice, it is expected that the different (+)-strand RNA viruses employ an RNA amplification strategy that combines, at least to some extent, both of these opposed modes of replication. The extent to which geometric amplification and the stamping machine modes of replication contribute to the overall amplification of viral RNA is of fundamental importance to the biology of RNA viruses. Moreover, the mode of amplification will have strong implications for important phenomena such as the ability to escape from host defense mechanisms or adaptation to new hosts, in short, for properties such as virulence and viral emergence. Despite this importance, little information on the preferred modes of replication used by different RNA viruses is available. Exceptional in this sense is the work of Chao et al. (2002). Analyzing the distribution of spontaneous mutations produced after a single burst of bacteriophage φ6, these authors showed that φ6 replicated mostly according to a stamping machine, although a minor fraction of the produced (+) progeny also served as templates for producing additional (–) strands.
In this work, the accumulation dynamics of (+) and (–) RNAs of the plant (+)-strand RNA virus Turnip mosaic virus (TuMV) during a single infection process of Nicotiana benthamiana protoplasts are analyzed and the contributions of geometric growth and the stamping machine mode of amplification are evaluated. TuMV belongs to genus Potyvirus within the family Potyviridae and is phylogenetically related to the Picorna-like supergroup of (+)-strand RNA viruses (Koonin et al. 2008). TuMV consists of a genomic RNA of approximately 10,000 nt, linked at the 5′ end to a viral protein (VPg) and with a poly(A) tail at the 3′ end. It encodes about 11 mature gene products that result from the processing of a large viral polyprotein by three viral proteases (Urcuqui-Inchima et al. 2001) and a second polypeptide derived from a translational read-through process (Chung et al. 2008).
To determine the accumulation dynamics of TuMV (+) and (–)-RNA strands, two experimental obstacles had to be overcome. The first is specific PCR amplification of the viral (–) strands, for the purpose of quantification, without interference from the most abundant (+) strands. This was achieved by optimizing the conditions of the reverse transcription (RT) reaction performed prior to quantitative real-time PCR (qPCR) and by employing RT primers tagged at the 5′ end with specific nonviral sequences (Plaskon et al. 2009). The second obstacle was to discriminate between (+) strands from the inoculum, and those resulting from viral amplification. This distinction is especially important immediately after transfection, when inoculum (+) strands could account for most of the (+)-strand genomic RNA present in the sample. This obstacle was overcome by starting infection from a virus cDNA clone under the control of Cauliflower mosaic virus (CaMV) 35S promoter and Agrobacterium tumefaciens nos terminator. The use of this construct ensured constitutive transcription of inoculum (+) strands at stable levels throughout the experiment, or at least until the infection finally exhausts the cellular resources or significantly shuts down cellular processes. As we show below, the constitutive expression of TuMV (+) RNA from the plasmid did not interfere with our ability to quantify the (+) molecules resulting from viral replication. Similarly, we show that no (–) strands were produced from the plasmid. A simple mathematical model describing viral RNA accumulation dynamics and correcting for the contribution of the viral (+) strands by continuous transcription from the 35S promoter was used to fit the experimental data. The quantitative data showed that in a single TuMV burst in protoplasts, viral RNA strands amplify asymmetrically with a final preponderance of the (+) strand of about 2 orders of magnitude. From the analyses of the model parameters we inferred that (+) and (–) amplification occur through a mixed strategy in which ∼93% of genomes are produced by stamping machine amplification and only ∼7% result from geometric growth.
Materials and Methods
Plasmids
Plasmid pTuMV contains an infectious TuMV cDNA clone obtained from calla lilly (Zantedeschia sp.) infected with the TuMV isolate YC5 (Chen et al. 2003), under the control of CaMV 35S promoter and A. tumefaciens nos terminator. The cloned TuMV sequence variant corresponds to GenBank accession no. AF530055.2 with a few sequence variations. pTuMV-VNN is a derivative of pTuMV in which the tripeptide GDD (5′-GGAGATGAT-3′, positions 5976–5984) in the active center of the viral RNA polymerase NIb was mutated to VNN (5′-GTCAATAAT-3′). pTuMV-GFP is another derivative of pTuMV in which the TuMV cDNA is tagged with a green fluorescent protein (GFP) cDNA in between the NIb and coat protein (CP) cistrons. The GFP cDNA includes an artificial NIaPro proteolytic cleavage site that mediates GFP release from the viral polyprotein. pCP3′UTR+ and pCP3′UTR-contain the same TuMV cDNA encompassing the CP cistron and the 3′-untranslated region (UTR) (from position 8757 to 9832 in AF530055.2) under the control of bacteriophage T3 RNA polymerase promoter in opposite orientations. In vitro transcription with T3 RNA polymerase of these plasmids linearized with XbaI produce two partial-length TuMV RNA molecules (CP cistron plus 3′ UTR) in (+) and (–) polarities.
Protoplast transfection
N. benthamiana Domin plants were grown under 16 hr light at 23° and 8 hr dark at 20°. For transfection experiments (Yoo et al. 2007), aliquots of 1 g of fully expanded leaves cut into 1.5- to 2-mm strips were vacuum infiltrated in 10 ml of enzyme solution (0.9% cellulase RS, 0.4% macerozyme R10, 20 mm MES pH 5.7, 0.4 m mannitol, 20 mm KCl, 10 mm CaCl2, and 0.1% BSA) for 5 min and incubated in the dark for 3 hr at 24°. Released protoplasts were filtered through a 75-nm nylon mesh, recovered by centrifugation at 700 rpm for 1 min, and washed by centrifugation in 10 ml of W5 solution (154 mm NaCl, 125 mm CaCl2, 5 mm KCl, and 2 mm MES pH 5.7). Protoplast concentration was adjusted to 105 ml−1 in W5, followed by incubation on ice for 30 min. Prior to transfection, protoplasts were pelleted and resuspended in MMg transfection solution (0.4 m mannitol, 15 mm MgCl2, and 4 mm MES pH 5.7) at a concentration of 106 ml−1. Aliquots of 100 μl protoplast suspension (105 protoplasts) were mixed with 10 μl DNA (30 μg of the corresponding plasmid) and 110 μl of PEG-Ca transfection solution (40% polyethylene glycol 4000, 0.2 m mannitol, 100 mm CaCl2, and 10% dymethyl sulfoxide). After 1 min incubation the transfection was stopped by adding 440 μl of W5 solution. The different aliquots of transfected protoplasts were combined, washed with W5 solution by centrifugation, and divided into a number of aliquots containing 2 × 105 protoplasts according to the time points in the experiment. Transfected protoplasts were incubated in a growth chamber under 16 hr light at 24° and 8 hr dark at 20°. At the selected time points, protoplasts were harvested by centrifugation at 700 rpm for 2 min, resupended in Trizol reagent (Invitrogen), and stored at –80° for RNA extraction.
RNA purification
Total RNA was purified using the Trizol reagent. Contaminating DNA was digested with DNase I (Fermentas). Treated RNA was extracted with phenol:chloroform (1:1) pH 8.0, precipitated with isopropanol, and resuspended in 12 μl H2O. RNA concentration was measured spectrophotometrically (Nanodrop, Thermo Scientific).
RNA quantification
(+) and (–) TuMV RNA was quantified by RT–qPCR using the quantified partial-length TuMV RNAs (CP plus 3′-UTR) of (+) and (–) polarities as standards. The (+)-RNA standard ran from 1.28 × 108 to 4 × 104 molecules at 1/5-fold dilution intervals. The (–) RNA standard ran from 6.2 × 106 to 2 × 103 molecules also at 1/5-fold dilution intervals. The Primer Express program (Applied Biosystems) was used for primer design. Aliquots of 100 ng of protoplast total RNA were reverse transcribed in triplicate in the presence of 250 nm either the (–) primer PI (5′-GGCCGTCATGGTGGCGAATAATAACCCCTTAACGCCAAGTAAG-3′, nonviral 5′ tag underlined, sequence complementary to TuMV GenBank accession no. AF530055.2 positions 9599–9620 not underlined) or the (+) primer PII (5′-GGCCGTCATGGTGGCGAATAACAATACGTGCGAGAGAAGCACAC-3′, nonviral 5′ tag underlined, sequence homologous to TuMV positions 9448–9470 not underlined) with Superscript III reverse transcriptase (Invitrogen) in 20-μl reactions for 30 min at 55°. Previous to reaction, primers were allowed to anneal by incubating 5 min at 70° and snap cooling on ice. Reverse transcription reaction was stopped by heating at 85° for 10 min. Sequence specific qPCR was performed in 20 μl final volume using the Maxima SYBR Green Master Mix reagent (Fermentas) at 95° for 10 min followed by 40 cycles of 15 sec at 95°, 1 min at 60°, and 25 sec at 79°. TuMV (+) RNA was quantified from 2 μl of the reverse transcription reaction performed with primer PI by using 250 nm primers PIII (5′-AATAAATCATAACAATACGTGCGAGAGAAGCACAC-3′, sequence homologous to TuMV positions 9448–9470 roman type) and PIV (5′-AATAAATCATAAGGCCGTCATGGTGGCGAATAA-3′, sequence equal to the 5′ tag of PI and PII underlined) and TuMV (–) RNA from 2 μl of the reverse transcription reaction performed with primer PII by using 500 nm of primers PIV and PV (5′-AATAAATCATAATAACCCCTTAACGCCAAGTAAG-3′, sequence complementary to TuMV positions 9599–9620 roman type). Primers PIII to PV contained 5′ flaps (italicized sequence) to improve qPCR (Afonina et al. 2007). Potential nonspecific amplification products were monitored by a one cycle incubation of 15 sec at 95°, 1 min at 60°, and 15 sec at 95°.
Mathematical model and data analyses
Mathematical modeling of the accumulation dynamics of (+) and (–) TuMV RNAs:
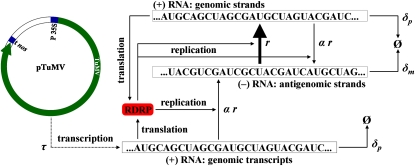
In this section we present a simple unstructured model describing the dynamics of RNA virus accumulation that allows for the analysis of different modes of amplification. This mean field model describes the change over time of three state variables: p35S, prepl, and m. Variable p35S denotes the concentration of the (+) RNA molecules transcribed from the 35S promoter used to initiate the infection. The other two variables, prepl and m, correspond, respectively, to the concentration of (+) and (–) RNA molecules produced by the viral replicase from the corresponding RNA template (see Figure 1 for a schematic description of the modeled system). The model is given by the following set of three ordinary differential equations:
| (1) |
| (2) |
| (3) |
with
| (4) |
Figure 1.—
Scheme of the dynamical system modeled with Equations 5 and 6. The model considers that after initiation of the cDNA transcription, a given sequence is replicated giving place to the complementary strand at a rate r. The parameter α takes into account the mode of replication. When α = 1, the replication is geometric whereas α close to zero represents the stamping machine. Degradation rates for the genomic and antigenomic strands are described by the parameters δp and δm, respectively. TuMV cDNA transcription from plasmid pTuMV is driven by CaMV 35S promoter (P 35S) and A. tumefaciens nos terminator (t nos) at a rate τ.
The function Φ imposes a logistic growth restriction to viral amplification due to finite cellular resources. Parameter K plays the role of the cellular carrying capacity (i.e., the maximum number of viral RNA molecules that can be produced in an infected cell). This type of growth constraint is a common assumption in replicators growing in finite systems (Murray 1989). The parameter τ > 0 is the rate of production of (+) RNA molecules from the cDNA under the control of the 35S promoter, which for simplicity is assumed to be time independent. The parameters δp > 0 and δm > 0 are the degradation rates of (+) and (–) RNA molecules, respectively. The amplification rates of the viral (+) and (–) RNA molecules by the viral replicase are given by the parameters r > 0 and rm > 0, respectively. To model the asymmetry in the amplification of both polarities, we introduce a parameter α ∈ (0, 1], so the replication rate of (–) strains can be expressed as a function of the replication rate of the (+) strands: rm = αr. With α = 1, both strands replicate at the same rate and thus replication is purely geometric. For values of α → 0, amplification will be closer to the stamping machine mode. Furthermore, it is plausible that as (+) RNAs accumulate in the cell, they may start inhibiting the synthesis of (–) strands by any kind of feedback regulatory mechanism. Mathematically, this can be conveniently described by a Hill function
where ψ measures the negative effect of (+) strands on the synthesis of (–) ones and θ is the Hill exponent. For simplicity, we assume that (+) strands do not cooperate in inhibiting the synthesis of (–) templates and thus θ = 1. If ψ = 0, (+) strands do not inhibit the synthesis of (−) ones and thus rm = αr. If ψ > 0, (+) strands inhibit the synthesis of (−) strands. In this case, the two extreme scenarios are: (i) if the concentration of (+) strands is low (p → 0), the rate of (−) synthesis is still given by rm = αr; (ii) if the concentration of (+) strands is very large (p → ∞), then rm → 0 and thus the synthesis of (−) strands has been effectively shutoff.
In practical terms, (+) RNA molecules synthesized from 35S transcription or viral replication are indistinguishable; therefore, the previous model can be reduced to a two-dimensional dynamical system by considering the whole pool of (+) RNA molecules as a single variable p = p35S + prepl. Then, from , we obtain
| (5) |
| (6) |
now with . Since the amplification of the viral strands by the viral replicase necessarily starts after the first (+) strands are transcribed from the cDNA, we assume as initial conditions p(0) = m(0) = 0.
Model-fitting algorithm:
Equations 5 and 6 were used to fit the data sets using a Monte Carlo simulated annealing (MCSA) method (Kirkpatrick et al. 1983). For each experiment, data values were first normalized by dividing each time series by the maximum value in the list (in all the cases for (+) strands). Equations 5 and 6 were then used to generate simulated time series using the fourth-order Runge–Kutta method with a constant time step size ∆t = 0.01 hr, and a total number of 8000 iterations, which resulted in a similar time scale to the one used in the experiments (i.e., 80 hr). The MCSA algorithm searches possible parameter configurations such as that the sum of the squares of the deviations between the experimental and the simulated data are minimized. Specifically, Sp and Sm are least-squares computed, respectively, from the data for (+) and (−) strands, with k ∈ {p, m}. Here yi corresponds to the experimental value at time i, and φk(xi, b) is the value of variable k obtained numerically from the model at time i and b = {α, r, τ, K, δp, δm, ψ} is a vector containing all the parameters of the mathematical model. The least-squares are computed by means of all the residuals for all the available replicas at each time point. For the simultaneous optimization of Sp and Sm a Pareto objective function, , was constructed with λ = 0.5. The following rules were applied during the optimization process: (i) small random modifications were introduced to all the parameters in vector b; (ii) using this modified b, the corresponding time series were obtained numerically from Equations 5 and 6; (iii) a new objective function (Snew) was computed; and (iv) if the new parameters improved S (i.e., Snew ≤ S), then the parameters were accepted and S = Snew. Otherwise, the new set of parameters was accepted with probability exp(−∆S/T), where ∆S = Snew − S, and T is a temperature parameter that decreases exponentially with the number of iterations (10−2 ≤ T ≤ 10−4). The process i–iv was iterated 105 times. The parameter values reported for each experimental set were computed as the median from 500 independent runs of the MCSA algorithm. The 95% confidence intervals were constructed from the 2.5% and 97.5% quantils.
Results
Strand-specific quantification of viral RNA by RT–qPCR
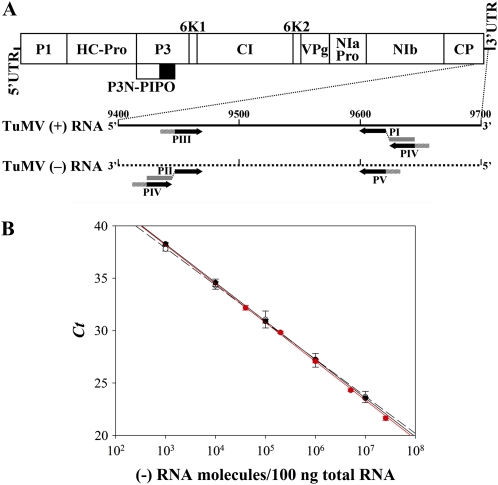
The quantification of TuMV (+) and (–) strands in protoplasts at short times post-transfection requires a technique with a low detection limit, such as RT–qPCR. However, it has been repeatedly demonstrated that this technique must be carefully optimized to achieve strand-specific detection (Bessaud et al. 2008; Plaskon et al. 2009; Tuiskunen et al. 2010). To quantify (+) and (–)-TuMV strands by RT–qPCR, the amplification of a 173-bp cDNA fragment at the end of CP cistron (positions 9448–9620 in GenBank accession AF530055.2) was selected using a qPCR primer design program. Two RNA species corresponding to the TuMV CP cistron plus the 3′-UTR in both (+) and (–) polarities were synthesized by in vitro transcription. These two RNAs were used as standards and to optimize the quantification protocol. Optimal strand-specific RT–qPCR amplification was obtained only when the RT reactions were performed at a temperature as high as 55° and when the RT primers were tagged at the 5′ ends with specific nonviral sequences used subsequently for the qPCR primers as described by Plaskon et al. (2009) (Figure 2A). qPCR primers also included AT-rich 5′ flaps to improve the quantification (Afonina et al. 2007) (Figure 2A). The control experiment in Figure 2B shows detection by RT–qPCR of different amounts of TuMV (–) RNA, ranging from 103 to 107 molecules, with no interference of 106 copies of complementary TuMV (+) RNA in a preparation of plant protoplast total RNA. The two standard curves obtained in the absence and in the presence of 106 TuMV (+) RNA molecules were similar, with slopes of –3.675 ± 0.030 and –3.539 ± 0.092 and R2 values of 0.999 and 0.991, respectively. The calculated amplification efficiencies were 87.12 and 92.03%, respectively. Figure 2B also shows the standard curve obtained for the RNA (+), which has a slope of –3.692 ± 0.042 (R2 = 0.998) and amplification efficiency of 86.58%.
Figure 2.—
(A) Diagram describing the primers used in the strand-specific RT–qPCR amplification to quantify the (+) and (–)-TuMV RNAs. The RT primers (PI and PII) were tagged at the 5′ end with specific nonviral sequences (shaded bars). The qPCR primers (PIII to PV) were tagged at the 5′ end with AT-rich flaps (hatched bars). Indicated in the diagram are the positions of TuMV genome untranslated regions (5′−UTR and 3′−UTR) and cistrons (P1, HC-Pro, P3, P3N-PIPO, 6K1, CI, 6K2, VPg, NIaPro, NIb, and CP). (B) Strand-specific quantification of TuMV RNAs by RT–qPCR. Black symbols correspond to the standard curves obtained for the RNA (–) in the absence (solid circles and continuous line) or in the presence (open circles and dash line) of a competing amount of 106 TuMV (+) RNA molecules. Red symbols correspond to the standard curves obtained for the RNA (+). The average of three replicate determinations of the Ct parameter is plotted vs. the amount of TuMV RNA molecules per 100 ng of plant total RNA evaluated spectrophotometrically. Bars, ±1 SD.
Transfection of N. benthamiana protoplasts with TuMV cDNA
To study the dynamics of (+) and (–) TuMV RNA accumulation during replication in single cells, we transfected N. benthamiana protoplasts. N. benthamiana is a well-established experimental host for this virus. The idea of using virions or purified viral RNA was discarded because this kind of inoculum cannot be entirely removed after transfection, and the remains would interfere with the subsequent quantification of viral RNA. Therefore, transfection with plasmid DNA containing an infectious TuMV cDNA clone under 35S promoter and nos terminator control was chosen. This inoculum does not interfere with subsequent RNA quantification. In this case, infection is started by the synthesis of copies of TuMV (+) RNA in transfected protoplasts. To control for transfection efficiency in different experiments, a plasmid containing the same TuMV cDNA clone tagged with GFP, TuMV-GFP, was used.
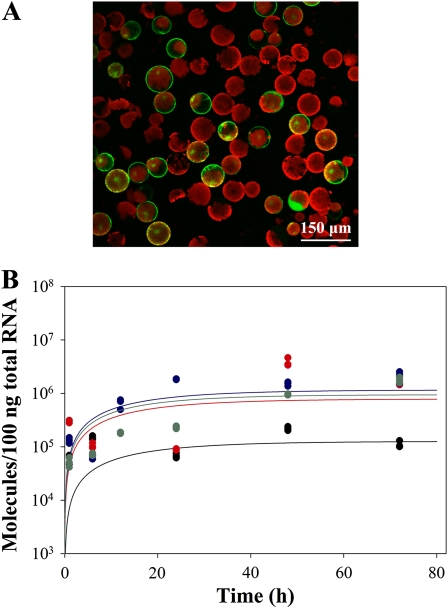
Protoplasts obtained from adult N. benthamiana leaves were transfected with plasmid DNA preparations at a ratio of 30 μg DNA per 106 protoplasts. Immediately after transfection, protoplasts were washed, aliquoted, and incubated in culture medium. At different times post-transfection total RNA was purified, minor amounts of contaminating DNA exhaustively removed by digestion with DNase I, and TuMV (+) and (–) strands quantified by RT–qPCR. When TuMV-GFP was transfected in a control experiment, a fraction of the protoplasts showed an intense green fluorescence 48 hr after transfection when observed under the fluorescence microscope (Figure 3A). Observation under the fluorescence microscope of the protoplast aliquots transfected with TuMV-GFP at 48 hr post-transfection indicated that the average transfection efficiency for this control plasmid in the three independent experiments was 37.5% (±2.5).
Figure 3.—
(A) N. benthamiana protoplasts infected by TuMV-GFP. Fluorescence micrograph at 48 hr post-transfection showing GFP expression in the fraction of protoplasts that resulted infected with TuMV-GFP. (B) Accumulation dynamics of (+) TuMV RNA in N. benthamiana protoplasts transfected with a plasmid expressing the replication-defective TuMV-VNN mutant. Plot of TuMV (+) RNA molecules in 100 ng of plant total RNA vs. time in four independent transfection experiments. Each experimental data correspond to the average of three RT–qPCR determinations. Different experiments are represented with different colors. Solid lines represent the best fit of Equation 7 to the control data.
Transfection of N. benthamiana protoplasts with replication-defective TuMV-VNN results in no accumulation of (–) strands
Plasmid-driven transcription of TuMV (+) RNA continued throughout the experiment, contributing to the overall amount of TuMV (+) RNA. Therefore, it is important to evaluate the contribution of this source of (+) RNA to the total amount as well as to confirm that no (–) strands are produced from the plasmid. To this end, a plasmid containing TuMV with the lethal triple mutation GDD to VNN in the active core of the viral RNA polymerase NIb, TuMV-VNN, was used. The amount of TuMV (+) RNA per 100 ng of plant total RNA was quantified in triplicate at different times post-transfection in four transfection experiments (Figure 3B). Very importantly, no (–) strands were detected at all in any of the four experiments, thus discarding the possibility of these strands being produced from the cDNA. Since (–) did not accumulate in this experiment, Equation 1 can be simplified to
| (7) |
and it can be fitted to the data shown in Figure 3B using the MCSA method, allowing us to estimate the corresponding parameters (the solid lines represent the best fittings). On average, the 35S promoter produced (+) strands at a rate τ = 0.0653 molecules/hr (95% CI: 0.0012, 0.0821) and strains were degraded at a rate δp = 0.0610 molecules/hr (95% CI: 0.0017, 0.0839). Synthesis and degradation of (+) strands reached an equilibrium value of K = 5.105 × 106 molecules (95% CI: 4.659 × 106, 5.543 × 106).
N. benthamiana protoplasts transfected with the wild-type TuMV accumulate RNAs of both polarities
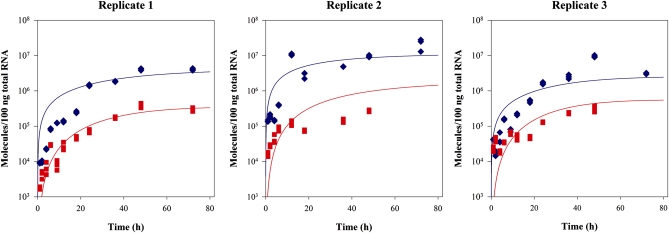
Using optimized RT–qPCR conditions that allow for strand-specific quantification of TuMV (+) and (–) RNA molecules, three independent transfection experiments were performed. For protoplasts transfected with TuMV, aliquots were taken at different times post-transfection, total RNA was purified, and the (+) and (–) TuMV RNA was quantified in triplicate. The number of TuMV (+) and (–) RNA molecules per 100 ng of plant total RNA was calculated from standard curves obtained under the same conditions with in vitro synthesized standards (Figure 4).
Figure 4.—
Accumulation dynamics of (+) and (–) TuMV RNA in infected N. benthamiana protoplasts. Plot of TuMV (+) (blue diamonds) and (–) (red squares) RNA molecules in 100 ng of plant total RNA vs. time in three independent transfection experiments. For each time point (+) and (–) RNAs were determined by triplicate. Solid lines represent the best fit of Equations 5 and 6 to the data: (+) strands in blue, (–) strands in red.
First, we sought for differences in the accumulation levels after transfecting protoplasts with wild-type TuMV (Figure 4) and with TuMV-VNN (Figure 3B). A general linear model was fitted to the accumulation data to assess for differences between the amounts of (+) RNA accumulated. Both the genotype of the virus in the inoculum and the experimental replicates were treated as random factors, with the second factor nested within the first. Time was treated as a covariable. First, a significant positive effect of time on the amount of (+) RNA measured was observed (χ2 = 225.677, 1 d.f., P < 0.001). Second, the accumulation of (+) RNA was, overall, 7.3-fold larger for TuMV than for the nonreplicative defective virus, a significant difference (χ2 = 25.812, 1 d.f., P < 0.001), reflecting the contribution of TuMV replication via intermediary (−) RNA in the former case. Finally, significant differences between replicates exist in both types of experiments (χ2 = 79.744, 5 d.f., P < 0.001). This difference is explained in terms of model parameters in the following section.
Therefore, we conclude that our experimental setup allows for (i) detecting the accumulation of (–) in a highly efficient manner and (ii) accounting for the accumulation of (+) strands due to viral replication from those produced by constitutive transcription from the plasmid.
Model fitting to experimental data and parameter determination
Figure 4 illustrates the results of the MCSA best fitting of Equations 5 and 6 to the experimental data. Table 1 shows the parameter values estimated for all three replicates as well as the values estimated after pooling together all the available data (last column). The three experiments rendered fully consistent estimates (overlapping 95% CI) for r, δp, δm, K, τ, and ψ and a minor discrepancy among experiments for α. Estimates of α were homogeneous for replicates 1 and 2, and significantly larger for replicate 3 (its 95% CI did not overlap with those obtained for the other two replicates). Indeed, this heterogeneity in α explains the significant differences among accumulation curves described in the previous section. In all cases, the 95% confidence intervals of the estimated parameters excluded zero, supporting their statistical significance.
TABLE 1.
Model parameters estimated by MCSA
| Parameter (units) | Replicate 1 | Replicate 2 | Replicate 3 | Average values |
| α | 0.0622 (0.0346, 0.1023) | 0.0654 (0.0094, 0.1114) | 0.1695 (0.1351, 0.2084) | 0.0743 (0.0264, 0.1941) |
| r (molecules/h) | 0.1217 (0.0937, 0.1707) | 0.1175 (0.0658, 0.1703) | 0.1220 (0.0981, 0.1691) | 0.1211 (0.0758, 0.1704) |
| δp (molecules/h) | 1.088 × 10−4 (1.790 × 10−6, 0.0076) | 0.0286 (0.0063, 0.0606) | 0.0040 (8.554 × 10−4, 0.0137) | 0.0049 (5.508 × 10−6, 0.0544) |
| δm (molecules/h) | 0.0081 (4.332 × 10−4, 0.0396) | 0.0184 (0.0012, 0.0674) | 0.0141 (0.0028, 0.0443) | 0.0121 (8.107 × 10−4, 0.0564) |
| K (molecules) | 4.694 × 107 (4.561 × 107, 4.887 × 107) | 3.061 × 107 (2.936 × 107, 3.222 × 107) | 3.537 × 107 (3.399 × 107, 3.659 × 107) | 4.694 × 107 (3.460 × 107, 3.158 × 108) |
| τ (molecules/h) | 0.0170 (0.0132, 0.0212) | 0.0132 (0.0086, 0.0204) | 0.0167 (0.0144, 0.0191) | 0.0163 (0.0094, 0.0204) |
| ψ (1/molecules) | 3.340 × 10−8 (4.154 × 10−9, 7.717 × 10−8) | 7.159 × 10−9 (6.880 × 10−10, 1.689 × 10−8) | 4.581 × 10−8 (5.486 × 10−9, 1.161 × 10−7) | 2.862 × 10−8 (1.602 × 10−9, 9.240 × 10−8) |
Each one of the three experimental replicates has been fitted to the model independently. Confidence limits represent the 95% confidence intervals obtained from 500 realizations of the numerical optimization process.
The observed asymmetry in the accumulation of both RNA polarities may result from two sources: (i) a preponderance of stamping machine, measured in our model by the parameter α, and (ii) any potential inhibition that (+) strands may have on the synthesis of (–) templates, measured by the parameter ψ. This second possibility, indeed, is particularly worrisome in our experiments due to the constant input of (+) RNA molecules transcribed from the plasmid. In all three cases, the amplification asymmetry parameter, α, was closer to zero than to one, thus indicating that TuMV replication was mainly dominated by the stamping machine. Indeed, the results are compatible with a picture in which, on average, 100 × (1 − 0.0743) = 92.57% of all TuMV genomes produced during a single cycle of cell infection are so by means of the stamping machine mode while only a minor proportion would result from additional rounds of geometric amplification. The estimated ψ value was significantly larger than zero, although very small. Indeed, the rate of synthesis of (–) strands would be halved only if the concentration of (+) strands becomes 1/ψ = 3.494 × 107 molecules, a value that is reached only at the very end of our experiments and is close to the carrying capacity K (Table 1). Therefore, we conclude that the observed asymmetry in the accumulation of both strains is mostly driven by the stamping machine mechanism of replication and not by the inhibition of the synthesis of (–) strands as (+) strands accumulated.
The comparison between the transcription rate from the cDNA 35S promoter, τ, and the synthesis of viral (+) RNAs by the viral replicase, r, shows that, on average, 7.4 times more molecules resulted from viral replication than from transcription of the cDNA. The difference between both rates was highly significant as confirmed by the nonoverlapping 95% CIs. This difference is in good agreement with the excess of (+) RNAs accumulated by the replicative virus relative to the nonreplicative virus (Figure 3B and related statistical analyses). On average, the degradation rate of the (+) RNAs, δp, was 2.5 times lower than that estimated for the (–) RNA molecules, δm. This asymmetry in the degradation rates could be easily explained by (+) RNAs being protected from degradation by RNases by the binding of VPg at 5′, the existence of the 3′-poly(A) tail and, obviously, encapsidation. However, the observed difference was not statistically significant due to the large overlap between the associated 95% CIs. The overall rate of (+) RNA synthesis (τ + r) was, on average, 28-fold greater than its degradation rate, δp, suggesting that for the time frame of the experiments, RNA degradation played a negligible role.
Finally, it is worth mentioning that the estimates of τ and δp obtained from the control experiments with TuMV-VNN (Figure 3B) did not statistically differ from those above (overlapping 95% CIs).
Discussion
The amplification dynamics of the (+) and (–) strands occurring during the replication of a (+)-strand RNA virus like TuMV is a fundamental parameter to understanding the accumulation of mutations in viral populations. Moreover, it is therefore relevant for understanding phenomena such as interactions between the virus and host defensive systems, and viral emergence or adaptation to new hosts. This dynamics also reflects certain aspects of virus molecular biology, such as the fraction of viral genomic RNA that acts as a template for amplification or translation, during each moment of the replication cycle. Pioneering studies have shown that in the case of (+)-strand RNA viruses, RNA replication is asymmetric and that the prevalence of (+)-strand results is several orders of magnitude higher than (–) strands from the replication process. In this work our aim is to establish the dynamics of (+) and (–)-strand accumulation of TuMV during a single-replication cycle in N. benthamiana protoplasts. Previous works have reported differences in the accumulation of (+) and (–)-sense strands for plant viruses (Palani and Lin 2007), but none of them provided dynamical accumulation data and, hence, it was not possible to make inferences about the underlying dynamics of production of strands of both polarities.
The RT–qPCR technique used in this work is suitable for detecting low levels of viral RNAs produced early in the infection process. However, as has been repeatedly reported, this technique lacks strand specificity (Afonina et al. 2007; Bessaud et al. 2008), presenting a serious challenge at determining both (+) and (–)-strand amplification dynamics. One of the reasons proposed to explain this lack of strand specificity is the ability of reverse transcriptases to use very short primers, including RNA primers, which facilitates heterologous priming and RNA self-priming during the RT reaction (Tuiskunen et al. 2010). Plaskon et al. (2009) solved this problem in the case of O'nyang-nyang virus RNA by using RT primers tagged with specific 5′-nonviral sequences and using one qPCR primer consisting of this nonviral sequence. The use of this strategy in our work (Figure 2A) allowed accurate quantification of as low as 103 molecules of TuMV (–) RNA in a preparation of total RNA from N. benthamiana protoplasts (Figure 2B). The qPCR primers used in this work also included AT-rich flaps (Figure 2A), previously shown to improve qPCR performance (Afonina et al. 2007).
Another methodological challenge for the accurate determination of the viral (+) and (–) RNA accumulation dynamics is the interfering effect of the material used to start the infection. Viral RNA coming from an in vitro transcription or a virion preparation cannot be entirely removed after transfection or infection, interfering with subsequent virus RNA determination. In this work this problem is solved by starting infection with a TuMV cDNA under the control of the 35S promoter and nos terminator. The use of a replication-defective TuMV mutant (TuMV-VNN) allowed for a correction for TuMV (+) RNA coming from 35S-driven transcription (Figure 3) vs. that coming from viral replication. Our mathematical analyses confirm the validity of this approach. In fact, the rate of production of TuMV (+) RNA by the viral replicase is about seven times larger than the production of transcripts driven by the 35S promoter.
Once the RNA accumulation curves were determined, we estimated by means of a dynamical mathematical model which part of the viral progeny comes from a geometric growth process and what part from a stamping machine amplification mode. Our results support the view that TuMV amplification follows a mixed strategy, which is largely dominated by the stamping machine mode (∼93%). What are the evolutionary consequences of such a conservative replication strategy? If replication was purely geometric, then the expected fraction of mutant genomes produced per infected cell would depend on the number of replication rounds, k, according to the expression 1 − e−ku, where u is the genomic mutation rate. By contrast, if replication proceeds as a pure stamping machine, this fraction is independent of k and given by the expression 1 − e−u. The estimates of k and u recently obtained for another closely related potyvirus, Tobacco etch virus (Tromas and Elena 2010), can be used to evaluate these two expressions: u = 0.045 and k = 13.4. In the case of a pure geometric model, 45.28% of genomes produced will be mutant, whereas in the case of a pure stamping machine, this number is reduced to 4.40%. Therefore, for a mixed replication model like that described here for TuMV, the fraction of mutant genomes can be computed as 0.9257 × 0.0440 + (1 − 0.9257) × 0.4528 = 0.0744. In other words, during TuMV replication, only 7.4% of the (+) RNA genomes produced will be mutants. Of course this computation should be taken with caution given the uncertainties associated with the actual values of k and u for TuMV.
By lowering the number of mutant genomes produced per cell infection, the stamping machine can be considered as a mechanism of mutational avoidance and, somehow, a way of increasing population robustness against mutations. Robustness is defined as a reduced sensitivity to perturbations affecting phenotypic expression. It has been proposed that several mechanisms may contribute to the robustness of RNA virus populations (Elena et al. 2006), some being intrinsic to virus replication (e.g., complementation, neutrality), while others are extrinsic and the consequence of the exploitation of cellular buffering mechanisms (e.g., heat-shock chaperones). Viruses as different as TuMV (here), φ6 (Chao et al. 2002), and φX174 (Denhardt and Silver 1966) have been shown to replicate mostly via the stamping machine mode, suggesting that selection may have operated on independent viral lineages to favor this replicative strategy, perhaps as a way of reducing the population mutational load.
Perhaps it needs to be highlighted that our experimental protocol allowed only for a single cycle of cell infection. Accordingly, our mathematical model simulates only the replication process within an infected cell, and what we demonstrate here is that intracellular TuMV amplification mainly follows a stamping machine strategy. However, it must be taken into consideration that within a multicellular host, virus population growth, as a first approximation, will still be a geometric process with rate R, where R stands for the average number of newly infected cells per already infected one. This population growth dynamic explains why viral population can reach very large sizes in very short times, despite that the actual RNA replication mechanism may be linear.
Our interdisciplinary work provides a dynamical characterization for the intracellular accumulation of viral RNA genomes and the estimates for key parameters tied to replication obtained from a simple mathematical model. The availability of biologically meaningful parameters obtained from in vivo quantification experiments is important for further investigations, especially for the fields of theoretical or computational biology.
Acknowledgments
Special thanks are due to Javier García-Andrade for his generous help and useful suggestions in protoplast transfection work, to Javier Carrera for help with the Monte Carlo simulated annealing algorithm, Mark P. Zwart for critical reading of the manuscript, and two anonymous reviewers for insightful comments and suggestions. F.M. is the recipient of a predoctoral fellowship from Universidad Politécnica de Valencia. This work has been supported by grants BIO2008-01986 (J.A.D.) and BFU2009-06993 (S.F.E.) from the Spanish Ministerio de Ciencia e Innovación, RGP2008/12 from the Human Frontier Science Program Organization and PROMETEO/2010/019 from the Generalitat Valenciana. We also acknowledge support from the Santa Fe Institute.
Literature Cited
- Afonina I., Ankoudinova I., Mills A., Lokhov S., Huynh P., et al. , 2007. Primers with 5′ flaps improve real-time PCR. Biotechniques 43: 770–774 [DOI] [PubMed] [Google Scholar]
- Bessaud M., Autret A., Jegouic S., Balanant J., Joffret M. L., et al. , 2008. Development of a Taqman RT-PCR assay for the detection and quantification of negatively stranded RNA of human enteroviruses: evidence for false-priming and improvement by tagged RT-PCR. J. Virol. Meth. 153: 182–189 [DOI] [PubMed] [Google Scholar]
- Chao L., Rang C. U., Wong L. E., 2002. Distribution of spontaneous mutants and inferences about the replication mode of the RNA bacteriophage φ6. J. Virol. 76: 3276–3281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C. C., Chao C. H., Chen C. C., Yeh S. D., Tsai H. T., et al. , 2003. Identification of Turnip mosaic virus isolates causing yellow stripe and spot on calla lily. Plant Dis. 87: 901–905 [DOI] [PubMed] [Google Scholar]
- Chung B. Y. W., Miller W. A., Atkins J. F., Firth A. E., 2008. An overlapping essential gene in the Potyviridae. Proc. Natl. Acad. Sci. USA 105: 5897–5902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Den Boon J. A., Diaz A., Ahlquist P., 2010. Cytoplasmic viral replication complexes. Cell Host Microbe 8: 77–85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denhardt D. T., Silver R. B., 1966. An analysis of the clone size distribution of φX174 mutants and recombinants. Virology 30: 10–19 [DOI] [PubMed] [Google Scholar]
- Drake J. W., 1993. Rates of spontaneous mutation among RNA viruses. Proc. Natl. Acad. Sci. USA 90: 4171–4175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake J. W., Holland J. J., 1999. Mutation rates among RNA viruses. Proc. Natl. Acad. Sci. USA 96: 13910–13913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy S., Shackelton L. A., Holmes E. C., 2008. Rates of evolutionary change in viruses: patterns and determinants. Nat. Rev. Genet. 9: 267–276 [DOI] [PubMed] [Google Scholar]
- Elena S. F., Sanjuán R., 2005. Adaptive value of high mutation rates of RNA viruses: separating causes from consequences. J. Virol. 79: 11555–11558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elena S. F., Carrasco P., Daròs J. A., Sanjuán R., 2006. Mechanisms of genetic robustness in RNA viruses. EMBO Rep. 7: 168–173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrer-Orta C., Arias A., Escarmís C., Verdaguer N., 2006. A comparison of viral RNA-dependent RNA polymerases. Curr. Opin. Struct. Biol. 16: 27–34 [DOI] [PubMed] [Google Scholar]
- Kirkpatrick S., Gelatt C. D., Jr., Vecchi M. P., 1983. Optimization by simulated annealing. Science 220: 671–680 [DOI] [PubMed] [Google Scholar]
- Koonin E. V., Wolf Y. I., Nagasaki K., Dolja V. V., 2008. The Big Bang of picorna-like virus evolution antedates the radiation of eukaryotic supergroups. Nat. Rev. Microbiol. 6: 925–939 [DOI] [PubMed] [Google Scholar]
- Laliberté J. F., Sanfaçon H., 2010. Cellular remodeling during plant virus infection. Annu. Rev. Phytopathol. 48: 69–91 [DOI] [PubMed] [Google Scholar]
- Murray J. D., 1989. Mathematical Biology. Springer Verlag, New York [Google Scholar]
- Palani P. V., Lin N. S., 2007. Northern analysis of viral plus- and minus-strand RNAs. Curr. Prot. Microbiol. 16: 16e3. [DOI] [PubMed] [Google Scholar]
- Plaskon N. E., Adelman Z. N., Myles K. M., 2009. Accurate strand-specific quantification of viral RNA. PLoS ONE 4: e7468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuán R., Nebot M. R., Chirico N., Mansky L. M., Belshaw R., 2010. Viral mutation rates. J. Virol. 84: 9733–9748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sardanyés J., Solé R. V., Elena S. F., 2009. Replication mode and landscape topology differentially affect RNA virus mutational load and robustness. J. Virol. 83: 12579–12589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thébaud G., Chadoeuf J., Morelli M. J., McCauley J. W., Haydon D. T., 2010. The relationship between mutation frequency and replication strategy in positive-sense single-stranded RNA viruses. Proc. R. Soc. London Ser. B 277: 809–817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tromas N., Elena S. F., 2010. The rate and spectrum of spontaneous mutations in a plant RNA virus. Genetics 185: 983–989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuiskunen A., Leparc-Goffart I., Boubis L., Monteil V., Klingström J., et al. , 2010. Self-priming of reverse transcriptase impairs strand-specific detection of dengue virus RNA. J. Gen. Virol. 91: 1019–1027 [DOI] [PubMed] [Google Scholar]
- Urcuqui-Inchima S., Haenni A. L., Bernardi F., 2001. Potyvirus proteins: a wealth of functions. Virus Res. 74: 157–175 [DOI] [PubMed] [Google Scholar]
- Yoo S. D., Cho Y. H., Sheen J., 2007. Arabidopsis mesophyll protoplasts: a versatile cell system for transient gene expression analysis. Nat. Protoc. 2: 1565–1572 [DOI] [PubMed] [Google Scholar]