Abstract
The deformity in idiopathic scoliosis (IS) is three dimensional in nature and effective correction involves all three planes. Even though the vertebral translation (VT) is an accepted element in the deformity along with vertebral rotation(VR) as reported by Asher and Cook (Spine (Phila Pa 1976) 20(12):1386–1391, 1995), Kotwicki et al. (Study Health Technol Inf 123:164–168, 2006) and Kotwicki and Napiontek (Pediatr Orthop 28(2):225–229, 2008), rib hump (rib hump index (RI)) and Cobb angle as reported by Aaro and Dahlborn (Spine (Phila Pa 1976) 6(6):567–572, 1981), it was assumed that VT was represented by adequately by Cobb angle and it was not analysed individually. We hypothesized that the Cobb angle and the VT measured in axial plane on CT scan and may not represent the same measurement and factors like coronal plane vertebral tilt,VR and vertebral deformation might affect them in different ways. Hence, VT should be considered as a separate variable and its relationship with VR, RI and Cobb angle should be investigated. Since the newer implants depend on curve translation and derotation for correction studying the role of VT and the relationships is important. VT, VR and RI were measured in CT scans of 75 patients with IS and correlated with Cobb angle. Regression analysis was used to identify the influence of the variables on each other. All the variables significantly correlated with one another but the correlation of Cobb and VT is not perfectly linear and it cannot be used to represent VT. VT influences RI much more than Cobb angle or VR. VT, therefore, merits further study treating it as an independent variable.
Keywords: Idiopathic scoliosis, Vertebral translation, Rib hump, Vertebral rotation, Cobb angle
Introduction
It is well known that the deformity in idiopathic scoliosis (IS) is three dimensional and correction involves all three planes. CT scan has proven to be a useful tool in analysis of the deformity and planning correction. Variables like Cobb angle,rib hump, vertebral rotation (VR) and vertebral translation (VT) which affect the curve have been studied [1, 2] and some authors have even noted that rib hump may be the first event [3–6]. The VR along the longitudinal axis has received attention in recent years due to the popularity of pedicle screw fixation [7–11]. Studies have also documented the relationship between VR, rib hump severity, quantified as rib hump index (RI) and Cobb angle [12, 13].
The senior author had noted VT in axial CT scan in number of cases of IS. While this is a known component of the deformity [13–16] and studies have shown that deformation of the vertebrae and VT have a linear relationship in opposite directions and occur along with VR [15, 16], analysis of VT has been neglected. It has been erroneously thought to be represented by Cobb angle alone [13].
We hypothesized that Cobb angle (supine) measured on radiographs cannot be used to represent VT and that VT measured on axial sections of CT scan will not vary in proportion to it since factors like coronal plane vertebral tilt, rotation, rib hump and vertebral deformation may affect the Cobb angle and VT differently. Hence, VT should be considered as a separate variable and its relationship with other factors should be investigated. It is even more important as the newer implants depend on vertebral derotation and translation for curve correction.
Materials and methods
Following approval from our institutional review board, we retrospectively reviewed the preoperative radiographs and CT scans of 75 patients: 20 males (26.67%) and 55 females (73.33%), with IS who subsequently underwent surgery for the same. The mean age of the patients was 17.6 years (range 5–63 years). 93.6% of curves were right sided and 6.33% were left sided.
All IS with documented onset before skeletal maturity were included. Previously operated patients, non-idiopathic scoliosis, adult scoliosis, IS with degenerative changes, those who underwent only conservative treatment or those who did not have a preoperative CT scan were excluded.
All patients were assessed with clinical and neurological examination by the same surgeon. Preoperative radiological assessment included standardised radiographs (full length spine supine AP, erect PA, lateral and bending views) and CT scan of the scoliotic spine. CT protocol used was 2 mm slice thickness using Somatom Sensation 16, Siemens AG, Erlangen, Germany. All CT scans were done in supine position on a cushion and were reported by the same radiologist. All radiological measurements were done using picture archiving and communication system (PiViewSTAR, InfiniitPACS, Version No:5.0.8.1, South Korea) by three fellowship-trained spine surgeons.
Cobb angle was measured on supine and erect radiographs. Lenke classification of the curve [17, 18] and risser sign were noted. Some conventions were adopted for measurements. In patients with multiple curve patterns or double thoracic curves, the main thoracic curve was used as the only measurement area to ensure uniformity. Lumbar structural scoliosis was not analysed because we were concerned with correlation of the parameters with rib hump. We felt that consideration of lumbar curve patterns may confound the results. In those cases with multiple curve patterns, the lumbar curve and proximal thoracic curve were taken into consideration only for the purpose of Lenke classification.
VR, VT and RI were measured in the axial sections of CT scan at the apex defined by the radiograph using methods detailed below. The VR was measured on axial CT sections with the protocol of Ho et al. [9, 19]. This was chosen because of the simplicity of measurement with easily identifiable landmarks and better intra and inter-observer reliability over Aaro and Dahlborn method on all except the abnormally titled vertebrae [10, 20, 21]. Rib prominence was measured using RI described by Gotze and Thulbourne and Gillespie and adapted by Aaro and Dahlborn [13, 22, 23].
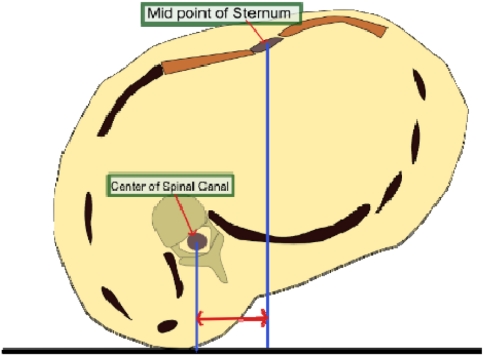
To measure the VT in axial plane of the CT scan, a simple method was evolved (Fig. 1). Midpoint of sternal width was marked at the apex of the curve in axial sections of the CT scan. The horizontal distance from the centre of the vertebral canal to the vertical line dropped form the sternal centre was measured in millimeters as the VT. The centre of sternum was chosen as it was identified as the ‘pole star’ bony point which was relatively stable in the midline to which we could refer to measure translation of the vertebra.
Fig. 1.
Measurement of the VT in axial section of the CT scan. Measured in millimeters as the horizontal distance between the line dropped from the centre of the spinal canal and the centre of the sternal width
Three surgeons measured the same data set; one surgeon repeating the measurement at an interval of 1 week. All surgeons were fellowship trained in spine surgery and were blinded to other’s measurements.
Statistical analysis
Statistical analysis was performed using SPSS Statistics (v 17.0) software package. Descriptive statistics was analysed. Correlation co-efficient was evaluated using Pearson’s correlation co-efficient (r2) for intra and interobserver analysis and correlation between all the variables. p value of less than 0.05 was considered significant.
Contribution of the variables to one another was assessed and the impact on each other was analysed with regression analysis, changing the dependant variable from Cobb (supine), VR, VT and RI. Adjusted R squared value was noted to to assess the adequacy of models, but no cut off value was decided. Instead, p value less than 0.05 was considered significant. Collinearity statistics was also noted in case of high correlation. Any correlation between the variables can confuse the conclusions derived by regression analysis. This could be brought out and correction done. High-tolerance values close to 1.0 and the lower VIF on collinearity statistics suggest that the variables do not interfere with regression analysis. Since the study included patients with ages of 5 years and 63 years, to discount the effects of early onset IS and degenerative changes in a long-standing idiopathic scoliosis, we redid the regression models with those two patients excluded and compared the results to the original set to assure ourselves of accuracy.
Observation and results
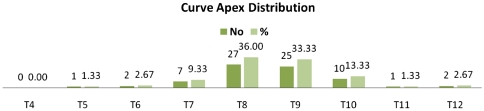
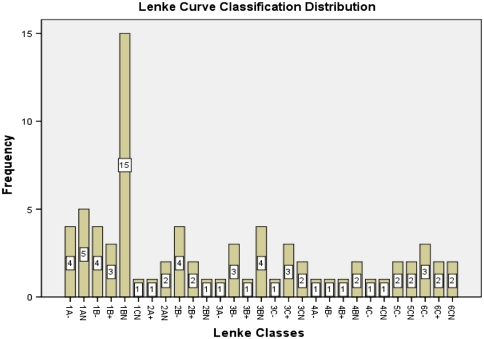
A total of 75 patients were measured. There were 20 males (26.67%) and 55 females (73.33%). The average age was 17.16 years (SD of 8.97, range of 5–63 years). There were 70 right sided thoracic curves (93.33%) and 5 left sided thoracic curves (6.67%). Maximum number of curves had an apex of T8 (27 no., 36%) followed by T9 with 25 no (33.33%) and T10 (10 no., 13.33%). Curve apex and Lenke classes were distributed as detailed in Figs. 2 and 3, respectively.
Fig. 2.
Distribution of the apex of the curves
Fig. 3.
Distribution of the Lenke classes in the patient group
Cobb angles
The mean Cobb angle (supine) was 50.29° (range of 21.75°–128.7°, SD of 20.46° Cobb angle (standing) averaged 61.14° (range of 24.31°–145°, SD of 22.06).
The intraobserver reliability of Cobb angle (supine) was very good (r = 0.99, p < 0.01) as was the interobserver reliability with values of, r = 0.997, r = 0.942 with p value <0.01 between observer one and two and observer one and three, respectively. There was also very good intra observer reliability in Cobb angle (standing) (r = 0.986, p value <0.01). The inter observer reliability was also very high; r = 0.998 and r = 0.936 with p value <0.01, between observer one and two and observer one and three, respectively.
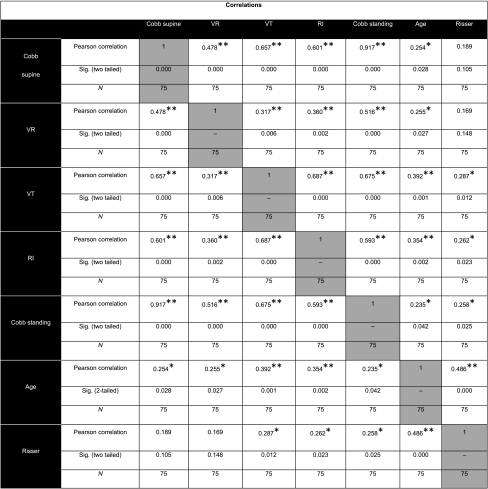
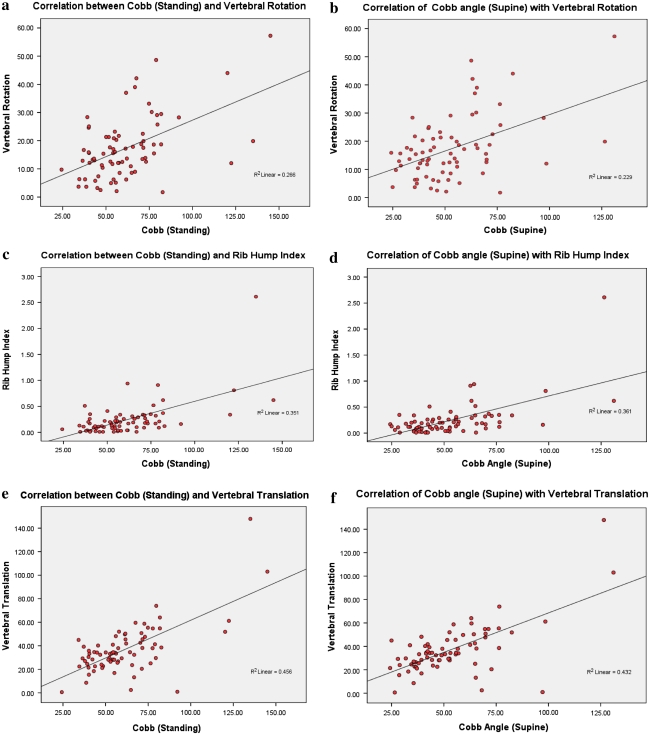
Correlation between Cobb angles (supine and standing) with VR, VT and RI was significant with p value <0.001 and age with p value of <0.05. The correlation of the Cobb angle (supine) and Risser stage was not statistically significant (Table 1; Fig. 4a–h).
Table 1.
Correlation matrix of Cobb angle (supine, standing), axial VR, RI, VT, risser stage and age of patient
Fig. 4.
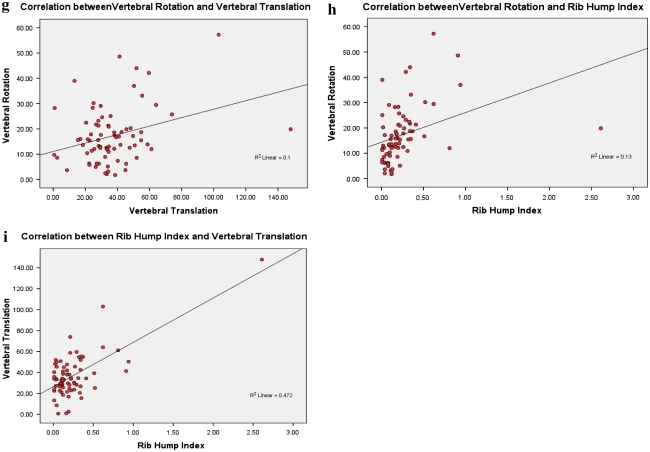
a Correlation between Cobb (standing) and vertebral rotation. b Correlation between Cobb (supine) and vertebral rotation. c Correlation between Cobb (standing) and rib hump index. d Correlation between Cobb (supine) and rib hump index. e Correlation between Cobb (standing) and vertebral translation. f Correlation between Cobb (supine) and vertebral translation. g Correlation between vertebral translation and vertebral rotation. h Correlation between rib hump index and vertebral rotation. i Correlation between rib hump index and vertebral translation
Vertebral rotation
The mean VR was 17.22° (range 1.72–57.24, SD 11.07). It had very good intraobserver reliability (r = 0.928, p value <0.01) and interobserver reliability (r = 0.932 and r = 0.973, p value of <0.01 between observer one and two and observer one and three, respectively).
The correlations of VR with Cobb angle (supine) (r = 0.478, p value <0.001), Cobb angle (standing) (r = 0.516, p value <0.001), RI (r = 0.36, p value = 0.002) and VT (r = 0.317, p value = 0.006) are statistically very significant. However, its r values with RI and VT are lower than its correlation with Cobb angle, indicating a weaker correlation of VR with RI and VT (Table 1; Fig. 4a–h).
Rib hump index
The mean RI was 0.24 (range 0.01–2.61, SD 0.34). The RI had a good intraobserver reliability (r = 0.71, p value <0.01) and interobserver reliability with r = 0.837 and r = 0.944, each with p value of <0.01, between observer one and two and observer one and three, respectively. The RI intraobserver reliability values were lower than the interobserver values. We did not re-measure RI as the intraobserver correlation was still significant (p < 0.01) and the interobserver reliability was very high.
There was statistically significant correlation of RI with VR (r = 0.36, p value = 0.002), VT (r = 0.687, p value <0.001), supine Cobb (r = 0.601, p value <0.001) and standing Cobb (r = 0.593, p value <0.001). It is noticeable that the VT seems to correlate better than other measures with RI. As noted above, VR has the least r value with RI among the variables studied (Table 1; Fig. 4a–h).
Vertebral translation
The mean VT was 36.9 mm. (range 0.59–148.86 mm, SD 20.95). The VT had very good intraobserver reliability (r = 0.96, p value <0.01) and interobserver reliability with r = 0.954 and r = 0.989, each with p value of <0.01, between observer one and two and observer one and three, respectively.
There was statistically significant correlation of VT with VR (r = 0.317, p value = 0.006), RI (r = 0.687, p value <0.001), supine Cobb(r = 0.657, p value <0.001) and standing Cobb (r = 0.675, p value <0.001). It is noticeable that the correlation of the VT with the Cobb (supine and standing), even though high, is not close enough to r = 1.0 indicating that, as hypothesized, VT does not vary in a linear manner with Cobb angle and hence it should probably be treated as an independent parameter (Table 1; Fig. 4a–h).
Regression analysis
Keeping the Cobb angle (supine) as the dependent variable, the predictors were analysed. Using the enter method of SPSS; a significant model emerged (p < 0.001 adjusted R square = 0.506.) (Table 2). VT had the highest predictive value and impact on Cobb angle (supine), signified by the high beta value and t value, and followed by VR. Interestingly, RI is not a strong predictor and does not have impact on Cobb angle (supine) and value was not statistically significant, as were Risser and age. Collinearity statistics were favourable (Table 2). However, it should also be noted that even though the present model is very significant (p < 0.001) it accounted for only 50.6% of the variance observed.
Table 2.
Regression coefficients with Cobb (supine) as the dependent variable
| Coefficientsa | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | t | Sig. | Collinearity statistics | |||
| B | Std. error | Beta | Tolerance | VIF | ||||
| All patients | ||||||||
| 1 | (Constant) | 27.747 | 4.962 | – | 5.592 | 0.000 | – | – |
| VR | 0.509 | 0.164 | 0.276 | 3.106 | 0.003 | 0.847 | 1.181 | |
| RI | 13.281 | 6.947 | 0.221 | 1.912 | 0.060 | 0.500 | 1.999 | |
| VT | 0.436 | 0.113 | 0.446 | 3.857 | 0.000 | 0.498 | 2.007 | |
| Risser | −0.164 | 1.170 | −0.013 | −0.140 | 0.889 | 0.751 | 1.331 | |
| Age | −0.144 | 0.226 | −0.063 | −0.639 | 0.525 | 0.680 | 1.471 | |
| Patients with aged between 5 and 63 years excluded | ||||||||
| 1 | (Constant) | 27.694 | 5.153 | – | 5.375 | 0.000 | – | – |
| VR | 0.584 | 0.166 | 0.313 | 3.526 | 0.001 | 0.818 | 1.223 | |
| RI | 14.623 | 7.082 | 0.245 | 2.065 | 0.043 | 0.460 | 2.173 | |
| VT | 0.409 | 0.111 | 0.421 | 3.688 | 0.000 | 0.495 | 2.020 | |
| Risser | −0.684 | 1.209 | −0.055 | −0.566 | 0.573 | 0.690 | 1.450 | |
| Age | −0.113 | 0.315 | −0.039 | −0.359 | 0.721 | 0.538 | 1.858 | |
aDependent variable: Cobb (supine)
Keeping the VT as the dependent variable, the predictors were analysed. Using the enter method of SPSS; a significant model emerged (p < 0.01 F = 19.866, adjusted R square = 0.56) (Table 3). Model’s adjusted R square value had improved when VT was used as the dependent variable. VT could be strongly predicted with Cobb (supine) and RI (p value <0.01). RI had the largest beta value and t value, suggesting that changes in small changes in values impact VT more than other variables. However, the VR, Risser and age were not significant predictors.
Table 3.
Regression coefficients with vertebral translation (VT) as the dependent variable
| Coefficientsa | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | t | Sig. | Collinearity statistics | |||
| B | Std. error | Beta | Tolerance | VIF | ||||
| All patients | ||||||||
| 1 | (Constant) | 3.715 | 5.763 | – | 0.645 | 0.521 | – | – |
| Cobb (supine) | 0.407 | 0.106 | 0.397 | 3.857 | 0.000 | 0.560 | 1.786 | |
| Risser | 0.610 | 1.128 | 0.048 | 0.541 | 0.590 | 0.754 | 1.326 | |
| Age | 0.326 | 0.216 | 0.140 | 1.513 | 0.135 | 0.698 | 1.432 | |
| VR | −0.121 | 0.169 | −0.064 | −0.718 | 0.475 | 0.749 | 1.336 | |
| RI | 25.202 | 6.185 | 0.409 | 4.075 | 0.000 | 0.589 | 1.697 | |
| Patients with aged between 5 and 63 years excluded | ||||||||
| 1 | (Constant) | 4.306 | 6.172 | – | 0.698 | 0.488 | – | – |
| Cobb (supine) | 0.413 | 0.112 | 0.401 | 3.688 | 0.000 | 0.520 | 1.922 | |
| Risser | 0.810 | 1.213 | 0.063 | 0.667 | 0.507 | 0.691 | 1.447 | |
| Age | 0.222 | 0.315 | 0.075 | 0.706 | 0.483 | 0.541 | 1.847 | |
| VR | −0.118 | 0.181 | −0.061 | −0.651 | 0.517 | 0.694 | 1.441 | |
| RI | 25.792 | 6.629 | 0.419 | 3.891 | 0.000 | 0.530 | 1.886 | |
aDependent variable: VT
The influence of VR on VT decreased to a statistically insignificant vale when test were repeated with patients aged 5 and 63 years were done. However, Cobb (supine) and RI retained the high significance levels.
In turn, RI was kept as the dependent variable and using the enter method a significant model emerged (p < 0.01 F = 15.249, adjusted R square = 0.525) (Table 4). RI could be strongly predicted with VT (p value <0.001). VT in addition had a higher beta and t value signifying that changes in VT can impact RI more than other variables. Interestingly, RI was not significantly impacted by changes in Cobb angle or VR in spite of good correlations obtained earlier. Risser and age were not significant predictors.
Table 4.
Regression coefficients with rib hump index (RI) as the dependent variable
| Coefficientsa | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | t | Sig. | Collinearity statistics | |||
| B | Std. error | Beta | Tolerance | VIF | ||||
| All patients | ||||||||
| 1 | (Constant) | −0.352 | 0.092 | – | −3.833 | 0.000 | – | – |
| Cobb (supine) | 0.004 | 0.002 | 0.228 | 1.912 | 0.060 | 0.485 | 2.061 | |
| VT | 0.008 | 0.002 | 0.474 | 4.075 | 0.000 | 0.509 | 1.966 | |
| Risser | 0.007 | 0.020 | 0.034 | 0.359 | 0.721 | 0.752 | 1.329 | |
| Age | 0.003 | 0.004 | 0.074 | 0.736 | 0.464 | 0.681 | 1.468 | |
| VR | 0.002 | 0.003 | 0.076 | 0.793 | 0.430 | 0.750 | 1.333 | |
| Patients with aged between 5 and 63 years excluded | ||||||||
| 1 | (Constant) | −0.403 | 0.091 | – | −4.449 | 0.000 | – | – |
| Cobb (supine) | 0.004 | 0.002 | 0.245 | 2.065 | 0.043 | 0.460 | 2.174 | |
| VT | 0.007 | 0.002 | 0.440 | 3.891 | 0.000 | 0.504 | 1.983 | |
| Risser | −0.002 | 0.020 | −0.009 | −0.092 | 0.927 | 0.686 | 1.457 | |
| Age | 0.011 | 0.005 | 0.225 | 2.121 | 0.038 | 0.573 | 1.744 | |
| VR | 0.000 | 0.003 | 0.000 | −0.001 | 0.999 | 0.690 | 1.450 | |
aDependent variable: RI
When we repeated the regression with patients with ages 5 and 63 years excluded, there was a shift in the relationship of Cobb (supine) with RI. The repeat analysis yielded a p value of 0.043 and it was significant. However, this is only slightly less that the significance level of 0.05 and the difference in the way VT and Cobb influenced to RI persisted as evidenced by the high beta and t value between VT and RI which was still much higher than that of Cobb (supine) and RI (Table 4).
Keeping VR as the dependent variable enter method yielded a significant model (p < 0.01 F = 4.769, adjusted R square = 0.203) (Table 5). There were several interesting findings. None of the variables, except the Cobb angle had any significant predictive value and impact on VR (p value <0.01). This is even more interesting in the light that these variables had significant correlations with each other. Even though the model was significant, it also had the lowest adjusted R squared value in the analysis performed. Even though there seems to be no universally agreed cut off point for adjusted R squared value, the current model with a value of 0.203 and its included variables, means that it could only explain about 20.3% of the variance observed in VR.
Table 5.
Regression coefficients with vertebral rotation (VR) as the dependent variable
| Coefficientsa | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Unstandardized coefficients | Standardized coefficients | t | Sig. | Collinearity statistics | |||
| B | Std. error | Beta | Tolerance | VIF | ||||
| All patients | ||||||||
| 1 | (Constant) | 2.509 | 4.101 | – | 0.612 | 0.543 | – | – |
| Cobb (supine) | 0.241 | 0.078 | 0.445 | 3.106 | 0.003 | 0.525 | 1.904 | |
| RI | 3.871 | 4.879 | 0.119 | 0.793 | 0.430 | 0.479 | 2.086 | |
| VT | −0.061 | 0.085 | −0.116 | −0.718 | 0.475 | 0.413 | 2.422 | |
| Risser | 0.144 | 0.804 | 0.021 | 0.179 | 0.859 | 0.751 | 1.331 | |
| Age | 0.167 | 0.155 | 0.135 | 1.078 | 0.285 | 0.687 | 1.455 | |
| Patients with aged between 5 and 63 years excluded | ||||||||
| 1 | (Constant) | −0.840 | 4.175 | – | −0.201 | 0.841 | – | – |
| Cobb (supine) | 0.268 | 0.076 | 0.500 | 3.526 | 0.001 | 0.513 | 1.950 | |
| RI | −0.007 | 4.948 | 0.000 | −0.001 | 0.999 | 0.433 | 2.312 | |
| VT | −0.053 | 0.082 | −0.103 | −0.651 | 0.517 | 0.414 | 2.415 | |
| Risser | 0.169 | 0.821 | 0.025 | 0.207 | 0.837 | 0.687 | 1.456 | |
| Age | 0.344 | 0.209 | 0.223 | 1.647 | 0.104 | 0.559 | 1.789 | |
aDependent variable: VR
The results were more or less similar with only the Cobb (supine) having any influence on VR when the regression was repeated with the patients with ages 5 and 63 years excluded. In fact the influence of RI on VR and VT on VR decreased further and were statistically insignificant. The influence of Cobb (supine) remained more or less the same at a high significance level.
Discussion
The apex vertebra distribution in our series for IS is comparable with other reported series [13]. In our series the highest number apex was at the level of T8 followed by T9. The relationship of scoliosis, VR and the RI has been well studied [1, 2, 10, 13]. Specifically, Aaro et al. [13] studied the relationship between Cobb angle, VR and RI and concluded that all factors were significantly correlated.Our results on correlations agree well with equivalent correlations in other series [1, 13] (Table 6).
Table 6.
Studies correlating vertebral rotation, vertebral translation and rib hump to Cobb angle
| Coob/VR | Cobb/RI | Cobb/VT | VR/VT | VR/RI | VT/RI | |
|---|---|---|---|---|---|---|
| Aora et al. [12] |
r = 0.68 p < 0.01 |
r = 0.34 p < 0.05 |
r* = 0.76 p < 0.01 |
– |
r = 0.60 p < 0.05 |
– |
| Kuklo et al. [1] |
r = 0.48 p = 0.003 |
r = 0.65 p < 0.0001 |
– | – |
r = 0.53 p = 0.002 |
– |
| Present study |
r = 0.478 p < 0.001 |
r = 0.60 p < 0.001 |
r = 0.657 p < 0.001 |
r = 0.317 p = 0.006 |
r = 0.36 p = 0.002 |
r = 0.687 p < 0.001 |
r* Aaro et al. used angular measure of MLdev on radiographs as an indirect measure of VT
Vertebral translation and its correlations
Clarifying the interrelationship of VT is important in an era where the implants correct the curves mainly by translation and derotation. We had hypothesised that VT cannot be represented by Cobb angle(supine) alone. As per our results, our hypothesis has been proven.
VT and its relation to variables like VR and deformation has been well described in literature. Kotwicki et al. [15, 16] have described the VT and its association with deformation and rotation. They found that the vertebral deformation accompanied the translation in a linear correlation with the phenomenas developing in opposite directions. Asher et al. [14] found that the vertebra translate and rotate away toward the apex and that translation occurred along with rotation. There was minimal antero-posterior translation. Acaroglu et al. [24] studied the actual apex, defined as the maximally translated vertebra and found that it was the most rotated in only a minority of the cases and the most rotated vertebra may be one or two level higher or lower to apex.
Inspite of these studies, we were unable to find any references which have studied the correlations between VT and Cobb angle, VR and RI, save the one by Aaro et al. [13]. Aaro et al. [13] measured the VT (MLdev in their notation) indirectly as the angular deviation of the apical vertebra from the sagittal plane on radiographs. Since VT correlated with Cobb angle (r = 0.76) it was concluded that Cobb angle gave fair representation of VT and VT was not analysed. Interestingly, even while reaching this conclusion, they have cited studies which state that Cobb angle was unreliable estimate and that VT should also be measured in addition to it [25, 26].
In our study, VT and the Cobb (supine) are closely related to each other and the correlation is significant (r = 0.657, p < 0.01). However, this is lower than the figure of (r = 0.76) Aaro et al. obtained in their study. Our contention to the conclusion of Aaro et al. that Cobb angle can be used as the lone frontal plane deformity estimate is that, the correlation, even while it is statistically significant, is not high enough to be perfectly linear to completely discard the variable VT from analysis. Doing so risks losing important differences in correlation that VT may have with other variables.
For example, VR behaves differently to Cobb angle (supine), VT and RI. VR had good correlation with Cobb angle (supine) (r = 0.478, p value <0.001), VT and RI but it has significant impact only on Cobb angle. The effect of VT and RI on VR further decreased when analysis was done after excluding the patients aged 5 and 63 years but the influence of Cobb (supine) on VR remained significant. It should be kept in mind that even though the regression model for VR is statistically significant, the adjusted R squared value was the lowest and the model accounted for only 20.3% of variance. This means that there may be other factors influencing in the relationships. Another example of the different behaviour exibited by VT and Cobb angle is that VT impacts RI and Cobb (supine) to the maximum extent. The impact of VT on RI is much more than that of Cobb angle (supine) on RI.
Thus, it is clear that if VT could be represented by Cobb angle (supine), VT would have followed the behaviour of Cobb angle with other variables closely in addition to having good correlations with it. Thus, VT seems to be an independent element that deserves more attention [14–16, 24].
Possible limitations and future improvements of the study
To answer the question that has not been adequately addressed we chose a large patient base and included all IS cases. Future studies can filter out the relationships in groupings like juvenile or adolescent IS, removing confounding elements, if any. We have included all curves with a structural thoracic element. Future studies can group them and study individual curve patterns possibly adding other variables and 3D CT imaging to bring out more details. Intraobserver RI measure had a lower reliability, but it was statistically very significant and had very good correlation with interobserver values, so we did not remeasure them. All the models were significant, but the adjusted R squared values could only explain 50–56% of the variance in the values observed. In the case of regression model of VR, the adjusted R square value was even lower at 0.203. Since all the models were significant statistically (p < 0.001) and there was no universally agreed cut off value for adjusted R squared value, we went ahead with the analysis. This possibly means that there are other variables which are influencing these variables. Inclusion of other variables like sagittal vertebral rotation, kyphosis and lordosis, antero-posterior VT could add more corroboration to conclusions.
Conclusion
Our hypothesis that VT cannot be represented by adequately with Cobb angle (supine) has been substantiated. The relationship of VT with other variables like RI, VR and Cobb angle has been analysed. Even though all variables had significant correlations, VT seems to impact RI to the greatest extent, even more than Cobb or VR. Considering that various studies have cited RI as the initial event in development of the curve and since the impact of VT on RI is significant, it is all the more important that VT should be analysed further. Analysis of the differences in groups of infantile, juvenile and adolescent IS will help further define the interrelationships.
Acknowledgments
None.
Conflict of interest All authors have contributed equally to this study and have no conflict of interest. All authors declare that they have no commercial interest which may pose a conflict of interest to this study.
References
- 1.Kuklo T, Potter BK, Lawrence L. Vertebral rotation and thoracic torsion in adolescent idiopathic scoliosis: what is the best radiographic correlate? J Spinal Disord Tech. 2005;18(2):139–147. doi: 10.1097/01.bsd.0000159033.89623.bc. [DOI] [PubMed] [Google Scholar]
- 2.Skalli W, Lavaste F, Descrimes J. Quantification of three-dimensional vertebral rotations in scoliosis: what are the true values? Spine. 1995;20(5):546–553. doi: 10.1097/00007632-199503010-00008. [DOI] [PubMed] [Google Scholar]
- 3.Grivas TB, Samelis P, Chadziargiropoulos T, Polyzois B. Study of the rib cage deformity in children with 10 degrees-20 degrees of Cobb angle late onset idiopathic scoliosis, using rib-vertebra angles–aetiologic implications. Study Health Tech Inf. 2002;91:20–24. [PubMed] [Google Scholar]
- 4.Patel A, Schwab F, Lafage V, Patel A, Obeidat MM, Farcy JP. Computed tomographic validation of the porcine model for thoracic scoliosis. Spine (Phila Pa 1976) 2010;35(1):18–25. doi: 10.1097/BRS.0b013e3181b79169. [DOI] [PubMed] [Google Scholar]
- 5.Grivas TB, Dangas S, Polyzois BD, Samelis P. The double rib contour sign (DRCS) in lateral spinal radiographs: aetiologic implications for scoliosis. Study Health Tech Inf. 2002;88:38–43. [PubMed] [Google Scholar]
- 6.Grivas TB, Vasiliadis ES, Mihas C, Savvidou O. The effect of growth on the correlation between the spinal and rib cage deformity:implications on idiopathic scoliosis pathogenesis. Scoliosis. 2007;2:11. doi: 10.1186/1748-7161-2-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stokes IAF, Bigalow LC, Moreland MS. Measurement of axial rotation of vertebrae in scoliosis. Spine. 1986;11:213–218. doi: 10.1097/00007632-198604000-00006. [DOI] [PubMed] [Google Scholar]
- 8.Kotwicki T, Krawczynski A, Lorkowska M, Frydryk K (2004) Clinical and radiological assessment of spinal rotation, International Research Society of spinal deformities, 207–211
- 9.Ho EKW, Upadlyay SS, Chan FL, Hsu LC, Leong JC. New methods of measuring vertebral rotation from computed tomographic scans. Spine. 1993;18:1173–1177. doi: 10.1097/00007632-199307000-00008. [DOI] [PubMed] [Google Scholar]
- 10.Ho E, Upadhyay SS, Chan FL, Hsu L, Leong J. New methods of measuring vertebral rotation from computed tomographic scans: an intraobserver and interobserver study on girls with scoliosis. Spine. 1993;18(9):1173–1177. doi: 10.1097/00007632-199307000-00008. [DOI] [PubMed] [Google Scholar]
- 11.Aaro S, Dahlborn M, Svensson L. Estimation of vertebral rotation in structural scoliosis by computer tomography. Acta Radiol Diagn. 1978;19:990–992. doi: 10.1177/028418517801900614. [DOI] [PubMed] [Google Scholar]
- 12.Aaro S, Dahlborn M. Estimation of vertebral rotation and the spinal and rib cage deformity in scoliosis by computer tomography. Spine (Phila Pa 1976) 1981;6(5):460–467. doi: 10.1097/00007632-198109000-00007. [DOI] [PubMed] [Google Scholar]
- 13.Aaro S, Dahlborn M. The longitudinal axis rotation of the apical vertebra, the vertebral, spinal, and rib cage deformity in idiopathic scoliosis studied by computer tomography. Spine (Phila Pa 1976) 1981;6(6):567–572. doi: 10.1097/00007632-198111000-00007. [DOI] [PubMed] [Google Scholar]
- 14.Asher MA, Cook LT. The transverse plane evolution of the most common adolescent idiopathic scoliosis deformities a cross-sectional study of 181 patients. Spine (Phila Pa 1976) 1995;20(12):1386–1391. [PubMed] [Google Scholar]
- 15.Kotwicki T, Napiontek M, Nowakowski A (2006) Transverse plane of apical vertebra of structural thoracic curve: vertebra displacement versus vertebral deformation. Study Health Technol Inf 123:164–168 [PubMed]
- 16.Kotwicki T, Napiontek MJ. Intravertebral deformation in idiopathic scoliosis: a transverse plane computer tomographic study. Pediatr Orthop. 2008;28(2):225–229. doi: 10.1097/BPO.0b013e3181647c4a. [DOI] [PubMed] [Google Scholar]
- 17.Lenke LG, Dobbs MB. Management of juvenile idiopathic scoliosis. J Bone Joint Surg Am. 2007;89:55–63. doi: 10.2106/JBJS.F.00644. [DOI] [PubMed] [Google Scholar]
- 18.Lenke LG, Betz RR, Harms J, Bridwell KH, Clements DH, Lowe TG, Blanke K. Adolescent idiopathic scoliosis: a new classification to determine extent of spinal arthrodesis. J Bone Joint Surg Am. 2001;83:1169–1181. [PubMed] [Google Scholar]
- 19.Ho EKW, Upadlyay SS, Ferris L, et al. A comparative study of computed tomographic and plain radiographic methods to measure vertebral rotation in adolescent idiopathic scoliosis. Spine. 1992;17:771–774. doi: 10.1097/00007632-199207000-00008. [DOI] [PubMed] [Google Scholar]
- 20.Göçen S, Aksu MG, Baktiroğlu L, Ozcan OJ. Evaluation of computed tomographic methods to measure vertebral rotation in adolescent idiopathic scoliosis: an intraobserver and interobserver analysis. Spinal Disord. 1998;11(3):210–214. [PubMed] [Google Scholar]
- 21.Lam GC, Hill DL, Le LH, Raso JV, Lou EH. Vertebral rotation measurement: a summary and comparison of common radiographic and CT methods. Scoliosis. 2008;3:16. doi: 10.1186/1748-7161-3-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thulbourne T, Gillespie R. The rib hump in idiopathic scoliosis. measurement, analysis and response to treatment. J Bone Joint Surg Br. 1976;58(1):64–71. doi: 10.1302/0301-620X.58B1.1270497. [DOI] [PubMed] [Google Scholar]
- 23.Götze HG. Significance of the rotation index for the prognostic evaluation of idiopathic thoracic scoliosis. Z Orthop Ihre Grenzgeb. 1975;113(4):563–565. [PubMed] [Google Scholar]
- 24.Acaroglu E, Yazici M, Deviren V, Alanay A, Cila A, Surat A. Does transverse apex coincide with coronal apex levels (regional or global) in adolescent idiopathic scoliosis? Spine (Phila Pa 1976) 2001;26(10):1143–1146. doi: 10.1097/00007632-200105150-00010. [DOI] [PubMed] [Google Scholar]
- 25.George K, Rippstein J. A comparative study of the two popular methods of measuring scoliotic deformity of the Spine. J Bone Joint Surg. 1961;43:809–818. [Google Scholar]
- 26.Lindahl O, Movin A. Measurement of the deformity in scoliosis. Acta Orthop Scand. 1968;39(3):291–302. doi: 10.3109/17453676808989462. [DOI] [PubMed] [Google Scholar]