Relation between Molecular Shape and the Morphology of Self-Assembling Aggregates: A Simulation Study

Abstract

Proteins can aggregate in a wide variety of structures, both compact and extended. We present simulations of a coarse-grained anisotropic model that reproduce many of the experimentally observed aggregate structures. Conversely, all structures predicted by our model have experimental counterparts (ribbons, multistranded fibrils, and vesicles). The model we use is that of a rodlike particle with an attractive (hydrophobic) stripe on its side. Our Monte Carlo simulations show that aggregate morphologies crucially depend on two parameters. The first one is the width of the attractive stripe and the second one is a presence or absence of attractive interactions at the particle ends. These results provide us with a generic insight into the relation between the shape of protein-protein interaction potential and the morphology of protein aggregates.

Introduction

In healthy organisms, proteins self-assemble into a wide variety of functional structures. Examples are the filaments and fibrils that form the cytoskeleton, the extracellular matrix, or the functional amyloid fibers that some organisms exploit (1–3). But protein self-assembly may also turn against its host. Examples are the amyloid aggregates that have been associated with Alzheimer's, Parkinson's, and other diseases (1,3). Irrespective of whether they are beneficial or pathogenic, linear protein aggregates share certain characteristics, even though they may consist of very different building blocks. The shared feature is that self-assembly is usually driven by interaction between hydrophobic patches on the exposed surface of the proteins. In the absence of self-assembly, these patches would be exposed to water. In the self-assembled structures, they are mostly buried. But, apart from these generic aspects, there are important differences between different aggregate-forming proteins. For instance, in fibers such as collagen, the protein building blocks are aligned along the fiber axis, whereas amyloid fibers typically have the building blocks oriented perpendicular to the fiber axes in a cross β-structure. In addition, the building blocks can vary substantially in size and shape.

An obvious question to ask is how aggregate morphology depends on the structure of the building blocks. At this generic level, this is not a question about detailed molecular structure, but rather about the overall shape of the self-assembling units and about the distribution of hydrophobic patches on their surface.

Insight into the role that these factors play is not only important to gain a qualitative understanding of self-assembly and aggregate formation, it may also help in the design of building blocks for novel self-assembling materials. In fact, as evolution is likely to have weeded out most “dangerous” self-assembling proteins, it is plausible that rational design may result in novel types of self-assembling molecules.

In the work reported here, we use coarse-grained computer simulations to explore the relationships among shape, hydrophobicity, and self-assembly. Such simplified models are computationally tractable, yet exhibit many of the key features that exist (or can exist) in properly functionalized proteins or other nanoscale particles.

Coarse-grained models are extensively used to study the collective behavior of systems that contain many proteins because fully atomistic simulations of such systems would be prohibitively expensive. In particular, atomistic simulations are too slow to map out complete phase diagrams of protein solutions. There is a wide variety of coarse-grained protein models that differ in the amount of microscopic detail that they retain. For recent reviews, we refer the reader to Tozzini (4), Sherwood et al. (5), Eom et al. (6), Trylska (7), Periole et al. (8), and Ayton and Voth (9).

In this study, we focus on models that describe an entire protein or peptide as a single, rigid particle with anisotropic interaction. The most widely studied model of this type is a sphere with short-ranged, patchy attractions (for a recent review, see Pawar and Kretzschmar (10)). Systems of spheres with a highly symmetric patch distribution may occur in different macroscopic phases: vapor, crystal, and (sometimes) liquid (11–13). If the patch distribution on the surface of the sphere is asymmetric, compact clusters may form (14,15). However, experiments indicate that proteins forming extended aggregates such as fibrils tend to have a nonspherical shape. The most generic model to describe such proteins is a particle with an anisometric hard core and a nonuniform distribution of hydrophobicity on the surface.

We also focus specifically on the aggregation of proteins with a prolate shape (α-helix or β-sheet strand). We represent such particles by a spherocylinder, i.e., cylinder with hemispherical caps at both ends. The spherocylinder account for the anisometric hard-core repulsion and phase diagram of such model can be found elsewhere (16–18). Attraction is accounted for by a hydrophobic patch. In particular, we focus on the situation where the hydrophobic patch runs lengthwise along the molecule. The other situation (one end of the molecule hydrophobic, the other hydrophilic) would correspond to regular surfactant systems that have been studied extensively (19–21). In our simulation, we vary the aspect ratio of the particles and the fraction of the surface covered by hydrophobic stripes. Below, we show that such simple model systems show a wide variety of self-assembled structures, many of which have been observed in experiment.

Methods

To study the self-assembly of patchy spherocylinders (PSCs), we performed Monte Carlo simulations. A sketch of a typical model particle is shown in Fig. 1. The interaction between two PSCs contains two ingredients—a repulsive interaction that depends only on the distance of closest approach between two spherocylinders, and an attraction that is angle-dependent:

$$U_{ij}=U_{rep}+U_{attr}.$$ (1)

The repulsive interaction was modeled using the Weeks-Chandler-Andersen potential (i.e., a shifted truncated Lennard-Jones potential):

$$U_{rep}\left(d_{ij}\right)=\{\begin{array}{cc}4ϵ\left[{\left(\frac{D}{d_{ij}}\right)}^{12}-{\left(\frac{D}{d_{ij}}\right)}^6+\frac{1}{4}\right]& d_{ij}\le \sqrt[6]{2}D\\ 0& d_{ij}>\sqrt[6]{2}D\end{array}$$ (2)

where ϵ represents strength of repulsion, D stands for diameter of the PSC, and d_ij is the closest distance between the line segments of length L in the middle of PSCs i and j (dotted segment in Fig. 1). The shape of the spherocylinder itself is swept out by moving a sphere with diameter D along the central line segment.

Figure 1.

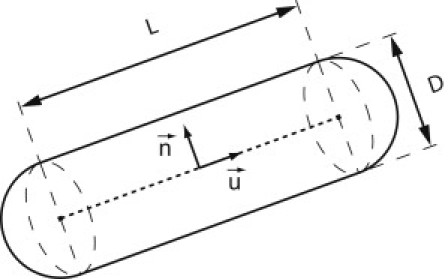
Schematic representation of a patchy spherocylinder (PSC). The letter L represents the length of the cylindrical part, D denotes its diameter, and $\overrightarrow{\mathrm{u}}$ is a unit vector along the spherocylinder axis. The vector $\overrightarrow{\mathbf{n}}$ is a unit vector normal to the spherocylinder axis defining the orientation of the attractive patch.

The functional form of the attractive part of the pair potential should reflect that there are two ways in which the attractive interaction between PSCs may be changed. The first, and most obvious, is that hydrophobic attraction can only act when the hydrophobic patches face each other. Hence, a rotation of a spherocylinder around its axis may change the attraction. This orientation dependence is a normal feature of patchy-particle models. The second, and less obvious, dependence reflects the fact that the hydrophobic attraction is expected to be strongest when the facing hydrophobic stripes are aligned and weakest when they are perpendicular. We take this orientation-dependence into account using a method that is inspired by (though not identical to) the method proposed by Savenko and Dijkstra (22).

We consider two variations of our striped spherocylinder model (see Fig. 2). Although the two models seem similar, they give rise to very different aggregation behavior. The first model that we consider, patchy spherocylinders-attractive endcaps (PSC-AE), has an attractive stripe that extends all along the spherocylinder (i.e., including hemispherical caps). The second model, patchy spherocylinders-no attractive endcaps (PSC-NE), has an attractive stripe that only runs along the cylindrical part of the spherocylinder. The distance dependence of the attractive potential is given by

$$U_{dist}\left(r_{ij}\right)=\{\begin{array}{ll}-\in \hfill & r_{ij}\le r_c-{\omega }_c\hfill \\ -\in {\text{cos}}^2\left[\frac{\pi \left(r_{ij}-r_c+{\omega }_c\right)}{2{\omega }_c}\right]\hfill & r_c-{\omega }_c<r_{ij}\le r_c\hfill \\ 0\hfill & r_{ij}>r_c,\hfill \end{array}$$ (3)

where r_c and ω_c are two parameters that, together, determine the range of the attraction. In what follows, we choose $r_c=D\sqrt[6]{2}+{\omega }_c$ and we consider both short-ranged and long-ranged attractions. For the short-ranged attraction, ω_c = 0.5D and for the long-ranged attraction, ω_c = 1.3D.

Figure 2.

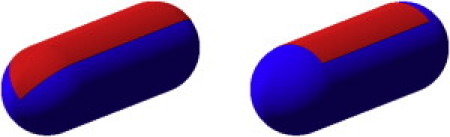
Graphical representation of the two PSC models. (Blue) The part of the surface that interacts as a hard spherocylinder. (Red) Attractive patches. (Left) PSC-AE (attractive endcaps). (Right) PSC-NE (nonattractive endcaps).

All Monte Carlo simulations were performed at constant number of particles (N), volume (V), and temperature (T). To update configurations, we use single-particle displacement and rotation moves. The systems studied in the simulations always contained 127 PSCs placed in a cubic cell. The value “127” may seem like a small number. However, as the aggregates are usually lower-dimensional, this number of particles is adequate. The simulations for a given aspect ratio were all performed at a fixed, low volume fraction ∼4%(see Tables 1–4).

Table 1.

Schematic phase diagram for the PSC-AE model with long-ranged interaction (see text)

PSC-AE long
L/D = 2
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	I	C
0.3	I	I	I	C	C	B
0.2	I	C	C	C	F4	B
0.1	C	C	C	F3	F4	B
L/D = 3
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	C	B
0.3	I	I	C	C	F4	B
0.2	C	C	C	F3	F4	B
0.1	F2	F2	2F2	F3	F4	B
L/D = 5
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	C
0.5	I	I	I	C	C	B
0.3	I	C	C	F3	F4	B
0.2	C	C	2F2	F3	F4	B
0.1	F2	F2	2F2	F3	F4	B

The first column contains the reduced temperature T^∗ ≡ k_BT/ϵ. The subsequent columns refer to different opening angles of the hydrophobic stripes. Table contains the results for different aspect ratios L/D. The letter I refers to a disordered (isotropic) phase. The letter C refers to the formation of clusters, F denotes fibers, and B bilayers.

Table 2.

Schematic phase diagram for the PSC-AE model with short-ranged interaction (see text)

PSC-AE short
L/D = 2
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	I	I
0.3	I	I	I	I	C	C
0.2	I	I	I	C	C	B
0.1	C	C	F3	F3	F4	B
L/D = 3
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	I	I
0.3	I	I	I	C	C	C
0.2	C	C	C	C	C	B
0.1	C	C	C	F3	F4	B
L/D = 5
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	C	C	C
0.3	I	C	C	C	C	B
0.2	C	C	C	C	C	B
0.1	C	C	C	F3	F4	B

The first column contains the reduced temperature T^∗ ≡ k_BT/ϵ. The subsequent columns refer to different opening angles of the hydrophobic stripes. Table contains the results for different aspect ratios L/D. The letter I refers to a disordered (isotropic) phase. The letter C refers to the formation of clusters, F denotes fibers, and B bilayers. Note that the 2F2 structure is not observed in this case.

Table 3.

Schematic phase diagram for the PSC-NE model with long-ranged interaction (see text)

PSC-NE long
L/D = 2
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	I	I
0.3	I	I	I	I	I	I
0.2	I	I	I	C	C	CS
0.1	C	C	C	C	C	CS
0.05	C	C	C	C	C	CS
L/D = 3
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	C	C
0.3	I	I	I	C	C	CS
0.2	C	C	C	C	C	CS
0.1	C	C	C	C	C	CS
L/D = 5
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	C	C	C
0.3	I	C	C	C	C	MS
0.2	C	C	C	C	C	PS
0.1	C	C	C	C	C	PS
L/D = 10
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	C	C
0.5	C	C	C	C	C	PS
0.3	C	C	C	C	C	PS
0.2	C	C	C	C	C	PS
0.1	C	C	C	C	C	PS

The first column contains the reduced temperature T^∗ ≡ k_BT/ϵ. The subsequent columns refer to different opening angles of the hydrophobic stripes. Table contains the results for different aspect ratios L/D. The letter I refers to a disordered (isotropic) phase. The letter C refers to the formation of clusters, PS denotes parallel stacks, CS crossed stacks, and MS mixed stacks.

Table 4.

Schematic phase diagram for the PSC-NE model with short-ranged interaction (see text)

PSC-NE short
L/D = 2
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	I	I
0.3	I	I	I	I	I	I
0.2	I	I	I	C	C	MS
0.1	C	C	C	C	C	MS
0.05	C	C	C	C	C	PS
L/D = 3
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	I	I
0.3	I	I	I	C	C	C
0.2	I	C	C	C	C	PS
0.1	C	C	C	C	C	PS
L/D = 5
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	I	I
0.5	I	I	I	I	C	C
0.3	I	I	C	C	C	PS
0.2	C	C	C	C	C	PS
0.1	C	C	C	C	C	PS
L/D = 10
T∗	30°	45°	60°	90°	120°	180°
1.0	I	I	I	I	C	C
0.5	C	C	C	C	C	PS
0.3	C	C	C	C	C	PS
0.2	C	C	C	C	C	PS
0.1	C	C	C	C	C	PS

The first column contains the reduced temperature T^∗ ≡ k_BT/ϵ. The subsequent columns refer to different opening angles of the hydrophobic stripes. Table contains the results for different aspect ratios L/D. The letter I refers to a disordered (isotropic) phase. The letter C refers to the formation of clusters, PS denotes parallel stacks, and MS mixed stacks. Note that the CS structure is not observed in this case.

We performed simulations for the following aspect ratios: L/D = 2, 3, 5, and 10. The angular width of the attractive stripe (including the switching region) varied from 30° to 180°. Unless stated otherwise, the initial configuration was an orientationally disordered fluid of PSCs. The initial configuration were equilibrated for (typically) 5.10⁶ sweeps (= moves per particle). After that, we sampled the equilibrium properties of the system during 5.10⁸ sweeps. The reduced temperature of the system (T^∗ ≡ k_BT/ϵ) was varied form T^∗ = 0.1 to T^∗ = 1.0. In what follows, all lengths are expressed in units of D. For a protein α-helix, D ≈ 1 nm and for rodlike colloids or viruses, D = 10–100 nm.

Results

The most striking feature of the simulation results presented below is the wide variety of aggregate shapes that are generated by this simple model, purely by modifying the opening angle of the attractive stripe. On the whole, we find that, although the aggregation behavior depends quantitatively on the aspect ratio of the spherocylinders, there is a usually qualitative similarity between the structures formed by PSCs with different aspect ratio. Hence, the key determinants in the aggregation behavior appear to be:

• 1.The angular width of the attractive stripes on the PSCs, and
• 2.The presence or absence of an attractive region of the spherical endcaps of the spherocylinders.

Below, we discuss our findings in more detail.

PSC-AE model

Fig. 3 shows a schematic phase diagram for spherocylinders with an aspect ratio L/D = 3 and an attractive stripe along the length of the cylindrical part of the particles that continues on the spherical endcaps. The figure shows that a wide variety of aggregate structures is observed as T^∗ and the opening angle of the attractive stripe are varied. At high temperatures, we find (not surprisingly) an orientationally disordered (isotropic) phase of PSCs. The stability range of the isotropic phase is indicated in the figure by I.

Figure 3.

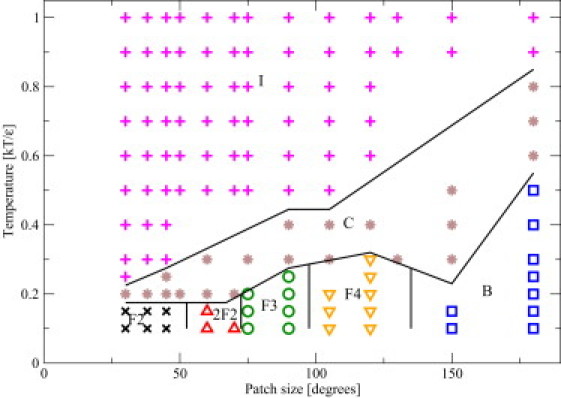
Schematic phase diagram of patchy spherocylinders with L/D = 3, at a volume fraction 4%. The model considered here has attractive endcaps and long-range attraction. The observed phases are: I, isotropic; C, cluster; Fn, fibers (n denotes the number of particles in the cross section of the fiber); B, bilayer. (Black lines) Schematic representation of boundaries between the points with different structures.

As the system is cooled down, we observe the formation of clusters (C). By clusters, we mean finite aggregates of small numbers of particles. Such finite aggregates are qualitatively different from the extended structures (fibers or sheets) that form at lower temperatures. Note also that the finite clusters are similar to surfactant micelles, although the morphology of the clusters formed is usually not the same. The PSC clusters are fairly disordered but their shape may already be indicative of the extended structures that form upon further cooling: Phases F2–F4 are fibers of aligned PSCs. The number n in Fn denotes the number of PSCs in the cross section of a single fiber. The phase denoted by B is a bilayer structure where the attractive stripes of the PSCs are oriented toward the middle of the bilayer. Interestingly, we observe both planar bilayers and bilayer vesicles, where the shape of a vesicle depends on the aspect ratio (L/D) of the building blocks. To rule out the possibility that the structures that we observe are determined by kinetics rather than equilibrium behavior, we checked for possible hysteresis effects. To this end, we started additional simulations where the initial configurations corresponded to bilayers, fibers, and clusters. In all cases, we found that the final structure did not depend on the initial configuration.

Fig. 4 shows a series of typical snapshots of the structures that we observed. We carried out additional simulations to check whether additional Fn structures with n > 4 would form between the F4 region and the B region in Fig. 3. In particular, we studied systems with patch widths of 130° and 140°. However, although we found some examples of F5 fibers, they were never a separate phase. Rather, they would appear in a mixture of bilayers or F4 fibers.

Figure 4.

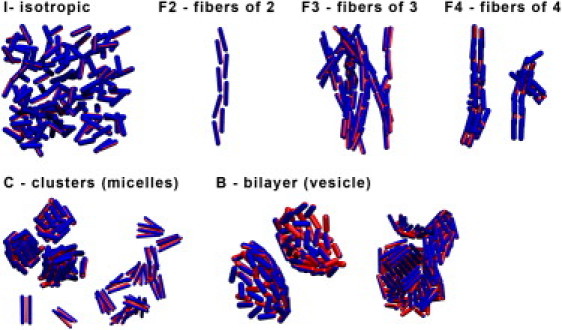
Snapshots of observed phases for the PSC-AE model. (Blue) PSCs. (Red spherocylinder) The attractive patch is represented with diameter corresponding to the patch size. The use of periodic boundary conditions allows us to display a cut through the vesicle structures.

Repeating the same simulations with other aspect ratios, we observed phase diagrams that were very similar to the L/D = 3 case (see Table 1). As the aspect ratio of the spherocylinders increases, the range of stability of the isotropic fluid phase shrinks. This is not surprising, as the maximum strength of the attractive interaction between PSCs increases with their length.

Changing the range of the attraction has a limited effect on the phase diagram (see Table 2). However, in the case of the shorter-ranged attraction, the 2F2 fibers were not observed for stripes with an opening angle of 60°. The reason is that rods with a 60°-wide stripe and long-ranged attraction form a somewhat unusual structure where two F2 fibers assemble to form a fiber with four strands.

Note that, at first sight, these 2F2 fibers do look similar to the F4 fibers that form when the hydrophobic patches have an opening angle of 120°. In the F4 case, all four spherocylinders in a fiber can interact with all contact neighbors, and so the attractive stripes would be, on average, oriented toward the geometrical center of the fiber (see Fig. 5). Contrast this with the 2F2 structure, in which the stripes are narrow (e.g., 60°) patches that do not point toward the geometrical center of the fiber. In the 2F2 case, the PSCs have a strong attractive interaction with only one nearest-neighbor and one additional attractive interaction over a larger distance corresponding to a diagonal partner in cross section (see Fig. 5). This is why we have chosen to describe a bundle of 2F2 fibers rather than the F4 fiber. Naturally, such 2F2 bundles can only form when the attractive interaction is sufficiently long-ranged, and therefore no 2F2 structures were observed for short-ranged interactions, as can be seen by comparison of Table 1 and Table 2.

Figure 5.

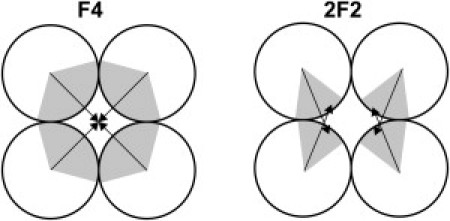
Two different structures of four-particle fibers. (Left) Structure corresponds to a wider angular patch. As a consequence, all neighboring particles can interact simultaneously and the patch is oriented toward the geometrical center of the fiber. We denote this structure as “F4”. (Right) Structure corresponds to the case of particles with a narrow attractive stripe. Particles interact strongly with one close neighbor at a time and interact weakly with the particle that is diagonally across from it. We denote this structure as “2F2”.

At very high L/D ratio, the interaction between the attractive ends will become very small compared to the interaction between two side-by-side aligned spherocylinders. Therefore, we expect that the phase behavior at higher temperatures will become similar to the model with nonattractive endcaps (PSC-NE), which is described in detail below.

PSC-NE model

Interestingly, there is an important qualitative difference between the structures formed by PSCs with an attractive patch on the spherical endcap (the PSC-AE model) and those formed PSCs that only have attractive stripes along the cylindrical part (the PSC-NE model).

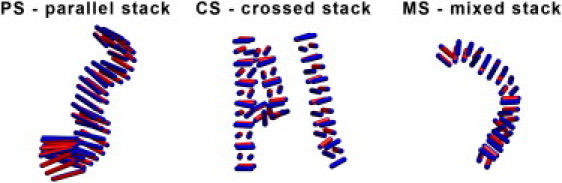
A schematic phase diagram for spherocylinders with an aspect ratio L/D = 3 and PSC-NE model is depicted in Fig. 6. The structures for other aspect ratios are summarized in Table 3. We note first of all that none of the fiber-structures observed in the case of attractive endcaps appear in the case where the spherical endcaps do not contribute to the attraction. Rather, we observe very different fiber structures where the PSCs are aligned perpendicular to the fiber axis. As in the case of the PSC-AE model, changing L/D results in the shift of the phase boundaries but, in addition, there are qualitative changes in the observed phase diagram. At smaller aspect ratios (L/D = 2 and L/D = 3), the PSCs form fibers consisting of a crossed stack (CS) of layers of aligned PSCs (see Fig. 7). In this structure, the spherocylinders are oriented perpendicular to the fiber axis and the PSCs in neighboring layers are perpendicular to each other. In one layer, a square forms with L PSC particles, resulting in area L×L.

Figure 6.

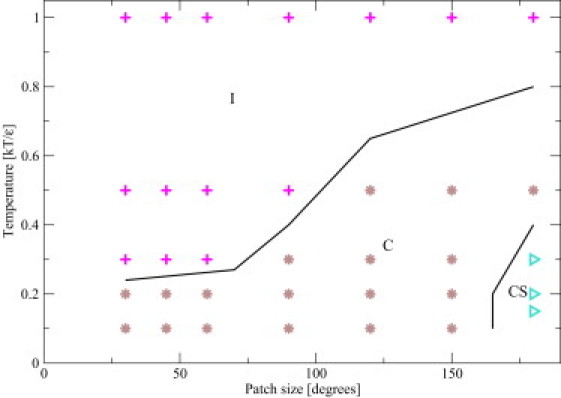
Schematic phase diagram of the PSC model with nonattractive endcaps (PSC-NE) and long-ranged attraction for L/D = 3 at a volume fraction of 4%. The observed phases are: I, isotropic; C, cluster; CS, crossed stack. (Black lines) Schematic representation of boundaries between the points with different structures.

Figure 7.

Snapshots of the aggregate structures of the PSC-NE model. (Blue) PSCs. (Red spherocylinder) The attractive patch is represented with diameter corresponding to the patch size.

PSCs with larger L/D ratios (5:10) form a very different structure: ribbons consisting of parallel dimers of PSCs. The cross section of such a parallel-stack ribbon is approximately equal to L × 2D. In one case (L/D = 5, T^∗ = 0.3, wedge angle = 180°), we observe mixed fibers that contain both parallel and crossed dimer regions. Not surprisingly, the crossed-stack structure has a higher bending rigidity than the parallel-dimer ribbon. Hence, the curvature of the mixed fibers is largely concentrated in the ribbons. Our simulations indicate that a wedge angle of 180° is at the boundary between flexible ribbons and rigid crossed stacks. This would suggest that, in this regime, the rigidity of fibers should be very sensitive to small changes in the intermolecular potential.

The structures formed by the PSC-NE model with short-ranged attraction interaction are similar to those exhibited by the same model with long-range attraction, with one exception: in the case of short-ranged attraction, we never observe crossed-stack fibers (see Table 4). The reason is that the CS phase is dependent on the interaction distance. If two spherocylinders can interact with each other at a distance such that another spherocylinder fits in between them, then the CS phase exists for L/D ≤ 4. We have tested this in a simulation and indeed, we have observed the CS phase under the following conditions: L/D = 4, T^∗ = 0.2, wedge angle = 180°.

Already at the cluster level, there are differences between the aggregates formed by the different PSC-NE particles: particles with a stripe-width of 30°–45° form clusters of dimers, while PSCs with larger stripe-widths form micellar clusters, where all PSCs were aligned.

Relation to experiments

The simulations discussed above show that a very simple coarse-grained model can account for a wide variety of aggregate structures. If the coarse-grained model that we use captures the essential physics of real proteins and peptides, we should expect that similar structures have been (or could be) observed in experiment.

We start by considering fibers made of α-helical peptides. Such structures have recently received much attention (for a review, see Woolfson (23)). One key difference between the experimental systems and the model studied here is that real peptides are chiral and that, as a result, all resulting structures are chiral. For instance, ribbons become twisted ribbons and fibers become coiled fibers. Of course, chirality can be taken into account in a coarse-grained model, but we instead focus our comparison on shorter stretches of fiber or ribbon, where the effects of chirality are not yet very pronounced.

In the review of Moutevelis and Woolfson (24), coiled-coil or collagenlike peptide structures were classified according to the complexity of their cross section. If we look at this experimental classification, we find that all structures predicted by our simple model are also observed in experiment. In particular, there are experimental structures corresponding to the F2, F3, and F4 fibers. In addition, there is experimental evidence of F5, F7, and F8 fibers. As explained in Moutevelis and Woolfson (24), the F5 structure is fairly rare (0.6% of all structures observed), hence it could easily have been missed in our fairly low-resolution search of parameter space. Note, however, that we did observe F5 structures in mixtures with F4 and bilayer structures. In addition, some of the structures they reported (24) (especially F7 and F8) may require the presence of more than a single attractive patch or stripe, something that is not captured in our very simple model (but that could obviously be accounted for by a straightforward extension of the model). Other, higher-order, assemblies reported in Moutevelis and Woolfson (24) (usually formed by connection or extension of the first-order assemblies) include structures that would also require additional patches in our model.

The simulations show that fibers with the F2–F4 structure can only form by a PSC-AE model with attractive endcaps. Without attractive ends, axially aligned particles cannot connect to form a fiber. Hence, such particles will either form finite aggregates or they have to align perpendicular to the axis of the fiber. Once the width of the attractive stripe in the PSC-AE model reached a critical size (150° in the case of L/D = 3), we do not observe an increase in the number of PSCs in direct contact or the formation of flat bilayers or bilayer vesicles. The credibility of our simple model would clearly be enhanced if there were experimental evidence for such bilayer vesicles. We have searched the Protein Data Bank (25) for possible vesicles made of bilayer of α-helices and, indeed, two structures (3BVF and 3GE4) seem to behave exactly as predicted: these proteins form vesicles where the structure is held together by the relatively large hydrophobic patches on the α-helices (see the Supporting Material).

Finally, we consider the structures formed by rodlike proteins that have no attractive interactions involving the endcaps (PSC-NE model). In this case, the simulations reveal a variety of stacks or ribbons where the proteins are oriented perpendicular to the fiber axis. In experiment, such structures are very common although, as mentioned before, they are usually chiral because of the chirality of their building blocks—something that is not accounted for in our model. An example of self-assembled of amphiphilic α-helices (i.e., “α-helical fibrils” (26)) has been recently reported. However, structures consisting of β-sheets (mainly cross-β structures) are more common. In fact, most of the amyloid structures are of this type. Note that the chirality and hydrogen bonding tend to increase the stiffness of such chiral structures with respect to the nonchiral structures presented here. The most common cluster structure of the PSC-NE model is a bundle structure, which is a common quaternary protein structure (e.g., 2A01 in the Protein Data Bank (25)). While our model suggests that all the above structures can be formed via hydrophobic interaction, this does not rule out the possibility that other interaction mechanisms (hydrogen bonds, salt bridges, charges, etc.) could result in the same structures. For example, structures involving β-sheets are usually stabilized by hydrogen bonds between the monomeric units.

Conclusions

We have presented a simple model for prolate proteins that reproduces a wide variety of protein-aggregation structures. Using Monte Carlo simulations, we identify two factors that play an important role in determining the morphology of protein aggregates:

• 1.The width of the attractive (hydrophobic) stripe on the side of the rodlike protein model; and
• 2.The presence or absence of attractive interactions mediated by the endcaps of the particles.

Our model does not include chirality and hence all resulting structures are nonchiral. However, it would be relatively straightforward to consider chiral models. If we disregard chirality, then the aggregate structures predicted by our model can all be identified with an experimentally observed protein-aggregate structures such as coiled coils, ribbons with cross β-structure, and protein vesicles. The model parameters corresponding to each structure provide us with a generic insight into the relation between the interaction potential of protein building blocks and the resulting aggregate morphology. Not all experimentally observed aggregate structures are reproduced by the simple model presented here, but it seems plausible that straightforward extensions of this model that go beyond a single hydrophobic stripe, could account for an even wider range of aggregate structures. Much of our discussion focused on the comparison between our simulations and the behavior of prolate proteins. However, our conclusions should apply equally well to structures formed by functionalized nanorods or rodlike viruses.

Appendix: Attraction between Striped Patchy Spherocylinders

Below, we describe the functional form that we have chosen to describe the attractive interaction between striped, patchy spherocylinders. We first define an interaction cutoff around the individual spherocylinders. The volume within this cutoff distance r_c is a spherocylinder with length L and radius r_c. When two spherocylinders are within range of the attraction, the axis of one spherocylinder (say i) intersects the cutoff volume of the other (say j), and vice versa. We denote the length of the line segments that are within the cutoff range by X_i and X_j, respectively. Of these segments, we delete the part (if any) that is not facing a hydrophobic patch on the other spherocylinder. The remaining line segments have lengths V_i and V_j, respectively (see Fig. 8). Clearly V_i and V_j are smaller for perpendicular spherocylinders than for parallel spherocylinders at the same distance. In our model, we assume that the attractive interaction between two spherocylinders is of the form

$$U_{attr}=U_{dist}\frac{V_i+V_j}{2D}{F}_1{F}_2,$$ (4)

where V_i and V_j are the length defined above. The values F₁ and F₂ (defined in Eq. 6 below) describe the dependence of the attraction on the orientation of the patches and U_dist(r_ij) describes the dependence of the attractive potential on the distance between the interaction segments V_i and V_j:

$$U_{dist}\left(r_{ij}\right)=\{\begin{array}{ll}-ϵ\hfill & r_{ij}\le r_c-{\omega }_c=D\sqrt[6]{2}\hfill \\ -ϵ{\text{cos}}^2\left[\frac{\pi \left(r_{ij}-r_c+{\omega }_c\right)}{2{\omega }_c}\right]\hfill & r_c-{\omega }_c<r_{ij}\le r_c\hfill \\ 0\hfill & r_{ij}>r_c.\hfill \end{array}$$ (5)

The value ϵ is a measure for the strength of the attraction, r_c represents a cutoff distance, and ω_c is a parameter that determines the distance over which the potential changes from −ϵ to 0. The scaling functions F_i (with $i=1,2$) in Eq. 4 are defined as:

$$F_1\left(\overrightarrow{{\text{r}}_{\text{ij}}},{\overrightarrow{\mathbf{n}}}_i\right)=\{\begin{array}{ll}0\hfill & {\overrightarrow{\mathbf{r}}}_{\mathit{ij}}^{\perp N}\cdot {\overrightarrow{\mathbf{n}}}_i\le C_1\hfill \\ \frac{1}{2}-\frac{{\overrightarrow{\mathbf{r}}}_{ij}^{\perp N}\cdot {\overrightarrow{\mathbf{n}}}_i-\left(C_2+C_1\right)/2}{C_2-C_1}\hfill & C_1<{\overrightarrow{\mathbf{r}}}_{\mathit{ij}}^{\perp N}\cdot {\overrightarrow{\mathbf{n}}}_{\mathit{i}}\le C_2\hfill \\ 1\hfill & {\overrightarrow{\mathbf{r}}}_{\mathit{ij}}^{\perp N}\cdot {\overrightarrow{\mathbf{n}}}_{\mathit{i}}>C_2.\hfill \end{array}$$ (6)

Here ${\overrightarrow{\mathbf{n}}}_i$ is a unit vector that specifies the orientation of the attractive stripe on spherocylinder i. The vector ${\overrightarrow{\mathbf{n}}}_{\mathit{i}}$ is perpendicular to ${\overrightarrow{\mathbf{u}}}_i$, the unit vector that specifies the orientation of spherocylinder i direction of PSC $\left({\widehat{\mathbf{u}}}_{\mathit{i}}\cdot {\widehat{\mathbf{n}}}_{\mathit{i}}=0\right)$ (Fig. 1). The vector ${\overrightarrow{\mathbf{r}}}_{\mathrm{i}\mathrm{j}}^{\perp \mathrm{N}}$ is a unit vector in the direction of the projection of $\overrightarrow{{\mathbf{r}}_{\mathbf{ij}}}$ perpendicular to ${\overrightarrow{\mathbf{u}}}_i$. The values C₁ and C₂ are constants, where C₂ represents half of the cosine of the opening angle of the wedge-shaped attractive patch. The value C₁ is the width of the linear switch function. (To give an example: a patch with total angular size 90° using an angular switch of 5° has C₁ = cos(90°/2) = cos (45°) = 1/√2 ≈ 0.707106781, and C₂ = cos(90°/2–5°) = cos (40°) = 0.766044443.)

Figure 8.

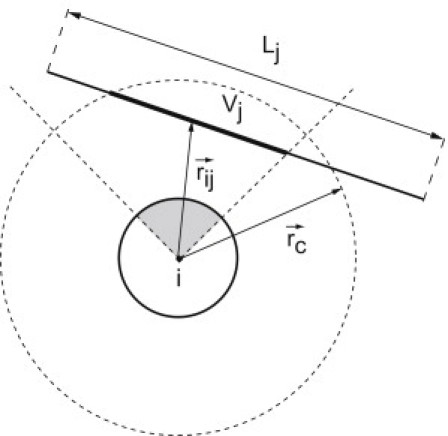
Schematic drawing of the intersection of patchy spherocylinder j line segment with the attractive patch of PSC i and its cutoff radius r_c. The cut results in an interactive line segment V_j. The expression $\overrightarrow{r_{ij}}$ is a vector from the geometrical center of interacting line segment V_i to the geometrical center of interacting line segment V_j.