On the Minimization of Fluctuations in the Response Times of Autoregulatory Gene Networks

Abstract

The temporal dynamics of the concentrations of several proteins are tightly regulated, particularly for critical nodes in biological networks such as transcription factors. An important mechanism to control transcription factor levels is through autoregulatory feedback loops where the protein can bind its own promoter. Here we use theoretical tools and computational simulations to further our understanding of transcription-factor autoregulatory loops. We show that the stochastic dynamics of feedback and mRNA synthesis can significantly influence the speed of response of autoregulatory genetic networks toward external stimuli. The fluctuations in the response-times associated with the accumulation of the transcription factor in the presence of negative or positive autoregulation can be minimized by confining the ratio of mRNA/protein lifetimes within 1:10. This predicted range of mRNA/protein lifetime agrees with ranges observed empirically in prokaryotes and eukaryotes. The theory can quantitatively and systematically account for the influence of regulatory element binding and unbinding dynamics on the transcription-factor concentration rise-times. The simulation results are robust against changes in several system parameters of the gene expression machinery.

Introduction

The quantitative levels of many proteins inside a cell are tightly regulated. The lag in response to an external or internal stimulus in attaining a given intracellular concentration is an important quantity in gene signaling, quorum sensing, genetic networks, switches, synthetic gene circuits, and gene memory devices (1–6). Raising the protein concentration beyond a certain threshold level in response to a signal subsequently triggers other signaling cascades. Transcriptional regulation plays an important role in determining the temporal evolution of protein levels and is orchestrated by the binding of transcription factor (TF) proteins to cis-regulatory elements such as promoters and enhancers.

The time required to achieve the n^th fraction of the steady-state concentration of a protein is a stochastic quantity and the mean first-passage time is often referred to as the rise-n-time. For precise regulation of cellular functions, the rise-times of the associated genes should be robust with respect to internal and external fluctuations. Even small delays in the rise times can have a significant effect on the cell or organism (5,7,8). In particular, given that transcription factors control the expression of multiple downstream genes, the TF concentrations need to be tightly regulated in a timely manner.

A large number of TFs interact with their own promoter sequences via the corresponding cis-acting regulatory elements, leading to self-regulatory loops that affect transcriptional regulation (9–12). Transcriptional autoregulatory networks play a critical role in fine-tuning the steady-state spatiotemporal protein concentrations (2,9,10,13–16), which are important for proper functioning, stabilization, development, and differentiation of the organism. Positive transcriptional autoregulation seems to be important for maintaining cellular memory and cell types across subsequent generations whereas negative transcriptional autoregulation seems to be important for maintaining the required in vivo concentrations of various proteins (1–3). Negative transcriptional autoregulation has also been shown to decrease the rise-n-time and the molecular number fluctuations associated with protein levels whereas positive autoregulation has been shown to increase both quantities (5,9,17).

In addition to the robustness of intracellular concentrations of various proteins in various types of self-regulatory loops, it is important to consider the robustness in the rise-n-times against internal and external fluctuations. Variations in the rise-n-times can play an important role in natural and synthetic gene networks. Although the effect of self-regulation on the extent of protein number fluctuations has been studied in detail (13–17), it is still not clear how self-regulatory loops influence the fluctuations in the rise-n-times associated with the building up of protein levels. In this work we seek to provide a theory to explain the following phenomena associated with the influence of transcriptional autoregulation on fluctuations in the rise-n-times:

• 1.The effect of promoter state fluctuations and the dynamics of mRNA synthesis on rise-n-times;
• 2.The influence of autoregulation on the fluctuations in the rise-n-times of gene expression systems;
• 3.The biologically relevant set of parameters which determine the robustness of the rise-n-times against fluctuations; and
• 4.The mechanism(s) by which gene expression systems are able to reduce the fluctuations in the rise-n-times.

Using theoretical and simulation tools, we show that a temporally efficient and responsively robust self-regulatory gene-network can be obtained by tuning the ratio of the lifetimes of mRNA and the corresponding TF protein.

Theory

A theoretical framework for autoregulation in gene expression

We consider the generalized autoregulated gene expression model described by the set of reactions illustrated in Fig. 1 A. In general, for a chemical reaction involving a molecule with concentration x, we consider its rate of creation (r_in) and elimination (r_out). We can write the stochastic kinetic equation describing the dynamics of concentration changes as a sum of a deterministic drift term that depends on r_in-r_out, and a diffusion term that depends on r_in and r_out (18–20). The stochastic chemical Langevin equation (CLE) is given by $dx/dt=r_{in}-r_{out}+\sqrt{r_{in}}{\xi }_{x,t}^{in}+\sqrt{r_{out}}{\xi }_{x,t}^{out}.$ Here ${\xi }_{x,t}^k$ are Gaussian noise terms for each of the chemical reactions and satisfy $\langle {\xi }_{x,t}^k\rangle =0$ and $\langle {\xi }_{x,t}^k{\xi }_{x,t^{\prime }}^k\rangle =\delta \left(t-t^{\prime }\right)$, where k = in or out.

Figure 1.

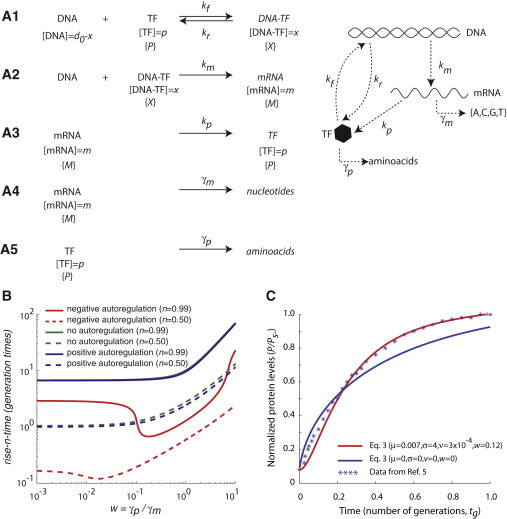
(A) Schematic description of the reactions analyzed in this work. (A1) Binding of the transcription factor protein (TF) to its cognate DNA sequence to form the DNA-TF complex. The concentration of promoter not bound by TF is denoted by d₀-x and the concentration of DNA bound by TF is denoted by x. The values k_f and k_r denote the kinetic constants for binding and unbinding, respectively. (A2) mRNA synthesis. The concentration of mRNA is denoted by m. The value k_m denotes the phenomenological kinetic constant for transcription. (A3) Protein synthesis. The concentration of the TF is denoted by p. The value k_p denotes the phenomenological kinetic constant for translation. (A4) mRNA degradation with kinetic constant γ_m. (A5) Protein degradation with kinetic constant γ_p. The variables x, m, and p are transformed into the dimensionless variables X, M, and P (see text). (B) Simulation results for the deterministic system of Eq. 3 (Γ = 0) Rise-n-time for the TF (the time required to reach the n^th fraction of the stationary state concentration) as a function of w (w = γ_p/γ_m, that is, the ratio of the decay rate constants for the protein and mRNA, respectively; shown in log scale) for positive autoregulation (blue), negative autoregulation (red), and no autoregulation (green). The rise-n-times are measured in terms of the number of generation times for n = 0.99 (solid lines) and n = 0.5 (dashed lines). Step size = 0.001. Δτ = 10⁻³, μ = 7 × 10⁻³, σ = 4, and ν = 3 × 10⁻⁴. Negative autoregulation shows a minimum rise-n-time as a function of w at w ∼ 0.2 (n = 0.99) or w ∼ 0.02 (n = 0.50). (C) Comparison of the theoretical predictions from the expressions in Eq. 3 and experimental results (deterministic case) The y axis shows the protein level normalized by the stationary state level in the negative autoregulation case. The x axis show time measured as the number of generation times. (Red line) Numerical integration of Eq. 3 with μ = 0.007, σ = 4, ν = 3 × 10⁻⁴, and w = 0.12; (blue line) prediction obtained when these parameters are 0. (Asterisks) Experimental data from Rosenfeld et al. (5,9). Because the experimental data starts from the initial value (P₀/P_s−) ∼ 0.08, we shifted the initial value of the simulated data to the same value at t = 0.

The reactions in Fig. 1 A refer to a gene that produces a transcription factor (TF) that can interact with its own promoter via binding at the corresponding regulatory elements along the DNA.

The first reaction describes the binding of the TF to its own free promoter (DNA) to form the DNA-TF complex. We denote by d₀ the total concentration of the promoter sequence (mols/liter, M) and by x the concentration of the DNA-TF complex. The phenomenological bimolecular rate constant k_f (M⁻¹ s⁻¹) and the unimolecular rate constant k_r (s⁻¹) characterize the binding and unbinding of the TF with its own promoter. The expression K_r/f = k_r/k_f (M) is the corresponding Michaelis-Menten-like constant. The second reaction describes the transcriptional process to form mRNA (concentration = m) and is characterized by the rate constant k_m (M s⁻¹). The third reaction describes the translation of the mRNA to form the TF protein (concentration = p) with a rate constant k_p (s⁻¹).

Reactions two and three describe the degradation of mRNA and TF; the intracellular lifetimes are characterized by the unimolecular decay rate constants γ_m (s⁻¹) and γ_p (s⁻¹), respectively. The reactions in Fig. 1 A are prone to fluctuations in the molecule numbers and the dynamics can be described in terms of a deterministic drift term controlled by the rate of production and degradation and a diffusion term. Because of these fluctuations, the first-passage time or rise-n-time to attain a given fraction n of the steady-state concentration (p = np_s±) is prone to variation. The stochastic CLEs corresponding to the set of chemical reactions in Fig. 1 A can be written as follows (18,19,21):

$$\begin{array}{l}dX/dt=k_{f}p\left(1-X\right)-k_{r}X+X_{\xi }/\sqrt{d_0};X_{\xi }=\sqrt{k_{r}X}{\xi }_{x,a,t}+\sqrt{k_{f}p\left(1-X\right)}{\xi }_{x,b,t}\hfill \\ dm/dt=k_m{\Omega }_{\pm }\left(X\right)-{\gamma }_{m}m+m_{\xi };m_{\xi }=\sqrt{k_m{\Omega }_{\pm }\left(X\right)}{\xi }_{m,a,t}+\sqrt{{\gamma }_{m}m}{\xi }_{m,b,t}\hfill \\ dp/dt=k_{p}m-{\gamma }_{p}p-k_f{d}_0\left(1-X\right)p+k_{r}X{d}_0+p_{\xi }+\sqrt{d_0}{X}_{\xi };p_{\xi }=\sqrt{k_{p}m}{\xi }_{p,a,t}+\sqrt{{\gamma }_{p}p}{\xi }_{p,b,t}\hfill \\ \langle {\xi }_{k,i,t}\rangle =0;\langle {\xi }_{k,i,t}{\xi }_{s,j,t^{\prime }}\rangle ={\delta }_{ks}{\delta }_{ij}\delta \left(t-t^{\prime }\right);k,s=\left\{x,m,p\right\};i,j=\left\{a,b\right\}\hfill \end{array}\}.$$ (1)

Here ξ are Gaussian white-noise terms associated with each of the chemical reactions and X = x/d₀ denotes the promoter occupancy (X ∈ [0,1]). In the negative autoregulation case, Ω₋ (X) = 1 − X reflects the microscopic probability of finding the free promoter. In the positive autoregulation case, Ω₊ (X) = X indicates the microscopic probability of finding the DNA-TF complex. In the absence of self-regulation, Ω(X) = 1.

Scaling and stochastic simulations of autoregulated gene expression

Although the scheme in Fig. 1 A can be directly simulated using the Gillespie algorithm (22) we use the CLE formalism (18) for the following reasons. We are interested in the distribution of the mean first-passage times associated with the building up of the TF protein to a certain preset fraction (n) of the steady-state value. The binding-unbinding dynamics of the protein with its own promoter is observed as a continuous process in the timescale of the synthesis of the mRNA and protein. We can use a continuous probability variable (such as X = x/d₀) to describe the promoter state dynamics to account for the promoter that is partially bound by the TF rather than a discrete Boolean type as described earlier (23,24). Because there is only one promoter associated with the gene of interest, using the Gillespie algorithm on such a system along the integer space and subsequently taking the ratio of bound/free number of promoters (= 0 or 1 at any time) with the total promoters (= 1) would result in Boolean type on-/off-states. The promoter state fluctuations mainly originate from the intrinsic randomness in the searching and arrival time of TF proteins and RNA polymerase at the promoter (25–28).

In the absence of autoregulation (Ω(X) → 1), the steady-state concentration of mRNA is m_s = k_m/γ_m. Defining the translational efficiency ε = k_p/γ_m, the steady-state TF concentration in the absence of autoregulation becomes p_s = εk_m/γ_p. An analytical solution to the system of Eq. 1 in the presence of autoregulation is not known but these equations can be stochastically simulated. To simplify this system of equations, we rescale the dynamical variables as follows:

$$\begin{array}{l}M=m/m_s,\hfill \\ P=p/p_s,\hfill \\ \tau ={\gamma }_{p}t.\hfill \end{array}$$ (2)

The validity of the CLE formalism can be ensured by adjusting the transformed time-step in such a way that the variables X, M, and P are observed as continuous type random variables in this timescale. With these variable transformations, the system of equations in Eq. 1 is reduced to the following dimensionless form:

$$\begin{array}{l}vdX/d\tau =P\left(1-X\right)-\mu X+X_{\Gamma };X_{\Gamma }=\sqrt{P\left(1-X\right)}{\Gamma }_{X,a,\tau }+\sqrt{\mu X}{\Gamma }_{X,b,\tau }\hfill \\ wdM/d\tau ={\Omega }_{\pm }\left(X\right)-M+M_{\Gamma };M_{\Gamma }=\sqrt{{\Omega }_{\pm }\left(X\right)}{\Gamma }_{M,a,\tau }+\sqrt{M}{\Gamma }_{M,b,\tau }\hfill \\ dP/d\tau =M-P-\sigma \left(\left(1-X\right)P-\mu X\right)+P_{\Gamma }+\sqrt{\sigma }{X}_{\Gamma };P_{\Gamma }=\sqrt{M}{\Gamma }_{P,a,\tau }+\sqrt{P}{\Gamma }_{P,b,\tau }\hfill \end{array}\}.$$ (3)

The expressions in Eq. 3 contain the following dimensionless parameters:

$$\begin{array}{l}w={\gamma }_p/{\gamma }_m,\hfill \\ \mu =K_{r/f}/p_s,\hfill \\ \sigma =k_f{d}_0/{\gamma }_p,\hfill \\ v={\gamma }_p/k_f{p}_s.\hfill \end{array}$$ (4)

The parameters ν and σ reflect the temporal coupling between the mRNA/protein dynamics and the binding-unbinding dynamics of TF molecules with the promoter. The ordinary perturbation parameter σ characterizes the strength of temporal coupling between the protein state dynamics with the promoter state fluctuations. The variable w represents the lifetimes of protein/mRNA and reflects the coupling between the mRNA and protein degradation dynamics. The variable μ, the Michaelis-Menten-like equilibrium constant measured in terms of the steady-state protein concentration p_s, is inversely proportional to the TF/promoter binding affinity and characterizes the strength of autoregulatory feedback.

The perturbation parameters w and v in the expressions in Eq. 3 are particularly important because they multiply the derivative terms, which describe, respectively, the dynamics of mRNA synthesis and the binding-unbinding dynamics of the TF to the promoter. Because p_s is proportional to the translational efficiency ε(ε = k_p/γ_m), both μ and ν are inversely proportional to ε. When the protein decay rate is high, both v and σ tend to 0 and the binding-unbinding dynamics of the TF is temporally uncoupled from the dynamics of protein-synthesis and decay. Further σ does not affect the rise-n-time of the transcription factor significantly because the change in the number of protein molecules due to promoter state fluctuations is negligible. In contrast, ν significantly affects the protein number fluctuations and fluctuations in the response times because the effect of varying ν is indirectly amplified through mRNA dynamics.

Furthermore, an increase in ν would decrease the rate at which promoter state occupancy shifts toward X = 1 (positive autoregulation) or X = 0 (negative autoregulation) as the TF level builds up. The decrease in the promoter state dynamics as v increases can be a consequence of either an increase in γ_p or a decrease in k_f. This means that there are not enough protein molecules to bind the promoter or there is a temporal slow-down in the autoregulatory feedback. This would eventually increase the rise-n-times in positive autoregulated networks and decrease the rise-n-time in negative autoregulated networks. The temporal slow-down in promoter state dynamics due to higher values of v can also lead to an overshooting behavior in the case of negative autoregulated network as observed experimentally by Rosenfeld et al. (9). For large values of w, an increase in w = (γ_p/γ_m), which may be a result of an increase in the protein decay rate and/or a decrease in the mRNA decay rate, leads to an increase in rise-n-times. Because the TF decays much faster, more time will be required to attain the n^th fraction of steady-state protein level, which in turn results in higher rise-n-times.

On the other hand, a decrease in w implies that the transcription factor protein will be stable over relatively longer times which in turn lead to an efficient binding and saturation of the promoter. This would result in an increase of rise-n-times in the case of negative autoregulated networks and a decrease of rise-n-times in the case of positive autoregulated networks under weak binding conditions (higher values of μ). Because the rise-n-time increases both at higher and lower values of w in the case of negatively autoregulated networks, one can eventually expect a minimum of rise-n-time at some optimum value of w. The system of expressions in Eq. 3 is completely characterized by this set of dimensionless perturbation parameters.

In the system of rate equations in Eq. 3, Γ are dimensionless Gaussian noise variables associated with the various reaction steps and satisfy the following constraints,

$$\begin{array}{l}{\Gamma }_{K,i,t}=\sqrt{{\lambda }_K}{\xi }_{k,i,t};\langle {\Gamma }_{K,i,\tau }\rangle =0;\langle {\Gamma }_{K,i,t}{\Gamma }_{S,j,t\prime }\rangle ={\lambda }_K{\delta }_{KS}{\delta }_{ij}\delta \left(t-t^{\prime }\right)\hfill \\ K,S=\left\{X,M,P\right\};i,j=\left\{a,b\right\};{\lambda }_X={\left(k_f{p}_s{d}_0\right)}^{-1};{\lambda }_M={\left({\gamma }_m{m}_s\right)}^{-1};{\lambda }_P={\left({\gamma }_p{p}_s\right)}^{-1}\hfill \end{array}\},$$ (5)

where λ_X/P/M are the noise strength parameters in the τ -space. Here X, M, P ∈ (0,1) during stochastic simulations, where X = 0, M = 0, P = 0, and X = 1, M = 1, P = 1 act as the reflecting boundaries and P = nP_s± (where n∈[0, 1]) is the absorbing boundary condition for the given mean first-passage time or rise-n-time problem under consideration. The deterministic steady-state concentration of TF levels P under the different autoregulation scenarios is given by

$$\begin{array}{l}{P}_s=1,\hfill \\ P_{s+}=1-\mu ,\hfill \\ P_{s-}=\left(1/2\right)\left(-\mu +\sqrt{{\mu }^2+4\mu }\right).\hfill \end{array}$$ (6)

In the limit when μ grows to infinity, we have lim_μ→∞ P_s− = P_s = 1. Similarly, when μ tends to zero, P_s+ also tends to 1.

Biologically relevant parameters characterizing autoregulated gene expression

For a given gene, d₀ = 1 molecule, p_s ∼ 10³ molecules, and m_s ∼ 10² molecules. In the τ-time space, we find γ_m ∼ 1/w and γ_p ∼ 1. We assume that under in vivo conditions, the protein interacts with its own promoter via a three-dimensional diffusion with a rate k_t ∼ 10⁶ M⁻¹ s⁻¹. The concentration of a single specific binding site or a protein molecule inside the Escherichia coli cell will be ∼2 nM and the number of collisions that can happen between a single TF protein with its own promoter will be in the order of k_f ∼ 10⁻³ molecules⁻¹ s⁻¹ (29). Here we have used the scaling 1 molecule = 2 nM inside the cellular volume. For a protein lifetime of ∼60 min, we find γ_p ∼ 3 × 10⁻⁴ s⁻¹. This means that in the transformed τ-space, k_f ∼ (10⁻³/γ_p) molecules⁻¹ γ_p¹. Upon substituting these values in the expressions in Eq. 5 we find the following empirical values:

$$\begin{array}{l}{\lambda }_X\sim {10}^{-4},\hfill \\ {\lambda }_M\sim w{10}^{-2},\hfill \\ {\lambda }_P\sim {10}^{-3}.\hfill \end{array}$$ (7)

Extension to dimers and protein-protein interactions

So far we have assumed that a single copy of the TF binds its own promoter and self-regulates its own expression. In several cases, a dimerized or multimerized protein binds its cis-regulatory modules and acts on the promoter (30). Under such conditions, the promoter occupancy variable X in the expressions in Eq. 3 will be modified as follows:

$$\begin{array}{l}\theta dY/d\tau =P^2-\varphi Y+\varphi \left(\mu X-Y\left(1-X\right)\right)+Y_{\Gamma };Y_{\Gamma }=\sqrt{P^2}{\Gamma }_{Y,a,\tau }+\sqrt{\varphi Y}{\Gamma }_{Y,b,\tau }+X_{\Gamma }\hfill \\ vdX/d\tau =Y\left(1-X\right)-\mu X+X_{\Gamma };X_{\Gamma }=\sqrt{Y\left(1-X\right)}{\Gamma }_{X,a,\tau }+\sqrt{\mu X}{\Gamma }_{X,b,\tau }\hfill \\ wdM/d\tau ={\Omega }_{\pm }\left(X\right)-M+M_{\Gamma };M_{\Gamma }=\sqrt{{\Omega }_{\pm }\left(X\right)}{\Gamma }_{M,a,\tau }+\sqrt{M}{\Gamma }_{M,b,\tau }\hfill \\ dP/d\tau =M-P-\left(P^2-\varphi Y\right)/\theta +P_{\Gamma }+Y_{\Gamma }/\sqrt{\theta };P_{\Gamma }=\sqrt{M}{\Gamma }_{P,a,\tau }+\sqrt{P}{\Gamma }_{P,b,\tau }\hfill \end{array}\}.$$ (8)

Here Y = p₂/p_s, where p₂ is the concentration of the freely available dimerized form of the protein while k_a and k_−a are corresponding forward and reverse rate constants associated with the dimerization reaction. Various other parameters and noise terms involved in the set of dynamical equations in Eq. 8 are defined as

$$\begin{array}{l}\theta ={\gamma }_p/k_a{p}_s,\hfill \\ \varphi =k_f{d}_0/p_s{k}_a,\hfill \\ \varphi =k_{-a}/k_a{p}_s,\hfill \\ {\Gamma }_{Y,a,\tau }=\sqrt{{\lambda }_Y}{\xi }_{y,a,t},\hfill \\ {\lambda }_Y={\left(k_a{p}_s\right)}^{-1}.\hfill \end{array}$$ (9)

The on-rate for the dimerization reaction will be diffusion-controlled and we estimate k_a ∼ 10⁶ M⁻¹ s⁻¹. Upon substituting the experimentally determined numerical values in the expressions in Eq. 9 we obtain the following empirical values:

$$\begin{array}{l}\theta \sim {10}^{-4},\hfill \\ \varphi \sim {10}^{-3},\hfill \\ \varphi \sim {10}^{-3}{e}^{-\alpha },\hfill \\ {\lambda }_Y\sim {10}^{-4}.\hfill \end{array}$$ (10)

Here α is the binding energy associated with the dimerization of TF proteins measured in terms of RT. The expressions in Eqs. 3–10 can be generalized to other systems including feed-forward, feedback, or cross-regulatory loops. In the latter case, two TFs such as A and B up-/downregulate each other's transcription. Under such conditions, the promoter occupancy rate equations for such a coupled system can be written as follows:

$$\begin{array}{l}{v}_{S}d{X}_S/d{\tau }_S=P_K\left(1-X_S\right)-{\mu }_S{X}_S+X_{S\Gamma };X_{S\Gamma }=\sqrt{P_K\left(1-X_S\right)}{\Gamma }_{X_S,a,{\tau }_S}+\sqrt{{\mu }_S{X}_S}{\Gamma }_{X_S,b,{\tau }_S}\hfill \\ w_{S}d{M}_S/d{\tau }_S={\Omega }_{\pm }\left(X_S\right)-M_S+M_{S\Gamma };M_{S\Gamma }=\sqrt{{\Omega }_{\pm }\left(X_S\right)}{\Gamma }_{M_S,a,{\tau }_S}+\sqrt{M_S}{\Gamma }_{M_S,b,{\tau }_S}\hfill \\ d{P}_S/d{\tau }_S=M_S-P_S-{\sigma }_S\left(\left(1-X_S\right)P_K-{\mu }_{S}X\right)+P_{S\Gamma }+\sqrt{{\sigma }_S}{X}_{S\Gamma }\hfill \\ P_{S\Gamma }=\sqrt{M_S}{\Gamma }_{P_S,a,{\tau }_S}-\sqrt{P_S}{\Gamma }_{P_S,b,{\tau }_S};P_A:\left(S=A,K=B\right);P_B:\left(S=B,K=A\right)\hfill \end{array}\}.$$ (11)

Here P_A and P_B are the scaled concentration terms associated with the two TF proteins which cross-regulate each other. Following the idea described in the expressions in Eq. 8, one can include the dimerization reaction between proteins A and B before cross-binding the respective cis-regulatory modules into the expressions in Eq. 11. The steady-state values of TF proteins which are required to set up the absorbing boundary condition for the mean first-passage time problem need to be numerically evaluated from Eqs. 8 and 11.

Stochastic simulations

The quantities that we want to calculate here are the mean and coefficient of variation ($CV=\sqrt{\text{variance}}/\text{mean}$) of the time required to attain the n^th fraction of the steady-state value of P. The estimated dimensionless parameters from empirical values are summarized in Table 1. We used the following numerical scheme (21) for the stochastic simulation of the expressions in Eq. 3,

$$\begin{array}{l}{X}_{k+1}=X_k+\left(P_k-\left(\mu +P_k\right)X_k\right)\Delta \tau /v+\sqrt{{\lambda }_X\Delta \tau }{X}_z/v;X_z=\sqrt{P_k\left(1-X_k\right)}{z}_{0,1,1}+\sqrt{\mu X_k}{z}_{0,1,2}\hfill \\ M_{k+1}=M_k+\left({\Omega }_{\pm }\left(X_k\right)-M_k\right)\Delta \tau /w+\sqrt{{\lambda }_M\Delta \tau }{M}_z/w;M_z=\sqrt{{\Omega }_{\pm }\left(X_k\right)}{z}_{0,2,1}+\sqrt{M_k}{z}_{0,2,2}\hfill \\ P_{k+1}=P_k+\left(M_k-P_k-\sigma \left(\left(1-X_k\right)P_k-\mu X_k\right)\right)\Delta \tau +\sqrt{{\lambda }_P\Delta \tau }{P}_z+\sqrt{\sigma }{X}_z;P_z=\sqrt{M_k}{z}_{0,3,1}+\sqrt{P_k}{z}_{0,3,2}\hfill \end{array}\},$$ (12)

where z are independent random values drawn from the standard normal distribution N(0,1). When the TF strongly binds with its own promoter, then the value of K_r/f under in vivo conditions is K_r/f ∼ (1–7) nM (9). This means that approximately three protein molecules are enough to bind and saturate 50% of their own promoter sequences inside the cellular volume and we estimate μ ∼ 7 × 10⁻³. The value of w = γ_p/γ_m seems to vary from w ∼ 10⁻¹ in the case of prokaryotes to w ∼ 10⁰ in the case of eukaryotes (25,29). Together with all these values, we also set the scaled time step as Δt = 10⁻³ and iterate w inside the range (0.01, 10.0) with a step size of Δw = 0.01 and n inside the range (0.1, 0.99) with a step size of Δn = 0.01.

Table 1.

Variables and parameters used in the stochastic simulations

Variable/parameter	Definition	Default values in t-space	Default values in τ = γpt space	Range examined
d0		1 molecule	1 molecule
ms	km/γm	100 molecules	100 molecules
ps	kmkp/γmγp	1000 molecules	1000 molecules
Kr/f	kr/kf	7 molecules	7 molecules
kf		10−3 molecules−1 s−1	4 molecules−1γp1
γm		2.5 × 10−3 s−1	8 (1/w = γm/γp) γp1
γp		3 × 0−4 s−1	1 γp1
ν	γp/kfps	0.0003	0.0003	5 × 10−5–0.004 in Figs. 3 and 4
σ	kfd0/γp	4	4	0–10,000 in Figs. 3 and 4
w	γp/γm	0.12	0.12	10−3–10 in Figs. 3 and 4
μ	Kf/r/ps	0.007	0.007	0.001–0.05 in Figs. 3 and 4
λM	1/γmms	1/γm102 molecules−1 s1	w10−2 molecules−1γp−1
λP	1/γpps	4 molecules−1 s1	10−3 molecules−1γp−1
λX	1/kfd0ps	1 molecules−1 s1	10−4 molecules−1γp−1

This table describes the variables and parameters used in the stochastic simulations (see text for details). The corresponding chemical reactions are shown in Fig. 1A. The values d₀ represent the number of promoters of a gene of interest inside the cell. The values m_s and p_s are the steady-state numbers of mRNA and protein molecules in the absence of autoregulation. The value K_r/f is the Michaelis-Menten-like equilibrium constant (the normalized and dimensionless form is μ) associated with the binding of the protein with its own promoter. The k_f is the forward rate constant associated with TF binding to DNA and k_r is the corresponding unbinding constant. The values γ_m and γ_p are the decay rate constants associated with the mRNA and protein molecules. The values ν and σ are the dimensionless parameters that reflect the temporal coupling between the mRNA/protein dynamics with the binding-unbinding dynamics of protein molecules with the promoter. The value w is lifetimes of protein/mRNA and reflects the coupling between the mRNA and protein dynamics; λ_X/P/M values are the noise strength parameters in the τ-space.

The value of the scaled time-step Δt = 10⁻³ plays critical role in capturing the effects of binding and unbinding of the transcription factor with its own promoter. In the real-timescale we find Δt = (10⁻³/γ_p) ≈ 4 s for a typical decay rate of the protein γ_p ∼ 3 × 10⁻⁴ s⁻¹, which corresponds to a lifetime of ∼60 min. One should note that Δt is already within the timescale that is required by the autoregulatory transcription factor to locate its specific promoter on DNA by searching via a combination of three- and one-dimensional diffusion dynamics inside the cell (25–27). Our numerical simulations show that the results do not change significantly whenever Δt < 10⁻³. The values of X, M, and P are confined inside (0,1); X = 0, M = 0, P = 0 and X = 1, M = 1, P = 1 act as the reflecting boundaries. The stochastic simulations are stopped whenever P = nP_s± (where n∈[0,1]), which is the absorbing boundary condition for a given value of n.

In the scaled dimensionless space, the rise-n-time is the scaled time τ required to attain the n^th fraction of the steady-state value of q. To convert τ into the original time variable t, which is measured in terms of the generation-time (t_g) of the organism, we use the transformation rule t_g = τ/ln2. All the statistical estimates associated with various rise-n-times were computed over 10⁵ stochastic realizations of the rescaled Langevin equations (see expressions in Eq. 3). The initial conditions for the negatively self-regulated and non-self-regulated gene expression systems were set to X₀ = 0, M₀ = 0, P₀ = 0, and τ = 0. We set the initial conditions to X₀ = 1, M₀ = 0, P₀ = 0, and τ = 0 for the simulation of positively self-regulated gene expression system.

Results and Discussion

We start by considering the deterministic case in Fig. 1 B. The rise-n-time associated with the negatively autoregulated gene expression system is shorter than the rise-n-time for the nonautoregulated and positively autoregulated cases. In the case of negatively autoregulated gene expression, there is an optimum value of w = γ_p/γ_m at which the rise-n-time is a minimum. This optimum becomes more prominent as n increases. When w is low, the mRNA levels decay faster than the transcription factor protein levels and there are very few mRNA molecules available for translation. In the negative autoregulation case, as the mRNA decay becomes slower, more proteins are produced per transcript, leading to faster blocking of the promoter by negative self-regulation—which, in turn, slows down the transcription factor protein production rate. In the positive autoregulation case, the promoter is further activated by protein production. In the strong binding scenario simulated in Fig. 1 B (μ = 0.007), as the protein level builds up and saturates the promoter, the system moves closer to the nonregulated case. With these strong-binding simulations, we obtain the following steady-state values: P_s− ≈ 0.0, P_s = 1, and P_s+ ≈ 0.993. This means that ∼10-times the rise-n-time will be required by the negatively autoregulated gene expression system to attain the steady-state concentration of the TF protein, similar to that of the positively or nonautoregulated gene network.

Fig. 1 C shows a single trajectory of the ratio (P/P_s−) for a negatively autoregulated network as a function of time. The quantitative results from the numerical integration agree well with the experimental data that were obtained on the negatively autoregulated E. coli TetR system (9). The fit from the numerical integration (μ = 0.007, σ = 4, ν = 3 × 10⁻⁴, and w = 0.12) is better than the one obtained from the deterministic analytical solution obtained by Rosenfeld et al. (9) for the conditions ν = 0, w = 0, and σ = 0. However, it should be noted that the model proposed here has more parameters than the one used in Rosenfeld et al. (9). These results argue that the feedback input functions for the protein dynamics (31), which are used in modeling various genetic networks, should also contain information about the mRNA dynamics.

After considering the deterministic conditions, we turn to the numerical simulations of the expressions in Eq. 3 under stochastic conditions (Fig. 2). Under negative autoregulation (Fig. 2 C), these simulations indicate that the rise-n-time attains a minimum at a value w = w_min,τ, which is a function of n (Fig. 2, C1 and C2). To characterize the fluctuations in the rise-n-times, we computed the coefficient of variation of the rise-n-time (CV_rise) which attained a minimum value (CV_min) around n ∼ (0.4–0.6) (Fig. 2, C3 and C4); we denote with w_min,ν the value of w at which this minimum was achieved. In contrast, the stochastic simulations of the gene expression system with positive autoregulation (Fig. 2 B) and without any autoregulation (Fig. 2 A) showed rise-n-times that were higher than the generation-time of the organism whenever $n\ge 0.5$. The simulation results for positive autoregulation and no-autoregulation are very similar here due to rapid saturation of the promoter by the transcription factor. In the absence of any autoregulation, the function Cv_min(n) was almost a constant whenever $n<0.8$ (Fig. 2, A and B).

Figure 2.

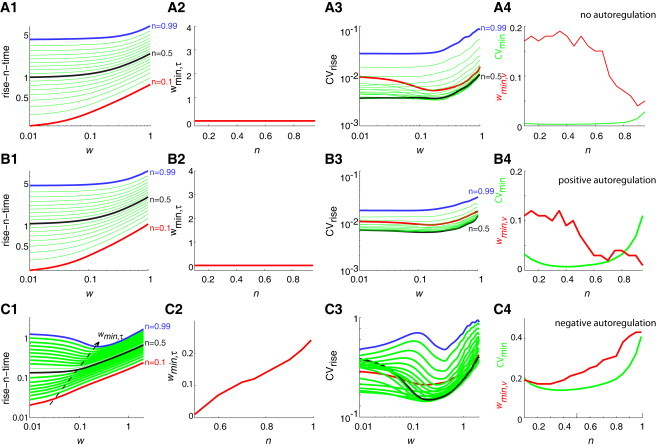
Effects of positive and negative autoregulation (stochastic simulations). Simulation results in the absence of autoregulation (A), in the presence of positive autoregulation (B), and in the presence of negative autoregulation (C). (A1–C1) Variation of the mean rise-n-times (in units of generation times, shown in log scale) for different values of w and n. Here the noise level parameters are μ = 0.007 and σ = 4, ν = 3 × 10⁻⁴, w is iterated with a step-size Δw = 0.01 (shown in log scale), the scaled time step was Δτ = 0.001, and n is iterated inside the interval 0.1–0.99 with Δn = 0.05. All the statistical quantities were computed over 10⁵ stochastic realizations (see Theory). (Red lines) n = 0.1. (Black lines) n = 0.5. (Blue lines) n = 0.99. In panel C1 and particularly for n > 0.3, the rise-n-time showed a minimum at w_min,τ < 10⁻². (A2–C2) Value of w_min,τ as a function of n. (A3–C3) Coefficient of variation of the rise-n-times (shown in log scale) as a function of w (shown in log scale) for different values of n. The value of CV attains a minimum when w → w_min,τ. Note that w_min,τ ≠ w_min,ν. (A4–C4) Both the parameters CV_min (green) and w_min,ν (red) are shown here as a function of n. The minimum value of CV_min occurs for different values of n in the negative and positive autoregulation cases. The noisy red curves can be attributed to the difficulty in defining a minimum w point for several of the curves in panels A3–C3.

Irrespective of the type of autoregulation, tuning of the parameters w and n can minimize the extent of fluctuations in the rise-n-times. The changes in the coefficient of variation in the rise-n-times for different values of n is 1–5% in the absence of autoregulation, 2–20% in the presence of positive autoregulation, and 10–50% in the presence of negative autoregulation (Fig. 2). Thus, autoregulatory loops increase the level of fluctuations in the response-times associated with the gene expression system. The increase in the fluctuations of the response-times is a consequence of promoter-state fluctuations introduced by the binding and unbinding of the autoregulating TF with the promoter sequences.

These theoretical results suggest that the optimum value of the parameter w that can be considered to design an efficient and robust negative autoregulatory gene expression network is inside the interval (0.1, 0.5), where fluctuations in the response-times are minimized. We asked whether this optimum range for w would be affected by changes in the other perturbation parameters by considering the deterministic version of the expressions in Eq. 3 with Γ = 0. The simulation results show that the optimum range of w is not significantly affected upon changing v, σ, μ, λ_X, λ_M, and λ_P. The effects of increasing the parameter v on the deterministic version of the expressions in Eq. 3 are shown in Fig. 3, A and B, the effects of changing σ are shown in Fig. 3, C and D, and the effects of changing μ are shown in Fig. 3, E and F. The minimum response-time values decrease as ν increases. Increasing ν in a negatively autoregulated network results in the overshooting of the synthesis of the TF protein as shown in Fig. 3 A.

Figure 3.

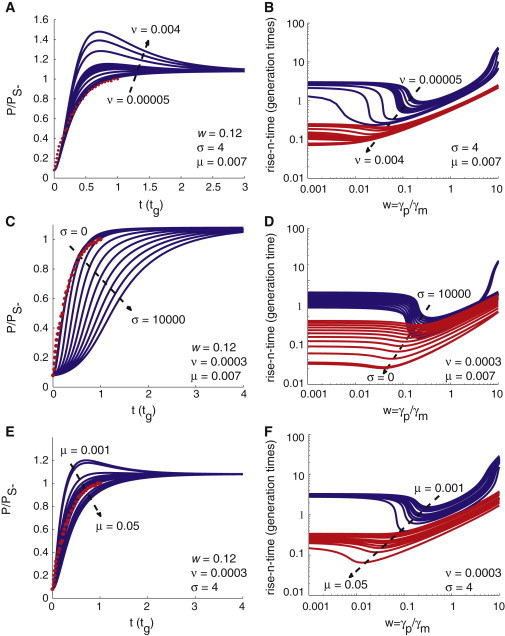
Effect of simulation parameters on rise-n-time and kinetics of negative autoregulation. We characterize the parameter landscape to describe how the rise-n-time and the kinetics of TF synthesis depend on the perturbation parameters w, ν, σ, and μ. We show these dependencies on several two-dimensional plots. All these plots were obtained by numerical integration of Eq. 3 for the negatively autoregulated network. (A, C, and E) Variation of protein synthesis levels as a function of the number of generation times (t_g). (Red asterisks) Experimental data from Rosenfeld et al. (9). (A) Curves show different values of parameter ν, ranging from 5 × 10⁻⁵ (top curve) to 0.004 (bottom curve) (σ = 4; μ = 0.007; w = 0.12; and ν = 0.004, 0.003, 0.002, 0.001, 0.0009, 0.0008, 0.0007, 0.0006, 0.0004, 0.0002, 0.0001, and 0.00005). Larger values of ν show evidence of overshooting in TF synthesis. (C) Curves show different values of the parameter σ ranging from 0 to 10,000 (ν = 3 × 10⁻⁴, w = 0.12, μ = 0.007; and σ = 0, 1, 2, 3, 4, 10, 100, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, and 10,000). When σ < 10³, the protein synthesis trajectory is not affected much. Beyond this value, the rise-n-time increases with σ. (E) Curves show different values of μ ranging from 0.001 to 0.05 (ν = 3 × 10⁻⁴, w = 0.12, σ = 4; μ = 0.05, 0.04, 0.03, 0.02, 0.01, 0.009, 0.008, 0.007, 0.006, 0.004, 0.003, 0.002, and 0.001). Lower values of μ show overshooting behavior in TF synthesis. (B, D, and F) Rise-n-times (log scale) as a function of parameter w (ranging from 0.001 to 10; shown in log scale). The characterization of the parameter variation in panels B, D, and F parallels the corresponding plots in panels A, C, and E. (Red curves) Rise-0.5-times (t_0.5−). (Blue curves) Rise-0.99-times (t_0.99−). The value of w at which the rise-n-times attain a minimum is a function of n and v. For a fixed ν we observe w_0.5− < w_0.99−. When ν  > 5 × 10⁻³, then the rise-0.5-times show very shallow minimum with w. With these parameter settings, for ν ≤ 3 × 10⁻⁴ and w ∼ 0.12, we find that t_0.5− ∼ 0.23t_g and t_0.99− ∼ t_g. These values are consistent with the experimental observations on negative self-regulation in transcription networks.

This result agrees with the experimental observations in Rosenfeld et al. (9). Increasing the value of μ in the negatively autoregulated network transforms the negatively autoregulated system to a non-self-regulated one. Decreasing μ can also lead to an overshooting behavior (Fig. 3 E) and increase the rise-n-time (Fig. 3 F). Because μ ∝ K_r/f and μ ∝ ε⁻¹, this means that an increase in the translational efficiency of the negatively autoregulated system would enhance the effects of negative self-regulation further. In the stochastic conditions, changing ν, μ, and σ values do not affect the optimum range of w_min,τ at which the coefficient of variation in the rise-n-times attains a minimum (Fig. 4). This suggests that this optimum range of w is also robust against the changes in the binding strength of the TF with its own promoter and the translational efficiency of the self-regulated gene network. Similarly, the optimum range of the parameter n that can be considered to attain the minimum level of fluctuations in the rise-n-times is in the interval 0.4–0.6.

Figure 4.

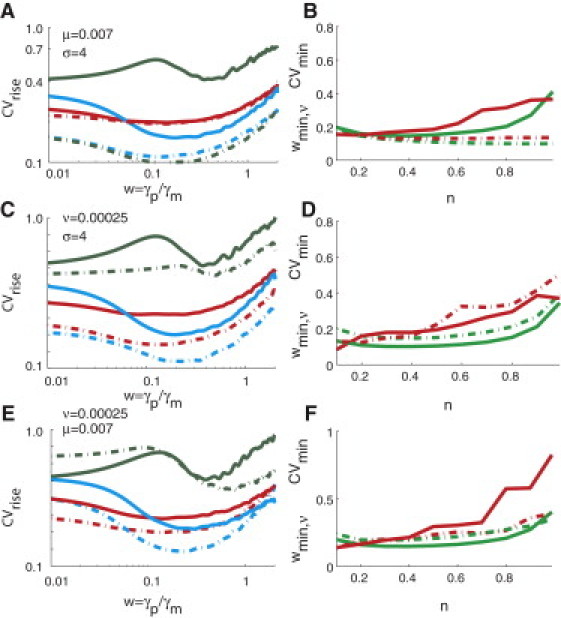
Robustness of optimum range of w against changes in other parameters (σ, μ, and ν) in negatively autoregulated network: We further characterize the parameter landscape to describe the dependence of the coefficient of variation of the rise-n-times on the perturbation parameters w, ν, σ, and μ. We show these dependencies on several two-dimensional plots. All these plots were obtained by numerical integration of Eq. 3 for the negatively autoregulated network. (A, C, and E) Curve color denotes different values of n (green, n = 0.1; blue, n = 0.5; and red, n = 0.99). (A) Variation of CV_rise (log scale) as a function of w (log scale) for ν = 0.00025 (solid curves) and ν = 0.025 (dashed-dotted curves). (σ = 4; μ = 0.007.) (C) Variation of CV_rise (log scale) as a function of w (log scale) for μ = 0.007 (solid curves) and μ = 0.07 (dashed-dotted curves). (σ = 4; ν = 0.00025.) (E) Variation of CV_rise (log scale) as a function of w (log scale) for σ = 4 (solid curves) and σ = 100 (dashed-dotted curves). (ν = 0.00025; μ = 0.007.) (B, D, and F) (B) Variation of CV_min (red) and w_min,τ (green) as a function n for ν = 0.00025 (solid curve) and ν = 0.025 (dashed-dotted curve). As ν increases, CV_min decreases monotonically. (D) Variation of CV_min (red) and w_min,τ (green) as a function n for μ = 0.007 (solid curve) and μ = 0.07 (dashed-dotted curve). (F) Variation of CV_min (red) and w_min,τ (green) as a function n for σ = 4 (solid curve) and σ = 100 (dashed-dotted curve).

In addition to reducing the rise-n-times, the negatively autoregulated gene-network is more efficient in synthesizing the protein whenever w falls between 0.1 and 1 because more protein is synthesized in less time. More generally, the simulations suggest that w is an important tuning parameter of the system as the complexity, compartmentalization, and size of the cell increases from prokaryotes to eukaryotes. Shorter mRNA lifetimes are sufficient in prokaryotes, where both transcription and translation are parallel processes. Longer mRNA lifetimes are necessary in eukaryotes because transcription and translation are spatially and temporally decoupled.

Studies on various prokaryotic systems show that the lifetimes of various mRNA molecules are in the range of 1/γ_m ∼ (1–5) min and the lifetimes of the TF proteins are 1/γ_p ∼ (1–60) min (23,24). Thus, the observed range of the parameter w (∼0.1 to ∼1) is within the optimum range to attain the minimum level of fluctuations in the rise-n-times as predicted by our theory. In eukaryotes (budding yeast), the lifetime of mRNA molecules is longer than in prokaryotes and the physiological range of w is inside interval 0.1–1, with a median of ∼0.3 (estimated over ∼2000 expressed genes) (24). The parameter w is positively correlated with the total noise of the protein expression system (32) and the condition w < 1 helps in reducing the protein number fluctuations by allowing averaging of the underlying mRNA fluctuations (24).

The robustness of various autoregulatory or cross-regulatory circuits against fluctuations in the response times can be fine-tuned by the parameters μ, σ, ν, and w. Here μ describes the strength of the feedback connection, σ describes the coupling strength between promoter state and protein dynamics, ν describes the speed of the feedback connection, and w describes the relative speed of mRNA degradation to protein degradation dynamics. These parameters and the corresponding equations governing expression levels and rise-n-times may help not only understand existing biological circuits but also design parts for synthetic biological circuits.

The total noise in protein numbers seems to be a linear function of w when the promoter state fluctuations are modeled as a binary dynamic variable (with respect to the current settings, X = 0 or 1) (24). Because here the time required by the gene expression system to produce a given number of TF proteins is a varying quantity, fluctuations in the response times should be directly proportional to the protein number fluctuations. This means that a decrease in w would steadily decrease the fluctuations in both the response times and protein numbers. On the other hand, this study suggests that the level of fluctuations in the response times is higher at lower and higher values of w than its optimum. This means that there is a trade-off between the requirements to reduce the extent of protein number fluctuations and fluctuations in the response times. These observations are consistent with our theoretical results, which indicate that the gene expression machineries of prokaryotes and eukaryotes are well optimized to minimize the extent of fluctuations in their response-times and protein numbers by setting the value of w inside 0.1–1.

Conclusions

We presented a theoretical framework to describe the dynamics of transcription and translation for TF proteins that bind their own promoters (autoregulatory loops). We simulated the theoretical equations to characterize the rise-n-times and their fluctuations and the overall robustness of the system to different biological parameters. We have shown that the binding-unbinding dynamics of the TF with its own promoter and the dynamics of synthesis of mRNA significantly influence the response-time associated with autoregulatory gene networks. We have also demonstrated that the level of fluctuations in the response-times associated with the building up of a TF to the n^th fraction of its steady-state concentration in the presence of negative, positive, or no autoregulation can be minimized by tuning the dimensionless parameter w = γ_p/γ_m, where 1/γ_m is the lifetime of the mRNA and 1/γ_p is the lifetime of the TF protein.