Rigidity Sensing Explained by Active Matter Theory

Abstract

The magnitude of traction forces exerted by living animal cells on their environment is a monotonically increasing and approximately sigmoidal function of the stiffness of the external medium. We rationalize this observation using active matter theory, and propose that adaptation to substrate rigidity results from an interplay between passive elasticity and active contractility.

Living cells respond to mechanical as well as biochemical cues. Rigidity sensing designates the web of complex mechanisms whereby a cell will adapt, as a function of the elastic modulus of its environment, diverse aspects of its phenotype, including motility, gene expression, proliferation, and fate after differentiation (1,2).

The traction forces that a cell exerts on a flat, elastic plate depend in a nontrivial way on the extracellular stiffness (3), being roughly proportional to the elastic modulus in a softer environment and saturating to a finite value for stiffer substrates (4). Similar force-rigidity data are obtained whether forces are measured locally (4) or globally (5–7) for both integrin-mediated (3,4) and cadherin-mediated (8,9) adhesion, and even when the traction forces are exerted by assemblies of cells in a monolayer epithelium (10). Single-cell rheology assays (6,7) show that cells respond to sudden changes in substrate rigidity too rapidly to be detected at the data acquisition rate. These observations call for a simple, generic explanation that is valid for short timescales where cell signaling cannot operate.

In the context of adhesion-dependent mechanosensing, Schwarz et al. (11) introduced a simple two-spring model, predicting that stiffer environments lead to stronger traction forces. A three-spring model was later proposed to explain the stiffness-dependent orientation of stress fibers in adherent cells (12), where contractility modulates cytoskeletal stiffness via a phenomenological polarizability coefficient. In this letter, we formulate and solve a simpler model derived from active matter theory, a generic description of living matter in which the mechanochemical transduction due to molecular motors (activity) plays a central role (13,14). We obtain a (static) force-rigidity relationship that agrees well with experimental data. We give an expression of the (dynamic) loading rate that we expect to be valid on timescales that are too short for cytoskeletal remodeling and protein recruitment to occur ($t\ll {10}^2$s (15,16)).

Model

On the basis of active matter theory, we formulate constitutive equations that take into account viscoelasticity, activity, and the polar nature of cytoskeletal biopolymers (13), and respect the principles of linear irreversible thermodynamics. In one spatial dimension, we write the stress of an homogeneous, elastic, and contractile material as the sum of an elastic and an active contribution: $\sigma ={\sigma }^{el}+{\sigma }_A$. The active stress ${\sigma }_A>0$ is proportional to $\Delta \mu$, the difference in chemical potential between the products and reagents of the chemical reaction that is responsible for mechanochemical transduction (ATP hydrolysis): ${\sigma }_A=\zeta \Delta \mu$, where ζ is a material parameter of the cytoskeleton (14). For simplicity, we restrict our description of the cytoskeleton to the linear regime and include 1), elasticity, described by a linear spring of length $l_C\left(t\right)$ at time t, rest length $l_C^0$, and spring constant k_C; and 2), activity, modeled by an active force $F_A={\sigma }_{A}S$ across a section of area S.

In the nonlinear regime, elastic moduli may also depend on activity, as hypothesized by Zemel et al. (12). The assumption that the rest length of elastic cytoskeletal structures is time-dependent due to motor activity (17) is also beyond the scope of the linear regime that we consider here.

The extracellular environment is represented by a linear spring of length $l_{\text{ext}}\left(t\right)$ at time t, rest length $l_{\text{ext}}^0$, and spring constant $k_{\text{ext}}$ (see Fig. 1). The traction force $F\left(t\right)$ exerted by the cell on its environment reads:

$$F\left(t\right)=k_{\text{ext}}\left(l_{\text{ext}}\left(t\right)-l_{\text{ext}}^0\right).$$ (1)

Figure 1.

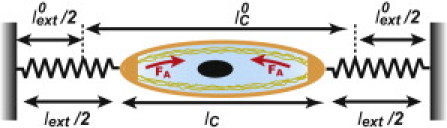
Schematic representation of the model.

The sign is chosen as $F>0$ for contraction. Under usual experimental conditions, the total length $l_{\text{tot}}$ of the system (cell + substrate) is constant: $l_{\text{tot}}=l_C\left(t\right)+l_{\text{ext}}\left(t\right)$. The force balance equation reads:

$$-F\left(t\right)+k_C\left(l_C\left(t\right)-l_C^0\right)+F_A=0.$$ (2)

Statics

The amplitude of the traction force at equilibrium reads:

$$F^{\text{eq}}=F_{\text{Sat}}\frac{k_{\text{ext}}}{k_{\text{ext}}+k_C}.$$ (3)

When $k_{\text{ext}}\gg k_C$, the traction force saturates to $F_{Sat}$, the sum of F_A and residual stresses $k_C\left(l_{\text{tot}}-l_{\text{ext}}^0-l_C^0\right)$:

$$F_{Sat}=F_A+k_C\left(l_{tot}-l_{ext}^0-l_C^0\right).$$ (4)

We expect the ensemble average of residual stresses to cancel: $\langle F_{\text{Sat}}\rangle =\langle F_A\rangle$. As long as $k_{\text{ext}}\ll k_C$, the traction force will be a linear function of $k_{\text{ext}}$: $F^{\text{eq}}\simeq \left(F_{\text{Sat}}/k_C\right)k_{\text{ext}}$.

Experimentally, a wide range of rigidities $k_{\text{ext}}$ can be obtained when the substrate is a dense array of cylindrical elastomer micropillars whose stiffness depends on their radius and height. Depending on the coating protein, traction forces are transmitted through integrin-mediated adhesions (with fibronectin) (3,4) or cadherin-mediated adhesions (with N-cadherin) (8,9). Fig. 2 shows that in both cases the experimental data are well fitted by the force-rigidity relation (Eq. 3). Note that the fitted values of saturation forces $F_{\text{Sat}}$ were not observed; rather, they correspond to values of $k_{\text{ext}}$ that are so large that the deflections of the pillars would fall below the experimental spatial resolution.

Figure 2.

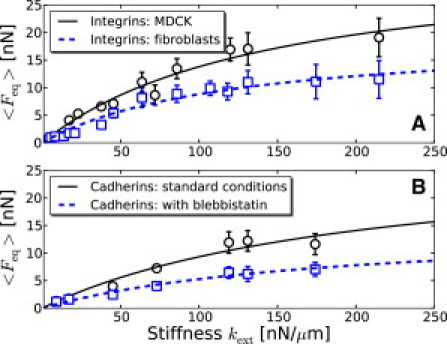
Experimental data (average traction force per pillar, markers) fitted with Eq. 3 (lines). (A) Integrin-mediated adhesions (Fig. 2, a and c, of Ghibaudo et al. (4)). MDCK cells (black circles): $F_{\text{Sat}}=34\pm 4\text{nN}$, $k_C=146\pm 30nN/\mu \text{m}$ (black solid line); fibroblasts (blue squares): $F_{\text{Sat}}=19\pm 3\text{nN}$, $k_C=119\pm 35\text{nN}/\mu \text{m}$ (blue dashed line). (B) Cadherin-mediated adhesions (Fig. 4 a of Ladoux et al. (9)). Standard conditions (black circles): $F_{Sat}=29\pm 10\text{nN}$, $k_C=209\pm 112\text{nN}/\mu \text{m}$ (black solid line); cells treated with blebbistatin (blue squares): $F_{\text{Sat}}=15\pm 8\text{nN}$, $k_C=183\pm 164\text{nN}/\mu \text{m}$ (blue dashed line). Error bars correspond to $95\%$ confidence levels.

The data encompass three cell types: Madin-Darby canine kidney (MDCK) cells, 3T3 fibroblasts, and C2 mouse myogenic cells. The cytoskeletal organization and adhesive properties of the cells vary substantially according to the type of adhesions and the range of substrate rigidity values. More-diffuse cortical actin dominates when the environment is softer, whereas actomyosin bundles are preferentially formed at higher rigidities (4,9). In all cases, our simple model captures the essence of the force-rigidity dependence and sums up biological variation into two quantitative parameters: the asymptotic traction force $F_{Sat}$ and the cytoskeletal stiffness k_C. The order of magnitude of the saturation force $F_{\text{Sat}}\sim 10nN$ corresponds to an active stress of the order of 10⁴ Pa. We obtain this value by neglecting possible residual stresses and using ${\sigma }_A\sim F_{\text{Sat}}/S$, where the section S of a micropillar is of order $S\sim 1\mu {\text{m}}^2$. The cytoskeletal rigidity is of the order of ${10}^2\text{nN}/\mu \text{m}$, corresponding to elastic moduli of the order of 10⁵ Pa, a value that is intermediate between moduli typical of cortical actin (18) and stress fibers (19) (we used $E\sim k_{C}d/S$ with $d\sim 1\mu \text{m}$).

When cells are treated with blebbistatin, an inhibitor of contractility, the value of $F_{\text{Sat}}$ is halved (Fig. 2 B). Inspection of Eq. 4 suggests that traction forces remain nonzero due to residual activity of myosin motors, as proposed previously (9), or to nonzero residual stresses, or to a combination of both effects. We note that the value of k_c is almost unchanged. However, assuming, as in Zemel et al. (12), that activity modulates cytoskeletal stiffness via a polarizability coefficient α leads to a ratio $F^{\text{eq}}/F_{\text{Sat}}=k_{\text{ext}}/\left(k_{\text{ext}}+\left(1+\alpha \right)k_C\right)$ that depends through α on cytoskeletal contractility. Experimental data (9) suggest that $F^{\text{eq}}/F_{\text{Sat}}$ is independent of the level of contractility, in agreement with our prediction (Eq. 3).

Dynamics

Using a biomembrane force setup in which micropipette aspiration controlled the external rigidity, Husson et al. (20) measured the loading rate exerted by T cells immediately after receptor engagement with a model antigen-presenting cell, and found it to be linear in $k_{\text{ext}}$. Motivated by this result, we turn to the dynamics of traction forces, and modify Eq. 2 by taking into account internal protein friction in a linear force-velocity relationship:

$$F_A\left(t\right)=F_S+\xi \frac{\text{d}{l}_C}{\text{d}t},$$ (5)

where F_S is the stall force, and ξ is a friction coefficient (21). Eliminating other variables in Eq. 2, we obtain a differential equation for the traction force:

$$\frac{\text{d}F}{\text{d}t}+\frac{F}{\tau }=\frac{F^{\text{eq}}}{\tau }$$ (6)

with a viscoelastic time $\tau =\xi /\left(k_{\text{ext}}+k_C\right)$. Integration from an initial time t₀ with initial force $F\left(t=t_0\right)=F^0$ gives $F\left(t\right)=F^{\text{eq}}+\left(F^0-F^{\text{eq}}\right)e^{-\left(t-t_0\right)/\tau }$. For zero initial force, we find that the initial loading rate is proportional to the substrate rigidity:

$${\frac{\text{d}F}{\text{d}t}}_{|\left(t-t_0\right)\ll \tau }\simeq \frac{F_{\text{Sat}}}{\xi }{k}_{\text{ext}}.$$ (7)

This is in agreement with the work of Husson et al. (20), where the initial time t₀ is set when pulling starts so that $F^0=0$. We checked that Eq. 7 still holds if we replace the linear force-velocity equation (Eq. 5) by Hill's (22) equation. Because $F_{Sat}$ is a function of activity, we predict that the loading-rate-rigidity data will be modified upon treatment with contractility agonists and antagonists.

Conclusion and Outlook

At low external rigidity, cell traction forces increase linearly with the stiffness of the substrate. Their constant ratio was first interpreted as a displacement regulated by the cell (3). We show that regulation is not necessary to explain the force-rigidity relationship. Within the framework of linear irreversible thermodynamics, we propose a minimal model whose consequences are consistent with available experimental data. We predict that both the saturation force $F_{\text{Sat}}$, exerted for large stiffness, and the constant displacement $F_{\text{Sat}}/k_C$, observed at low stiffness, depend on the contractility level. Our description is relevant for several types of adhesive structures and cytoskeletal organization. In contrast to Schwarz et al. (11), we ignore the dynamics of adhesive contacts through which force is transmitted to the substrate. Other monotonically increasing functions of stiffness that depend on two parameters also fit the same experimental data. It is our hope that this work will foster further quantitative experiments to confirm—or disprove—our model.

To treat the dynamics of traction forces, we include internal friction and obtain an initial loading rate proportional to external stiffness, as observed experimentally (20). In accord with single-cell rheology assays (6,7), the loading rate $\text{d}F/\text{d}t$ responds instantaneously to variations of $k_{\text{ext}}$.

Our analysis shows that the simplest equations of active matter dictated by symmetry and conservation laws are sufficient to describe a behavior that at first sight might seem to require a more elaborate regulation. This suggests that other features, such as stress fiber diameter and equilibrium with the rest of the actin-myosin system, can be described within the general framework of active gels. We hope that extensions of our model will facilitate a quantitative understanding of how more-complex cell processes depend on extracellular rigidity. Including membrane elasticity and cortical tension in an appropriate geometry may explain why the initial loading rate exerted by T cells upon receptor engagement saturates for stiffer environments (20). The dynamics of wetting of the microplate by the cell must be taken into account to describe traction forces exerted during cell spreading (5,6). Finally, biochemical signaling, protein recruitment, and remodeling of adhesive and cytoskeletal structures act over longer timescales (15,16) and may enhance the mechanical effects described here.