Dynamics of Calcium Sparks and Calcium Leak in the Heart

Abstract

We present what we believe to be a new mathematical model of Ca²⁺ leak from the sarcoplasmic reticulum (SR) in the heart. To our knowledge, it is the first to incorporate a realistic number of Ca²⁺-release units, each containing a cluster of stochastically gating Ca²⁺ channels (RyRs), whose biophysical properties (e.g., Ca²⁺ sensitivity and allosteric interactions) are informed by the latest molecular investigations. This realistic model allows for the detailed characterization of RyR Ca²⁺-release properties, and shows how this balances reuptake by the SR Ca²⁺ pump. Simulations reveal that SR Ca²⁺ leak consists of brief but frequent single RyR openings (∼3000 cell⁻¹ s⁻¹) that are likely to be experimentally undetectable, and are, therefore, “invisible”. We also observe that these single RyR openings can recruit additional RyRs to open, due to elevated local (Ca²⁺), and occasionally lead to the generation of Ca²⁺ sparks (∼130 cell⁻¹ s⁻¹). Furthermore, this physiological formulation of “invisible” leak allows for the removal of the ad hoc, non-RyR mediated Ca²⁺ leak terms present in prior models. Finally, our model shows how Ca²⁺ sparks can be robustly triggered and terminated under both normal and pathological conditions. Together, these discoveries profoundly influence how we interpret and understand diverse experimental and clinical results from both normal and diseased hearts.

Introduction

Ca²⁺-induced $\text{C}{\text{a}}^{2+}$ release (CICR) forms the basis for the translation of electrical signals to physical contraction in cardiac myocytes during the process known as excitation-contraction coupling. In heart, L-type Ca²⁺ channel current is amplified by triggering Ca²⁺ release from the intracellular Ca²⁺ store (i.e., sarcoplasmic reticulum, SR) primarily via the ryanodine receptor, type 2 (RyR) Ca²⁺ channel. These Ca²⁺-activated RyRs are located on the SR membrane and largely arranged in paracrystalline arrays (10–300 RyRs) that are separated from the sarcolemmal membrane (SL) by the small (15-nm) dyadic subspace (1,2).

During systole, RyRs are activated by Ca²⁺ influx via adjacent voltage-sensitive L-type Ca²⁺ channels (LCCs). Together, the LCC and RyR clusters form a functional unit of Ca²⁺ release known as the Ca²⁺-release unit (CRU), which is essential to the local control of Ca²⁺ release during excitation-contraction coupling (3). The synchronized opening of clustered RyRs results in elevations of local (i.e., subspace) [Ca²⁺] known as “Ca²⁺ sparks”. During diastole, in the absence of LCC Ca²⁺ influx, spontaneous Ca²⁺ sparks are rare but still easy to observe using a Ca²⁺ indicator where the Ca²⁺-spark rate reflects the finite opening rate of the RyR channel (4).

Another form of Ca²⁺ release, “invisible” by standard confocal imaging methods, is the “nonspark” event, which involves the opening of a single RyR (e.g., “Ca²⁺ quark”) or a few RyRs that fail to trigger a full Ca²⁺ spark (5).

A third RyR-based Ca²⁺ release pathway is attributed to a small population of diffusely distributed RyRs termed “rogue” RyRs, which are located away from the junctional cleft (2,6,7). Here, we present a mathematical model that identifies and characterizes these three forms of visible and invisible diastolic RyR Ca²⁺ release, in a coherent manner. This SR Ca²⁺ leak or loss of Ca²⁺ from the SR is experimentally observed (8,9) but flawed in earlier mathematical models. In our fully stochastic model, the simulation now matches the biology and provides what we believe to be new insight into the mechanisms by which SR Ca²⁺ leak operates in intact cells. This model is fully informed by the latest molecular investigations of heart cells, heart nanoanatomy, and recent characterizations of channels, transporters, and buffers.

SR $\text{C}{\text{a}}^{2+}$ leak is attributed to RyRs, Ca²⁺permeant channels whose open probability is controlled by [Ca²⁺]_i, [Ca²⁺]_sr, phosphorylation state, and other factors. In this manner, SR Ca²⁺ content is regulated by Ca²⁺ leak and the sarco/endoplasmic reticulum Ca²⁺-ATPase (SERCA) Ca²⁺ pump. [Ca²⁺]_sr is observed to change in response to diverse diseases (e.g., heart failure and arrhythmia) (10,11) and phosphorylation by kinases such as protein kinase A or Ca²⁺-calmodulin-dependent kinase II (12,13). Additionally, RyR mutations such as those related to catecholaminergic polymorphic ventricular tachycardia can also underlie changes in RyR behavior and thus change SR Ca²⁺ content (14). These conditions are frequently found to be arrhythmogenic and contribute to Ca²⁺ waves, Ca²⁺ alternans, and other forms of cellular instability (11). The dynamics of SR Ca²⁺ leak are thus critical to our understanding of heart function during both physiological and pathophysiological conditions. Computational models offer an explicit means to investigate nanoscale events related Ca²⁺ leak not easily measured under experimental settings.

The physiological mathematical model of Ca²⁺ leak presented here provides fundamentally new, to our knowledge, and important findings that change our understanding of Ca²⁺ signaling at the nanoscopic and cell-wide level. The five major new findings of this model include the following:

• 1.We observe the presence of an “invisible” Ca²⁺ leak that is quantitatively consistent with earlier unexplained experimental findings (15).
• 2.We find that the fully stochastic activation and termination of RyR-based Ca²⁺ release within the ventricular myocyte allows us to properly account for SR Ca²⁺ leak, obviating the inclusion of an ad hoc, non-RyR-mediated Ca²⁺ leak flux.
• 3.[Ca²⁺]_sr levels are demonstrated to depend critically on RyR open probability (P_o) and vice versa. This reconciles modeling concepts and findings with new experimental results relating to pump/leak balance.
• 4.Single RyR openings, although brief, are frequent (∼3000 cell⁻¹ s⁻¹) and often fail to trigger a full Ca²⁺ spark (∼130 cell⁻¹ s⁻¹), suggesting that Ca²⁺ spark fidelity in response to both single LCC and RyR openings is actually quite low.
• 5.Simulations predict that increased RyR activity can, somewhat paradoxically, lead to increased SR Ca²⁺ leak even in the presence of decreased [Ca²⁺]_sr.

Taken together, this model accounts for how the molecular-level characteristics of individual RyRs influence the emergent property of cellular SR Ca²⁺ leak, and lays the foundation for fully spatially resolved modeling of Ca²⁺ signaling in single cells.

Methods

Model formulation

Here we present a whole-cell model for CICR in cardiac myocytes, which builds and expands upon the local SR Ca²⁺ release model previously introduced by Sobie et al. (16). Both the RyR cytosolic [Ca²⁺]_i sensitivity and luminal SR [Ca²⁺] ([Ca²⁺])_sr dependency have been updated to reproduce recently reported single channel gating behavior (17). The previous ad hoc formulation of cooperative gating has been replaced with an energetic coupling formulation (18) derived from allosteric behavior observed in biological systems (19,20). Our model (see Fig. 1) consists of 20,000 independent Ca²⁺ release units (CRUs), each containing a cluster of stochastically gating RyRs that are instantaneously coupled via local subspace [Ca²⁺] ([Ca²⁺]_ds). These CRUs are coupled via a bulk myoplasmic [Ca²⁺]_i, which also includes a small fraction (5%) of diffusely distributed, nonjunctional or “rogue” RyRs. SERCA pumps Ca²⁺ from the myoplasm back into the SR (21). The SR itself is composed of junctional SR (JSR) and network SR (NSR) components, each with appropriate volumes and Ca²⁺ buffers. The sarcolemma (SL) has a background Ca²⁺ leak and two transsarcolemmal calcium transporters (the Na⁺-Ca²⁺ exchanger, and the plasmalemmal Ca²⁺-ATPase) to extrude Ca²⁺ from the cell.

Figure 1.

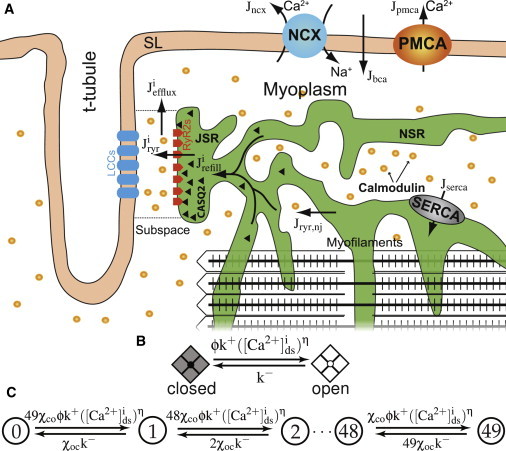
Diagram of SR Ca²⁺ leak model and release site schematic. (A) Model compartments and Ca²⁺ fluxes (solid arrows). (B) Transition-state diagram for the two-state Markov chain describing a single RyR. (C) Transition-state diagram for the Markov chain representing the RyR cluster where each state indicates the number of open RyRs (N_o) in the CRU (e.g., 0, 1, 2, …48, 49).

Although we also envision a cluster of L-type Ca²⁺ channels (LCCs) apposing the RyR cluster that trigger the CRUs during electrical activity, the LCCs have been disabled for this simulation that focuses on diastolic Ca²⁺ signaling when LCCs are quiescent. We are assuming minimal or no mitochondrial Ca²⁺ buffering (22), therefore potential contributions of this organelle to Ca²⁺ handling are omitted. The mathematical description of key elements is presented below. The seeming novelty of this model lies in the details of its formulation and the inclusion of the known properties and functions of each model component that had been overlooked, ignored, or strategically excluded in prior models. We have consequently identified several major findings—believed by us to be entirely new—as described above and presented below.

RyR model

In this study, the RyR signaling that underlies cardiac EC coupling is studied by observations of Ca²⁺ sparks in resting cells in which LCCs are quiescent. The dyad, or dyadic subspace, is a restricted space located between the transverse tubule and JSR membranes that contains a cluster of RyRs that gate stochastically, display coupled gating (23), and have a P_o that depends both cytosolic and luminal [Ca²⁺] (17). Here, each Ca²⁺-activated RyR is represented by a two-state Markov chain containing one closed (C) and one open (O) state. Transitions from C to O are dependent on both [Ca²⁺]_ds and junctional SR [Ca²⁺]([Ca²⁺])_jsr (see Fig. 1 B), with k⁺ as the association rate constant for [Ca²⁺]_ds binding with units of μM^−η s⁻¹, and k⁻ as the corresponding dissociation rate constant in s⁻¹. A luminal regulation function (ϕ = ϕ_m[Ca²⁺]_sr + ϕ_b) serves to modify the channel opening rate where [Ca²⁺]_sr is the luminal [Ca²⁺] associated with each RyR (which is [Ca²⁺]_jsr [Ca²⁺]_sr and [Ca²⁺]_nsr for junctional and nonjunctional RyRs, respectively).

Combining 49 of these identical two-state RyRs into a cluster and assuming they are instantaneously coupled via [Ca²⁺]_ds yields a M = 50 state release site where each state indicates the number of open RyRs (N_o) for the CRU (0 ≤ N_o ≤ 49), as shown in Fig. 1 C where terms on the arrows are transition rates. In these rate terms, χ_oc and χ_co represent mean-field allosteric coupling factors (18) given by

$${\chi }_{\text{oc}}=\text{exp}\left\{-a_{\ast }0.5\left[N_{\text{c}}{\epsilon }_{\text{cc}}-\left(N_{\text{o}}-1\right){\epsilon }_{\text{oo}}\right]\right\},$$ (1)

$${\chi }_{\text{co}}=\text{exp}\left\{-a_{\ast }0.5\left[N_{\text{o}}{\epsilon }_{\text{oo}}-\left(N_{\text{c}}-1\right){\epsilon }_{\text{cc}}\right]\right\},$$ (2)

where a_∗ represents the average allosteric connectivity (based on a 7 × 7 grid with nearest-neighbor coupling), and ε_cc is a dimensionless free energy of interaction (units of k_BT) that specifies the change in free energy experienced by a channel in state C when allosterically coupled to another channel in state C, and similarly for ε_oo. The coefficients N_c (number of closed RyRs) and N_o serve to partition allosteric coupling between the forward and reverse transitions. In addition to dyadic RyRs, a small fraction (5%) of RyRs are assumed to be found away from the junction as diffusely distributed, single channels.

SERCA formulation

SERCA consumes ATP to pump Ca²⁺ into the SR from the myoplasm. Here, we have implemented a SERCA formulation recently developed by Tran et al. (21). The SERCA flux takes the form, J_serca = 2v_cycleA_p, where v_cycle is the cycling rate per pump molecule (see the Supporting Material) and A_p is the concentration of SERCA molecules per liter cytosol. The Tran-Crampin SERCA formulation was selected because it provides a realistic representation of SERCA-dependent Ca²⁺ flux that displays physiological behavior at low [Ca²⁺]_i (see Fig. S6 A in the Supporting Material) and is sensitive to changes in [Ca²⁺]_sr (see Fig. S6 B), which is essential when allowing RyR-based leak to balance SERCA. Whole-cell Ca²⁺ dynamics obtained using this SERCA formulation is provided in the Supporting Material.

Concentration balance equations

The Markov chain Monte Carlo model used here consists of 2N + 2 (N = 20,000) ordinary differential equations representing the time-evolution of (Ca²⁺) in the bulk myoplasm ([Ca²⁺]_i), the NSR ([Ca²⁺]_nsr), the JSR ([Ca²⁺]_jsr), and the dyadic subspace ([Ca²⁺]_ds) compartments, and N Markov chains representing the stochastic RyR clusters (see Fig. 1 A). The concentration balance equations and formulation for all fluxes can be found in the Supporting Material. The flux through the RyR cluster associated with the i^th CRU is given by

$$J_{\text{ryr}}^{\text{i}}=N_{\text{o}}^{\text{i}}{\nu }_{\text{ryr}}\left({\left[\text{C}{\text{a}}^{2+}\right]}_{\text{jsr}}^{\text{i}}-{\left[\text{C}{\text{a}}^{2+}\right]}_{\text{ds}}^{\text{i}}\right),$$ (3)

where 1 ≤ i ≤ N, v_ryr is the RyR Ca²⁺ release rate in s⁻¹, and Nⁱ_o is the number of open RyR channels at the i^th release site. Similar to previous work (24,25), model parameters lead to rapid equilibrium of [Ca²⁺]_ds with the [Ca²⁺]_i and [Ca²⁺]_jsr allowing [Ca²⁺]_ds to be approximated using an algebraic expression of [Ca²⁺]_i, [Ca²⁺]_jsr, and N_o (see Eq. S23 in the Supporting Material).

Results

Ca²⁺ signaling in heart cells involves interactions among many proteins in a spatially and temporally complex environment as suggested in Fig. 1 A. Teasing apart the causal links in this cellular environment is aided enormously by mathematical models informed by experimental results. Here, we present results from a whole-cell model of SR Ca²⁺ signaling that seeks to investigate local Ca²⁺ dynamics using fresh modeling elements constrained and informed by the recent experimental findings described below.

RyR Ca²⁺ sensitivity and allosteric coupling

SR Ca²⁺ release in cardiac myocytes is a multiscale process ranging from small invisible Ca²⁺ leak events due to brief openings of a single RyR, to microscopic Ca²⁺ sparks involving numerous RyRs at single a CRU, to cell-wide [Ca²⁺]_i transients involving release from numerous CRUs within the cell. This process depends critically on the sensitivity of the RyRs to local cytosolic and luminal [Ca²⁺] as well as interactions between neighboring channels (i.e., allosteric coupling). It has been shown that Ca²⁺ sparks result from synchronized openings of clustered RyRs (4), mediated by [Ca²⁺]_ds with a strong dependence on [Ca²⁺]_sr (26). Clustered RyRs undergo probabilistic interactions here referred to as “allosteric coupling” but first described more rigidly as “coupled gating” (23). In our sticky-cluster model (16), we attempted to capture this known property of RyR gating by including an ad hoc formulation for cooperativity among the RyRs and demonstrated that this feature enabled robust Ca²⁺ spark termination. Here, we have implemented an energetic coupling formulation (18) based on models of protein-protein interactions (19).

Fig. 2 shows how the sensitivity of single RyR channels to be triggered by Ca²⁺ depends on the local [Ca²⁺]_i (Fig. 2 A), local [Ca²⁺]_sr (Fig. 2 B), and also on allosteric coupling between the individual RyRs within the CRUs (Fig. 2, C and D). When plotted as a function of [Ca²⁺]_i (Fig. 2 A), the steady-state single RyR P_o is an increasing function of [Ca²⁺]_i with a half-maximal point (K_m) of ∼12 μM when [Ca²⁺]_sr is held constant at 1 mM (solid line). This result corresponds well with results from lipid bilayer measurements (solid circles) that display a K_m of 12.2 μM and a Hill coefficient of 2.6 (27). Fig. 2 B shows how the RyR P_o increases as a function of increasing [Ca²⁺]_sr when [Ca²⁺]_i is held constant at 8 μM, which also agrees well with a corresponding experimental observation (solid squares) from Qin et al. (17).

Figure 2.

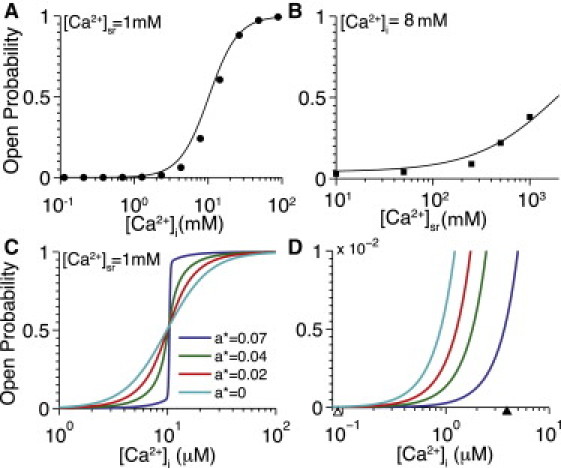
Single channel RyR Ca²⁺ sensitivity and influence of allosteric coupling on RyR steady-state open probability (P_o). (A) Single channel RyR P_o as a function of cytosolic [Ca²⁺] ([Ca²⁺]_jsr = 1 mM). (Solid line) Model result in which data points (solid circles) indicate best fit; normalized P_o (K_d = 12.2 μM, η = 2.6) from Fig. 1B in Qin et al. (27). (B) Single RyR P_o as a function of luminal [Ca²⁺] ([Ca²⁺]_ds = 8 μM). (Solid line) Model result in which data points (solid squares) indicate experimental results from Fig. 3B in Qin et al. (27). (C) P_o for a cluster of 49 RyRs as a function of [Ca²⁺]_i with varying levels of average RyR allosteric connectivity (a_∗). As a_∗ increases, P_o exhibits steeper dependence [Ca²⁺]_i. (D) Zoom of Fig. 2C showing lower [Ca²⁺]_i levels. For reference, markers on x axis indicate the diastolic [Ca²⁺]_i and peak [Ca²⁺]_ds resulting from a single open RyR (blue triangle and red triangle, respectively).

Fig. 2 C displays the steady-state P_o for a cluster of RyRs versus [Ca²⁺]_i with varying levels of average RyR allosteric connectivity (a_∗) and Fig. 2 D shows the same behavior for low [Ca²⁺]_i levels. Note that decreasing a_∗ is equivalent to removing allosteric interactions between some RyRs. In the absence of coupling (i.e., a_∗ = 0), RyRs are coupled only by [Ca²⁺]_ds and exhibit higher P_o at low local [Ca²⁺]_i, similar to isolated RyR channels. However, with the allosteric coupling levels used in this study (i.e., a_∗ = 0.07; blue line), clustered RyRs display decreased P_o at low cytosolic [Ca²⁺]_i due to stabilization of closed channels by the allosteric interactions. Because closed channels have a stabilizing influence on their neighbors, the RyR cluster is more likely to remain closed at low [Ca²⁺]_i and transition rapidly from all-closed to all-open at elevated [Ca²⁺]_i. Note, we also observed that N_RyR has a modest impact on CRU P_o (see Fig. S2).

Local Ca²⁺ dynamics

In our previous model (16), we showed that SR Ca²⁺ release events via a cluster of cooperatively gating RyRs with both cytosolic and luminal Ca²⁺ sensitivity provided robust Ca²⁺ sparks with characteristics comparable to those observed experimentally including frequency, duration, termination, and restitution (4). However, this single CRU model did not attempt to characterize the leak of Ca²⁺ out of the SR nor was the dynamic Ca²⁺ sensitivity examined. The formulation of RyR gating presented here as new and the inclusion of a thermodynamically constrained SERCA formulation allows significant insights into the dynamics of SR Ca²⁺ leak shown below.

Fig. 3 and Fig. S3 show diastolic Ca²⁺ sparks and nonspark Ca²⁺-release events as measured by [Ca²⁺]_ds (Fig. 3 A and Fig. S3 A), stochastic RyR gating as measured by N_o (Fig. 3 B and Fig. S3 B), and Ca²⁺ blinks as measured by [Ca²⁺]_jsr (Fig. 3 C and Fig. S3 C). In Fig. 3, all 20,000 CRUs were simulated and the traces shown depict release activity recorded in a subpopulation of randomly selected CRUs (i.e., 10% of total) over a period of 200 ms. In this subpopulation, out of the 58 CRUs that exhibited release activity, only five produced Ca²⁺ sparks during that period of time. This is representative of the whole-cell behavior, which resulted in 132 Ca²⁺ sparks cell⁻¹ s⁻¹. The five CRUs displaying Ca²⁺ sparks did not interact directly and were coupled only via [Ca²⁺]_i. Fig. 3 shows not only the [Ca²⁺]_ds changes due to Ca²⁺ sparks (colored lines) but also the changes in [Ca²⁺]_ds due to the opening of individual RyRs within CRUs that did not lead to Ca²⁺ sparks (gray lines). In the latter case, CRUs that do not display Ca²⁺ sparks are still capable of SR Ca²⁺ leak through uncoordinated openings of single or small groups of RyRs that would likely be invisible experimentally. We also tested a wide range of CRUs sizes (16 ≤ N_RyR ≤ 100) and found robust Ca²⁺-spark triggering and termination (see Fig. S3 and Fig. S4).

Figure 3.

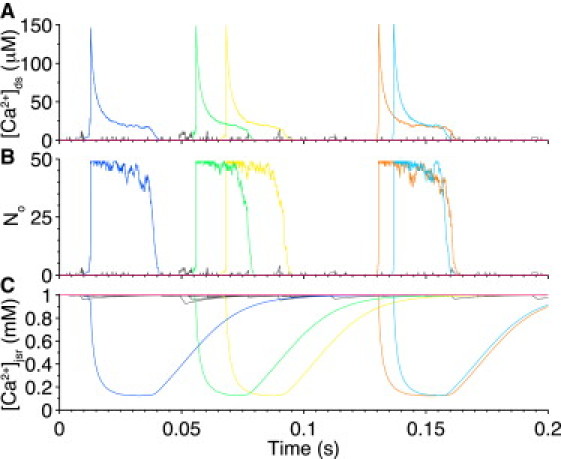
Local Ca²⁺ dynamics. (A) Subspace [Ca²⁺] ([Ca²⁺]_ds) associated with each RyR cluster during spontaneous, diastolic Ca²⁺ release events. (B) N_o at each CRU. (C) Junctional SR [Ca²⁺] ([Ca²⁺]_jsr) present on the luminal side of RyR cluster. (Each colored line represents a different CRU where a Ca²⁺ spark is observed and nonspark RyR activity is shown in shading.) Note: For visual clarity, only 10% of total CRU activity is displayed here.

Dynamics of Ca²⁺-spark triggering and termination

The model demonstrates that diastolic Ca²⁺ sparks arise from elevations in [Ca²⁺]_ds caused by brief but frequent openings of single RyRs. The stochastic nature of RyR gating also allows for prolonged openings of single RyRs that increase the probability of a Ca²⁺ spark due to sustained periods of elevated [Ca²⁺]_ds. Fig. 4 A shows the details of the RyR currents (I_RyR) that underlie the Ca²⁺ spark dynamics in Fig. 3, and Fig. 4 B provides a closer view of these I_RyR events. The current associated with a Ca²⁺ spark (I_spark) peaks at ∼10 pA (see Fig. 4 A) whereas the current associated with an individual RyR (I_quark) peaks at 0.2 pA (see Fig. 4 B). These values are consistent with experimental results (28). Examination of the upstroke of I_spark reveals a stepwise increase in I_RyR that precedes the regenerative CICR rise to the peak of the I_spark. Ca²⁺ sparks arise from frequent I_quark events within each CRU. However, there are many I_quark records that do not initiate an I_spark and some that even trigger one or more RyR to open without triggering a Ca²⁺ spark. This recruitment pattern is clearly consistent with the stochastic nature of local CICR and with the inference that RyR clusters are relatively difficult to trigger (29,30).

Figure 4.

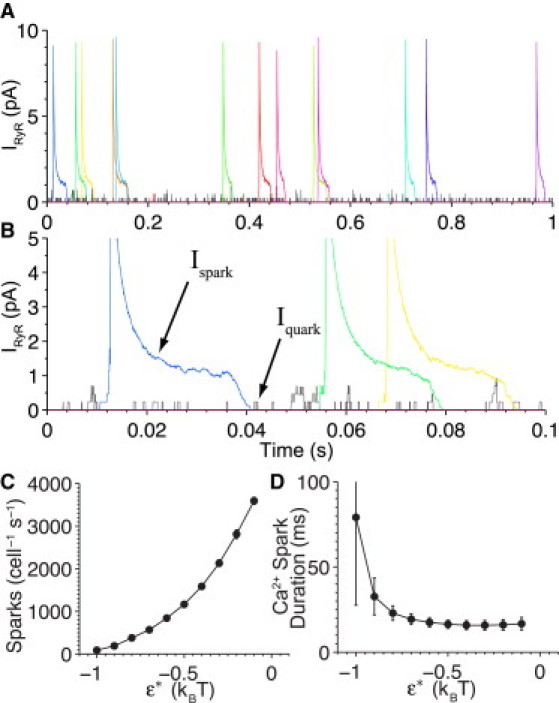
Dynamics of diastolic Ca²⁺ spark triggering and termination. (A) Spontaneous RyR Ca²⁺ current in pA during a 1-s simulation. (B) Zoom of RyR current showing spark initiation and termination profiles. (Colored lines) Different CRUs, respectively, where a Ca²⁺ spark is observed. (Shading) Nonspark RyR activity for the remaining CRUs. Note: For visual clarity, only 10% of the whole cell activity is displayed here. (C) Number of Ca²⁺ sparks as function of the strength of allosteric coupling (coupling strength is assumed to be symmetrical, i.e., ε_∗ = ε_cc = ε_oo). (D) Average Ca²⁺ spark duration versus ε_∗.

During I_spark, [Ca²⁺]_jsr declines because Ca²⁺ moves from the JSR to the dyadic subspace via the open RyRs, causing I_RyR to decrease. This can be readily appreciated by examining the fluctuations in I_RyR produced during the initial phase of a Ca²⁺ spark as compared to fluctuations visible near the end of each Ca²⁺ spark (see Fig. 4 B). Consequently, fluctuations in the release current due to the gating of individual RyRs becomes increasingly small during the final phase of I_spark. Eventually [Ca²⁺]_jsr (see Fig. 3 C) is depleted to a point where the Ca²⁺ spark terminates stochastically—facilitated by allosteric coupling and reduced RyR reopenings due to lower [Ca²⁺]_ds and [Ca²⁺]_jsr.

Although this result is consistent with the termination mechanism proposed in Sobie et al. (16), many of the key elements appear novel. For example, the clear character of I_quark and how it initiates I_spark reveals that triggering of a Ca²⁺ spark is not an all-or-none process as we had previously hypothesized (16). Significantly, Fig. 4, A and B, shows that the overwhelming majority of single RyR gating activity does not lead to Ca²⁺ sparks. The duration of these nonspark, single-channel events are consistent with the biophysical properties of the RyR (e.g., its inherent closing rate) that display mean open times in the range of 1–4 ms in lipid bilayer experiments (31). Ca²⁺ released via this mechanism is likely to go unaccounted for experimentally and lends itself to the concept of invisible leak. A closer examination of this nonspark leak mechanism is presented below.

The effect of allosteric coupling strength (ε_∗) on frequency and duration of Ca²⁺ sparks is examined in Fig. 4, C and D. Note that decreasing ε_∗ is analogous to increasing the amount by which RyR interactions stabilize both closed and open channel pairs. Ca²⁺-spark rate rises exponentially and Ca²⁺-spark duration decreases as coupling strength is lowered (i.e., increased ε_∗). This demonstrates that RyRs exhibit elevated activity in the presence of weak allosteric coupling—caused by the increased opening rate of uncoupled channels (see Fig. 2 C). Although the Ca²⁺-spark rate is very sensitive to ε_∗, the average spark duration is much less sensitive to ε_∗, suggesting that RyR luminal [Ca²⁺] dependency is playing the dominant role for Ca²⁺-spark duration and termination. Note, simulations indicate that complete removal of allosteric coupling yields Ca²⁺-spark rates much higher than those observed in FK506-based uncoupling experiments (32). This supports the idea that RyR-RyR coupling may involve factors in addition to FKBP12.6.

Visibility of SR Ca²⁺ leak

Although SR Ca²⁺-release events originating from a fully activated cluster of RyRs are easily detectable experimentally (4), Ca²⁺ release by an individual or even a few RyRs is well below the experimental detection threshold (16). I_quark is comparable to unitary LCC current at −30 mV (i.e., 0.2 pA). This local Ca²⁺-signaling mass is far less than that of a Ca²⁺ sparklet (33)—which is detectable because of its long mean open time (≥10 ms due to channel agonists) and high external (Ca²⁺) (20 mM) or special optical conditions (e.g., the 100-nm-thin optical section of total internal reflection microscopy) or both. In Fig. 5, the visibility of Ca²⁺ release due to I_spark and I_quark is assessed in the presence of realistic noise (see Sobie et al. (16)). In Fig. 5 A, a simulated linescan image of the SR Ca²⁺ release activity shown in Fig. 5 B (black line, right axis) is given. Although the signal due to the I_spark event is clearly visible, the signal emitted by the two I_quark events (generated by one and four open RyRs) that precede the Ca²⁺ spark cannot be discerned. The fluorescent profile (Fig. 5 B (blue line, left axis)) suggests that such SR Ca²⁺ release events that fail to induce a full Ca²⁺ spark are likely to go undetected. We also generated a simulated Ca²⁺ spark/blink pair (see Fig. S5) for comparison with recent experimental measurements (34). Below, we examine the propensity of these nonspark occurrences during diastole.

Figure 5.

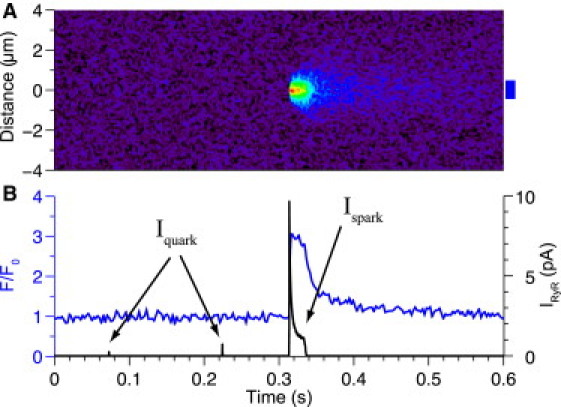
Experimental detection of SR Ca²⁺ release. (A) Simulated linescan of I_RyR activity. (B) Time course of I_RyR exhibiting both spark (I_spark) and nonspark (I_quark) events (black line) and the corresponding fluorescence profile (F/F₀) of Fluo3 (blue line). The F/F₀ profile was obtained by averaging fluorescence from a 1-μm-wide region (blue box). Simulated linescan based on previously published methods (see Sobie et al. (16) and Smith et al. (40)).

Ca²⁺-spark latency and fidelity

The cardiac SR Ca²⁺-leak pathway includes both Ca²⁺ sparks and nonspark SR Ca²⁺-release events. The nonspark events occur when RyR channels open but do not trigger enough RyRs to produce a Ca²⁺ spark. Statistical analysis of all spontaneous Ca²⁺ release events provides information on SR Ca²⁺-leak dynamics such as Ca²⁺-spark latency (the time from spark initiation to spark peak) and fidelity (the probability of individual RyR openings triggering a full Ca²⁺ spark). During diastolic simulations (see Figs. 3 and 4) the time required to reach the peak of a Ca²⁺ spark varies from less than a millisecond to several milliseconds and decreases as a function of N_o (Fig. 6 A). The fidelity of Ca²⁺-spark triggering has been anticipated by the examples of I_quark and I_spark shown in Fig. 4, A and B. Single RyR openings occur at a rate of ∼3000 cell⁻¹ s⁻¹; however, most fail to trigger a Ca²⁺ spark.

Figure 6.

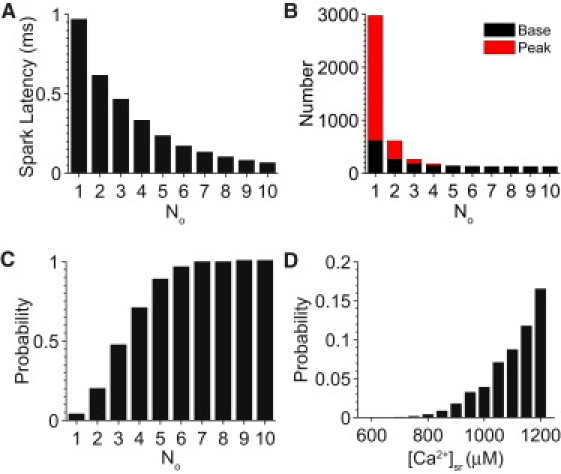
Analysis of Ca²⁺ spark latency and fidelity. (A) Average mean time to spark peak as a function of the N_o. (B) Number of Ca²⁺ release events versus the N_o where events are segregated between events that lead to additional RyR openings (solid bars) and events that do not (shaded bars). Note that the bar above N_o = 10 also corresponds to the number of Ca²⁺ sparks during the simulation. (C) Probability of triggering a spark as a function of peak N_o. (D) Histogram of the probability of a single RyR opening triggering a spark as a function of [Ca²⁺]_sr.

Fig. 6 B shows a histogram of the number of Ca²⁺-release events versus the N_o involved in the event. Some events serve as the base for triggering additional RyRs to open (solid bars) whereas other events peak at N_o and then terminate (shaded bars). Note that most (85%) of the 20,000 CRUs have no RyRs that open at all during the 1-s simulation. There are between 100 and 150 diastolic Ca²⁺ sparks cell⁻¹ s⁻¹ in rat ventricular myocytes (4) and this is faithfully reproduced by the model. Of the ∼3000 RyR opening events, only ∼130 lead to Ca²⁺ sparks, indicating that the fidelity of an I_quark triggering an I_spark is low. This is further illustrated in Fig. 6 C, which shows the likelihood of a Ca²⁺ spark increases with N_o, but is quite low (∼5%) when N_o = 1. This indicates the probability of a single or a few open channels to trigger a Ca²⁺ spark is small under normal conditions but increases rapidly as [Ca²⁺]_sr is increased (see Fig. 6 D). In summary, Fig. 6 shows that Ca²⁺ sparks are a dynamic balance between the regenerative nature of CICR and the stabilizing influence of allosteric coupling on the RyR channels.

SR Ca²⁺ leak in permeabilized cells

SR Ca²⁺ content is known to influence the rate of diastolic loss of Ca²⁺ from the SR (9). To examine SR Ca²⁺ leak and its dependence on Ca²⁺ sparks and I_RyR, we mimicked the inhibition of SERCA by thapsigargin (TG) and observed the loss of Ca²⁺ from the SR under permeabilized conditions (similar to experiments by Zima et al. (8)). Fig. 7 A shows the temporal decline in [Ca²⁺]_sr and Ca²⁺-spark rate after SERCA inhibition. The high cytosolic [Ca²⁺]_i (150 nM) used in these permeabilized cell experiments results in an elevated Ca²⁺ spark rate (∼1000 sparks cell⁻¹ s⁻¹)—six times the Ca²⁺ spark rate seen in rat myocytes during diastole. In Fig. 7 A Ca²⁺ sparks cease after [Ca²⁺]_sr falls below 700 μM. However, even in the absence of Ca²⁺ sparks, Ca²⁺ continues to leak from the SR. The model suggests that this is due to the background I_RyR that is experimentally “invisible” (see Fig. 5), and the SR loses half of its Ca²⁺ within 5 min of SERCA inhibition.

Figure 7.

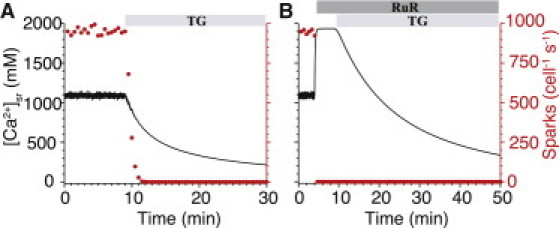
Effect of SERCA inhibition on SR [Ca²⁺]. (A) Simulated effect of SERCA inhibition by thapsigargin (TG, A_p = 0) on [Ca²⁺]_nsr (black line) and whole-cell Ca²⁺ spark rate (red circles). (B) Simulated effect of a RyR-specific antagonist, ruthenium red (RuR) on [Ca²⁺]_nsr (black line) and whole-cell Ca²⁺ spark rate (red circles), before and after SERCA inhibition by TG. In each case, [Ca²⁺]_i was fixed at 150 nM to mimic experimental conditions in permeabilized cells (see Zima et al. (8)). RuR is modeled here by disabling all but 2% of the RyRs in the model cell and giving the functional RyRs the kinetics of nonjunctional, rogue RyRs (v_ryr = 0, v_ryr,nj = 1.01 s⁻¹).

To further investigate invisible leak, 98% of the RyRs in the cell were disabled by ruthenium red (RuR)—completely preventing the generation of Ca²⁺ sparks (Fig. 7 B). During the brief period when most RyRs were blocked but SERCA remained active, [Ca²⁺]_sr increases to nearly twice its initial value due to the shift in pump/leak balance. However, after SERCA inhibition, Ca²⁺ still leaks out of the SR via the nonspark pathway even as [Ca²⁺]_sr declines below 1 mM, albeit at a much slower rate than in Fig. 7 A. These simulations suggest that the unidentified leak pathway highlighted by Zima et al. (8) may, in fact, be incomplete inhibition of the cell's nearly 1,000,000 RyRs.

Dependence of SR Ca²⁺ leak on SR Ca²⁺ content

The opening of RyRs depends on both [Ca²⁺]_i and [Ca²⁺]_sr and makes experimental analysis of SR Ca²⁺ leak complicated. However, the model allows us to directly examine how SR Ca²⁺ leak varies based on changes in [Ca²⁺]_sr. Fig. 8 shows the characteristics of SR Ca²⁺ leak in our whole-cell SR Ca²⁺ release model and its Ca²⁺-spark and -nonspark Ca²⁺ leak-pathways via junctional and nonjunctional rogue RyRs.

Figure 8.

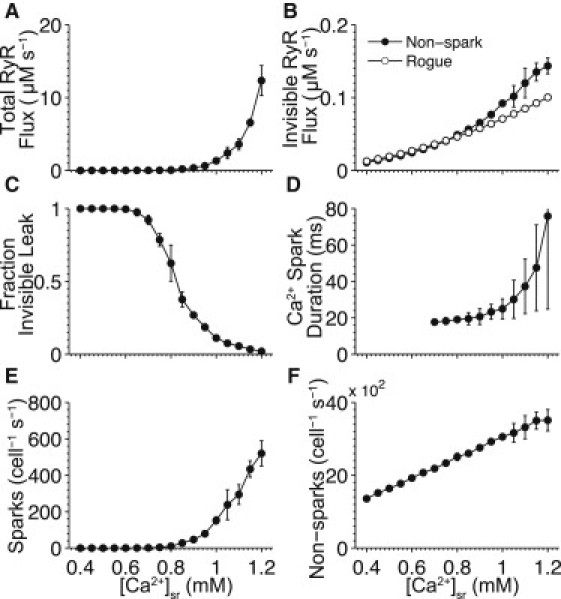
Effect of SR Ca²⁺ load ([Ca²⁺]_sr) on SR Ca²⁺ leak. (A) Total integrated RyR flux during a 1-s simulation. (B) Integrated nonspark RyR flux via junctional RyRs (solid line, solid circles) and nonjunctional RyRs (solid line, open circles). (C) Fraction of RyR flux not associated with a Ca²⁺ spark (e.g., nonspark RyR flux divided by total RyR flux). (D) Average Ca²⁺ spark duration. (E) Ca²⁺ spark rate. (F) Number of nonspark events versus [Ca²⁺]_sr. The junctional nonspark flux is defined as RyR activity that does not precede a Ca²⁺ spark. (Data points) Average over 10 simulations. (Error bars) Standard deviation from the mean. Note that [Ca²⁺]_i was held constant at 90 nM.

A pivotal role of [Ca²⁺]_sr is governing the overall RyR-mediated SR Ca²⁺ efflux as shown in Fig. 8 A. The low overall Ca²⁺ leak seen at low [Ca²⁺]_sr (≤ 800 μM) is due not only to decreased RyR opening rates but also decreased Ca²⁺-spark triggering fidelity caused by reduced I_RyR. The contribution of nonspark Ca²⁺ leak to this process is shown in Fig. 8 B. For [Ca²⁺]_sr levels used here (i.e., rodent), Ca²⁺ sparks dominate SR Ca²⁺ leak whereas at lower [Ca²⁺]_sr levels (i.e., larger mammals) SR Ca²⁺ leak is primarily via the invisible, nonspark pathway. Not surprisingly, the frequency of both Ca²⁺ sparks and nonspark Ca²⁺-release events are increasing functions of [Ca²⁺]_sr (Fig. 8, E and F), with Ca²⁺ sparks exhibiting an approximately exponential increase. Note that this rapid rise of Ca²⁺-spark rate at elevated [Ca²⁺]_sr levels would likely eventually give way to propagating Ca²⁺ waves in a fully spatial model. This rapid increase in Ca²⁺-spark rate at elevated [Ca²⁺]_sr levels is due to increased Ca²⁺-spark fidelity (ability of I_quark to trigger I_spark) and RyR [Ca²⁺]_i sensitivity. In summary, Ca²⁺ sparks dominate SR Ca²⁺ leak under normal SR Ca²⁺ load; however, at lower [Ca²⁺]_sr, the nonspark-based leak contributes a greater fraction of the overall leak. Note that rogue RyRs can be excluded from this model with modest effect on results.

SR Ca²⁺ leak under pathological conditions

Pathological conditions such as heart failure are often associated with SR Ca²⁺ mishandling due to downregulation of SERCA and/or excessive phosphorylation of RyR. With this in mind, simulations were conducted with the model to study the effects of these two changes, the goal being to acquire novel insights into the development of the pathology. Fig. 9 demonstrates the effect of phosphorylation on SR Ca²⁺ leak, simulated via changes in the RyR opening rate (k⁺) and changes in SERCA's [Ca²⁺]_i sensitivity (K_d,i).

Figure 9.

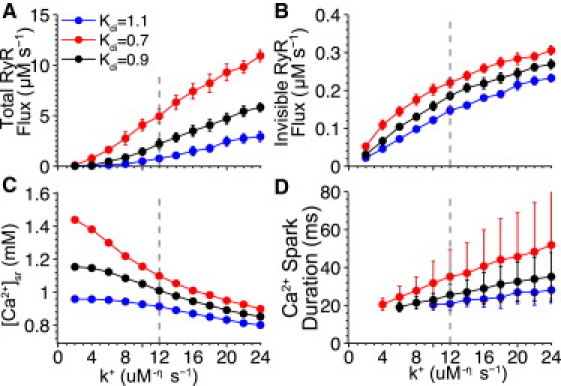
Effect of pathology on SR Ca²⁺ leak modeled by adjusting RyR opening rate (k⁺) and SERCA's [Ca²⁺]_i sensitivity (K_d,i). (A) Total integrated RyR flux during a 1-s simulation. (B) Integrated nonspark RyR release flux via both junctional and nonjunctional RyRs. (C) Steady-state [Ca²⁺]_sr. (D) Average Ca²⁺ spark duration versus k⁺. In all simulations, [Ca²⁺]_i was fixed at 90 nM and [Ca²⁺]_nsr was allowed to equilibrate to its steady-state value. (Data points) Average of 10 simulations. (Error bars) Standard deviation from the mean. (Vertical dashed lines) Parameter values under normal conditions.

In all simulations, [Ca²⁺]_i was fixed at 90 nM and [Ca²⁺]_sr was allowed to equilibrate to its steady-state value. The whole-cell Ca²⁺-leak rate is shown to increase with RyR phosphorylation levels (Fig. 9 A), and similarly for nonspark-based leak (Fig. 9 B). This response, along with the decrease in steady-state [Ca²⁺]_sr shown in Fig. 9 C, is expected and is attributed to the phosphorylation-induced increase of the RyR open probability. The model suggests that Ca²⁺ sparks produced at these diminished SR Ca²⁺ levels are of longer durations (Fig. 9 D) and exhibit greater variability—which is, to our knowledge, a novel prediction that has yet to be tested experimentally. Also, simulations show that increased RyR activity can, somewhat paradoxically, lead to increased SR Ca²⁺ leak even in the presence of decreased [Ca²⁺]_sr (see Fig. 9, A and C).

Discussion

We have presented what we believe to be a new mathematical model that successfully and robustly characterizes Ca²⁺ sparks and Ca²⁺ leak in the heart during diastole. The model includes a realistic number of CRUs each containing a cluster of stochastically gating RyRs with properties constrained by experimental observations. The CRUs function independently of each other but are sensitive to the [Ca²⁺] in the cytosol, through which they combine to produce whole-cell phenomena as observed experimentally. The model presented here improves upon our previous Ca²⁺-spark model (16) that modeled Ca²⁺ sparks from a single CRU incorporating RyR regulation by subspace and luminal calcium. It incorporates improved RyR Ca²⁺ sensitivity and allosteric interactions as well as complete descriptions of diastolic Ca²⁺ cycling. It embodies several well-characterized properties of Ca²⁺ sparks (duration, termination, activation, and sensitivity to Ca²⁺ and [Ca²⁺]_sr). In doing this, it describes and characterizes SR Ca²⁺ balance including both Ca²⁺ spark- and nonspark-based SR Ca²⁺ leak. The work provides a conceptual framework and tools for an improved understanding of a number of perplexing issues previously presented by us and others as noted below.

Importantly also, the stochastic model of Ca²⁺ sparks and Ca²⁺ leak during diastole, which (to our knowledge) we present here as new, lays the foundation for more complex dynamic models with fully integrated, spatially resolved, time-dependent Ca²⁺ signaling.

Inactivation of RyR not needed

There is no need for Ca²⁺-dependent RyR inactivation to terminate Ca²⁺ sparks as demonstrated here and in our previous model (16). Ca²⁺ sparks terminate stochastically facilitated by [Ca²⁺]_jsr depletion and RyR allosteric coupling. Although the physical self-association of RyRs in biochemical preparations of RyRs supports the physical interactions among the homotetramers, superresolution imaging and additional experiments are needed to explore this aspect. Finally, to date, no Ca²⁺-dependent inactivation process involving RyRs has been demonstrated experimentally with the right timing to account for the termination of Ca²⁺ efflux from a CRU. Moreover, recent experimental studies on Ca²⁺-spark termination argue against the involvement of Ca²⁺-dependent inactivation in spark termination (35,36).

Leaky RyR

That RyRs open during diastolic conditions as individual channels to produce I_quark and as ensembles to produce I_spark is consistent with this new Ca²⁺ spark model. Indeed, it is necessary to include such properties of RyRs in the model to reproduce the recent experimental observation that when SERCA is blocked, [Ca²⁺]_sr decreases due to both spark-mediated and nonspark-mediated mechanisms (8). The need for pump-leak balance in the SR has been nicely demonstrated both experimentally (8,9) and in the model here. The model also suggests how increased phosphorylation of the RyR during heart failure might increase the leakiness of the RyRs. Additionally, despite nonjunctional RyRs having increased P_o due to the lack of allosteric coupling, they contribute only a small fraction of the total SR Ca²⁺ leak in this model.

SERCA

The Tran-Crampin SERCA formulation reproduces the experimental observation that Ca²⁺ uptake into the SR depends on both [Ca²⁺]_i and [Ca²⁺]_sr (37,38). The model predicts virtually no backflux of Ca²⁺ under physiological conditions, allowing entirely RyR-based leak to balance SERCA—providing a simple yet physiological system of pump/leak balance to the model. However, we acknowledge that the system may indeed be more complex (i.e., other leak pathways such as IP₃Rs may also contribute to SR Ca²⁺ leak).

Ca²⁺-induced Ca²⁺ release

The manner by which Ca²⁺ sparks are produced suggests that the process is dominated by Ca²⁺-induced Ca²⁺ release (CICR). The initial probabilistic opening of a single RyR depends on its sensitivity to both [Ca²⁺]_i and [Ca²⁺]_sr. The opening and closing rates also depend on modulatable properties of RyR and those of interacting proteins (see above). The increase in [Ca²⁺]_ds produced by the initial RyR opening is the primary trigger for diastolic Ca²⁺ sparks. However, during EC coupling the triggering is due largely to the increase in [Ca²⁺]_ds from the opening LCCs in the sarcolemmal or transtubule membranes opposite the RyR cluster in the CRU. Our simulations suggest that when either a single RyR or LCC opens, the local RyR cluster is unlikely to be triggered. This feature, which is required here to reproduce the phenomenon of invisible RyR-mediated leak (7,8,15), has been suggested previously based on analysis of voltage-clamp experiments (29,30). As the intrinsic sensitivity of RyR increases due to phosphorylation, mutation, or other change, the remarkable stability of the system can change. Ca²⁺ instability of CICR may arise when [Ca²⁺]_sr becomes elevated or when RyR Ca²⁺ sensitivity increases. Exploration of the features of instability will be addressed in a spatially resolved Ca²⁺-spark model.

Ca²⁺-spark characteristics

An important part of this model is to fit all major features of the experimental findings, in respect to Ca²⁺ sparks and SR Ca²⁺ leak, with the simplest model possible. These goals were achieved even as we constrained the behavior of RyRs and SERCA by their measured biophysical properties. The Ca²⁺-spark rate is similar to that observed in rats during diastole. Ca²⁺-spark characteristics for other species are largely the same, except for the Ca²⁺-spark rate, which is lower. Only modest changes to the model are needed to lower the Ca²⁺-spark rate. For example, slight reductions in diastolic [Ca²⁺]_sr dramatically decrease Ca²⁺-spark rate.

Trigger characteristics

The likelihood of a Ca²⁺ spark occurring due to the opening of a single RyR is <10%. During the upstroke of a cardiac action potential, RyRs are triggered by openings of the voltage-gated LCCs. Given that a single LCC opening is known to contribute roughly the same Ca²⁺ current as an individual RyR and LCC openings are brief (∼0.5 ms) (33), therefore many LCCs must open during systole in order to trigger a spark. However, during systole, LCC openings are well synchronized by depolarization, ensuring adequate Ca²⁺ influx to trigger Ca²⁺ sparks. In fact, the presence of seven LCCs per CRU (consistent with the LCC/RyR ratio of 1:7 (39)) allows for robust triggering of the CRUs during a simulated depolarization (see Fig. S1).

In summary, the relatively simple mathematical model of Ca²⁺ sparks put forward by Sobie et al. (16) has been advanced significantly by the improvements in RyR Ca²⁺ sensitivity, inclusion of a physiological SERCA formulation, and the incorporation of these Ca²⁺-handling mechanisms into a detailed whole-cell model of CICR. This self-consistent, and to our knowledge, new model is highly constrained by experimental observations and forms the basis for a new generation of Ca²⁺ signaling simulations.