Improvement of Structure-Based Potentials for Protein Folding by Native and Nonnative Hydrogen Bonds

Abstract

Pure Gō models (where every native interaction equally stabilizes the folded state) have widely proved their convenience in the computational investigation of protein folding. However, a chemistry-based description of the real interactions also provides a desirable tune in the analysis of the folding process, and thus some hybrid Gō potentials that combine both aspects have been proposed. Among all the noncovalent interactions that contribute to protein folding, hydrogen bonds are the only ones with a partial covalent character. This feature makes them directional and, thus, more difficult to model as part of the coarse-grained descriptions that are typically employed in Gō models. Thanks to a simplified but rigorous representation of backbone hydrogen bonds that we have recently proposed, we present in this article a combined potential (Gō + backbone hydrogen bond) to study the thermodynamics of protein folding in the frame of very simple simulation models. We show that the explicit inclusion of hydrogen bonds leads to a systematic improvement in the description of protein folding. We discuss a representative set of examples (from two-state folders to downhill proteins, with different types of native structures) that reveal a relevant agreement with experimental data.

Introduction

According to the principle of minimal frustration (1,2), the folding pathway is funnel-shaped and is encoded in the native structure of the protein. As the relationship between the native structure and the kinetic and thermodynamic properties of the folding process is experimentally well established (3–5), many simulation models, known as Gō (or structure-based) potentials, have been suggested considering only native interactions (6–8). This simplified view of the system energetics is usually accompanied by intermediate resolution descriptions of the chain geometry, where each amino acid is represented by a few centers of interaction (frequently just the α-carbons). Regardless of their dual simplicity, these so-called coarse-grained Gō models (9–12) have shown a remarkable ability to describe protein folding, in addition to profiting from a manageable definition and a reduced computational cost.

In some cases, however, Gō models fail due to the oversimplification of the protein energetics (13–16), especially if there are intermediates involving nonnative interactions (17) or alternative stable structures such as aggregates (18). This highlights the importance of the chemical nature of the interactions themselves and the role of nonnative interactions in the ruggedness of the folding funnel (19). As a result, a kind of second-generation Gō models that explicitly consider individual interactions have arisen (20,21). The resulting potentials enhance the accuracy of the original Gō models and provide a more detailed tool for protein folding studies.

If we evaluate each type of interaction individually, the backbone hydrogen bonds deserve special attention. In terms of biological relevance, they have a role all their own, as they guide the secondary structure formation and are said to be determinant in the protein structure specificity (22,23). In addition, their partially covalent nature makes them directional and stronger than other interactions such as hydrophobic ones.

The combination of a reduced but accurate representation of hydrogen bonds and a Gō-type potential seems, then, especially appealing. The lack of an explicit definition of amide and carbonyl groups in α-carbon models makes single-bead hydrogen-bond representations quite elusive, so-seldom has this combination been reported (24). Instead, hydrogen bonds have sometimes been inserted as directional modifiers of the native interaction strength (25), although this alternative misdescribes the directionality of hydrogen bonds in strands (26). In other examples, more centers of interaction per amino acid for either hydrogen bond (27) or Gō interactions (28) are necessary, leading to more complex and time-consuming potentials. In any case, previous works have focused on the structural description of proteins or specific cases like protein aggregation (28), but no rigorous analysis about the effect of hydrogen bonds on protein folding has been carried out to our knowledge.

In this article, we aim to fill this gap and evaluate the general impact of a hydrogen-bond-explicit definition on Gō models, using only an α-carbon representation and paying special attention to the effect on the folding thermodynamic and structural characteristics. The strength of our work lies in a careful election of the potentials. As a Gō model, we have used a potential from Prieto et al. (12) that has been successfully applied to many cases, displaying good agreement with experimental data and a remarkable cooperativity by itself (29–32).

The election of the hydrogen-bond potential is particularly problematic. Although many reduced models have been propounded lately (33–35), they are usually forced to sacrifice an accurate geometry for a single bead representation (36). These topology distortions make them unsuitable for the combination with α-carbon Gō models, as they are somehow incompatible by definition. Rather, we have used a hydrogen-bond model recently introduced by ourselves in Enciso and Rey (37), which has been especially designed to mirror the geometric characteristics of natural hydrogen bonds and reproduces the formation of secondary structures in peptidic systems. By using this approach, the hydrogen-bond potential in this work models both native and nonnative hydrogen bonds, whereas the rest of native interactions are considered through the structure-based potential. In this way, we treat hydrogen-bond interactions in a rigorous way and introduce some frustration in the folding pathway at the same time.

If we pursue the obtention of a realistic thermodynamic view of protein folding, the combination of these two potentials raises a number of questions. First, we must resolve whether the inclusion of hydrogen bonds in this kind of simplified simulation model has any impact on the folding process characteristics. Secondly, we must determine whether this impact induces any kind of bias in the general protein behavior, or instead results in broad applicability.

In this article, we analyze the folding characteristics of a representative bunch of globular proteins. We analyze some proteins widely studied both experimentally and theoretically that, presenting different native structures, have led us to obtain a general overview of our combined potential characteristics. We then go on to focus on proteins where our previous experience shows that pure Gō models fail in their description (e.g., results depending on the experimental structure (31) or downhill folders predicted as two-state ones with Gō models, see below).

We have found that the specific consideration of hydrogen bonds leads to a better description of the folding thermodynamics than the Gō model on its own, reproducing the experimental folding characteristics more accurately, even in the absence of sequence-dependent terms.

Methods

The model

In this work, proteins are described through an off-lattice representation where each amino acid i is represented by a hard sphere centered at the α-carbon position. Each unit is linked to its neighbors by a virtual bond vector of length 3.8 Å, corresponding to a trans peptide bond. An auxiliary vector h_i perpendicular to the plane defined by adjacent virtual bond vectors of each bead i is also defined (see Fig. 1 in Enciso and Rey (37)).

Figure 1.

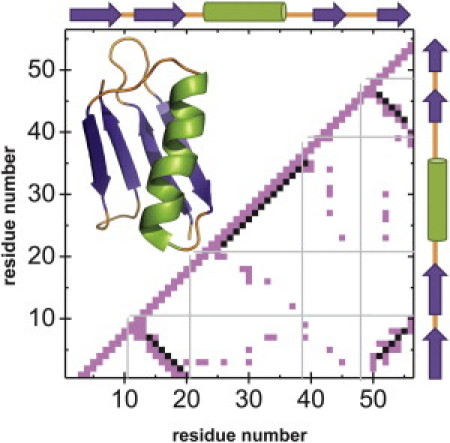
Cartoon and contact map of the immunoglobulin-binding domain of streptococcal protein G (PDB code 2GB1), where the different secondary structure regions have been marked (shaded lines and schematic images along the axes). (Mauve squares, online color only) Presence of a Gō contact between residues; (black squares) initial Gō contacts that have been removed due to the detection of a native hydrogen bond. Note that hydrogen bonds are detected in every secondary structure region, according to the PDB header.

Interactions between bead pairs are defined in terms of a Gō potential (12) and a hydrogen-bond one (37). Because they have been thoroughly described elsewhere, only their main features will be discussed here.

We have used a Gō model, proposed by our group some years ago, that has provided excellent results in folding studies (29–32,38). It consists of a harmonic well potential centered at the native distance between α-carbons, $d_{ij}^{nat}$ (where i and j are the interacting beads). There are two kinds of interactions: local interactions (between residues i and i + 2 and residues i and i + 3) that are always present and preserve the intrinsic chain rigidity of a polypeptidic system and the proper chirality; and long-range interactions (between i and j, where j > i + 3) that are only considered if there is a contact in the native state (i.e., the native distance between any pair of heavy atoms from the referred amino acids is <4.5 Å, according to the experimental PDB structure (39)). One interesting characteristic of our structure-based model is that it reproduces a cooperative transition in proteins that experimentally have been shown to fold via a two-state process. Actually, we have previously checked that the lack of cooperativity that is sometimes assigned to simple models with only one bead per residue and pairwise interactions (see, e.g., Chan et al. (40) and references therein) is partially due to the mathematical form of the attraction basin (12). Our model was designed to correct, at least partially, those effects, by using a narrow attractive well. With that definition, we have been able to reproduce both folding processes with rather narrow, cooperative folding transitions, as well as downhill folding processes, in reasonable agreement with experimental results (30,32).

On the side of hydrogen-bond interactions, we have used a very recent model, also introduced by ourselves, that has proved its ability in the obtention of secondary structure elements for peptides (37). The special care in the geometric characteristics of the secondary structures (as similar as possible to those appearing in native proteins) makes it ideal for our study.

The hydrogen-bond energy between any pair of residues i and j (where j > i + 2 and j ≠ i + 4) is evaluated in a two-part process: first, we check three geometrical restrictions (i.e., length of the tentative hydrogen bond between beads, represented by the distance r_ij between the corresponding beads, orientation between auxiliary vectors, determined by |cos(h_i · h_j)|, and relative orientation between the auxiliary vectors and the tentative hydrogen bond, given by |cos(h_i . r_ij)| and |cos(h_j . r_ij)|). Then, if the value of each restriction falls within certain limits, a steplike potential applies. The acceptable ranges and the interaction strength differ depending on the kind of hydrogen bond (either helical or β-type). Although their numerical ranges are described in detail elsewhere (Table I in Enciso and Rey (37)), we include here the main data:

• For the first restriction, 4.7 Å ≤ r_ij ≤ 5.6 Å.

• For the second restriction, 0.74 ≤ |cos (h_i · h_j)| ≤ 0.93 if it is a local interaction, and 0.75 ≤ |cos (h_i · h_j)| ≤ 1.0 if it is not.

• For the third restriction, 0.92 ≤ |cos(h_{i or j} · r_ij)| ≤ 1.00 if it is a local interaction, and 0.94 ≤|cos(h_{i or j} · r_ij)| ≤ 1.0 if it is not.

This hydrogen-bond potential follows the same philosophy of other models previously used in the literature (33,34,41). We have checked, however, that in a reasonable temperature range our model provides elements of secondary structure with a more natural structure than those obtained with previously reported models, when only the hydrogen-bond interactions are taken into consideration (37). We should also mention that, as described, our hydrogen-bond model is only defined as a pairwise interaction, without any additional term enforcing cooperativity, as it has been included in other implementations of coarse-grained models for hydrogen-bond interactions (41).

We remark that hydrogen bonds can be formed between every pair of residues, regardless of their relative positions in the native structure. Thus, we are not only defining hydrogen bonds in a more accurate way, but also considering the ruggedness of the folding funnel within our potential definition.

Logically, some Gō contacts also correspond to the formation of hydrogen bonds in the native state. In these cases, the Gō contact is removed from our interaction definition to avoid overstabilizations, turning the detection of native hydrogen bonds into a relevant part of this work. As the Gō potential is based on the PDB structure, we pursue a hydrogen-bond definition fully consistent with the PDB information. This information is indirectly included in the PDB file headers through the secondary structure assignments, but the precise hydrogen-bonded pairs are not stated. To obtain them, we first tried to use the usual methods for hydrogen-bond detection (e.g., DSSP (42) or STRIDE (43)), but we found that they present slight differences with these PDB headers. Being that our hydrogen-bond potential is able to detect nearly 90% of native hydrogen bonds (as defined by PDB headers) in raw (unminimized) PDB structures (37), we decided to let our system relax under the effect of both the full Gō and hydrogen-bond potentials. In this way, we are able to obtain relaxed structures that are fully compatible with these headers and show no remarkable distortions (their root mean-square deviation compared to the original PDB structure is <0.5 Å, computed from the α-carbon positions).

Once all the native hydrogen bonds are detected, they are removed from the Gō potential definition, resulting in a decrease in the number of Gō contacts (compared to the pure Gō potential) when the combined potential is built. As an example, the resulting contact map for the B domain of protein G (PDB code 2GB1 (44)) is shown in Fig. 1. The mauve squares (online color only) correspond to Gō contacts and the black ones are native interactions that have been removed from the Gō potential because they correspond to native hydrogen bonds (see legend of Fig. 1 for a further explanation).

The relative weight of Gō and hydrogen-bond interactions has been properly modulated as a model parameter (w_HB = 2.0 w_GO) to give optimal results. We have performed several tests, obtaining similar upshots within a 25% variation of this value.

Data generation

To study the characteristics of the whole energetic and structural landscape for our model, we have used a parallel tempering (45) Monte Carlo simulation algorithm, as previously described (12). We have carried out single-chain numerical experiments with 20–30 temperatures each, depending on the system size and complexity. Each full simulation starts from a completely extended conformation for each chain and consists of 5 × 10⁶ Monte Carlo cycles at every temperature after 3 × 10⁶ equilibration cycles. In each cycle, every bead of the system is subjected to a trial Monte Carlo move.

The results presented here correspond to statistical averages over the sampling at every temperature and over different independent runs. For each system, three or five independent runs have been carried out.

Trajectory analysis

Once the simulations are completed, the thermodynamic analysis of our numerical results has been performed by the weighted-histogram-analysis method (WHAM) (46). We have converted the reduced units used in the calculations to real ones by correlating the experimental denaturation temperature of each protein (taken from the literature) to our transition temperature, computed as the maximum of the calculated heat capacity curve. Once the temperature is rescaled, the energy conversion is straightforward.

Results and Discussion

Our purpose is to evaluate whether an explicit consideration of hydrogen bonds improves the thermodynamic properties of folding in combination with classical Gō models. Thanks to an accurate single-bead hydrogen bond (37), we aim to know whether this approach improves aspects like cooperativity and free energy barriers along the folding process. Furthermore, we want to estimate whether this effect is a kind of a priori bias or provides a correct modulation of the free energy landscape of the transition for a given protein. For that purpose, we have structured this section according to different questions, from the most basic to more subtle and specific ones.

Do hydrogen bonds have any effect on folding for a single coarse-grained model like ours?

To find out, we started with the study of a classical test system (12,47–49), a paradigm of a two-state folder: the immunoglobulin binding domain of streptococcal protein G, also called GB1. We used the NMR-resolved structure, with PDB code 2GB1 (44,50) (note that, from now on, we will refer to each protein by its code).

In panel I of Fig. 2, we show a cartoon representation of 2GB1, as well as its heat capacity curve versus temperature (Fig. 2, I a), and the free energy profile versus total energy at the transition temperature resulting from WHAM calculations (Fig. 2, I b). Generally speaking, sharp maxima in heat capacity curves indicate cooperative foldings, whereas free energy profiles provide the energy distributions of the native and denatured states at a given temperature (in this case, the transition temperature), as well as the related free energy barrier. Regarding the semiquantitativeness of our results, two-state folders have free energy barriers greater than 5 kJ·mol^–1 (51); smaller barriers lie below or very close to thermal fluctuations and indicate a downhill folding.

Figure 2.

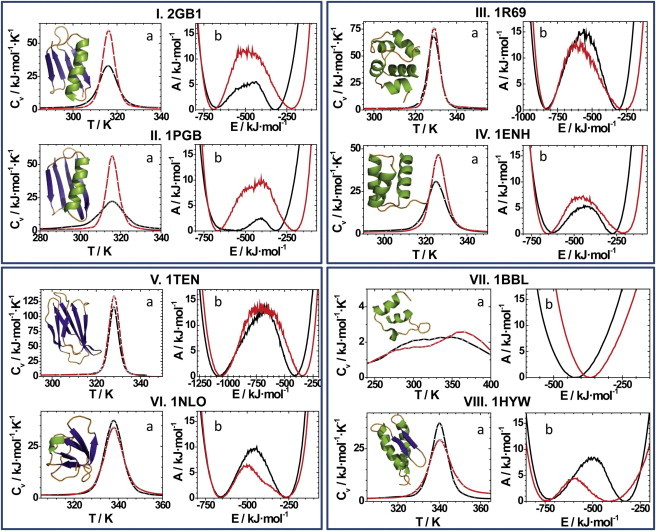
Heat capacity curves (a) and free energy profiles (b) of the studied proteins for the plain Gō model (black) and the combined Gō model with hydrogen bonds (red). In each rectangular section, two proteins are compared: (I) 2GB1 and (II) 1PGB (same protein whose structure has been determined by a different method); (III) 1R69 and (IV) 1ENH (two helical proteins); (V) 1TEN and (VI) 1NLO (β proteins); and (VII) 1BBL and (VIII) 1HYW (downhill proteins).

In each plot of Fig. 2, the black curve represents the results computed using the pure Gō potential, used as reference, whereas the red curve comes from the combination of Gō and hydrogen-bond interactions introduced in this work. As we can see in Fig. 2 I a, both heat capacity curves present a sharp peak, typical of cooperative transitions as it has been experimentally found for GB1. Hydrogen bonds enhance this cooperativity, also increasing the free energy barrier (see Fig. 2 I b), despite the fact that this cooperativity is not explicitly included in our model definition of the hydrogen-bond interactions. By exploring the minima corresponding to the folded and unfolded states in the free energy profiles, we can connect the differences imposed by the presence of the hydrogen bonds to a better definition of the native state (mediated by the specific definition of hydrogen bonds in the native structure) merged with a destabilization of the denatured one, where the removal of the Gō contacts that form native hydrogen bonds reduces the residual native structure in the denatured state.

Gō models strongly depend on the specific experimental structure, leading to different results for the same protein depending on the specific definition of the structure (30,38). Encouraged by the good results on 2GB1, we can raise our next question.

Can hydrogen bonds correct this logical but undesirable feature of plain Gō models?

The case of GB1 is particularly representative, as it has been observed (30) that the previously studied NMR structure (2GB1) leads to different results compared with the x-ray one (1PGB (52)). The results for 1PGB are shown in Fig. 2 II. If we start focusing on the black curves, we can clearly appreciate the differences between 2GB1 and 1PGB, where the latter one presents an incorrect barrierless folding (free energy barrier at ∼3 kJ·mol^–1) and a poorly defined native state at the transition temperature. The inclusion of hydrogen bonds (red curves) has a clear effect, sharpening the description of the energetics of the native state. As a result, we recover an almost identical transition to the 2GB1 case, proving that the explicit consideration of hydrogen bonds provides fully comparable results for this protein, independently of the experimental structure used to define the Gō potential.

After these results, we could think that the explicit consideration of hydrogen bonds in the model always leads to an increase in the free energy barrier, independently of the protein itself. As this has been also suggested for all-α proteins (27), this will be our following task, leading to another question.

Do hydrogen bonds insert a particular bias in the free energy surface for protein folding in our model?

To try to answer this, we have undertaken the study of the folding process for some α-proteins. As an example, we show, in Fig. 2 III, the amino terminal domain of phage 434 repressor (PDB code 1R69 (53,54)), an all-α protein that presents a cooperative folding (55). In our results, differences between the former model and the new one are rather subtle, but still meaningful. In both cases, we obtain a sharp heat capacity peak, distinctive of two-state folders. In the free energy curves, the combined potential shows a slight reduction in the barrier that refutes the hypothesis of a systematic barrier increase. For this protein, there are no changes in the native basin between both models, but the denatured basin presents the already observed shift toward higher energies, linked to the removal of some Gō contacts. This is accompanied by a widening of this basin, leading to a slight reduction in the free energy barrier as a net effect, as already mentioned. The broadening of the denatured basin has a structural source: it is due to the presence of some residual helical structure that, interestingly, has been claimed to be essential for the folding of this protein (55). In Fig. 3 a we show the frequency of hydrogen bonds that we have detected in our simulations for the denatured state of 1R69 at the transition temperature. It presents a low proportion of helical contacts that are not circumscribed to those present in the native state.

Figure 3.

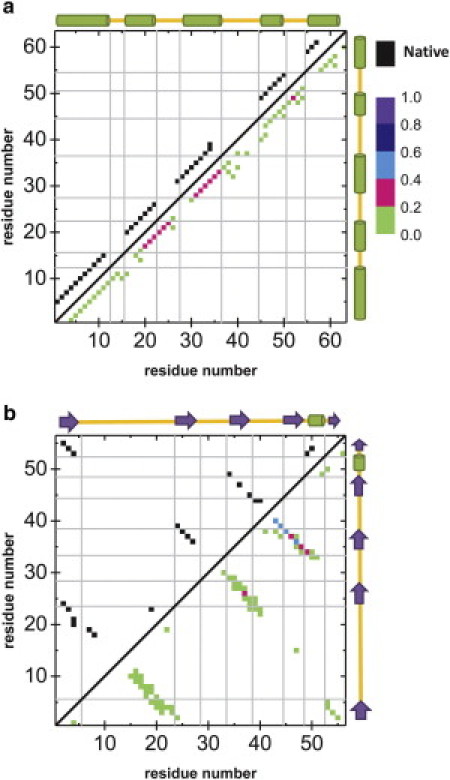
Maps of hydrogen-bond frequency in the denatured state of (a) 1R69 and (b) 1NLO. (Upper triangles) Hydrogen bonds that are detected in the native state. (Lower triangles) Frequency of appearance of hydrogen bonds in the denatured state of the given protein, according to the legend displayed. (Similarly to Fig. 1, the shaded lines and the sketches over the axes indicate secondary structure elements.)

As a matter of fact, a remaining helical content has been stated to be a general feature of the denatured state of helical proteins (56). The lack of an explicit consideration of hydrogen bonds in pure Gō models may result in a vague representation of residual helicity in the denatured state. Our approach surmounts this lack of specificity, dealing with these interactions in a more rigorous way. As an additional example, we show in Fig. 2 IV the engrailed homeodomain (PDB code 1ENH (57,58)). Numerous experimental and computational studies state that 1ENH is a two-state folder that nevertheless presents a high folding rate. In this protein, the residual structure is also thought to play an important role in the folding transition (59). The pure Gō results from our reference model show a relatively low heat capacity peak and a free energy barrier of ∼5 kJ·mol^–1, edging the downhill limit. Adding hydrogen bonds leads to a small increase in the folding cooperativity. In addition, the free energy barrier grows up to 7 kJ·mol^–1, typical of two-state folders: the widening in the denatured state with the combined model (also observed here) is counterbalanced by a better defined native state. In conclusion, the introduction of hydrogen bonds in this kind of protein implies the retention of some residual helical structure, providing a general broadening of the denatured basin but without forcing any systematic bias on the thermodynamical folding properties, which still depend on the intrinsic characteristics of the analyzed protein.

Once the impact of hydrogen bonds in helical proteins is correctly understood, how do they affect β-proteins?

We studied a fibronectin type III domain from human tenascin (PDB code 1TEN (60,61)), a typical example of two-state folder whose folding pathway has been thoroughly studied (62,63). Our results are shown in Fig. 2 V and only reveal minor changes when hydrogen bonds are applied. The free energy profile indicates that the native state is slightly better defined (narrower), whereas the denatured one shows no broadening, evidencing that hydrogen bonds do not induce any artifactual residual structure in this case (hydrogen bond map not shown).

Within β-proteins, we have also performed numerical simulations on the SH3 domain (PDB code 1NLO (64)) due to its biological relevance in aggregation studies and its well-established properties (two-state folder with a relatively high folding rate, comparable to helical proteins (65)). Our results, plotted in Fig. 2 VI, show that the heat capacity curves are typical from two-state folders, either including or omitting hydrogen bonds. However, the free energy barrier (tightly linked to the folding rate) gets considerably lower if hydrogen bonds are considered. The origin of this change lies now in the presence of a very broad denatured state, where many configurations within this basin share some residual hydrogen-bond interactions. The corresponding hydrogen-bond frequency map of Fig. 3 b mostly locates them in the distal loop of the protein (residues 39–44). Interestingly, this region is part of the structure of the transition state of this protein and is thought to be experimentally stabilized by a hydrogen-bond interaction (66). Moreover, it has been found that the distal loop plays a determinant role in the dimerization of the SH3 domain (67), showing therefore the importance of hydrogen-bond interactions in the folding and aggregation of this protein.

Up to this point, our systematic study has focused on two-state folders, which are thought to be the most common ones within living organisms. However, some small proteins can also exhibit a downhill folding where the free energy barrier is negligible (51).

Can hydrogen bonds contribute to a better description of barrierless folders?

We started by simulating the most common example of downhill folder, the E3 binding domain of the dihydrolipoamide succinyltransferase core from the 2-oxoglutarate dehydrogenase multienzyme complex of Escherichia coli, also known as BBL protein (PDB code 1BBL (68)). We have previously studied this protein with the plain Gō model, showing that downhill folding processes can be adequately simulated with this approach (30). However, the effect of hydrogen bonds is unknown. The results shown in Fig. 2 VII are characteristic of downhill folders, with a very broad and shallow heat capacity curve and without any barrier in the free energy profile at the transition temperature. This also proves that the inclusion of hydrogen bonds in our simulations does not induce free energy barriers if they are not present in the real system.

The success in the previous cases fostered our study of the gpW protein (PDB code 1HYW (69)). This α + β protein experimentally presents a very small folding barrier, showing an overall downhill folding (70,71). Knowledge-based potentials have given quite elusive results (72), and so does our plain Gō model. Shown in the black curves on Fig. 2 VIII, it exhibits a clear two-state behavior. However, the inclusion of hydrogen bonds (red curves) flattens the heat capacity curve and considerably reduces the free energy barrier down to ∼4 kJ·mol^–1, a typical result of a downhill protein with a barrier smaller than the thermal fluctuations. Moreover, we get an additional confirmation that our hydrogen-bond interactions do not systematically enhance the cooperativity of the folding transition. Instead, they seem to correct some deficiencies of our structure-based model to describe the thermodynamics of the folding transition in several proteins from different structural families and with distinct folding behaviors, making the simulation results of the new combined model closer to the experimental evidence in every case tested.

Summary and Conclusions

Structure-based potentials have traditionally proved their broad applicability in the study of protein folding when nonnative interactions may play a minor role. However, to take these effects into account, these models are recently adapting their interaction descriptions to the chemistry of the particular interactions (20,21). Among them, hydrogen bonds deserve special attention not only because of their biological relevance but also due to the partially covalent nature that makes them directional and stronger than other interactions. This directionality is responsible for the difficulty in achieving an accurate description in computational models with only one center of interaction per amino acid.

In this work we have undertaken this task thanks to a hydrogen-bond model in which this dichotomy is specifically tackled (37), mixed with a Gō potential of proven good quality (12). We have centered this study on the comparison of the resulting combined potential compared to the plain Gō model. Our aim has been to find out whether the inclusion of hydrogen bonds can improve the thermodynamic description of protein folding. Therefore, we have studied a set of representative cases pursuing two aims:1), check whether the good properties of Gō models remain, and 2), find out whether there is a perceptible improvement in the thermodynamic description of protein folding.

Regarding the first aim, we studied a well-known case where the Gō potential had previously proved its aptitude: the two-state folder 2GB1 (12). The introduction of hydrogen bonds does not imply any kind of undesirable effect, maintaining the general two-state scenario and even enhancing the free energy barrier of folding, even though our hydrogen-bond model does not explicitly include a term enhancing cooperativity.

Our model with hydrogen bonds does not only have a modulating role on systems where the Gō model already presented adequate results. We have also applied this approach to proteins where simple Gō potentials do not give a proper description of their folding process. Being the same protein as 2GB1, the example of 1PGB is particularly illustrative because the Gō model used here predicts a completely different (downhill) folding (31). In this case, our combined potential is able to correct this Gō artifact, presenting again a two-state folding identical to 2GB1.

Once our approach was found valid for general cases, we carried out a systematic analysis of folding events using proteins with different types of native structures. To illustrate this, we have shown a couple of examples of all-α (1R69 and 1ENH) and all-β (1TEN and 1NLO) proteins. The role of hydrogen bonds in all-α proteins is especially relevant, as a residual helical content has been observed in the denatured state of many of them (55,56,59). This effect, which the pure Gō model cannot properly reproduce, is correctly modeled when hydrogen bonds are explicitly considered. Interestingly, they do not force changes in the height of the free energy barriers, but correctly modulate them in agreement with experimental results.

In relation to all-β proteins, no systematic remaining structure is observed in their unfolded state, like in 1TEN. In 1NLO, however, some residual structure is observed. Interestingly, these partial interactions are not a model artifact, but they seem to have a biological meaning: they are mainly placed in regions experimentally stabilized by hydrogen bonds in the transition state and with a crucial role in the folding of this protein. Thus, the folding of this protein according to our model constitutes a valuable example of the synergistic effect of this combined potential and its applicability to protein folding studies.

Although we have mainly focused on two-state folders, the combined potential seems to work well in downhill folders too. We studied 1BBL, a typical example where our Gō potential had already given correct results (30). We checked that the introduction of hydrogen bonds does not have any undesirable effect, and downhill behavior is conserved. Our last challenge has been to determine whether the combined potential can simulate downhill folders even when the Gō potential cannot detect them. For that purpose, we studied 1HYW, a downhill protein with a small folding barrier where the Gō model predicts a two-state transition. Interestingly, the insertion of hydrogen bonds considerably reduces it, reaching the downhill range.

As a general view, we can conclude that all these profitable results are mainly based on three issues: a better definition of the native state in most cases; a certain removal of Gō-like residual structure in the denatured state; and a partial retention of helical structure in the denatured state (if this kind of structure is preponderant in the native conformation). As a result, the protein thermodynamics is not biased but adequately modulated according to the intrinsic characteristics of the protein itself: In some cases, the cooperativity of the folding transition is increased when hydrogen bonds are included. In other proteins, the folding barrier is not substantially modified, or it is even reduced. In all the cases, our hydrogen-bond model has contributed to make the simulation results of the combined model closer to the experimental evidence than the results from our Gō model alone.

In conclusion, we have successfully combined a Gō potential and a hydrogen-bond model to simulate the thermodynamic properties of the folding process for a representative set of proteins. Our results, that semiquantitatively match experimental data, show that this combination of potentials is an excellent candidate for carrying out these and other folding studies.