Abstract
We introduce and discuss a novel approach called back-calculation for analyzing force spectroscopy experiments on multimodular proteins. The relationship between the histograms of the unfolding forces for different peaks, corresponding to a different number of not-yet-unfolded protein modules, is exploited in such a manner that the sole distribution of the forces for one unfolding peak can be used to predict the unfolding forces for other peaks. The scheme is based on a bootstrap prediction method and does not rely on any specific kinetic model for multimodular unfolding. It is tested and validated in both theoretical/computational contexts (based on stochastic simulations) and atomic force microscopy experiments on (GB1)8 multimodular protein constructs. The prediction accuracy is so high that the predicted average unfolding forces corresponding to each peak for the GB1 construct are within only 5 pN of the averaged directly-measured values. Experimental data are also used to illustrate how the limitations of standard kinetic models can be aptly circumvented by the proposed approach.
Introduction
During the last decade, single-molecule force spectroscopy experiments based on optical tweezers or atomic force spectroscopy have acquired increasing importance for characterizing properties of individual proteins, as well as protein complexes. Among the hundreds of such studies carried out so far, it is particularly worth mentioning force spectroscopy investigations of multimodular proteins. These constructs typically consist of a series of protein modules that are covalently linked at their ends (see, e.g., (1–12)). Upon pulling the constructs at both ends, a series of unfolding events are observed. The forces at which the unfolding events occur carry a wealth of information about the unfolding mechanics and kinetics of the construct modules (3,13,14). Customarily, this information is extracted by analyzing the force distribution obtained by gathering together the succession of unfolding forces over repeated stretching experiments and analyzing them with different methods, such as Monte Carlo simulation and regression to zero force (5,15–19). The scope and utility of these commonly employed analysis techniques can be considerably extended by examining separately the distribution of the forces associated with the first, second, etc., unfolding event in the constructs. This approach, which so far has been applied only limitedly (5,20), is particularly appropriate and useful when the construct consists of repeats of the same type of globular protein (such as I27 or GB1). In fact, because of the identical nature of the modules, it is expected that the forces associated with the various unfolding events depend on the number of unfolded modules still present on the molecule, but that the statistical distributions should nevertheless be tied by a definite relationship, as pointed out in previous studies (5,20,21,22). To the best of our knowledge, such dependence has not yet been adequately explored or exploited in experimental contexts. Furthermore, one may envisage using only the limited information contained in the experimental distribution of one single group of unfolding forces to predict with high accuracy the average unfolding forces of all other groups. This issue also has not been addressed before, and we therefore investigate it in this study.
The problem is here attacked at two levels. First we adopt a simplified analytical scheme, which implicitly relies on a standard kinetic model for the unfolding of the protein modules (Evans's theory). This method, which builds on a treatment introduced in previous studies (20,21,23), combines a transparent analytical formulation with the simplicity of implementation and use. Yet the simplifying assumptions that allow for the exact analytical treatment of the model come at a disadvantage, since the predicted probability distributions for the unfolding forces of the various peaks can be significantly different from the measured ones.
This limitation can be overcome by using the alternative and more general phenomenological approach introduced and discussed here for the first time that we know of. The scheme, based on the bootstrap statistics and termed back-calculation, is parameter-free and does not rely on any specific kinetic model. The method merely uses the probability distribution of forces associated with one of the unfolding events (the first, the second, etc.) and predicts the distribution of forces of all other events. The method is validated against data obtained from stochastic simulations (both Langevin and Monte Carlo) and from atomic force microscopy (AFM) experiments carried out on multimodular GB1 constructs. In all cases, the average forces associated with any unfolding event are well predicted by back-calculation. Deviations from the experimental measured values are of only 5 pN, a quantity that is smaller than the uncertainty typically associated with experimental estimates for protein unfolding forces.
Materials and Methods
Experiment
Our experiments were performed on multimeric constructs consisting of eight GB1 modules, hereafter denoted as (GB1)8, and dissolved in Tris/HCl buffer (10 mM, pH 7.5) at a concentration of ∼20 μg/ml (1,2,24). The force-extension curves of (GB1)8 were measured by means of a commercially available AFM system (Picoforce AFM Nanoscope IIIa, Bruker, Madison, WI) using a V-shaped silicon nitride cantilever (NP, Bruker). The spring constant of the lever was measured from thermal fluctuation measurements (25) as part of the AFM calibration procedure and was found to be equal to 0.0575 N/m. The constructs were pulled along the x direction at the speed x = 2180 nm/s. Further details of the standard experimental protocol that was followed can be found in a recently published note (21).
A typical experimental force-extension curve is presented in Fig. 1. Because the AFM tip will not necessarily pick the construct at its free end, the number of modules trapped between the anchored end and the AFM tip can be <8. As a matter of fact, among the curves presenting a clear detachment peak, the most numerous group was the one displaying six unfolding peaks. We therefore limited considerations to this set of force-extension curves. The curves were analyzed using Hooke (26) an open-source software package designed to analyze the force spectroscopy curves. Hooke was further used to analyze the data from Langevin simulations of the stretching of multimodular protein constructs (see below).
Figure 1.
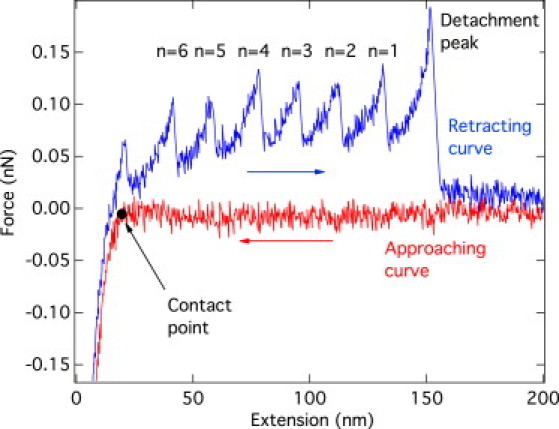
Typical force-extension curve recorded in an AFM stretching experiment on a (GB1)8 construct. The lower curve shows the force as the AFM tip approaches the substrate until the contact is established. The upper curve represents the force while the tip is retracted from the substrate and shows a series of unfolding events of the construct picked up by the tip. Notice that this trace displays six unfolding events. The effect of an aspecific interaction at the beginning of the retracting trace is observed. The peak forces leading to the unfolding of the various modules are measured with respect to the background provided by the constant part of the retracting curve.
Numerical simulations
Two different computational approaches, namely Monte Carlo and Langevin simulations, were used to study the mechanical unfolding of multimodular protein constructs. In both cases, the pulled construct is assumed to be anchored at one end while the other is pulled at fixed speed. The end-to-end distance of each protein module projected along the pulling direction, x, is used as an effective order parameter to describe the module state. This corresponds to considering the system as being effectively one-dimensional, as in the sketch of Fig. 2 a. This is a good approximation, since for the typical unfolding forces at play in our experiments, the end-to-end distance of our construct, as obtained from a wormlike-chain (WLC) model, is expected to be almost equal to its contour length, so that fluctuations in the y and z directions can be neglected.
Figure 2.
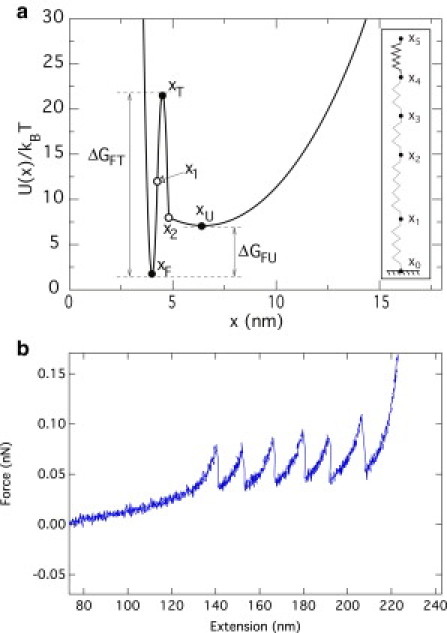
(a) Illustration of the anharmonic spring potential for one module of the construct in the Langevin simulation (see Eq. 1). A large value of A, equal to 100 pN × nm2, was used in Eq. 1 to enforce the constraint that the modules cannot be stretched beyond the nominal GB1 contour length, Lc = 18 nm. The reference end-to-end separation of the folded state, xF, is set equal to 4 nm and the the end-to-end separation between the folded state and the transition (T) state, , is 0.5 nm. The reference end-to-end separation of the unfolded state, xU, is equal to . Consistent with what has been established in previous studies, the barrier separating the folded and transition states is set equal to , whereas the barrier between the folded and unfolded states has the value , with the temperature, T, equal to 300 K (i.e., pN nm). For simplicity, the curvature, kT, is set equal to kF. The value of kF in turn is set to pN/nm to ensure the continuity of the potential and its derivative at the midpoint, , where the first two parabolas in Eq. 1 meet. The value of kU was set to be much smaller than kF, at kU = kF/500 = 2.69 pN/nm. The value of x2 was finally obtained by the requirement of continuity of the potential. To avoid an excessive parameterization of the model, flexible linkers in the construct are described as unfolded protein modules. (Inset) Protein model used in Langevin simulations. (b) A force-extension curve obtained with the Langevin simulation applied to a model construct that initially comprised six folded modules intercalated by seven linkers (each linker has the same length as an unfolded module).
Depending on the value of the end-to-end separation, each module is considered as being folded (F) or unfolded (U); these two states are separated by a barrier of potential energy whose height is modulated by the applied tensile force. The effective potential energy, U(x), is modeled explicitly in the Langevin scheme, where one integrates the stochastic equation of motion for each of the tethered modules in the construct that is being pulled. By contrast, no explicit representation of the construct is considered in the Monte Carlo approach. The latter, in fact, is employed to model the succession of discrete unfolding events occurring at force-dependent rates.
The two methods clearly embody rather different strategies for simulating the stretching experiments and, also in view of the different parameters used in the corresponding stochastic simulations, are useful to probe the generality and transferability of the back-calculation method (BC) proposed here.
A detailed description of the two methods is provided hereafter.
Langevin simulations
With reference to the sketch in the inset of Fig. 2 a, the anchored end of the construct is located at x0 = 0, while the other end (x4 in the sketch) is attached to the moving AFM tip. For simplicity, to parallel what is done in the Monte Carlo scheme below, the latter is modeled as a Hookean spring (x4–x5 in the sketch) with spring constant kAFM = 0.01 N/m. Each protein module behaves as an anharmonic spring; the associated free-energy profile, U(x), is shown in Fig. 2 a and described by the expression
| (1) |
The model parameters are chosen to be consistent with the overall shape of the potential energy typically found in proteins (27) and are provided in the caption to Fig. 2. In particular, the contour length of each module is equal to the nominal contour length of GB1, Lc = 18 nm, the reference end-to-end separation of the folded state is xF = 4 nm, and its distance to the transition state is Δx = 0.5 nm.
In multimodular protein constructs, each protein module is connected to the next via a short peptidic linker of length 1.5 nm. To keep at a minimum the number of parameters in the model, we described these linkers, which clearly do not undergo any transition upon stretching, by unfolded protein modules. To do so, we initially prepared the pristine construct as a succession of folded modules with initial end-to-end separation equal to xF, intercalated with unfolded modules with initial end-to-end separation equal to xU. The potential energy barrier separating the F and U states is sufficiently high that an initially unfolded module will not spontaneously refold over the short timespan of the model stretching experiment.
The total potential energy of the homomeric module chain composed of n protein modules, ℓ linkers, and the AFM tip is given by
| (2) |
The time evolution of the key construct positions, follows the overdamped Langevin dynamics:
| (3) |
where γ = 4.4 × 10−5 pN s/nm is the friction coefficient appropriate to yield (according to Kramer's theory) a spontaneous unfolding rate (at zero applied force) equal to koff = 10−2 s−1. is a Gaussian white noise with zero mean and variance equal to (kB is the Boltzmann constant and K is the temperature). Notice that the derivative of the potential U (entailed by the derivative of H) is not continuous in x2.
The stochastic equations of motion were integrated numerically with a time step of 1 ns. After an initial equilibration, the position of the AFM tip, is moved at constant velocity, , with ν = 500 nm/s. This velocity value is commonly employed in stretching simulations and falls in the typical range of pulling velocities used in experiments (28). The typical time span required to unfold all the n = 6 modules in the constant-velocity simulation was 0.25 s.
The force/extension curve of the system is obtained by recording the restoring force experienced by the AFM tip, , as a function of the AFM tip position, , as shown in Fig. 2 b. Several hundred such curves were collected and analyzed with Hooke after performing a time average over windows of duration 0.15 ms to mimic the finite time resolution of a typical experiment.
Monte Carlo simulations
As anticipated at the beginning of the section, the Monte Carlo approach (here implemented as in studies by Rief and colleagues (28,29) and Zinober and colleagues (30)) provides a phenomenological approach to the kinetics of mechanical unfolding. The advantage of its transparent formulation is balanced by the highly simplified nature of the model. In particular, by contrast with the Langevin modeling of biopolymer stretching employed here and in other approaches (31), no explicit representation of the module constructs is considered, and the linkers are not accounted for. In addition, the pulling action is assumed to act equally on all the n modules, causing the same steady increase of the end-to-end separation for each of them. Notice that because of the limited sound velocity in the chain, this condition is only approximately realized in Langevin schemes and experiments (where other effects, such as viscosity, can be at play). In any case, the lower the pulling rate the better the approximation is expected to be.
Within the above assumption, the end-to-end distance (equal to zero at the initial time, t = 0) of each one of the n modules at time t is equal to . In this study, we considered n = 6 and v = 500 nm/s, and the effective spring constant of the AFM tip is set to kAFM = 0.01 N/m. Notice that kAFM is smaller than the nominal spring constant of the tip used in our typical stretching experiments. This is because kAFM stands for an effective spring that, in addition to the AFM tip, accounts for stiffness of the folded modules, which are not explicitly included in our Monte Carlo scheme. With this simplified description, the loading rate is not dependent on the number of folded modules, which brings the Monte Carlo closer to the BC assumptions, as discussed later. We underline that our goal here is to provide a benchmark for the BC and not to reproduce the experimental data, so a qualitative picture is satisfactory at this stage. The instantaneous force experienced by each module is computed from the theoretical force-extension curve, fWLC(x) of an equilibrated WLC with contour length Lc = 18 nm (appropriate for GB1) and a persistence length of lp = 0.4 nm. The progressive loading of the modules is followed at time increments of duration Δt = 1.6 × 10−5 s. At the (discrete) time, t, the probability that one of the modules yields and becomes unfolded is computed within the Evans approximation (13) disregarding the refolding probability:
| (4) |
where kB is the Boltzmann constant and T = 300 K is the system temperature. The effective values koff = 0.11 s−1 and Δx = 1.44 Å are obtained from a fit of the experimental data using Evans's theory as in Benedetti et al. (20). The fitting procedure ensures that the unfolding forces fall in a range similar to the experimental ones, although a precise match is neither expected nor sought. The Monte Carlo scheme consists of drawing a random number, uniformly distributed in the [0,1] interval, for each of the n protein modules and comparing it with p(t). An unfolding event occurs when one of the n random numbers is smaller than p(t). The associated unfolding force is recorded and the calculation is next repeated with the n – 1 modules. The statistical distribution of the unfolding forces for each value of n was obtained from 1000 repeats of the Monte Carlo unfolding simulations.
Analytically solvable model
Simple analytical expressions for the probability distributions of the unfolding forces, and the associated mean values and variance, as a function of the number of domains, n, can be obtained by introducing a further simplification besides the ones introduced for the Monte Carlo scheme. Specifically, each protein module is treated as a harmonic spring (as in the Langevin approach) rather than a WLC, and the unfolding process follows the Bell-Evans theory. Within these assumptions, the probability distribution of unfolding forces has been previously worked out both for single-chain stretching (see, e.g., Hummer and Szabo (23)) and for multimodular constructs (20,21). For completeness, and for the purposes of better discussing the phenomenological BC method, an analogous derivation is provided here.
Let us consider a model construct consisting of harmonic springs: the n0 initially folded modules have spring constant equal to kF, whereas the remaining ℓ have a smaller spring constant, kU, as appropriate for unfolded modules. The model construct is subject to the AFM pulling action (the AFM tip is again modeled as a harmonic spring with constant kAFM). Because the tip is pulled at constant velocity, v, the tensile force experienced at time t by each construct is equal to
| (5) |
where is the effective spring constant of the construct in series with the AFM tip and its inverse decreases with n as . Here is the inverse spring constant of the completely unfolded construct, and A is a correction term that describes the dependence of the spring constant on the number of folded modules.
Following Evans's theory, the survival probability that any one module has remained folded up to time t is equal to (23)
| (6) |
The probability that all the n modules have remained folded up to time t, or equivalently up to the loading force , is simply obtained by raising the above expression to the power n,
| (7) |
By differentiating Sn with respect to f, one obtains the probability distribution, , for the force at which the first unfolding event occurs in a chain of n modules.
The sought expression is
| (8) |
where the proportionality factor, containing the normalization of the probability distribution, was omitted.
Since the function above is typically nonnegligible only for positive f, we can compute its average and variance integrating over , which leads to the analytical result
| (9) |
| (10) |
where is the Euler-Mascheroni constant.
We remark here that the variance is independent of the number of folded modules, n, in the construct. This result is related to the empirical observation that in typical stretching experiments of a single protein construct, the variance of the unfolding force is largely independent of the loading rate (23).
If the dependence of the spring constant on the number of folded modules can be neglected, the average unfolding force acquires a particularly simple expression:
| (11) |
where the parameters a and b are obtained from the average force and variance for a given n: and .
Finally, we notice that for all values of n, the expression of Eq. 8 corresponds to a Gumbel extremal distribution (32) with the fat tail extending toward low values of the force, f. Accordingly, the viability of the analytical model to capture the statistical properties of the unfolding forces measured for a given value of n can be ascertained by checking whether the forces follow the Gumbel distribution. To address this point, we employed the Anderson-Darling test and computed the significance level to which one can support the null hypothesis that the data originate from a Gumbel distribution. According to custom, the threshold of 5% statistical significance was used to accept or reject the null hypothesis.
Back-calculation
The previous analytical results rely on a definite kinetic model (Evans's theory) and on the harmonic modeling of the elastic response of the AFM tip and the protein modules. These effects could be included in a more general theoretical framework which, however, would not yield simple analytical calculations.
This difficulty can be circumvented using a simple and physically appealing phenomenological approach, which we term the back-calculation method, described hereafter. The method is parameter-free, as it relies on the knowledge of the empirical probability distribution of the unfolding forces at one particular value of n. This reference distribution can be used straightforwardly to predict the average value of the force and its variance at all other values of n. The scheme is best illustrated assuming that the reference distribution is the one for n = 1, . This distribution is directly obtained from the data gathered in the stretching experiments or from the stochastic simulations (Fig. 3). In the same spirit of the Monte Carlo and the analytically solvable model, we assume that the loading rate is sufficiently low that at any given time, all modules experience the same instantaneous tensile force applied at their ends, f, and that each of them can unfold independently from the others. We also assume that the stiffness of the construct, defined as the derivative of f with respect to its length, is not dependent on the number of folded constructs, n. This is equivalent to considering A = 0 in the analytical model, and it is realistic for investigated cases (for counterexamples, see King et al. (21)). Under these assumptions, without resorting to any kinetic model or lengthy stochastic simulations, the average unfolding force associated with the nth peak, , is computed by drawing n random numbers distributed according to and taking the smallest of them as the force at which one of the n modules first unfolds. The average value of the unfolding force, (and its variance), is clearly obtained by repeating the batch force sampling process several times.
Figure 3.
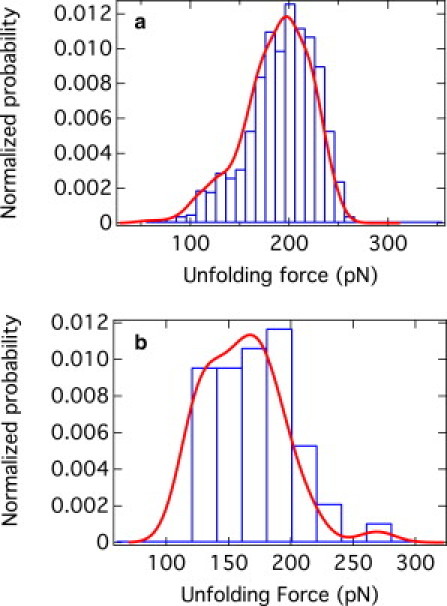
Normalized probability distribution of the unfolding forces for the n = 1 peaks (i.e., near the detachment point) obtained for (a) Monte Carlo simulation and (b) GB1pulling experiments. The continuous line in both cases represents the Gaussian KDE estimated from the raw data. The histograms are both normalized.
One may use the ordered list of N measurements to construct a cumulative probability distribution interpolated linearly between consecutive measured values. The cumulative distribution is next straightforwardly used (see Chapter 7.3 in Press et al. (33)) to sample, with the correct weight, the n force values. Describing the process in terms of the cumulative distribution has also the following important advantage. It is possible to exploit the simple relationship of Eq. 7 (which is based on the assumption of independence and hence valid regardless of the specific underlying kinetic process) to generate data for unfolding forces of the nth peak starting from the data obtained for a peak with a different order, say mth.
In fact, indicating by
the cumulative distribution for the unfolding forces of the mth peak, it can be determined that the corresponding cumulative distribution for the nth peak is
| (12) |
It is important to stress that the above relationships are of high conceptual and practical interest for recovering the distribution of unfolding forces of one peak, say n = 1, starting from a peak of higher order, say m = 2. A detailed description of how this backward extrapolation can be practically implemented in a numerical scheme is provided in the Appendix, and the results are provided in the Supporting Material. The results discussed hereafter are produced with a more refined method where the probability is obtained from fitting the histogram of the raw force measurements with a convolution of Gaussians using the kernel density estimation (KDE) (34) (Fig. 3). Data are sampled according to this distribution using either the cumulative distribution, or the rejection scheme (see Chapter 7.3 in Press et al. (33)).
Results and Discussion
For all the three systems of interest (the GB1 experiment and the Monte Carlo and Langevin simulations), we analyzed the data of the force-versus-extension (or equivalently force-versus-time) curves. In all three cases, the data pertained to the stretching of constructs of n0 = 6 modules, and therefore, the few curves that did not display a clear presence of six force peaks were discarded.
The peaks were indexed in an inverse order with respect to their order of appearance in the stretching experiment. Specifically, the peak of order n = 6 corresponds to the peak observed first (when six folded modules were present before the unfolding event), whereas peak order n = 1 corresponds to the unfolding event for which only one module was present before the unfolding event and occurring immediately before the construct detachment from the support. The peak force data for each value of n were next considered (see Benedetti et al. (20) for details on the automated peak division procedure) and used to compute the histograms reflecting the force distribution. The probability distribution is obtained with a convolution of Gaussians using the KDE method mentioned in the Methods section. The resulting normalized distribution of the forces, pn(f), at which a single module unfolds in the Monte Carlo scheme and GB1 experiments is shown in Fig. 3. The best-fit Gaussian convolutions were used to obtain a robust estimate of the average unfolding force and its standard deviation (SD) at each value of n. The results are provided in Tables 1–3 and Figs. 4–6.
Table 1.
Unfolding forces from Monte Carlo simulations
| Comparison with n = 1 back-calculated values | ||||||
|---|---|---|---|---|---|---|
| n | 6 | 5 | 4 | 3 | 2 | 1 |
| Average, Monte Carlo data | 142 | 146 | 150 | 157 | 166 | 187 |
| Average, n = 1 BC | 138 | 142 | 148 | 156 | 168 | — |
| SD, Monte Carlo data | 40 | 35 | 35 | 35 | 37 | 35 |
| SD, n = 1 BC | 29 | 31 | 32 | 31 | 33 | — |
All values are given in pN.
Table 2.
Unfolding forces from Langevin simulations
| Comparison with n = 1 back-calculated values | ||||||
|---|---|---|---|---|---|---|
| n | 6 | 5 | 4 | 3 | 2 | 1 |
| Average, Langevin simulation | 70 | 73 | 74 | 78 | 84 | 92 |
| Average, n = 1 BC | 70 | 72 | 74 | 78 | 83 | — |
| SD, Langevin simulation | 16 | 14 | 13 | 13 | 14 | 15 |
| SD, n = 1 BC | 11 | 11 | 12 | 13 | 14 | — |
All values are given in pN.
Table 3.
Unfolding forces for GB1
| Comparison with n = 1 and n = 2 back-calculated values | ||||||
|---|---|---|---|---|---|---|
| n | 6 | 5 | 4 | 3 | 2 | 1 |
| Average, experiment | 124 | 128 | 129 | 137 | 146 | 162 |
| Average, n = 1 BC | 121 | 125 | 128 | 134 | 143 | — |
| Average, n = 2 BC | 123 | 127 | 131 | 137 | — | 160 |
| SD – experiment | 25 | 30 | 31 | 31 | 30 | 31 |
| SD, n = 1 BC | 17 | 18 | 19 | 21 | 25 | — |
| SD, n = 2 BC | 21 | 21 | 22 | 24 | — | 36 |
Accuracy in prediction of the SD is improved when data from n = 2 are used. All values are given in pN.
Figure 4.
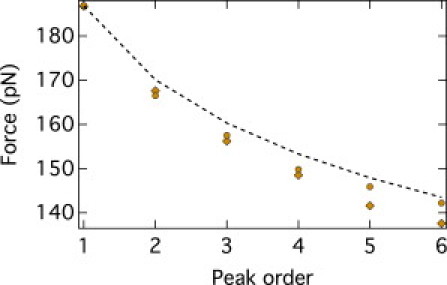
Average unfolding force versus peak order for the Monte Carlo (circles) and BC (diamonds) from the distribution of unfolding forces of the peak order n = 1 stemming from the Monte Carlo simulation and kinetic model (dashed line). The statistical error (mean ± SD) is the same size as the symbols, ∼0.5 pN.
Figure 5.
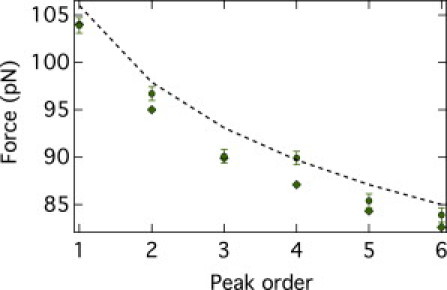
Average unfolding force versus peak order for the Langevin (circles) and BC (diamonds) from the distribution of unfolding forces of the peak order n = 1 stemming from the Langevin simulation and kinetic model (dashed line). The statistical errors (mean ± SD) are shown with error bars for the Langevin simulation, whereas for the BC data, the errors are the same size as the symbols (∼0.5 pN).
Figure 6.
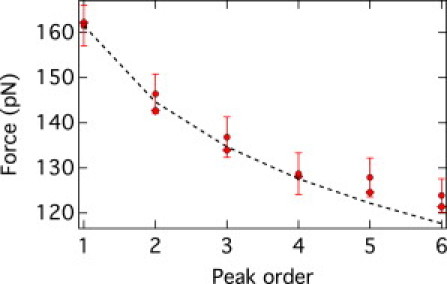
Average unfolding force versus peak order for the GB1 experimental data (circles) and BC (diamonds) from the distribution of unfolding forces of the peak order n = 1 stemming from the experiments and kinetic model (dashed line). The statistical errors (mean ± SD) are shown with error bars, whereas the BC data have errors of the same value as the size of the symbols (∼0.5 pN).
The best-fit distribution for the last surviving peak, n = 1, was typically used as input for the back-calculation and analytically solvable methods to obtain predictions for the average unfolding forces at all values of n. For the case of highest practical interest, namely, the GB1 experiment, the distribution of unfolding forces of all other peaks, , was also used to predict the unfolding forces of other peaks (see Table S1 in the Supporting Material).
Monte Carlo data
We start by discussing the application of the method to data generated using the Monte Carlo procedure. Of the three sets of data (from experiment and Langevin and Monte Carlo simulations), this set is the one that is expected to be most appropriately captured by back-calculation. The Monte Carlo scheme indeed builds on the identical kinetic status of all the modules, and during this process, only the total contour length changes, with very mild effect on the loading rate.
By using the n = 1 data, it is indeed seen in Table 1 that the mean values of the predicted and measured unfolding forces are in good agreement for all peaks n = 2…6, with differences always <5 pN. The agreement is readily perceived in Fig. 4, where it is seen that the BC data up to n = 4 fall within the statistical uncertainty of the Monte Carlo data, and only the forces predicted at n = 5 and n = 6 present SDs of ∼2.5 from the Monte Carlo data.
A more challenging quantity to compare is the second moment of the distribution, which is the variance or, equivalently, the SD. For the latter quantity, the agreement is still good. The deviation of the Monte Carlo and back-calculated values, , is typically within 10% and is worst for the last peak, n = 6, for which it is 16%.
The results of the analytical model present an accord with the Monte Carlo data that is comparable with their agreement with the BC. This is illustrated by the dashed line in Fig. 4, which reports the analytical predictions based on the Monte Carlo data for n = 1 (data for this case and other values of n are provided in the Supporting Material). The good accord is nontrivial in view of the fact that the simplified analytical treatment describes the folded protein domains as harmonic springs, whereas the Monte Carlo data were generated employing a WLC model for each domain. We carried out the Anderson-Darling statistical test described in the Methods section and established that the Monte Carlo data for n = 1 (and higher values, too) are compatible with an underlying Gumbel distribution. This reinforces the applicability of the simplified analytical scheme in the model Monte Carlo context.
Langevin data
The same analysis was repeated for the data generated using the Langevin scheme, which contains several differences from the Monte Carlo scheme. Specifically, the Langevin scheme does not enforce either Evans's kinetics or the same precise behavior of all folded modules in the chain. In addition, it accounts for the presence of model linkers between the folded modules, and finally, values of and are appreciably different from those in the Monte Carlo case.
As is visible from Table 2 and Fig. 5 also for the Langevin context, the performance of the back-calculation method is good and, with the exception of the point for the fourth peak (which compared to the trend of the other data points appears to be an outlier), the average predicted values of unfolding forces are all within about one SD of the Langevin data. As for the Monte Carlo data, the predicted SDs are also consistent with the measured ones, and the largest relative error, again found for the peak with the largest extrapolation, n = 6, is 14%.
As shown in Fig. 5, the performance of the analytical model based on the n = 1 data is not dissimilar from that of the back-calculation (the detailed results are again reported in the Supporting Material). Indeed, also in this context, the Anderson-Darling test indicates that distributions of the unfolding forces are compatible with a Gumbel distribution.
Experimental data on (GB1)8
Finally, we turned to the experimental data, which clearly represent the greatest challenge. Because of the complex interplay of the several factors that impact on the stretching process, and because the pulling rate is not particularly low, it may not be expected a priori that the system unfolding response might be well captured by the back-calculation. In particular, it is not obvious a priori that the unfolding events of various peaks in the chain can be appropriately described as statistically independent events. In fact, correlations can arise in nearby protein moduli because of the limited sound velocity in the chain or because of contact interactions. Moreover, given the small number of experimental samples, 47 measurements for each force peak, it is not simple to obtain a reference histogram from the experiment or to pin a distribution, even when using the KDE interpolation scheme. Thus, any defect in the starting distribution is consequently amplified by the back-calculation method.
Despite these caveats, the predictive capability of the back-calculation method for the average unfolding forces was found to be very good also in this case. The level of agreement can be appreciated by examining Table 3 and Fig. 6. The increasing underestimation, as a function of n, of the sample SD (predicted from the n = 1 peak) is probably ascribable to the fewer-than-expected measurements at low forces. This is readily demonstrated by starting the back-calculation from the second peak, n = 2, which by covering lower values of unfolding forces can reproduce very well not only the mean unfolding forces at all other values of n, but also the corresponding SDs.
In light of this consideration, the very good consistency of the back-calculation data with the measured distribution is very remarkable, and testifies to the robust applicability of the method.
It is particularly instructive to discuss the performance of the analytical method as well. Neither the average unfolding forces nor their SDs are dissimilar from the experimental ones (see Fig. 6 and Supporting Material). However, unlike in the cases for the Monte Carlo and Langevin data, this agreement does not stand up to closer statistical scrutiny.
In fact, the Anderson-Darling statistical test indicates that the experimental data do not follow the Gumbel extremal statistics entailed by the analytical model at each value of n (see Eq. 8). In fact, the null hypothesis for the n = 1 peak is supported with a confidence level of <1%. The same applies for the n = 2 peak as well (in spite of the fact that a more and more pronounced Gumbel-like character is expected as n increases).
The above observations demonstrate the utility of the back-calculation approach in the context of practical interest. Indeed, the phenomenology of systems such as multimodular constructs of GB1 can be too rich to be well accounted for by Evans's theory. In such contexts, a good control/prediction of the unfolding forces for varying numbers of surviving modules can be made only starting from the phenomenological distribution.
Conclusions
We present a systematic investigation of the statistical properties of the forces associated with the first, second, etc., unfolding events in a multimodular construct. We introduced a phenomenological scheme, termed back-calculation, which, using as sole input the distribution of the forces associated with a certain unfolding event (e.g., the first), predicts the force distribution of all other events. We stress that the method follows a bootstrap approach starting from the raw force-extension measurements. In particular, it does not rely on any model of mechanical response for protein unfolding kinetics.
At a general level, it is shown that the standard procedure of analyzing experimental stretching data by grouping together forces associated with all unfolding events, could be more profitably replaced by considering the events separately with equal order of appearance. To the best of our knowledge, the possibility of applying such a scheme to analyze experimental data has not been explored before. Second, a comparison of the experimental distributions of unfolding forces with that predicted by standard kinetic models reveals appreciable discrepancies, thus preventing their use as reliable descriptors of the mechanical unfolding process. This fact is consistent with previous independent investigations (27).
In addition, the approach has several implications for the design/analysis of stretching experiments of multimodular constructs. First, its simplicity makes the back-calculation particularly appealing as a simple and transparent scheme for the interpretation of experimental data. In this respect, an interesting applicative avenue is offered by heterogeneous multimodular constructs, for which the back-calculation can offer a term of reference apt for highlighting composition-dependent modulations of the mechanical response. Second, it offers a simple, parameter-free phenomenological approach for predicting the distributions of the various unfolding peaks using a negligible computational effort. In this respect, it presents major advantages compared to the more computationally intensive stochastic (Monte Carlo or Langevin) numerical approaches. Finally, it can be applied to the design of biomaterials starting from their molecular modular components (e.g., choosing an appropriate number of repeats), with unfolding forces falling in a desired range, or to precondition a pulling experiment (choice of pulling speed, stiffness of the AFM tip) so that the mechanical response is profiled with a desired resolution. A study of the latter aspects is underway.
The numerical implementations (C programming language) of the back-calculation techniques are available upon request from the authors.
Acknowledgments
This work was supported by the Swiss National Science Foundation (grant No. 205320-131828) and by the Italian Ministry of Education (MIUR).
Appendix
The procedure used to predict the force distribution for peak n given a set of experimental measurements for peak m is discussed here in detail. As a first step, an ordered table , with , is built that contains the N measured forces for peak m.
To resample new data from the same distribution, the procedure is as follows:
Extract a uniform random number .
Find i such that .
The extracted force is computed as .
The last step is based on a liner interpolation of the cumulate of the distribution.
To extract data corresponding to the distribution of a different peak n, which can be larger or smaller than m, the procedure has to be modified as follows:
Extract a uniform random number .
Compute .
Find i such that .
The extracted force is computed as .
Supporting Material
References
- 1.Cao Y., Li H.B. Polyprotein of GB1 is an ideal artificial elastomeric protein. Nat. Mater. 2007;6:109–114. doi: 10.1038/nmat1825. [DOI] [PubMed] [Google Scholar]
- 2.Cao Y., Lam C., Li H.B. Nonmechanical protein can have significant mechanical stability. Angew. Chem. Int. Ed. 2006;45:642–645. doi: 10.1002/anie.200502623. [DOI] [PubMed] [Google Scholar]
- 3.Carrion-Vazquez M., Oberhauser A.F., Fernandez J.M. Mechanical and chemical unfolding of a single protein: a comparison. Proc. Natl. Acad. Sci. USA. 1999;96:3694–3699. doi: 10.1073/pnas.96.7.3694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sandal M., Valle F., Samorì B. Conformational equilibria in monomeric α-synuclein at the single-molecule level. PLoS Biol. 2008;6:e6. doi: 10.1371/journal.pbio.0060006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brockwell D.J., Beddard G.S., Radford S.E. Mechanically unfolding the small, topologically simple protein L. Biophys. J. 2005;89:506–519. doi: 10.1529/biophysj.105.061465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Marszalek P.E., Lu H., Fernandez J.M. Mechanical unfolding intermediates in titin modules. Nature. 1999;402:100–103. doi: 10.1038/47083. [DOI] [PubMed] [Google Scholar]
- 7.Li H., Linke W.A., Fernandez J.M. Reverse engineering of the giant muscle protein titin. Nature. 2002;418:998–1002. doi: 10.1038/nature00938. [DOI] [PubMed] [Google Scholar]
- 8.Carrion-Vazquez M., Li H.B., Fernandez J. The mechanical stability of ubiquitin is linkage dependent. Nat. Struct. Mol. Biol. 2003;10:738–743. doi: 10.1038/nsb965. [DOI] [PubMed] [Google Scholar]
- 9.Li H., Carrion-Vazquez M., Fernandez J. Point mutations alter the mechanical stability of immunoglobulin modules. Nat. Struct. Mol. Biol. 2000;7:1117–1120. doi: 10.1038/81964. [DOI] [PubMed] [Google Scholar]
- 10.Lee G., Abdi K., Marszalek P.E. Nanospring behaviour of ankyrin repeats. Nature. 2006;440:246–249. doi: 10.1038/nature04437. [DOI] [PubMed] [Google Scholar]
- 11.Oberhauser A.F., Hansma P.K., Fernandez J.M. Stepwise unfolding of titin under force-clamp atomic force microscopy. Proc. Natl. Acad. Sci. USA. 2001;98:468–472. doi: 10.1073/pnas.021321798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sorce B., Sabella S., Pompa P.P. Single-molecule mechanical unfolding of amyloidogenic β2-microglobulin: the force-spectroscopy approach. ChemPhysChem. 2009;10:1471–1477. doi: 10.1002/cphc.200900220. [DOI] [PubMed] [Google Scholar]
- 13.Evans E., Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys. J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Garg A. Escape-field distribution for escape from a metastable potential well subject to a steadily increasing bias field. Phys. Rev. B. 1995;51:15592–15595. doi: 10.1103/physrevb.51.15592. [DOI] [PubMed] [Google Scholar]
- 15.Imparato A., Sbrana F., Vassalli M. Reconstructing the free energy landscape of a polyprotein by single-molecule experiments. Europhys. Lett. 2008;82:58006. [Google Scholar]
- 16.Oberhauser A.F., Carrión-Vázquez M. Mechanical biochemistry of proteins one molecule at a time. J. Biol. Chem. 2008;283:6617–6621. doi: 10.1074/jbc.R700050200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Best R., Brockwell D.J., Clarke J. Force mode AFM as a tool for protein folding studies. Anal. Chim. Acta. 2003;479:87–105. [Google Scholar]
- 18.Brockwell D.J., Beddard G.S., Radford S.E. The effect of core destabilization on the mechanical resistance of I27. Biophys. J. 2002;83:458–472. doi: 10.1016/S0006-3495(02)75182-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Aioanei D., Samorì B., Brucale M. Maximum likelihood estimation of protein kinetic parameters under weak assumptions from unfolding force spectroscopy experiments. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:61916. doi: 10.1103/PhysRevE.80.061916. [DOI] [PubMed] [Google Scholar]
- 20.Benedetti F., Sekatskii S.K., Dietler G. Single-molecule force spectroscopy of multimodular proteins: a new method to extract kinetic unfolding parameters. J. Adv. Microsc. Res. 2011;6:1–6. [Google Scholar]
- 21.King W.T., Su M.H., Yang G.L. Monte Carlo simulation of mechanical unfolding of proteins based on a simple two-state model. Int. J. Biol. Macromol. 2010;46:159–166. doi: 10.1016/j.ijbiomac.2009.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dietz H., Berkemeier F., Rief M. Anisotropic deformation response of single protein molecules. Proc. Natl. Acad. Sci. USA. 2006;103:12724–12728. doi: 10.1073/pnas.0602995103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hummer G., Szabo A. Thermodynamics and kinetics of single-molecule force spectroscopy. In: Barkai E., Brown F.L.H., Orrit M., Yang H., editors. Theory and Evaluation of Single-Molecule Signals. World Scientific; Singapore: 2008. pp. 139–175. [Google Scholar]
- 24.Li H. Engineering proteins with tailored nanomechanical properties: a single molecule approach. Org. Biomol. Chem. 2007;5:3399–3406. doi: 10.1039/b710321m. [DOI] [PubMed] [Google Scholar]
- 25.Florin E., Rief M., Gaub H. Sensing specific molecular interactions with the atomic force microscope. Biosens. Bioelectron. 1995;10:895–901. [Google Scholar]
- 26.Sandal M., Benedetti F., Samorì B. Hooke: an open software platform for force spectroscopy. Bioinformatics. 2009;25:1428–1430. doi: 10.1093/bioinformatics/btp180. [DOI] [PubMed] [Google Scholar]
- 27.Schlierf M., Rief M. Single-molecule unfolding force distributions reveal a funnel-shaped energy landscape. Biophys. J. 2006;90:L33–L35. doi: 10.1529/biophysj.105.077982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rief M., Gautel M., Gaub H.E. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 1997;276:1109–1112. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- 29.Rief M., Fernandez J.M., Gaub H.E. Elastically coupled two-level systems as a model for biopolymer extensibility. Phys. Rev. Lett. 1998;81:4764–4767. [Google Scholar]
- 30.Zinober R.C., Brockwell D.J., Smith D.A. Mechanically unfolding proteins: the effect of unfolding history and the supramolecular scaffold. Protein Sci. 2002;11:2759–2765. doi: 10.1110/ps.0224602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Berkovich R., Garcia-Manyes S., Fernandez J.M. Collapse dynamics of single proteins extended by force. Biophys. J. 2010;98:2692–2701. doi: 10.1016/j.bpj.2010.02.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gumbel E. Dover; Mineola, NY: 2004. Statistics of Extremes. [Google Scholar]
- 33.Press W., Teukolsky S., Flannery B. Cambridge University Press; Cambridge, United Kingdom: 2007. Numerical Recipes, 3rd ed.: The Art of Scientific Computing. [Google Scholar]
- 34.Silverman B.W. Chapman & Hall/CRC; Boca Raton, FL: 1986. Density Estimation for Statistics and Data Analysis. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


