Abstract
Before they enter preschool, children vary greatly in their numerical and mathematical knowledge, and this knowledge predicts their achievement throughout elementary school (e.g., Duncan et al., 2007; Ginsburg & Russell, 1981). Therefore, it is critical that we look to the home environment for parental inputs that may lead to these early variations. Recent work has shown that the amount of number talk that parents engage in with their children is robustly related to a critical aspect of mathematical development - cardinal-number knowledge (e.g., knowing that the word “three” refers to sets of three entities; Levine, Suriyakham, Rowe, Huttenlocher, & Gunderson, 2010). The present study characterizes the different types of number talk that parents produce and investigates which types are most predictive of children’s later cardinal-number knowledge. We find that parents’ number talk involving counting or labeling sets of present, visible objects is related to children’s later cardinal-number knowledge, whereas other types of parent number talk are not. In addition, number talk that refers to large sets of present objects (i.e., sets of size 4 to 10 that fall outside children’s ability to track individual objects) is more robustly predictive of children’s later cardinal-number knowledge than talk about smaller sets. The relation between parents’ number talk about large sets of present objects and children’s cardinal-number knowledge remains significant even when controlling for factors such as parents’ socioeconomic status and other measures of parents’ number and non-number talk.
Introduction
Children display substantial variation in their mathematical knowledge as early as age four (e.g., Dowker, 2008; Ginsburg & Russell, 1981; Klibanoff, Levine, Huttenlocher, Vasilyeva, & Hedges, 2006; Starkey, Klein, & Wakeley, 2004; West, Denton, & Germino-Hausken, 2000). These early differences suggest that the numerically-relevant input parents provide may be an important factor in young children’s numerical development. Indeed, the amount of parent number talk predicts preschool children’s knowledge of the cardinal meanings of the number words, a critical aspect of mathematical development, even controlling for parents’ socio-economic status (SES) and other aspects of parents’ and children’s number and non-number talk (Levine et al., 2010). The present study seeks to elaborate on this finding by determining whether children’s cardinal-number knowledge is influenced not only by the amount of parent number talk, but also by the quality of that talk. In particular, we will address two major questions about parent number talk during naturalistic parent-child interactions. First, does number talk that references present objects predict children’s later number knowledge to a greater extent than number talk that does not? Second, what are the roles of number talk about small sets, in the subitizing range (1 to 3 items), and larger sets (4 to 10 items) in predicting children’s number knowledge? By addressing these questions, we hope to illuminate the nature of the parent-child number interactions that are most helpful to children as they learn the cardinal meanings of the number words.
Learning the exact cardinal meanings of the number words is a difficult and protracted process for preschool-aged children. Knowing that a number word refers to sets of a specific number of items (e.g., that “two” refers to sets of two items and that “three” refers to sets of three items) is far from a trivial problem for children at this age. Children who can reliably count to 10 are often unable to correctly produce, label, or point to a specific set size, even for small numbers such as 1, 2, and 3 (e.g., Wynn, 1990, 1992b). Children learn the cardinal meanings of the number words slowly and in order, taking about a year from the time they can successfully produce a set of size “one” to the time they can produce sets of size “four” or more (Wynn, 1992b). Once they can produce set sizes greater than “four”, children have discovered the “cardinal principle”, that the last number reached when counting a set of objects represents the numerosity of the whole set (Gelman & Gallistel, 1978). Acquiring the cardinal principle is a major milestone in children’s mathematical development, after which children can correct their errors when producing sets of a given numerosity, match highly dissimilar sets based on their numerosities, and understand that adding one to a set increases its numerosity by exactly one (Le Corre & Carey, 2007; Le Corre, Van de Walle, Brannon, & Carey, 2006; Mix, 2008; Wynn, 1990, 1992b). Although all typically-developing children eventually master the cardinal principle, the age at which they do so varies widely. Some children master the cardinal principle before age 3, enabling them to correctly produce and label sets of any size within their count list; by age 4, others have only mapped the meaning of “one” to a set of one object, and are unable to reliably produce sets of 2 or higher when asked to do so (Sarnecka & Lee, 2009). In other words, by the time children are 4 years old, there is already a 1- to 2-year gap in math knowledge between children who are more or less mathematically advanced.
Such early individual differences in children’s mathematical knowledge would be of little concern if they were easily overcome by schooling. However, this does not appear to be the case based on a report that mathematical knowledge at the start of kindergarten predicts later math achievement through at least fifth grade (Duncan et al., 2007). The predictive power of early math knowledge for later school achievement underlines the importance of understanding the sources of variation in children’s development of cardinal-number knowledge. Because this variation arises before entry into formal schooling, we examine the early home environment for mathematically-relevant interactions between parents and children that may influence children’s development. In particular, we seek to elaborate on the finding that the amount of parent number talk predicts children’s cardinal-number knowledge (Levine, et al., 2010) by characterizing the types of number talk in which parents engage with their children. In doing so, our goal is to determine whether certain types of parent number talk are more predictive of children’s cardinal-number knowledge than others. In Levine et al.’s (2010) study, each number word was assumed to have equal predictive power regardless of the context. Thus, the utterances “there are five bears” and “I’ll be there in two seconds” were given equal weight in predicting children’s number knowledge. Yet it is clear that these utterances differ in many ways and may not be equally informative to a child learning the cardinal meanings of the number words.
One dimension on which number talk can vary is whether the talk is related to counting (e.g., “one, two, three”), labeling cardinal values of sets (e.g., “the octopus has eight legs”), or other uses (e.g., “high five”). The majority of parent number talk falls into counting or labeling cardinal values of sets (Levine et al., 2010), and there are strong theoretical reasons to believe that both of these types of talk are critical to numerical development, since knowledge of the cardinal principle requires understanding counting, cardinal values, and the relationship between them (Gelman & Gallistel, 1978). In fact, input in which counting and labeling set sizes are used together appears to facilitate children’s learning of the cardinal principle (Mix, Sandhofer, & Moore, 2009). Since we believe that both counting and labeling set sizes are important for numerical development, and because the frequencies of these two types of input are positively correlated in parents’ talk, we collapse between them in our main analyses. In investigating differences in the numerical input that parents provide, we focus on two other types of variation in parent number talk: 1) the physical context, i.e., whether or not the parent is counting or labeling a set that is present and visible to the child; and 2) the set size, i.e., whether the counted or labeled set is small (set sizes 1–3) or large (set sizes 4–10).
First, there are compelling reasons to believe that parents’ number talk that refers to present objects will be more informative than number talk that does not. Labeling the cardinal values of sets of present objects (e.g., “you have two dolls”) may facilitate mapping number words onto relevant set sizes by allowing the child to see concrete exemplars paired with the appropriate number word, whereas labeling the cardinal values of non-present objects (e.g., “we saw your two friends yesterday”) may be more difficult for children to map onto the relevant set size. The presence of concrete exemplars may be especially important given the particular difficulty of learning number words. That is, since number words refer to properties of a set rather than to properties of a single object, children may have more difficulty extracting the commonalities between different exemplars of “three” (e.g., three crackers, three cars) than between different exemplars of “car”, because the sets of “three” are more difficult to align and compare (Kotovsky & Gentner, 1996; Mix, Sandhofer, & Baroody, 2005). Further, children’s nonverbal numerical skills, such as matching sets based on set size, develop earlier for sets of visible objects than for stimuli that are present but ephemeral, such as sounds (e.g., Mix, Huttenlocher & Levine, 1996). The developmental advantage for numerical reasoning with present objects in nonverbal tasks suggests that children may be quicker to map number words to set sizes with present-object sets than with other types of sets such as sounds, actions, or non-present objects.
Counting present objects should also facilitate children’s acquisition of the cardinal principle, since knowledge of the cardinal principle entails an understanding of the relationship between counting and the cardinal values of sets (Carey, 2009; Gelman & Gallistel, 1978). While rote counting (e.g., counting while playing hide-and-go-seek) may facilitate learning the correct sequence of the count list, counting present objects provides information not only about the verbal sequence of the count list, but also about the counting principles such as one-to-one correspondence (that each item in a set should be given one and only one tag; Gelman & Gallistel, 1978) as well as visual information regarding the size of the set being enumerated. Thus, there are strong theoretical reasons to believe that both counting and labeling the cardinal values of present-object sets are critical types of numerical input, and should be more informative than either counting or labeling set sizes without present-object referents.
The second major aspect of parents’ number talk that we investigate is the size of the sets that parents reference. Set size may be a critical variable in the development of cardinal-number knowledge because small and large sets are thought to be represented by two qualitatively different nonverbal numerical systems, which we will refer to as the small-exact-number system and the large-approximate-number system (e.g., Carey, 2009; Feigenson, Dehaene & Spelke, 2004; Spelke & Kinzler, 2007; Xu, 2003). Using the small-exact-number system, sets of 3 items or fewer (e.g., objects, events, sounds) can be discriminated by human infants (e.g., Feigenson & Carey, 2003; Wynn, 1992a, 1996). This discrimination ability is hypothesized to rely on a system that continuously tracks individual items, but has a limited capacity of about 3 items (e.g., Feigenson, Dehaene & Spelke, 2004). Using the large-approximate-number system, sets of 4 or more items can be represented approximately and discriminated up to a given ratio limit, which decreases with age (e.g., Lipton & Spelke, 2003, 2004; Xu & Arriaga, 2007; Xu & Spelke, 2000; Xu, Spelke & Goddard, 2005).1
Given that children have two distinct systems for nonverbally representing large and small sets, how does their learning of exact cardinal number word meanings relate to each system? According to the bootstrapping theory, the small-exact-number system is the critical component (Carey, 2009). This theory holds that children first learn the mappings between the number words 1, 2, and 3 and their nonverbal representations in the small-exact-number system (Carey, 2009). They also learn the verbal count list, and eventually use their knowledge of the count list and of the cardinal meanings of the first 3 number words to form the crucial inductive inference, that for every increase of one word in the count list, the set size referred to by that word increases by exactly one. One possible implication of this theory is that parents’ labeling of small sets (size 1–3) should be most predictive of children’s later number knowledge, because this type of input should accelerate children’s learning of the cardinal meanings of the first 3 number words and therefore accelerate their induction of the cardinal principle as well.
Although exposure to small-number talk is almost certainly vital for learning the meanings of the words 1, 2, and 3, we ask whether exposure to number talk about large sets (4–10) also contributes to children’s development of cardinal-number knowledge. We propose that children do not infer the cardinal principle based solely on their knowledge of the count list and the cardinal meanings of the words 1, 2, and 3. Rather, children benefit from exposure to number talk about sets of size 4 or greater when learning the cardinal principle. The rationale is as follows. Children can learn the cardinal meanings of the words 1, 2, and 3 by directly mapping the number words onto their corresponding nonverbal representations in the small-exact-number system. Because the small number words map directly onto the child’s pre-existing nonverbal representations, the child can learn the cardinal meanings of the small number words individually, without understanding the ordinal relations between these numbers or their connection to the count list (e.g., Le Corre & Carey, 2007; Sarnecka & Carey, 2008; Sarnecka & Lee, 2009). As a result, children who are exposed primarily to number talk about sets of size 1, 2, and 3 may succeed in learning these direct mappings, but have little or no need to go beyond those mappings to infer the cardinal principle.
Although children could conceivably map large number words onto their pre-existing large-approximate-number representations before learning the cardinal principle, empirical evidence shows that that children do not do so until about 6 months after they have learned the cardinal principle (Condry & Spelke, 2008; Le Corre & Carey, 2007). Thus, prior to learning the cardinal principle, children who are exposed to large number words cannot map these number words onto either their small-exact-number system or their large-approximate-number system.
This situation may be especially informative for children’s learning of the cardinal principle for several reasons. First, in a pragmatic sense, exposure to large-number talk is motivational; if children were never exposed to large-number talk, there would be no system for them to figure out and no reason for them to use their inferential capacities to discover the cardinal principle. Hearing large-number talk, which they are not able to map directly onto a nonverbal representation as they did with the numbers 1, 2, and 3, may create the motivation to figure out what the larger number words mean and how they map onto set sizes. Second, large-number talk in which parents count and label the same set (e.g., “there are four sticks, one, two, three, four”) provides an opportunity for children to notice that the cardinal label applied to the set matches the last word in the count list applied to the same set. In contrast, while counting and labeling a small set of objects (e.g., “there are three balls, one, two, three”) could provide the same information about the cardinal principle, in this case the count list is redundant because the child can know that the word “three” refers to a set of 3 items without counting. Children may be particularly motivated to learn when given information that conflicts with their pre-existing representations, a phenomenon known as representational discrepancy (Levine, Kwon, Huttenlocher, Ratliff, & Dietz, 2010; Opfer & Siegler, 2007). When large sets are the focus of parents’ number talk, children are in this situation. In contrast, when small sets are involved, there is no discrepancy with the child’s current state of knowledge, and so the child may not attend to the relation between counting and cardinal values in these cases. Third, counting large sets provides more sequential exemplars of the counting principles (e.g., stable-order and one-toone correspondence) than counting small sets, which may improve children’s learning of these principles.
For all of these reasons, our theory suggests that while parent number talk about small sets should help children learn to correctly label sets of size 1, 2, and 3, it may not be sufficient for them to learn the cardinal principle. Parent number talk about large sets may be a critical source of input for learning the cardinal principle. This large-number talk may enhance children’s performance on problems that require knowledge of the numbers 4 and above as well as on problems that require knowledge of the low numbers, since children who have learned the cardinal principle perform better than children who have not even on tasks involving small numbers (e.g., Negen & Sarnecka, 2009).
It is important to note that small-number talk is quite frequent in parent-child interactions, while large-number talk is relatively rare (Levine, et al., 2010; Sarnecka, Kamenskaya, Yamana, Ogura, & Yudovina, 2007). In addition, large-number counting (e.g., “one, two, three, four”) necessarily includes small-number counting. Therefore, in examining the impact of large-number talk on children’s number knowledge, we are effectively investigating differences between children who only (or primarily) hear small-number talk and children who hear both small-number and large-number talk in the home.
We analyze parents’ number talk at child ages 14–30 months, which is prior to the age at which children typically begin to learn the cardinal meanings of the number words (e.g., Sarnecka & Lee, 2009). We deliberately analyze parental input at these early ages to avoid, insofar as possible, the possibility that parents’ number talk is driven by children’s own interest in number words and activities. Given that our study is correlational, however, any relations that are found concerning parent input and child knowledge need to be tested in an experimental study in order to conclude that the relations are causal in nature. Our outcome measure occurs at child age 46 months, when many but not all children have discovered the cardinal principle (e.g., Sarnecka & Lee, 2009). Since we expect the variation in the outcome measure at this age to primarily reflect whether children have learned the cardinal principle or not, we predict that parents’ number talk about large sets will be more predictive of children’s cardinal-number knowledge than parents’ number talk about small sets, for the reasons discussed above.
Method
Participants
Forty-four children participated in this study (24 males, 20 females). Children were drawn from a larger sample of 63 families in a longitudinal study of language development. The families were selected to be representative of the demographics of the Chicago area in terms of race/ethnicity and income levels. All children were being raised as monolingual English speakers. Families were included in the study if they completed the measure of child cardinal-value knowledge (Point-to-X task, described below) at child age 46 months, if they had data for all five sessions from child ages 14 to 30 months, and if they interacted with the same caregiver during those sessions. From the larger sample of 63 families, 2 were excluded because the child did not complete the outcome measure (Point-to-X) at 46 months, 7 were excluded because they were missing one or more sessions, and 10 were excluded because two caregivers were present during one or more sessions or the caregiver changed over the course of the study. The demographics of the remaining subset reflect those of the entire sample.
Procedure
Families were visited in the home every four months between child ages 14 and 58 months. Only data from the 14–30 month sessions were analyzed for this study. At each session, children and their caregivers were videotaped for 90 minutes engaging in their typical daily activities, and the experimenters did not mention our interest in numerical development. There were 5 sessions (child ages 14, 18, 22, 26, and 30 months) for a total of 7.5 hours of parent-child interaction. All speech was transcribed. The unit of transcription was the utterance, defined as any sequence of words preceded and followed by a pause, change in conversational turn, or change in intonational pattern. All dictionary words, as well as onomatopoeic sounds (e.g., woof-woof) and evaluative sounds (e.g., uh-oh), were counted as words. Transcription reliability was established by having a second coder transcribe 20% of the videotapes. Reliability was assessed at the utterance level and was achieved when coders agreed on 95% of transcription decisions.
Measures
Measures of parent number talk
Transcripts were searched by computer for uses of the number words “one” through “ten.” Because the word “one” can be used both numerically and non-numerically, all instances of the word “one” were manually coded as either numerical or non-numerical. A second researcher coded 20% of the sessions and achieved 99% reliability. Numerical uses of “one” included counting (e.g., “one, two, three”), cardinal values (e.g., “one truck”), references to Arabic numerals (e.g., “That’s the number one”), and references to time or age (e.g., “one minute”, “when you turned one”). We applied relatively strict criteria and coded all other uses of “one” as non-numerical. These uses included deictics (e.g., “this one”), anaphoric uses of “one” (e.g., “that’s the pretty one”), and some idioms (e.g., “one of these days”). Overall parent number talk included all numerical uses of “one” plus all uses of the words “two” through “ten.”
Parent number talk was further divided into instances, which were defined such that each counting sequence (string of sequential number words) was coded as one instance of number talk. For example, if a parent counted “one, two, three, four” it would be coded as one instance. For all other types of number talk (e.g., labeling cardinal values of sets, labeling Arabic numerals, etc.), each number word was coded as one instance. For example, if a parent said, “You have two red sticks and two blue sticks” it would be coded as two instances of number talk. Although previous research has analyzed parent number talk using number word tokens (Levine et al., 2010), we chose to use instances here due to the nature of our analyses. Because we plan to divide parents’ number talk into categories based on the size of the set being referenced (small=1–3, large=4–10), it was important to ensure that parents’ counting of larger sets would not be over-weighted. By using instances instead of tokens, a parent who counted “one, two” and later counted “one, two, three, four, five” would have 1 instance of small-number counting and 1 instance of large-number counting. If we had used tokens as the unit of analysis, this parent would have 2 tokens of small-number counting and 5 tokens of large-number counting, which would confound the size of the set and the amount of parent number input. By using instances, we eliminate this confounding.2
Number talk instances were further classified based on three cross-cutting variables: 1) whether parents were counting or labeling cardinal values of sets; 2) whether objects were present or not and 3) whether the set size enumerated was small (1–3) or large (4–10). The combinations of these three variables yielded 8 categories of parent number talk, which are listed with examples in Table 1. When determining whether objects were present, we considered “objects” to include both parts of objects (e.g., ears) and whole objects (e.g., dolls), and to include both physical objects and pictures of objects. Objects were considered “present” if they could be visually apprehended by the child, including objects that were simultaneously visible (e.g., a picture of two bees) and sequentially visible (e.g., blocks being placed in a bucket one at a time). Events such as jumps were not considered objects.
Table 1.
Examples of each type of parent number talk.
| Type of parent number talk | Example |
|---|---|
| Counting with present objects, small sets (1–3) | One, two bees. [pointing to pictures in a book] |
| Counting with present objects, large sets (4–10) | We got one, two, three, four, five, six, seven, eight more hats. [counting blocks with pictures of hats on them] |
| Counting without present objects, small sets (1–3) | One, two, three, whoo! [mother picks up child] |
| Counting without present objects, large sets (4–10) | One, two, three, four, five. [playing hide-and-go-seek] |
| Cardinal values with present objects, small sets (1–3) | Oh, you got two bugs. [child holding two stuffed animal bugs] |
| Cardinal values with present objects, large sets (4–10) | Four sticks. [child holding four drumsticks] |
| Cardinal values without present objects, small sets (1–3) | We never really get through one whole story. |
| Cardinal values without present objects, large sets (4–10) | Mom said four songs and we did four songs. |
| All other | High five! |
All other uses of number words were grouped together as “all other,” which primarily included references to Arabic numerals (e.g., “that’s a four”), time (e.g., “one second”), the child’s age (e.g., “you’ll love this when you’re four”), and conventional nominatives (e.g., “high five”). Twenty percent of the transcripts were coded for reliability of the categorization of number talk by two researchers who agreed on 82 percent of number instances. Disagreements were resolved by the more experienced coder.
Although the target length for all sessions was 90 minutes, the actual length varied due to parents’ schedules or experimenter error. Mean session length was 88.5 minutes (SD=4.9; range=44.4 to 101.3). Only 14 sessions (6%) were less than 85 minutes in length. Nevertheless, to account for variation in session length, parents’ number talk was pro-rated based on actual session length to reflect the amount of number talk that would be expected to occur if the session had been exactly 90 minutes long.
Measures of parent non-number talk
We included a measure of parents’ other (non-number) talk as a control for the overall amount of language the parent provided to the child. This measure included the number of total word tokens produced by the parent, excluding number word tokens, and was pro-rated to reflect a session length of 90 minutes.
Cardinal-value knowledge: Point-to-X task
The Point-to-X task (Wynn, 1992b), a measure of cardinal-value knowledge, was administered at child age 46 months. The task consisted of 16 items, administered in either a forward or backward fixed random order. For each item, children were shown a piece of paper, divided in half by a vertical line, with a set of squares on the left and right sides (the side of presentation was counter-balanced across subjects). Each set of squares was vertically arrayed and represented the cardinal values 1 through 6. Some items contained pairs of sets with adjacent numerosities (e.g., 3 vs. 4) and some contained pairs of sets with nonadjacent numerosities (e.g., 3 vs. 5). For each item, children were asked to “Point to X,” where X referred to one of the two cardinal values on the page. Children were not told to count the objects, but were allowed to count if they spontaneously did so. Each child’s score was the number of items correct out of 16.
Vocabulary comprehension: Peabody Picture Vocabulary Test
The Peabody Picture Vocabulary Test, a vocabulary comprehension task, was administered at child age 54 months (PPVT-III, Dunn & Dunn, 1997). Each item on this multiple-choice task requires children to point to one of four pictures that matches an orally-presented word. The PPVT-III is a widely-used, nationally-normed test, and is similar in presentation and response format to the Point-to-X task. The sample size for analyses involving the PPVT is 43, since one child did not complete the task.
Socioeconomic status
As a control variable, we created a measure of socioeconomic status (SES) based on family income and the primary caregiver’s (PCG’s) years of education. When parents reported that the father and mother were both PCGs, the maximum years of education attained by either parent was used. Mean family income was $61,818 (SD=$31,542, range=less than $15,000 to over $100,000) and mean education was 15.9 years, equivalent to a bachelor’s degree (SD=2.1 years, range=10 [less than high school] to 18 [Masters degree or higher]). Family income and PCG’s education were positively related (r(42)=0.48, p=.001) and were combined into one SES variable using Principle Components Analysis. This analysis found one component, our composite SES score, which accounted for 74 percent of the original variance and weighted education and income positively and equally. The composite SES score has a mean of 0 (SD=1). Families with high scores on the SES composite have a high annual income level and a PCG with a high level of education.
Results
Because the measures of amount of number talk and non-number talk were not normally distributed, they were transformed using the natural logarithm, ln(n+1), for all analyses involving correlations, regressions, and comparisons of means. This was done in order to ensure normally distributed, linear relations between measures.
Description of parents’ number talk
We first sought to characterize the amount and types of parent number talk observed in our sample. Means and standard deviations of each type of parent number talk, by session, are reported in Table 2. Number talk was relatively infrequent but increased over time, with parents producing an average of 9.12 instances of total number talk (SD=9.76) during the 14-month session and almost twice that number, 17.22 instances (SD=17.61), during the 30-month session. Cumulatively across all five sessions, parents produced an average of 65.76 instances of total number talk (SD=44.3), with a range from 4 to 168 instances. The most frequent type of number talk was cardinal values with present objects, small sets, with parents producing an average of 25.89 instances (SD=19.76) over the 5 sessions. Although the frequency of each type of parent number talk increased from the 14- to the 30-month session, this increase was only significant for 2 types of talk: cardinal values without present objects, small sets (t(43)=3.69, p=.001) and cardinal values without present objects, large sets (t(43)=2.27, p<.05).
Table 2.
Means and standard deviations of parent number talk instances, by child age and type of number talk (N=44).
| Child Age (Months) | ||||||
|---|---|---|---|---|---|---|
| 14 | 18 | 22 | 26 | 30 | Total | |
| Counting with present objects, small sets (1–3) | 0.58 (1.05) | 0.67 (1.29) | 0.71 (1.53) | 1.21 (3.38) | 1.18 (2.80) | 4.34 (5.75) |
| Counting with present objects, large sets (4–10) | 0.40 (1.11) | 0.35 (0.84) | 0.30 (1.14) | 0.93 (2.78) | 0.66 (1.45) | 2.64 (3.46) |
| Counting without present objects, small sets (1–3) | 0.45 (1.02) | 1.15 (2.59) | 1.23 (2.43) | 0.55 (1.46) | 0.46 (0.98) | 3.83 (5.28) |
| Counting without present objects, large sets (4–10) | 0.12 (0.40) | 0.28 (0.64) | 0.36 (0.95) | 0.30 (0.60) | 0.43 (0.93) | 1.49 (1.59) |
| Cardinal values with present objects, small sets (1–3) | 3.89 (3.49) | 5.37 (5.80) | 4.43 (5.31) | 5.80 (5.56) | 6.41 (7.40) | 25.89 (19.76) |
| Cardinal values with present objects, large sets (4–10) | 0.66 (1.73) | 0.92 (2.35) | 0.76 (2.45) | 0.68 (1.24) | 1.00 (2.47) | 4.04 (6.05) |
| Cardinal values without present objects, small sets (1–3) | 0.67 (1.13) | 1.01 (1.39) | 1.76 (2.00) | 1.25 (1.84) | 1.73 (2.03) | 6.42 (5.19) |
| Cardinal values without present objects, large sets (4–10) | 0.02 (0.16) | 0.02 (0.15) | 0.07 (0.34) | 0.18 (0.66) | 0.22 (0.53) | 0.51 (1.06) |
| All other | 2.33 (5.77) | 2.10 (3.67) | 2.19 (2.90) | 4.84 (10.27) | 5.13 (8.83) | 16.60 (18.14) |
|
| ||||||
| Total | 9.12 (9.76) | 11.87 (10.43) | 11.81 (11.36) | 15.75 (19.82) | 17.22 (17.61) | 65.76 (44.31) |
Since parent number talk was a relatively rare occurrence, it was necessary to aggregate the data in order to create more stable measures of parent number talk that could be used to predict children’s later cardinal-number knowledge. We did so by combining the data for all 5 sessions and by collapsing our 9 fine-grained categories into 5 larger categories. As described in the Introduction, we combined parents’ use of counting and labeling cardinal values because these uses were positively correlated (r(42)=.59, p<.001) and because both are important for children’s learning of the cardinal principle (Gelman & Gallistel, 1978)3. For simplicity, we refer to the combination of counting and cardinal values simply as “number talk”. This aggregation resulted in 5 larger categories of cumulative parent number talk: (1) number talk with present objects, small sets (1–3), (2) number talk without present objects, small sets (1–3), (3) number talk with present objects, large sets (4–10), (4) number talk without present objects, large sets (4–10), and (5) all other (see Table 3 for descriptive statistics). Number talk about present objects with small sets (1–3) was the most common, with parents producing an average of 30.2 instances (SD=22.6) across the five sessions. Consistent with the large range of variation found in total number talk, the range for talk about present objects with small sets was very broad, from 1 to 93 instances. Similarly large variation was found in parents’ use of each of the other four categories of number talk (see Table 3). While all parents produced at least one instance of small-number present-object talk, 1 parent (2 percent) never produced small-number non-present-object talk, 13 parents (30 percent) never produced large-number present-object talk, and 11 parents (25 percent) never produced large-number non-present-object talk. In addition, positive correlations were found between the amount of parent number talk in each of the 5 categories (Table 4).
Table 3.
Descriptive statistics showing, for each aggregated type of number talk (including both counting and labeling cardinal values of sets), parents’ instances of number talk, instances of number talk per 1,000 utterances, and the percent of number talk instances of that type across the 5 sessions (N = 44).
| Raw number talk instances | Number talk instances per 1,000 parent utterances | Percent of number talk instances | ||
|---|---|---|---|---|
| Mean (SD) | Median (Range) | Mean (SD) | Mean (SD) | |
| Number talk with present objects, small sets (1–3) | 30.23 (22.59) | 25 (1–93) | 5.56 (2.78) | 44.5 (15.1) |
| Number talk without present objects, small sets (1–3) | 10.25 (7.96) | 8 (0–32) | 2.03 (1.37) | 16.5 (9.3) |
| Number talk with present objects, large sets (4–10) | 6.67 (7.19) | 5 (0–28) | 1.23 (1.21) | 8.3 (7.2) |
| Number talk without present objects, large sets (4–10) | 2.01 (1.90) | 2 (0–7) | 0.46 (0.49) | 3.9 (4.0) |
| All other | 16.60 (18.14) | 12 (0–79) | 3.63 (3.77) | 26.8 (19.6) |
|
| ||||
| Total | 65.76 (44.31) | 57 (4–168) | 12.92 (6.93) | |
Table 4.
Correlations between instances of parent number talk by type (N=44).
| 1. | 2. | 3. | 4. | |
|---|---|---|---|---|
| 1. Number talk with present objects, small sets (1–3)a | - | |||
| 2. Number talk without present objects, small sets (1–3)a | .74*** | - | ||
| 3. Number talk with present objects, large sets (4–10)a | .69*** | .51*** | - | |
| 4. Number talk without present objects, large sets (4–10)a | .26~ | .24 | .30~ | - |
| 5. All othera | .34* | .22 | .43** | .22 |
p<.10;
p<.05;
p<.01;
p<.001
The natural logs of parent number talk instances were used in these analyses to correct for non-normality in the measures.
Parents’ SES was significantly correlated with number talk about small sets with present objects (r(42)=.42, p<.01) and small sets without present objects (r(42)=.40, p<.01). Although parents’ SES was not significantly correlated with talk about large sets with present objects, the relation was in the expected direction (r(42)=.23, p=.13). There was no relation between parents’ SES and talk about large sets without present objects (r(42)=.06, p=.68), or all other number talk (r(42)= −.18, p=.23). We focus our further analyses on the first 4 categories that are relevant to our hypotheses, which include all number talk about counting and labeling set sizes, the two broad categories that account for the large majority (73 percent) of parents’ total number talk (SD=19.6 percent).
Performance on the Point-to-X task
On our 16-item measure of cardinal-value knowledge, the Point-to-X task, children averaged 12.55 items correct (SD=2.96; 78.4 percent). Thirty-one of the 44 children (70 percent) scored significantly above chance on the task (score of 11 or more, p<.05). On the 4 items where both target and distractor were sets of size 4 or higher, children averaged 2.55 items correct (SD=1.02; 63.8 percent). On the 12 items where at least one set size was 3 or less, children averaged 10.00 items correct (SD=2.42; 83.3 percent). Children’s lower performance on items where both target and distractor were sets of size 4 or higher is consistent with our hypothesis that much of the variation in performance at this age is related to children’s knowledge of the cardinal principle, which is required for successful performance on these high-number items.
For the 32 children for whom video records of the Point-to-X task were available, we recorded whether children engaged in overt verbal counting. Two researchers independently coded 20% of the subjects and achieved reliability of 98%. Eleven of the 32 children (34 percent) engaged in overt verbal counting on at least one item. However, three of these children used immature counting strategies such as counting both sets (e.g., counting to 5 on a 2 versus 3 item) or counting incorrectly (e.g., counting 3 items as “four, five, six”). The 8 remaining children who engaged in mature overt verbal counting scored significantly higher on the 4 items where both numbers were 4 or greater (M=3.1, SD=1.4) than the immature counters and non-counters (M=2.3, SD=0.9) (t(30)=2.03, p=.05). In contrast, the difference between mature counters (M=10.4, SD=2.8) and others (M=9.5, SD=2.5) was not significant on the 12 items where at least one number was 3 or less (t(30)=0.84, p=.41). Consistent with previous research (e.g., Le Corre, et al., 2006), children who were able to correctly deploy a counting strategy were more successful, especially on the higher-numbered items.
Relations between types of parent number talk and children’s cardinal-value knowledge
We conducted a series of regression analyses to determine the relations between each of the 4 types of parent number talk of interest and the child’s later cardinal-number knowledge as assessed by the Point-to-X task4 (Table 5). First, we found that parents’ SES was a significant predictor of children’s number knowledge (β=.49, p<.001), accounting for 24 percent of the variance in children’s Point-to-X performance (Model 1). Next, we asked whether each of the 4 types of parent number talk were significant predictors of children’s later number knowledge, controlling for parents’ SES. We found that, controlling for parents’ SES, parent talk about small sets of present objects significantly predicted children’s later number knowledge (β=.33, p<.05), accounting for an additional 8.9 percent of the variance (Model 2). In contrast, parent number talk involving small sets (1–3) without present objects was not a significant predictor of children’s number knowledge after controlling for parents’ SES (β=.18, n.s.) (Model 3).
Table 5.
A series of regression models predicting child cardinal-value knowledge at 46 months based on 4 types of parent number talk, controlling for parent SES (N = 44).
| Child Cardinal-value knowledge (Point-to-X Score) – 46 months | |||||||
|---|---|---|---|---|---|---|---|
| Parameter estimate (standardized) | |||||||
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | Model 7 | |
| Parent SES | 0.49*** | .35* | .42** | .40** | .48*** | .38** | .38** |
| Number talk with present objects, small sets (1–3)a | .33* | .07 | |||||
| Number talk without present objects, small sets (1–3)a | .18 | ||||||
| Number talk with present objects, large sets (4–10)a | .41** | .37* | .38* | ||||
| Number talk without present objects, large sets (4–10)a | .16 | ||||||
| Parent other word tokens a | .06 | ||||||
|
| |||||||
| R-squared stat (%) | 24.4 | 33.3 | 27.1 | 40.1 | 26.8 | 40.3 | 40.3 |
|
| |||||||
| F-stat | 13.5*** | 10.3*** | 7.6** | 13.7*** | 7.5** | 9.0*** | 9.0*** |
| F-stat degrees of freedom | (1, 42) | (2, 41) | (2, 41) | (2, 41) | (2, 41) | (3, 40) | (3, 40) |
p<.10;
p<.05;
p<.01;
p<.001
The natural logs of these measures were used to correct for non-normality.
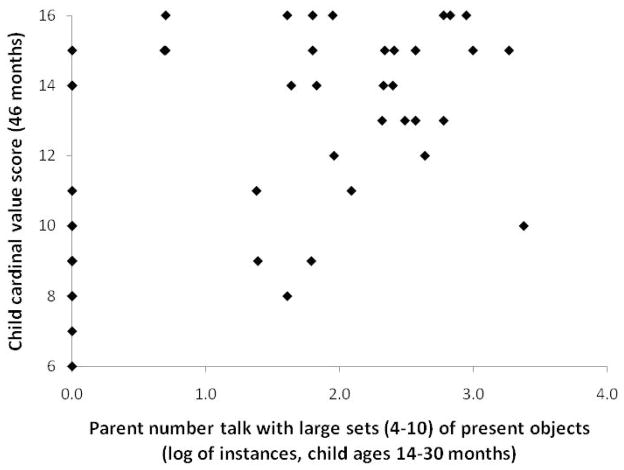
Moving to parent number talk about large sets (4–10), we again found that number talk involving present objects was a significant predictor of children’s cardinal-number knowledge (β=.41, p<.01), accounting for an additional 15.7 percent of the variance over and above parents’ SES (Model 4). However, number talk involving large sets without present objects again did not predict children’s cardinal-number knowledge after controlling for parents’ SES (β=.16, n.s.) (Model 5). Thus, for both number talk about small numbers and about large numbers, only talk that referenced present objects was significantly related to children’s later number knowledge.
Our next analysis sought to determine whether present-object number talk with large sets (4–10) or with small sets (1–3) was more predictive of children’s overall cardinal-number knowledge. To do so, we ran a regression model including three predictors: parents’ SES, parents’ present-object talk about small sets, and parents’ present-object talk about large sets (Model 6). We found that present-object talk about large sets remained a significant predictor of children’s cardinal-value knowledge (β=.37, p<.05) while present-object talk about small sets did not (β=.07, n.s.). In other words, controlling for SES and the amount of talk about small numbers of present objects, additional talk about large numbers of present objects predicted children’s cardinal-number knowledge.
Finally, in order to eliminate the possibility that the effect was driven by parents who provided more verbal input in general, we ran a model controlling for parents’ overall non-number talk (Model 7). We found that controlling for SES and parents’ overall amount of non-number talk, parents’ large-number present-object talk remained significant (β=.38, p<.01). Thus, parent number talk involving large sets of present objects appears to be an important and robust predictor of children’s later cardinal-number knowledge. This is especially striking because it is a relatively small portion of parents’ total number talk, representing only 8.3 percent of number talk instances (SD=7.2 percent). Nevertheless, this small subset of number talk accounts for an additional 15.7 percent of the variance, over and above the effect of SES, in children’s cardinal-value knowledge at 46 months (Model 4).
Specific relations between parent number talk and high- vs. low-number Point-to-X items
We hypothesized that small-number talk may help children learn numbers in the subitizable range, whereas large-number talk should be especially helpful for children’s learning of the cardinal principle. Since our Point-to-X task included a range of set sizes, we asked whether parents’ large- and small-number talk predicted children’s performance on specific items of the Point-to-X task in a way that was consistent with these hypotheses. We expected that small-number talk would predict performance on items where at least one set was size 3 or less (12 low-number items: 2 trials each of 1 vs. 2, 2 vs. 3, 2 vs. 4, 3 vs. 4, 3 vs. 5, and 3 vs. 6), but would not predict performance on items where both sets were greater than 3 (4 high-number items: 2 trials each of 4 vs. 5 and 5 vs. 6). We expected that large-number talk would predict performance on the high-number items5 as well as the low-number items, as discussed in the Introduction.
We conducted separate regression analyses with the outcome measure being either the 12 low-number Point-to-X items or the 4 high-number Point-to-X items. We also restricted our analyses to present-object talk since this type of number talk was found to be most informative to children in our previous models. As predicted, controlling for parents’ SES, parents’ small-number present-object talk significantly predicted children’s performance on the low-number items on the Point-to-X task (β=.36, p<.05) but did not significantly predict performance on the high-number items (β=.11, p=.50)6. This is consistent with the hypothesis that parents’ talk about sets of size 1, 2, and 3 can help children learn these particular cardinal values, but may not be sufficient for them to learn the cardinal principle.
Controlling for parents’ SES, parents’ large-number present-object talk predicted children’s performance on the high-number items (β=.27, p=.07) as well as the low-number items on the point-to-X task (β=.38, p<.01). Again, this is consistent with the hypothesis that parents’ use of large-number talk may be particularly helpful to children’s learning of the cardinal principle, which in turn strengthens their knowledge of the low numbers.
Relations between types of parent number talk and child vocabulary knowledge
We also were interested in investigating the specificity of these effects to the domain of numbers. In other words, is parent large-number present-object talk related specifically to children’s number knowledge, or is it related to their language development more generally? To test this possibility, we asked whether parents’ use of each of the 4 types of number talk was related to children’s vocabulary knowledge at age 54 months. Consistent with previous research, children’s vocabulary knowledge was correlated with parents’ SES (r(41)=.58, p<.001) (e.g., Huttenlocher, Haight, Bryk, Seltzer & Lyons, 1991) and parents’ overall word tokens (excluding number words) (r(41)=.52, p<.001). Moreover, in a partial correlation controlling for parents’ SES and overall non-number talk, we found no significant correlations between children’s vocabulary knowledge and any of the 4 types of parent number talk (all p’s>.35).
Discussion
Parents varied a great deal in the amount and types of number talk they produced. Importantly, the amount of number talk parents devoted to counting or labeling sets of present objects, especially when those sets consisted of higher numbers of items (4–10), was specifically predictive of children’s later cardinal-number knowledge. This result is striking because although parents’ overall amount of number talk has been shown to predict children’s number knowledge (Levine et al., 2010), we find that a very small subset of this number talk (8.3 percent) explains more of the variation in children’s later number knowledge (15.7 percent over and above SES) than the totality of parent number talk (11.4 percent over and above SES) (Levine, et al., 2010). We also carefully considered alternative explanations, and found that the relation between large-number present-object talk and children’s number knowledge held even controlling for parents’ use of small-number present-object talk, parents’ SES and parents’ non-number talk. Thus, the relation was not driven by parents’ use of present-object number talk in general nor by parents’ overall amount of linguistic interaction with their children. In addition, parents’ number talk did not predict children’s vocabulary knowledge once parents’ SES and overall talkativeness was controlled, indicating that children whose parents talked more about large sets of present objects did not have more advanced verbal development in general. Rather, parents’ number talk with large sets of present objects predicted children’s later cardinal-number knowledge in what appears to be a domain-specific fashion.
Our results suggest that not all types of parent number talk are equally important in promoting the development of children’s number knowledge. First, we find that number talk in which parents either count or label perceptually present sets of objects is more related to children’s development of cardinal-number knowledge than number talk that does not. This is consistent with accounts of early word learning in which joint attention to visible objects can provide crucial information to children learning a new word (e.g., Baldwin, 2000; Tomasello & Todd, 1983). It is also consistent with findings that in nonverbal contexts children have more difficulty making numerical judgments for ephemeral sets, such as sounds or actions, than for sets of visible objects, at least for small sets (Mix, 1999; Mix, Huttenlocher & Levine, 1996). In addition, number talk that involves present objects allows parents to model the counting principles whereas rote counting does not (Gelman & Gallistel, 1978).
Second, we find that within number talk about present objects, talk about sets that fall outside the range governed by the small-exact-number system (i.e., sets of size 4 to 10) is the strongest predictor of children’s later cardinal-number knowledge. Parents’ large-number talk predicts children’s performance on tasks involving both small (1–3) and large (4–6) set sizes. These results are consistent with our hypothesis that large-number talk is important for children’s learning of the cardinal principle, since knowledge of the cardinal principle is required for success on tasks involving large numbers and is associated with improved performance on tasks involving small numbers as well (e.g., Negen & Sarnecka, 2009). While parents’ small-number talk predicts children’s performance on items involving small numbers (1–3), it does not predict performance on items involving larger numbers, suggesting that small-number talk alone is not sufficient for children to learn the cardinal principle. As discussed in the Introduction, number talk in which parents count or label large sets of present objects may contribute to learning the cardinal principle in multiple ways, such as creating motivation to learn, providing examples of the correspondence between counting and numerical labeling, and providing examples of the counting principles.
These results suggest that children whose input includes a lot of small-number talk but not very much large-number talk may learn the small numbers quickly, but then become stalled when faced with the problem of learning the cardinal principle; as a result, children who receive large-number input in addition to small-number input may surpass them. These predictions can be tested through experimental training studies designed to mimic different patterns of parental input. While we controlled for a number of variables in order to rule out alternative explanations of the relation between parent number talk and child cardinal-number knowledge, we cannot fully eliminate the possibility that another factor, such as children’s own interest in numerical interactions, explains the relations that we have observed. Thus, controlled experimental studies are critical to concluding that number talk about large sets of present objects is causally related to children’s cardinal-number knowledge.
The results presented here also have important policy implications, showing that parents’ engagement in numerically-relevant behaviors in the home seems to have an impact on children’s early mathematical development. However, parents may not realize how important their behaviors are for their children’s mathematical development. For example, the vast majority of parents of preschool- and kindergarten-aged children believe that school is primarily responsible for children’s mathematics skill (Evans, Fox, Cremaso, & McKinnon, 2004). Further, nearly all parents overestimate their child’s numerical knowledge and fail to realize that their child, who typically can count to 10, does not understand important numerical concepts such as the cardinal principle (Fluck, Linnell, and Holgate, 2005). Finally, parents are often unsure about how to promote their child’s numerical development. Almost three-quarters of parents of preschoolers express uncertainty about early mathematics teaching and learning, saying things like “I don’t really know what level she should be at…” (p. 252, Cannon & Ginsburg, 2008).
Together, these findings suggest that there is significant room for improvement in both the quantity and quality of parents’ numerical interactions with their children. Yet unlike literacy, for which there has been a strong push for parents to read to their preschool children, there has not been such a concerted effort to encourage parents to engage in numerical activities with their preschool children or to inform them about the kinds of interactions that support children’s mathematical development (National Research Council, 2009). If experimental studies corroborate our findings, encouraging parents to engage in counting and labeling not only very small sets of objects but also somewhat larger sets of objects may help children with the difficult task of figuring out the relationship between counting and the cardinal meanings of the number words. In summary, the current study provides an initial step in identifying the kinds of early number talk that hold promise for improving children’s mathematical understanding. Follow-up studies are important to test the hypotheses raised about the optimal ways to teach early numeracy skills, which in turn will allow policy-makers to provide precise, evidence-based recommendations to parents and early childhood educators about children’s early mathematics learning.
Figure 1.
Scatter plot displaying the relation between parent number talk with present objects and large sets (4–10) (log of instances) at child ages 14–30 months and child cardinal value score (Point-to-X task) at 46 months (N = 44).
Acknowledgments
This research was supported by National Institute of Child Health and Human Development Grant P01HD40605 and National Science Foundation Science of Learning Center Grant SBE 0541957, the Spatial Intelligence and Learning Center (SILC), to Susan Levine, and by National Center for Education Research Grant R305C050076 to Elizabeth Gunderson. We thank Kristi Schonwald, Jodi Khan, and Jason Voigt for administrative and technical support, and Laura Chang, Elaine Croft, Hannah Degner, Kristen Duboc, Jennifer Griffin, Elizabeth Hickey, Lauren King, Max Masich, Erica Mellum, Jana Oberholtzer, Lilia Rissman, Rebecca Seibel, Yini Shi, Calla Trofatter, Kevin Uttich, Julie Wallman, and Kristin Walters for help in data collection, transcription, and coding. We also are grateful to the participating children and families.
Footnotes
Some research suggests that older children and adults may be able to represent sets of size 4 using the small-exact-number system (e.g., Cowan, 2001; Scholl, 2001). If we instead define small-number talk as size 1–4 and large-number talk as size 5–10, the significance levels of the results reported below remain at least at p<.06.
Nonetheless, the pattern of results remains the same if tokens are used instead.
Predicting children’s cardinal number knowledge from instances of counting alone or from instances of cardinal values alone produced the same pattern of results. All results that were significant at the p<.05 level for the aggregate measure of counting plus cardinal values were also significant at least at the p<.07 level when conducted separately for instances of number talk involving counting and for instances of number talk involving labeling the cardinal values of sets.
All regression models were checked for violations of model assumptions, including linearity, normality, homoscedasticity, independence of errors, and collinearity. No violations were found. Since some predictors were significantly intercorrelated as described above, we used the variance inflation factor (VIF) to identify possible instances of collinearity. All VIF’s were less than 2.3, well below suggested cutoff levels of 5–10 (Stine, 1995).
The strictest test of this hypothesis would use only the items where both numbers are higher than 4, since children can learn the cardinal meaning of “four” before learning the cardinal principle (e.g., Sarnecka & Lee, 2009). However, our task included only 2 such items (5 vs. 6 with targets 5 and 6) and chance level was 50%, yielding too much noise in the data to estimate the effects of parent input on only these two items. In addition, children who understand “4” but not the cardinal principle are relatively rare, and often perform more similarly to children who know the cardinal principle than to those who do not (e.g., Sarnecka & Carey, 2008).
The results reported here are based on linear regression models. Since the item-level data were categorical, we also conducted hierarchical logistic regression models, with items nested within subjects, and the results were the same.
References
- Baldwin DA. Interpersonal understanding fuels knowledge acquisition. Current Directions in Psychological Science. 2000:40–45. [Google Scholar]
- Blevins-Knabe B, Musun-Miller L. Number use at home by children and their parents and its relationship to early mathematical performance. Early Development and Parenting. 1996:35–45. [Google Scholar]
- Cannon J, Ginsburg HP. “Doing the math”: Maternal beliefs about early mathematics versus language learning. Early Education and Development. 2008;19(2):238–260. [Google Scholar]
- Carey S. The Origin of Concepts. Oxford: Oxford University Press; 2009. [Google Scholar]
- Condry KF, Spelke ES. The development of language and abstract concepts: The case of natural number. Journal of Experimental Psychology: General. 2008;137(1):22–38. doi: 10.1037/0096-3445.137.1.22. [DOI] [PubMed] [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24(01):87–114. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Dowker A. Individual differences in numerical abilities in preschoolers. Developmental Science. 2008;11(5):650–654. doi: 10.1111/j.1467-7687.2008.00713.x. [DOI] [PubMed] [Google Scholar]
- Duncan GJ, Claessens A, Huston AC, Pagani LS, Engel M, Sexton H, et al. School readiness and later achievement. Developmental Psychology. 2007;43(6):1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Dunn LM, Dunn LM. Peabody Picture Vocabulary Test. 3. Circle Pines, MN: American Guidance Service; 1997. [Google Scholar]
- Evans MA, Fox M, Cremaso L, McKinnon L. Beginning reading: The views of parents and teachers of young children. Journal of Educational Psychology. 2004;96(1):130–141. [Google Scholar]
- Feigenson L, Carey S. Tracking individuals via object-files: evidence from infants’ manual search. Developmental Science. 2003;6:568–584. [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Fluck M, Linnell M, Holgate M. Does counting count for 3- to 4-year-olds? Parental assumptions about preschool children’s understanding of counting and cardinality. Social Development. 2005;14(3):496–513. [Google Scholar]
- Gelman R, Gallistel CR. The child’s understanding of number. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Ginsburg HP, Russell RL. Social class and racial influences on early mathematical thinking. Monographs of the Society for Research in Child Development. 1981;46:1–72. [Google Scholar]
- Goldin-Meadow S, Nusbaum H, Kelly SD, Wagner S. Explaining math: Gesturing lightens the load. Psychological Science. 2001;12:516–522. doi: 10.1111/1467-9280.00395. [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Haight W, Bryk A, Seltzer M, Lyons T. Early vocabulary growth: Relation to language input and gender. Developmental Psychology. 1991;27(2):236–248. [Google Scholar]
- Iverson JM, Goldin-Meadow S. Gesture paves the way for language development. Psychological Science. 2005:367–371. doi: 10.1111/j.0956-7976.2005.01542.x. [DOI] [PubMed] [Google Scholar]
- Klibanoff RS, Levine SC, Huttenlocher J, Vasilyeva M, Hedges LV. Preschool children’s mathematical knowledge: The effect of teacher “math talk”. Developmental Psychology. 2006:59–69. doi: 10.1037/0012-1649.42.1.59. [DOI] [PubMed] [Google Scholar]
- Kotovsky L, Gentner D. Comparison and categorization in the development of relational similarity. Child Development. 1996;67(6):2797–2822. [Google Scholar]
- Le Corre M, Carey S. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition. 2007;105:395–438. doi: 10.1016/j.cognition.2006.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Corre M, Van de Walle G, Brannon EM, Carey S. Re-visiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology. 2006:130–169. doi: 10.1016/j.cogpsych.2005.07.002. [DOI] [PubMed] [Google Scholar]
- Levine SC, Gunderson EA, Huttenlocher J. Mathematical development during the preschool years in context: Home and school input variations. In: Stein NL, Raudenbush S, editors. Developmental Science Goes to School: Implications for Education and Public Policy Research. New York: Taylor and Francis; (in press) [Google Scholar]
- Levine SC, Kwon M-K, Huttenlocher J, Ratliff KR, Dietz K. Children’s understanding of ruler measurement and units of measure: A training study. Paper presented at the Annual Meeting of the Cognitive Science Society.2009. [Google Scholar]
- Levine SC, Suriyakham LW, Rowe ML, Huttenlocher J, Gunderson EA. What counts in the development of young children’s number knowledge? Developmental Psychology. 2010;46(5):1309–1319. doi: 10.1037/a0019671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense: Large number discrimination in human infants. Psychological Science. 2003;14:396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Discrimination of large and small numerosities by human infants. Infancy. 2004;5(3):271–290. [Google Scholar]
- Mix KS. Preschoolers’ recognition of numerical equivalence: Sequential sets. Journal of Experimental Child Psychology. 1999;74(4):309–332. doi: 10.1006/jecp.1999.2533. [DOI] [PubMed] [Google Scholar]
- Mix KS. Surface similarity and label knowledge impact early numerical comparisons. British Journal of Developmental Psychology. 2008;26:13–32. [Google Scholar]
- Mix KS, Huttenlocher J, Levine SC. Do preschool children recognize auditory- visual numerical correspondences? Child Development. 1996;67:1592–1608. [PubMed] [Google Scholar]
- Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal quantification in early childhood. Advances in Child Development and Behavior. 2005;33:305–346. doi: 10.1016/s0065-2407(05)80011-4. [DOI] [PubMed] [Google Scholar]
- Mix KS, Sandhofer CM, Moore JA. How input helps and hinders acquisition of the cardinal word principle. Paper presented at the Society for Research in Child Development (SRCD) Biennial Meeting; Denver, Colorado. 2009. [Google Scholar]
- Negen J, Sarnecka BW. Young children’s number-word knowledge predicts their performance on a nonlinguistic number task. In: Taatgen NA, van Rijn H, editors. Proceedings of the 31th Annual Conference of the Cognitive Science Society; Austin, TX: Cognitive Science Society; 2009. pp. 2998–3003. [Google Scholar]
- National Research Council. Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press; 2009. Mathematics Learning in Early Childhood: Paths Toward Excellence and Equity. [Google Scholar]
- Opfer JE, Siegler RS. Representational change and children’s numerical estimation. Cognitive Psychology. 2007:169–195. doi: 10.1016/j.cogpsych.2006.09.002. [DOI] [PubMed] [Google Scholar]
- Sarnecka BW, Carey S. How counting represents number: What children must learn and when they learn it. Cognition. 2008;108:662–674. doi: 10.1016/j.cognition.2008.05.007. [DOI] [PubMed] [Google Scholar]
- Sarnecka BW, Kamenskaya VG, Yamana Y, Ogura T, Yudovina JB. From grammatical number to exact numbers: Early meanings of “one,” “two,” and “three” in English, Russian, and Japanese. Cognitive Psychology. 2007;55:136–168. doi: 10.1016/j.cogpsych.2006.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarnecka BW, Lee MD. Levels of number knowledge during early childhood. Journal of Experimental Child Psychology. 2009 doi: 10.1016/j.jecp.2009.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholl BJ. Objects and attention: The state of the art. Cognition. 2001;80:1–46. doi: 10.1016/s0010-0277(00)00152-9. [DOI] [PubMed] [Google Scholar]
- Spelke ES, Kinzler KD. Core knowledge. Development Science. 2007;10:89–96. doi: 10.1111/j.1467-7687.2007.00569.x. [DOI] [PubMed] [Google Scholar]
- Starkey P, Klein A, Wakeley A. Enhancing young children’s mathematical knowledge through a pre-kindergarten mathematics intervention. Early Childhood Research Quarterly. 2004:99–120. [Google Scholar]
- Stine R. Graphical interpretation of variance inflation factors. The American Statistician. 1995;49(1):53–56. [Google Scholar]
- Tomasello M, Todd J. Joint attention and lexical acquisition style. First Language. 1983;4:197–212. [Google Scholar]
- West J, Denton K, Germino-Hausken E. NCES 2000–070. Washington, DC: National Center for Education Statistics; 2000. Fall. America’s Kindergartners: Findings from the Early Childhood Longitudinal Study, Kindergarten Class of 1998–99. 1998. [Google Scholar]
- Wynn K. Children’s understanding of counting. Cognition. 1990;36:155–193. doi: 10.1016/0010-0277(90)90003-3. [DOI] [PubMed] [Google Scholar]
- Wynn K. Addition and subtraction by human infants. Nature. 1992a;358:749–750. doi: 10.1038/358749a0. [DOI] [PubMed] [Google Scholar]
- Wynn K. Children’s acquisition of the number words and the counting system. Cognitive Psychology. 1992b;24:220–251. [Google Scholar]
- Wynn K. Infants’ individuation and enumeration of actions. Psychological Science. 1996;7(3):164–169. [Google Scholar]
- Xu F. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition. 2003;89(1):B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Arriaga RI. Number discrimination in 10-month-old infants. British Journal of Developmental Psychology. 2007;25:103–108. [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES, Goddard S. Number sense in human infants. Developmental Science. 2005;8(1):88–101. doi: 10.1111/j.1467-7687.2005.00395.x. [DOI] [PubMed] [Google Scholar]