Alteration and Reorganization of Functional Networks: A New Perspective in Brain Injury Study

Abstract

Plasticity is the mechanism underlying the brain’s potential capability to compensate injury. Recently several studies have shown how functional connections among the brain areas are severely altered by brain injury and plasticity leading to a reorganization of the networks. This new approach studies the impact of brain injury by means of alteration of functional interactions. The concept of functional connectivity refers to the statistical interdependencies between physiological time series simultaneously recorded in various areas of the brain and it could be an essential tool for brain functional studies, being its deviation from healthy reference an indicator for damage. In this article, we review studies investigating functional connectivity changes after brain injury and subsequent recovery, providing an accessible introduction to common mathematical methods to infer functional connectivity, exploring their capabilities, future perspectives, and clinical uses in brain injury studies.

Introduction and Historical Background

The Nervous system’s great ability to carry out the complex task of perception, presumes the cooperation of different structures while processing information from several sources, both external and internal. To process information the presence of specialized areas is required and, even for handling simple information, the coordination of different structures allowing global information processing. Therefore, perception supposes different brain areas processing hierarchically and simultaneously working in different time and frequency scales. Hebb (1949) suggested that elements of higher cognitive processes, such as concepts, words, and mental images, are represented in the brain as cortical cell networks (i.e., connected neural populations composing functional units). These neurons may be sparsely distributed over extensive cortical areas, even recruiting neurons from both hemispheres (transcortical assemblies). The information processing requires segregation (specialized brain areas) but also and importantly integration, to reach a global cooperation between such areas. Moreover, nervous system is dynamic and able to react to continuous environmental changes, integrating information, and generating real time responses. The brain is the complex network by excellence.

Segregation–integration dichotomy

During the last century, research under information processing theory has been greatly influenced by segregation–integration dichotomy. While segregation indicates a high functional specialization of each brain region, integration highlights the idea of a global structure and cooperative behavior. Neither of these views alone adequately account for the multiple levels at which interactions occur during brain functioning. Modern views conceive the human brain as a system merging the local specialization with global integration (Tononi et al., 1994). Several experimental evidences about the segregation and integration in the brain have been documented (for a review see Engel et al., 1997; Mountcastle, 1998), principally in the cerebral cortex. Under this framework, the study of brain functioning is based on the idea that the brain is a complex network of dynamical systems with abundant interactions between local and distant brain areas. The coexistence of integration and segregation has been studied theoretically. Sporns and Tononi groups (Tononi et al., 1992, 1994; Sporns et al., 2000a,b, 2002) proposed a measure based on entropy and mutual information (MI), called neuronal complexity, able to capture the coexistence of such fundamental processes for the brain organization. These theoretical findings relate to connectivity and complexity in the nervous system.

Synchronization as mechanism of interaction

A balance between segregation and integration arrived with the concept of synchrony. Complexity and synchrony compete with each other since synchrony increases at expenses of complexity (Buzsaki, 2006). Historically, concepts like synchronization or complexity rose in neuroscience at a cellular level, specifically with visual cortex neurons. Perception and cognition of a complex stimulus could not be simply explained as with feature detection of basic stimulus by specialized brain areas. Moreover, when several objects are simultaneously perceived, an activation pattern indicates perception of a set of features but there is no information about the way in which such features are combined to compose perception of different objects (the “superposition catastrophe”). The need for combination of perceived features into object representations is called the binding problem. Nonetheless, due to the combinatorial constraint, binding cannot be achieved by the activity of neurons sensitive to certain feature combinations. An alternative is the representation by a network of associated neurons distributed over large areas of the brain. Theoretical studies (Von der Malsburg, 1981), animal experiments and human neurophysiological data have contributed to the belief that the base for binding mechanism implemented in the brain is synchronization, or temporal binding.

Major measurable single neuron activity consists of spike trains that in most cases have an oscillatory character. According to the theory of temporal binding, activation of a neural assembly consists in the synchronization of oscillatory activity in associated cells. Temporal tuning of the spikes may not affect the neuronal firing mean rates, so synchronization could be suitable as a marker for belonging-together of features that are represented by single neurons. This way, the concept of binding has been introduced into the perception framework, in order to understand underlying mechanisms for sensory integration (i.e., features into an object representation) and segmentation (i.e., features distinguishing different objects). The theory of binding must be interpreted in the context of functional integration of specialized and spatially separated brain areas (Varela et al., 2001). Large-scale cooperation in the brain seems to be necessary to achieve perception-related object representations as well as more complex cognitive processes.

Mathematically, the synchrony concept refers to the relation between temporal structures of two signals. Complementarily, synchrony may be defined by the temporal window where some trace of an earlier event is retained, altering the response to a subsequent event (Buzzsaki and Draguhn, 2004). Therefore the dynamic phase between two local networks seems to be a signature of cross communication between groups of neurons (Singer and Gray, 1995; Varela et al., 2001; Fries, 2005, 2009; Singer, 2009). Synchronization concept could be one the most common mechanisms for information communication in the human brain since biological systems tend to economize resources, and synchronization of local and distant networks can be readily accomplished by oscillators involved in coupling rhythms with a low energy cost (Buzzsaki and Draguhn, 2004). All these findings suggest that oscillation-based synchrony is probably the most energy-efficient physical mechanism for temporal coordination in the brain (Buzzsaki and Draguhn, 2004).

Functional connectivity

An approach to the understanding of the dynamical nature of connections among neural assemblies could be the concept of functional connectivity (Friston, 1994), referring to the statistical interdependencies between physiological time series simultaneously recorded in various brain areas. Functional connectivity is an essential concept for the study of brain functioning and its deviation in an individual from normal patterns could be used to give an indication of damage. Bi- and multi-variate analysis of time series in order to study interdependence have been applied to local field potential (LFP), electroencephalographic (EEG) and magnetoencephalographic (MEG) recordings, functional magnetic resonance (fMRI), and are considered reliable techniques to study functional connectivity between different brain regions. Linear and non-linear methods such as coherence function, Phase Synchronization Indexes, or synchronization likelihood (SL) have been successfully applied to the study statistical dependencies between neurophysiological time series.

Functional Connectivity Methods

Several statistical techniques have been developed to study interactions in both time and frequency domains, and in both linear and non-linear frameworks (for an extensive review see Pereda et al., 2005). We shortly present an introduction to available statistical methods for inferring functional connectivity from continuous time series (LFP, EEGs, or MEGs recordings) and a brief introduction to functional connectivity in fMRI. An adaptation of such methods for point processes, as spike trains, can be found in Jarvis and Mitra (2001). For the sake of unification from now on we will consider X(t) and Y(t) as two neurophysiological series (EEG or MEG, for example), describing the electric or magnetic field per time step (according to the sampling frequency). A common method to characterize association, but not very used nowadays, is the correlation coefficient A tool widely understood but which provides very limited knowledge about the functional properties of the neural network. This tool, which has been principally applied to spike trains (Brody, 1999), works in time domain and estimates the probability for time association between signals. In general, two signals X(t) and Y(t) will be correlated if we can predict the variations of one of them as a function of the other one. This phenomenon can be estimated by the correlation coefficient

$$C_{XY}\left(\tau \right)=\underset{u}{\int }\widehat{X}\left(u\right)\widehat{Y}\left(u-\tau \right)du$$ (1)

where $\widehat{X}$ is the zero-mean, normalized transform of the signal X(t). High values of C_XY(τ), close to 1 indicate that X(t) reproduces the variations of Y(t), with a time delay τ that can be different from zero. Time delay between two linearly connected signals can be inferred by means of the delay value that maximizes previous function. However, this delay is not directly related with the propagation time of the electrical signal (Quian Quiroga et al., 2000). A measure of linear correlation between signals is the cross-correlation function at zero delay (Pearson’s product).

This tool works in time domain, estimating probability for time association between signals. However, neurophysiological data’s spectral content can provide very valuable information. To deal with this advantage, a transformation from time to spectral domain is required, being the Fourier transform the most commonly used. In this case signals can be narrowly band-passed around a certain frequency, estimating the correlation coefficient between the band-passed signals, i.e., their coherence. Two signals are said to be synchronous if their rhythms coincide. The concept of synchrony has been applied to signals that had a dominant oscillatory mode, either originally or after filtration around a chosen frequency.

Time and spectral coherence

Spectral coherence

A well-known method for functional connectivity estimation is spectral coherence (SC). Equivalent to correlation coefficient in spectral domain, SC measures linear association between signals, interpreting data in the frequency domain, where the corresponding second order (linear) parameter is the cross-spectrum between two processes, f_XY(λ). The cross-spectrum can be considered as the correlation between processes X(t) and Y(t) at frequency λ, being X(t) and Y(t) two time series as, for example, EEG recordings. If the cross-spectrum vanishes for all frequencies, the two processes will be linearly independent. Therefore, SC will quantify the two signals association with the normalized measure:

$$|R_{XY}\left(\lambda \right){|}^2=\frac{f_{XY}\left(\lambda \right)}{\sqrt{f_{XY}\left(\lambda \right)f_{XY}\left(\lambda \right)}}$$ (2)

Two linearly independent processes (uncorrelated) have vanishing SC for all or certain frequencies, whereas |R|² = 1 indicates a perfect linear relationship between two processes. Coherence is sensitive to both phase and amplitude relationships between signals (Varela et al., 2001). Phase synchrony measures the relationship between phases without any influence from amplitudes. Coherence has widely been applied, principally to EEG and MEG data (for a extensive review see for example Shaw, 1984; Dumermuth and Molinari, 1991).

A disadvantage with SC occurs when networks composed by more than two signals (for example, 32 EEG channels) are considered. First attempt to incorporate the information of more than two systems (an extension of bivariate analysis) was made by adding a third component, called partial coherence. This approach is based on the idea of subtracting linear influences from other processes, obtaining a partial relation between two time series. In such a case, the method will have to be able to discern whether a couple of brain areas are directly connected or such connections take place via other systems (indirect connections). Further on, for inferring if two signals have direct or indirect connection, partial spectral coherence (PSC) can be used (Dahlhaus et al., 1997). This later is based on the association measure (cross-spectrum) between two signals after the linear effect of the other systems has been subtracted. PSC is defined as:

$$|R_{XY∕C}\left(\lambda \right){|}^2=\frac{g_{XY}\left(\lambda \right)}{\sqrt{g_{XY}\left(\lambda \right)g_{XY}\left(\lambda \right)}}$$ (3)

where g(λ) = f⁻¹(λ) is the inverse of the spectral density matrix, and C denotes other systems. To decide whether two signals are directly or indirectly coupled the same criterion as that for the SC could be applied. Partial coherence, R_XY/C(λ), represents the coherence fraction between X(t) and Y(t) that is not shared with C. For example, if C contributes to the linear interaction between X(t) and Y(t), then partial coherence R_XY/C(λ) will be smaller than ordinary coherence, R_XY(λ). Note that partial coherence is a linear method and an eventual failure of its reduction might be caused by non-linear interaction between signals.

Time-spectral coherence

A more sophisticated alternative to Fourier Transform is the wavelet transform (WT), able to perform a simultaneous time–frequency representation of non-stationary time signals. The continuous WT of a signal X(t), similarly to the Fourier Transform, involves its projection onto a set of basic functions, obtained by rescaling and translating along the time axis the so-called mother wavelet Ψ. As with the Fourier Transform, this new representation is defined by the wavelet coefficients W(p,z), which can be obtained as:

$$W\left(p,z\right)=\frac{1}{\sqrt{p}}{\int }_{-\infty }^{\infty }X\left(t\right){\Psi }^{*}\left(\frac{t-z}{p}\right)dt$$ (4)

where parameter z defines localization, and p defines the wavelet timescale, playing the role of the rhythmic component period. The choice of the mother wavelet function Ψ depends on the research aim (Torrence and Compo, 1998; Mallat, 1998), however, a very common function to study rhythmic components of a signal is the Morlet wavelet function. In order to avoid edge artifacts at the beginning and at the end of the time interval in the wavelet spectrum estimation of a finite-length time series, we consider the cone of influence (COI), defined as the region in the (p,z) plane where the wavelet power is decreased by e² (Torrence and Compo, 1998). WT allows performing a time–frequency analysis of rhythmic components in a signal, and hence estimate the wavelet coherence for a pair of signals, a normalized measure of association between two time series (Grinsted et al., 2004):

$$C_{XY}\left(p,z\right)=\frac{{\left|S\left[W_{XY}\left(p,z\right)∕p\right]\right|}^2}{S\left[E_X\left(p,z\right)∕p\right]S\left[E_Y\left(p,z\right)∕p\right]}$$ (5)

where E_X is the wavelet power spectrum of the signal X(t) and S is a smoothing operator (for details see Torrence and Webster, 1998; Grinsted et al., 2004). For instance, if two linearly independent MEG signals have insignificant coherence, C_XY(p,z) ≈ 0, whereas C_XY(p,z) = 1 indicates a perfect linear relationship between the signals at the p scale and z localization, similarly to SC. The global wavelet coherence, $C_{XY}^G$, can be obtained by time averaging local (time-dependent) coherence

$$C_{XY}^G\left(p\right)=\frac{1}{T}{\int }_0^T{C}_{XY}\left(p,z\right)dz$$ (6)

where T is the length of the signal. Global coherence provides an unbiased and consistent estimation of the coherence (Percival, 1995).

Granger causality based methods

The above mentioned methods provide very useful information about functional connectivity, but they have a limitation, while assuming that connections have to be symmetrical. To deal with this disadvantage the concept of Granger causality is known to gage the direction of information flow (causal relations). In this framework several methods have been proposed: the partial directed coherence (PDC; Sameshima and Baccalá, 1999) and the directed transfer function (DTF; Kaminiski and Blinowska, 1991), among others.

Granger causality (Wiener, 1956; Granger, 1969) between two time series reads: “an observed time series X(t) granger-causes another series Y(t), if the knowledge of past of X(t) significantly improves the prediction of Y(t).” According to the definition, an appropriate framework for studying neural connectivity is the auto-regressive (AR) model:

$$X_i={\displaystyle \sum _{j=1}^p{A}_j{X}_{i-j}+{\text{ε}}_i}$$ (7)

where X represents each signal, A is the prediction (casualty) coefficients matrix, ε is the innovation (white noise), and p is the order of the model (usually estimated by the Akaike criterion). Generally, predictability can be interpreted in terms of causality coefficients. Based on these coefficients several methods have been proposed to estimates network connectivity patterns. Kaminiski and Blinowska (1991) proposed a frequency domain normalized measure called DTF. It depends on the transfer function matrix H = (1 − A)⁻¹ as:

$${\text{DTF}}_{XY}^2\left(\text{λ}\right)=\frac{{\left|H_{XY}\left(\text{λ}\right)\right|}^2}{{\displaystyle \sum _{m=1}^k{\left|H_{Ym}\left(\text{λ}\right)\right|}^2}}$$ (8)

Directed transfer function can be interpreted as the influence of system X(t) on Y(t) and it is bounded to the range [0, 1], where k is the number of signals. Direct causality (DC) was introduced by the same authors (Kaminski et al., 2000). If A_XY(t) ≠ 0 for some t, we can conclude on the existence of interaction directed from system j to i. Therefore, in order to evaluate the interaction from system X(t) over Y(t) we calculate:

$${\text{DC}}_{XY}^2={\displaystyle \sum _{t=1}^p{A}_{XY}^2\left(t\right)}$$ (9)

However the main drawback of the DTF, is that it does not allow detecting the indirect connections. To solve this limitation, a modified version of this measure called direct directed transfer function (dDTF) has been introduced (Korzeniewska et al., 2003). This new measure takes into account the PSC defined in Eq. 3, R_XY/C(λ), and is based on the normalization in frequencies:

$${\text{dDTF}}_{XY}^2\left(\text{λ}\right)=\frac{{\left|H_{XY}\left(\text{λ}\right)\right|}^2}{{\displaystyle \sum _{\text{freq}}{\displaystyle \sum _{m=1}^k{\left|H_{XY}\left(\text{λ}\right)\right|}^2}}}{\left|R_{XY/C}\left(\text{λ}\right)\right|}^2$$ (10)

Sameshima and Baccalá (1999) proposed a measure called PDC which is based on the inverse of the coefficients matrix $Ā:$

$${\text{PDC}}_{XY}\left(\lambda \right)=\frac{{Ā}_{XY}\left(\lambda \right)}{\sqrt{{ā}_X{\left(\lambda \right)}^H{ā}_Y\left(\lambda \right)}}$$ (11)

where ${ā}_j$ represents column j of the matrix $\overline{A}$. This measure works in frequency domain and allows discerning indirect connections.

Partial directed coherence is based on the elements of A, thus its computation does not require a matrix inversion. However, since DTF is based on the elements of the transfer function matrix (H) it is less computationally efficient and robust than PDC. On the other hand, PDC is normalized with respect to the total inflow of information, whereas DTF is normalized with respect to the total outflow of the information.

The first step for connectivity estimation through these methods is to fit the AR model (multivariate auto-regressive, MAR). Therefore, their outcome depends on the reliability of the fitting, which requires choicing a model order and an optimal epoch length (a guide for model order selection can be found in Marple, 1987). A critical question is the selection of the time window length to be analyzed. MAR model assumes stationary signals, a very few times satisfied assumption in neurophysiology (for alternative solutions see Arnold et al., 1998; Ding et al., 2000; Liang et al., 2000). Another case that needs attention is when dealing with two time series. In this case causality has to be interpreted carefully. As advised by Granger, causality can only be inferred if both signals contain the fundamental information for the network. This assumption is difficultly satisfied in real data but in most of the experimental cases neurophysiologic data is recorded from multiple sites simultaneously. A multivariate modeling framework can be then used to infer causality instead of a pair wise analysis. In comparison with correlation or coherence, the statistical properties of the Granger-based methods have not been yet deeply investigated (for example, how the pre-processing of the data affects the causality). Causality measures have to be interpreted only in a statistical sense, since they completely depends on the estimation of the model parameters.

Phase synchrony

Two coupled Non-linear Oscillators may have their phases synchronized even when their amplitudes are uncorrelated. When a signal X(t) is transformed into the frequency domain (by means of the Fourier transform, for example) instantaneous amplitude Am(t) and phase ϕ(t) of X(t) appear as clearly separated entities:

$$X^{\prime }\left(\lambda ,t\right)=\text{Am}\left(t\right)exp\left(i\left(\lambda t+{\varphi }_x\left(t\right)\right)\right)$$ (12)

This separation allows focusing on phase as a measurement containing all the information about the temporal structure of brain activity. In this case, perfect synchrony between X(t) and Y(t) means that ϕ_x(t) = ϕ_y(t). And the interaction between the dynamics of two brain signals can be observed by their instantaneous phase difference

$${\varphi }_{xy}\left(t\right)=|n{\varphi }_x\left(t\right)-m{\varphi }_y\left(t\right)|$$ (13)

where n and m are integers that indicating the ratios of possible frequency locking. Generally the case n = m = 1 is studied but evidence for 1:2 and 1:3 phase synchrony have also been reported. Phase locking therefore becomes an indicator of the dynamic phase relationship between two local networks independently of their amplitude (Lachaux et al., 1999).

Synchronization likelihood

Synchronization likelihood is a general measure of the statistical interdependencies between two time series (Stam et al., 2002). To infer functional interactions between X(t) and Y(t) it is assumed that the more X(t) and Y(t) “resemble” each other, the stronger X(t) and Y(t) interact. This “resemblance” is usually quantified by the correlation coefficient or coherence. However it has been shown that X(t) and Y(t) can interact, even when X(t) and Y(t) do not “resemble” each other in a simple way (Rulkov et al., 1995). SL aims to quantify the generalized synchronization by detecting non-linear and linear dependencies between two signals. SL relies on the detection of simultaneously occurring patterns, which can be complex and widely different, in the two signals.

$$\text{SL}=\frac{n_{XY}}{\left(W_x-W_y+1\right)p_{\text{ref}}}$$ (14)

where n_XY is the number of simultaneous repetitions in channels X(t) and Y(t), W_x and W_y are the corresponding time windows and p_ref denote the percentage of vectors that are considered close enough to the signal to represent the same state of the system (for the election of parameters see Montez et al., 2006). SL ranges from 0 (no synchronization) to 1 (complete synchronization).

Mutual information

This measure is based on the concept of Shannon entropy, which can be defined as the average amount of information gained from a measurement that specifies one particular value. Given M possible outcomes Xi, each of them with probability pi, then the entropy’s is given by:

$$I_X=-{\displaystyle \sum _{i=1}^M{p}_i\log p_i}$$ (15)

The MI between two signals is defined as:

$${\text{MI}}_{XY}=\sum p_{ij}log\frac{p_{ij}}{p_i{p}_j}$$ (16)

where p_ij is the joint probability of X = Xi and Y = Yj. It is a measure of the information shared by X and Y (i.e., how much information is provided by one signal by knowing the values of the other) This measure is also called “transinformation” or “redundancy”). Thus, MI = 0, (p_ij = p_ip_j) for independent signals and whereas for identical signals the value of MI is the uncertainty contained in one of them alone. A limitation of MI is that it requires long time series, a constraint that can result in conflict with the stationary assumption.

Phase lag index and imaginary part of coherence

A common approach, in order to avoid the influence of a common source (see discussion below), is the use of correlation measures which are not sensitive to volume conduction like the phase lag index (PLI; Stam et al., 2007) or the imaginary part of the coherency (Nolte et al., 2004).

The main aim of the PLI method is to estimate the phase synchronization invariant under the presence of common sources (Stam et al., 2007) by discarding phase differences centered around 0 ± π. The PLI is a measure of the asymmetry of the phase difference distribution between two signals. This distribution is flat if no phase coupling exists between two time series whereas any deviation from this flat distribution indicates phase synchronization. This asymmetry supposes the presence of a consistent non-zero phase difference between brain signals, however such phase difference cannot be explained by the influences of common sources since these influences are effectively instantaneous. PLI is based on an index of the asymmetry of the phase difference distribution, given by:

$$\text{PLI}=\left|\langle \text{sign}\left[\Delta \varphi \left(t\right)\right]\rangle \right|$$ (17)

where Δϕ(t) is the time series of the phase differences. The PLI ranges between 0 and 1. PLI vanishes when no coupling or coupling with a phase difference centered around 0 ± π exists, however PLI equal to 1 indicates perfect phase locking at a value of Δϕ(t) different from 0 ± π. To know which of the two signals is leading in phase is necessary to omit the absolute value.

Based on the idea that coherence of non-interacting sources is necessarily real, it has been shown that the imaginary part of coherency could be a suitable technique to study interactions among brain areas avoiding common source problems (Nolte et al., 2004). The imaginary part of coherency is only sensitive to synchronizations of two systems which are time-lagged to each other and it does not capture artifactual interactions if volume conduction does not cause a time-lag.

Functional connectivity from fMRI data

Functional connectivity magnetic resonance imaging (fcMRI) is a technique able to study Connectivity between different brain areas by means of the blood oxygen level-dependent (BOLD) signal. This method has been used in resting-state (Greicius, 2008) and task-state (Lee et al., 2009). In this case, connectivity can be inferred through correlations across subjects, blocks, runs, trials, or individual BOLD time points (Friston et al., 2003; Fox and Raichle, 2007).

The most common method to calculate fcMRI is seed-based correlations. An arbitrary amount of regions of interest (ROI) are defined, and in each one, all signals voxel’s are averaged. A connectivity matrix is created by calculating the correlation between each pair of ROI’s signals. An additional approach takes place by applying independent components analysis (ICA) which considers all voxels at once. The mathematical algorithm underlines independent systems and therefore spots the ones that are correlated. A linear and bayesian approach to determine the effective connectivity is the dynamic causal modeling (DIC; Friston et al., 2003) containing three sets of parameters for the implicit causal model which mediate: (a) the influence of extrinsic inputs on the states, (b) intrinsic coupling among the states, and (c) the inputs to modulate that coupling.

An evaluation of the different functional connectivity methods (David et al., 2004) has demonstrated that the sensitivity of techniques depend upon frequency specificity of coupling (broad vs. narrow band) and the nature of the functional connectivity (linear vs. non-linear). Such analysis suggested that methods based on generalized synchronization concept, maybe the most sensitive but only in case of broad-band analysis. However, in narrow-band analysis, MI was found to be the most sensitive method to disclose frequency-specific couplings. Measures based on generalized synchronization and phase synchronization are the most sensitive to non-linear coupling.

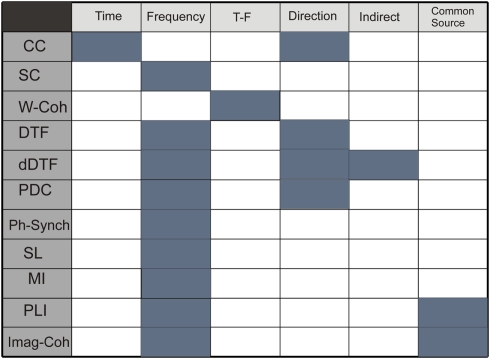
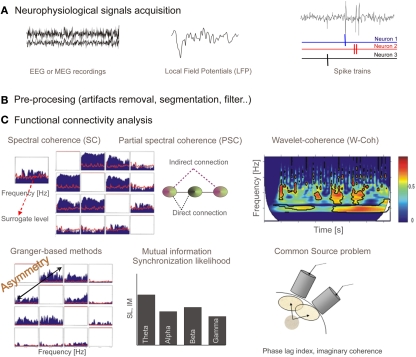
Figure 1 summarizes the properties of functional connectivity methods and Figure 2 illustrates the mathematical steps to infer on functional connectivity. Some free software toolbox are available, for example EEGLAB (Delorme and Makeig, 2004)¹ or FIELDTRIP² packages. Adaptation of some of the methods explained before to point processes (as spike trains) can be found in Jarvis and Mitra (2001) and for fMRI in Statistical Parametric Mapping³.

Figure 1.

Table describing properties of methods: time domain, frequency domain, simultaneous time and frequency domain, direction of the coupling, detection of indirect and direct connections, and no sensibility to common source influence. Functional connectivity methods: CC, correlation coefficient; SC, spectral coherence; W-Coh, wavelet coherence; DTF, directed transfer function; dDTF, direct directed transfer function; PDC, partial directed coherence; Ph-Synch, phase synchrony; SL, synchronization likelihood; MI, mutual information; PLI, phase lag index; Imag-Coh, imaginary part of coherence.

Figure 2.

(A)Neurophysiological signals acquisition: EEG or MEG recordings are continuous time series representing electric or magnetic field in the scalp. Local field potentials (LFP) is a macroscopic scale recording generated by the electrical mixed transmembrane currents produced by neurons. From the extracellular recordings and using sorting spikes algorithms, spike trains corresponding to simultaneously recorded neurons can be obtained. (B) These recordings have to be pre-processed in order to filter, remove artifacts, or establish time windows. (C) Output from different functional connectivity methods. Spectral coherence (SC) provides coupling per frequency, and it is bounded in the interval (0, 1). Red line shows surrogate level, needed to conclude a statistically significant association. Partial spectral coherence (PSC) is proposed as a tool able to distinguish between direct and indirect (via another system) connections. We show the representation for four systems (note the symmetry). Wavelet coherence, similarly to spectral coherence, provides a measure for the coupling between a pair of sensors but in this case in both time and frequency domains. Representation of the wavelet coherence for a pair of system is a 3D plot (time, frequency, and coherence). Granger-based methods are developed to provide information flow direction. In this case the representation is similar to one from SC or PSC (for four sensors) but now connections from sensor x to sensor y are not the same as connections from sensor y to sensor x (asymmetry). Mutual information and synchronization likelihood provide a measure of coupling between a pair of signals. When signals are filtered in spectral bands of interest we obtain a bar diagram as a possible representation. Finally, we represent, for illustrative purpose, a scheme of the common source (volume conduction) problem. It has to be assumed that when dealing with nearby sensors a high probability of capturing activity of common sources will exist, and therefore spurious strong correlation could arise. Some methods (phase lag index or the imaginary part of coherence) have been proposed to overcome this problem.

A MATLAB toolbox, Granger causal connectivity analysis (GCCA) has recently been proposed (Seth, 2010).

Threshold decision: surrogate data test

The application of a frequency domain identification method (either SC, PSC, DTF, or PDC for example) results in a function Ψ(λ) defining coupling probability between a pair of systems at frequency λ. A significantly high value for Ψ(λ) means that both systems are likely to interact at that frequency. Although high amplitudes of the connectivity function Ψ(λ) usually indicate the presence of consistent coupling between two signals. This effect could be caused by a random casual variation in signals. Consequently statistical significance should be cross-checked for the observed coupling value. In order to conclude positively on the connectivity (synchrony) between two signals, Ψ(λ) should be higher than the significance level obtained under the null hypothesis assumption, assuming time series are statistically independent (i.e., we have to estimate the level of random leak between these channels). An evaluation of the significance level can be performed by a surrogate data test (Theiler et al., 1992; Schreiber and Schmitz, 2000) with Monte Carlo simulation to establish a 95% confidence interval. The surrogate time series are obtained from the original by randomizing phase relations whereas other first order characteristics are kept intact (Korzeniewska et al., 2003). Under this approach the connectivity measure was recalculated using surrogate data builded by randomizing phase relations with statistical properties as close as possible to the original data. The procedure is as follows: the signal is transformed into the frequency domain by a Wavelet or Fourier Transform; each amplitude is then multiplied by eiϕ, where ϕ is independently chosen for each frequency in the interval [0, 2π]; phase is symmetrized so that ϕ(−f) = ϕ(f) to get a real inverse transform and finally the inverse transform, i.e., the surrogate data, is obtained, which has the same power spectrum than the original signal but with random phases.

Source space

A key problem concerning signal connections eventually occurs when different sensors sample signals originated by common sources. This has major consequences for results interpretation in terms of interactions among brain regions. When dealing with scalp measures, it should be assumed that nearby sensors have high probabilities of capturing common sources activity, showing spurious strong correlation. In the other hand, when analysis is done in sensor space it could be difficult to interpret the anatomical meaning of the brain areas to which sensors are assigned. For instance, a sensor located over the frontal cortex does not mean that necessarily the signal recorded there actually has its origin in the frontal cortex. The measured magnetic field with MEG is much less distorted by biological tissue than the electric potentials from EEG and thus a much more direct relation in the sensor space between the original source and the captured signal could be expected. Because a direct relation between sensor position and immediate brain region underneath cannot be fully assumed, it should be considered that labels describing brain regions and the ones used to describe connectivity profiles could be subjected to some spatial deviations. Several attempts have been proposed to overcome these two problems: the common source problem and the anatomical correspondence problem and both arise from the sensor space analysis. The first approach is the use of correlation measures not sensitive to common source influence, like the PLI (Stam et al., 2009) or the imaginary part of the coherency (Nolte et al., 2004) described in Section “PLI and Imaginary Part of Coherence,” or very recently: Haufe et al. (2011) have proposed a novel technique to assess functional brain connectivity in EEG or MEG signals by analyzing the sparsely connected sources and which can overcome the problem of common source by modeling neural data. The later problem could be faced by studying functional connectivity in the source space in order to estimate brain sources generating the sampled oscillatory activity. This approach’s main benefit derives from dealing with interactions between anatomically defined regions but it is limited by the choice of an appropriate model for source reconstruction and a suitable source reconstruction algorithm, which could influence interdependencies between sources (Hadjipapas et al., 2005; Stam et al., 2009). Very recently, new methods have been proposed to estimate the source activity (Nolte and Muller, 2010; Haufe et al., 2010). This novel approach to solving the EEG–MEG inverse problem is based upon a decomposition of the current density into a small number of spatial basis fields. Finally a third approach is based on the use of time series analysis techniques to remove interdependencies between signals. A baseline random coherence subtraction has been proposed (Nunez et al., 1997) as well as the use of surrogate data to control spurious levels. An alternative and practical approach is to analyze functional connectivity in the sensor space, grouping then sensor pairs in local and long-distance couplings, grouping them, for instance, in regions Frontal, Right Temporal, Left Temporal, Central, and Occipital.

Application of Functional Connectivity Methods to Brain Injury Study

The knowledge of the neurophysiological mechanism underlying brain’s potential capability to compensate for lesions is a priceless information for optimal rehabilitation strategies. Studies using different clinical techniques support the concept of functional reorganization after brain injury, comparing most of them, local activation degree, and pattern, in patients with good recovery. However, published data is sometimes contradictory (Barbro, 2008) since the heterogeneity of tasks and techniques generates a great results diversity (Kelly et al., 2006). It seems necessary to study brain injury and recovery from a different perspective than the local activity approach. Probably by analyzing connectivity changes between different brain areas. A possible framework to study brain strategies for brain injury recovery is based on the idea that brain is a complex network of dynamical systems with abundant interactions between local and more distant brain areas (Varela et al., 2001).

Focal brain lesions can produce deficits by two basic mechanisms: local cortical dysfunction at the lesion area, and remote cortical dysfunction due to interruption of the connection between areas. Based on this phenomenon we have cited, as example, several studies reporting evidence of functional connectivity pattern alteration after brain injury.

Using a multimodal approach that combines clinical, structural, functional imaging, and neurophysiological information, Gerloff et al. (2006) studied brain reorganization in recovered patients after capsular stroke. Reorganization is studied in this paper from the point of view of recruitment of areas not previously involved in a hand movement task, since their main goal is the study of the incorporation of primary motor cortex in contralesional hemisphere in motor function. In this study cortico-cortical connectivity is inferred by means of SC from EEG recordings but also cortico-spinal connectivity using transcranial magnetic stimulation (TMS). EEG coherence analysis allowed them to conclude that stroke supposed a connectivity decrease in the stroked hemisphere but an increase in the contralesional hemisphere. It is suggested that contralesional hemisphere is functionally integrated in the reorganized cortical network subserving recovered hand movements after stroke. Moreover, EEG spectral power analysis (local activity) evidenced involvement of contralesional primary motor cortex in after stroke reorganization, showing that the right central region was more active in patients than in controls in beta band during movement preparation and execution. Increased contralesional activity could facilitate control of recovered motor function, similarly to complex movements in healthy subjects.

Using a combination of TMS and positron emission tomography (PET), Chouinard et al. (2006) examined primary motor area (M1) changes and its effective connectivity in stroke patients with chronic motor deficits who underwent movement therapy. Simultaneously with improvements observed in motor tests before and after therapy, authors found changes in TMS local response in the ipsilesional and contralesional M1, changes in the strength of interhemispheric connectivity between M1s, and changes in the effective connectivity of the ipsilesional and contralesional M1s with non-primary motor areas, the basal ganglia, and thalamus motor nuclei. TMS effects, when applied over the ipsilesional motor cortex, are observed in both the ipsilesional and contralesional cortex. This could indicate effective connectivity changes between both hemispheres, very important for hand movement coordination. As showed before, by Gerloff et al. (2006), recovered stroke patients recruit resources in the intact hemisphere to fulfill motor task.

Dancause et al. (2005) examined cortical connections of the ventral premotor cortex after injury to M1 (ischemic infarct to the contralateral M1 hand area). Results for experiments with animals suggest that M1 injury causes axonal sprouting near ischemic injuries and the establishment of novel connections within a distant target, supporting the hypothesis that after a stroke, cortical areas distant from the injury undergo major neuroanatomical reorganization.

Regarding hand motion recovery, Grefkes et al. (2007) studied subcortical stroke impact on the interaction of cortical motor areas within and across hemispheres by means of effective connectivity from fMRI and dynamic causal modeling. During voluntary hand movements generation in patients, significant disturbances in the effective connectivity of motor areas was reported. Motor deficit of patients with a single subcortical lesion is associated with pathological interhemispheric interactions among key motor areas. Authors concluded that a dysfunction between ipsilesional and contralesional M1 underlies hand motor disability after stroke. In monkey studies, Frost et al. (2003) studied the role that intact tissue plays in functional remodeling in cerebral cortex after an ischemic infarct in the hand representation of primary motor cortex. Their results suggest that cortical injury causes neurophysiologic reorganization of remote cortical areas and that the greater the damage to reciprocal intracortical pathways, the greater the plasticity in intact areas is. Reorganization in non-lessoned tissue may provide a neural substrate for adaptive motor behavior, playing an important role in function recovery.

Hall et al. (2010a) studied the action of sub-sedative doses of zolpidem on the neuronal network oscillatory activity in a patient which suffered a stroke a long time ago, that caused major damage to the left hemisphere causing motor and cognitive deficits. Pharmaco-MEG analyzes revealed robust and persistent pathological theta and beta oscillations within the lesion and its surrounding cortex. Administration of zolpidem (hypnotic drugs) correlated with the desynchronization in theta and beta oscillations in all regions of the lesioned hemisphere and was coincident with marked improvements in cognitive and motor function. Very recently, Hall et al. (2010a) have demonstrated that diazepam (non-specific GABAergic modulator) modulates theta, alpha, beta, and gamma frequency oscillations in specific regions of the cortex in healthy volunteers. These results could have therapeutic applications in the treatments and in the characterization of neuronal network function in health and disease.

Brain tumors impact on spatial patterns of functional connectivity, is one of the more studied brain injury aspects, proving that brain tumors alter the functional connectivity and the topology of the network. Bartolomei et al. (2006) found alterations in patients synchronization, even in not focal yet involved intra-hemispheric connectivity. A remarkable result concerns the dependency of the reported changes on the spectral band. In particular, decreasing high frequency long-distance connections with increasing slower bands for local connectivity were found. Similarly, Bosma et al. (2009) studied the neurophysiological mechanisms underlying cognitive dysfunction in low-grade glioma (LGG) patients. Such patients show higher short and long-distance synchronization in theta band. These results, correlated with neurocognitive tests performance, allow concluding that strength and spatial widespread brain connectivity changes could be responsible for cognitive dysfunction in glioma patients.

Some decades ago, Wada test (intra-arterial amobarbital procedure) was frequently used to determine language dominance and memory capacity in temporal lobe epilepsy (TLE) surgery candidates, since activity in one of the brain hemispheres is selectively suppressed. Douw et al. (2009) explored the effect of Wada test on functional connectivity patterns in pharmaco-resistant epilepsy, tumors, or mesial temporal sclerosis patients. Slow-band-based connectivity increased over the hemisphere ipsilateral after injection while contralateral and interhemispheric interaction decreased. However, higher spectral bands connectivity increased. Reported results, therefore indicate that functional connectivity in both injected as well as contralateral hemispheres is strongly altered by this procedure.

Functional connectivity in persistent vegetative state patients was studied by Cauda et al. (2009), reporting a dysfunctional default mode network (see Power et al., 2010 for a description of default network), with decreased connectivity in several brain regions including the dorsolateral prefrontal cortex and anterior cingulated cortex. Such alterations are especially significant in the right hemisphere, supporting the view that right hemisphere default and resting-state play an important role in self-consciousness. The clinical problem of how to separate patients in minimally conscious state (MCS) from patients with severe neurocognitive disorders (SND) which show signs of awareness was explored by Pollonini et al. (2010) by means of functional connectivity. Results showed that SND group has a larger number of connections compared to MCS group, in all frequency bands. Two connections are significantly different in the two groups of patients: slow waves between the left temporal and parieto-occipital areas and beta band input to the frontal areas from all other cortical areas. Subjects classification according to functional connectivity in all frequency resulted in 100% classification accuracy of all subjects. A pathological increase of connectivity strength from the cingulate cortex to the primary and supplementary motor areas during a movement task is observed in tetraplegic patients (Cona et al., 2009).

Traumatic brain injury has also been treated by means of functional connectivity. Kumar et al. (2008) studied working memory deficits present in patients with mild traumatic brain injury. Authors found that the different stages of working memory were associated with poor fronto-parietal, fronto-temporal, and temporo-parietal connectivity as well as poor interhemispheric connectivity in the frontal and temporal regions in the patients. These results allow suggesting that the inter- and intra-hemispheric functional connectivity is impaired in such patients during working memory performance.

Recently, Castellanos et al. (2010) evaluated brain injury impact on spectral and spatial patterns of functional connectivity. Networks are compared with those after neurorehabilitation, providing evidence for the notion that reorganization of such networks restores functional connectivity patterns in these patients after recovery. A loss of local and long distant slow-band-based connectivity from patients following a traumatic brain injury and those after rehabilitation was observed and conversely, an increase in alpha- and beta-band-based connectivity was found. Additionally, a correlation between network reorganization and cognitive recovery (measured by psychological test) was found. This study suggested that those changes in functional connectivity at the neurophysiological level are related with behavioral level changes observed. A topological (Castellanos et al., 2011) analysis of the same data showed that reorganization architecture depends on the spectral band (being most pronounced in alpha band). The graph theory based measures indicate that energetic cost could be a recovery suitable marker. Also at a topological level, it may be inferred that functional networks structure evolves in parallel toward brain recovery as correlations do with neuropsychological scales.

Some computational models study brain injury and posterior recovery. Butz et al. (2009) paper proposes a detailed model considering neurons firing properties (synapses formation, axonal arbors, etc.). A very interesting matter is addressed in such work: how rehabilitation strategies must be designed to take full advantage of plasticity according to continuous or paused stimulation, comparing adult with juvenile networks. In the study by Alstott et al. (2009) localized structural lesion effects on the network were computationally studied, where lesion is implemented as sequential single node deletions (random and targeted) and localized area removal, or by removing all nodes and their connections within a spatially defined region around a central location. As shown by the authors, lesions along the cortical midline, the temporo-parietal junction, and the frontal cortex result in the largest and more widespread effects on functional connectivity. In addition, lesions influenced the coupling between regions outside the lesion itself, including the contralateral hemisphere. Honey and Sporns (2008) investigated relationships between inter and intra regional couplings using two different dynamical cortical models. Their results show that high-degree nodes produce the largest and most extensive effects on cortico-cortical interactions in both models. This result seems to be common in all models studying the effect of damage.

Future Perspective and Conclusion

Brain networks show complex system architecture, with a balance between segregation and integration of information. Oscillatory activity in the brain can be measured simultaneously at multiple sites, allowing the estimation of functional connectivity as well as capturing the global structure of the neural system. During the last few years, the idea of studying brain network’s properties applying graph theory concepts (for example, small-world properties have been applied to the study of brain healthy and pathological states. At a multivariate level, graph theoretical analysis is being currently used to capture neural systems global structure and the interplay between segregation and integration, with recorded brain sites and the connections between them representing the vertices and the edges of the network, respectively (Boccaletti et al., 2006). Complex systems, such as the brain network structure, share certain key organizational principles (Bullmore and Sporns, 2009). Thus, small-world architecture seems to be a common feature of many complex systems (Watts and Strogatz, 1998) and there is evidence that structural and functional brain networks show this pattern of organization (Palva et al., 2009; Stam et al., 2009; Gerloff and Hallet, 2010). Small word structure is characterized by a dense intra-modular connectivity and a reduced amount of intermodular connections. Its dynamical properties (such as high clustering and short average path lengths) have been associated with information transmission efficiency and parallel processing providing an optimal model to a better understanding of the segregation and integration problem. Besides the abovementioned properties, there are other useful parameters to quantify the topological and dynamical properties of complex networks, such as modularity, hierarchy, centrality, and the idea of network hubs, which may be very useful to characterize brain networks (see Costa, 2006; Bullmore and Sporns, 2009 for reviews).

The present review aims to support functional connectivity as a possible framework to study how brain is altered after injury (traumatic injury, stroke, tumor, for example) and the principles governing recovery strategies. Although a brain injury supposes the loss of cortical regions, literature also shows how a focal brain lesion induces changes in both adjacent and in spatially distant brain regions (Nudo et al., 1996; Witte and Stoll, 1997; Lee and van Donkelaar, 2006). One of the mechanism proposed as responsible for functional reorganization has been the rewiring of the anatomical connections by retraining, compensating, and/or substituting brain functioning (Wilson, 2008). Reorganization can also be interpreted as the recruitment of areas previously not, or less, engaged in a given task, in order to substitute for directly lesioned or disconnected areas (Merzenich and Jenkins, 1993; Nudo et al., 1996; Cramer et al., 1997; Rossini et al., 1998). The point of view that we would like to support in this work is that such spatially localized (focal) damage induces alteration in the damaged brain area but also in distant, but linked brain regions. For this purpose functional connectivity methods could be a valuable tool to study brain injury impact since it supposes a spatially global measure.

Most of the studies reviewed focus their results at a cortical level, principally due to the recording techniques constraints (as EEG or MEG). However, long rage white matter pathway interruption could probably be causing most of the connectivity changes observed in the cortex. For example, the computational works by Alstott et al. (2009) reporting widespread changes along the cortical midline, the temporo-parietal junction, and the frontal cortex are probably due to a structural interruption of long range white matter connectivity pathways such us a arcuate fasciculum and corpus callosum. This supports the use of a multimodal imaging approach, since it provides complementary, rather than just mutually validating information. Each technique assesses different aspects of information processing (PET, EEG, MEG) and functional connectivity (EEG, TMS).

Although the application of network analysis to the brain injury study are quite recent, clinical studies cited in this work provided evidence for alteration occurring at interactional level as a consequence of a brain injury. For example, the pathological increase of slow waves-based connectivity and the increase of higher bands-based connectivity have been reported in studies of tumors (Bartolomei et al., 2006; Bosma et al., 2009). Moreover, in this study the postoperative decrease of theta synchronization could be interpreted as a tendency toward a “normalized” state of the theta band after tumor resection (idea confirmed by the decrease of seizure frequency). The role of spectral bands in brain interactions underlying cognitive processes is a fundamental subject even nowadays. Modulation of brain rhythms showed by Hall et al. (2010b) regarding spectral dynamics are very relevant, because the study of spectral dynamics modulation induced by drugs can raise further relevant information according cognitive neuroscience and therapeutic consequences. This work determines the spatial profile of power changes across the cortex following drug administration. The role of the oscillations on the synchronization of the networks could be a factor that regulates the emergence and coordination of functional networks, which is a topic of relevant importance in future research. In the stroke patient case reported by Hall and colleagues, authors show that motor and cognitive impairments are related to increased low-frequency oscillations. The administration of zolpidem produces a desynchronization of such pathological slow rhythm restoring cognitive function. This patient showed an improvement of WAISS-III assessments carried out after zolpidem administration. The characterization of the cognitive status after brain injury by means of a neuropsychological assessment is a very common way to diagnose the effects of brain lesion. However, the correlation between changes observed in the test score and neurophysiological changes can provide evidence for a parallel evolution between them, and supposes an evidence supporting the idea of functional interactions as a mechanism that captures brain injury’s impact. The work by Castellanos and colleagues, show a correlation between network reorganization and cognitive recovery. A reduction of delta-band-based connections and the increment of those based on alpha band, correlated with Verbal Fluency scores, as well as Perceptual Organization and Working Memory indexes, respectively. Additionally, changes in connectivity values based on theta and beta bands correlated with Patient Competency Rating Scale.

Effectiveness of rehabilitation therapies is – even today – a great subject of debate. Comparative studies of efficiency over different neurorehabilitation programs and the later revision of how these strategies can be designed to take advantage of brain plasticity could intensify treatment outcomes. However, based on the Declaration of Helsinki principles, a treatment that already has demonstrated benefits for a particular population of patients should not be denied just by experimental reasons. It hinders the possibility of test different rehabilitation programs in human patients. It is for this reason, that computational models can be useful. Models, as those proposed by the Butz et al. (2009), Alstott et al. (2009), or Honey and Sporns (2008) are valuable platforms to assay critical aspects of a rehabilitation program, as for example, the frequency for rehabilitation sessions, the starting point after lesion, or the influence of age and educational level. Some of these aspects are tested by Butz and colleagues, concluding that pauses in stimulation are essential to allow for a spontaneous network reorganization that is required for a lasting compensation of a lesion. Computational level results, might help with the development of rehabilitation strategies. Related to this issue, arises the question about how it can be used to guide treatment. An objective measure of the impact of a brain injury, for example the functional connectivity, along post-injury period could provide an objective marker for recovery. Deviation from a defined healthy reference, can be established as an indication of lesion, and therefore a not-complete recovery. Brain injury impact over the network might establish evolutional profiles at behavioral, cognitive, motor, and functional level. It could increase our predictive and prognostic capability and support the assignment of a certain program (strength degree, length), as well as the election of optimal pharmaceutics strategies among different possibilities.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.