The Role of Bundle Sheath Extensions and Life Form in Stomatal Responses to Leaf Water Status^,,

Abstract

Bundle sheath extensions (BSEs) are key features of leaf structure with currently little-understood functions. To test the hypothesis that BSEs reduce the hydraulic resistance from the bundle sheath to the epidermis (r_be) and thereby accelerate hydropassive stomatal movements, we compared stomatal responses with reduced humidity and leaf excision among 20 species with heterobaric or homobaric leaves and herbaceous or woody life forms. We hypothesized that low r_be due to the presence of BSEs would increase the rate of stomatal opening (V) during transient wrong-way responses, but more so during wrong-way responses to excision (V_e) than humidity (V_h), thus increasing the ratio of V_e to V_h. We predicted the same trends for herbaceous relative to woody species given greater hydraulic resistance in woody species. We found that V_e, V_h, and their ratio were 2.3 to 4.4 times greater in heterobaric than homobaric leaves and 2.0 to 3.1 times greater in herbaceous than woody species. To assess possible causes for these differences, we simulated these experiments in a dynamic compartment/resistance model, which predicted larger V_e and V_e/V_h in leaves with smaller r_be. These results support the hypothesis that BSEs reduce r_be. Comparison of our data and simulations suggested that r_be is approximately 4 to 16 times larger in homobaric than heterobaric leaves. Our study provides new evidence that variations in the distribution of hydraulic resistance within the leaf and plant are central to understanding dynamic stomatal responses to water status and their ecological correlates and that BSEs play several key roles in the functional ecology of heterobaric leaves.

Stomata close in response to changes in water status throughout the soil-plant-atmospheric continuum, including declines in soil water status (Davies and Zhang, 1991; Comstock and Mencuccini, 1998), reduced xylem hydraulic conductance proximal to leaves (Saliendra et al., 1995), and increased evaporative water loss (Mott and Parkhurst, 1991). Stomatal dynamics and closure in response to atmospheric drought can contribute to adaptation to dry habitats (Franks and Farquhar, 1999; Cunningham, 2004). It is unclear, however, where water status is sensed or how it is transduced into changes in stomatal conductance (g_s). The similarity of stomatal responses to hydraulic supply and demand (Saliendra et al., 1995; Comstock and Mencuccini, 1998; Cochard et al., 2002) suggests that part of the regulation of g_s results from negative feedback from water status within the leaf (Buckley, 2005). The resolution of these questions may require greater focus on functional aspects of leaf anatomy, in particular the hydraulic coupling of the epidermis with the rest of the leaf.

During natural transpiration, water potentials may vary greatly over small spatial scales within leaves, because of large and varying resistances in the pathways for water flow to the sites of evaporation (Mott, 2007; Zwieniecki et al., 2007; Peak and Mott, 2011). Some of this variation involves xylem hydraulic resistance within the leaf (Nardini et al., 2003; Brodribb and Holbrook, 2004; Sack et al., 2004; Lo Gullo et al., 2005). However, there can be substantial resistance downstream of xylem conduits. For example, among 10 tropical forest tree species, 11% to 74% of leaf hydraulic resistance (r_leaf) resided outside the xylem (Sack et al., 2005). Helianthus annuus showed strong diurnal variation in r_leaf, with half the resistance extravascular and modulated by irradiance and circadian rhythms, probably via changes in aquaporin expression and/or activation (Nardini et al., 2005). Reduction of r_leaf by light coincided with the up-regulation of aquaporins in Juglans regia (Cochard et al., 2007). Other data (Zwieniecki et al., 2007) suggest that r_leaf downstream of the xylem includes at least two components, representing flow into separate “fast” and “slow” pools of water at low and high resistance, respectively. Zwieniecki et al. (2007) proposed categorizing leaves based on the extent to which the epidermis and/or mesophyll are hydraulically sequestered from the xylem.

Evidence is mixed about the importance of these phenomena for stomatal function. Changes in water potential caused by reduced humidity can be propagated laterally within a leaf, inducing changes in g_s in areas that experience constant humidity (Mott et al., 1997; Mott and Franks, 2001). Similarly, stomata can respond to changes in transpiration rate in distant regions of the same leaf (Buckley and Mott, 2000) or plant (Pataki et al., 1998; Pepin et al., 2002; Brooks et al., 2003). Long-distance responses include transient wrong-way opening movements similar to those generated by local hydraulic perturbations, which suggests that the long-distance responses are mediated by hydraulic signals. However, Mott (2007) reported that stomatal responses to humidity were independent on the two surfaces of amphistomatous leaves of Vicia faba and Xanthium strumarium: when humidity was changed at one surface only, stomata on that surface responded but stomata on the other surface did not. This suggests that changes in water potential near one surface may not propagate to the opposite surface, which in turn suggests that stomata in opposing epidermes on broad leaves might be hydraulically sequestered from one another and from the xylem. Peak and Mott (2011) hypothesized that guard cells themselves are hydraulically sequestered from the epidermis and instead sense humidity in the stomatal pore directly. An alternative explanation is that the hydraulic resistance between the epidermis and the bulk leaf tissue, including the xylem, can be very large, consistent with the observation that epidermal turgor pressure responded to humidity at the perturbed surface but not at the unperturbed surface in V. faba (Mott, 2007; turgor was not measured for X. strumarium).

The hydraulic resistance between the epidermis and the rest of the leaf may vary strongly across species, and especially between homobaric and heterobaric leaves. The latter possess bundle sheath extensions (BSEs) that connect the epidermis and vascular bundles (Wylie, 1952). BSEs can help distribute light through thicker leaves, enhancing photosynthesis (Nikolopoulos et al., 2002), and they may limit lateral CO₂ diffusion within the leaf (Terashima, 1992; Morison et al., 2007). BSEs are more common in xeric, high-light species and upper canopy trees (Kenzo et al., 2007) and in deciduous woody species than in herbs (Wylie, 1952; McClendon, 1992). Scoffoni et al. (2008) found that the reduction of r_leaf by light was much stronger in heterobaric than homobaric species (averaging 58% versus 20%, respectively). This suggests the BSEs are in the hydraulic pathway and can provide additional flow paths that may reduce r_leaf in heterobaric leaves relative to homobaric leaves. Thus, as Wylie (1952) hypothesized based on their anatomy, BSEs may contribute significantly to water flow in heterobaric leaves by facilitating water transport to the epidermis. It is surprising that the role of BSEs in stomatal control has received so little attention.

Well-known features of stomatal behavior can provide insight about the roles of BSEs in leaf hydraulics and the control of water loss. In most angiosperm leaves, stomatal closure following either increased evaporative demand or reduced water supply is preceded by opening movements known as “wrong-way responses” (WWRs; Fig. 1). The WWR is caused by an initial reduction in epidermal back pressure on stomata (Darwin, 1898; Cowan, 1972), whereas the subsequent closure (“right-way response” [RWR]) results from a slower but larger decline in guard cell turgor pressure that may be caused by solute release from guard cells (Losch and Schenk, 1978; Ehret and Boyer, 1979; Grantz and Zeiger, 1986; Buckley and Mott, 2002a, 2002b; Powles et al., 2006). The rate of stomatal opening during the WWR depends on the time constant for changes in epidermal turgor pressure, P_e. The rate of change of P_e is:

where ψ_b, ψ_e, and ψ_m are water potentials of the bundle sheath, epidermis, and mesophyll; r_be and r_me are the resistances to the epidermis from the bundle sheath and mesophyll, respectively; E is transpiration rate and f_e is the epidermal transpiration fraction; and ε_e and v_e are epidermal elastic modulus and volume, respectively (for a derivation of Eq. 1, see Supplemental Data S2). Equation 1 suggests that stomatal opening rate due to reduced P_e will scale with 1/r_be for a step change in supply (ψ_b) and with f_e for a step change in demand (E). However, increased demand may also reduce ψ_b, so the opening rate following a change in E may also scale with 1/r_be, but to a lesser extent.

Figure 1.

A representative response of stomatal conductance (g_s) of Olea europea to a step increase in evaporative demand from 15 to 25 mmol mol⁻¹ (decrease in relative humidity from 52% to 20%) at t₁, followed by leaf excision at the petiole at t₄. The points in time and corresponding g_s values used to calculate the WWR and RWR parameters (t₁–t₆ and g₁, g₂, g₄, and g₅; note that g₃ ≡ g₁ and g₆ ≡ g₄) as described in “Materials and Methods” are represented diagrammatically.

This predicts that low r_be should increase WWR opening rates for both supply and demand perturbations, but more so for supply responses. Thus, we hypothesized that the rates of stomatal opening during excision WWRs (V_e) and humidity WWRs (V_h), as well as their ratio (V_e/V_h), will be greater in heterobaric than homobaric leaves. Similarly, because soil to leaf hydraulic resistance is greater in woody than herbaceous species (Turner et al., 1984; Mencuccini, 2003; Sack et al., 2003), we hypothesized that V_e, V_h, and V_e/V_h will be greater in herbaceous than woody species. To assess the degree and functional significance of hydraulic sequestration of the epidermis as affected by BSEs and plant growth habit, we tested these hypotheses by measuring stomatal responses to humidity and leaf excision in leaves of 10 homobaric and 10 heterobaric species, each group containing five herbaceous and five woody species (Table I). In addition, because our hypotheses arose from inspection of Equation 1, they may not account for some effects (e.g. ψ_b, P_e, and π_e will change during the time period used to calculate V_e and V_h); therefore, we assessed the theoretical plausibility of our hypotheses by simulating our experiments in a dynamic compartment-resistance model of water flow and stomatal control (diagrammed in Fig. 1 and presented in detail in Supplemental Data S1).

Table I. Species used in this study.

Species	Family
Heterobaric, woody
Umbellularia californica	Lauraceae
Vitis vinifera	Vitaceae
Photinia × fraseri	Rosaceae
Nerium oleander	Apocynaceae
Viburnum opulus ‘Roseum’	Adoxaceae
Heterobaric, herbaceous
Helianthus annuus	Asteraceae
Hordeum vulgare	Poaceae
Phaseolus vulgaris	Fabaceae
Solanum lycopersicum	Solanaceae
Glycine max	Fabaceae
Homobaric, woody
Hedera helix	Araliaceae
Olea europea	Oleaceae
Cotoneaster horizontalis.	Rosaceae
Euonymus fortunei ‘Colorata’	Celastraceae
Ligustrum japonicum ‘Texanum’	Oleaceae
Homobaric, herbaceous
Vicia faba	Fabaceae
Nicotiana tabacum	Solanaceae
Tradescantia pallida	Commelinaceae
Chlorophytum comosum ‘Variegatum’	Agavaceae
Ocimum basilicum	Lamiaceae

RESULTS

Transient WWRs to humidity and leaf excision were observed in 51 of 58 leaves and 19 of 20 species studied. One of three individuals of Ocimum basilicum and Phaseolus vulgaris failed to show WWRs to humidity, and one of three individuals of Chlorophytum comosum and Euonymus fortunei and all three individuals of Tradescantia pallida showed no WWR to leaf excision. Where WWRs were observed, we found wide ranges for most WWR parameters (for definitions of parameters, see “Materials and Methods”). The humidity and excision WWR sizes (W_h and W_e) varied 29- and 484-fold across species, respectively. The WWR response lengths (L_h and L_e) varied 15.9- and 18.8-fold, respectively. The rates of stomatal opening (V_h and V_e) varied 100- and 190-fold, respectively. The size of steady-state humidity responses (R_h) varied by 109-fold. Similarly wide variation was observed in these parameters when they were expressed relative to initial g_s. The W_h,rel and W_e,rel varied 107- and 61-fold, respectively; V_h,rel and V_e,rel varied 66- and 149-fold, respectively; and R_h,rel varied 40-fold. These results are given in detail by species in Supplemental Table S1 and summarized by group (leaf type and life form) in Table II. A substantial part of the total variance in the data set, ranging from 22% to 60%, occurred within species (i.e. among replicates of the same species) for all parameters except V_h, V_e, and R_h,rel (Table II).

Table II. Means ± se of stomatal response parameters measured in heterobaric and homobaric species, and results of ANOVA (species nested within homobaric versus heterobaric nested within woody versus herbaceous).

Trait		Symbol	Units	Variancea	Woody	Herbaceous	Heterobaric	Homobaric	Simulatedb
									1× rbe	10× rbe	20× rbe
Initial stomatal conductance		g1	mol m−2 s−1	44c	0.071 ± 0.012c	0.120 ± 0.021	0.108 ± 0.022c	0.087 ± 0.016	0.083	0.074	0.067
Relative RWR to humidity		Rh	%	37d	29.3 ± 2.8e	21.8 ± 2.1	22.9 ± 2.2d	28.2 ± 3.0	25.9	27.6	29.1
WWR parameters
Rate of openingf	Humidity	Vh/10−5	mol m−2 s−2	22d	8.58 ± 1.45c	19.7 ± 7.3	20.2 ± 7.3c	8.1 ± 1.2	3.7	4.2	4.5
Excision	Ve/10−5	mol m−2 s−2	27d	13.2 ± 9.9g	41.0 ± 17.5	41.7 ± 15.8g	9.4 ± 1.9	13.2	9.8	7.2
Relative size	Humidity	Wh,rel	%	51c	43.6 ± 19.4e	24.3 ± 5.93	42.8 ± 19.5d	25.0 ± 5.7	8.9	10.9	13.1
Excision	We,rel	%	46g	62.5 ± 16.7d	113 ± 79	138 ± 77g	37.7 ± 9.1	19.0	18.3	17.4
Length	Humidity	Lh	min	45c	9.70 ± 1.73c	6.97 ± 1.48	7.73 ± 1.32e	8.94 ± 1.94	7.2	7.0	7.0
Excision	Le	min	60g	7.89 ± 1.57e	5.57 ± 1.17	7.00 ± 1.30d	6.46 ± 1.56	4.9	5.0	5.3
Ratio of sizes		We/Wh	–	57c	2.22 ± 0.36c	4.73 ± 2.10	4.77 ± 2.08e	2.18 ± 0.46	2.14	1.68	1.33
Ratio of opening rates		Ve/Vh	–	56c	1.59 ± 0.31e	3.22 ± 1.34	3.23 ± 1.20e	1.40 ± 0.24	3.58	2.32	1.62

^aPercentage of variance occurring within rather than among species.

^bSimulations used the model described in the Supplemental Data and the parameter values in Table III, except r_be, which was increased by factors of 10 and 20 in the simulations under the headings 10× r_be and 20× r_be, respectively.

^cP < 0.01.

^dP > 0.05.

^eP < 0.05.

^fActual opening rates (mol m⁻² s⁻²) were 10⁻⁵ times those given in the table.

^gP < 0.001.

WWR Kinetics

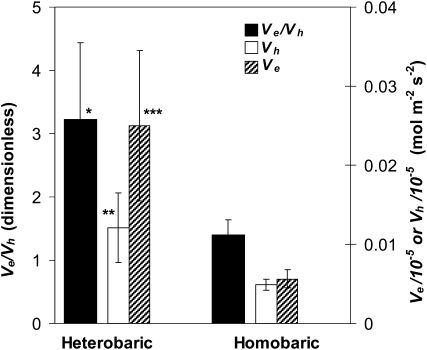
Heterobaric and homobaric species showed strong differences in WWR parameters. Consistent with our hypothesis, the ratio of the rates of stomatal opening during WWRs to excision and humidity (V_e/V_h) was more than twice as large for heterobaric than homobaric species (3.23 ± 1.20 versus 1.40 ± 0.24; P < 0.05; means ± se; Fig. 3; Table II). This difference arose because opening during WWRs to excision was 4.4 times faster in heterobaric than homobaric leaves (V_e/10⁻⁵ = 41.7 ± 15.8 versus 9.4 ± 1.9 mol m⁻² s⁻²; P < 0.001; Fig. 3) and despite the fact that opening during WWRs to humidity was also 2.5 times faster in heterobaric leaves (V_h/10⁻⁵ = 20.2 ± 7.3 versus 8.1 ± 1.2 mol m⁻² s⁻²; P < 0.01; Fig. 3). Notably, faster opening was not consistently associated with shorter WWRs: although humidity WWRs were shorter in heterobaric than homobaric species (P < 0.05), excision WWRs did not differ significantly in length (Table II).

Figure 3.

Rates of opening during WWRs to humidity (V_h; white bars) and leaf excision (V_e; hatched bars) and the ratio of those rates (V_e/V_h; black bars) in heterobaric and homobaric species. n = 10 species and 29 experiments in each group. Values shown are means ± se. * P < 0.05, ** P < 0.005, *** P < 0.001.

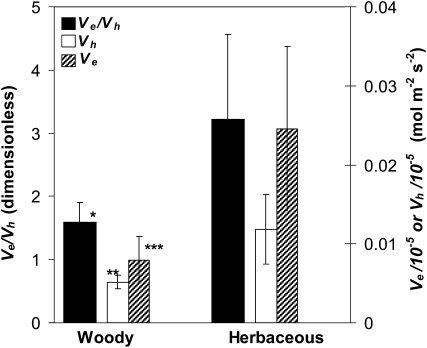
We also found that the hypothesized differences in WWR kinetics between woody and herbaceous species, V_h, V_e, and V_e/V_h, were 2.3, 3.1, and 2.0 times greater, respectively, in herbaceous than woody plants (P < 0.005, P < 0.001, and P < 0.05, respectively; Fig. 4; Table II). In this case, faster opening was associated with shorter humidity and excision WWRs (P < 0.005 and P < 0.05, respectively; Table II).

Figure 4.

Rates of opening during WWRs to humidity (V_h; white bars) and leaf excision (V_e; hatched bars) and the ratio of those rates (V_e/V_h; black bars) in woody and herbaceous species. n = 10 species and 29 experiments in each group. Values shown are means ± se. * P < 0.05, ** P < 0.005, *** P < 0.001.

The faster opening we observed in heterobaric than homobaric and in herbaceous relative to woody species was linked partly, but not entirely, with higher initial g_s (Table II). Thus, V_h and V_e were correlated with g₁, with relationships that appeared to be exponential (equations V_h = 0.00242 e^{8.2472∣·g1}, r² = 0.402; and V_e = 0.00334 e^{6.7698∣·g1}, r² = 0.145; P < 0.001 and P = 0.005, respectively; Supplemental Fig. S1). We determined whether BSEs and life form affected V_e and V_h independently of g₁ by determining the residuals of V_h and V_e against g₁ from these equations and testing for differences in these residuals using the nested ANOVAs (see “Materials and Methods”). For V_h and V_e, the residuals differed between heterobaric and homobaric (P = 0.064 and P < 0.001, respectively) and between woody and herbaceous species (P < 0.005 and P < 0.001, respectively). Supplemental Figure S2 shows mean residuals by species, leaf type, and life form. These findings indicated differences in rates of stomatal opening between leaf and plant types that were independent of differences in g₁.

WWR and RWR Sizes

The sizes of WWRs differed between plant types in some cases. Thus, WWRs in response to excision were 3.7 times larger in heterobaric than homobaric species (W_e,rel = 138% ± 78% versus 38% ± 9%, respectively; P < 0.001; Fig. 5), but WWRs in response to humidity did not differ significantly in size between heterobaric and homobaric species (W_h,rel = 43% ± 20% versus 25% ± 6%, respectively; Fig. 5; Table II). Humidity WWRs were significantly larger in woody than herbaceous species (44% ± 19% versus 24% ± 6%, respectively; P < 0.05; Fig. 6; Table II). However, the ratio of WWR sizes was significantly greater in heterobaric than homobaric (4.77 ± 2.08 versus 2.18 ± 0.46; P < 0.05) and in herbaceous than woody plants (4.73 ± 2.10 versus 2.22 ± 0.36; P < 0.005; Fig. 5; Table II).

Figure 5.

Relative sizes of WWRs to humidity (W_h,rel; white bars) and leaf excision (W_e,rel; hatched bars) and the ratio of those sizes (W_e/W_h; black bars) in heterobaric and homobaric species. n = 10 species and 29 experiments in each group. Values shown are means ± se. * P < 0.05, *** P < 0.001. ns, Nonsignificant.

Figure 6.

Relative sizes of WWRs to humidity (W_h,rel; white bars) and leaf excision (W_e,rel; hatched bars) and the ratio of those sizes (W_e/W_h; black bars) in herbaceous and woody species. n = 10 species and 29 experiments in each group. Values shown are means ± se. * P < 0.05, ** P < 0.005. ns, Nonsignificant.

Steady state or RWRs in response to humidity were significantly larger in woody than herbaceous species (R_h,rel = 29.3 ± 2.8 versus 21.8 ± 2.1; P < 0.05; Table II), but heterobaric and homobaric species did not differ significantly (Table II).

Modeling Analysis

Using the baseline parameter set (Table III), in which the resistance from the bundle sheath to the epidermis, r_be, was assumed equal to that between the bundle sheath and the mesophyll, the model predicted V_e/V_h = 3.58 (1× r_be under “Simulated” in Table II). Using the same parameters but with resistance to the epidermis increased 10- or 20-fold (10× r_be and 20× r_be under “Simulated” in Table II), the model predicted V_e/V_h = 2.32 and 1.62, respectively. All three simulations predicted larger WWRs in response to excision than humidity, but this difference declined as r_be increased (W_e/W_h = 2.14, 1.68, and 1.33 at 1×, 10×, and 20× r_be, respectively). The absolute rates of opening and WWR sizes predicted by the model were smaller than we observed (Table II).

Table III. Variables and parameters in the leaf model used in this study.

Parameter/Variable Name	Symbol	Units	Baseline Value
Dynamic state variables
Epidermal volume	ve	m3 m−2leaf	–
Guard cell volume	vg	m3 m−2leaf	–
Mesophyll volume	vm	m3 m−2leaf	–
Bundle sheath volume	vb	m3 m−2leaf	–
Guard cell osmotic content	ng	mol m−2leaf	–
Calculated state variables (i = e, g, b, m)
Turgor pressure	Pi	MPa	–
Osmotic pressure	πi	MPa	–
Water potential	ψi	MPa	–
Stomatal conductance to water vapor	gs	mol air m−2 s−1	–
Transpiration rate	E	mmol water m−2 s−1	–
Parameters
Hydraulic resistances (leaf area basis)
Leaf	rleaf	MPa m2 s mmol−1	0.08
Soil-leaf xylem	rsx	MPa m2 s mmol−1	0.232 or ∞a
Extraxylar	rox	MPa m2 s mmol−1	0.032
Bundle sheath-mesophyll	rbm	MPa m2 s mmol−1	0.0116
Xylem-bundle sheath	rxb	MPa m2 s mmol−1	0.0116
Bundle sheath-epidermis	rbe	MPa m2 s mmol−1	0.0232
Mesophyll-epidermis	rme	MPa m2 s mmol−1	0.0232
Epidermis-guard cell	reg	MPa m2 s mmol−1	0.126
Values at incipient plasmolysis
Leaf symplastic volume	vtotal	m3 m−2leaf	1.3 × 10−4
Epidermal volume fraction	veo/vtotal	–	0.31
Bundle sheath volume fraction	vbo/vtotal	–	0.062
Guard cell volume fraction	vgo/vtotal	–	0.0085
Mesophyll volume fraction	vmo/vtotal	–	0.62
Epidermal osmotic pressure	πeo	MPa	0.6
Mesophyll osmotic pressure	πmo	MPa	0.6
Bundle sheath osmotic pressure	πbo	MPa	0.6
Miscellaneous
Pressure-conductance scaling factor	χ	mol air m−2 s−1 MPa−1	0.11
Guard cell pressure-volume coefficients	c1, c2	MPa, –	4.1, 6.7
Epidermal pressure-volume coefficient	c3, c4	MPa	−13.4, 7.4
Maximum mesophyll elastic modulus	εm	MPa	15.3
Guard cell osmoregulatory rate constant	α	mol s−1 MPa−1	0.005
Hydroactive sensitivity [∂(πg,ss − πe)/∂Pe]	B	–	4
Fraction of evaporation from epidermis	fe	–	0.5
Fraction of evaporation from mesophyll	fm	–	0.5
Fraction of evaporation from bundle sheath	fb	–	0
Fraction of evaporation from guard cells	fg	–	0
Leaf-air water mole fraction difference	Δw	mmol water mol−1 air	15 or 25b

^ar_sx was changed to infinity to simulate leaf excision.

^bΔw was changed from 15 to 25 mmol mol⁻¹ to simulate reduced humidity.

We assessed parameter sensitivity by a series of simulations (Fig. 7) in which individual parameter values were doubled relative to their baseline values in Table III. This analysis suggested that V_e/V_h should be sensitive to changes in several parameters, including r_be. Specifically, increases in epidermal osmotic pressure at incipient plasmolysis (π_eo), guard cell volume fraction (v_go/v_total), or maximum mesophyll elastic modulus (ε_m) would strongly increase V_e/V_h, whereas increases in the rate constant for guard cell osmoregulation (α), the sensitivity of guard cell osmotic pressure to epidermal turgor at steady state (B), or the soil-leaf xylem resistance (r_sx) would strongly reduce V_e/V_h. Doubling epidermal transpiration fraction (f_e) reduced V_e/V_h by a similar degree as doubling r_be. V_e/V_h was minimally sensitive to other parameters. The absolute sensitivities of V_e and V_h differed widely among parameters. Notably, doubling α had no effect on V_h but reduced V_e by over 30%. Doubling symplastic volume (v_total) reduced both V_h and V_e by about 45%. The similar effects of f_e and r_be on V_e/V_h had different causes: f_e increased V_h with little effect on V_e, whereas r_be reduced V_e with little effect on V_h. Increasing π_eo enhanced V_e much more than V_h; the opposite was true for B (Fig. 7).

Figure 7.

Sensitivity of rates of opening during WWRs to humidity (V_h; white bars at right) and leaf excision (V_e; hatched bars at right) and the ratio of those rates (V_e/V_h; black bars at left) to doubling of individual parameter values in the model described in the Supplemental Data. All parameters except the one listed on a given row in this figure took on the baseline values given in Table III. Parameters are ordered with respect to their effect on V_e/V_h. b.s., Bundle sheath; g.c., guard cell.

We also assessed the sensitivity of V_e/V_h to a wider range of r_be values (Fig. 7). These simulations used a range of values of B and α, because we could not estimate these parameters from the literature yet sensitivity analysis found them to be important in WWR kinetics. Simulated values of V_e/V_h coincided with observed means for heterobaric and homobaric species at approximately 2.5 and 26 times the baseline value of r_be, respectively, under baseline values of B (4) and α (0.005 s⁻¹); at approximately 1 and 16 times baseline r_be for high B (6); and at 6 and 26 times baseline r_be for low α (0.0025). (Similar trends were predicted at low B [2] and high α [0.01], but in neither case could simulations span the range of observed mean V_e/V_h values for both leaf types if r_be were constrained to 30 times baseline.) From these three ranges, we tentatively estimated that a 4- to 16-fold reduction of r_be by BSEs (26/6 ≈ 4, 26/2.5 ≈ 10, 16/1 = 16) could explain observed differences in WWR kinetics between heterobaric and homobaric leaves.

We repeated the preceding analysis (data not shown) by increasing r_sx to estimate the change in r_sx needed to reduce V_e/V_h by half, as observed for woody plants in comparison with herbaceous plants. For high α (0.01 s⁻¹), a 6-fold increase in r_sx reduced V_e/V_h by half. At other values of α and B, doubling r_sx reduced V_e/V_h by 12% to 20%; however, further increases in r_sx caused sustained oscillations in g_s (data not shown).

DISCUSSION

We hypothesized that BSEs and growth habit would impact strongly on stomatal responses. Thus, BSEs in heterobaric leaves should increase the rates of stomatal opening during transient WWRs to V_e and V_h, but more so for excision, such that the ratio V_e/V_h should be greater in heterobaric than homobaric leaves. Our hypotheses were based on inspection of Equation 1 in the introduction and therefore unavoidably omitted some dynamic complexity. However, a more rigorous analysis based on a dynamic compartment-resistance model (Figs. 7 and 8) also predicted that V_e and V_e/V_h should be larger in plants with low r_be.

Figure 8.

Sensitivity of the ratio of opening rates during WWRs to leaf excision and humidity (V_e/V_h) to variation in the hydraulic resistance from the bundle sheath to the epidermis (r_be) in the model described in the Supplemental Data. The ordinate is multiples of r_be relative to its baseline value in Table III (0.0232 MPa m⁻² s⁻¹ mmol⁻¹). The solid line shows baseline values for all parameters other than r_be; dashed lines show simulations assuming values of guard cell osmotic sensitivity to epidermal turgor (B) different from baseline values, as shown; dotted lines show simulations using values of guard cell osmoregulation rate constant (α) different from baseline values, as shown. Areas shown in gray are observed values (means ± 1 se) of V_e/V_h for heterobaric (HE) and homobaric (HO) species.

Our results supported these hypotheses for the impacts of BSEs. The V_e, V_h, and the ratio V_e/V_h were greater in heterobaric than homobaric leaves, as predicted. These results suggest that BSEs reduce the sensitivity of epidermal turgor (P_e) to changes in either hydraulic supply or demand for the epidermis, but more so for changes in hydraulic supply. We also predicted larger V_e, V_h, and V_e/V_h in herbaceous than woody plants because of the smaller total resistance of water supply to the epidermis in woody species. Our results supported those predictions as well.

Our data and model analyses support the hypothesis that BSEs substantially reduce hydraulic resistance to the epidermis. To estimate the size of that effect, we determined how widely r_be needed to vary to reproduce the mean values of V_e/V_h observed for heterobaric and heterobaric leaves (Fig. 8). On this basis, we estimated that a 4- to 16-fold reduction in r_be by BSEs could explain our observations. This is consistent with previous estimates of the extravascular fraction of r_leaf (30%–50%; Sack et al., 2005) and of the effects of high irradiance on r_leaf in heterobaric leaves (reductions of 58% versus 20%, respectively; Scoffoni et al., 2008), which suggest that BSEs reduce r_be by 5- to 24-fold (this is derived in Supplemental Data S5).

Effect of Parameters Other Than r_be on WWR Properties

Comparison of our results with the model suggested that parameters other than r_be may also vary systematically between heterobaric and homobaric leaves. Parameter sensitivity analysis showed that increasing total symplastic volume per unit leaf area (v_total) would reduce both V_h and V_e independent of their ratio. This is also evident from inspection of Equation 1, and it reflects the ability of volume to buffer changes in turgor pressure. One study did in fact find thicker leaves in homobaric than heterobaric woody species (Liakoura et al., 2009), which is consistent with higher v_total and thus with our finding of smaller V_e and V_h in homobaric species. Another possibility is that π_eo and B covary and are larger in heterobaric leaves (these are, respectively, epidermal osmotic pressure at incipient plasmolysis and the sensitivity of guard cell osmotic gradient to P_e in the steady state), as these parameters both increase V_e and V_h but have opposing effects on their ratio V_e/V_h (Fig. 7).

Sensitivity analysis indicated four other parameters with greater effects than r_be on V_e/V_h: guard cell volume fraction (v_go/v_total), maximum mesophyll elastic modulus (ε_m), guard cell osmoregulatory rate constant (α), and soil-leaf xylem resistance (r_sx). Like π_eo and B, v_go and α have strong but opposing effects on V_e/V_h in the model. However, α modulates rates of adjustment in guard cell osmotic content, which v_go translates into osmotic pressure; thus, one may expect α and v_go to covary, which would tend to cancel both parameters’ effects on V_e/V_h. Doubling ε_m increased V_e/V_h by 10%, so a 10-fold increase in ε_m could potentially explain the observed approximately 100% difference in V_e/V_h between heterobaric and homobaric leaves. This is unlikely, however, because even doubling ε_m increased it to 30.6 MPa, which exceeds the range of values commonly reported in plants (Niinemets, 2001; Saito and Terashima, 2004). Increases in another parameter, r_sx, reduced the absolute magnitudes of both V_e and V_h, with a greater impact on V_e than V_h. These effects are qualitatively identical to those of r_be and can be understood on a similar basis.

Doubling the epidermal transpiration fraction (f_e) reduced V_e/V_h by a similar degree as doubling r_be. This arose mainly from increased V_h in the case of f_e but from decreased V_e in the case of r_be (Fig. 7). This bears out the analysis of Equation 1, which suggested that increased f_e and decreased r_be should accelerate stomatal opening after demand and supply perturbations, respectively. The actual value of f_e is unknown and highly debated (Tyree and Yianoulis, 1980; Maier-Maercker, 1983; Grantz, 1990). Our analysis suggests that if f_e differs systematically with leaf type, one would expect larger f_e in homobaric than in heterobaric leaves. That seems reasonable, as BSEs prevent evaporation from the epidermal cells that they subtend. However, evaporation from BSEs likely cannot explain trends in V_e/V_h with leaf type, because the effect of bundle sheath transpiration fraction (f_b) was negligible in the model (data not shown).

Other parameters generally had smaller effects than r_be on V_e, V_h, and V_e/V_h. Doubling the resistance from the bundle sheath to the mesophyll (r_bm) slightly increased V_e/V_h due to a small increase in V_e and decrease in V_h. These effects are opposite those of r_be, and this is because the ratio r_be/r_bm essentially partitions water supply between the epidermis and mesophyll. Epidermal volume fraction (v_eo/v_total) very slightly reduced both V_e and V_h, consistent with Equation 1, and bundle sheath volume fraction (v_bo/v_total) had negligible effects on V_e and V_h. Xylem to bundle sheath resistance (r_xb) had effects qualitatively identical to, but much smaller than, those of r_sx (i.e. reduced V_e and V_h and increased V_e/V_h), which is logical, given that r_sx and r_xb are in series and proximal to the bundle sheath. Increased epidermis to guard cell resistance (r_eg) slightly increased V_e but not V_h. V_h was minimally affected because r_eg has two opposing effects: it slows both the hydropassive and hydroactive declines in guard cell turgor (which increase and decrease opening rate, respectively) by impeding water movement. However, whereas the humidity WWR peaks when the hydroactive response overcomes the epidermal mechanical advantage, the excision WWR peaks when the epidermis reaches zero turgor, which means hydroactive kinetics have less influence on V_e than on V_h.

The model assumes a linear dependence of g_s on guard cell turgor, whereas g_s (and WWR size) may be mechanically limited to a maximum upper value. Thus, if heterobaric and homobaric species differed systematically in the proximity of their initial g_s to that theoretical maximum, this could introduce a bias in WWR size and, transitively, in the parameters of WWR kinetics. Although we did not attempt to quantify maximum g_s per se, we sought to minimize variations in the proximity of initial to maximum g_s by measuring all leaves at the same high irradiance (600 μmol m⁻² s⁻¹, which exceeded that prevailing in the greenhouse during plant growth and acclimation prior to measurement).

The Cause of Wide Variation in WWR Parameters

Although we found strong effects of leaf type on most WWR parameters, there was large variation in those parameters, both among and within species. This variation could not be explained by differences in growing or measurement conditions. Some of this variation may relate to the mechanical advantage (m) of epidermal cells, which varies among and within species, the latter in relation to changing P_e (Franks et al., 1995, 1998; Franks and Farquhar, 2007). Technical challenges have limited measurements of m to a few species. We note that one would expect the qualitative effects of P_e-dependent changes in m to be consistent among replicate leaves from a given species; however, we found that WWR parameters often diverged even within species in this study, which suggests variation in factors other than m.

Notably, variation in WWR parameters has been reported previously. Powles et al. (2006) reported consistent differences in excision WWR size and duration between Photinia × fraseri individuals kept outdoors versus in a glasshouse in the days prior to measurement. They used a modeling analysis to attribute those effects to differences in the lag time preceding the guard cell hydroactive response. They also found that WWR size and length were positively correlated, as we did in this study. Those findings suggest that the time constant for relaxation of xylem-epidermis water potential gradients is correlated with the lag time preceding the guard cell hydroactive response (otherwise, longer WWRs would also be smaller). Thus, variation in WWR such as observed in these studies is consistent with variation in the hydraulic resistance of flow pathways proximal to the guard cells, including r_be and r_eg.

Some within-species variation in WWR kinetics may be genetic in origin. Sinclair et al. (2008) measured r_leaf and excision responses in three genotypes of Glycine max, and one genotype had distinctively slower WWRs than the others. Interestingly, the “slow” genotype also displayed larger r_leaf, a more nearly homeostatic transpiration rate at high Δw (larger R_h,rel), and failure of xylem hydration to mitigate either of those effects. Those results are consistent with our hypothesis that greater extravascular hydraulic resistance should slow stomatal movements after supply perturbations. They also suggest that extravascular resistance is substantial and can vary within species.

Differences in the Hydraulic Connection of the Epidermis to the Rest of the Leaf: Implications for Stomatal Control

WWRs were shorter in heterobaric leaves. This suggests that BSEs help reduce transient water loss after increases in evaporative demand. This may mitigate transient declines in leaf water potential and the associated risk of xylem cavitation, which would otherwise require further stomatal closure, limiting carbon gain. Thus, BSEs could enhance drought tolerance, which is consistent with their greater ecological distribution in high irradiance than in shade species (Kenzo et al., 2007).

Notably, not all land plants exhibit WWRs: they are apparently absent among extant ferns and lycophytes, which are also insensitive to abscisic acid (Brodribb and McAdam, 2011), a hormone known to induce stomatal closure in response to progressive soil drought in most seed plants (Davies et al., 1987; Raschke, 1987). This suggests that stomatal hydromechanics are fundamentally different in seedless plants and seed plants: whereas the former have strictly passive control of g_s in relation to water status, seed plants require metabolic or other mechanisms to amplify passive changes in guard cell turgor to overcome the epidermal mechanical advantage (Buckley, 2005). Not surprisingly, then, guard cell osmoregulation in seed plants is highly complex and adaptable (Zeiger et al., 2002; Nilson and Assmann, 2007). Our finding that BSEs can affect stomatal dynamics, together with evidence that extravascular resistance is large and dynamic (Nardini et al., 2005; Sack et al., 2005; Cochard et al., 2007) and located partly in BSEs (Scoffoni et al., 2008), suggests that BSEs may contribute to the regulatory challenges posed by seed plants’ unique stomatal mechanics.

One likely role for a variable BSE resistance would be to reversibly amplify changes in epidermal water potential caused by changes in evaporative demand or water supply. “Apparent feed-forward” behavior of stomata (Franks et al., 1997), in which water loss actually declines at high evaporative demand, may be necessary for optimal stomatal control under certain conditions (Buckley, 2005). Feed-forward could result from increased hydraulic resistance (Oren et al., 1999; Buckley and Mott, 2002b; Buckley, 2005), perhaps via modulation of r_be. Variation in r_be could also help reconcile the observation that stomata respond independently to humidity in the two epidermes of amphistomatous leaves (Mott, 2007) with other data that showed strong hydraulic coupling of stomatal behavior over much greater distances (Heath and Russell, 1954; Schulze and Kuppers, 1979; Mott et al., 1997; Buckley and Mott, 2000). Clarity on this issue awaits further study on the phenomenology of r_be in relation to the external and leaf environment.

Differences in Steady-State Humidity Responses

This study also provided measurements of steady-state stomatal responses (RWRs) to reduced humidity. Relative RWR size (R_h,rel) did not differ significantly between heterobaric and homobaric leaves, but it was greater in woody than herbaceous species. This is consistent with an earlier study comparing humidity responses in six nonwoody and seven woody species (Franks and Farquhar, 1999). For a step change from Δw_low to Δw_high in our model, R_h,rel is:

where M is net epidermal mechanical advantage, χ is a turgor-to-conductance scaling factor, and R is the effective hydraulic resistance from the soil to the epidermis. (Eq. 2 is derived in Supplemental Data S3.) Thus, greater R_h,rel may reflect greater R, a more sensitive guard cell response (B), smaller mechanical advantage, or higher stomatal density (which largely determines χ) in woody plants. The latter is unlikely, as high χ also implies high initial g_s, whereas we found lower g₁ in woody than herbaceous plants. The model predicted greater R_h,rel in plants with greater r_sx, r_xb, r_be, and f_e (all of which influence R) and greater B, confirming Equation 2, and smaller R_h,rel in plants with high π_eo (data not shown). However, the effects of r_sx and B were about 25 to 30 times greater than those of r_be and f_e, and the next largest effects were 30 times smaller still, suggesting that RWRs in response to humidity are primarily affected by R and B. As whole plant resistance is generally greater in woody species (Turner et al., 1984; Mencuccini, 2003; Sack et al., 2003), we suspect that greater R is the most likely cause for larger RWRs in woody than herbaceous species.

CONCLUSION

We found that rates of stomatal opening during transient WWRs were greater in heterobaric than in homobaric leaves and that this difference was greater during excision than humidity responses. Theoretical analysis showed this pattern to be consistent with the hypothesis that BSEs reduce hydraulic resistance between the bundle sheath and epidermis (r_be). We estimated r_be to be on the order of 4 to 16 times greater in homobaric than heterobaric leaves by applying a theoretical model to our results; we estimated a similar range (5 to 24 times) from published measurements of effects of light on leaf hydraulic resistance in heterobaric versus homobaric leaves. Our results further support the view that BSEs substantially affect the hydraulic and stomatal functioning of leaves. Furthermore, we found stronger steady-state humidity responses in woody than herbaceous species, consistent with their greater hydraulic resistance. These findings indicate that the coupling of bulk leaf and xylem water status with the epidermis impacts the dynamics of stomatal responses to dry air and that leaf tissue variation can have strong impacts on these responses across species and life forms.

MATERIALS AND METHODS

Plant Material

Plants of diverse herbaceous and woody species (Table I) were obtained from local nurseries in Sonoma County, California, or grown from seed in the Sonoma State University Burr Greenhouse. Plants were acclimated in the greenhouse (64%–92% relative humidity and 21°C ± 3°C) at least 10 d prior to measurements. One healthy, young, fully expanded leaf from each plant was measured for stomatal responses for three plants per species, except Glycine max and Ligustrum japonicum, for which one leaf from each of two plants were measured. Herbaceous plants grown from seed were sown in 10-cm-square pots filled with soil:vermiculite:perlite (8:1:1) and provided slow-release fertilizer (Osmocote). Other plants were kept in the 4- or 20-L pots and soils in which they were purchased from nurseries. No plants were root bound.

Gas Exchange

Stomatal conductance was measured using an open-flow, single-pass gas-exchange system. Gases from tanks (Praxair) were mixed with mass flow controllers (FMA-5400 series; Omega) and partially humidified by bubbling through degassed, deionized water before injecting 1% CO₂ in air from a tank (Praxair) with a mass flow controller. The gas stream was then split. Part passed through the reference cell of an infrared gas analyzer (IRGA; Li-Cor 7000; Li-Cor) and a chilled-mirror dewpoint hygrometer (General Eastern DEW-10; General Electric), and the remainder was passed through a mass flowmeter (FMA-2809; Omega) and a sealed chamber containing the leaf before entering the IRGA sample cell. Pressures were monitored with a bubbling manometer proximal to the IRGA and balanced by adjusting flows with valves.

The leaf chamber (of nickel-plated aluminum) used two high-speed fans to circulate air over the leaf, producing a boundary layer conductance of 0.85 mol air m⁻² s⁻¹. The chamber lid was a glass window (12.7 × 8.0 cm) in a high-density polyethylene frame. Leaf temperature was controlled by circulating water from a water bath through channels in the chamber body and monitored with two copper-constantan thermocouples appressed to the lower leaf surface. The photosynthetic photon flux density at the leaf surface was measured with a GaAsP photodiode (G1118; Hamamatsu) previously calibrated to a quantum sensor (LI-190; Li-Cor).

Experimental Protocol

Each experiment measured a humidity response followed by an excision response for the same leaf (Fig. 1). A plant was brought to the laboratory in the morning (7:00–8:30 am), and one healthy, young, fully expanded leaf was clamped in the chamber and allowed to equilibrate at 600 μmol m⁻² s⁻¹ photosynthetic photon flux density, 25°C leaf temperature, 15 mmol mol⁻¹ leaf-air water vapor mole fraction difference (Δw; =52% relative humidity), and 370 μL L⁻¹ ambient CO₂ (c_a). Stomatal conductance (g_s) was logged every second. After g_s reached a steady state (defined as 10 min without a directional trend), Δw was increased to 25 mmol mol⁻¹ (=20% relative humidity) in a single step by adjusting the mixing ratio of humidified and dry air with mass flow controllers. After g_s reached a new steady state, the leaf was excised at the petiole and gas exchange was logged for an additional 60 min.

Correction for Mixing and Desorption Lags

After humidity is reduced, mixing lags and vapor desorption can affect water vapor differential for a time. To correct for this, we measured time courses of IRGA output after a step reduction in humidity identical to that applied in leaf experiments with and without the leaf chamber in the sample line. We characterized the lag due to chamber mixing and desorption by comparing sample signals with and without the chamber and fit a two-phase exponential model to their difference between 1 and 5 min after the humidity change (r² = 0.9987); that model showed a half-time of 9 s and a 95% time of 51 s. We characterized differences in sample versus reference line mixing lags by comparing sample and reference signals without the chamber and fit a second-order polynomial to their difference between 1 and 5 min after the change (r² = 0.994; P < 0.0001). For each leaf experiment, we discarded data from less than 1 min after the Δw change and applied the corrections to measured water vapor differentials over the remaining time course.

Calculation of Parameters Describing Stomatal Responses

We quantified features of stomatal movements during WWRs and RWRs as described below and illustrated in Figure 1. For humidity responses, we recorded the initial value of g_s (g₁) at the time of the humidity change (t₁), the time and value of g_s at the peak of the WWR (t₂ and g₂), and the time at the end of the WWR (t₃, defined as the time at which g_s first dropped below g₁; note that g₃ ≡ g₁). For excision responses, we recorded the g_s value (g₄) at the time of excision (t₄), the time and g_s value at the WWR peak (t₅ and g₅), and the time at the end of the WWR (t₆). We calculated the absolute size of each WWR (W) as W_h = g₂ − g₁ for humidity and W_e = g₅ − g₄ for excision and the length of each WWR (L) as L_h = t₂ − t₁ and L_e = t₅ − t₄. We calculated the rate of opening during each WWR (V) as V_h = W_h/L_h and V_e = W_e/L_e. We also calculated the size of humidity RWRs (R_h) as R_h = g₁ − g₄; we did not attempt to quantify an RWR to excision. To normalize for differences in initial g_s, we also calculated percentage relative sizes of WWRs and RWRs and opening rates (W_rel, R_rel, and V_rel) by dividing W_h, R_h, V_h, and V_e by g₁ and W_e by g₄ and multiplying by 100. Data for each trait were analyzed using a nested ANOVA, with species nested within heterobaric versus homobaric leaf type and nested within woody versus herbaceous life form (Minitab release 15). Data were incremented by 1 and log transformed before analyses to allow the inclusion of zero values and to increase normality and heteroscedasticity (Sokal and Rohlf, 1995). Additionally, as WWR parameters were linked with g₁ (see “Results”), we determined whether BSEs and life form affected V_e and V_h independently of g_1. We determined correlations of V_e and V_h on g₁ and tested for differences in the residuals of those correlations using the nested ANOVAs (Sokal and Rohlf, 1995).

Dynamic Model of Water Flow and Stomatal Control

We simulated water flows, stomatal movements, and transpiration in leaves subjected to the experimental protocol described above using a physical model based on the conservation of mass in an explicit compartment/resistance network (Fig. 2). Complete details and parameter estimation are given in the Supplemental Data and briefly summarized here.

Figure 2.

Resistance/compartment diagram used to derive the dynamic model of water flow and stomatal control described in “Materials and Methods” and the Supplemental Data. The liquid phase resistances between the soil (s), xylem (x), bundle sheath and BSEs (b), epidermal (e), mesophyll (m), and stomatal guard cell (g) compartments are depicted, as are the fractional evaporation of water from the mesophyll, epidermis, and guard cells (arrows).

The model contains five state variables: symplastic volumes for four leaf water pools (mesophyll, epidermis, guard cells, and the bundle sheath, including BSEs in heterobaric species) and guard cell osmotic content (osmotic contents in other pools are assumed constant). The volumes determine turgor and osmotic pressures passively. Flows are calculated from water potential differences and resistances among pools. Each pool supports a fixed fraction of total evaporation (Table III), which is proportional to VPD and stomatal aperture. Aperture is a function of guard cell and epidermal turgor pressures. Xylem capacitance is assumed negligible, so xylem water potential is quasi-steady state with respect to other pools. The only active process is dynamic modulation of guard cell osmotic content to seek a “target” value of osmotic pressure (π_g) proportional to epidermal turgor (P_e), which overcomes the epidermal mechanical advantage and causes a negative steady-state relationship between g_s and VPD. WWRs arise because P_e necessarily declines before π_g. The existence of this hypothesized “hydroactive feedback” is supported by a great deal of evidence (Losch and Schenk, 1978; Ehret and Boyer, 1979; Grantz and Zeiger, 1986; Buckley and Mott, 2002a, 2002b; Powles et al., 2006) and is the basis of previous models (Haefner et al., 1997; Buckley et al., 2003).

We derived a baseline set of parameter values (given in Table III) from the literature, for Vicia faba where possible, as described in Supplemental Data S4. V. faba is a homobaric species in our study and is common in the stomatal literature. The parameter that captures the hypothesized role of BSEs (r_be, bundle sheath-epidermis resistance) has not been directly measured. Therefore, we initially assumed r_be to be equal to the resistance from the bundle sheath to the mesophyll (r_bm), and the baseline parameters represent a heterobaric leaf. However, we varied r_be among simulations to assess its potential role in stomatal dynamics.

We used this model to simulate our experimental protocol and assessed the sensitivity of predicted WWR kinetics to parameters in the model relative to a simulation using the baseline parameter set.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. Correlations of opening rates with initial conductance.

• Supplemental Figure S2. Residuals from correlations of opening rates with initial conductance.

• Supplemental Table S1. Detailed wrong-way response parameters by species.

• Supplemental Data S1. Description of the dynamic compartment/resistance model.

• Supplemental Data S2. Derivation of Equation 1 in the text (rate of change of epidermal turgor pressure).

• Supplemental Data S3. Derivation of Equation 2 in the text (relative size of steady-state humidity response).

• Supplemental Data S4. Estimation of baseline parameter values used in the model.

• Supplemental Data S5. Estimation of irradiance-dependent change in extravascular resistance in heterobaric leaves.