Measurement of Regional Specific Lung Volume Change Using Respiratory-Gated PET of Inhaled ¹³N-Nitrogen

Abstract

Regional specific lung volume change (sVol), defined as the regional tidal volume divided by the regional end-expiratory gas volume, is a key variable in lung mechanics and in the pathogenesis of ventilator-induced lung injury. Despite the usefulness of PET to study regional lung function, there is no established method to assess sVol with PET. We present a method to measure sVol from respiratory-gated PET images of inhaled ¹³N-nitrogen (¹³NN), validate the method against regional specific ventilation (sV̇), and study the effect of region-of-interest (ROI) volume and orientation on the sVol–sV̇ relationship.

Methods

Four supine sheep were mechanically ventilated (tidal volume V_T = 8 mL/kg, respiratory rate adjusted to normocapnia) at low (n = 2, positive end-expiratory pressure = 0) and high (n = 2, positive end-expiratory pressure adjusted to achieve a plateau pressure of 30 cm H₂O) lung volumes. Respiratory-gated PET scans were obtained after inhaled ¹³NN equilibration both at baseline and after a period of mechanical ventilation. We calculated sVol from ¹³NN-derived regional fractional gas content at end-inspiration (F_EI) and end-expiration (F_EE) using the formula sVol = (F_EI − F_EE)/(F_EE[1 − F_EI]). sV̇ was computed as the inverse of the subsequent ¹³NN washout curve time constant. ROIs were defined by dividing the lung field with equally spaced coronal, sagittal, and transverse planes, perpendicular to the ventrodorsal, laterolateral, and cephalocaudal axes, respectively.

Results

sVol–sV̇ linear regressions for ROIs based on the ventrodorsal axis yielded the highest R² (range, 0.71–0.92 for mean ROI volumes from 7 to 162 mL), the cephalocaudal axis the next highest (R² = 0.77–0.88 for mean ROI volumes from 38 to 162 mL), and the laterolateral axis the lowest (R² = 0.65–0.83 for mean ROI volumes from 8 to 162 mL). ROIs based on the ventrodorsal axis yielded lower standard errors of estimates of sVol from sV̇ than those based on the laterolateral axis or the cephalocaudal axis.

Conclusion

sVol can be computed with PET using the proposed method and is highly correlated with sV̇. Errors in sVol are smaller for larger ROIs and for orientations based on the ventrodorsal axis.

Regional specific lung volume change (sVol), defined as regional tidal volume divided by regional end-expiratory (EE) gas volume, is a key variable in lung mechanics and in the pathogenesis of ventilator-induced lung injury. sVol provides information directly associated with tidal aeration and lung strain and allows for the estimation of regional elastance and ventilation (1,2). Consequently, several methods have been developed to assess sVol or related quantities with CT (2–6) and MRI (7–10). PET allows for the assessment of regional lung shunt (11–13), ventilation-to-perfusion ratios (14–19), and neutrophilic inflammation (20,21). However, there is currently no method to quantify sVol with PET. Availability of such a technique would be valuable to investigate disease processes such as ventilator-induced lung injury.

Recent CT studies have shown that sVol is linearly correlated with specific ventilation (sV̇) in mechanically ventilated healthy supine sheep (2,5). These studies indicate that measurements of sVol can be validated through their relationship with sV̇. Indeed, regional sV̇ depends directly on volume change (sV̇ = ΔV/[V·Δt], where V is volume and t is time), and measurement of sV̇ from ¹³N-nitrogen (¹³NN) washout with PET is well established (14,16–18). Those CT studies also indicated that the accuracy of sVol depends on the volume of regions of interest (ROIs) due to registration effects. In addition, evidence of anisotropic lung expansion (22) and vertical gradients in lung volume and ventilation in supine humans and animals (23,24) implies that sVol accuracy may also depend on ROI orientation, that is, if ROIs are delineated by dividing the field of view with equispaced coronal, sagittal, or transverse planes.

Equilibration of inhaled ¹³NN in the lungs leads to a distribution of ¹³NN in proportion to regional gas volume. In this study, we present a method based on respiratory-gated PET of equilibrated ¹³NN to compute regional sVol from end-inspiratory (EI) and EE images of regional gas volume. The method is validated through comparisons against regional sV̇ in mechanically ventilated sheep at different levels of lung inflation. We also study the influence of ROI size and orientation on the relationship between sV̇ and sVol and quantify the contributions of each Cartesian axis to total aeration and ventilation heterogeneity.

MATERIALS AND METHODS

Animal Preparation

The protocols of this study were approved by the Subcommittee on Research Animal Care of the Massachusetts General Hospital. Four sheep weighing 20.2 ± 1.9 kg were premedicated with intramuscular ketamine (5 mg/kg) and midazolam (1–2 mg/kg). General anesthesia was induced with an intravenous bolus of propofol (2–4 mg/kg) and fentanyl (5–10 μg/kg) and maintained with a continuous infusion of propofol and fentanyl titrated to blood pressure and heart rate. Pancuronium (0.1 mg/kg) was used for muscle paralysis at induction and repeated every 90 min. Femoral arterial and internal jugular venous lines were introduced for monitoring of blood pressures, blood sampling, and fluid infusion. Animals were anticoagulated with intravenous heparin (a 2,000-U bolus and 1,000 U hourly) to prevent blood clotting in the catheters and pulmonary embolism. A mainstream flow and pressure analyzer was connected to the endotracheal tube for measurement of tidal volume (V_T) and airway pressure and computation of respiratory system compliance (Noninvasive Cardiopulmonary Management System, model 7300; Respironics). After preparation, sheep were transported to the PET suite.

Experimental Protocols

To study the relationship between sVol and sV̇ under distinct physiologic conditions, we chose to analyze data on 4 sheep from 2 separate experimental protocols. For both protocols, V_T was within recommended clinical values (V_T = 8 mL/kg), with an inspired oxygen fraction of 0.3, inspiratory-to-expiratory time ratio of 1:2, and respiratory rate between 20 and 28 breaths per minute to maintain normocapnia (P_aCO₂ = 35–45 mm Hg). The first protocol aimed to maximize regional aeration heterogeneity in healthy sheep by using zero end-expiratory pressure (ZEEP group, n = 2) along a 16-h period. The second protocol aimed at simulating a clinical condition of mild lung injury with low-dose endotoxin (10 ng·kg⁻¹·min⁻¹) while maximizing homogeneity of lung aeration through the use of positive end-expiratory pressure (PEEP group, n = 2). PEEP was adjusted according to a recently proposed strategy to maximize alveolar recruitment while limiting hyperinflation (25) by setting PEEP to the value at which a plateau pressure of 30–32 cm H₂O was achieved with constant V_T. These sheep were ventilated for 4 h. For both protocols, PET images were obtained as described below at baseline and at the end of the mechanical ventilation period. Endotoxin infusion was initiated after acquisition of baseline images in the PEEP group.

PET Protocol

For all PET scans, sheep were positioned supine in the camera (Scanditronix PC4096; GE Healthcare), with the most caudal slice adjacent to the diaphragm dome. The camera collected 15 transverse slices of 6.5-mm thickness over a 9.7-cm-long axial field, providing 3-dimensional data for an estimated 70% of the total lung volume (15). Transmission scans of 10 min were obtained using a uniform rotating pin source of ⁶⁸Ge to correct PET emission scans for tissue attenuation and to measure lung density (26). We acquired an initial emission scan of an intravenous injection of a ¹³NN-saline bolus (~1,000 MBq), consisting of 22 frames (8 × 2.5 s, 10 × 10 s, and 4 × 30 s). During the first 60 s, the animal was kept in apnea to allow the tracer to diffuse from the blood and accumulate in alveolar airspaces. This scan provided images of pulmonary blood flow (15), which were used for the delineation of lung tissue in the field of view.

A previously described closed-circuit rebreathing system (18) was used to administer ¹³NN gas. A period of 6–10 min was allowed to ensure complete tracer equilibration in regions of low ventilation. Because of its low solubility in water and tissue (partition coefficient water/air = 0.018 at 37°C), inhaled ¹³NN remains confined to alveolar airspaces and conducting airways, with the tracer concentration in a region after equilibration being proportional to the gas volume of that region.

Respiratory-gated emission scans of intrapulmonary ¹³NN were obtained after tracer equilibration (mean activity, 303.4 ± 92.5 kBq/mL). Gating was based on thresholding of the inspiratory pressure signal using a custom LabView interface (version 8.2; National Instruments). Respiratory cycles were divided into 6 bins of equal duration, each bin containing counts from the same phase of the respiratory cycle. A scanning period of 5 min was used to acquire PET data over several breaths. EI and EE frames were selected from the resulting 6 gated image frames on the basis of maximum and minimum tracer activity in the field of view.

A washout scan of the inhaled ¹³NN was acquired after the gated imaging to assess regional ventilation. Starting from tracer equilibrium in the lungs, an imaging sequence consisting of 16 frames (12 × 10 s and 4 × 30 s) was started. The washout was initiated at 60 s into the sequence by switching the breathing system to tracer-free gas.

PET images were reconstructed with a voxel size of 2 × 2 × 6.5 mm using the standard convolution backprojection algorithm and were filtered with an in-plane, low-pass Hanning kernel, yielding an effective volumetric resolution of 1.1 cm³.

Definition of Lung Fields for Analysis

Volumetric masks of lung fields were delineated separately for the EI and EE frames by initially including all voxels whose ¹³NN activity exceeded a threshold value of 40%–50% of the highest activity within the frame; including perfused but poorly aerated lung regions viewed in the ¹³NN bolus infusion scan; and refining the masks manually to exclude the trachea, the 2 main bronchi, and partial-volume effects along the edges of the lung and near the heart. Caudal slices containing a significant volume of diaphragm were also excluded from the analysis.

Computation of Regional Specific Volume Change

Regional tidal sVol (defined as [V_EI − V_EE]/V_EE, where V_EI = end-inspiratory gas volume and V_EE = end-expiratory gas volume of a region) was computed as proposed by Fuld et al. (2):

$$\text{sVol}=\frac{{\text{F}}_{\text{EI}}-{\text{F}}_{\text{EE}}}{{\text{F}}_{\text{EE}}(1-{\text{F}}_{\text{EI}})},$$ Eq. 1

where F_EI and F_EE are the mean fractional gas content (F_gas) of a region at end-inspiration and end-expiration. F_gas represents the fraction of the volume of a region occupied by gas. Equation 1 is based on F_gas measurements rather than absolute volume measurements. This method of computing sVol is less sensitive to errors in precise delineation of ROIs than methods based on absolute volumes (2).

F_EI and F_EE were calculated from the gated ¹³NN images. For this, the 6 gated image frames were averaged to produce a single image of mean regional tracer activity during the entire respiratory cycle. The corresponding transmission scan, which was obtained at mean lung volume, was processed as previously described (27) to construct an image of the average regional F_gas. Finally, the scaling factor between ¹³NN activity from gated emission scans and F_gas from the transmission scan was computed as the mean ratio of F_gas to ¹³NN activity in all voxels with F_gas greater than 0.5. Such regions were chosen for their higher signal-to-noise ratio and to exclude partial-volume effects near lung edges.

ROIs for analysis were defined by dividing the EI and EE lung fields along 3 Cartesian axes (ventrodorsal, laterolateral, and cephalocaudal). ROIs were generated from 1-, 2-, or 3-dimensional grids based on equidistant divisions of those axes (Supplemental Fig. 1; supplemental materials are available online only at http://jnm.snmjournals.org). Thus, ROIs divided along the ventrodorsal axis (i.e., VD ROIs) were separated by equispaced coronal planes, along the laterolateral axis (i.e., laterolateral ROIs) were separated by equispaced sagittal planes, and along the cephalocaudal axis (i.e., cephalocaudal ROIs) were separated by equispaced transverse planes. For multidimensional division, equispaced planes along either 2 or 3 axes formed a grid of ROIs. The number of divisions along a given dimension ranged from 2 to the number required to produce ROIs of single-voxel thickness along that dimension. Larger numbers of divisions produced ROIs with smaller mean volumes. Corresponding ROIs in the EE and EI lungs fields were used to compute sVol.

Calculation of Regional sV̇

Regional sV̇ was estimated by fitting the ¹³NN kinetics during washout with a monoexponential curve:

$$\text{A}(\text{t})={\text{A}}_0·{\text{e}}^{-\text{s}·\stackrel{.}{\text{V}}\text{t}},$$ Eq. 2

where A(t) = tracer activity as a function of time, A₀ = tracer activity at start of washout, sV̇ = regional specific ventilation, and t = time.

Because the PET image data represent cumulative decay counts over specific time intervals, we used an integral-based approach and least-squares linear regression to estimate A₀ and sV̇ (28). Finally, to compare experiments with different respiratory rates (RR), per-breath specific ventilation (sV̇_B) was computed as:

$${\text{s}\stackrel{.}{\text{V}}}_{\text{B}}=\frac{\text{s}\stackrel{.}{\text{V}}}{\text{RR}}.$$ Eq. 3

Spatial Dependence of F_gas and sV̇

We computed voxel-level F_gas from transmission scans and sV̇ from washout scans (as described above) to assess their dependence on spatial position. A linear regression model (Eq. 4) was used to estimate the contributions of each Cartesian axis to the total variability in these voxel-level values.

$$P_{\mathit{ijk}}=\mu +x_i+y_j+z_k+{\epsilon }_{\mathit{ijk}}.$$ Eq. 4

For each voxel value of F_gas or sV̇ (P_ijk), the model accounts for contributions of the global mean (μ); specific position along the laterolateral (x_i), VD (y_j), and cephalocaudal (z_k) axes; and a non-Cartesian component (ε_ijk). The fractional contribution of each axis was computed as the variance related to position along that axis divided by the total variance. Finally, contributions from each axis were normalized such that their sum was equal to 1.

Sensitivity of Mean Regional F_gas to ROI Position

Differences in tissue content of ROIs at end-inspiration and end-expiration could lead to errors in the assessment of sVol. To estimate the magnitude of this effect, we calculated mean F_gas within ROIs as their boundaries were shifted similarly to displacements caused by lung motion or heterogeneous regional expansion. We divided the lung field of a ZEEP animal into 5 ROIs along each of the 3 Cartesian axes and examined mid lung ROIs. The mean F_gas of each ROI was computed in its original position and after shifts of 6 mm along its axis of division. In addition, a cubic 18-mL ROI resulting from 3-dimensional division of the lung field was shifted along all 3 axes by 6 mm.

Statistical Methods

Results are expressed as mean ± SD. The square of the Pearson product-moment correlation coefficient (R²) was used to quantify the correlations between sVol and sV̇_B. ROIs with volume less than the mean − 1 SD in each experiment, usually located at the edges of the lung, had an undue effect on R² calculations and were excluded from the analysis. Standard errors of estimates (SEEs) of sVol from sV̇_B were computed to quantify and compare the predictive value of sVol for different ROI orientations and sizes. Distributions of the differences between predicted and measured sVol were compared using an ANOVA model including animal, time point, ROI volume, and orientation as independent variables. Values of P less than 0.05 were considered significant.

RESULTS

Sheep mechanically ventilated with PEEP showed larger mean airway pressure and peak inspiratory pressure than those ventilated with ZEEP (Table 1). In all animals, respiratory system compliance decreased from baseline to the end of the experiment.

TABLE 1.

Ventilator Settings and Respiratory Measurements

Ventilator setting	ZEEP group				PEEP group
	Sheep 1 baseline	Sheep 1 end	Sheep 2 baseline	Sheep 2 end	Sheep 3 baseline	Sheep 3 end	Sheep 4 baseline	Sheep 4 end
VT (mL)	193	176	157	165	186	185	168	159
PEEP (cm H2O)	0.0	0.0	0.0	0.0	13.3	14.5	18.9	18.3
PIP (cm H2O)	13.4	22.0	15.9	19.4	29.0	35.0	32.2	37.0
MAP (cm H2O)	3.0	4.5	3.2	3.7	16.6	19.2	22.1	22.2
Crs (mL/cm H2O)	17.1	9.1	12.9	10.4	17.9	14.6	16.5	14.8

PIP = peak inspiratory pressure; MAP = mean airway pressure; C_rs = respiratory system compliance; End = after 16 h of mechanical ventilation for ZEEP group and 4 h for PEEP group.

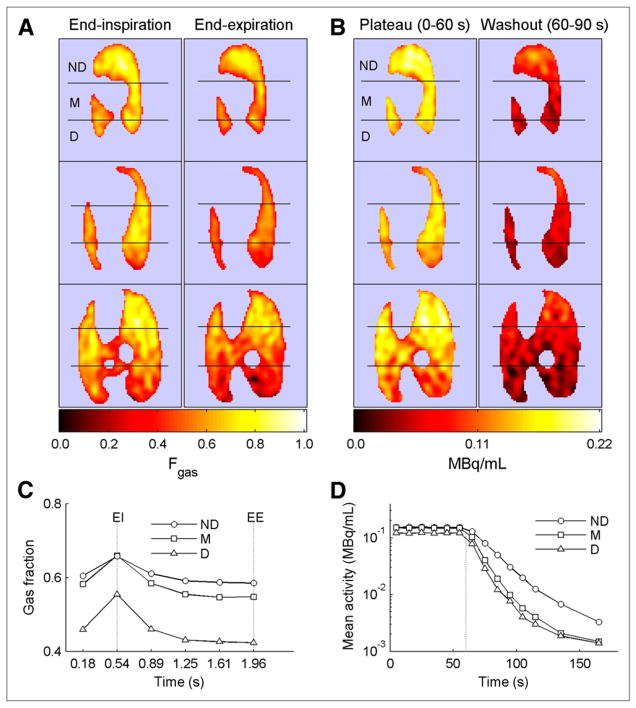
Respiratory gating yielded a sequence of frames along the breathing cycle consistent with changes in regional lung volume in all studied ROIs (Fig. 1). There were notable regional differences in gas content and tracer kinetics during ¹³NN equilibrium and washout. The nondependent regions had the highest gas content throughout the respiratory cycle (Figs. 1A and 1C) and demonstrated the slowest washout rate (Figs. 1B and 1D). The dependent and middle regions had smaller gas contents, particularly at end-expiration (Figs. 1A and 1C) and exhibited faster washout rates than the nondependent regions (Figs. 1B and 1D).

FIGURE 1.

PET scans and tracer kinetics in animal ventilated with zero EE pressure and tidal volume of 8 mL/kg. Hot color scale is used in all images, with black equaling zero regional activity and white equaling maximal regional activity. Left side in image corresponds to left side in animal. (A) EI and EE frames of regional gas volume from respiratory-gated ¹³NN PET scans, shown in 3 transverse slices of lung from apex (top) to base (bottom). Lungs are divided into 3 isogravitational ROIs: nondependent (ND), middle (M), and dependent (D). (B) Images of ¹³NN content at mean lung volume during ¹³NN equilibrium (plateau) and during first 30 s of washout. Rate of decrease in tracer activity in dependent and middle regions is higher than that in nondependent regions. (C) Respiratory-gated gas fractions in nondependent, middle, and dependent regions. Maximum gas fraction occurs at EI, whereas minimum occurs at EE. (D) ¹³NN wash-out kinetics for same lung regions. Vertical dotted line indicates washout start.

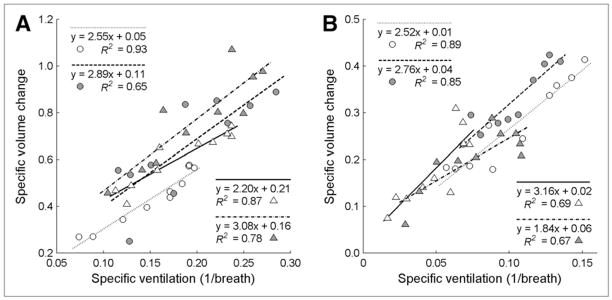
The relationship between sV̇_B and sVol in 10 VD ROIs showed a strong linear correlation for all time points in both groups (Fig. 2). R² for all experiments ranged from 0.65 to 0.93, with an average of 0.79 ± 0.11. All linear correlations were significant at P less than 0.01. The mean slope of the regression lines was 2.63 ± 0.45, and the y-intercept was 0.08 ± 0.07. The average ROI volume among both ZEEP and PEEP experiments for 10 VD ROIs was 49 mL. Experiments with ZEEP (Fig. 2A) showed a larger range of sV̇_B and sVol than those with PEEP (Fig. 2B) and also tended to have higher y-intercepts (P < 0.06). This presence of positive y-intercepts dependent on PEEP level is consistent with a theoretical prediction of the relationship between sV̇_B and sVol (Supplemental Appendix).

FIGURE 2.

Relationship between sV̇_B and sVol in 10 ventrodorsal ROIs for each sheep at baseline (empty symbols) and after ventilation (filled symbols). Note different axis scales for experiments with ZEEP (A) and experiments with PEEP (B), with each sheep in these groups represented by different symbol. R² ranged from 0.65 to 0.93, with average of 0.79 ± 0.11. For ZEEP experiments, sV̇_B and sVol values, ranges, and y-intercepts tended to be higher than for PEEP experiments.

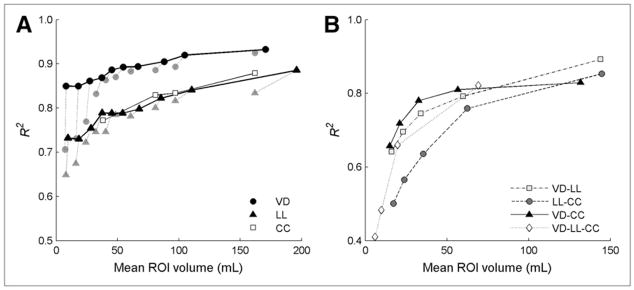
In ROIs divided along only 1 axis, the R² values between sV̇_B and sVol were dependent on both the ROI volume and the orientation (Fig. 3A). For all orientations, R² increased with ROI size. Removal of volumetric outliers was particularly important to improve R² in VD and laterolateral ROIs for volumes less than 50 mL. VD ROIs yielded the highest R² (>0.85 for all volumes), cephalocaudal ROIs yielded the next highest R² (>0.76 for all volumes), and laterolateral ROIs produced the lowest R², which were still greater than 0.73 even for the smallest mean volumes.

FIGURE 3.

Coefficients of determination (R²) between sV̇_B and sVol in ROIs generated by either unidimensional (A) or multidimensional (B) division of lung field along ventrodorsal (VD), laterolateral (LL), or cephalocaudal (CC) axes. Gray symbols in A for VD and LL axes represent values of R² before removal of volumetric outliers. Effect of removing outliers is larger for smaller ROIs. R² generally decreased with reduction in mean ROI volume. In B, all combinations including divisions along VD axis have similarly high R² (>0.64) at 15 mL and above.

The dependence of R² on ROI size and orientation was also present when ROIs were generated by multidimensional division of the field of view along either 2 or 3 axes (Fig. 3B). R²s were highest when VD divisions were combined with divisions along the other axes, with R² greater than 0.64 for all such combinations at mean ROI volumes greater than or equal to 15 mL. Combining divisions along the laterolateral and cephalocaudal axes yielded R² greater than 0.50 for mean ROI volumes greater than 17 mL. Below 25 mL, R² seemed to decrease more rapidly with further reduction in ROI volume.

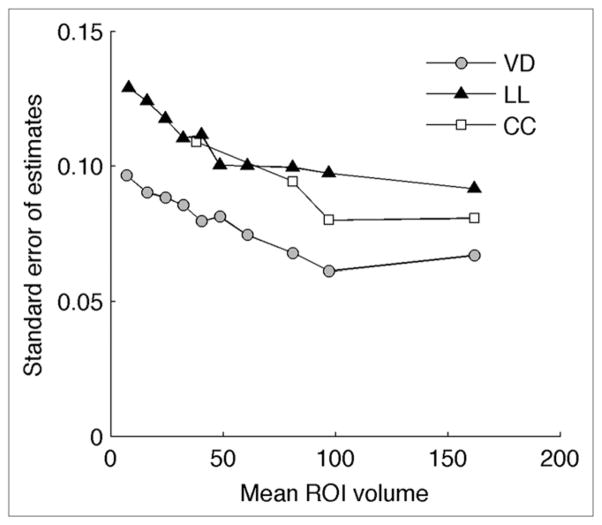
VD ROIs yielded significantly lower differences between measured sVol and sVol predicted from sVol–sV̇_B regressions than laterolateral (P < 0.001) and cephalocaudal (P < 0.001) ROIs. This result is consistent with the SEEs of sVol from sV̇_B for different ROI orientations, which are lowest for VD ROIs at all ROI volumes (Fig. 4). For all orientations, SEEs generally decreased with increase in mean ROI volume. Overall, SEEs at all volumes were below 0.10 for VD, 0.13 for laterolateral, and 0.11 for cephalocaudal ROIs.

FIGURE 4.

SEEs of sVol from sVol–sV̇_B regression lines. SEEs were lower for ventrodorsal (VD) than for laterolateral (LL) and cephalocaudal (CC) orientations. For all orientations, SEEs increased for smaller ROI volumes.

The contributions of the different axes to total variance in voxel-level F_gas and sV̇ were studied separately for experiments with ZEEP and PEEP (Supplemental Fig. 2). For both conditions, position along the VD axis exhibited the most influence on both variables, with the laterolateral axis having the next largest influence. For F_gas, PEEP acted to homogenize the influences of the different axes. In contrast, the contribution of the VD axis to total sV̇ variance appeared to be even larger for PEEP than for ZEEP experiments.

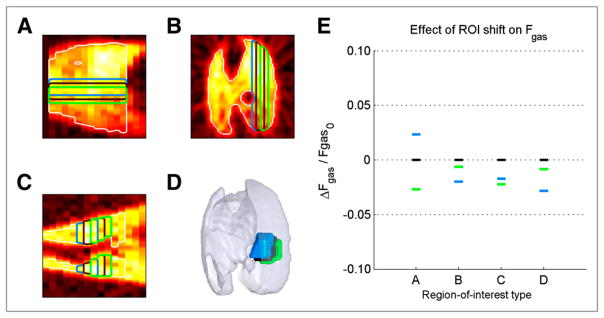
Shifting ROI boundaries along their axes of division resulted in small changes in mean regional F_gas (Fig. 5). Relative changes in F_gas when shifting boundaries along only 1 axis were under 2.7% for all cases. In addition, shifting the cubic ROI resulted in a maximum relative change in F_gas of only 2.8%.

FIGURE 5.

Effect of ROI boundary shifts on mean regional F_gas. (A–D) ROIs used to compute mean F_gas, divided along the ventrodorsal axis (A, sagittal plane), laterolateral axis (B, transverse plane), cephalocaudal axis (C, coronal plane), and combining all directions (D, 3-dimensional view). (E) Mean regional gas fractions for each ROI type in A–D (represented by respective colors) demonstrated small changes in F_gas as result of ROI boundary shifts.

DISCUSSION

The following are the 2 main results of this study in supine mechanically ventilated sheep. First, PET-based regional measurements of lung specific volume change derived from respiratory-gated images of equilibrated inhaled ¹³NN are strongly correlated with specific ventilation computed from the subsequent ¹³NN-washout. Second, correlation between regional specific lung volume change and specific ventilation is highest, and SEEs of sVol from sV̇_B are lowest, for larger ROIs and for ROIs divided along the VD axis.

Lung tissue strain is a fundamental variable in pulmonary mechanics and an important promoter of lung injury and dysfunction (20,21,29,30). Consequently, CT and MRI techniques were developed to assess regional volume changes (2–10). Respiratory-gated PET has been applied to image thoracic tumors (31–33). However, there has been limited use in the assessment of lung function (16), limiting, among others, accurate estimates of lung ventilation (14). Our results support the use of respiratory-gated PET to assess sVol. PET methods to quantify regional function (11–19,23,26,34) and inflammation (20,21) can be combined with the proposed method, providing inherent coregistration and a valuable tool to study lung dysfunction and injury during mechanical ventilation.

sVol and sV̇_B assess different quantities. sVol measures tidal changes in mean regional gas fraction over multiple breaths and primarily depends on true changes in regional gas volume. It is also affected by regional blood volume, lung motion, partial-volume effects, and the quality of coregistration between EI and EE images. sV̇_B is also mainly influenced by regional volume changes. Additionally, it is affected by partial-volume effects and by factors unique to sV̇_B including serial and parallel dead space, intraregional gas mixing, and pendelluft. A lower sVol–sV̇_B correlation could result from any of the listed factors influencing each measurement independently. Because the major factor contributing to both sVol and sV̇_B is the regional tidal volume, high sVol–sV̇_B correlations reflect a systematic assessment by both variables of regional tidal volume. Because correlation coefficients are affected by range, we also computed SEEs to quantify the dispersion of the predictions of sVol with sV̇_B. Those results confirmed the trends found with correlation coefficients in the comparisons among ROI orientations and sizes.

Importantly, CT measurements of sVol based on the same principles used in this study were correlated with direct assessments of sVol obtained with parenchymal markers (2). These direct validation data, combined with our results, provide a strong indication that sVol and sV̇_B measured with PET are both useful to assess regional lung volume changes during mechanical ventilation. Because sVol is the variable most directly associated with regional volume changes, it is the preferred method. When respiratory gating is unavailable, sV̇_B provides information about regional volume changes, if factors unique to sV̇_B can be assumed to be unimportant.

Our measurements of R² were computed from data derived from all animals and time points, providing a measure of the global correlation between sV̇_B and sVol. The use of data from multiple animals provides a large range of values in both sV̇_B and sVol for each ROI configuration, such that the values of R² are indicative of the predictive power of one variable from the other. This is supported by the fact that the SEEs of the sVol–sV̇_B regressions, which are not affected by the range of the variables, are consistent with the data on R², showing smaller errors for VD and larger ROIs.

sVol–sV̇_B correlations were higher for larger ROI volumes. Such results are compatible with the reduction of imaging noise on estimates of F_gas and sV̇_B with larger regions. In addition, larger ROIs tend to reduce the effect of coregistration error between gated EI and EE images and between the gated images and the sV̇_B measurements at mean lung volume.

The orientation of ROIs was also an important determinant of the sVol–sV̇_B correlation. VD ROIs lead to larger R² and smaller SEEs than laterolateral or cephalocaudal ROIs of the same size. In fact, R² values greater than 0.85 were found for VD ROIs less than 10 mL. This result is consistent with our finding of a high contribution of the VD axis to total heterogeneity in regional F_gas and sV̇. Our results expand previous findings (2,23,24) by suggesting that VD variability in F_gas and sV̇ predominates in supine sheep even when submitted to high levels of PEEP and that a substantial fraction of total sVol heterogeneity is also associated with the VD axis.

The low sensitivity of sVol measurements to lung motion is an important characteristic of the presented method. Because current PET cameras do not allow for high-resolution tracking of anatomic tissue references as done with CT (2–5), registration errors between images at different lung volumes due to lung motion could be problematic. However, the method to compute sVol used in our study relies on the assessment of regional F_gas, which varies smoothly with lung position. We showed that registration errors do not significantly compromise the measurements of F_gas and sVol. The same advantage has been demonstrated for CT assessment of sVol (2). Errors in mean F_gas could become important, with significant density heterogeneity at length scales similar to the ROI size.

Another important feature of the method is that sVol results from dynamic gated scans acquired over several minutes of steady-state breathing. These scans represent the time-averaged regional gas content better than a single-breath measurement, relevant in the presence of significant interbreath variability. Multibreath acquisition of gated images may also improve the sVol–sV̇_B correlation, because sV̇_B is measured over several breathing cycles. Another factor improving sVol–sV̇_B correlations is that both measurements derive from ¹³NN imaging. In contrast, CT measurements use lung density to compute sVol and xenon as a radiodense contrast agent to assess ventilation (2,4,5). In this case, density changes may be due to either changes in xenon concentration or movement of tissue components into and out of the field of view, resulting in a potential increase in measurement error (35).

Removal of outlier ROIs (volume < mean − 1 SD) had a notable effect on improving R² at low mean ROI volumes. On average, these ROIs corresponded to a negligible fraction of the total lung field (~0.5%). Such ROIs were usually at the edge of the lung field and were significantly influenced by partial-volume effects because of their small size (<2 mL).

We fit a nonzero intercept line to the experimental sVol–sV̇_B data, in contrast to a previous study (2), because the presence of a dead space leads to a positive intercept in the sVol–sV̇_B regression (Supplemental Appendix). Intercepts were larger in the sVol–sV̇_B lines for the ZEEP than for the PEEP group. PEEP leads to a larger increase in regional lung volume than in dead space (36), decreasing the dead space–to–lung volume ratio. Simulations describing the effect of this decrease on the sVol–sV̇_B relationship substantiated this finding (Supplemental Appendix), indicating that our PET measurements of sVol and sV̇_B are accurate enough to quantify details in the sVol–sV̇_B relationship.

CONCLUSION

We presented a technique for the assessment of regional lung expansion using respiratory-gated PET of inhaled ¹³NN and compared its measurements with those derived from the subsequent ¹³NN washout. Measurements of regional volume changes using gated imaging were highly correlated with per-breath specific ventilation computed from inhaled ¹³NN washout, suggesting that both of those variables provide reliable assessments of regional tidal lung volume change in the studied conditions. Errors in the estimates of regional lung volume change depend on ROI size and orientation and decrease with increasing volume and with the orientation of the ROIs used for analysis, being smallest for VD ROIs.