Structural and Dynamical Characteristics of Peptoid Oligomers with Achiral Aliphatic Side Chains studied by Molecular Dynamics Simulation

Abstract

All-atom molecular dynamics simulations of N-substituted glycine peptoid oligomers with methyl and methoxyethyl side chains have been carried out for chain lengths of 5, 10, 20, and 50 residues in aqueous phase at room temperature. The (ϕ, ψ backbone dihedral angle distributions in the Ramachandran plots show that helical structures, similar to polyproline type I and type II helices, are the most favorable conformations in most peptoid oligomers studied. The left-handed helical structures are shown to be increasingly favored as the oligomer chain length grows. A significant population of cis amide bond configuration has been identified in the peptoid oligomers. By combining the analysis of ϕ and ω backbone dihedral angles, we determined the relative composition of the four major conformations favored by the backbone dihedral angles. The trans α_D conformation is found to be most favored for all peptoid oligomers studies. The time correlation functions of the end-to-end distance highlight a rigid backbone structure relative to side chains for peptoid oligomers. The transition between right-handed and left-handed helical conformation is found to be very rare, and between cis and trans isomerism in amide bond completely absent in the simulation time scale. The radii of gyration for all peptoid oligomers have been found to be consistently larger in comparison to the peptide counterparts, suggesting slightly open structures for peptoids relative to peptides, while the fluctuations in the radius of gyration support a rigid backbone structure of peptoids.

1. INTRODUCTION

Peptoids are a synthetic peptidomimetic biopolymer class with a small modification to peptides in molecular structure in which side chains are attached to amide nitrogen adjacent to C_α carbon in the backbone. Recently there has been growing interest in peptoid class oligomers due to their unique conformational properties and potential for a variety of applications in biomedicine and materials science.^1-11 Example includes polypeptoids grafted onto surfaces through a biomimetic peptide of a mussel adhesive protein with 3,4-dihydroxy-L-phenylalanine(DOPA)-lysine(LYS) sequence, which have been shown to exhibit excellent anti-fouling properties against protein adsorption on a titanium oxide surface and enhanced biocompatibility.^12,13 Recent finding of rapid cellular uptake¹⁴ increased the potential of peptoids for various biological applications. The advantages of peptoids over peptides include facile synthesis protocol¹⁵, flexible design option for side chain structure^16,17, high resistance to chemical or enzymatic degradation^18,19, and better biocompatibility.²⁰

One of the most distinct features in the molecular structure of peptoids is on the backbone nitrogen atom. In contrast to the case of peptides, the backbone nitrogen atom in peptoids is bound to an alkyl side chain and hence, lacks the ability to function as a hydrogen bond donor. Therefore, the intramolecular hydrogen bond between carbonyl oxygen and the hydrogen atom on the backbone nitrogen in peptides, which often plays a crucial role in folding of peptides and proteins, does not exist in peptoids. The absence of backbone hydrogen bonds in peptoids allows the side chain-induced local interactions, such as excluded volume effect, stereo chemistry, and aromatic resonance effect, to take a central role in the folding process of the backbone.^21-23 Side chain interactions can also control the conformational flexibility generated by the methylene group at C_α position. It has been shown that such a unique interaction mechanism in peptoids can lead to the formation of backbone structures that are dramatically different from those of peptides.^24-26

Despite the growing interest in peptoids for the potential applications in wide areas, information available on the structural and dynamical characteristics of this class of molecules is relatively limited. In order to improve the performance of this promising new material in various technological applications, understanding the detailed mechanisms of functionality at a molecular level is crucial. For example, understanding the exact mechanism of surface anti-fouling at a molecular level is essential to establish a rational molecular design strategy to develop peptoids with optimal anti-fouling functionality. Theoretical and computational studies can provide detailed information on structural and dynamical properties of the material at a molecular level, which can advance the understanding of complex mechanisms of various functionalities in different applications. Previous computational studies on peptoids include molecular mechanics calculations of disarcosine and other dipeptoids carried out by Simon et al.²⁷, ab initio quantum mechanical calculations of basic structural units of peptoids and peptides by Moehle and Hofmann²⁸, quantum mechanical and semi-empirical calculations of peptoid oligomers with aromatic chiral side chains by Armand et al.²⁹, and ab initio molecular orbital theory applied to study helical propensity of sarcosine hexamers by Baldauf et al.³⁰ Recently, Butterfose et al. calculated the conformational energy landscape of small peptoids by performing quantum mechanical and molecular mechanics calculations.³¹ Despite the detailed conformational information of small molecules available from those approaches, quantum mechanical and molecular mechanics calculations are computationally very demanding and the applications of the techniques have been limited to relatively small peptoid molecules. On the other hand, technical applications of peptoids in laboratory often involve long chains, with the number of residues sometimes going well over 10 monomer units. Furthermore, most quantum mechanical and molecular mechanics calculations have been carried out in vacuum environment, leaving out the effects of solvent which can play a crucial role in some applications.

In order to bridge the gap between the previous computational studies dominated by quantum mechanical and molecular mechanics calculations and typical laboratory applications, we carried out full-atomistic molecular dynamics (MD) simulations of peptoid oligomers with different chain lengths in bulk aqueous phase, with explicit water molecules. In the following, we first describe the simulation methodology followed by the presentation of the computational results. We analyze the effects of side chain variations and chain length on the peptoid structure, and discuss the implications in comparison with the peptide counterparts. Dynamical properties of backbone and side chains are presented for the first time, to the best of our knowledge. Analysis of the dihedral angle distributions provides detailed insight into conformational preferences of the peptoid oligomers and the role of side chains.

2. METHODS

We performed MD simulations of a series of two different peptoid species, one with methyl (CH₃-) side chains (sarcosine, abbreviated as SAR) and the other with methoxyethyl (CH₃OC₂H₅-) side chains (N-methoxyethyl glycines, abbreviated as PMP), and of their peptide counterparts in an aqueous environment at room temperature with fully atomistic resolution using GROMACS³² simulation package. The molecular structures of the peptoids explored in this study are shown in Figure 1. Four different chain lengths with 5, 10, 20, and 50 monomer units for each peptoid/peptide species have been simulated in order to study the effect of chain length on structure and dynamical properties of the peptoids. Hence a total of 16 different molecules, including 4 sarcosines, 4 PMP’s, and their peptide counterparts, have been simulated in this study. We also carried out replica-exchange MD simulations for all 16 species in order to improve sampling efficiency, the results of which were virtually identical in structural characteristics compared with those from regular MD simulations.

Figure 1.

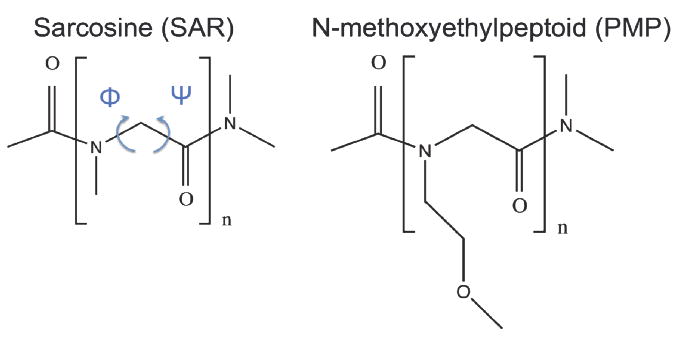
Molecular Structure of the sarcosine (SAR) and N-methoxyethyl glycine (PMP) explored in this study. The definitions of ϕ and ψ backbone dihedral angles are shown in blue arrows. The chain lengths n = 5, 10, 20, and 50 have been studied in this work.

2.1 Regular MD

Each peptoid and peptide oligomer of interest was generated by first building a monomer unit, and then linearly attaching monomer replicas one after another until a desired chain length was reached. The N-terminal of each peptoid/peptide molecule was capped by an acetyl group (CH₃CO-), and the C-terminal by an amine group (NH₂-).

The Optimized Potential for Liquid Simulations (OPLS) force field parameters³³ were used to describe interactions among the atoms. The force field assignments of peptoid molecules were done with close reference to the standard assignments for amino acids and other relevant molecular classes, such as tertiary amides. The force field assignments using the standard OPLS parameters generated the net total charge on each peptoid monomer that matches its neutral formal charge. The improper dihedral potential of the backbone O_i-1-C_i-1-N_i-C_αi dihedral angle in peptoids is the only interaction that does not have the exact matching parameter in standard OPLS force field due to the different nature of the backbone nitrogen atom in peptoids. The potential parameter for peptides, 43.932 kJ/mol energy barrier, was used for this particular improper backbone dihedral interaction, meaning that we imposed the same strength of planarity for amide bonds in peptoids as in peptides. The detailed atomic force field assignments are summarized in Table S1 (Supporting Information).

Each oligomer was first energetically stabilized by steepest descent algorithm, followed by an equilibration for at least 1 ns in vacuum at temperature 300 K. The molecule collapsed from the initial linear conformation to a complex entangled conformation after equilibration. The molecule was then immersed in a 10×10×10 nm³ cubic box of TIP4P water molecules, and a simulation was run for production for 50 ns in canonical (NVT) ensemble at constant temperature 300 K. A typical snapshot at the completion of a simulation for PMP 20mer is shown in Figure 2.

Figure 2.

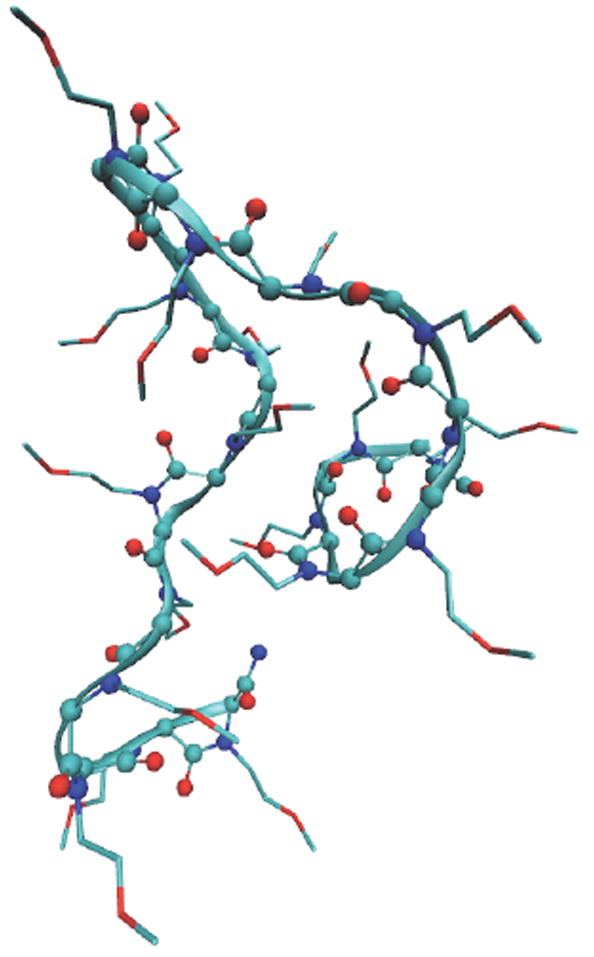
A typical snapshot at the completion of the regular MD simulation for PMP 20mer. The backbone is shown in a ball-and-stick model overlaid with a ribbon representation, and the side chains are shown in lines. The carbon atoms are shown in green color, oxygen in red, nitrogen in blue. Hydrogen atoms are not shown.

2.2 Replica Exchange MD

The replica exchange MD simulations^34-36 were performed for a temperature range 300-350K. A temperature series for each simulation system was generated according to the scheme developed by Patriksson et al.³⁷ in order to produce uniform exchange probability for all replicas during replica exchange simulations. The targeted exchange probability was set at P_exch = 0.3, and the total number of temperature values generated is 17, 22, 32, 43 for 5mer, 10mer, 20mer, and 50mer, respectively. Each replica exchange simulation ran for 20 ns. In order to test the effect of initial conformation we ran a replica exchange MD simulation for PMP 20mer with a linear initial configuration in aqueous phase for 20 ns, and the results were essentially the same for the backbone dihedral angle distribution and other features of interest. We present results mostly from replica exchange MD simulations in this report, except for the analysis of dynamical characteristics.

3. RESULTS AND DISCUSSION

Ramachandran plot, a two-dimensional graphical representation of the backbone (ϕ, ψ) dihedral angle distribution of amino acid residues, is widely used to identify secondary structure of peptides and proteins. The definition of the backbone dihedral angles, ϕ and ψ, is shown in figure 1. It is well known that polyalanine has a propensity to form an α-helical structure, in equilibrium with β-structures (β-sheet and β-hairpin) and random coil states, depending on detailed conditions. The Ramachandran plot for polyalanine 50mer from the replica exchange MD simulations (Figure 3a) shows a significant population of α-helical structure with (ϕ, ψ) backbone dihedral angles around (-80°, -25°) and some β-sheet structure around (-90°, 150°) and (-150°, 150°), which matches well with typical Ramachandran plot for polyalanine in the literature.³⁸ The Ramachandran plots of polyalanine 5mer, 10mer, 20mer, and 50mer from both regular and replica exchange MD simulations show that the α-helical structure is increasingly more favored over β-sheet structure as the chain length increases. (not shown)

Figure 3.

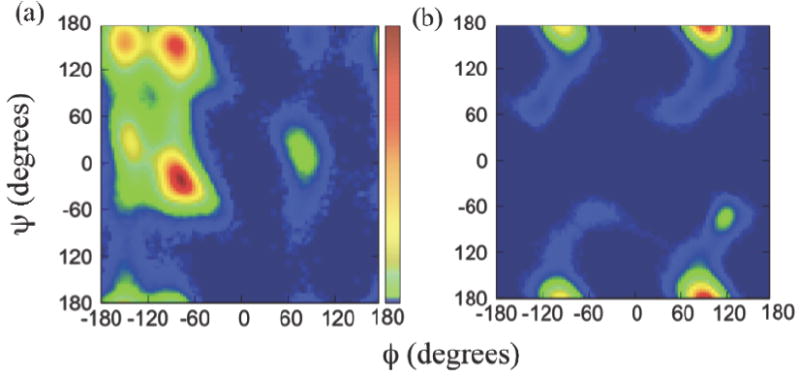
The (ϕ, ψ) Ramachandran plots of (a) polyalanine and (b) sarcosine 50mers, obtained from the replica exchange MD simulations. The scale bar in (a) represents from no population in blue color to the highest population in red.

The Ramachandran plot of sarcosine 50mer, the peptoid counterpart of polyalanine, is shown in figure 3b. The difference in the backbone dihedral angle distributions between peptide and its peptoid counterpart is dramatic. The backbone dihedral angle pairs (ϕ,ψ) of sarcosine 50mer are heavily populated near (±90°, ±180°), while the polyalanine 50mer has small or no population in these regions. It is worth mentioning that a switch of the side-chain position from C_α to the adjacent amide nitrogen atom generates such a huge difference in backbone dihedral distribution and the secondary structure for the peptoid oligomer. Such changes may result from intrinsic structural characteristics of peptoids such as the tertiary amide nature of the backbone nitrogen atom, the lack of backbone hydrogen bonding, and achirality of C_α.

The Ramachandran plot of sarcosine 50mer has main features that are very similar to the conformational energy landscape for sarcosine dimer reported by Butterfose et al.³¹ and agrees well with the experimental data for a series of peptoid oligomers therein. First, the four population maxima near (±90°, ±180°) in conventional Ramachandran scale from -180 to 180° in figure 3b match well with two energy minima near (±90°, 180°) in the conformational energy landscape plotted in scale from 0 to 360° in figure 1 of reference 31. Additionally, the dihedral angles located outside the four maxima in Ramachandran plot in figure 3b are distributed over the regions around the maxima that closely resemble the moderate energy valleys extending from two minima in the conformational energy landscape for disarcosine.³¹ The achiral backbone structure of peptoids means that a given (ϕ, ψ) combination is equivalent to (-ϕ, -ψ), which is confirmed by the center-symmetric nature of both the Ramachandran plot of sarcosine 50mer in figure 3b and the conformational energy landscape for disarcosine by Butterfose et al.³¹ Such similarities between the Ramachandran plot of sarcosine 50mer and the conformational energy landscape for sarcosine dimer imply that the conformational propensity of a basic peptoid dimer unit may be applied to longer-chain peptoid oligomers as a prime folding principle that governs the overall conformation of the longer-chain oligomers. This means that the overall conformation of long-chain peptoid oligomers are mainly driven by local interactions at an individual monomer level rather than long-range intramolecular interactions among monomer units separated far apart in a chain, as commonly observed in secondary structures of standard peptides. Such a locality of the conformational driving force for peptoids may be understood at least in part by the lack of intramolecular hydrogen bonds in peptoid backbone.

The heavily populated combinations of backbone dihedral angle pair (ϕ, ψ) for sarcosine 50mer near (±90°, ±180°) in figure 3b have previously been assigned to cis α_D and trans α_D conformations and their mirror images.^{30, 31} The cis α_D conformation near (-90°, ±180°) is a structure similar to polyproline type I helix, a compact right-handed helix featuring cis amide bonds that is relatively rare in standard peptides. As pointed out in the earlier discussion, the achirality of peptoid backbone structure equally allows a left-handed helical mirror image of the cis α_D conformation near (90°, ±180°). On the other hand, the trans α_D conformation near (90°, ±180°) is similar to polyproline type II helix, an extended left-handed helix with trans amide bonds, which is quite common in peptides and proteins. The polyproline type II helix plays important roles in many biological processes.^{39, 40} Again, a right-handed polyproline type II helix, a mirror image of trans α_D conformation, can exist near (-90°, ±180°). The small population near (120°, -75°) has been previously assigned as C_7β helix, which is energetically less stable than α_D helix. ^{30, 31} Since the (ϕ, ψ) range of cis α_D conformation and of the mirror image of trans α_D conformation overlap each other at around (-90°, ±180°), further analysis is necessary in order to determine the relative composition of the two conformations. The same applies to the mirror image of cis α_D conformation and trans α_D conformation, both sharing a region near (90°, ±180°) in backbone dihedral angles.

The Ramachandran plots of the sarcosine oligomers with different chain lengths reveal that there is a steady increase in relative population of the backbone conformations with ϕ ≈ 90° coupled with a decrease of the conformations with ϕ ≈ -90° as the chain length increases, as shown in figure 4a. Namely, the maximum probabilities of the backbone conformations near ϕ = -90° and ϕ = 90° are almost the same at around 0.07 for sarcosine 5mer, while the conformations near ϕ = 90° are favored by more than three times over those near ϕ = -90° for sarcosine 50mer. The conformations near ϕ = -90° and ϕ = 90° for 10mer and 20mer have peak probabilities roughly halfway between those for 5mer and 50mer, while the chain-length dependence between 10mer and 20mer is much smaller than between 5mer and 50mer. Such a little change in the backbone conformation distributions between 10mer and 20mer is probably due to the limited sampling of the conformations in our simulations. As pointed out earlier, the conformations near ϕ = 90° correspond to trans α_D conformation and mirror image of cis α_D conformation, both of which are left-handed helices. Therefore, figure 4a reveals that the left-handed helical conformations, or trans α_D conformation and mirror image of cis α_D conformation, are increasingly favored over the right-handed helices, or cis α_D conformation and mirror image of trans α_D conformation, for sarcosine oligomers as the chain length increases. Figure 4b is the cumulative sum of the ϕ angle probabilities along ϕ angle coordinate for sarcosine oligomers, featuring two plateaus typical for a two-component system, representing the relative composition between the left-handed (trans α_D plus mirror image of cis α_D) and the right-handed (cis α_D plus mirror image of trans α_D) helices for each sarcosine oligomer. The analysis of the amide bond isomerism, to be discussed later, can offer an additional compositional resolution, allowing a complete determination of the compositions for all four main helical conformations.

Figure 4.

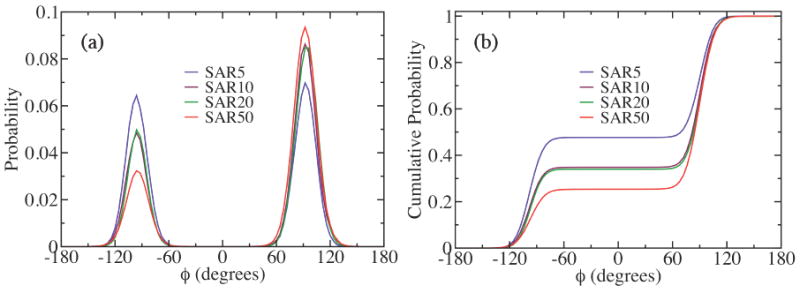
(a) The probability distributions of the ϕ backbone dihedral angle, and (b) the cumulative probability distributions of (a) for sarcosine oligomers with different chain lengths, obtained from the replica exchange MD simulations.

In the case of PMP oligomers, PMP 5mer and 10 mer have scattered Ramachandran signals and show no significant populations in specific helical conformations, while PMP 20mer and 50mer show Ramachandran patterns similar to those of sarcosine oligomers with left-handed helices favored over right-handed helices. (Figure 5) It is rather surprising that sarcosine oligomers favor left-handed helices over right-handed ones as chain length increase, considering that the achirality of the peptoid backbone should in principle result in equal preference between left-hand and right-hand helices. The reason of such propensity for left-hand helices in peptoid oligomers is likely that the system is trapped in a local free energy minimum and cannot get out of it within the simulation time scale. In order to test this hypothesis, we artificially created an initial structure of the sarcosine 10mer with more right-handed than left-handed backbone helical components, and carried out both regular MD at 300K and replica exchange simulation for a temperature range of 300-350K for 50 ns each. We monitored how the artificial initial helical preference evolves in time. The results show that the larger population of the right-handed helix conformation that we imposed initially on the backbone is more or less preserved throughout the entire simulation time in both regular MD simulation and replica exchange simulation, with the fraction of the right-handed helical conformation, denoted by P_RH in figure S2 in Supporting Information, mostly remain intact at ~0.7 in the regular MD case before jumping to even higher value near 0.8 at the final few nanoseconds of the simulation, while the fraction fluctuates marginally around 0.6-0.7 for replica exchange simulation. Further, the difference in the average probability distributions of the ϕ backbone dihedral angles between regular MD and replica exchange simulations is marginal. (Figure S3 in Supporting Information) These results suggest that it may take much longer time in regular MD or much larger temperature range in replica exchange MD for the peptoid oligomers discussed in this work to reach a true equilibrium.

Figure 5.

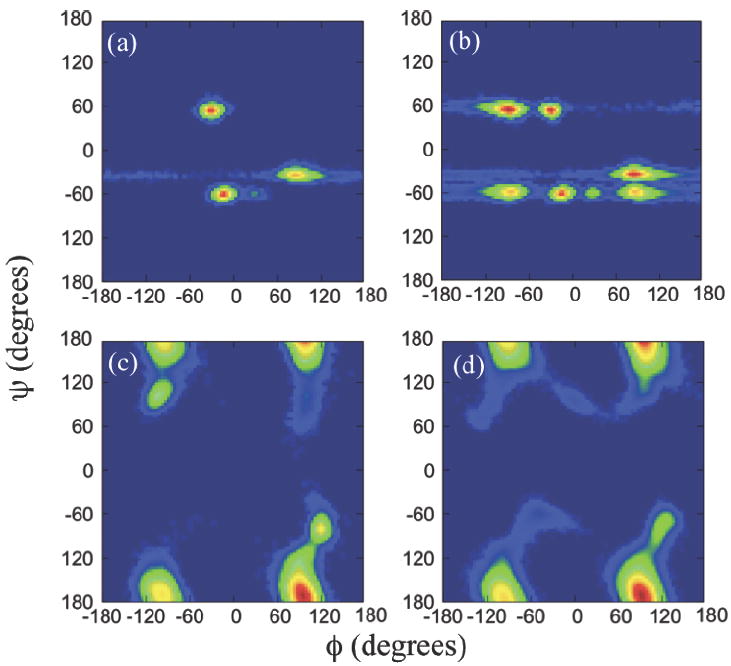
The (ϕ, ψ) Ramachandran plots of PMP (a) 5mer, (b) 10mer, (c) 20mer, and (d) 50mer, obtained from the replica exchange MD simulations. The color scales are the same as those in Fig. 3(a).

To test the temperature effect in replica exchange simulation, we ran another replica exchange simulation of sarcosine 10mer with 82 replicas for a larger temperature range of 300K-600K for 50 ns. The results show that the backbone dihedral composition for the right-handed helix increased to 47.3% for the 300-600K temperature range, compared with 34.8% for the 300-350K temperature range. So the propensity for left-handed helix decreased as a larger temperature range was used for replica exchange simulation. (Figure S4 in Supporting Information) Apparently the higher temperatures allowed the molecule to escape a local free energy minimum and cross some free energy barriers to sample a larger conformational space. The results again suggest that the conformational symmetry breaking of the peptoids in this work is likely to be the result of the molecules being trapped in local minima at the given simulation conditions. Estimating the magnitudes of the free energy barriers for the helical conformational transitions in the peptoid oligomers would be certainly interesting. However it is beyond the scope of this work.

Figure 5 shows the Ramachandran plots of PMP oligomers with different chain lengths. The Ramachandran plots of PMP oligomers with methoxyethyl side chains display the same tendency as sarcosine oligomers of having no similarity to those of peptide counterparts. Comparing figure 5d with figure 3b, one can also notice that the PMP 50mer and SAR 50mer have quite similar Ramachandran plots. Such a similarity in Ramachandran plots is also found between PMP 20mer and SAR 20mer.(not shown) On the other hand, the PMP 5mer and 10mer exhibit scattered distributions of backbone dihedral angles, suggesting dramatically different backbone conformations from those of the sarcosine counterparts that have similar Ramachandran plots as SAR 20mer or 50mer. (not shown) Since the only difference between PMP and sarcosine is the side chain, the dramatic difference in Ramachandran plots for PMP 5mer and 10mer is likely induced by the long, bulky, hydrophilic methoxyethyl side chains on relatively short backbones. Longer chains such as PMP 20mer and 50mer show (ϕ, φ) distributions which are very similar to those of sarcosine counterparts, with a slight increase in C_7β conformation near (120°, -75°) and (-120°, 75°), indicating that the variation in the side chains has little or no effect on the backbone conformation of the longer-chain peptoid oligomers investigated in this study.

It is well known that the backbone amide bonds in standard α-peptides are predominantly in trans configuration and highly planar. In peptoids, however, the amide bonds can readily populate both trans and cis conformations, increasing the conformational diversity in peptoid backbone structure and allowing an access to conformations that are mostly excluded for peptides.^{23, 26} Sui et al. studied the kinetics and equilibration of cis-trans isomerization of the amide bonds in short N-acetylated peptoids using NMR spectroscopy.⁴¹ They found that the fraction of cis conformation in model peptoid monomers range around 30%, and the exchange rate between cis and trans conformations strongly depends on the location of the amide bonds in a given peptoid chain.

We calculated the average relative populations of cis and trans conformations of the backbone amide bonds in both sarcosine and PMP peptoid oligomers from the simulations, and the results are summarized in figure 6. The ω angle that defines the amide bond dihedral configuration shows significant populations of cis conformation (ω = 0°) for both sarcosine and PMP peptoid oligomers except for sarcosine 5mer. The fraction of cis conformations in sarcosine oligomers ranges from 0% (5mer) to 26.3% (20mer), while PMP oligomers overall contain higher fractions of cis amide conformations, ranging between 20.4% (50mer) and 66.7% (10mer). Direct correlation between the fraction of cis amide conformations and chain length is not apparent. However, the exceptionally high cis fraction in PMP 5mer (50.0%) and 10mer (66.7%) may be related with the less structured, scattered backbone conformations implied in their Ramachandran plots in figure 5a and 5b. With higher content of cis conformation that is relatively higher in energy compared to trans conformation, the PMP 5mer and 10mer should form conformations energetically less favorable, likely driven by the bulky side chains, as was discussed above.

Figure 6.

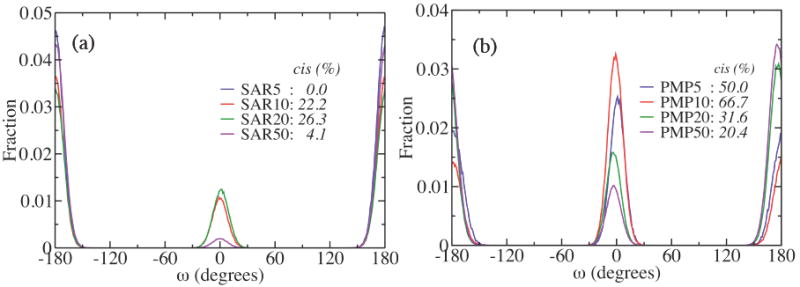
The ω angle distributions obtained from the replica exchange MD simulations for (a) sarcosine and (b) PMP oligomers for the chain lengths n = 5, 10, 20, and 50. The amide bond is in cis conformation for ω around 0°, and trans for ω around ±180°.

By combining the information on the relative fraction of cis vs. trans conformations in amide bonds (Figure 6), which allows us to resolve cis α_D and trans α_D conformations, and the information on the relative fraction of right-hand and left-hand helices available via the population distribution against ϕ angle (Figure 4), we are able to resolve all four major helical conformations in each peptoid oligomer. We can also calculate their relative compositions, with an assumption that every backbone dihedral angle combination in each monomer residue falls into one of the four major helical conformation classes, and other minor populations, such as C_7β, can be ignored. For instance, in case of sarcosine 50mer, the total fraction of dihedral conformations that favors the left-handed helix is calculated as 74.6% by integrating the peak intensity around ϕ = 90° in figure 4a or directly from the cumulative probability in figure 4b. Multiplying this fraction by the fraction of trans amide bond conformations of 95.9% from figure 6a gives 71.5% of the entire dihedral angle pairs favoring “trans and left-handed” helical structure, i.e. trans α_D conformations. This means that an average 36 monomers out of the total 50 monomers in sarcosine 50mer favor trans α_D conformation. One may vary the range of the dihedral angles that defines each helical structure and carry out similar analysis to obtain results with different level of conformational resolution. Table 1 summarizes the relative compositions of helical handedness (right vs. left), the fractions of amide bond isomers (cis vs. trans), and the overall average fraction of each of the four major helical conformations, determined by this approach, in the four sarcosine oligomers, PMP 20mer, and PMP 50mer. The compositions of PMP 5mer and 10mer cannot be determined due to the scattered pattern of their backbone dihedral angles, which prohibits the composition analysis of helical handedness.

Table 1.

The compositions of the major helical conformations in sarcosine and PMP oligomers.

Oligomer	Right-hand helix (%)	Left-hand helix (%)	cis amide bond (%)	trans amide bond (%)	cis αD (%)	trans αD Mirror (%)	cis αD Mirror (%)	trans αD (%)
SAR 5mer	47.7	52.3	0.0	100.0	0.0 [0]	47.7 [2]	0.0 [0]	52.3 [3]
SAR 10mer	34.8	65.2	22.2	77.8	7.7 [1]	27.1 [3]	14.5 [1]	50.7 [5]
SAR 20mer	34.0	66.0	26.3	73.7	8.9 [2]	25.1 [5]	17.4 [3]	48.6 [10]
SAR 50mer	25.4	74.6	4.1	95.9	1.0 [0]	24.4 [12]	3.1 [2]	71.5 [36]
PMP 20mer	30.0	70.0	31.6	68.4	9.5 [2]	20.5 [4]	22.1 [4]	47.9 [10]
PMP 50mer	28.1	71.9	20.4	79.6	5.7 [3]	22.4 [11]	14.7 [7]	57.2 [29]

^*The integer in bracket is the approximate number of monomers in each chain that favors the given conformation.

^**SAR = sarcosine; Mirror = mirror image.

The results in Table 1 show that trans α_D helix is the most favored conformation in all peptoid oligomers, while cis α_D helix is the least favored. This is consistent with the results from quantum mechanical calculations by Baldauf et al.³⁰, which show that trans α_D conformation is the lowest energy configuration among different helical structures and cis α_D becomes increasingly less favored as chain length grows. Since peptoids are center-symmetric with achiral backbone structure the same energetic hierarchy applies to the mirror-image conformations, which can explain the higher fraction of mirror image conformation of trans α_D compared to the mirror image conformation of cis α_D in all peptoid oligomers, except for PMP 20mer where the two conformations occupy similar fractions. Overall, this suggests that, in peptoids, the backbone ω angle for amide bond plays a more decisive role in defining a conformational propensity than the ϕ backbone dihedral angle associated with the helical handedness. This is reasonable because the change in helical handedness in achiral peptoids causes no difference in energy, while trans/cis isomerism of amide bonds induces a significant energetic difference.³⁰

Dynamical characteristics of the peptoid oligomers have been probed via the time correlation functions of the end-to-end distance for the peptoid backbone and the side chains. The time correlation function C(t) of a quantity A(t) is defined as

$$C(t)=\frac{<\delta A(\tau )\delta A(\tau +t)>}{{\sigma }^2(A)},$$ (1)

where δA = A − < A > and σ²(A) =< A² > − < A >², with the bracket representing the ensemble or time average.⁴² The time correlation functions, C(t), of the end-to-end distances for the backbone and the side chains in PMP 20mer, as shown in figure 7, behave in very different ways. That is, the correlation function for the backbone decays very slowly and remains strongly correlated within the given time range of 20 ns. On the other hand, the time correlation functions of the methoxyethyl side chains decay very fast and become completely uncorrelated within 40 ps (the inset in Figure 7). Two drastically different time scales of the end-to-end distance time correlations of the backbone and the side chains imply that the motions of the peptoid backbone and the side chains correspond to very different dynamical regimes. While the methoxyethyl side chains have relatively fast motion and large flexibility, the backbone appears to be quite rigid and the dynamics of it seems much slower. The distinct separation of time scales in dynamics between the side chains and the backbone in the peptoid oligomers is reminiscent of the feature well established in protein dynamics.^43-45 It has been found that the relaxations of side chains in proteins range in the tens of picosecond time scale, while backbones have much slower relaxations with a few tens of microseconds. While the general time scales of the backbone relaxations in proteins are far beyond the time scales of our simulations, the distinct trends in the end-to-end distance time correlation functions between the side chains and the backbone strongly suggest that the peptoid oligomers have dynamical characteristics similar to those of proteins. Simulations that are ~100 times longer would be needed to investigate the backbone equilibrium behaviors, which is far beyond our computational capability.

Figure 7.

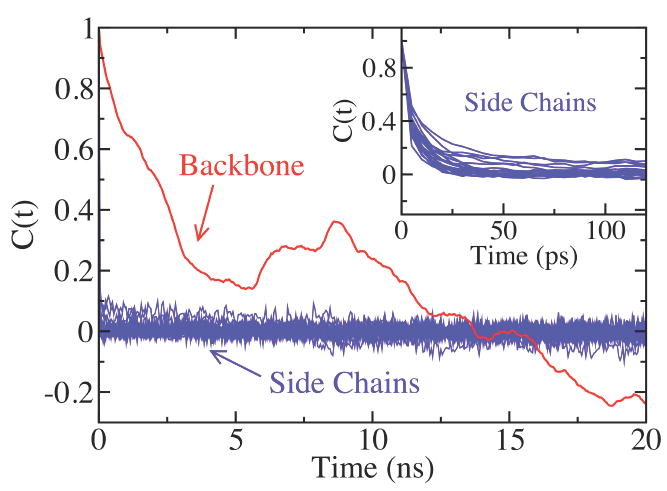
The time correlation functions of PMP 20mer from the regular MD simulation. The time correlation function for the backbone is shown in red, and for side chains in blue. The inset is a zoom-up view of the early-time behavior of the time correlation functions for the side chains. The time correlation functions were calculated for the final 40 ns of the simulation.

Figure 8 shows the snapshots of the sarcosine 50mer backbone structure in ribbon representation at the beginning, in the middle, and at the end of the replica exchange simulation. The monomer segments that change their helical handedness from left-handed to right-handed or vice versa are marked in red color. Seven monomer residues out of the total fifty residues in the chain have successfully crossed the energy barrier eight times (monomer No. 43 made two transitions) between two energy minima at around ϕ = ±90° and made conformational transitions among the three structures. No transition was observed between trans and cis configurations in amide bonds during the simulation. The rigidity of the peptoid backbone structure can be confirmed by the rare transitions of the ϕ angles between left-handed and right-handed helices and no transition between cis and trans amide bond conformations. Meanwhile, the backbone dihedral angles ϕ, ψ, and ω have been observed to fluctuate widely in time during the simulation; as much as about ±30° from the angles that are ideal for the helical conformations, which is the main reason that a well-defined helical conformation is visually not identified in the chain during the simulation despite the fact that, as shown in Table 1, the fraction of the backbone dihedral angles favoring trans α_D conformation is above 70% for sarcosine 50mer. The dihedral angles favoring four different major helical structures randomly mix along the chain, which also hinders the formation of a stable, well-defined helical conformation in chain segments. Similar patterns were observed for the other sarcosine oligomers, with transitions occurring even less for shorter chains. The PMP oligomers showed similar features, with backbone dihedral angles of an individual monomer fluctuating significantly around the optimal angles for helical structures, while the actual transitions between different helices and between cis and trans amide bonds are either very rare or none. The rate constants of the cis-trans transition for amide bonds in some peptoids have been reported to be in the range of 0.030~0.37 s^-1,⁴¹ so it is reasonable that no isomeric transition in amide bonds was observed in our simulations.

Figure 8.

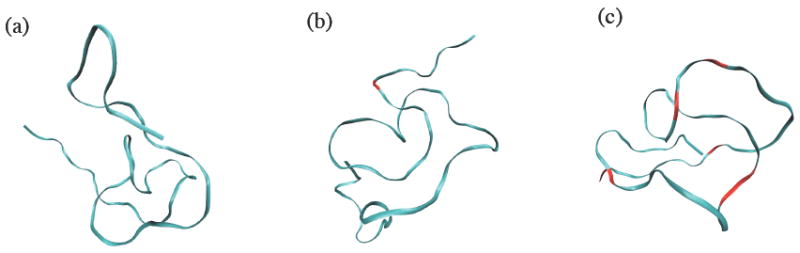
Snapshots of the backbone structure of sarcosine 50mer in ribbon representation at time (a) t = 0, (b) 10 ns, and (c) 20ns, taken from the replica exchange MD simulation. Shown in red color are the locations of monomer residues that made transitions between right-handed and left-handed helices from the previous snapshot.

Figure 9 shows the average radius of gyration, <R_g> for sarcosine and PMP oligomers compared with the peptide counterparts for different chain lengths N, obtained from the replica exchange MD simulations. The <R_g> of peptoid oligomers are consistently larger than those of peptide counterparts. A similar trend has been observed in the regular MD simulations. This implies that the peptoids are relatively open in structure compared to peptides, which may partly be the effect of the lack of intramolecular hydrogen bonds in peptoid backbone. On the other hand, the average fluctuations of <R_g>, represented by the error bars in figure 9, show mixed results with no clear trend in comparison to peptide counterparts. This suggests that the backbone rigidity of peptoids may be as high as that of peptides, and the fluctuation of the backbone conformation is comparable to that of the more compact peptide counterparts despite the relatively open structure of the peptoids.

Figure 9.

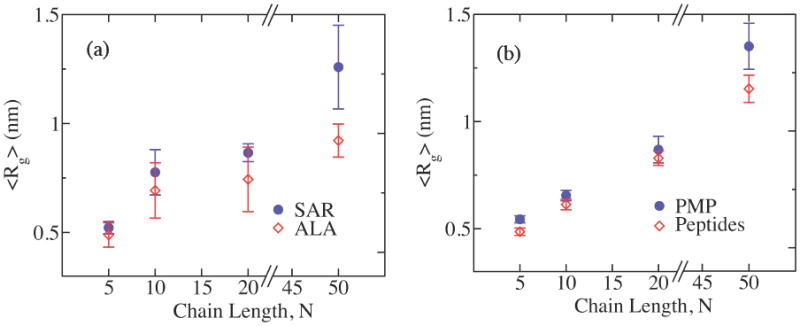
The average radius of gyration, <R_g>, and fluctuations, i.e. the error bars, of R_g for (a) sarcosine and (b) PMP oligomers (blue circles) compared with the peptide counterparts (red open diamonds) for the chain lengths N = 5, 10, 20, and 50, obtained from the replica exchange MD simulations.

The comparison of the temporal profiles of R_g(t) and the end-to-end distance, R_e(t), reveals that each structural quantity can measure the properties of the global conformation of the peptoids with a different sensitivity. Figure 10(a) shows the temporal profiles of R_g(t) and R_e(t) of PMP 50mer in the final 40 ns of the simulations. The overall trend of the two profiles is very similar; they both decrease in the beginning until around 25 ns, then steadily increase until near 45 ns to reach the maxima before decreasing again until the end of the simulations. However, the magnitude of the change in the course of the simulation time is very different between the two quantities; R_g(t) changes relatively little in the range roughly between 1.2 nm and 1.35 nm, while R_e(t) changes much more dramatically between around 0.75 nm and 2 nm. Since both quantities measure the properties of the global conformation of the molecule, as supported by the similar overall temporal trend shown in figure 10(a), we argue that R_g(t) is relatively insensitive to changes in the global conformation of PMP 50mer probably because the conformational fluctuations average out over the entire molecule, while R_e(t) is much more susceptible to the changes in global conformation of the molecule, and hence, is an indicator more sensitive to the conformational changes not only at the level of chain terminals but also at the larger, global scale of the molecule. Figure 10(b) shows two different backbone structures of PMP 50mer at minima and maxima R_g and R_e(t) at times t = 25 ns and 45 ns, indicated by arrows I and II, respectively, in figure 10(a). The conformational changes in the global scale between the two structures in figure 10(b) are apparent, and they are much better captured by R_e(t) compared with R_g(t).

Figure 10.

(a) The time evolutions of radius of gyration (R_g(t), solid blue line) and the end-to-end distance (R_e(t), dotted red line) of PMP 50mer from the regular MD simulations, showing similar overall trends, but with significantly different ranges of fluctuations. (b) The snapshots of the backbone conformations I and II at times t = 25 ns and 45 ns, respectively, near the minima and the maxima for both R_g(t) and R_e(t), as marked with the arrows in (a).

The power-law dependencies of the mean values for some properties of polymers against chain length are well established for different classes of polymers, and provide for a measure of the universal nature of the dependency of the structural properties with number of segments.⁴⁶ Identifying the scaling behavior of such quantities against chain length can, therefore, provide valuable insight into the fundamental nature of the polymer of interest. Even though our peptoids are relatively short, we attempted to determine the scaling behavior of the radius of gyration, i.e. ${\langle R_g^2\rangle }^{1/2}\propto N^{\upsilon }$ where N is the chain length and ν is the scaling exponent, for PMP and SAR by using the data from the replica exchange MD simulations. We found ν to be around 0.4 (0.40 for PMP, 0.37 for SAR), which are between the scaling exponent for a random walk, ν=1/2, and a compact-globule for which ν=1/3. In comparison, the scaling exponents for the peptide counterparts are found as 0.28 for the alanine oligomers, and 0.39 for the peptide counterparts of PMP, each of which is consistently smaller than the expoent of the peptoid counterpart, reflecting the compact nature of peptide oligomers in comparison with peptoids. The scaling exponent of the alanine oligomers is anomalously small and the fitting quality of the data is poor (data not shown), which may be due to the limited incomplete samplings in the current simulations. While the relatively small number and range of chain lengths explored in the study hinder a fair assessment of real scaling exponents, the results appear to suggest that the peptoid chains take relatively collapsed structures that are more compact than random walks (Gaussian chains), but still contain a significant amount of empty space inside. This is consistent with the relatively open structure for peptoids as suggested above.

5. SUMMARY

We have presented the results of the fully atomistic MD simulations of a series of peptoid oligomers with different side chains in aqueous phase with explicit water molecules. To our knowledge, this work is the first application of the classical MD simulation approach to the peptoid-class molecules. The standard OPLS force field parameters have been used without modification for peptoid oligomers in this study. Recent studies^47,48 on proteins and peptides indicate that the standard force field parameters need modifications in order to reproduce the experimentally observed quantities. Therefore it is plausible that the standard force field parameters used for peptoids in this work might also require similar refinements in order to achieve a level of accuracy good enough to reliably predict the system properties. The lack of detailed experimental information does not enable us to measure the accuracy of the force fields and it may be interesting to perform such experiments in order to optimize, if necessary, the force field parameters for peptoids.

The analysis of the simulation results shows that peptoids have unique backbone dihedral angle distributions drastically different from the peptide counterparts. The backbone dihedral angles favoring helical conformations, similar to polyproline type I and type II, have been found to be highly populated. It was found that the backbone dihedral angles favoring the right-handed helical conformation are increasingly more populated as the chain length grows. Unlike in peptides, a significant fraction of amide bonds in peptoid oligomers was found to take cis isomeric configuration, which enables the molecule to take unique conformations inaccessible for peptides. The relative compositions of the four major helical structures have been determined from the distributions of backbone dihedral angles, ϕ and ω. The results show that trans α_D helix and its mirror image conformation is the most favored, while cis α_D conformation is the least favored, which is consistent with the previous studies based on quantum mechanical calculations.

The end-to-end distance correlation times reveal that the peptoid backbone is rigid and dynamically slow despite the lack of backbone intramolecular hydrogen bonds. The side chains, on the other hand, are highly mobile. The detailed analysis of the backbone dihedral angle sequences in individual snapshots suggests that the transitions between different helical conformations are rare or non-existent during the simulations, while the high degree of temporal fluctuations of the backbone dihedral angles and the random mixing of dihedral angles favoring different conformations severely hinder the formation of a well-defined helical conformation in the peptoid chains. The peptoids are considered to assume more open, swollen structures compared to peptides as suggested from the average radius of gyration. The temporal profiles of R_g(t) and R_e(t) suggests that the end-to-end distance is a better representation of the global conformational changes of the peptoid. Finally, the dependence of the radius of gyration on chain length suggests that the peptoids have average structures that are more compact than Gaussian chains but more open than collapsed globules.

The finding of this work can serve to explain the ability of the peptoids to act as non-fouling agents when end-grafted to surfaces¹³, in particular the ability of the side chains to freely relax in relatively short time scales, as well as the variation of the structure of the backbone between different, but well defined configurations.