Medical ultrasound: imaging of soft tissue strain and elasticity

Abstract

After X-radiography, ultrasound is now the most common of all the medical imaging technologies. For millennia, manual palpation has been used to assist in diagnosis, but it is subjective and restricted to larger and more superficial structures. Following an introduction to the subject of elasticity, the elasticity of biological soft tissues is discussed and published data are presented. The basic physical principles of pulse-echo and Doppler ultrasonic techniques are explained. The history of ultrasonic imaging of soft tissue strain and elasticity is summarized, together with a brief critique of previously published reviews. The relevant techniques—low-frequency vibration, step, freehand and physiological displacement, and radiation force (displacement, impulse, shear wave and acoustic emission)—are described. Tissue-mimicking materials are indispensible for the assessment of these techniques and their characteristics are reported. Emerging clinical applications in breast disease, cardiology, dermatology, gastroenterology, gynaecology, minimally invasive surgery, musculoskeletal studies, radiotherapy, tissue engineering, urology and vascular disease are critically discussed. It is concluded that ultrasonic imaging of soft tissue strain and elasticity is now sufficiently well developed to have clinical utility. The potential for further research is examined and it is anticipated that the technology will become a powerful mainstream investigative tool.

1. Introduction

On the one hand, ultrasonic imaging is a mature medical technology. Nearly 22 per cent of all the 38 million imaging procedures carried out in 2009–2010 in National Health Service hospitals in England (population 51 million) were ultrasonic investigations, which was second only to those carried out with traditional X-radiography and fluoroscopy, and 30 per cent more than all of those using X-ray computed tomography, magnetic resonance imaging (MRI) and nuclear medicine techniques combined [1]. Ultrasonic imaging is generally real time, it is highly acceptable to most patients, exposures used in current practice are considered to be safe and the equipment is generally less expensive than that of other imaging technologies.

On the other hand, ultrasonic imaging techniques are the subject of intense research activity and the capabilities of new approaches to provide novel information of considerable actual and potential clinical value are highly attractive. For instance, although most contemporary ultrasonic imaging techniques are limited to the display of anatomy, tissue motion and blood flow, the emerging technology of ultrasonic imaging of soft tissue strain and elasticity aims at providing information about the mechanical properties of tissues, such as their hardness or stiffness.

It is the mechanism of the contrast in the image which is one of the most important characteristics that distinguishes the practical capabilities and limitations of one particular imaging technology from those of others [2]. For instance, the contrast in X-ray imaging owes its origin fundamentally to differences in the atomic numbers of the materials which make up the structures being imaged, whereas that in MRI corresponds to the distribution of protons and differences in their relaxation times. In traditional ultrasonic imaging (see §5), the signals which form the image are basically owing to reflection and scattering of ultrasound where there are differences in the characteristic impedances of the media being imaged. The characteristic impedance is equal to the product of the density and the longitudinal wave speed in the medium: the latter depends on the bulk modulus of the medium (see equation (3.4)). Consequently, techniques for imaging strain and elasticity (i.e. Young's or shear modulus) provide unique information.

The only technology that currently comes anywhere near to competing with ultrasonic elastography is magnetic resonance elastography (MRE) [3,4]. MRE is not restricted by the presence of bone or gas, is sensitive to motion in three dimensions with high-speed volume acquisition, can be carried out by relatively unskilled practitioners and the interpretation of its results is quite straightforward. In comparison with this, ultrasonic estimation of soft tissue strain and elasticity is generally more accurate and precise, it is relatively fast, access to the scanners is much more convenient for patients and practitioners, and the overall cost per investigation is much lower.

2. A brief history of palpation in medical diagnosis

Depending on the symptoms, when a patient first seeks medical advice, the doctor, after taking the clinical history, very often begins to make a diagnosis by means of a physical examination. Classically, this has three aspects: palpating the abdomen, percussing the chest and listening with a stethoscope.

In the process of palpation, the practitioner applies manual pressure to the patient's skin and in this way senses the position, hardness, mobility and pulsation of structures within the body.

In ancient Egyptian medicine, palpation was considered to be of fundamental importance. Quoting from the Ebers papyrus,¹ which dates from about 1550 BC, and commenting on other sources [5], ‘Palpation of the pulse was very important and noted in the papyri. Also that of the abdomen was no less important: “If thou examinest a man suffering from a resistance in his cardia [meaning the viscera], and thou findest that it goes and comes under thy fingers like oil in a leather bag…then thou shalt examine him lying extended on his back. If thou findest his belly warm and a resistance in his cardia, thou shalt say to him: it is a liver case. Thou shalt prepare the secret herbal remedy which is made by the physician…” The palpation of tumors was detailed and painstaking…Wounds were also felt with the same care: a fractured skull was compared to a punctured earthen jar, the pulsations of the brain were compared to those of an open fontanelle. Fractures were distinguished from luxations by feeling crepitus under the fingers’.

Similarly, palpation has always been important in traditional Chinese medicine. Touching the body to detect the pulse in the radial artery and, from the character of the pulsations, to diagnose disease conditions is a highly refined art which dates back at least to about 500 BC, the time of the physician Bian Que [6].

In Western medicine, it may be surprising that the practice of palpation was not put on a reputable basis until the 1930s. Quoting from Shorter [7], reporting the experience of Karl Stern, a resident physician in Frankfurt in the 1930s: ‘There was, quite aside from the world of sight, an entire world of touch which we had never perceived before. In feeling differences of the radial pulse, you could train yourself to feel dozens of different waves with their characteristic peaks, blunt and sharp, steep and slanting, and the corresponding valleys. There were so many ways in which the margin of the liver came up towards your palpating finger’.

Thus, nowadays, medical practitioners glean much useful information from manual palpation. Essentially, what they detect is the elasticity of tissue, and the differences in the elasticities of different tissues, sensed though the displacement of tissue (i.e. strain) resulting from applied pressure (i.e. stress), whether the origin of the applied pressure is internal (e.g. owing to a pulse of blood travelling along an artery) or external (e.g. owing to the hand of the examiner).

Manual palpation, although an indispensable part of the contemporary routine physical examination of the patient, does have its limitations. It is usually capable of detecting the pulsation of superficial arteries, such as the radial and carotid arteries. Within the abdomen, however, palpation can generally only detect structures or abnormal masses which are quite large in size and which have elasticities that differ from those of neighbouring tissues by considerable amounts; it becomes increasingly unreliable for those which are smaller and deeper. Moreover, the interpretation of palpation is completely subjective: it does not provide any quantitative data.

There are some types of cancer for which appropriate groups of supposedly normal individuals are encouraged regularly to examine themselves by manual palpation for signs of abnormality. Thus, young men should palpate their scrotums to search for changes which might be an early warning of testicular cancer, and women should examine their breasts in case a lump should indicate the presence of a malignant tumour. Similarly, digital rectal examination by a skilled practitioner can usefully reinforce the reliability of the diagnosis of prostate cancer. The reasons why this kind of examination is justified are that malignant tumours are, in general, harder than their surrounding normal tissues and that, although the false-negative and false-positive rates are rather high, the benefits of early diagnosis and treatment can far outweigh the costs—both financial and social—of false-positives.

3. An elementary tutorial on elasticity

The elasticity of a material describes its tendency to resume its original size and shape after being subjected to a deforming force or stress. Fluids resist a change in volume, but not in shape: they possess only volume elasticity. Solids resist changes in shape and volume: they possess rigidity or shear elasticity, as well as volume elasticity. The change in size or shape is known as the strain, which is expressed as a ratio (e.g. the change in length per unit length). The strain is produced by a system of forces; the force acting on unit area is known as the stress.

The basic principles of elasticity can be found in most textbooks on materials science (e.g. [8]). In summary:

For a homogeneous isotropic solid, the ratio of stress/strain is a constant, called the modulus of elasticity. Three moduli (with units of N m⁻², or Pa) are commonly used to define its elasticity:

Young's modulus (longitudinal elasticity), E = (stress)/(strain).

Shear or torsion modulus (rigidity), G.

Bulk or volume modulus (volume elasticity), K.

When a material is stressed, its breadth may contract as its length extends. This is defined by a constant called Poisson's ratio, which is given by

Three linear elastic constitutive equations define the relationships between these four constants,

3.1

3.2

3.3

Solids can support mechanical waves in four principal modes, depending on the way in which the particles in the solid move during wave propagation. In longitudinal (or compressional) waves, the particles move in the direction of propagation, whereas in transverse (or shear) waves, they move in the direction normal to the direction of propagation. The other principal wave modes are surface and plate waves, but these are hardly relevant to propagation in biological soft tissues and so they are not given further consideration here.

The speeds at which mechanical waves propagate in a solid are given by the following equations:

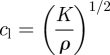3.4

and

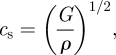3.5

where c_l is the longitudinal wave speed, c_s is the shear wave speed and ρ is the tissue mass density.

For homogeneous isotropic solids subjected to increasing tension, Hooke's law (i.e. strain is directly proportional to stress) applies, until the elastic limit is reached and, eventually, fracture failure occurs.

Some materials exhibit both elastic and viscous properties when subjected to stress and the relationship between stress and strain is time dependent. A viscoelastic material can be simply modelled as an elastic component coupled with a viscous component which acts as a damper that delays the stress–strain response without affecting its asymptotic value. Yet, other materials exhibit poroelastic properties. A porous material is one in which a solid matrix is permeated by an interconnecting network of fluid-filled pores. When considering the stress–strain relationship in a poroelastic material, the matrix can be modelled with elastic properties and the fluid is spatially redistributed over time in the material in order to accommodate its deformation.

4. The elasticity of biological tissues

The basic component of biological tissue is the cell, which is typically 5–10 µm in diameter. Enclosed within the cell wall (which itself is far from being a simple membrane) is the cytoplasm, which contains microscopic structures such as the nucleus and the mitochondria. There are five primary types of soft tissues. These are: epithelial tissue, which is made up of cells packed tightly together to form continuous sheets that serve as the linings of structures and organs; connective tissue, usually containing strands of collagen, which supports and adds structure to the body; parenchymal tissue, which is the functional tissue of organs; muscle tissue, which has the ability to contract in response to electrical signals; and nerve tissue, which has the ability to generate and conduct electrical signals.

In addition to the soft tissues, there are several kinds of hard tissues, principally bone and teeth. The mechanical properties of vertebrate hard tissues have been extensively studied (e.g. [9,10]). Hard tissues are not readily amenable to ultrasonic measurement, however, because of their relatively high densities and ultrasonic attenuations, and so are outside the scope of the present paper.

An organ is a structure that contains at least two types of tissues functioning for a common purpose. Examples of organs include skin, liver, kidney, heart and brain. The mechanical properties of tissues cannot realistically be described in terms of simple agglomerations of homogeneous cells; rather, tissues have microscopic and macroscopic organizations which need to be considered in the context of their multiple scales.

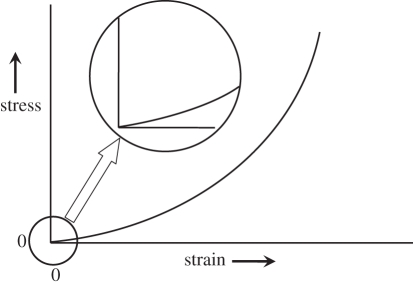
Figure 1 shows the typical relationship between stress and strain in soft tissues. With the stress increasing from zero, the strain increases rapidly as free fluid is exuded, after which the ratio of stress over strain (Young's modulus) can be considered to be linear for small changes (i.e. for strains of less than a few per cent), but the elastic modulus becomes progressively greater with increasing strain. Consequently, the conditions under which any particular value was measured need to be specified. A further complication is that tissue may be viscoelastic (which may manifest itself as hysteresis on relaxation of the stress), poroelastic, anisotropic or contractile, or any combination of these, quite apart from being normal or modified by disease. Other factors which may be relevant are the age of the tissue, its temperature, and whether it is in vivo, in vitro or fixed.

Figure 1.

Idealized stress–strain relationship for soft tissues. The inset (with stress on a magnified scale) shows that, when tissue is stressed, the strain initially increases rapidly (corresponding to the elimination of free fluid), after which the relationship is effectively linear over a small increase in stress. With further increase in stress, the tissue becomes strained decreasing rapidly (as it approaches the limit of its elasticity). The practical implication of this is that, in order to obtain reproducible and useful values of Young's modulus, the tissue needs to be slightly statically preloaded and the measurement needs to be made over a small increment in stress (i.e. in the linear region).

The literature is bereft of data for the bulk modulus of soft tissues. Surprisingly, standard biomechanics textbooks (such as [11]) are almost completely silent in this respect. Indeed, it seems that the best that can be done to gain insight into this is to use equation (3.4) to calculate the probable range of K from published values of the speed of sound (c_l) and density (ρ) for soft tissues. Even after 20 years since its publication, there is one book [10] which is arguably still the best source of reference. Omitting data for ‘soft tissues’ such as the lens of the eye, cartilage, skin and tendon, but including all other normal and pathological soft tissues, values for c_l range from 1412 m s⁻¹ in fat to 1629 m s⁻¹ in muscle; the corresponding values for ρ are 916 and 1060 kg m⁻³, respectively. Substituting these values for c_l and ρ in equation (3.4) gives an indication of the value of K; thus, K for soft tissues must range from about 1800 MPa in fat to about 2800 MPa in muscle.

In the literature, it is usual for values of Young's modulus to be reported, rather than those of shear modulus. For soft tissues, however, Poisson's ratio is usually between 0.490 and 0.499. This is because tissue is almost incompressible. Consequently, from equation (3.2),

4.1

It is the value of G which is required for the calculation of shear wave speed from equation (3.5) and so, in this review, equation (4.1) is used for convenience whenever conversion from values of E to those of G—and vice versa—is necessary.

It is rather disappointing that the published data for Young's moduli of biological tissues, many of which are listed in table 1, are often of only limited quantitative use. There are wide variations, particularly between those reported by different authors—even for tissues of the same types. Some of these differences may be owing to the sometimes indiscriminate treatment of large strains in Lagrangian (i.e. relative to the original length) or Eulerian (i.e. relative to the strained length) representations (this is not problematic with small strains). Moreover, the data are sparse (table 1 is actually quite a comprehensive compendium). Nevertheless, it can reasonably be concluded that typical values of Young's modulus are about 10 kPa for parenchyma, 20 kPa for muscle and 50 kPa for connective tissue. Table 1 also includes data for rubber (which might intuitively be thought to have elasticity similar to that of soft tissue, but clearly does not) and for a water-based material consisting of gelatin and agar (which is one of the family of tissue-mimicking materials: see §6.3).

Table 1.

Published values of Young's modulus for various types of tissues and other relevant materials. Where the range of conditions of measurement were specified by the authors, the data are for low static preloading, low strain and low frequency. Ca, carcinoma.

tissue	type	E (kPa)	reference
breast	unspecified	29	[12]
		21–23	[13]
	adipose	19	[14]
		1.9	[15]
	ductal Ca	25	[14]
	in situ	12	[15]
	glandular	33	[14]
	fibrous	110	[14]
		1.8	[15]
	invasive Ca	93	[14]
cervix	unspecified	30–90	[16]
kidney	unspecified	10	[17]
		6	[13]
liver	unspecified	13	[18]
		10–17	[19]
		7–10	[13]
		1–3	[20]
		0.4–1.7	[21]
	normal	10	[22]
		0.6–1.1	[23]
	focal nodular	1.1–2.5	[23]
	hyperplasia
	chronic hepatitis	35	[18]
	cirrhosis	52	[18]
		1.1–4.9	[23]
	VX2 Ca	0.3–0.9	[20]
	cholangiocarcinoma	3–12	[23]
muscle	unspecified	14–16	[13]
		10–40	[20]
		7–57	[24]
		1.2–1.8	[21]
	intercostal	100	[22]
	cardiac (systole)	100	[25]
	cardiac (diastole)	10	[25]
	along fibres	13	[26]
	across fibres	5.3	[26]
	VX2 Ca	2–8	[20]
prostate	unspecified	0.8–4.0	[20]
	normal	62–69	[14]
		17	[27]
	benign prostatic	36	[14]
	hypertrophy
	carcinoma	100	[14]
		24	[27]
thrombus	unspecified	8–38	[28]
uterus	unspecified	30–90	[16]
	leiomyoma	60–220	[16]
rubber	soft	990–3000	[29]
agar 3% +		70–100	[20]
gelatin 3%

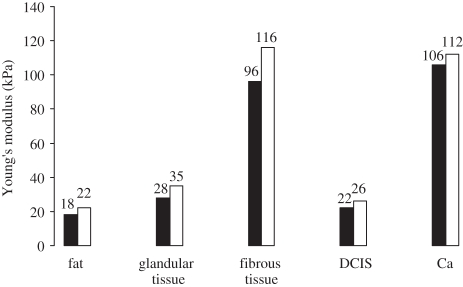
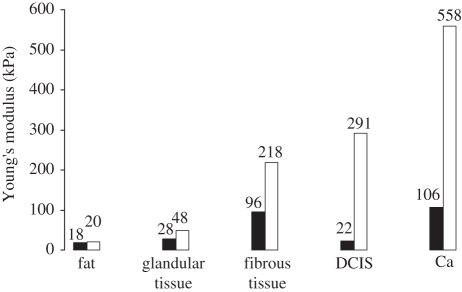
Although the origins of many of these data are inadequately specified, those in Krouskop et al. [14] are a notable exception. For various types of breast tissues, figure 2 summarizes the results of their mechanical measurements at loading frequencies of 0.1 and 4 Hz with 5 per cent static loading, and figure 3, summarizes those for static loadings of 5 and 20 per cent with a 0.1 Hz loading frequency. From figure 2, it is apparent that Young's modulus is not greatly dependent on the loading frequency, at least below 4 Hz, irrespective of the tissue type. For some types of tissues, however, figure 3 shows that Young's modulus is highly dependent on the degree of static loading and that the ratios of Young's moduli of different types of tissues (i.e. their dynamic range) are greater at higher static loadings.

Figure 2.

Young's moduli of different types of breast tissues, measured with the same static preloading (5%) but at two loading frequencies (0.1 Hz, black bars; 4 Hz, white bars). Although the measured value of Young's modulus increases slightly with the loading frequency, the effect is not particularly marked. The practical implication of this is that, provided that the rate of change of the tissue displacement for the measurement is slow (i.e. quasi-static), static conditions can be assumed to apply. Data from Krouskop et al. [14]. DCIS, ductal carcinoma in situ.

Figure 3.

Young's moduli of different types of breast tissues, measured at the same (quasi-static) loading frequency (0.1 Hz) but at two levels of static preloading (5%, black bars; 20%, white bars). The measured value of Young's modulus increases markedly with the level of static preloading. The practical implication of this is that, in order to obtain reproducible measurements of Young's modulus, the level of static preloading (provided that it is sufficient for the free fluid to be eliminated) should be kept as small as practicable. Data from Krouskop et al. [14].

It has been stated [30] that the shear modulus (which is approx. equal to one-third of Young's modulus) of soft tissues varies over several orders of magnitude, whereas the variation in the bulk modulus is significantly less than one order of magnitude. This generalization has been perpetuated in the subsequently published literature. Within groups of broadly similar types of tissues, however, the shear modulus data which they quoted are actually in narrower ranges, not much exceeding one order of magnitude. What is really important is that Young's moduli of different types of tissues, including abnormal tissues, may be markedly different in structures in which the lack of significant difference in bulk moduli makes tissue characterization by traditional ultrasonic scanning problematic (see §5). In the breast, for example, the bulk modulus hardly varies in different types of tissues from about 2000 MPa, whereas Young's modulus typically ranges from about 20 kPa in fatty tissues to about 100 kPa in carcinoma.

5. The physical principles of pulse-echo and doppler ultrasound

The evolution of medical ultrasonics can be traced through contemporary reviews (see [31–36]). For an up-to-date tutorial, see Halliwell [37]. A brief summary of the physical principles is given below.

In order to be clinically useful, an ultrasonic imaging system typically needs to be able to resolve structures of around a millimetre in size at depths of up to around 150 mm. Ultrasound travels at a speed of about 1500 m s⁻¹ in soft tissues; this means that the frequency needs to be in the low megahertz range because the wavelength, which is one of the factors that determine the spatial resolution and which is inversely proportional to the frequency, is, for example, 0.5 mm at 3 MHz. A narrow beam of ultrasound is radiated by an aperture which is, say, at least 10 times the wavelength in size; a transducer, typically polarized lead zirconate titanate, produces a pulse of ultrasound when excited by a brief electrical pulse. The tissue to be imaged contains reflectors and scatterers that give rise to echoes which may be detected by the transducer, delayed in time according to their distances from the transducer (i.e. by about 1.33 µs mm⁻¹).

The attenuation of ultrasound in soft tissues is about 0.2–0.5 dB cm⁻¹ MHz⁻¹. Thus, attenuation increases with both distance and frequency, and this limits the penetration (i.e. the depth from which the echoes have amplitudes sufficient to be detected above the noise) at any given frequency. In practice, this means that a frequency of about 3 MHz is optimal for abdominal scanning, where a penetration depth of up to 150 mm may be appropriate.

Thus, pulse-echo ultrasonic imaging is based on the principle that a directional beam of pulsed ultrasound can be generated and that echoes may be detected from reflectors and scatterers in the beam, delayed in time according to their depths.

Pulse-echo information is commonly displayed as: an A-scan (with the ultrasonic beam in a fixed position within the tissues and with the echoes being displayed as deflections of the ultrasonic timebase); a two-dimensional B-scan (with the beam being swept through a two-dimensional plane within the tissues and with the position and direction of the ultrasonic timebase on the display, brightness-modulated by the echoes, being coupled to that of the ultrasonic beam); or as an M-mode trace (with the beam in a fixed position within the tissues, within which echo-producing targets are moving along the beam, to produce a time-position recording by having a slow-speed timebase moving orthogonally to the direction of the brightness-modulated ultrasonic timebase on the display). B-scanning is usually performed in real time (i.e. typically at a frame rate of more than 20 s⁻¹); by acquiring echoes from a volume of tissue, three-dimensional imaging is also possible.

If the ultrasound is reflected or scattered by targets with a component of motion along the axis of the ultrasonic beam (e.g. by pulsatile blood flow), the echoes that are received are shifted in frequency by the Doppler effect. For physiological target velocities, the Doppler shift frequency lies in the audible range. The operator may simply listen to these signals or, by pulsing the ultrasound to provide depth information, the signal may be processed, for instance, to code two-dimensional B-scans with colour according to the relevant values of blood flow velocity.

The reflection and scattering of ultrasound on which pulse-echo and Doppler techniques depend occur (according to the size of the target in relation to the wavelength of the ultrasound) where there are changes in the characteristic impedance of the constituents of tissue. The characteristic impedance of a material is equal to ρc_l, where ρ is its density and c_l is the longitudinal wave speed. The important point here is that, as equation (3.4) shows, the speed of sound c_l depends on the bulk modulus K and not on the shear modulus G, so the contrast in pulse-echo images conveys no direct information about Young's modulus of the tissue.

6. Techniques for ultrasonic imaging of soft tissue strain and elasticity

6.1. Introduction

6.1.1. Historical origins

The study of the behaviour of vibrating body tissue has a long history. For instance, the theory to characterize the propagation of shear, longitudinal and surface waves in which soft tissue was treated as an elastic viscous compressible medium was developed nearly 60 years ago [38]. It was not until some 30 years later, however, that imaging technologies—led by ultrasonic technology—reached a stage of refinement which enabled the results of this and related work to begin to be exploited to provide information of actual or potential clinical value, with the near-simultaneous publication of the first independent descriptions of the measurement of soft tissue motion using the correlation between sequential ultrasonic echo wavetrains [39,40].

The A-scan from blood (and, by extension, that from any collection of randomly distributed scatterers, such as those in solid soft tissues) owes its origin to the scatterers in the volume corresponding to the resolution cell (i.e. the volume of tissue instantaneously occupied by the ultrasonic pulse as it travels along the beam through the tissue) [41]: the ultrasound scattered by blood flowing in a direction perpendicular to the ultrasound beam decorrelates according to the blood flow velocity and the width of the ultrasonic beam. By experimentally measuring the value of the correlation coefficients between A-scans acquired at known tissue displacements, it was subsequently shown that tissue motion in the liver owing to blood vessel pulsation could be observed and it was speculated that the motion was dependent on the elasticity of tissue and that the method, despite being subject to large error, might be used to determine the state of the tissue, both in diffuse conditions and in localized lesions [39]. Only the limitations of the autocorrelation of demodulated A-scans were discussed and, thus, the opportunity was missed to comment on the possibility that cross-correlation of A-scans might have a role in directly observing tissue displacement, strain and elasticity.

In the study of Wilson & Robinson [40], the motion of liver tissue induced by vascular pulsation was also observed: both the phase changes and the autocorrelation functions were estimated. It was concluded that relative elastic properties of tissues could be inferred from these measurements and that this might provide clinically useful diagnostic information.

A paper was published in 1983 by Fujimoto and his colleagues—in Japanese—which seems to have been the first to describe the use of dynamic tests ultrasonically to estimate the compressibility and mobility of breast tumours, by applying pressure with the probe of a two-dimensional scanner. Based on this paper, it was subsequently shown [42] that breast masses which deform easily and are mobile are usually fibroadenomas, whereas those which deform easily but are fixed are usually cysts and those which are both incompressible and fixed are almost certainly carcinomas.

Measurements of the velocity of externally excited low-frequency (about 10 Hz) mechanical waves propagating in tissue, made using a one-dimensional ultrasonic pulsed Doppler system, gave estimates that were in very close agreement with the values of the elastic modulus obtained using a commercial testing machine at strains of up to 20 per cent for the relaxed muscle in the legs in volunteers [43]. This approach was further developed [44] using higher excitation frequencies (between 100 and 300 Hz) and a two-dimensional real-time ultrasonic imaging system. The Doppler signals were analysed to generate two-dimensional phase maps, from which the velocities of the low-frequency shear waves propagating in an agar phantom containing graphite powder scatterers and in porcine muscle were calculated in the direction normal to the moving phase fronts. At excitation frequencies below about 175 Hz, the measured values were almost independent of frequency, implying that the effect of shear elasticity dominated over that of shear viscosity. This important paper ended with the presentation of in vivo images of a human liver. It was concluded that ‘Although these results are preliminary ones, it may be said that the method proposed here gives a useful information [sic] about mechanical properties of the tissues’. The dependence of velocity on elasticity was recognized (see equation (3.5)), but the possibility of elasticity imaging was not specifically mentioned.

There are several methods that involve the use of ultrasound by which the elasticity of soft tissues can be investigated, but which are outside the scope of this review. For instance, neither Doppler tissue imaging of the myocardium [45]—which is essentially a variant of ultrasonic Doppler colour flow imaging, with the rejection filter threshold selected to display the relatively strong echoes from the tissue rather than the weaker echoes from the blood and which provides information about myocardial dyskinesia—nor the measurement of the arterial blood flow pulse wave velocity [46]—which increases with hardening of the vessel—depend on the direct measurement of either the localized tissue strain or the localized shear wave speed. Except where reference to such topics helps the context, they are not discussed in this review.

Thus, the foundations on which ultrasonic imaging of soft tissue strain and elasticity are built had been firmly laid by the end of the 1980s. The remainder of §6 describes the various approaches which have subsequently been developed and, in many cases, introduced into clinical practice.

6.1.2. Overview of strain and elasticity imaging approaches

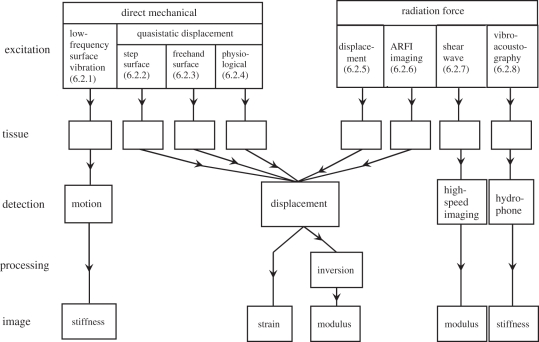
As illustrated in figure 4, the first stage in elastography involves the excitation of the tissues. Excitation can be by direct mechanical means or by ultrasonic radiation force. The excitation results in (quasi)static or dynamic tissue displacement, the latter being accompanied by the generation of shear waves. Detection of the effects of excitation can be by the ultrasonic Doppler effect, by ultrasonic pulse-echo methods or by acoustic emission. Finally, the resultant information can be displayed as images, either directly of the spatial distributions of strains or shear waves or of elastic moduli or tissue stiffnesses. Usually, the elastograms² (whether of strain, elastic modulus or stiffness) can be fused with the corresponding ultrasonic B-scans, as this facilitates the identification of the anatomical structures to which they relate.

Figure 4.

Overview of approaches to elastography. The methods of excitation are classified broadly as being by direct mechanical action or by radiation force: the section number in the paper corresponding to each technique is shown. The method of detecting and processing the effect of the excitation is also shown for each technique, as is the characteristic (stiffness, strain or (Young's) elastic modulus), which is displayed in the corresponding image. ARFI, acoustic radiation force impulse.

Tissue strain is a surrogate for tissue stiffness, where stiffness can be considered to be the representative of what might be felt with manual palpation: low tissue strain corresponds to high tissue stiffness and vice versa. Thus, in practice, clinically useful information can often be provided by strain imaging. In the simplest of geometries, if both the stress and the strain are known, the elastic modulus is given by their ratio. In real anatomical and pathological situations, however, the boundary conditions are such that the estimation of the shear modulus is far more complicated: the inverse problem that needs to be solved is to identify what distribution of elastic modulus would be consistent with the observed distributions of stress and strain.

Generally, in mechanical excitation methods (often called low-frequency or quasi-static displacement methods), the displacement is kept so small that the resultant tissue strain is never more than a few per cent, and usually very much less. The ultrasonic measurement of the displacement depends on the deterministic nature of ultrasound backscattered by tissue. The wavelength of the ultrasound (for example, about 500 µm in soft tissues at the typical frequency of 3 MHz) is very much greater than the size of the small scattering structures which are the origin of the speckle, which characterizes ultrasound backscattered by solid soft tissues [48]. Consequently, the assumption that the echoes from a small volume of tissue can retain coherence even when their phase changes as the result of displacement may have at least limited validity, and this is the basis of the ultrasonic measurements such as those made by cross-correlation of echo wavetrains acquired before and after the application of stress. Moreover, because the magnitude of the strain is small, it is a reasonable assumption that the echoes from any given small volume of tissue before and after being strained can be meaningfully cross-correlated.

If the compressor used for direct mechanical excitation is bigger than the homogeneous tissue specimen and free-slip conditions exist, the situation is quite straightforward. It becomes more complicated when the compressor is smaller than the specimen, as, in practice, it usually is: it may not then be realistic to assume that the compression is uniaxial [49].

Radiation force excitation methods depend on the fact that, when an ultrasonic wave is absorbed or reflected, a force in the direction of propagation of the wave is the result. With complete absorption, the relationship is

6.1

where F is the force, W is the ultrasonic power and c_l is the longitudinal speed of propagation. For example, complete absorption of an ultrasonic wave travelling in water (or soft tissue) with a power of 1 W results in a force of about 0.7 mN, which is roughly equal to the force of gravity acting on a mass of 70 mg. As illustrated in figure 4, there are several ways in which this phenomenon can be applied in elastography.

As tissue volume can be considered to be incompressible, measurements in only one direction in a three-dimensional volume are sufficient to allow Young's modulus to be determined. (Modest precompression of tissue is necessary to minimize the blood and free fluid volume, so that the tissue can then be assumed to be incompressible.) Another necessary assumption is that the tissue is locally homogeneous; inaccurate results are obtained near boundaries between different kinds of tissues and this may limit the window size for cross-correlation. Internal and external tissue boundaries can have marked effects on the distribution of applied stresses and this can make it problematic quantitatively to analyse strain images [50]. An advantage of radiation force excitation is that focused ultrasound can produce highly localized motion and regions containing boundaries can usually be avoided.

Dynamic methods are limited by the ability to propagate shear waves deep into tissue because of their relatively rapid attenuation. Static methods have the opposite problem: movement at any point in tissue will affect all other points and this must be taken into account in the estimation of Young's modulus.

In elastography, the signal-to-noise ratio (SNR_e) and the contrast-to-noise ratio (CNR_e) of the target to the background are commonly used to assess the accuracy of strain estimation methods. These are defined as follows [51,52]:

6.2

and

6.3

where μ is the mean measured strain and σ is the standard deviation in the measured strain in the region of interest.

6.1.3. A brief summary of some relevant published reviews

Some reviews of elastography that have already been published are as follows (in chronological order):

1996

This landmark review [53] was published soon after the opening of the era of ultrasonic imaging of soft tissue strain and elasticity. It is remarkable for its prescience in the areas of elasticity data, source excitation, tissue models and boundary conditions.

1998

In this review [54], the principles of quasi-static step displacement ultrasonic elastography are discussed in the context of medical image processing. Some early clinical results are presented.

1999

This review [55] was written as an introduction for mechanical engineers and others (as distinct from clinicians) to the then quite novel concept of elastography. It is a comprehensive treatment of the contemporary state of the art.

2002

This review [56] aimed to expose, to a mainly clinical readership, the creation and display of ‘elastograms’ showing local strains, Young's moduli and Poisson's ratios in tissues subjected to quasi-static displacements.

2003

This review [57] discusses several methods of estimating tissue hardness using internal or external means of applying stress and several associated methods of detecting the resulting strain, aimed at imaging mechanical characteristics of tissue. Both ultrasonic and magnetic resonance techniques are considered.

2003

This is a tutorial [58] intended primarily to introduce ultrasonic elastography to academic clinical radiologists. The concept of quasi-static freehand scanning with software to produce strain images is discussed and some examples of using the technique in the differential diagnosis of breast lesions are included.

2004

This review [59] briefly discusses the state of the art in ultrasonic elastography, in the context of the then newly available quasi-static near-real-time freehand scanners. The author foresaw the development of 10 clinically useful applications, of which perhaps four have now come to fruition.

2005

In this paper [60], the authors reviewed what they considered to be the major classes of excitation stimuli (step compression, cyclic quasi-static compression, harmonic and transient shear wave excitation) used in elasticity studies and demonstrated that they all produce responses that fall within a common spectrum of elastic behaviour. This commonality arises because the tissue responses are all governed by the same underlying physics.

2009

This review [61] focuses on three different kinds of mechanical stimuli used in quasi-static elastography, namely steady-state, low-frequency and physiological excitations. The author identified most of the then commercially available scanners with freehand quasi-static elastography capability and pointed out that the realization of fully satisfactory elastic modulus imaging still required enhancements to be made in spatial resolution and signal-to-noise ratio.

2011

This is a 20 year perspective [62] of imaging the elastic properties of tissue, supported by 175 literature references. The authors summarized the basic principles (with relevant equations) and the timeline of what they saw to have been the major innovations in the technology; although the emphasis is on methods based on ultrasound, they also touched on MRE and optical coherence elastography. They concluded with a brief overview of clinical results and a short discussion of future directions.

6.2. Techniques for ultrasonic elastography

6.2.1. Low-frequency surface vibration

‘Sonoelasticity imaging’ is the term coined to describe the ultrasonic elastography method in which a low-frequency (typically 10–1000 Hz) mechanical vibrator is applied to the skin surface and the motion induced in the underlying tissues is detected by a pulsed Doppler system [63]. Because stiff tissues respond differently from soft tissues, regions of high stiffness can be displayed in contrast to those of low stiffness. A problem with this is that, although stiff lesions are not highlighted in the image, neither are other regions from which no signal is detected: this can lead to errors in clinical diagnosis. This approach was subsequently refined [64] and it was hypothesized that, by varying the excitation frequency within the range 10–1000 Hz and with colour Doppler imaging, it should be possible to reject artefacts owing to respiration. The authors concluded that ‘the combined external vibration and Doppler ultrasound detection approach appears to be the leading candidate for imaging the relative elastic properties of discrete regions of tissue’. This speculative conclusion was supported by experimental data reported in a companion paper [20]. The method was subsequently extended to three dimensions [65].

The detection by ultrasonic B-scanning of shear waves induced directly by mechanical vibration of a phantom at frequencies in the range 300–400 Hz has been demonstrated [66]. Coincidentally, a systems approach was presented to the quantitative estimation of Young's modulus in soft tissues from sequences of vibrating ultrasonic B-scan images [67]. Independently, a probe was constructed consisting of an ultrasonic A-scan transducer which also acted as a transiently vibrating piston, so that a single pulse of low-frequency shear waves was induced in the tissue from which echoes were acquired [68]. Although this approach required compensation for the physical motion of the ultrasonic transducer, the values of Young's modulus estimated from the measured shear wave speeds were close to those expected, both for phantoms and for human biceps muscles during contraction and relaxation. In what seems to have been an extension of this work, a technique was described for two-dimensional real-time imaging to detect the shear waves generated by two vibrating rods, one at each side of a linear array transducer [69]. A particularly novel aspect of this approach was that all the elements in the transducer array were excited simultaneously to transmit a flat beam which insonated the entire image plane, so that very high frame rate (up to 10 000 frames per second) two-dimensional imaging of the entire shear wave field was achieved. (It can be seen now that this was an important step in the development of supersonic shear imaging, as described in §6.2.7.) Heterogeneous phantom shear modulus distribution maps were reconstructed by means of an inversion algorithm and it was predicted that this approach would be useful for breast cancer detection. The problem of shear modulus reconstruction in dynamic elastography has been discussed [70]: although the authors validated their theory with MRI data, their conclusions are relevant to ultrasonic elastography.

It was discovered that interfering shear waves, generated by two surface vibrators with slightly different frequencies, produced moving interference patterns (termed ‘crawling waves’) [71]. It was then demonstrated that images of shear wave velocity distribution could be derived from these crawling waves detected by ultrasonic B-scan imaging [72]. The authors used a one-dimensional kernel and estimator that computed the local shear wave velocity independently of the shear wave displacement data in neighbouring regions. Subsequently, it was shown that a two-dimensional shear velocity estimation algorithm was more accurate and robust [73] and this was further validated by in vivo studies of healthy human muscle [74].

6.2.2. Step (quasi-static) surface displacement

In this approach, a force is applied (usually to the skin surface) for a time which is sufficiently long for the induced tissue strains effectively to become stabilized (quasi-static) and the resultant compression (longitudinal) and shear (lateral) tissue displacements are measured ultrasonically. The force may be generated by a mechanical actuator and may be applied as a single displacement or in a sequence of incremental steps, with displacement measurements being made with each step.

The tissue motion and deformation which result from applied stress are not limited to a single dimension. Moreover, most tissues are anisotropic and viscoelastic. For these reasons, one-dimensional strain measurement is likely only to provide a partial picture of the complete situation. Thus, the lateral strain should be estimated in order to acquire two- or even three-dimensional data, although currently this is seldom the case.

The method seems first to have been comprehensively described in 1991 [47]. The aspiration is to produce two-dimensional images of the distribution of the elastic modulus in tissue in vivo. Recognizing that the estimation of the elastic modulus from measurements of displacement requires the solution of the inverse problem, however, the technique is often used simply to produce real-time images corresponding to the distribution of tissue strain.

Using cross-correlation for time-shift estimation, strain images were created from 40 to 60 A-scan line pairs obtained with 1–2 mm lateral translations of a 2.25 MHz transducer between the pairs [47]. The compressor consisted of the front face of the transducer attached to an annulus to increase its overall size to 44, 89 or 127 mm. Slight precompression was followed by step displacements of 0.5–1.0 mm for each line pair. Elastograms of various configurations of phantoms and of a bacon (i.e. cured pork belly) slab were presented and it was rather modestly concluded that ‘the method could become useful in a number of applications’.

Following their early work, Ophir and his colleagues have published the results of their subsequent research in numerous papers, the extent of which preempts their detailed review. (Their papers on elastography, published since 1991, of which there are more than 110, are listed in http://www.elastography.com.) For instance, they contributed to the development of strain estimators, from studies of signal correlation [75], envelope decorrelation [76] and temporal stretching [77–80], through zero-crossing tracking [81], to spectral cross-correlation and parametric spectral estimation [82,83]. Their papers on multi-resolution imaging [84] and axial resolution [85] are also relevant to these studies. They analysed the stress distributions owing to external compressors, with and without apodization [48,86,87]. There are many papers on contrast, noise and resolution in ultrasonic elastography [88–96]. They tackled the problems of lateral resolution and out-of-plane displacement [97–99] and demonstrated the feasibility of generating images of poroelasticity [100–102]. The paper by Doyley et al. [103] is representative of their work on modulus elastography.

The publications of Ophir and his colleagues are the most numerous in the literature on the subject of surface step displacement techniques for ultrasonic elastography. Some principal publications of others on this topic are outlined in the remainder of this subsection.

Papers by other authors [104–108] are concerned with cross-correlation. Generally, this research involved external surface displacement, although there is one example in which an angioplasty balloon containing an intravascular ultrasonic scanner was used to stress the wall of the coronary artery [109], allowing plaques to be classified as hard, soft or homogeneous. Later, a compliant balloon catheter with an integrated intravascular scanner was used to demonstrate ex vivo images of thrombus and plaque [110]. It seems likely, however, that satisfactory in vivo application would require motion compensation, which remains problematic.

Recently, the performances of the more important strain estimation strategies involving two-dimensional windows of ultrasonic radio-frequency and signal envelope data have been evaluated [111]. The authors compared a single-resolution approach with a coarse-to-fine approach, both by finite-element modelling and experimentally, and they quantified the accuracy of measurements and the detectability of targets in axial and lateral dimensions, using the signal-to-noise and contrast-to-noise ratios (equations (6.2) and (6.3)). The coarse-to-fine approach outperformed single-step displacement for strains larger than 1 per cent. On a coarse scale, the envelope data gave the better results.

Simple one-dimensional ultrasonic displacement estimates of the elastic moduli of muscle, liver and plasticized polyvinyl-chloride specimens have been compared with values obtained using an Instron model 1122 universal testing machine [21]. With the Instron device, the stress–strain response was initially linear in all cases, for strains of up to 5 per cent; with these values as the reference, errors in ultrasonically determined displacement estimates of Young's modulus were typically of the order of 25 per cent, although these errors were substantially reduced when the size of the compressor was taken into account, and when multiple compression levels with small strain increments were applied. Subsequently, it was demonstrated that the optimal strain increment for multi-compression in relatively homogeneous tissue is about 0.35 per cent, but it was concluded that an increment of 0.15 per cent is more appropriate for a large dynamic range [112].

With the simple static approach, it is the time or phase lag at the peak of the correlation function which corresponds to the displacement. In practice, however, high displacement gradients and out-of-image-plane tissue motion combine to reduce the correlation coefficient. It was demonstrated that, for strains greater than 1 per cent, the correlation coefficient often falls below 0.9, and the uncertainty in determining the cross-correlation peak in the presence of noisy echo signals increases significantly [113]. This deteriorating performance is at least partly owing to ‘peak hopping’: by applying a dynamic programming procedure to find the most likely sequence of the consequentially hidden states in the sequence of measurements with strains of up to 6 per cent, significant improvement was demonstrated [114]. For larger strains of up to 10 per cent, it was shown that a wavelet-based peak search algorithm can provide acceptable results [115].

Conditioning the data by companding (signal compression or expanding) allows relatively large displacements to be analysed while also minimizing additive noise and losses from misregistration [116]. Companding works by measuring the local tissue displacements from one- and two-dimensional correlation lags, typically at three spatial scales, and appropriately compressing or expanding the echo signals to enable them to be cross-correlated. Satisfactory results can be obtained with strains as large as 5 per cent. Even better results can be obtained by iterative adaptive meshing [117] or optical flow processing [118], but at higher computational cost. In clinical practice, however, it is often appropriate to apply larger strains, which can enhance lesion detectability, and to accept that the images which are obtained are essentially qualitative.

Except in idealized conditions that consequently are clinically unrepresentative, the accuracy of lateral displacement tracking is one of the factors that determine the performance of displacement elastography. An obvious way to improve the accuracy of this estimate is to increase the sampling rate in the lateral direction. An alternative approach is to first synthesize a lateral phase signal from the A-scan lines that are available and then to estimate the lateral displacement by zero-crossing detection [119]. More traditionally, a linear transducer array with a wide transmitted beam has been used to acquire high frame-rate images (similar to the technique used for supersonic shear imaging: see §6.2.7), and this demonstrated results comparable to those obtained using slower line-by-line image acquisition [120,121]. A review of the effects of various parameters on lateral displacement estimation [122] concluded that the jitter error is minimized by small A-scan line spacing, wide bandwidth and spline interpolation.

Much of the published work on elastography neglects the fact that many tissues have poroelastic properties. Poroelasticity is due to the presence of mobile liquid within the tissue. In practice, this can often be ignored if the tissue is subjected to precompression before the displacement owing to further loading is estimated. In reality, however, complete characterization of a poroelastic material with a linearly elastic solid phase requires the measurement of Young's modulus, Poisson's ratio and the permeability of the solid matrix to the liquid which perfuses its pores [123]. Even though the pores are too small to be imaged directly using currently available techniques, both the volume fraction of the liquid and its resistance to flow through the pores are likely to be of diagnostic significance. Thus, in a study of the time evolution of the strain within cylindrical samples of tofu (bean curd) during sustained compression, parametric images were obtained which represented Poisson's ratio and the time-dependent elastic modulus [124].

It is fortunate that strain images are often sufficiently informative to be of clinical utility. Intuitively, however, images of distribution of Young's modulus would be probably both more reproducible and more useful for tissue characterization. In order to obtain a quantitative image of the elastic modulus with quasi-static displacement, the strain and displacement fields must be measured and inverted based on an assumed model of the soft tissue mechanics. Thus, theoretically predicted and experimentally verified internal displacement and strain images have been obtained for a linear elastic model with complex boundary conditions [125]. Subsequently, this approach was developed and used to demonstrate the reduction of artefacts by a reconstruction procedure involving the solution of partial differential equations describing the mechanical equilibrium of a deformed medium [126], and in the presence of nonlinearity [127].

Using the multi-compression approach, elastic modulus images have been produced by a coarse-to-fine strategy, initializing the process by the axial strain distribution [128]. Using the confidence of displacement estimates as a weighting factor, the inverse problem of elasticity reconstruction was solved and an accuracy of 1 per cent was achieved in the estimate from phantom data. The clinical feasibility of the method was demonstrated by in vivo breast imaging.

Although the approach was limited to studies of phantoms with controlled axial movement of the probe, encouraging results have been reported using a two-dimensional capacitive micromachined ultrasonic transducer array [129]. It was concluded that three-dimensional tracking provided robust measurements of displacement and it was predicted that volume data acquisition with two-dimensional arrays will lead to a significant advancement in the capabilities of elasticity imaging systems.

6.2.3. Freehand (quasi-static) surface displacement

The force exerted by the probe in contact with the skin varies as a natural consequence of freehand real-time ultrasonic B-scan imaging: this causes variation in tissue displacement which can be used for quasi-static elasticity imaging. This approach seems first to have been described in 2001 [130]. The authors found that the strain sensitivity and contrast-to-noise ratio of freehand elastograms were comparable to those produced by mechanically induced probe displacement, although the signal-to-noise ratio and the dynamic range were somewhat worse. Using a similar freehand scanning technique [131], it was shown that high-quality elastograms could readily be obtained with in vivo breast studies: real-time simultaneous display of B-mode and strain images assisted in the process and the preliminary results suggested that the strain image sequences for various breast pathologies were unique.

Side-by-side display of real-time B-scan and strain images facilitates the identification of anatomical features in relation to their elastic properties. In most commercially available scanners, however, the strain image is overlaid on the B-scan as a ‘colour wash’, where colour corresponds to strain and brightness is partly determined by the signal amplitude [132]. It requires a skilled operator to obtain good quality images with this simple approach. With the use of a normalization stage in the processing, however, good pseudostrain images can be produced with a wide range of probe motions, rather than having to rely on smooth manual compressions [133]. An alternative approach has been developed [134] called ‘assisted freehand ultrasound’ (AFUSON). In this, the AFUSON device is held in stationary contact with the patient's skin by the operator and the ultrasonic probe, the body of which is housed within the device, is axially mechanically displaced in a sequence of 0.25 mm increments over a distance typically of 2–5 mm. Compared with completely freehand acquisition, this semi-automatic system reduces out-of-plane motion decorrelation by 50 per cent and lateral motion by 30 per cent, and increases within-scan repeatability by 50 per cent.

Using a commercially available ultrasonic scanner equipped with software for freehand elastography and a tissue-mimicking phantom, the impact of the dynamic range of the elasticity, the size of the region of interest, the frequency of probe movement, the rejection of elastogram noise, the frame rate and the image persistence, and smoothing on imaging performance have been investigated [135]. Perhaps unsurprisingly, it was found that the dynamic range of the elasticity had the greatest effect on target visualization.

Using a linear ultrasonic transducer array with motor-driven sector scanning in the orthogonal direction, three-dimensional volumes of ultrasonic radio-frequency data have been acquired before and after the application of a slight manual increment in the pressure of the probe [136]. The total data acquisition time was rather less than 2 s. Three-dimensional windows were used to track the tissue displacement in all directions and three-dimensional kernels for least-squares gradient estimates. It was shown that the sequential image volumes were aligned sufficiently well for good signal correlation and that there was adequate axial strain variation to produce satisfactory strain estimates.

6.2.4. Physiological displacement

The idea of making use of the arterial pressure pulse to gain insight into the elasticity of the vessel wall is not a new one. For instance, a paper describing the measurement of the changing diameter of the carotid artery in a normal volunteer by means of M-mode ultrasound was published in 1990 [137]. An example of the subsequent controversy which accompanied these kinds of techniques concerning their accuracies can be found in Stadler et al. [138].

It was then demonstrated that strain images of the wall of an arterial phantom could be estimated by cross-correlation of ultrasonic radio-frequency A-scans acquired by intravascular ultrasonic scanning (IVUS) during the passage of a pressure pulse simulating cardiac action [139]. In these experiments, the IVUS catheter was positioned at the centre of the lumen. When used in vivo, however, this is generally not the case and it was only at end-diastole that elastograms with sufficient reliability for plaque characterization could be obtained [140]. Motion compensation in IVUS elastography is a persistent problem [141].

The prospect of transcutaneous strain imaging based on internal deformation of tissue in proximity to pulsating blood vessels has been investigated [142]. Following experiments with phantoms containing flow channels, strain images were produced in tissue in the neighbourhood of the brachial artery in vivo and it was concluded that this approach has a potential role in real-time non-invasive measurement of relative pressure or vascular elasticity.

6.2.5. Radiation force displacement

The idea of using focused ultrasonic radiation force to displace tissue and thus to acquire information about localized stiffness seems first to have been published in 1990 [143]. The tissue was displaced by the radiation force; when the ultrasound was switched-off, the recoil of the tissue was observed with an ultrasonic pulse-echo system. Empirically, it was found that the recoil rate was related to the stiffness of the tissue. This approach was later refined [144] and it was demonstrated that the time–displacement curves acquired from a phantom exhibited a viscoelastic response which was consistent with the Voigt model. By studying the dynamics of single laser-induced bubbles subjected to pulsed ultrasonic radiation force, it was also shown that the maximum bubble displacement is inversely proportional to Young's modulus of the embedding medium [145].

With the growth of interest in the use of high-intensity focused ultrasonic surgery (HIFUS) [146,147], the possibility of monitoring minimally invasive therapeutic tissue ablation by ultrasonic radiation force imaging has recently begun to be investigated [148]. In this application, the technique is known as ‘harmonic motion imaging for focused ultrasound’. By modulating the amplitude of the HIFUS beam at a frequency typically of 15 Hz and simultaneously acquiring M-mode recordings (a process that is dependent on efficient filtering of the imaging signals), the displacement amplitude can be seen to be reduced as the lesion is formed, because of its increasing hardness.

The fundamental concept of radiation force displacement underpins the techniques described in §§6.2.6 and 6.2.7. These two approaches are sufficiently mature to merit separate discussions.

6.2.6. Acoustic radiation force impulse imaging

It was not until the technique that is called acoustic radiation force impulse (ARFI) imaging was described in 2002 [149] that the feasibility of using short-duration acoustic forces (pushing pulses) to cause localized displacements deep within tissue and to track these displacements by ultrasonic cross-correlation, thus mapping viscoelastic properties point by point but otherwise in a way similar to that used in surface displacement methods, began widely to be appreciated. With a modified diagnostic ultrasonic scanner and a linear transducer array, a focused beam was used to apply pushing pulses to a volume of about 2 mm³ for up to 1 ms per pulse, with which, typically, the resultant displacement was about 10 µm. Each tracking line was divided into a series of short search regions and the location of the peak in the cross-correlation function between a kernel in the first tracking line and the corresponding position in the second tracking line was used to estimate the axial displacement. Using this system, the first two-dimensional in vivo ARFI breast images were produced, co-registered with the corresponding B-scans.

In ARFI imaging, the lateral profile of the pushing beam and, consequently, that of the radiation force is roughly Gaussian. The effect of the resultant distribution of the tissue displacement within the tracking beam has been analysed and it was shown that, with cross-correlation, the estimate is typically equal to the square root of the peak displacement [150].

Simplistically, ARFI images represent the spatial distribution of tissue stiffness. As the tissue recoils at the focal point following the application of a pushing pulse, shear waves propagate away from this region [151]. By measuring the speed of these shear waves, the local value of the shear modulus can be estimated from equation (3.5); using this method in a phantom, ARFI imaging estimates differed from direct measurements of the elastic modulus by not more than about 20 per cent. The image contrast for spherical inclusions is greatest immediately after force cessation: it increases as the size of the focal region is decreased but frame rate and thermal considerations impose trade-offs with the hypothetical safety of the technique [152]. Because the process of data acquisition typically requires 1–3 ms per tracking line pair, physiological motion can degrade the quality of in vivo images. This effect can be minimized by using tracking beams with lower ultrasonic frequencies, and by adopting scanning strategies that take account of this motion [153]. Model-based motion compensation, although not without limitations, can also be helpful [154].

ARFI imaging has been compared with quasi-static surface displacement elastography [155]. ARFI images were found to be more homogeneous in both the background and within inclusions, and they had better contrast, particularly for soft inclusions and beyond boundaries in the media at which slip could occur.

In considering the safety of ARFI imaging, the peak temperature increase with a typical regime was estimated to be about 0.14°C for each pushing pulse [149]. Assuming that an increase in temperature of up to 1°C is acceptable [156] and considering the spatial distribution of the pushing beams during two-dimensional scanning, it was concluded that this regime did not pose an increased risk to the patient over that with traditional B-scan imaging. Further analysis [157] confirmed the safety of the method for the particular pulsing regime which was used and also showed that, although the thermal expansion of the tissue is negligible, the change in the speed of sound may be appreciable; this is also relevant to the related topic of thermal strain imaging [158]. The thermal problem can be ameliorated by tracking tissue displacements with parallel receiver beam-forming [159].

6.2.7. Radiation force induction of shear waves

It was first reported in 1998 both that acoustic shear waves could be induced remotely in tissue by the radiation force of a focused ultrasonic beam and that these shear waves could be detected, optically or by magnetic resonance, and displayed as an image, from which their speed and, hence, the elasticity of the tissue could be estimated [30]. It was concluded that the ultrasonic exposure necessary to induce detectable shear waves could be below the threshold for bioeffects. It was also speculated that the shear waves might be able to be visualized with ultrasound. Subsequently, it was confirmed that it was thus practicable to measure the shear wave speed point by point by axial translation of the focused beam, from which a two-dimensional image of Young's modulus could be displayed [160]. Later, a time-to-peak lateral displacement estimator was developed as an alternative to correlation-based algorithms for the measurement of shear wave speed and it was demonstrated that this could be used to estimate Young's modulus in the livers of normal volunteers [161].

A technique known as ‘spatially modulated ultrasound radiation force’ (SMURF) imaging has been developed [162]. Using a linear array transducer, a single reference A-scan line is first acquired at some specified position along the array. Two radiation force pushing pulses are then transmitted in rapid succession: they are focused at the same depth but separated laterally by an appropriate distance. A series of A-scan lines is then acquired, in the same position as the reference A-scan line; correlation processing of these A-scans allows the time between the induced shear wave peaks to be estimated. The method (which is reminiscent of the crawling wave technique described in §6.2.1) has been reported to be fast and accurate in the measurement shear modulus in a phantom and in ex vivo porcine liver [163].

The remote localized induction of shear waves in tissue by a strongly focused beam of ultrasound, the measurement of their speed by ultrasound and the fast two-dimensional imaging of Young's modulus was first demonstrated in 2004 [164]. With 4 MHz 100 µs pulses applied to groups of elements in a linear array transducer with appropriate timing to form a focused beam sequentially at typically five discrete points along the beam axis, shear waves are induced which interfere constructively to create a wavefront analogous to the Mach cone of an aircraft travelling at supersonic speed. Thus, the source of the shear waves may be thought of as travelling along the beam axis at, relative to that of the shear waves, supersonic speed. By time-sharing the operation of the linear array transducer, all the transducer elements are then excited simultaneously by pulses with a duration appropriate for imaging and a set of about 50 two-dimensional images of the propagating shear wavefront is acquired at a frame rate of 5000 s⁻¹ by parallel processing of echoes received by appropriate groups of elements across the array. Thus, the local values of the shear wave speed can be estimated, from which a Young's modulus map can be constructed. Moreover, again by timesharing, B-scan images can also be acquired and displayed parametrically with the elasticity data. In practice, for breast scanning, all this can be achieved within about 20 ms per frame, corresponding to a frame rate of 50 s⁻¹, which effectively is real time. Because of the mechanism by which the extended shear wavefront is created, the method is called ‘supersonic shear imaging’.

By modelling the propagation of radiation force-induced low-frequency (50–500 Hz) shear waves (such as that used in supersonic shear imaging), the dependence on the viscoelasticity of tissue was demonstrated [165]. This led to the speculation that viscoelasticity maps might be more informative than maps of Young's modulus, considering that elasticity by itself has not proved to be completely adequate for tumour characterization.

6.2.8. Vibroacoustography

A variant of the use of focused ultrasonic radiation force to displace localized regions with tissue has been described [166]. The foci of two ultrasonic beams are arranged to coincide at the beam cross-over point within the tissue. The two beams have slightly different frequencies (typically differing by 25 kHz) and so the tissue in the focal region experiences a radiation force which fluctuates at the beat frequency. The tissues which are only in either one beam or the other also experience radiation forces, but these do not fluctuate and so only the tissue in the beam cross-over region vibrates at the beat frequency. The amplitude of this tissue vibration depends on the local stiffness of the tissue, so that the associated acoustic emission at the beat frequency, when detected by an external hydrophone, can be used to create an image of spatial stiffness distribution when the focal point is scanned in a two-dimensional plane.

Three methods of stress field formation for vibroacoustography have been compared [167]. The use of a single amplitude-modulated focused transducer has the major disadvantage that the oscillating radiation force acts on the transducer itself and this generates a signal which tends to mask that owing to acoustic emission from the tissue. With a confocal transducer, the central element is smaller than the concentric annulus and so it has a greater focal depth of field. Physically, the optimal arrangement is for the beams produced by separate transducers to cross over at the position of their coincident foci, but this may not be convenient for clinical application. The most promising compromise for clinical use is probably to use a linear transducer array [168], but the possibility that a disc-shaped sector array [169] might be used in some situations should not be discounted.

Vibroacoustography has been compared with other dynamic radiation force methods of elastography [170]. The conclusion was that vibroacoustography can detect displacements as small as a few nanometres, whereas displacements of at least a few micrometres are necessary with other ultrasonic methods; this is because the hydrophone detector is highly sensitive. A consequence of this is that the ultrasonic intensity can be low, giving confidence in the safety of the method. The spatial resolution of vibroacoustography is proportional to the width of the main lobe of the stress field (typically 700 µm at 3 MHz). Another important advantage of vibroacoustography is that, unlike other contemporary ultrasonic methods, it can detect small hard inclusions, such as microcalcifications.

Although vibroacoustography has many desirable attributes for the investigation of the mechanical properties of tissue, it suffers from the major disadvantage that data have to be acquired separately from each point within the imaged tissue. Even with the rapid beam steering possible with a linear array transducer, the low frequency of the mechanical vibration (typically 10–25 kHz) places a physical constraint on the minimum two- and three-dimensional scanning times.

6.3. Tissue-mimicking materials and phantoms for evaluating the performance of techniques for ultrasonic imaging of soft tissue strain and elasticity

The convenient, reliable and reproducible evaluation of the performance of techniques for ultrasonic imaging of soft tissue strain and elasticity is dependent on the use of consistent tissue-mimicking materials. This is because the characteristics of real tissues, whether in vivo, in vitro or fixed, cannot be standardized in any meaningful way.

For practical use, tissue-mimicking materials are usually fabricated into phantoms, which may be simple test objects or designed to simulate relevant anatomical structures both in the overall shape and by incorporating components with differing characteristics. By the time that the potential of ultrasonic elastography began to be of interest, phantoms for B-scan ultrasonography were already in widespread use and commercially available. In that application, water-based gels [171] satisfy the requirements for speed of sound (about 1540 m s⁻¹), attenuation (about 0.5 dB cm⁻¹ MHz⁻¹) and backscatter coefficient (between 10⁻⁵ and 10⁻², between 2 and 7 MHz).

Tissue-mimicking phantoms for evaluating the performance of techniques for ultrasonic imaging of soft tissue strain and elasticity need as closely as possible to match the characteristics of real tissues with respect to speed of sound, density, attenuation, scattering, Young's modulus, Poisson's ratio and viscosity; and these characteristics need to have the appropriate frequency and temperature dependencies. The materials are also required to be non-toxic and stable over time.

Water-based gelatin gels containing n-propanol can provide a wide range of stiffnesses approximating to those of soft tissues [172]. The addition of formaldehyde or paraformaldehyde increases the melting point of the gel (paraformaldehyde generates cross-links more rapidly than formaldehyde) and also increases the stiffness in a predictable fashion. This slightly increases the speed of sound, which is typically in the range 1550–1600 m s⁻¹. Graphite powder or glass beads can be added to produce the desired attenuation and scattering characteristics.

Although water-based gelatin gels are suitable for the construction of solid phantoms, they tend to rupture easily with increasing stress. This makes them rather unsuitable for use as, for example, wall-less blood vessel phantoms. It has been proposed that this problem could be avoided using polyvinyl alcohol cryogel (PVA-C), which acquires its properties by a freeze–thaw process [173]. This material can be modified to have a speed of sound in the range 1500–1600 m s⁻¹ and an attenuation of 1–3 dB cm⁻¹ at 5 MHz. It is virtually incompressible and has been reported to have elasticity close to that of a pig aorta. Detailed information about this material is available [174,175]. Polyacrylamide gel is a similarly useful material [176].

The temporal stability of oil-in-gel dispersions, in which the base aqueous materials were either gelatin or a mixture of agar in gelatin, for use as elastography phantoms has been reported [177]. Depending on their formulation, these materials have been produced with Young's moduli of 5–130 kPa, speeds of sound of 1492–1575 m s⁻¹ and attenuation coefficients of 0.14–0.47 dB cm⁻¹ MHz⁻¹. The stiffness of these phantoms remained unchanged within 1–2% over periods of at least eight months.

Although the usual requirement is for phantoms that mimic parenchymatous tissues and those with similar mechanical characteristics, there are some applications in which different properties are desirable. For example, using typical electrophoresis gel production protocols, the preparation of low-concentration acrylamide-based phantoms mimicking the mechanical characteristics of the vitreous body of the eye has been described [178]. With acrylamide concentrations of 1.6–1.7%, the speed of sound was 1499–1510 m s⁻¹ and the attenuation coefficient was 0.07–0.14 dB cm⁻¹ MHz⁻¹; the elastic modulus was roughly proportional to the gel concentration and could be adjusted to be similar to that of the vitreous body.

Recently, it has been reported that a material composed of a mixture of styrene–ethylene/butylene–styrene copolymer in mineral oil, with the addition of silica or graphite powder scatterers, can be used satisfactorily to mimic the mechanical and acoustical properties of soft tissues [179]. This material, which has proved to be stable over a period of at least 16 months, can be formulated to have Young's modulus in the range 2.2–150 kPa, speed of sound from 1420 to 1464 m s⁻¹, and an attenuation coefficient from 0.4 to 4.0 dB cm⁻¹ at 3.5 MHz.

Simplistically, it is assumed that the stress–strain relationship in tissue is linear and this is realistic in the case of small strains and considering the rather qualitative nature of clinical elastography. It is apparent that a wide variety of materials exists for use as phantoms for ultrasonic elastography. There are several manufacturers of commercial phantoms and, for them, the choice of material must often be governed by proprietary considerations. Individual researchers tend naturally to use the formulations which they themselves have developed and with which they are familiar. For instance, a breast phantom (actually, of cylindrical shape) has been constructed for ultrasonic elastography, using dispersions of microscopic droplets of safflower oil in solid aqueous gelatin [180]. Bound and unbound fibroadenomas, small cancers, large cancers, glandular tissue and fat were simulated by changing the volume per cent of the oil, from 10 per cent for simulated fibrodenomas to 70 per cent for simulated fat, to produce progressively harder inclusions of appropriate sizes.

Phantoms are invaluable in the development of elastography systems and for the assessment of their performance. None of the existing phantom materials perfectly simulates the relevant ultrasonic and mechanical properties of soft tissues of any kind and the search for better tissue-mimicking materials is continuing.

7. Emerging clinical applications

7.1. Overview

The literature on established and emerging clinical applications of ultrasonic estimation and imaging of soft tissue strain and elasticity is by no means confined to the biomedical ultrasonic journals. In §7.2, a few examples drawn from diverse publications are reviewed, not only to illustrate some of the uses of ultrasonic imaging of strain and elasticity in the context of several clinical specialties, but also to demonstrate situations in which the various techniques have been shown to be applicable or to have promise for the future.

Apart from studies carried out using the specialized and advanced equipment which exists in some research laboratories, most clinical work is necessarily performed using one or other of the scanners with elasticity imaging capability which are commercially available. In general, such machines are high-end real-time B-scanners with additional software to derive elastograms, which depend on the changing probe pressure experienced during freehand scanning.

Supplementary information about many clinical applications can be found in a review paper [181], which, although it was published 4 years ago, is still a very useful source of reference.

7.2. Applications in clinical specialties

7.2.1. Breast disease

Palpation of the breast is commonplace whenever the presence of a lesion is a possibility. As a diagnostic test, however, it has not been shown to be effective in reducing breast cancer mortality. Moreover, X-ray mammography and newer techniques such as MRI (even in younger women with denser breasts, in whom X-ray mammography tends to be unreliable), whether alone or in combination, miss some cancers and also have significant false-positive rates [182].

B-scan ultrasonography is in the same category, although its performance can be improved using microbubble contrast agents [183] and ultrasonic colour Doppler imaging can be helpful [184]. Where malignancy is suspected, biopsy is usually needed to obtain a definitive diagnosis. The deficiencies of all these techniques have stimulated the investigation of the potential clinical advantages of ultrasonic elastography of the breast in the context of both asymptomatic and symptomatic lesions.

Using quasi-static compression of about 1 per cent, with side-by-side display of the ultrasonic two-dimensional B-scans and the elastograms, it was possible to distinguish between malignant lesions and 73 per cent of fibroadenomas and 56 per cent of solid benign lesions [185]. In another study, a commercial ultrasonic scanner with freehand compression for elastography was used to examine histologically proven focal breast lesions [186]. With B-scanning, the sensitivity was 96 per cent and the specificity was 56 per cent; the corresponding figures with elastography were 81 and 89 per cent. When the qualitative results of elastography were replaced by calculations of the ratios of the strains in normal and suspect areas of the images, the sensitivity increased to 90 per cent, while the specificity was unchanged at 89 per cent.

The presence of microcalcifications in breast lesions is a strong indicator of malignancy, but their visualization is practically impossible using traditional ultrasonography. Vibroacoustography, however, has been shown [187] to be capable of imaging microcalcifications (of about 110 µm in diameter) in ex vivo human breast tissue specimens.

Using a commercially available scanner with freehand ultrasonic elasticity imaging capability, earlier results [181] were confirmed by comparing the apparent sizes of lesions as estimated from traditional B-scans and from elastograms [188]. It was found that, if the suspect B-scan area was greater than that of the elastogram, the lesion was likely to be benign, and vice versa for malignant lesions, with a specificity of 95 per cent.

Using the assisted freehand ultrasonic technique (see §6.2.3), the concept of ‘slip imaging’ for breast lesion assessment was introduced [189]: axial strain imaging was supplemented by the measurement of lateral displacement or slip, to provide an estimate of lesion mobility. Although this resulted in a reduction in sensitivity, both the diagnostic accuracy and the specificity increased.

Using a commercially available scanner with ARFI imaging capability, it was demonstrated that ultrasonic strain imaging improved the classification of benign and malignant breast masses, in comparison with ultrasonic B-scanning alone [190]. It was concluded that strain imaging can be helpful in deciding whether or not a lesion should be biopsied.

As an example of the results of preliminary clinical studies, it has been demonstrated that supersonic shear imaging is a promising technique for quantitative mapping of breast tissue elasticity [191]. The technique has the advantage of being less operator dependent than freehand compression, because the mechanical excitation is generated by the system itself.

The clinical applications of ultrasonic elastography in the differential diagnosis of breast lesions have been pragmatically reviewed [192].

7.2.2. Cardiology

Originally, echocardiography was used to assess valvular function and, indeed, that is still one of its principal clinical applications. In order to obtain insight into cardiac performance, however, echocardiographic techniques were evolved to study the regional behaviour of the myocardium. For this, the first important advance was the development of tissue Doppler imaging [45], but this is often difficult to interpret because of its angle dependency.

The thickening and thinning of the myocardium during the cardiac cycle can be estimated by ultrasonic pulse-echo imaging: the myocardium becomes thicker when the ventricles contract during systole and thinner when they relax during diastole. This simple approach is not very satisfactory, however, because the heart rotates and is displaced as well as being deformed during ventricular contraction and relaxation.

Regional ultrasonic myocardial strain and strain rate measurements have been in clinical use for more than 10 years [193]. During this time, the technique has evolved from being based on simple continuous one-dimensional measurements of the thickness of the myocardium over the cardiac cycle, through two-dimensional [194] to three-dimensional [195] approaches, providing increasingly complete pictures of cardiac function. These developments have reached an advanced stage of refinement with the application of two-dimensional speckle tracking (see [196]) and they have been supplemented by the results of investigations of, for example, the image frame rate necessary to track tissue motion satisfactorily [197].

This discussion of ultrasonic myocardial strain and strain rate measurements has been kept at a superficial level, because the topic is not strictly within the scope of the present paper. While it is true that the change in thickness of the myocardium during the cardiac cycle is properly described as the myocardial strain, and that the rate of change of strain is the myocardial strain rate, it must be clearly understood that these changes are accompanied by cyclical changes in the actual value of Young's modulus of the myocardium, as well as in the myocardial blood volume. This is quite different from the situation which prevails in tissues that are not contractile, in which Young's modulus is simply passively dependent on the static and dynamic loading, and which is the main thrust of the present paper.

Logically, a reasonable objective would be to continuously measure the instantaneous regional value of Young's modulus of the myocardium over the cardiac cycle. This is because the value of Young's modulus depends on the degree of myocardial contraction: it can be expected to be characteristically cyclical in normally functioning myocardium, but relatively constant in infarcted tissue. With contemporary techniques, it is not possible to track the rapidly moving myocardium to allow the localized strain to be estimated by cross-correlation, let alone to model factors such as the ventricular pressure sufficiently realistically to allow the instantaneous regional value of Young's modulus of the myocardium over the cardiac cycle to be estimated.

It is apparent, however, that there is a reasonable prospect of measuring the instantaneous regional value of Young's modulus of the myocardium over the cardiac cycle, by means of supersonic shear imaging. Thus, by applying a linear transducer array directly to the exposed myocardium in an experiment on sheep, the shear wave velocity was measured in a small region at a rate of up to 20 s⁻¹ [25]. In this way, it was possible to estimate the values of Young's modulus, which varied cyclically from about 10 kPa in diastole to about 100 kPa in systole. The effect of local ischaemia following coronary artery ligature was also observed: a region of weakened contractility was noted. The clinical implications of this work are truly exciting.

7.2.3. Dermatology

High-resolution ultrasonic B-scanning of the skin is well established in clinical practice; using frequencies of 20–100 MHz, applications include wound healing assessment, tumour staging and response, boundary definition, eczema and ageing studies [198].

In order to be clinically useful, ultrasonic skin elastography needs to have a resolution comparable to that of ultrasonic skin B-scanning (laterally, better than around 100 µm). In this context, it was demonstrated that the greyscale level in 15–40 MHz B-scans increases markedly with increasing strain, whereas the attenuation markedly decreases [199].

An instrument with a 50 MHz focused transducer surrounded by a small annulus vibrating at 300 Hz which generated shear waves in the skin with which it was in contact has been described [200]. This allowed the local elasticity to be estimated from the shear wave velocity, which was recovered from phase analysis of the ultrasound backscattered by the displacement field. Measurements within the dermis are not influenced by the overlying layers and so the method can be expected, for instance, to provide insight into the ageing processes of the skin.

As an alternative means of changing the pressure on the skin in a step-wise fashion for high-frequency (20 MHz) ultrasonic elasticity imaging, a fluid-filled chamber with an opening in contact with the skin has been used [201]. The chamber accommodated the transducer and a linear scanning mechanism. The pressure in the chamber could be adjusted in steps from 0 to −11 kPa (i.e. 0 to −110 mbar): the negative pressure not only served to decompress the tissue in a step-wise fashion, but also helped to keep the device in contact with the skin. It was apparent that, in normal skin, resistance to decompression is primarily owing to the dermis and not to the subcutaneous fat. Differences were found when imaging burns and a nevus. Moreover, the consequences of any tendency for the tissue to become engorged by blood and free fluids were not addressed.

7.2.4. Endocrinology

Ultrasonic elastography of the thyroid has been shown to be feasible using carotid artery pulsation (e.g. [202]). With this technique, the ratio of ultrasonically estimated strain near the carotid artery to that of the suspect region of tissue was shown to be higher for papillary carcinoma than for nodular goitre. It was speculated that this might be clinically useful for guiding fine-needle aspiration biopsy in order to reduce the possibility of false-negative results in patients with suspicion of malignancy.

7.2.5. Gastroenterology

Traditional imaging techniques often fail to detect hepatic metastases. This is particularly so with B-scan ultrasonography. Although microbubble contrast agents can improve the reliability of B-scan ultrasonography [203,204], the cost is not trivial and their use involves logistical and regulatory difficulties. This, combined with the fact that surgeons often discover unsuspected hard malignant lesions when they are able to palpate the exposed liver directly, has encouraged the development of ultrasonic elastography for transabdominal liver scanning.

With a 40 Hz mechanical vibrator in contact with the skin close to a real-time ultrasonic scanner with a curvilinear array transducer, the Doppler signals have been used to estimate the two-dimensional shear wave velocity distribution [18]. In the right lobe of the liver, the average velocities were 6.0 m s⁻¹ in healthy volunteers, 9.8 m s⁻¹ in those with chronic hepatitis and 11.9 m s⁻¹ in those with cirrhosis (the ribs prevented data acquisition from the left lobe). These are clinically useful distinctions.

The external application of quasi-static and vibration excitation for elasticity imaging is feasible only for structures at rather limited distances from the abdominal wall. In appropriate circumstances, this problem can be avoided using endoscopic ultrasonic elastography, which has been shown to give promising results in cases of tumours situated close to the gastrointestinal tract [205]. The possibility that this approach might improve the accuracy of guiding biopsy in the differential diagnosis of focal pancreatic masses, especially in the presence of chronic pancreatitis, is particularly attractive.

The application of ARFI imaging at depths which are clinically realistic for abdominal imaging (including liver, gallbladder and hepatic vessels) in adults was first reported in 2005 [206]. Encouraging results were obtained. The technique allowed co-registration of the strain images with B-scan and colour Doppler images. Motion due either to changing pressure on the hand-held transducer or to vascular pulsation, respiration or digestion, however, was one of the problems, particularly because the line-by-line process of data acquisition was necessarily slow; to some extent, linear motion filters were helpful. Also, it was concluded that the heating effect of the pushing pulses was within accepted safety limits. Recently, it was demonstrated, using a commercially available scanner with ARFI imaging capability, that better diagnostic performance than that achieved with B-scanning alone in the detection and assessment of chronic liver disease was obtained when it was supplemented by elastography [207].

At the current stage in the development of ultrasonic elastography, it is apparent that the supersonic shear imaging technique has important advantages over other approaches in the assessment of abdominal structures. For instance, it was found, in intercostal studies of the liver, that the technique was highly reproducible and repeatable, and superior to ARFI imaging [22]. A particular advantage of the technique was that, because of its very high frame rate (up to 50 frames per second), no significant motion artefacts were observed. Moreover, it was possible to assess the mechanical behaviour of the liver over quite a large bandwidth (typically 50–400 Hz); in this way, shear wave dispersion could be demonstrated, opening up the prospect of shear wave spectroscopy.

Twenty years ago, it could be more dangerous for a patient with suspected appendicitis to have an ultrasonic scan than not to have one; this was because of the high false-negative rate of diagnostic ultrasonography at that time [208]. However, with modern equipment, the results of B-scan ultrasonography are now much more reliable; in one study, the addition of freehand elastography was reported to improve the sensitivity in the detection of acute appendicitis from about 88 per cent to 100 per cent [209]. This result is particularly encouraging, because the study was done with a commercially available machine.

As an adjunct to freehand elastography, in an approach which significantly reduces the level of the skill required to produce useful results, a 50 Hz mechanical vibrator has been developed which, when applied to the abdominal wall over the liver, induces shear waves in the liver which can be detected by a 5 MHz pulse-echo transducer mounted at the tip of the low-frequency vibrator [210]. In this way, the propagation of the shear wave can be observed over time, so that the shear wave speed can be estimated directly. The technique has been used in the study of cirrhosis in patients with hepatitis C [211], hepatitis B [212], biliary liver disease [213], alcoholic liver disease [214], non-alcoholic fatty liver disease [215] and hepatic steatosis [216].

7.2.6. Gynaecology

Transvaginal B-scan ultrasonography is often the first-line imaging technique in the investigation of suspected gynaecological abnormalities.

Uterine fibroids are a common cause of dysfunctional bleeding. They are composed of the same smooth muscle fibres as the uterine wall, but they are very much denser. As a result, they are often poorly visualized on traditional transvaginal ultrasonography, so that their number and size can be wrongly estimated; this may cause difficulties during any subsequent surgery. Using a commercially available machine with small movements of the probe inducing tissue displacement, it was concluded that real-time ultrasonic elastography could provide detailed mapping and characterization of fibroids [217]. That is useful in itself, but an important problem in cases of dysfunctional bleeding is the possibility that it may not be due to fibroids, but to adenomyosis or other causes, for which the treatment is different. The frequency-dependent complex elastic moduli of human uterine tissue have already been characterized [16] and some promising results have been obtained with ex vivo uteri [218].

7.2.7. Minimally invasive surgery

Radio-frequency ablation is one of several approaches to the clinical management of metastastic lesions in the liver. One of the challenges with this technique is to ensure that all the malignant cells have been destroyed, and this cannot be assessed reliably by traditional ultrasonography. A method has been described in which the ablation probe itself was used as the tissue displacement device for ultrasonic elastography, thus minimizing the problems of lateral slippage and non-axial motion experienced with other displacement approaches and imaging during the respiratory cycle [219]. It was shown that the elastograms obtained in this way correlated well with histological examination. Using externally applied low-frequency vibration, good correspondence was demonstrated between three-dimensional elastography and gross pathology in lesions induced by radio-frequency ablation in in vivo pig livers [220].

HIFU is becoming an established technique for trackless ablation of deep tissues [147]. It can be effective in the treatment of tumours of the breast, kidney, liver, pancreas, prostate and uterus. One of the major problems with HIFU, however, is that of predicting the positions of the regions of ablation and monitoring their formation. This can be done quite well with MRI [221], but that technique is relatively expensive and rather inconvenient. It was proposed that, by running the HIFU transducer at a power below that necessary to form a lesion but sufficient to heat the tissue, it might be possible to use a diagnostic scanner to detect the resultant tissue strain by the associated shift in the time-position of the backscattered ultrasound and thus to determine the location at which the lesion would be formed. In an in vitro study, it was concluded that this was likely to be feasible, provided that means could be found to compensate for the physiological motion which could be expected to occur in vivo [222]. In another approach, which was based on earlier work [223], it was demonstrated that, even without breath-holding, elastograms of the prostate could be obtained using a transrectal ultrasonic probe by changing the volume of liquid in the coupling balloon, after HIFU had been used to treat the prostate with the transrectal device [224]. In some patients, good correlation was found between MRI and ultrasonic strain imaging of the lesion. The method using externally applied vibration in pig livers also showed good correspondence between three-dimensional elastography and pathological findings for HIFU lesions [220].

In an in vivo experiment with mice, a harmonic motion imaging system consisting of a HIFU transducer with a coaxial phased-array imaging probe to detect the backscattered ultrasound from the focal region while the HIFU beam was amplitude modulated at a frequency of 15 Hz was used [225]. This modulated the radiation force so that the tissue displacement and, hence, the tissue strain image could be obtained in real time. In this way, the changes in tissue stiffness accompanying thermal lesioning could be monitored.

7.2.8. Musculoskeletal studies

Skeletal muscle tissue is anisotropic, with the fibres being aligned with the direction of contraction. The results obtained using the sonoelastic imaging technique in the determination of muscle elasticity have been reported [24]. Using the device previously described [200] (see §7.2.2), it was found that the shear wave velocity perpendicular to the fibres in contracted human biceps muscle was 12 m s⁻¹, which was four times slower than that parallel to the fibres [226]. Subsequently, using supersonic shear imaging, the concept of muscle hardness in the quantitative assessments of neuromuscular pathology and rehabilitation began to be explored [227]. Because this technique gives rise to a wide frequency spectrum (about 100–800 Hz) of shear waves, the viscoelasticity can be estimated with a single acquisition. The hope is that ultrasonically estimated viscoelasticity might reduce the need for biopsy in the diagnosis of neuromuscular diseases which, although rare, have very significant impact on life expectancy. Following the presentation of the first results of in vivo ultrasonic measurements of skeletal muscle viscoelasticity [73], a complete set of quantitative in vivo parameters describing the mechanical properties of normal contracted and relaxed muscle has been reported [228]. For instance, using a Voigt's model to represent the loading in biceps muscle, the shear modulus parallel to the fibres was estimated to increase from about 6 to 100 kPa when the loading increased from 0 to 4 kg; the corresponding decrease transverse to the fibres was from 1.6 to 1.1 kPa. For the viscosity, the corresponding changes were from 0.7 to 3.8 Pa s and from 0.9 to 2.5 Pa s, respectively. Of course, the shear modulus of muscle is strongly dependent on loading and this again highlights the caution with which the data presented in table 1 need to be applied.

The rare muscle diseases classified as idiopathic inflammatory myopathies are characterized by slow but progressive muscle weakness, fatigue, falling, pain and tenderness. Clinically, it is difficult to distinguish between polymyositis, dermatomyositis and inclusion body myositis [229]; the results of biochemical tests are often equivocal, biopsy is not a trivial procedure and MRI is unreliable as well as being expensive and not readily accessible. Using a commercial ultrasonic scanner with freehand elastographic capability, however, it was concluded that the results were sufficiently promising to merit further investigation [230].

The time-dependent local strain response of the affected arms of patients with lymphoedema has been compared with that of their contralateral arms [231]. Although the results were not unequivocal, they indicated the possibility that poroelasticity imaging might prove to be useful in the diagnosis and study of the condition.

Cleft lip and/or cleft palate occur in around one per 700–1000 live births [232]. Cleft lip is usually surgically corrected in the neonatal period, by reconstruction of the upper lip and restoration of the circular muscle. The success of the procedure depends mainly on the continuity and functionality of the muscle and the amount and position of the residual scar tissue. It is difficult to distinguish between the muscle and the scar tissue by B-scan ultrasonography. It has been demonstrated, however, that ultrasonic elastography, using the natural voluntary movement of the lip to strain the tissue, is capable of making this distinction, as the scar tissue is compressed when the muscle expands [233].

The results of ultrasonic quasi-static strain measurements on Achilles tendons of rabbit showed that better correlation with histology in both normal and inflamed tendons was obtained using strain measurement than with B-scan ultrasonography [234]. In healthy volunteers and using a commercial scanner with freehand elastographic capability, excellent correlation was found with the hardness of Achilles tendons; it was concluded that the role of the method in the assessment of tendinopathy should be investigated [235]. It was observed that the reproducibility of elastograms obtained using this technique was better in the longitudinal than in the transverse direction [236]. It was also reported that there could be different values of elasticity in the same apparently normal tendon and it was suggested that this might be the result of presymptomatic damage.

Both the compressive and the tensile components of strain in bovine anterior cruciate ligaments and at the ligament–bone insertions, using the technique of quasi-static ultrasonic elastography, have been demonstrated [237].

7.2.9. Radiotherapy

In prostate brachytherapy, in which radioactive seeds are implanted in the gland in order to irradiate the malignant tissue, the dosimetry depends critically on having information about the precise locations of the seeds. X-radiography, X-ray computed tomography, MRI and B-scan ultrasonography all have deficiencies in this respect. One way in which this can be done is to vibrate the seeds with a low-frequency magnetic field and thus to detect them with two-dimensional power Doppler imaging [238]. Of course, this is not strictly an elastographic technique.

However, the feasibility of imaging brachytherapy seeds in a gel phantom by means of vibroacoustography has been demonstrated [239]. Remarkably good contrast resolution was obtained when the excitation frequency was selected to coincide with the resonant frequency of the seeds. The potential of the method, a practical clinical procedure, deserves to be explored.

Gel dosimetry is an established technique for the verification of complicated ionizing radiation fields, such as those used in intensity-modulated radiotherapy. For example, ionizing radiation changes the magnetic properties of certain polymer gels so that the dose to which they have been exposed can be deduced from magnetic resonance images [240], but the cost and limited access to MRI scanners restrict the utility of this approach. Exposure to ionizing radiation also modifies the elasticity of the material, however, and the possibility that ultrasonic elastography could be used for gel dosimetry has begun to be explored [241]. Following the irradiation of part of a scatter-loaded gel block with a 21 Gy dose of 6 MV photons, the shear moduli of irradiated and un-irradiated regions were estimated by ultrasonically measuring the displacement resulting from compression. The results were complicated by the boundary conditions but suggested that, with further development, the approach could become clinically useful.

7.2.10. Tissue engineering

Using a 50 MHz ultrasonic quasi-static elasticity microscope [242], elasticity micrographs of two model systems commonly used for tissue engineering have been obtained [243]. It was possible to identify the upper cell layer of a tissue-engineered smooth muscle sample separately from its supporting matrix, and collagen microspheres embedded in an otherwise homogeneous gel could be clearly depicted. The conclusion was that there are many potential tissue engineering applications for ultrasonic elasticity micrography.

7.2.11. Urology

A quasi-static compression rig for ultrasonic elastography was used in in vitro experiments with a goat kidney and a rabbit model of nephritis and the changes in the elasticity of the kidney with renal damage and concomitant scarring could be detected before this was revealed by renal function tests [244]. Early loss of transplanted kidneys is usually the result of acute rejection, but long-term loss is often owing to chronic fibrosis. Thus, in patients with renal transplants, a technique for assessing the degree of fibrosis could provide a clinically useful indication of overall graft health. The results of freehand transabdominal ultrasonic elastography in the study of two kidney transplant patients with secondary end-stage renal disease, one owing to diabetes and the other to lupus nephritis, revealed a threefold difference in renal cortical strain [245]. More data are needed but the approach does seem to have clinical potential.

Current imaging techniques are unreliable both in the screening of the disease and in the differential diagnosis of abnormalities of the prostate gland. Consequently, the ‘gold standard’ for the assessment of the prostate is needle biopsy, which is not only very unpleasant for the patient and expensive for the service provider, but also not without risks and errors. In experiments with prostatectomy specimens, it was found that three-dimensional ultrasonic elastography performed considerably better than B-scanning in the detection of prostate cancer [246]. Similarly, it was concluded that ultrasonically estimated tissue elasticity is a promising biomarker for prostate cancer [247]. Of course, the results of neither of these studies are confirmation that the method will be useful in clinical practice. Using ARFI imaging to examine freshly excised human prostate glands, it was possible to visualize the internal structures and it was demonstrated that malignant lesions, benign hyperplasia, calcification and atrophy all had characteristic appearances [248]. At the least, that technique holds out promise for the more accurate guidance of biopsy and the consequential reduction in the false-negative rate of the procedure. The clinical applications, such as they are, of ultrasonic elastography in the differential diagnosis of prostate lesions have been pragmatically reviewed [192].

7.2.12. Vascular disease

In the UK, more than 44 per cent of all deaths are owing to causes connected with the heart and the cardiovascular system [249]. A very substantial proportion of these deaths are due to atherosclerosis of the coronary and carotid arteries. Plaques form in these arteries and, if they rupture, the resultant emboli can have catastrophic consequences. The characterization of atherosclerotic plaques and the identification of those which are vulnerable to rupture is a huge challenge for B-scan ultrasonography. For instance, some correlation was found between the texture of ultrasonic images of excised carotid artery plaques and their histology [250]; however, that work served more to demonstrate the limitations of histology as a ‘gold standard’ than to justify the utility of the ultrasonic approach in the clinical management of individual patients.

Arteries pulsate in response to changing blood pressure during the cardiac cycle. Following preliminary encouraging results [140], data obtained with a radially steered-array real-time IVUS B-scanner with echo-tracking and motion compensation processing for the creation of ultrasonic elastograms [251] demonstrated good correlation between low strain values and regions of calcification identified in atherosclerotic plaques in coronary arteries. A major difficulty with this approach is that of gross tissue motion and related artefacts, which tend to obscure the displacements that occur within the plaque itself. A technique aimed at motion compensation based on block matching and optical flow has been described [141] and this represents a further step towards the practical clinical application of the method.

Although intravascular ultrasonic scanning might seem to be the obvious way of attempting to produce arterial wall strain images with blood pulse pressure displacement, it has the disadvantage of being invasive and the disposable catheters are expensive. Encouraging results have been obtained with transcutaneous ultrasonic scanning [252]; for instance, it was possible to distinguish between the arteries of healthy young individuals and those of elderly patients with asymptomatic carotid stenoses. Promising results were also obtained using transcutaneous elastography of carotid artery plaques [253]. This may lead to clinically convenient identification of plaque composition and vulnerability, with relatively low cost and high patient acceptability, and seems to deserve to be explored.

The results of a pilot study in which ARFI imaging provided measurements of the mechanical properties of carotid and politeal arteries have been presented [254]. It was concluded that the detection and discrimination of hard and soft plaques might be helpful in the selection of treatment strategies and that the arterial stiffness in regions without atheroma might be a predictor of cardiovascular risk. A particularly encouraging report [255] was that, in experimentally induced calcifications in porcine femoral arteries, acoustic emission signals could be detected by means of vibroacoustography. This seems likely to prove to have been a clinically important development.

Using the supersonic shear imaging technique, it was shown, in a healthy volunteer, that the shear modulus of the wall of the carotid artery is about 60 per cent higher in systole than it is in diastole [256]. This finding supports the idea that the method might be valuable in the clinical assessment of arterial stiffness.

Thermal strain imaging has been shown to be capable, in principle, of identifying lipid pools within atherosclerotic plaques. The method depends on the differential changes in the speed of sound resulting from exposure to microwave pulses producing small increases in temperature (typically 1–2°C), detected during intravascular scanning. A major problem with this approach is that of bulk motion and tissue deformation; for this, compensation techniques have begun to be developed [257].

Venous thromboembolism is the most common cause of death among patients in hospital although, potentially, it is preventable [258]. The incidence of the condition is 1–3 per 1000 per year. Characteristically, a clot develops in a deep vein in the leg, after which parts of the clot detach, to be transported by the circulation to cause the often fatal complication of pulmonary embolism. Ultrasonic Doppler colour flow imaging with compression is nowadays accepted to be the best test when the presence of deep vein thrombosis is suspected. The operator obtains transverse images of the leg, showing arteries and veins, and applies pressure to the probe: if the vein collapses before the artery, there is no clot, and vice versa if there is a clot. Clinically, however, there is then a further problem. If the clot is acute, the patient should be given intravenous heparin to disperse it, followed by oral anticoagulant; but if the clot is chronic, only oral anticoagulant should be prescribed. Using a rat model, good correlation has been demonstrated between the age-related Young's modulus of thrombus determined by ultrasonic elastography and that subsequently directly measured ex vivo [28]. This suggests that ultrasonic thrombus elastography might be used to select the appropriate therapy for patients with deep vein thrombosis.

8. Conclusions and future prospects

Although ultrasonic elastography is a relatively new technology, it already has a place in the clinic. In particular, there are two approaches—freehand surface displacement (§6.2.3) and supersonic shear imaging (§6.2.7)—which seem currently to be the most useful, at least partly because they are both implemented in commercially available machines. Moreover, the use of freehand vibration-assisted elastography (§7.2.7) has achieved considerable popularity.

Looking into the future of elastography, Konofagou [59] anticipated that, during the decade to 2014, significant progress would be made in 10 areas. Already, she has been at least partially vindicated in her predictions concerning: the imaging of normal tissues with distinct, symmetric or ordered structure, such as kidney and prostate; viscoelastic and poroelastic applications for time-dependent mechanical property assessment; temperature monitoring and lesion detection in HIFU applications; early detection of normal or pathological myocardial or intravascular function; and localized radiation force techniques that can provide a direct motion-to-elastic-modulus relationship. This progress, however, leaves much still to be done, not only in these five areas, but also in the five other areas which she judged to be important: the characterization of tumour type based on ‘signature’ images such as mobility and shear strain; fast algorithms and fast acquisition hardware with handheld feedback for the most efficient clinical application of elastography; full three-dimensional deformation imaging using two-dimensional arrays and four-dimensional ultrasonic data with the latest scanners; monitoring of acupuncture needling effects to assess the mechanism behind needle/tissue coupling; and applications at cellular level through the use of higher frequency transducers or the acoustic microscope for small organ and tissue engineering applications.

Most recently, Parker et al. [62] concluded that there are not only opportunities for the development of elastographic techniques (such as through the enhancement of the capability of commercially available scanners and the emergence of stand-alone devices, and advances in estimators that go beyond relative stiffness and Young's modulus to provide insight into viscosity, anisotropy, nonlinearity, dispersion and their changes with disease), but also through progress in developmental models of diseases that link genetic, cellular and gross pathological changes with observations of biomechanical properties.

Indeed, there are troubling uncertainties and lacunae in the published data on the biomechanical properties of tissues in health and disease: a major effort is needed to collect, classify and disseminate the information which is available and to fill the gaps by making the requisite measurements. Other areas in which research needs to be pursued include the safety of all the different approaches to elastography, and the standardization of system performance and analytical approaches.

In summary, soft tissue strain and elasticity imaging is already a useful adjunct to real-time and Doppler ultrasonic scanning techniques. Moreover, it is the subject of intense contemporary research activity and can confidently be expected to become a powerful mainstream investigative tool.