The effect of individual variation on the structure and function of interaction networks in harvester ants

Abstract

Social insects exhibit coordinated behaviour without central control. Local interactions among individuals determine their behaviour and regulate the activity of the colony. Harvester ants are recruited for outside work, using networks of brief antennal contacts, in the nest chamber closest to the nest exit: the entrance chamber. Here, we combine empirical observations, image analysis and computer simulations to investigate the structure and function of the interaction network in the entrance chamber. Ant interactions were distributed heterogeneously in the chamber, with an interaction hot-spot at the entrance leading further into the nest. The distribution of the total interactions per ant followed a right-skewed distribution, indicating the presence of highly connected individuals. Numbers of ant encounters observed positively correlated with the duration of observation. Individuals varied in interaction frequency, even after accounting for the duration of observation. An ant's interaction frequency was explained by its path shape and location within the entrance chamber. Computer simulations demonstrate that variation among individuals in connectivity accelerates information flow to an extent equivalent to an increase in the total number of interactions. Individual variation in connectivity, arising from variation among ants in location and spatial behaviour, creates interaction centres, which may expedite information flow.

1. Introduction

Interactions are used to transfer information among humans [1], other animals [2] and cells, such as neurons. The structure of the interaction network, who interacts with whom and how often, influences the flow of information on the network [3]. Many animals use social networks to coordinate group behaviour [1,4,5]. Social insect colonies operate without central control. Individuals use local cues, including interactions with others, resulting in the regulation of the colony's activities [6–8] and possibly affecting its fitness [9]. Examining the interaction network structure of social insects can reveal the significance of various individuals to information transmission. For example, certain individuals may engage in more interactions than others and function as information hubs [10].

Ants vary in task performance and task fidelity [11–14] and so, like other social insects [15,16], ants may vary in how often each individual interacts with others. ‘Key individuals’, such as catalysts, may enhance the task performance of other workers [17], as demonstrated in honeybees. In honeybees, vibration behaviour performed by certain individuals modulates the search of other nestmates for new nest sites [18], possibly through increasing the interaction rate among nestmates [19]. Only few such examples of key individuals have been studied and little is known about what dictates who becomes a key individual and why individuals vary in their connectivity.

The spatial distribution of workers in the nest may produce variation among individuals in the frequency of interaction. For example, honeybees spatially segregate by age, leading to more interactions among individuals of similar age [20]. Specific locations, such as arena edges [21], can facilitate interactions. Most behavioural tasks are location-specific; for example, brood care occurs where broods are kept [22–24] and foraging wherever food is available [23]. As a result, ants performing the same task might interact more with one another than with ants from a different task [25]. Thus, the location of an ant within a nest, and how long it spends there [26], might dictate how many nestmates it encounters and who they are.

How an ant moves around influences its interaction rate. Theory predicts that the greater an ant's standard deviation of turning angle, or ‘turning index’ [27,28], the more tortuous its trajectory, the less ground it covers and the less likely it is to interact with other ants per time unit [29]. Empirical studies, however, show a positive relationship between turning index and encounter rate. Workers of the Argentine ant, Linepithema humile, increase both their turning index and their encounter rate as local density increases [28], and in Messor sancta, interaction rate is positively related to turning index [27].

Individual variation in connectivity, defined as the number of interactions, may have an important function. While the total number of interactions influences information transmission rate [8,30], network structure is also important. Networks exhibiting heterogeneity in connectivity have a right-skewed degree distribution: a few individuals have many connections, and most individuals have few connections. Such networks with highly connected nodes, or hubs, facilitate rapid disease transfer [31,32], efficient air-traffic flow [33], problem-solving in human groups [1] and the rate of neuron activation, synchronization and response times in neural networks [34]. Other attributes of network structure, beyond the scope of the present work, may also expedite or slow down the rate of information transfer [1,34].

The speed of information flow on a social insect network can determine how fast a colony responds to stimuli and achieves a collective decision [35]. For example, in the rock ant, Temnothorax albipennis, the more individuals visit the location of a new nest site, the higher the recruitment to the new nest, the more information about the nest's location arrives at the nest, and the faster the colony will move into it, thus decreasing exposure to the danger associated with emigration [36]. Other collective behaviours, such as response to a predator, or foraging, may benefit from the rapid dissemination of information throughout the colony. However, rapid dissemination of disease, which may travel on the same interaction network as information, can have detrimental consequences [25].

Here, we examine the structure of an interaction network in the red harvester ant, Pogonomyrmex barbatus, to determine whether there is individual variation in the number of ant encounters, with few highly interactive ants. Harvester ants interact using brief antennal contacts [6,37], and the rate of interaction influences the task and activity of the ant. For example, patrollers leave the nest early each morning and travel around the foraging area [38]. Returning patrollers interact with foragers in the entrance chamber, just inside the nest entrance, and this stimulates the foragers to leave the nest [39,40]. Later, the intensity of foraging depends on the rate at which returning foragers interact with inactive foragers in the entrance chamber [41,42].

We examine the structure of the interaction network in the entrance chambers of laboratory nests, and use a computer simulation to illustrate the consequences of the observed structure. We ask whether (i) ant interactions occur uniformly throughout the entrance chamber; (ii) the spatial distribution of interactions results solely from the ants' paths, or instead ants preferentially associate with or avoid one another; (iii) the distribution of ant interactions is random with all individuals having a similar number of interactions, or right-skewed with few highly connected individuals and many individuals with few interactions; (iv) individual variation in the number of interactions can be explained merely by variation in the duration of observation; (v) individual variation persists after accounting for the duration of observation; and (vi) the shape of an ant's path and its location within the entrance chamber is associated with its interaction frequency. We then use a computer simulation to illustrate the possible function of the interaction network structure, showing how individual variation in connectivity, total number of interactions or a dynamic probability of interactions each affects the speed of information flow.

2. Methods

2.1. Empirical observations

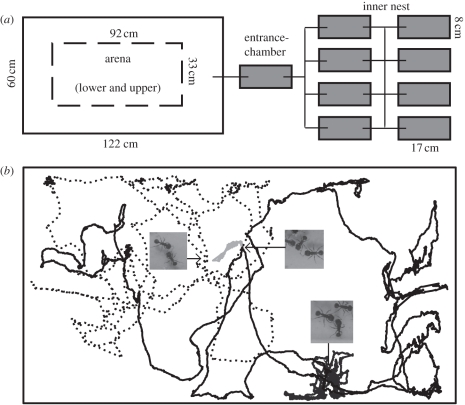
To determine the structure of the interaction network exhibited by ants, we observed two queen-right laboratory housed colonies of P. barbatus. Each colony was housed in a nest consisting of 7–10 closed plastic boxes (17 × 8 × 4 cm each) with plaster flooring, connected using Tygon tubing and kept in the dark using red mylar. The nest chambers were connected to an open, two-storey foraging arena, 122 × 60 cm in the bottom and 92 × 33 cm in the top. The nest chambers were connected to the foraging arena with one closed plastic box that was kept in the dark with no plaster floor, the entrance chamber (figure 1a). This entrance chamber is where ants meet as they come in and go out of the nest, and appears to function analogously to the chamber just inside the nest entrance in the field [36]. One colony, ‘Beth’, was collected from the field near Rodeo, NM, in the summer of 2007; the other colony, ‘Gozde’, was collected in summer 2008. Observations were made in September 2009.

Figure 1.

(a) Laboratory nest structure, grey shading denotes dark chambers. (b) Walking trajectories of four ants in the entrance chamber. The photos and arrows show interactions among these four ants that were identified using the trajectory data. The turning index (standard deviation of turning angle) for the paths shown are light grey, 131°; dark grey, 122°; solid black, 101°; dotted black, 92°.

To measure interactions, ants were filmed in the entrance chambers, and interactions were recorded using image analysis. We made one 5 min film of the entrance chamber of each colony, using a Canon Vixia H20 camera at 30 frames s⁻¹. To remove debris that could interfere with the image analysis, we cleaned the chamber one week prior to filming. Within 2–3 days, the number of ants in the chamber and their behaviour, including walking through the chamber, resting in it and transporting food from the outside, were similar to that observed before cleaning. While filming, the red mylar was removed from the covers of the entrance chamber and the inner nest to improve visibility. Removal of the mylar had no apparent effect on the behaviour of the ants. Food was not provided in the foraging arena for 4 days prior to filming. Both colonies had food stored in chambers further inside the nest, past the entrance chamber.

The path of each ant as it moved was automatically identified from the film using GemVident, a Java-based image analysis Multi-Target tracking software that we developed [43]. The image analysis software assigned each ant a unique identification number. Each ant entering the entrance chamber during the observation was assigned a unique number upon entry, so that an ant that left the entrance chamber and returned to it during the observation was counted as two ants. Because ant re-entry rate is low, it has little effect on our results (details in the electronic supplementary material). To ensure that each track represents the continuous movement of a single ant within the entrance chamber, we manually corrected any tracking errors introduced by the automated algorithm when the view of an ant was obstructed and the ant was lost by the tracking system. Correction was conducted by overlaying the ant walking trajectories on the movie images and advancing them both frame-by-frame, using custom software written in Matlab v. 2008a (The MathWorks Inc., MA). We identified 131 ants and their trajectories for Beth and 72 for Gozde (figures 1b and 2b).

Figure 2.

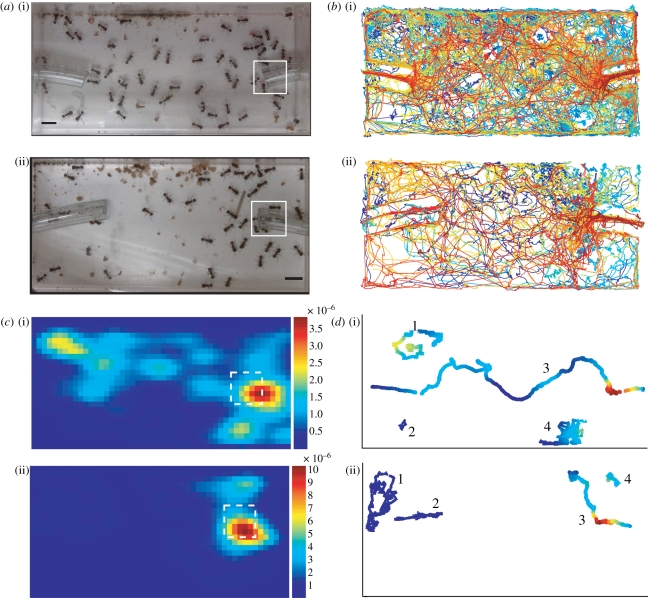
Spatial analysis of the entrance chamber for the two study colonies ((i) Beth; (ii) Gozde). (a) Images of the entrance chamber. Left tube leads to the foraging arena, right tube leads to the inner nest. White squares are the ROI around the entrance leading to the inner nest. (b) All ant trajectories. Each ant is represented in a different colour. (c) The utilization distribution map of ant interactions. Colour represents the interaction density estimate at each location. The dashed squares are in the same location as the solid squares in (a). (d) Trajectories of four ants illustrating the interpolation of the interaction density onto the ant trajectories. Trajectory colour represents the interaction density in each location and is on the same colour-scale as in (c). Numbers are used to distinguish the four ant trajectories.

We used the resulting trajectories to automatically identify interactions among ants. An interaction was defined as a physical contact between an ant's antennae and any part of another ant. To determine the spatial and temporal criteria characterizing an interaction between two ants, we haphazardly chose five interactions for each colony from the films. We overlaid the trajectories on the film and measured the distance between the trajectories of the interacting ants and the time they spent adjacent to each other during the interaction. We used the average shortest distance between the two trajectories measured and the shortest interaction duration. Based on these measurements, we characterized an interaction between two ants as two trajectories within 55 pixels or less, approximately two-thirds of an ant length, that remained at this distance for at least 5 frames (0.2 s) (figure 1b). A total of 3145 ant interactions were identified in Beth and 1483 in Gozde (see interaction examples in figure 1b). To verify that the interactions determined automatically fit the definition above, we visually examined 26 per cent of the automatically identified interactions for each colony. The false-positive error rate was 0.75 per cent in Gozde and 3.75 per cent in Beth. Analysis showing this false-positive error rate would not affect our results and an example of the process used to check the automatic interactions is provided in the electronic supplementary material.

2.2. Spatial distribution of interactions

To examine whether ant interactions were homogeneously distributed in space, we tested whether more interactions than expected at random occurred in the region of the chamber that was closest to the entrance of the tube leading to the inner nest (figure 2a). We chose this region because preliminary data suggested that ant interactions were most likely to occur in this region. However, the region used in our statistical analysis was not defined using the location of the interactions, but using the location of the tube leading to the inner nest. For each of the two colonies, we defined a region of interest (ROI) around the tube entrance leading to the inner nest, based on an image of the entrance chamber (figure 2a). The spatial position of the ROI in relation to the chamber walls differed slightly in the two colonies because of differences in the plastic tube's shape, but the size of the ROI was the same for both (figure 2a). To test whether ants interacted significantly more in the ROI than elsewhere in the entrance chamber, we ran a Monte Carlo test. Our null hypothesis was that there were as many or fewer interactions in the ROI as in any other similar-sized area elsewhere in the entrance chamber. We randomly selected, with replacement, 100 000 squares the size of the ROI throughout the entrance chamber and summed the number of interactions over the entire 5 min observation for each colony, within each square. We computed the probability that the number of interactions in the randomly selected squares was greater than or equal to the number of interactions in the ROI.

To further investigate whether the spatial heterogeneity of interactions we found was due solely to heterogeneity in the ants' positions (figure 2b), or whether ants regulate their interactions and either avoid other ants or preferentially interact with them, we ran another Monte Carlo test. Our null hypothesis was that after taking into account the ants' locations, there will be as many or fewer interactions in the ROI as in any other similar-sized area elsewhere in the entrance chamber. To quantify ant locations we used for each ant its position in all the frames of the video for the duration it was visible, using a rate of 30 frames s⁻¹. We randomly selected, with replacement, 100 000 squares of the same size as the ROI throughout the entrance chamber. We calculated the probability that the ratio between the number of interactions and the square of the number of ant positions (interactions/positions²) in the randomly selected squares was greater than the same ratio in the ROI. The denominator of this ratio is squared because an interaction requires two ants to meet (see also [28]). If this ratio is greater in the ROI than elsewhere in the chamber, the result will indicate that ants preferentially interact in the ROI, more than expected based on their movements alone. No significant difference in this ratio across the chamber will indicate that the spatial distribution of interactions is a result of the ants' movements alone and that ants do not preferentially contact or avoid one another.

2.3. Individual variation in interactions

We examined whether the structure of the interaction network identified in each of the two colonies was random or included some individuals that were much more interactive than others. We constructed an interaction network for all the ants in the entrance chamber and examined its structure. We computed for each ant its weighted degree (WD), defined as the total number of interactions with any other ant, including repeated interactions, also known as ‘strength’ [44,45]. We used the Akaike Information Criterion (AIC) [46] as a likelihood-ratio test [47] to determine whether a Poisson, a geometric, a negative binomial or a power-law distribution best fits the observed WD distribution. If a Poisson (bell-shaped) distribution best fits the WD distribution, this indicates a random network structure with little individual variation [48]. A geometric fit to the WD distribution indicates a network structure with right-skewed connectivity, i.e. few individuals with many interactions and many individuals with few interactions. Both the Poisson and the geometric distributions are special cases of the negative binomial distribution. A negative binomial distribution will provide a better fit to the WD distribution because it is more general and has two parameters instead of one. If r of the negative binomial distribution is 1, the distribution is geometric and as r approaches infinity, the negative binomial distribution approaches a Poisson distribution. Finally, if a power-law distribution fits the WD distribution, this indicates more extreme individual variation in connectivity than the geometric distribution, i.e. the highly interactive individuals have more interactions than in the geometric fit [47,49].

To determine what produced the observed WD distribution, we examined the relationship between WD, i.e. an ant's number of interactions, and how long it was observed. We used a generalized linear model (GLM) to test whether WD was associated with the duration for which an ant was observed and colony identity. We included colony identity in the model to account for colony-specific attributes such as size and age. We predicted that the longer an ant was observed in the entrance chamber, the more nestmates it will encounter.

Because the number of interactions an ant experienced depended on the length of time it was observed, in the subsequent analyses we examined variation among ants in interaction frequency, i.e. WD per unit time. We used the AIC [46] as a likelihood-ratio test [47] to determine whether an exponential or a Gaussian distribution best fits the interaction frequency distribution. A good fit to the continuous equivalent of a geometric distribution, the exponential distribution, indicates a right-skewed interaction frequency distribution, i.e. few individuals with high interaction frequency and many individuals with low interaction frequency. A good fit to the continuous equivalent of the Poisson distribution, the Gaussian distribution, indicates no individual variation in interaction frequency.

We then examined how interaction frequency depends on the ant's spatial behaviour: the shape of its path and its location. Because the colony in which we observed more trajectories showed significantly more interactions overall, we also included colony identity as an effect in this analysis. Theoretical work predicts a negative relationship between an ant's turning index and its interaction rate [29]. We computed the turning angle between each two steps in an ant's trajectory; a step was defined as the line traversed by an ant between two successive frames. We then calculated the turning index, or standard deviation of turning angle, for each trajectory (figure 1b), as in Gordon [28]. To consider the effects of location, because interactions were heterogeneously distributed throughout the entrance chamber, we examined whether an ant that passed through regions of high interaction density was likely to have a high interaction frequency. We first mapped the interaction density throughout the chamber, by creating a utilization distribution map of all ant interaction locations using a kernel density estimate [50] (figure 2c). We then interpolated the interaction density onto the ant trajectories (figure 2d) and computed the average interaction density of each trajectory. Because of the large number of interactions used to create the utilization distribution map (3145 for Beth and 1483 for Gozde), the contribution of each individual ant (131 ants in Beth and 72 in Gozde) to the interaction density was very small, so we did not exclude the same ant's interactions when interpolating the interaction density onto its trajectory. We ran a GLM to examine the relationship between interaction frequency and turning index, average trajectory interaction density and colony identity.

2.4. Model

We used an agent-based computer simulation to illustrate how individual variation in interaction number, and total number of interactions, each affect the flow of information among ants. We compared the speed of information flow in four models that varied in the probability of ant interactions. (i) Uniform: null model in which all ants have an identical and consistent probability of interacting with one another. (ii) Highly Interactive Uniform (UniformHI): to illustrate the effect of increasing the total number of interactions on information flow, ants have an identical and consistent probability of interacting with one another which is greater than that of the Uniform model. (iii) Skewed: to illustrate the effect of individual variation in interaction probability on information flow, ants vary in their probability of interaction with nestmates, and the probability of interaction does not change over time. (iv) Changing: to illustrate the effect of a dynamic probability of interaction on information flow, ants start with a uniform probability of interaction and each ant increases its probability of interaction once, when it becomes informed, as detailed below.

In each of the simulations, 100 ants interacted for 1000 timesteps, and each simulation was repeated 100 times for each of the four models. We assigned each ant a status, informed or not informed, depending on its number of interactions. At the beginning of each simulation, 10 random ants were assigned an ‘informed’ status. During each timestep, we allowed a maximum of 10 interactions, which corresponds to the number of interactions per second we observed (average: 4.5, range: 0–14 for Gozde; average: 9.5, range: 3–26 for Beth). Each ant was allowed no more than one interaction per timestep. Ants that interacted 10 times with informed individuals became informed themselves. In our model the ants did not forget; once an ant became informed, it remained informed for the duration of the simulation.

The probability that two ants interacted depended on the product of their individual interaction probabilities. For the Uniform, UniformHI and Skewed models, the probability that each ant interacted with another in a given timestep was pre-assigned at the beginning of the simulation. In the null Uniform model, all ants were assigned an individual probability of interaction of 0.03. In the UniformHI model, all ants were assigned an individual interaction probability of 0.039, 1.3 times the Uniform one. In the Skewed model, ants were assigned individual interaction probabilities following an exponential distribution with a mean of 0.03, assigning most ants a low individual interaction probability and few ants a high probability. In the fourth model, Changing, ants were initially assigned a lower individual interaction probability than that of the Uniform model, 0.0275. Once an ant became informed, its individual interaction probability increased 1.3-fold to 0.0358. The average individual probability of interaction in the Changing model was similar to that of the Uniform model, 0.03. Each ant changed its individual interaction probability only once, effectively maintaining very low individual variation in interactions in the Changing model, as in the Uniform model. For more details on parameter choice and for the source code of the simulation, see the electronic supplementary material.

The total number of interactions in the Uniform, Skewed and Changing models was similar, to control for the effect of total number of interactions and allow a valid comparison among the different network structures. However, there was some variation in the total number of interactions because the number of interactions at each timestep was not fixed. We compared the total number of interactions in the four models using a one-way analysis of variance (ANOVA) and a Tukey's test for multiple comparisons.

The simulation output was used to illustrate the effect of interaction probability and the total number of interactions on information flow speed. To quantify the speed of information flow, we recorded the number of informed ants in each timestep. We determined the time at which 50 per cent of the ants become informed (T50) as in O'Donnell & Bulova [50]. We compared speed of information flow among the four models using a one-way ANOVA and a Tukey's test for multiple comparisons. By comparing the speeds of the Skewed, UniformHI and Changing models to the Uniform model we can distinguish whether what speeds up information flow is the interaction network structure (Skewed), the total number of interactions (UniformHI) or a dynamic change in interactions (Changing).

Spatial analysis, Monte Carlo tests, simulations and model-fitting were conducted in Matlab v. 2008a (The MathWorks Inc., MA, USA); other statistical analysis was conducted in JMP 8.0 (SAS, NC, USA).

3. Results

A total of 131 distinct trajectories were identified in the first colony, Beth, with 3145 interactions. In the second colony, Gozde, we identified 72 trajectories and 1483 interactions (figures 1b and 2b).

3.1. Spatial distribution of interactions

The spatial distribution of interactions was heterogeneous. Significantly more interactions occurred near the chamber entrance leading to the inner nest (the ROI) than elsewhere in the entrance chamber (Monte Carlo test, p < 0.01 for both colonies; figure 2c).

The spatial distribution of interactions corresponded to the spatial distribution of ant positions, showing that ants do not actively seek or avoid contact with others. The Monte Carlo test showed no significant difference between the ROI and the rest of the entrance chamber in the ratio between the number of interactions and ant positions squared (interactions/positions²) (Monte Carlo test: Beth: p = 0.11; Gozde: p = 0.34).

3.2. Individual variation in interactions

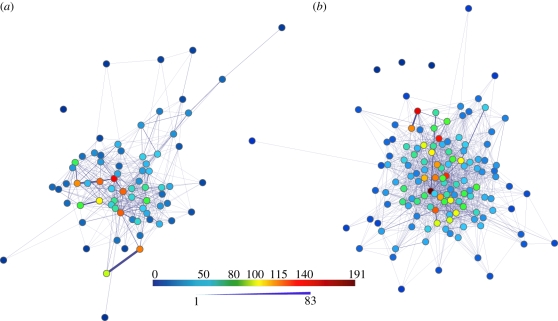
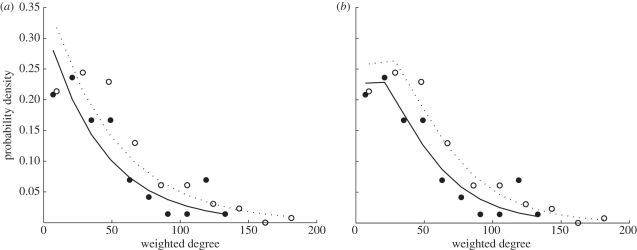
Most ants had few interactions and few ants had many interactions (figure 3). The structure of the ants' interaction network fits a discrete, right-skewed, geometric WD distribution and a negative binomial distribution with r ≈ 1 (figure 4). The observed WD distributions showed a better fit with the geometric and negative binomial distributions than with the Poisson or power-law distributions, for both colonies (Beth: negative binomial AIC = 1260 < geometric AIC = 1277 < power-law AIC = 1626 < Poisson AIC = 3908; Gozde: negative binomial AIC = 672 < geometric AIC = 679 < power-law AIC = 783 < Poisson AIC = 2201; figure 4). The good fit to the negative binomial distribution with r values close to 1 (Beth: r = 1.65; Gozde: r = 1.49) and to the geometric distribution shows that the distribution of interactions is right-skewed, i.e. few individuals have many contacts while most have few. The negative binomial distribution fits the WD distribution slightly better than the geometric distribution, because the negative binomial has two parameters while the geometric distribution has only one. Of the three models that have only one parameter (Poisson, geometric and power-law), the geometric distribution best fits our data. The lack of fit with a Poisson distribution shows that individuals differ in the number of interactions, while the lack of fit with the power-law distribution shows that the highly interactive individuals do not have many orders of magnitude more interactions than the rest of the population.

Figure 3.

Interaction network among ants in the entrance chamber of two laboratory housed colonies ((a) Gozde; (b) Beth). Each ant is represented as a node in the network. Node colours reflect the WD of an ant (same colour scale for both colonies). Edge thickness corresponds to the number of interactions. Network layout is ‘Spring embedded’ in which the distance between nodes corresponds to how tightly they are connected. Networks were created using Cytoscape 2.6.2.

Figure 4.

WD distribution of the interaction network in the entrance chamber of two laboratory housed colonies. Open circles (Beth) and closed circles (Gozde) represent binned weighted degree for each colony. The dotted (Beth) and solid (Gozde) lines are the fits of (a) a geometric distribution to the data; (b) a negative binomial distribution to the data. (See figure S6 in the electronic supplementary material for a representation of this figure on a log-linear scale).

The ants' WD increased with the duration of observation, and the two colonies differed in the total number of interactions (GLM: p < 0.0001, r² = 0.35). The longer an ant was observed in the entrance chamber, the greater is its WD (p < 0.0001, T = 10.16). The average (±s.d.) duration of a trajectory was 150 ± 115 s for Beth and 173 ± 119 s for Gozde. Furthermore, Beth, the colony with more identified trajectories, had a significantly greater average WD than Gozde (p < 0.01, T = 2.61).

To account for variation among ants in the duration of observation, subsequent analysis used the WD per time unit, or interaction frequency. The distribution of interaction frequencies, which takes into account the duration of observation, was right-skewed, similar to the WD distribution. The distribution of ant-interaction frequency (a continuous variable) fits an exponential distribution better than a Gaussian distribution for both the colonies (Beth: exponential AIC = −7.9220 < Gaussian AIC = −0.1621; Gozde: exponential AIC =−10.4501 < Gaussian AIC = −0.1621).

Variation in ant-interaction frequency was associated with path shape and spatial position. As predicted [29], interaction frequency decreased with turning index, i.e. the more tortuous an ant's trajectory, the less likely it was to interact with other ants per time unit. This is probably because ants that turn around more are likely to cover less ground. Furthermore, the more time an ant spent in regions with many interactions (interaction hot-spots), the greater is its interaction frequency. The interaction frequency was significantly correlated with the turning index, average trajectory interaction density and colony identity (GLM: p < 0.0001, r² = 0.4). Interaction frequency decreased with turning index (p < 0.0001, T = −6.35) and was positively correlated with average trajectory interaction density (p < 0.0001, T = 9.24). The colonies differed in interaction frequency, as they did in interaction number (p < 0.0001, T = 4.28, Beth > Gozde).

3.3. Model

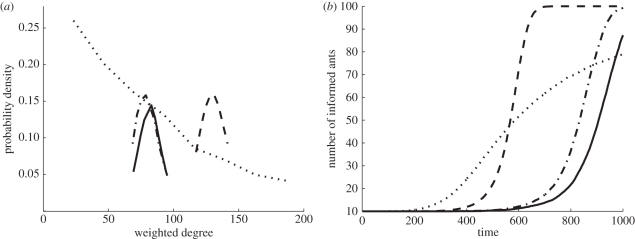
Of the four models we tested, only the Skewed model produced a network with individual variation in the number of interactions. The Uniform, UniformHI and Changing models produced networks with no individual variation in the number of interactions. Like the network we observed, the WD distribution of the simulated Skewed model fit a geometric distribution better than a Poisson distribution (AIC Poisson = 652 300 > AIC geometric = 106 780; figure 5a). The WD distributions for the other three models—Uniform, UniformHI and Changing—like those of random networks [48], fit a Poisson better than a geometric distribution (Uniform: AIC Poisson = 71 348 < AIC geometric = 108 240; UniformHI: AIC Poisson = 75 809 < AIC geometric = 117 370; Changing: AIC Poisson = 76 125 < AIC geometric = 107 820; figure 5a). The interaction probability of the UniformHI model was greater than that of the Uniform model, so its Poisson WD distribution had a higher mean (Uniform: 82 ± 9 < UniformHI: 130 ± 11), but they both had a similar interaction network structure (figure 5a). The Changing and Uniform models differed slightly in the interaction structure because the Changing model's interaction probability was not constant throughout the simulation. However, their mean WD was similar (Uniform: 82 ± 9 ≈ Changing: 80 ± 11) allowing a comparison among the speed of information flow in these two models that illustrates the effect of changing the probability of interaction in response to information without being affected by increasing the total number of interactions.

Figure 5.

(a) WD distribution resulting from the four models: Uniform (solid), Changing (dotes and dashes), Skewed (dotted) and UniformHI (dashed). (b) Number of informed ants at each time-step of the simulation (averaged over 100 simulation runs) for the four models, same legend as in (a).

In all the four models, the increase over time in numbers of informed ants followed a logistic curve (figure 5b). At first, there were many uninformed ants, and in most interactions, ants switched from uninformed to informed status. This led initially to rapid information flow. As the simulation progressed, and informed ants did not forget and change the status back to uninformed, fewer uninformed ants were available, and the information flow slowed down. Such a logistic process is similar to the recruitment rate dynamics in O'Donnell & Bulova's [51] model of task performance.

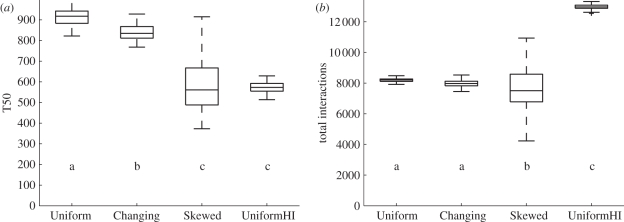
The speed of information flow of the Skewed and UniformHI models was much faster than that of the Uniform model, while the speed of information flow in the Changing model was only slightly faster than that of the Uniform model (ANOVA: p < 0.0001, F = 526; Tukey's test: Uniform–UniformHI: p < 0.00001; Uniform–Skewed: p < 0.00001; Uniform–Changing: p < 0.0001; figure 6a). There was no difference between the UniformHI and the Skewed models in the speed of information flow (Tukey's test: p = 0.26; figure 6a).

Figure 6.

(a) Boxplot of the T50, averaged for the 100 simulations for each of the four models. Models with different lower case letters are significantly different (Tukey's test p < 0.0001). (b) Boxplot of the total number of interactions, averaged for the 100 simulations of each of the four models. Models with different lower case letters are significantly different (Tukey's test p < 0.05).

The total number of interactions was higher in the UniformHI model than in the Skewed, Changing and Uniform models (ANOVA: p < 0.0001, F = 1399. Tukey's test: UniformHI–Uniform: p < 0.00001; UniformHI–Skewed: p < 0.00001; UniformHI–Changing: p < 0.00001; figure 6b). The Skewed model had slightly fewer interactions than the Uniform and Changing models (Tukey's test: Skewed–Uniform: p < 0.0001; Skewed–Changing: p = 0.046; figure 6b). This slight difference in the total number of interactions may be owing to the high variance among simulation runs of the Skewed model, which results from the high variance in individual interaction probabilities in the Skewed model and the random assignment of ‘informed’ status to the first 10 ants. There was no difference between the Uniform and Changing models in the total number of interactions (Tukey's test: Uniform–Changing: p = 0.11; figure 6b).

4. Discussion

The interaction networks we observed in harvester ants had right-skewed WD distributions: few ants engaged in most of the interactions while most ants engaged in few interactions. Interestingly, many other biological systems exhibit variation in connectivity, with right-skewed distributions such as exponential, geometric or power-law degree distributions [3,47–49]. Previous work on social insects shows that some individuals are more interactive than others in honeybees [20] and rock ants [52], as in other animals [53–55]. However, little is known about the functional importance of these highly interactive individuals and what processes lead certain individuals to engage in more interactions than others. In harvester ants, it appears that variation among ants in interactions arises from the ants' spatial behaviour.

We found that an ant's number of interactions depended on its time in the entrance chamber and on colony identity. However, even after taking these factors into account, there was further variation among ants in interaction frequency. We observed significantly more interactions in the colony with more identified trajectories. Colony size influences interaction number and network structure in other ant species [21] and in wasps [15]. However, we observed only two colonies, so further work is needed to examine the relationship between colony size, or other colony-specific characteristics, and the network structure of harvester ants.

Interaction frequency, i.e. the number of interactions per unit time, depended on path shape. We found that the more convoluted an ant's path, i.e. high turning index, the less ground it covers, and the fewer other ants it meets. This is consistent with the predictions of Adler & Gordon [29] on differences in interaction frequency among groups of ants, in which all ants in the group had a particular turning index. We found further that variation in path shape, within a group, also accounts for the variation in interaction frequency.

Interaction frequency depended on location as well as path shape. The spatial distribution of ant interactions was heterogeneous throughout the entrance chamber. Most interactions occurred at a specific, functionally significant, location: the tube linking the entrance chamber and the inner nest. Interaction hot-spots were observed at this location in two laboratory nests, suggesting that this is an important location for information exchange. The interaction hot-spots emerged from the ants' walking trajectories, resulting from the way the colonies respond to nest structure [56,57]. Further observation of nests with a different structure is required to test the effect of nest structure on the location of ant interactions.

The longer an ant spent in the interaction hot-spot, the greater its rate of interactions. Previous work on other social insects shows that differences among individuals in movement patterns can restrict them to particular nest areas [26], and lead to differences in task performance [22–24]. Here we found that an ant's location can also determine whether it becomes one of the more interactive individuals in the interaction network. The relationship between an ant's number of interactions and its spatial behaviour is consistent with the possibility that each ant's interactions are Poisson-distributed, while variation among ants is gamma-distributed, leading to the observed negative binomial WD distribution overall. Further work is needed to determine the causes of individual variation in movement patterns.

Other processes, in addition to spatial behaviour, may contribute to individual variation in connectivity. For example, a behavioural rule in which all ants tolerate a certain number of uninformed contacts before they stop contacting other ants, i.e. a Bernoulli process, would lead to a negative binomial WD distribution. Most commonly, animals socially assort based on genetic relatedness to form family groups. However, social assortment and variation in interactions can also be determined by reproductive state [58], dominance rank [54,59], familiarity [60], behavioural traits [61], task [4,37,62], body size [63] and location [64]. In ants, the structure of interaction networks may depend on colony age, the amount of brood and stored food or ecological conditions such as seasonal changes. Further work is needed to determine when and how the structure of the network changes. We do not know whether the role of a highly interactive individual is transient or whether certain individuals persist in this role. In either case, variation among individuals in interaction frequency may facilitate rapid information transfer within a colony.

The speed at which information flows in a network dictates how fast a group collectively responds to environmental stimuli and therefore may have fitness consequences. As illustrated, when comparing our models, an interaction network structure with variation among individuals in interaction frequency (Skewed model) can expedite information flow to an extent equivalent to an increase in the total number of interactions (UniformHI model), and to a greater extent than dynamically increasing the interaction probability in response to environmental cues (Changing model). Thus, variation among individuals in connectivity can facilitate rapid information flow without increasing the total number of interactions. Networks with variation among individuals in interaction frequency have faster information flow than uniform networks because the highly interactive individuals reduce the number of interactions required to connect distant nodes [1,3,31,32,34]. The speed of information flow was similar in the two models (Uniform and Changing) with a Poisson degree distribution, in which there was no or little variation among individuals in interaction frequency, and a similar total number of interactions.

Most other models on information networks in social insects [26,29,51] have not considered individual variation in connectivity. Our model extends these studies by introducing individual variation in interaction probability, and by illustrating its effect on information flow speed. Naug & Camazine's [25] model examined the effect of variation on disease transmission in social insects and showed, in contrast with ours, that heterogeneity reduces the speed of disease transmission. Their model used only two interaction variants, one within and the other among tasks but no further variation among individuals, producing a modular network with uniform clusters that are loosely connected to one another. Information, or disease, flowing on such a modular network is less likely to pass through the weak connections among clusters, and thus is slower than a uniform network in which all connections are identical.

Our simulations illustrate that variation among individuals in interaction frequency increases information flow. The presence of unusually interactive individuals has an effect on information flow similar to that of two other, not mutually exclusive, well-studied processes: increasing the total number of interactions, and dynamically increasing interaction rate in response to environmental cues. Both of these processes increase the speed of information flow by increasing the rate at which individuals interact [51,65]. Empirical studies show that social insects increase the number of interactions in response to environmental information, as in our Changing model. Encountering a food source increases the number of interactions in fire ants, Solenopsis invicta [66,67], honeybees, Apis mellifera [68] and rock ants, T. albipennis [52]. Increasing the total number of interactions, as in our UniformHI model, speeds-up the transmission of disease in bumblebees [16]. Empirical studies are still needed to determine how individual variation in connectivity, as in our Skewed model, contributes to information flow in social insects. Understanding the structure of interactions among animals and the role of each individual in these networks can shed light on how information flows in a group and how collective behaviours arise.