Evolution of social learning when high expected payoffs are associated with high risk of failure

Abstract

In an environment where the availability of resources sought by a forager varies greatly, individual foraging is likely to be associated with a high risk of failure. Foragers that learn where the best sources of food are located are likely to develop risk aversion, causing them to avoid the patches that are in fact the best; the result is sub-optimal behaviour. Yet, foragers living in a group may not only learn by themselves, but also by observing others. Using evolutionary agent-based computer simulations of a social foraging game, we show that in an environment where the most productive resources occur with the lowest probability, socially acquired information is strongly favoured over individual experience. While social learning is usually regarded as beneficial because it filters out maladaptive behaviours, the advantage of social learning in a risky environment stems from the fact that it allows risk aversion to be circumvented and the best food source to be revisited despite repeated failures. Our results demonstrate that the consequences of individual risk aversion may be better understood within a social context and suggest one possible explanation for the strong preference for social information over individual experience often observed in both humans and animals.

1. Introduction

While there has been extensive research in the evolution of individual decision-making under risk and, independently, in the evolution of social learning, the interaction between these two processes has received relatively little attention. It is widely accepted that individuals living in a group may acquire information about their environment individually, through processes such as trial and error, or socially, by observing others in the group and learning from the latter's experience. In recent decades, the strategic use of individual and social learning has been a focus of interest for evolutionary biologists, psychologists and anthropologists (e.g. [1–6]). While social learning saves the costs of individual learning (in terms of time and errors), it also bears the potential risk of learning others' maladaptive behaviour [7]. Consequently, the availability to the population of reliable public information is often considered as the main constraint on the success of social learning [8–10].

Obtaining reliable information is undoubtedly a major constraint on any learning process, either individual or social. Among the well-known obstacles confronting individual learners is the emergence of cognitive biases as a result of the sampling process (e.g. [11–14]). One such bias may arise from failures: an action resulting in a relatively poor outcome is likely to be avoided in subsequent sampling steps, in what is known as risk aversion or ‘the hot stove effect’ [15,16]. Consequently, an action that has variable rewards and which may initially appear to offer a low return, will be abandoned in favour of alternative actions even if the expected value of the former is higher. A scenario where actions that are on average the most rewarding are also the most variable is likely in a foraging situation. As food items with high nutritional value are more rare and are likely to be depleted first [17–20], searching for them may involve repeated failures even though on average they are optimal choices. Although being risk-averse may under some circumstances be adaptive [21], in this situation it leads to sub-optimal behaviour (e.g. [22]). In the present study, we suggest that this phenomenon may result in an important (and so far overlooked) evolutionary advantage to social learning over individual learning.

In a seminal analysis of the evolution of individual and social learning, Rogers [23] showed that individual and social learning achieve a mixed evolutionarily stable strategy (ESS) where their fitnesses are equal, but the mean population fitness at the ESS point is the same as that of a population containing only individual learners. This result seemed paradoxical [23,24] in light of the conventional view of social learning as a key contributor to the evolutionary success of human populations. Later, it was suggested that this conflict (known as Rogers' paradox) can be resolved if social learning is not used indiscriminately, but applied under appropriate circumstances—an assertion supported by both observations of animals and theoretical work (reviewed in [25–27]; see also [24,28,29]). Nevertheless, theoretical work has shown that Rogers' paradox is generally robust [2,24,29–31], and some experimental work indicates that animals may rely on public information and discard personal information even when it is maladaptive for them to do so ([32–36]; see also [7,37,38]). This suggests that the tendency to rely on social information may reflect a general evolved response. It has also been suggested that social learning may be advantageous in changing environments (see [30]), but this is also the case for individual learning [39]. Thus, while some rate of environmental change can promote the evolution of social learning, it cannot fully explain its advantage over individual learning.

A clear advantage for social learning has been demonstrated recently by Rendell et al. [40]. In an effort to search for the most effective strategy of learning from others, Rendell et al. launched a tournament among social learning strategies. Strategies entered by external participants competed against each other to determine to what extent and under what conditions it is best to use social or individual learning. The tournament's most successful strategies, including the winner, were strategies that relied heavily on social learning. The advantage of social learning demonstrated by Rendell et al. was based on the fact that individuals whose behaviour was copied by others demonstrated the highest-payoff behaviour in their repertoire, thereby inadvertently selecting the best information to be used by social learners. The mean fitnesses of populations containing a number of strategies were found to be positively correlated with the frequencies of social learning. However, populations fixed on only one of the winning strategies, employing social learning as their main learning method, had a lower mean fitness than populations fixed on strategies that relied less heavily on social learning. These complex results are nevertheless expected from this kind of modelling, where social learners are information parasites whose success depends on the quality of information produced by individual learners (see discussion in [40]).

In the present study, we suggest that an advantage to social learning over individual learning may result from a different mechanism, involving risk sensitivity. In a variable environment where choices with high expected payoffs are associated with high risk of failure, social learners can circumvent the problem of risk aversion if they learn where to forage by watching individuals that have already found food. Consequently, they acquire better information than individual learners, prevail and increase population mean fitness even in the absence of individual learners (contrary to Rogers' paradox). This is likely when social foragers are engaged in a producer–scrounger game (described in [41,42]) in which producing (independent search) facilitates individual learning, while scrounging (joining others' food discoveries) facilitates social learning [7,8,27,43].

To investigate the hypothesis that social learning may have an advantage over individual learning in a risky environment, we used agent-based evolutionary simulations, combining a producer–scrounger game with explicit individual and social learning rules for associating different food patch types with experienced reward. We tested which learning strategy was most successful: exclusive individual learning, exclusive social learning or combined individual and social learning (where the term ‘exclusive’ entails using only one type of learning; an individual using the exclusive social learning strategy will therefore engage only in social learning, and although it can produce new information for others when it searches for food, it will not use this information to learn individually). We also investigated whether the advantage of social learning in a risky environment was related to learning complexity, in terms of the extent of details in memory representation [44], or to the frequency of learning errors. Finally, we analysed the performance of each learning strategy and confirmed an increase in the population mean fitness as social learning evolved.

2. The model

The fitness consequences of a learning strategy depend on a dynamic process involving stochastic sampling errors that influence successive sampling steps and eventually produce a wide distribution of possible outcomes. This makes analytical modelling impractical and it is therefore common to study the performance of learning rules by means of computer simulations (e.g. [13,16,45–47]). Formal analysis is even more difficult in the situation we study here, where learning strategies are evolving in the context of a frequency-dependent game. This is because the learning success of a focal individual can influence the payoffs, and indicates the learning process of other players. In order to capture this highly dynamic process, we use agent-based evolutionary simulations in which learning and social strategies are encoded by genes carried and expressed by individuals that are engaged in a virtual social foraging game. While the conclusions that can be drawn from such simulations may be limited to the range of tested parameters, there is increasing recognition that such simulations may be superior to the analytical models in realistically complex situations (reviewed by [48,49]). Accordingly, and in line with recent suggestions to view computer simulations as experimental research [50], our analysis may be regarded as a demonstration that is valid for a certain range of realistic conditions. Our model for learning rules and social foraging strategies was inspired by observations on the house sparrow, Passer domesticus, in our own research group (see [51,52]), as well as by previous work on social foraging in this species (e.g. [41,53–55]), but it may be applied to all social foragers.

A detailed description of the model following the ODD (Overview, Design concepts, Details) protocol [56,57] is provided in the electronic supplementary material, appendix A. Most readers may find the description below sufficiently informative.

2.1. The population

We simulated a population of n haploid agents. Each agent is defined by four genetic loci: (i) a foraging strategy locus, F, which defines the agent's probability of applying the producer or scrounger strategy; (ii) a learning rule locus, L, which determines the resolution at which the agent studies the environment; (iii) an individual learning locus I, which determines whether the agent learns while producing; and (iv) a social learning locus C, which determines whether the agent learns while scrounging (see the detailed description of all genes given below). The four genes give rise to 24 possible genotypes, but owing to epistatic effects they produce only 10 phenotypes (tables 1 and 2). All agents have the same lifespan, namely one generation composed of J foraging steps executed simultaneously by all agents during a ‘producer–scrounger game’ (see below). All agents end their lives at the end of the game and there is no overlap between generations. Fitness is determined according to the agents' accumulated payoffs during the J steps of the game, and the top 50 per cent of agents are then selected to reproduce asexually, each giving rise to two genetically identical offspring (an extension of this type of model to include sexual reproduction is in Arbilly et al. [58]). After production of the new generation, mutation occurs at a rate μ = 1/n at each locus. The population is followed through G generations. It should be clear that although we assume for simplicity that individuals are engaged in a single game of J steps during their lifetimes, similar results would be expected for repeated games of J steps during each lifetime as long as learning starts anew for each new game (i.e. repeated games are independent). The assumption that learning starts anew every generation may be realistic when the relevant cues for finding food change over time or change when the environment changes.

Table 1.

Symbols used in the simulations.

symbol	description
F1	foraging allele: pure producer (always applies the producer strategy)
F2	foraging allele: part-time scrounger (0.5 probability of being a producer)
L0	learning rule allele: non-learning
L1	learning rule allele: complex learning rule
L2	learning rule allele: simple learning rule
I0	individual learning allele: no individual learning
I1	individual learning allele: individual learner
C0	social learning allele: no social learning
C1	social learning allele: social learner
n	number of agents in the population
J	number of steps in the game (equivalent to each agent's lifespan)
G	number of generations in the simulation
μ	mutation rate
α	memory factor within the learning rule (weight of past events)
β	probability that a scrounger erroneously joins unsuccessful producers
θ	probability of associating socially acquired information with the wrong patch type

Table 2.

Genotypes and the phenotypes they produce as a result of epistatic interaction.

genotypes	phenotype
F1L0I0C0, F1L0I0C1, F1L0I1C0, F1L0I1C1, F1L1I0C0, F1L1I0C1, F1L2I0C0, F1L2I0C1	1. pure producer, non-learner
F1L2I1C0, F1L2I1C1	2. pure producer, simple learning rule
F1L1I1C0, F1L1I1C1	3. pure producer, complex learning rule
F2L0I0C0, F2L0I0C1, F2L0I1C0, F2L0I1C1, F2L1I0C0, F2L2I0C0	4. part-time scrounger, non-learning
F2L2I1C0	5. part-time scrounger, exclusive individual learning, simple learning rule
F2L1I1C0	6. part-time scrounger, exclusive individual learning, complex learning rule
F2L2I0C1	7. part-time scrounger, exclusive social learning, simple learning rule
F2L1I0C1	8. part-time scrounger, exclusive social learning, complex learning rule
F2L2I1C1	9. part-time scrounger, both individual and social learning, simple learning rule
F2L1I1C1	10. part-time scrounger, both individual and social learning, complex learning rule

2.2. The environment

The simulated environment consists of four food patches E₁, E₂, E₃ and E₄. The four patches are visually distinguishable from one another, but patches E₁ and E₂ have a common visual characteristic, for example, the same colour, and so do patches E₃ and E₄; therefore, these can be viewed as E₁₂ and E₃₄, respectively (see illustration in table 3). We assume that the relative frequencies of E₁ and E₂ within E₁₂ and of E₃ and E₄ within E₃₄ are equal. Each patch is represented by two parameters: the probability of finding food items in the patch, and the nutritional value of these items (table 3). The two parameters were set to be negatively correlated, so that the best food (the food with the highest nutritional value) is the least likely to be found. This environmental set-up represents a non-trivial learning task and is likely to be common in nature (valuable food items may be depleted sooner and become less common). To simplify the simulation, patch parameters remained constant throughout the game (no depletion during the game), and the environment had no spatial structure.

Table 3.

Food patch parameters and expected values. E₁₂ and E₃₄ represent perceptual unification of two patches based on a common visual cue (e.g. colour or shape); the black square and triangle and the white circle and pentagon represent possible visual characteristics of the patches that may cause perceptual unification based on colour. The shapes and colours are shown here only for illustrative purposes.

	patch
	E1	E2	E3	E4	E12	E34
parameter	▪	▴	○		▪ ▴	○
nutritional value	4	1.500	0.750	0.250
probability of finding food	0.250	0.333	0.500	1
expected value	1	0.500	0.375	0.250	0.750	0.313

2.3. Foraging strategy

The foraging strategy locus (F) determines the agent's probability of applying a producer strategy at each step of the producer–scrounger game described below, with the complementary probability of applying a scrounger strategy. Following preliminary simulations showing the emergence of a bi-allelic population (see explanation in the ODD protocol format of appendix A), we assumed two alternative foraging alleles: F₁, whose carriers have a probability 1.0 of adopting a producer strategy, and F₂, whose carriers have a probability of 0.5 of applying the producer strategy and 0.5 of applying the scrounger strategy (i.e. follow others). The F₁ and F₂ alleles were assigned randomly with equal probability to the n individuals in the first generation.

2.4. Learning strategy

An agent's learning strategy is defined by two genes: The I gene determines whether the agent applies individual learning (I₁ allele) or does not (I₀ allele), and the C gene determines whether the agent applies social learning (C₁ allele) or does not (C₀ allele). The social learning gene C is irrelevant for pure producers (F₁ carriers) as social learning takes place while scrounging from others (table 2). However, part-time scroungers (F₂ carriers) may exclusively adopt individual learning (I₁C₀ genotype), exclusively adopt the social learning strategy (I₀C₁ genotype) or use a strategy combining both individual and social learning (I₁C₁). In the first generation, all agents are assigned the non-learning alleles I₀ and C₀ and alleles I₁ and C₁ are introduced into the population by random mutation.

2.5. Learning rules

Learning may take place both when an agent acts as a producer and when it acts as a scrounger (see above). The value of the food item it has obtained (zero in the case it has obtained no food) updates the agent's memory, and this information is used in the agent's subsequent producing steps to decide in which patch to search for food. Memory is updated using a linear operator rule [59–61], also known as the weighted return rule [16], which yields for each patch a weighted average of the most recently acquired payoff and previous payoffs, according to the equations:

where M_i,t is the value of patch E_i in the agent's memory at step t, and Y_t is the updating vector: Y_i,t equals the payoff obtained at step t if patch E_i was visited at step t (i.e. only the memory of the visited patch is updated, while memories for the other patches do not change). Here, α (0 ≤ α ≤ 1) is a memory factor describing the weight given to the agent's past experience. Note that when learning individually (while producing), Y_i,t is the payoff the producer initially obtains. When learning socially (while scrounging), Y_i,t might be viewed as the payoff the scrounger observes to be obtained by the producer, or the payoff the scrounger actually receives (i.e. after deducting the finder's share, see game description below). Although the usual definition of social learning is the former [27], we model it here as the latter, as we believe that in a realistic producer–scrounger game, it is much easier for scroungers to obtain information on what they actually received than on what the producer found. However, we also carried out simulations in which scroungers updated their memory using their observation of what the producer found; these show qualitatively similar results, and are presented in the electronic supplementary material, appendix B. For the first step, M_i,1 are set to be the mean of expected values of all four patches (M_i,1 = 0.53 for all i).

Following Arbilly et al. [44], who found that learning complexity may interact with the performances of social foraging strategies, two learning rules are defined by the alleles at the learning rule locus. The first is a complex learning rule (allele L₁) that views the environment in full detail, as composed of the four food patches E₁, E₂, E₃, E₄. The second is a simple learning rule (allele L₂) that views the environment as composed of only two patches, E₁₂ and E₃₄ (table 3). Note that with the complex learning rule, individuals can potentially learn to prefer the patch with the highest expected value (table 3; patch E₁, expected value = 1.0), while with the simple learning rule they can at best learn to prefer the E₁₂ combination (with an expected value of 0.75). Thus, if applied successfully, complex learning should be better than simple learning. However, as complex learning divides its sampling steps between four patches in memory representation (rather than two), it is more likely to involve sampling errors when the total number of learning steps is small (see extensive analysis of this aspect in [44]). Assuming that complex learning is more costly, a fractional deduction of 0.01 from the cumulative payoff was made for all agents carrying the L₁ allele (see [44] for the analysis of different levels of this cost). A third allele L₀ results in no learning, and for carriers of L₀, patch information is not stored in memory and the patch in which to forage when producing is chosen at random (with an expected payoff of M_i,t = 0.53 that remains constant throughout the game). In the first generation, all agents are assigned allele L₀, and alleles L₁ and L₂ are introduced into the population by random mutations. Note that for carriers of the non-learning allele L₀, the learning genes I and C that were described above (learning individually and/or socially) are not relevant.

To account for the possibility that learning while scrounging from others may be inaccurate, we include θ as the probability of attributing the scrounged payoff in the scrounger's memory to a different patch from the one in which it was actually obtained. The payoff can be erroneously attributed with equal probability to any of the other patches.

2.6. Decision rule

When producing, the agents decide in which patch to forage based on the information acquired and updated according to the learning process described above. We used the exponential (logit) response rule (following [62–65]) according to which at step t, patch E_i is chosen with a probability based on its relative weight in memory (M_i,t), using the expression:

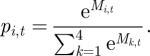This expression holds for complex learners (L₁ carriers) that distinguish between all four patches; simple learners (L₂ carriers) use the same expression but k goes from 1 to 2 (rather than from 1 to 4). The patches' variability results in highly dynamic memory values that do not necessarily approximate the patches' nutritional value; the use of an exponential ratio prevents choice rigidness in the case of values that are close to zero, and allows more frequent sampling of seemingly less attractive patches than a simple ratio.

2.7. The producer–scrounger game

As described above, the agents' lifespan is composed of J steps. Each step begins with a choice of foraging strategy (producing or scrounging) according to the agent's foraging allele (see above). Agents with allele F₁ (they always search), or agents with allele F₂ (they use the producer strategy with a probability of 0.5), choose a patch to forage in (based on the above learning and decision rules) and receive a payoff (or not) according to patch parameters described in table 3. Agents with allele F₂ that act as scroungers are then assigned to producers to simulate a scrounging process. We first assume that at each step, scroungers are able to distinguish successful producers from producers that failed to find food, and join only successful producers that can be identified by their feeding behaviour (see [66] for supporting evidence). We also include a probability β of erroneous joining (i.e. joining producers that did not find food) and examine its effect on the results. A producer in our game can be joined by only one scrounger, and the payoff is divided between the two agents (such that a finder's share, namely half the payoff, always goes to the producer). Since assignment of scroungers to producers is completely random, it is possible for a scrounger to be left with no payoff if the producer to which it was assigned has already been joined by another scrounger, while some producers may not be joined by any scroungers. This game structure is somewhat different from a game in which any number of scroungers can join a producer (see [59,67]), but it leads to the same frequency-dependent dynamics typical of a producer–scrounger game.

3. Results

3.1. Coevolution of individual and social learning in the producer–scrounger game

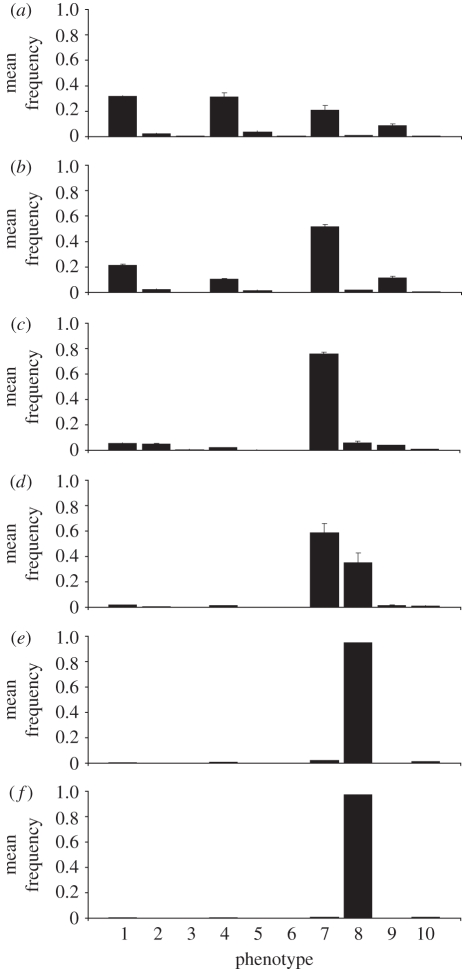
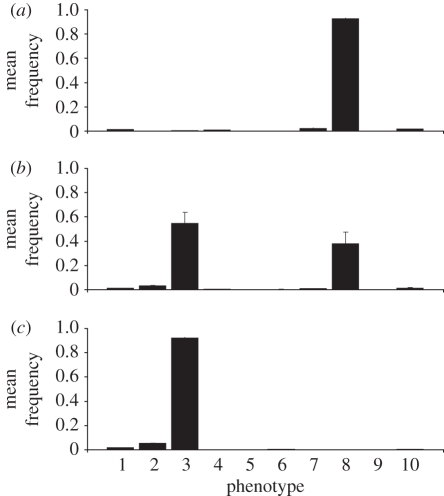
We initially investigated the coevolution of individual and social learning in the producer–scrounger game without any of the errors that may disturb the social learning process (θ = 0 and β = 0, i.e. assuming that social learners identify patch types correctly, and join only producers that found food). An analysis of phenotype frequencies for various values of J, the number of steps, is shown in figure 1 (results of the same simulations where social learners' memory is updated with the observed producer's finding appear in electronic supplementary material, appendix B, figure A). All populations begin on average as half pure producers (F₁) and half part-time scroungers (F₂), which are all non-learners (L₀I₀C₀), but as long as learning has an advantage over non-learning (J > 5, figure 1b–f), the part-time scroungers that are also exclusively social learners (F₂I₀C₁ genotype) evolve to dominate the population almost completely. Whether the exclusively social learners evolve to apply the simple or the complex learning rule depends on the number of learning steps available to them: for example, for J ≥ 70, complex learning is always the sole learning rule allele (figure 1e); for J = 30 steps, the simple learning rule L₂ is the fitter rule (figure 1c) and for J = 50, the two rules may evolve alternately, with some advantage to the simple learning rule (figure 1d).

Figure 1.

Mean phenotype frequency and standard error in generations 1501–3000, across 10 repeats of the simulation for each value of the number of steps J ((a) J = 5; (b) J = 10; (c) J = 30; (d) J = 50; (e) J = 70; (f) J = 100). Population size n = 300, number of generations G = 3000, memory factor α = 0.5, probability of erroneous joining β = 0, probability of social learning error θ = 0. Phenotypes 1–10 are as described in table 2. Phenotypes 7 and 8 are the part-time scroungers that apply exclusively social learning using simple and complex learning rules, respectively. Missing error bars imply that the standard error is too small to be visible. Complete fixation of dominating strategies was prevented by recurrent mutations.

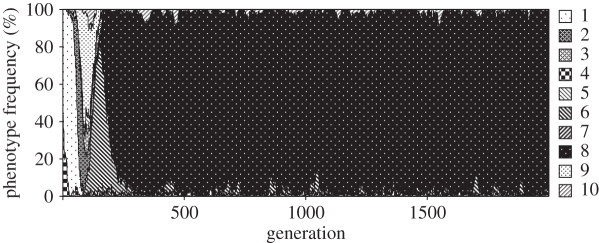
An example of typical evolutionary dynamics within generation lifespan J = 70 is shown in figure 2, and illustrates how within a few hundred generations, part-time scroungers dominate the population almost completely, employing social learning as their only learning strategy and using a complex learning rule (the F₂L₁I₀C₁ genotype). Although individual learning evolved in some cases for a short period within the first 500 generations in various allelic combinations, it became extinct as soon as the exclusive social learning genotype I₀C₁ evolved.

Figure 2.

Example of evolutionary dynamics of individual and social learning in one population. Population size n = 300, J = 70 steps, number of generations G = 2000, memory factor α = 0.5, probability of erroneous joining β = 0, probability of social learning error θ = 0. Phenotype numbers are as specified in table 2. Phenotype 8, F₂L₁I₀C₁, which dominates the population from approximately generation 250, is the part-time scrounger that applies exclusive social learning and a complex learning rule.

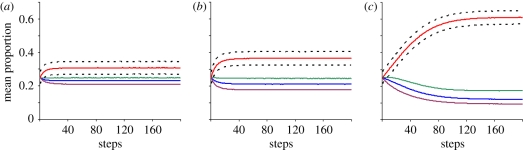
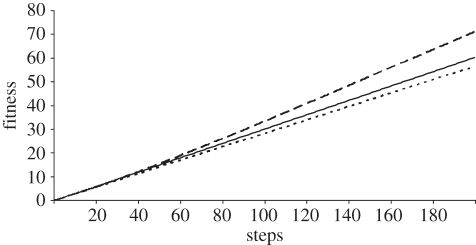
To understand why exclusive use of social learning was the most successful strategy, we explored the patch choice distribution developed by each learning strategy during the game. Using a non-evolutionary simulation, we analysed the distribution of patch choice by each strategy during repeated one-generation games of different lengths (different number of steps J), in populations of part-time scroungers. We compared exclusively social learners, exclusively individual learners and players that learn both individually and socially with all players using the complex learning rule. The results of this analysis are depicted in figure 3. Since patch E₁ has the highest expected payoff (table 3), a successful learning process based on the complex learning rule should lead to its preference over the other three patches. As expected, a qualitative preference is produced by all three strategies, but the magnitude of this preference varies. For games longer than J = 37 steps, exclusively social learners developed a stronger preference for the correct patch (E₁) than players using the other two strategies (compare figure 3c with figure 3a,b). As a result, exclusively social learning also yielded consistently higher mean fitness (cumulative payoff) than the other two strategies (figure 4).

Figure 3.

Patch choice mean distribution for different learning strategies as a function of the number of steps J in one generation of the game. Mean choice proportions for each J are calculated for 10 000 repeats of the simulation. Population size n = 300, number of generations G = 1 (non-evolutionary simulation), memory factor α = 0.5, probability of erroneous joining β = 0, probability of social learning error θ = 0. The black dotted lines indicate the standard deviation of E₁ patch preference. (a) Exclusively individual learning. (b) Combined individual and social learning. (c) Exclusively social learning. Red lines, E₁; green lines, E₂; blue lines, E₃; purple lines, E₄.

Figure 4.

Mean fitness (cumulative payoff) of the three learning strategies as functions of the number of steps J, in pure strategy populations. Fitness of each strategy at each point is the mean for 10 000 populations. Population size n = 300, number of generations G = 1 (non-evolutionary simulation), memory factor α = 0.5, erroneous joining β = 0, social learning error θ = 0. Dotted lines, exclusively individual learning; continuous lines, combined individual and social learning; dashed lines, exclusively social learning.

It is important to note that patch choice for each learning strategy (and its fitness consequences) was analysed in populations applying that strategy alone (pure populations). Thus, the better patch choice among exclusively social learners must have been a result of socially acquired information alone without any individually produced experience (see §4).

3.2. Learning from unsuccessful others

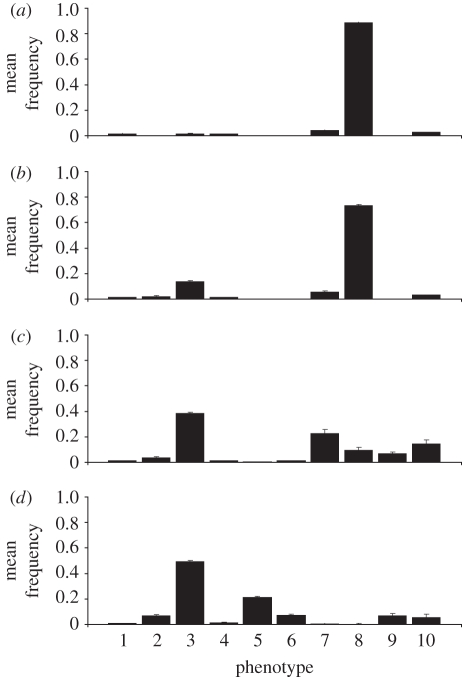
So far, we have assumed that scroungers join only producers that have found food (β = 0) and therefore learn socially to associate patch type with the nutritional value of the food item (minus finder's share—see model description) but never learn socially to associate this patch type with a complete failure (i.e. with a zero payoff). This situation changes when scroungers erroneously join producers who did not find food (β > 0), and as a consequence, experience some of the payoff variability from the high-risk high-reward patches. The effect of β on the success of exclusively social learning indicates that part-time scroungers can afford erroneous joining of up to 10 per cent and still maintain exclusively social learning (figure 5; see also electronic supplementary material, appendix B, figure B). However, as β increases (e.g. β = 0.15, 0.2), the population is gradually taken over by pure producers that use the complex learning rule and do not engage in any social learning (figure 5, phenotype 3). The evolutionary dynamics of each of the 10 runs with β = 0.15 (figure 5b) are not shown here, but were dominated by the exclusively social learner phenotype once it evolves; however, this could take a long time (more than 2000 generations in two of the cases, and in two cases out of the 10 it did not happen at all).

Figure 5.

Mean phenotype frequency for different probabilities ((a) β = 0.1; (b) β = 0.15; (c) β = 0.2) of erroneous joining. Means are calculated for generations 1501–3000 across 10 repeats of each simulation. Population size n = 300, generation lifespan J = 70 steps, number of generations G = 3000, memory factor α = 0.5, probability of social learning error θ = 0. Phenotypes 1–10 are as described in table 2 (successful phenotypes here: phenotype 8, part-time scrounger that applies exclusive social learning and a complex learning rule; phenotype 3, pure producer that uses a complex learning rule).

3.3. Errors in learning from others

As mentioned earlier, with probability θ, a social learner may erroneously attribute the scrounged payoff acquired in a particular patch to a different patch type from the one in which it was actually found. Simulation results for various values of θ are presented in figure 6 (see also electronic supplementary material, appendix B, figure C). Values of θ ≤ 0.2 do not reduce the success of exclusively social learners (phenotype 8, figure 6a). As θ increases to 0.5 (figure 6b,c), the frequency of exclusively social learners decreases and their place is taken by the pure producer-complex learner phenotype 3, as well as by part-time scroungers applying the combined individual and social learning strategy (phenotypes 9 and 10). Interestingly, when exclusive social learning decreases in frequency, it also evolves an association with the simple learning rule rather than with the complex learning rule (figure 6c, phenotype 7). The specific timing of this switch in terms of the value of θ depends on the relation between the number of steps J and complex learning cost γ (which was set here to 0.01): exclusive social learning will evolve an association with the simple learning rule at lower values of θ if we increase the complex learning cost γ, and at higher values of θ if we increase the number of steps J. However, the results remain qualitatively similar (not shown, see related analysis in [44]). At θ = 0.7 (figure 6d), the error in socially acquired information makes social learning disadvantageous, and part-time scroungers evolve into exclusively individual learners (phenotype 5).

Figure 6.

Mean phenotype frequency for different probabilities ((a) θ = 0.2; (b) θ = 0.3; (c) θ = 0.5; (d) θ = 0.7) of social learning error. Means are calculated for generations 1501–3000 across 10 repeats of each simulation. Population size n = 300, generation lifespan J = 70 steps, number of generations G = 3000, memory factor α = 0.5, probability of erroneous joining β = 0. Phenotypes 1–10 are as described in table 2 (successful phenotypes here: phenotype 8, part-time scrounger that applies exclusively social learning and a complex learning rule; phenotype 3, pure producer that uses a complex learning rule).

4. Discussion

4.1. Social learning as an exclusive means to acquire information

Our simulations show that in a variable environment where high payoffs are associated with greater risk, social learning may have an advantage over individual learning, to the extent of becoming the population's only means of acquiring information. This case is indeed extreme; however, we believe that it provides an important insight into the evolution of individual and social learning. Individual learners update their memory with their personal experience, which includes successes and failures in their searching (producing) activity. Failures (with zero payoffs) are most likely to occur in the patches that are, on average, the most highly rewarding (E₁ and E₂; table 3). Remembering these failures, individual learners may develop an aversion towards those patches and avoid them in their subsequent producer steps. Moreover, several learning models (e.g. [13,16]) have shown that this risk aversion emerges again after each failure, despite occasional successful episodes. In our simulation, this effect is responsible for maintaining the low level of average E₁ preference among individual learners (figure 3a,b). Exclusively social learners, on the other hand, update their memory only while scrounging from others, and do not remember (by definition) their own failures as producers. Thus, as long as the chance of erroneously joining an unsuccessful producer (β) is zero, exclusively social learners remember only successful experiences. This circumvents the development of risk aversion to variable patches, and allows development of a strong preference for the E₁ patch, which offers food items with the highest nutritional value (i.e. the highest payoff when food is found). Since E₁ is also the patch with the highest expected reward (despite its high risk), part-time scroungers that learn to prefer it during their searching steps enjoy the best payoffs and hence have the highest fitness. Note that relying even partly on individual learning was sufficient to reduce the proportion of correct choices (compare figure 3b and 3c) and consequently to reduce fitness (figure 4). These dynamics also account for the success of learning over non-learning in games as short as J = 10 steps when exclusively social learning is possible (figure 1). Other simulations (not shown) have shown that exclusively individual learning requires games to be about twice as long in order to evolve, as it requires a longer sampling period to overcome the error resulting from risk aversion (see also [68], and extensive analysis in [44]).

The risk aversion we see in our simulation is somewhat related to a phenomenon known as the ‘hot stove effect’ [15], or ‘stickiness’ [12], where aversive experiences prevent future exploration of a potentially good option. It is also related to learners' tendency to underweight rare events and to choose the option that has been better most of the time [14,69]. However, while these phenomena describe maladaptive outcomes of individual learning, our study suggests that the same learning rules may become highly adaptive when applied in the context of social learning.

Finally, we have shown both in evolutionary and non-evolutionary simulations that in the absence of erroneous joining (β = 0) and social learning error (θ = 0), a population composed purely of exclusively social learners is the most fit. This may seem surprising since, unlike previous models where exclusively social learning was facilitated by information transfer from one generation to the next (e.g. [70]), in our model all the information had to have been generated anew at every generation without individual learning. If there are no individual learners in the population, who produces the information? We assume that all agents are born naive, with no knowledge about the environment, and in their first step as producers they choose a patch randomly. Nevertheless, if successful, this random choice produces new information for potential scroungers who will register this success (as they are all social learners) and will take it into account when choosing a patch as producers; then they too will be joined by scroungers if they succeed in obtaining a payoff. Thus, the only source of information available to the population derives from the random successes that become public information.

While we demonstrated the advantage for exclusively social learning in an environment where the highest expected payoff is associated with both the lowest probability of finding food and the highest nutritional value, we can show that for this advantage to persist, the patches learned by social learners do not necessarily have to be those with the highest possible expected payoff. It is sufficient that they are better on average than the safe patches. For example, replacing the second best patch (E₂) with a patch that offers nutritional value of 19 with a probability of 0.05 (expected value = 0.95), resulted in a situation where exclusively social learners still prevailed but learned to prefer this second best patch (unpublished simulations). This is to be expected because learning only from successful foraging events led social learners to prefer the patch with the highest nutritional value without being able to tell its expected payoff. Nevertheless, as long as this patch is better on average than the patch preferred by individual learners, social learners will prevail. On the other hand, in a situation where the patch offering the highest nutritional value has a worse average payoff, exclusive social learning will result in maladaptive choices and therefore will not evolve (unpublished simulations).

4.2. Errors diminishing the success of social learning

We also examined the effect of increasing the erroneous joining probability β. The part-time scrounger exclusively social learner F₂L₁I₀C₁, withstood erroneous joining probabilities of up to 0.15 (although with delayed takeover). Interestingly, the failure of exclusively social learners with β ≥ 0.2 is mainly a result of inefficient scrounging rather than a result of inefficient learning. Part-time scroungers were already subject to the risk of not finding a successful producer to join. Adding a substantial probability of joining unsuccessful producers reduced their chances of success even further. Indeed, as a result, they were replaced by pure producers that were not affected by β, and could actually benefit indirectly from the fact that more scroungers would fail to join them when they did find food. The assumption that scroungers will mostly attempt to join successful producers is critical for our result—both in maintaining part-time scroungers in the population and in finding that exclusively social learning is the fittest learning strategy (since its rapid acquisition of information relies on joining successful producers). This assumption is common in simulations of the producer–scrounger game (e.g. [59,67]), and is also supported by recent observations in house sparrows, where 68 per cent of scrounging events in flocks of adult sparrows resulted in the recovery of food, while the probability of finding food by chance was only 16 per cent [66]. In light of these experimental and theoretical results, it is likely that indiscriminate joining would be rather costly and should occur only to a limited extent.

To account for the possibility that social learning while scrounging is cognitively more difficult and may be subject to errors, we considered the effect of learning errors during scrounging steps (with probability θ). Some experimental evidence suggests that scrounging from others may inhibit the learning of foraging cues [71–73], but in some species scrounging does not seem to present such a problem [74,75]. In either case, our analysis suggests that learning errors during scrounging are quite affordable for part-time scroungers; they will adhere to exclusive social learning even at a learning inaccuracy as high as 40 per cent. However, we found that this rate of learning errors during scrounging selects for using a simple rather than a complex learning rule. This is consistent with our previous analysis of the evolution of simple and complex individual learning rules, where simple learning prevailed when the effective number of learning steps was relatively small [44]. The effect of learning errors while scrounging may be similar because it reduces the number of effective learning steps.

Considering how cognitive abilities may evolve, it is quite likely that they begin as low-performance abilities, that is, with high error frequency, and improve through selection over the course of generations. In that sense, it is interesting that low performance of exclusively social learning (with θ as high as 0.5) is nevertheless beneficial enough for social learning to evolve, hinting perhaps that even if this sort of ability initially appears in a population in a primitive form, it will have no trouble spreading and improving (i.e. decreasing θ) quite rapidly.

4.3. Rogers' paradox, risky payoffs and the evolution of social learning

The notion that social learning accelerates knowledge acquisition compared with individual learning is hardly new. Learning by observing successful others can save various costs of individual exploration, including the cost of time. However, our model demonstrates not only that social learning can expedite knowledge acquisition but also that by ignoring personal experience and relying solely on social information, a more adaptive behaviour can develop. These results overcome the paradox described by Rogers [23] and that has been debated extensively in the literature (e.g. [2,3,24,29,70,76]). Our results demonstrate that in a variable environment, where the most rewarding behaviour comes with a risk, Rogers' paradox may not exist. On the contrary, a learning strategy involving individual learning is not adaptive, and exclusive use of social learning produces better knowledge and increases the population's mean fitness. Of course, this scenario is rather extreme; a situation where the individual completely disregards its personal experience is not very plausible. Yet, our results highlight the potential importance of the interaction between variable payoffs and social learning for understanding the evolution of both learning rules and social learning.

Finally, there is evidence that animals (and humans) frequently rely on socially acquired information more than on their own individual experience, to the extent of adopting maladaptive behaviours [7,32–38]. The advantage of exclusively social learning in a variable environment demonstrated by our results suggests one possible explanation for this phenomenon.