Skip to main content
PMC home page
Human Molecular Genetics logoLink to Human Molecular Genetics
. 2011 Jul 14;20(20):4069–4075. doi: 10.1093/hmg/ddr309

Adult height variants affect birth length and growth rate in children

Lavinia Paternoster 1,*,†, Laura D Howe 1,†, Kate Tilling 3, Michael N Weedon 4, Rachel M Freathy 1,4, Timothy M Frayling 4, John P Kemp 1, George Davey Smith 1, Nicholas J Timpson 1, Susan M Ring 2, David M Evans 1,†, Debbie A Lawlor 1,†
PMCID: PMC3177650  PMID: 21757498

Abstract

Previous studies identified 180 single nucleotide polymorphisms (SNPs) associated with adult height, explaining ∼10% of the variance. The age at which these begin to affect growth is unclear. We modelled the effect of these SNPs on birth length and childhood growth. A total of 7768 participants in the Avon Longitudinal Study of Parents and Children had data available. Individual growth trajectories from 0 to 10 years were estimated using mixed-effects linear spline models and differences in trajectories by individual SNPs and allelic score were determined. The allelic score was associated with birth length (0.026 cm increase per ‘tall’ allele, SE = 0.003, P = 1 × 10−15, equivalent to 0.017 SD). There was little evidence of association between the allelic score and early infancy growth (0–3 months), but there was evidence of association between the allelic score and later growth. This association became stronger with each consecutive growth period, per ‘tall’ allele per month effects were 0.015 SD (3 months–1 year, SE = 0.004), 0.023 SD (1–3 years, SE = 0.003) and 0.028 SD (3–10 years, SE = 0.003). By age 10, the mean height difference between individuals with ≤170 versus ≥191 ‘tall’ alleles (the top and bottom 10%) was 4.7 cm (0.8 SD), explaining ∼5% of the variance. There was evidence of associations with specific growth periods for some SNPs (rs3791675, EFEMP1 and rs6569648, L3MBTL3) and supportive evidence for previously reported age-dependent effects of HHIP and SOCS2 SNPs. SNPs associated with adult height influence birth length and have an increasing effect on growth from late infancy through to late childhood. By age 10, they explain half the height variance (∼5%) of that explained in adults (∼10%).

INTRODUCTION

Twin and family studies have shown adult human height to be highly heritable (80–90%) (1–3). Twin studies also suggest that the genetic contribution to height varies throughout childhood with birth length and early growth appearing to have stronger environmental influences than later growth and height which appears to be more strongly influenced by genetic variation (4).

Many genome-wide association studies (GWASs) have successfully identified loci associated with adult height (5–12). A recent meta-analysis which included 133 653 European subjects in the genome-wide scan and 50 074 subjects in follow-up identified 180 single nucleotide polymorphisms (SNPs) associated with adult height, explaining ∼10% of the variation (12). However, none of these studies has related these SNPs to height growth in childhood.

The balance of genetic and environmental influences on growth is likely to differ across childhood. Birth size may be influenced more by maternal size and the intrauterine effects of maternal behaviours such as smoking than genetics, although birth length has been shown (through correlations with paternal size) to be more genetically influenced than other aspects of fetal growth, such as weight (13). Infancy is then considered to be a canalization period, whereby growth shifts an infant's size from their birth size to their genetically determined size and growth pattern. Thus, in the first 2 years of life, many infants exhibit height centile-crossing, i.e. a child whose height at one time point sits on a low centile of the population distribution of height may well have a height on a higher centile of the population distribution at a later time point, and vice versa. Later in childhood, height tends to follow a stable pattern in terms of the centile of the population distribution, which is assumed to be the genetically determined growth pattern (14). Thus, it is possible that genetic variation has relatively less influence on birth length and growth in infancy, and more influence on growth later in childhood. This, however, has not yet been empirically tested using data from longitudinal cohort studies and SNPs identified from GWAS.

A recent study of 3538 individuals (15) took 48 height-associated SNPs and evaluated their associations with several features of growth: adult height, peak height velocity in infancy (PHV1) and peak height velocity in puberty (PHV2). They formally tested all SNPs for an interaction with age (infancy versus puberty) and found evidence of such an interaction with four SNPs—rs10946808 (HIST1H1D) and rs6854783 (HHIP) which were most strongly associated with PHV1 and rs11107116 (SOCS2) and rs12459350 (DOT1L) which were most strongly associated with PHV2. Of these, they described previous biological evidence that supported their findings for the age interactions with HHIP and SOCS2. That study therefore demonstrates that the SNPs identified in the adult study are associated with growth patterns in infancy and that they may affect different time periods. However, that study focussed on growth patterns at two sensitive time periods, infancy and puberty, and did not explore associations of the SNPs with rates of growth between infancy and puberty or the association between these SNPs and birth size. Another recent study analysed the association between SNPs from 46 previously reported adult height loci in children and found nominally significant associations for 15 loci (16), but that study analysed together all children between the ages of 0 and 18 years (preventing identification of age-specific effects) and does not have repeat measures on the same children. It therefore remains unclear at what age in childhood the adult height SNPs begin to affect growth.

In this study, we examine the association of the 180 height SNPs identified in the original GWAS of European adults (12) (and the combined allelic score of these) on birth length and individual growth trajectories from birth to age 10 in the Avon Longitudinal Study of Parents and Children (ALSPAC) cohort. We also test the hypothesis that the associations differ according to birth length.

RESULTS

Data on growth and genotypes were available for 3994 boys and 3774 girls (55% of the total ALSPAC cohort—differences between those included and excluded are shown in Supplementary Material, Table S1). There were a median of eight measurements per child (inter-quartile range 6–11 measurements), with most children having measurements across each of the growth periods (Supplementary Material, Table S2).

There was an association of the allelic score with birth length [each ‘tall’ allele increases birth length by 0.026 cm (95% CI 0.020–0.033) P = 1 × 10−15] (Table 1 and Supplementary Material, Table S4). In a regression of birth length on allelic score (adjusting for sex), there was little statistical evidence for a sex difference (interaction P = 0.158). The allelic score explained ∼2% of the variation in birth length (R2= 0.017).

Table 1.

Association results for the allelic score and birth length and growth

Birth length 0–3 months 3 months–1 year 1–3 years 3–10 years
Mean birth length, cm (SD) or growth rate, cm per month (SD) 50.49 (1.525) 3.73 (0.232) 1.64 (0.139) 0.81 (0.074) 0.53 (0.036)
Beta coefficients (SE), in cm 0.0264 (0.0033) 0.0020 (0.0015) 0.0021 (0.0006) 0.0017 (0.0002) 0.0010 (0.0001)
Beta coefficients (SE), in SD 0.0173 (0.0022) 0.0086 (0.0065) 0.0151 (0.0043) 0.0230 (0.0027) 0.0278 (0.0028)
P-values 1 × 10−15 0.175 3 × 10−4 6 × 10−17 2 × 10−37
Open in a new tab

Coefficients (standard error) are reported as the cm and SD mean difference in birth length or growth per month per ‘tall’ allele. The between growth periods heterogeneity P-value was P = 0.0004.

There was no association between the allelic score and early growth (0–3 months), but there was increasing evidence for an association with growth in the next three periods. Each ‘tall’ allele increases growth by 0.0021 cm (95% CI 0.0009–0.0032) or 0.015 SD per month between 3 months and 1 year (P = 0.0003), by 0.0017 cm (95% CI 0.0013–0.0021) or 0.023 SD per month between 1 and 3 years (P = 6 × 10−17), and by 0.0010 cm (95% CI 0.0009–0.0012) or 0.028 SD per month between 3 and 10 years (P = 2 × 10−37) (Table 1 and Supplementary Material, Table S4). Aggregated over the 3 months to 10 years period, this translates into a 0.14 cm growth difference per ‘tall’ allele. In a regression of height at age 10 on the allelic score (adjusting for sex), each tall allele was associated with an increase in height of 0.16 cm (95% CI 0.14–0.17, P = 6 × 10−90), with little statistical evidence for a sex difference (interaction P = 0.78). The allelic score explained ∼5% of the variation in height at age 10 (R2= 0.051).

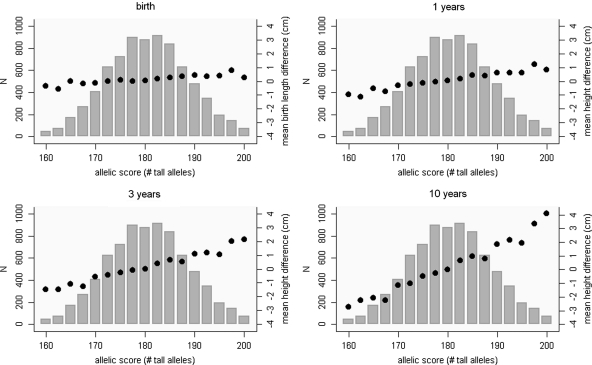
Plots of the mean height differences at birth, 1, 3 and 10 years, by allelic score show approximate linear relationships (Fig. 1). The mean height difference between individuals with 170 or fewer ‘tall’ alleles (representative of the bottom 10% of individuals’ allelic score in our population) and individuals with 191 or more ‘tall’ alleles (representative of the top 10%) at age 10 is 4.7 cm (or 0.8 SD) (full growth trajectories for simulated 10th and 90th centile individuals are shown in Supplementary Material, Fig. S1).

Figure 1.

Figure 1.

Open in a new tab

Mean birth length and height at 1, 3 and 10 years, by allelic score. Birth lengths and height at exact ages were predicted from a multilevel model that did not include the allelic score. Mean height differences were calculated as the mean predicted height minus the mean height (separately for boys and girls) for that age (by allelic score). Bars represent the distribution of the allelic score.

Only two individual SNPs showed a significant association (P < 5.6 × 10−5) for either birth length or a growth period (Supplementary Material, Table S4). The C allele of rs3791675, in the EFEMP1 gene, was associated with an increased growth rate of 0.0048 cm (95% CI 0.0026–0.0071, P = 2 × 10−5) per tall allele per month in the fourth growth period (3–10 years). This SNP also showed some evidence for an association (P = 0.001) in the third growth period (1–3 years), but little evidence for association with birth length or the first two growth periods (though heterogeneity by growth period P = 0.104). The C allele of rs6569648, in the L3MBTL3 gene, was associated with an increased birth length of 0.19 cm per tall allele (95% CI 0.10–0.28, P = 3 × 10−5), but there was little evidence for association with any of the four growth periods (heterogeneity by growth period P = 0.017). However, there were no significant differences between growth periods for any of the SNPs (heterogeneity P > 0.0003 for all SNPs, Supplementary Material, Table S4) and we may have low power for these individual SNP analyses.

A previous study (15) has reported an interaction with age for four of the loci studied here (HIST1H1D, HHIP, SOCS2 and DOT1L). We found some evidence of an association (0.009 cm per C allele per month, P = 0.003) in the expected direction in the third growth period (1–3 years) for rs7689420 in the HHIP gene, but no association (P = 0.198) with growth in later childhood (3–10 years), although there was little statistical evidence of heterogeneity by growth period (P = 0.214) (Supplementary Material, Table S2). We found some evidence of an association (0.004 cm per T allele per month, P = 4 × 10−4) in the fourth growth period (3–10 years) for rs11107116 near the SOCS2 gene, but little evidence for association with birth length (P = 0.352) or growth during infancy (first 3 growth periods all P-values > 0.25). There was suggestive statistical evidence for heterogeneity by growth period for this SNP (P = 0.020) (Supplementary Material, Table S2). However, we found little evidence of association between rs806794 (in the histone cluster) or rs12982744 (in the DOT1L gene) and birth length, or any of the growth periods (and heterogeneity by growth periods were P = 0.857 and P = 0.691, respectively).

Although we have low power to detect associations with individual SNPs in each growth period, when we analyse the association between these SNPs and height at age 10, there is evidence of association for many individual SNPs (rs3791675 in EFEMP1, rs11830103 in SBNO1, rs6449353 near LCORL, rs11205277 near SF3B4, rs6470764 near GSDMC, rs7689420 in HHIP, rs11259936 in ADAMTSL3, rs2856321 in ETV6, rs4800452 near CABLES1, rs1708299 in JAZF1; Supplementary Material, Table S5), suggesting that the very small associations observed in each growth period aggregate to produce real differences of up to 0.6 cm per allele by this age.

We hypothesized that the associations between the allelic score and growth may differ according to thirds of birth length, such that the effect of the allelic score on postnatal growth would be strongest in those of lower birth length (i.e. an interaction between allelic score and birth length on growth). Despite some suggestion that the effect of allelic score differs by tertile of birth length, there is little statistical evidence that the coefficients differ (Supplementary Material, Table S6).

DISCUSSION

Patterns of height and growth are controlled by a number of mechanisms, which vary from infancy into early adulthood. Although birth length does appear to have some genetic component (13), maternal size (determined by her genes and environment), behaviours during pregnancy and health and foetal nutrition are suggested as key determinants of birth length, whereas genetics, nutrition and illnesses affect growth more after birth (14). It is thought that growth in the first 2 years of life is more susceptible to environmental influences than growth later in childhood which is primarily genetically determined (14). GWASs have now identified SNPs robustly associated with adult height (5–12), some of which have also been shown to be associated with peak height velocity either infancy or puberty or both (15). To our knowledge, this is the first study to look at the association of these SNPs with growth trajectories from birth to 10 years, and to examine the age at which these SNPs begin to influence height and height growth.

We have shown that an allelic score derived from a set of known adult height-associated SNPs (12) is associated with birth length and with childhood growth from ∼1 year onwards. This contrasts with earlier work from the same cohort showing that socioeconomic influences on child height operate primarily through differences in birth length, but have little effect on postnatal growth (17). These findings together suggest that birth length and very early growth appear to be influenced by environmental factors and somewhat by genetic factors, whereas growth later in childhood appears to be more genetically determined, consistent with the literature (14).

These findings suggest that the association observed in previous work between these SNPs and adult height is not just due to processes affecting later growth, such as timing, duration and velocity of the pubertal growth spurt, but that this genetic component of height is at least operating in part from before birth and increasingly so from 3 months of age. In fact whereas the original paper reported that these SNPs explain ∼10% of adult height variation, we show that by age 10 this same set of SNPs already explains ∼5% of height variation. We have purposefully modelled growth up to age 10 only to capture pre-pubertal growth; questions on age at menarche and Tanner scoring of breast, penis and pubic hair suggest that at this age the vast majority of the children (at least 95%) were pre-pubertal. Thus, our results suggest that these genetic variants are affecting pre-pubertal growth.

Four loci studied here have previously been shown to have an interaction with age (HIST1H1D, HHIP, SOCS2 and DOT1L) (15). We show supportive evidence for two of these interactions (although none of these reached statistical significance). In our data, rs7689420 (HHIP) is associated with infancy growth (1–3 years), but not later childhood growth and rs11107116 (SOCS2) is only associated with later childhood growth (3–10 years) and not earlier growth. The previous studied had shown a HHIP SNP to be associated with PHV1, but not with PHV2 and the same SOCS2 SNP to be associated with PHV2 and not PHV1. We cannot claim an exact replication of the previous study findings for these SNPs as the previous study compared associations of these variants with infant growth and the pubertal growth spurt, and as noted above, we have purposefully examined associations with growth from birth to pre-puberty. However, of the four loci for which they found evidence of an age interaction, it was these two for which there is previous biologically relevant evidence. The HHIP gene is a component of the hedgehog signal transduction pathway involved in embryogenesis and early development (18) and the SOCS2 has been shown to have a role in growth hormone signalling, which may be important in ‘childhood growth’ but not ‘infancy growth’ (19). We also identified two other genes with evidence of association only during specific growth periods. rs3791675, in EFEMP1, showed association only during the 3–10-year growth period and rs6569648 in L3MBTL3 showed association only with birth length. However, the differences between associations at different growth periods for these SNPs were not significant and these findings will need to be replicated further in future early growth studies.

The differing ages at which individual SNPs show their effects might suggest that it is inappropriate to use the allelic score to study genetic growth across time periods. However, despite the differing effects, our analysis of the allelic score demonstrates the ages at which the majority of these SNPs have their effect on growth and shows that between the ages of 1 and 10 years, this score is associated with growth rates. Although some observations about the effects of individual SNPs across ages can be made, this study lacks power to rigorously investigate this. However, the score provides a useful and powerful summary of the association of ‘adult height’ genetic variation with growth in childhood. Another reason for lack of power for the birth length analyses specifically is that measurement error for length in infancy is greater than for later height measurements. Post hoc power calculation indicates that the minimal effect sizes that we would be able to detect, with 90% power and an alpha of 5%, for the association with allelic score are 0.0068 cm per allele for birth length and 0.0010, 0.0006, 0.0003 and 0.0002 cm per allele per month for the four growth periods, respectively. The minimal per-allele effect sizes we would be able to detect with the same power and alpha for individual SNPs vary between 12 and 20 times larger than those for the allelic score (depending on a theoretical minor allele frequency range of 0.5–0.1, Supplementary Material, Table S7).

Although we found little statistical evidence of an interaction between birth length and allelic score for the association with infancy and childhood growth rates, this hypothesis is worthy of further investigation in future large studies of the genetic effects of early childhood growth.

This study demonstrates the involvement of 180 known adult height SNPs in childhood growth. These SNPs appear to have some influence on birth length and are consistently associated with childhood growth from age 1 year, such that by age 10 they appear to explain half the variance (∼5%) of that explained in adults (∼10%).

MATERIALS AND METHODS

ALSPAC participants

ALSPAC is a longitudinal population-based birth cohort that recruited pregnant women residing in Avon, UK, with an expected delivery date between 1st April 1991 and 31st December 1992. A total of 14541 women were enrolled, with 14062 children born, of which 13988 were alive at 1 year (13617 singletons). The cohort, including its representativeness, is described in detail on the website http://www.alspac.bris.ac.uk and elsewhere (20). Both mothers and children have been extensively followed from the eighth gestational week onwards using a combination of self-reported questionnaires, medical records and physical examinations. A random sub-sample of the children from the last 6 months of recruitment (‘Children in Focus’ group—∼10% of the total cohort) were invited to clinics between ages 4 months and 5 years; all children were invited to clinics from age 7 years onwards. Biological samples including DNA have been collected. Ethical approval was obtained from the ALSPAC Law and Ethics committee and relevant local ethics committees, and written informed consent provided by all parents.

Genotyping

A total of 9912 subjects were genotyped using the Illumina HumanHap550 quad genome-wide SNP genotyping platform by 23 and Me subcontracting the Wellcome Trust Sanger Institute, Cambridge, UK and the Laboratory Corporation of America, Burlington, NC, USA. Individuals were excluded from further analysis on the basis of having incorrect gender assignments; minimal or excessive heterozygosity (<0.320 and >0.345 for the Sanger data and <0.310 and >0.330 for the LabCorp data); disproportionate levels of individual missingness (>3%); evidence of cryptic relatedness (>10% IBD) and being of non-European ancestry (as detected by a multidimensional scaling analysis seeded with HapMap 2 individuals, EIGENSTRAT analysis revealed no additional obvious population stratification and genome-wide analyses with other phenotypes indicate a low lambda). The resulting data set consisted of 8365 individuals (84% of those genotyped). SNPs with a minor allele frequency of <1% and call rate of <95% were removed. Furthermore, only SNPs which passed an exact test of Hardy–Weinberg equilibrium (P > 5 × 10−7) were considered for analysis. Genotypes were subsequently imputed with MACH 1.0.16 Markov Chain Haplotyping software, using CEPH individuals from phase 2 of the HapMap project as a reference set (release 22).

Growth measurements

Length/height data for children were available from several sources. Birth length (crown-heel) was measured for almost the whole cohort by ALSPAC staff who visited newborns soon after birth (median 1 day, range 1–14 days), using a Harpenden Neonatometer (Holtain Ltd.). From birth to 5 years, measurements are also available for the majority of the cohort from health visitor records, which form part of standard child care in the UK. In this cohort, we had up to four measurements taken on average at 2, 10, 21 and 48 months of age, which we have demonstrated in previous work to have good accuracy (21). For a random 10% of the cohort, we also have measurements from Children in Focus clinics, held between the ages of 4 months and 5 years of age. At these clinics, crown-heel length was measured up to 25 months using a Harpenden Neonatometer (Holtain Ltd.) and from 25 months standing height was measured using a Leicester Height Measure (Seca). From age 7 to 10 years, all children were invited to annual clinics, at which standing height (without shoes) was measured to the last complete mm using the Harpenden Stadiometer (Holtain Ltd.). Across all ages, parent-reported child heights are also available from questionnaires.

Modelling of growth trajectories

Growth trajectories were modelled using all available height measurement sources. Implausible height measurements (>4 SD from the mean for gender- and age-specific category) were re-coded as missing (101 measurements from 96 individuals, ∼0.1% of all available measurements). All other available measures were used in analyses. To account for the likely reduced accuracy of parent-reported measurements (22), a binary indicator of measurement source (research clinic or health records versus parent-reports from questionnaires) was included in all models.

Individual growth trajectories were estimated using a mixed-effects linear spline model [two levels: measurement occasion (age) and individual], fitted using the statistical package MLwiN version 2.10 (www.cmm.bristol.ac.uk/MLwiN/index.shtml) (17), using the Stata command runmlwin (23) (http://www.bristol.ac.uk/cmm/software/runmlwin/). Such models allow for the change in magnitude and variance of height over time and use all available data from all eligible children under a missing at random assumption. They also allow for individual variation in growth trajectories, since random effects allow each individual to have different intercepts and slopes. Models for growth between birth and 10 years were constructed for boys and girls combined, with an interaction between gender and each growth period such that boys and girls are allowed to have different birth lengths and growth rates in each period. We identified three spline points (four growth periods) that defined periods of approximately linear growth: between birth and 10 years: 0–3 months, 3–12 months, 12–36 months and 36–120 months. Full details of the statistical methodology are presented in the Supplementary Material. Over 60 000 height measurements were included in the models, with the median number of individual measurements being 8 (Supplementary Material, Table S2). The growth trajectory models demonstrated good fit, with the differences between actual and predicted measurements tending to be small (Supplementary Material, Table S3). Growth rates were fastest in early infancy and declined throughout childhood (e.g. growth rate in the first 3 months of life was 3.73 cm/month and between 3 and 10 years of age was 0.53 cm/month, Table 1).

Statistical analysis

For the individual SNPs, we used the dosages (in terms of estimated number of ‘tall’ alleles) from the imputed data. An allelic score was constructed by summing across all 180 SNPs the dosages of ‘tall’ alleles, as reported in ref. (12).

Genetic differences in the growth trajectories were estimated by including a statistical interaction between age and genotype (each SNP and the allelic score) in the multilevel model, and estimating whether there were differences between genotypes in terms of the constant term (representing birth length) and each of the slopes for the growth periods. Thus, the associated P-values test the null hypothesis of no difference in birth length or growth in each period per allele, and the coefficients represent the mean difference in birth length or growth rate per allele. The effect of genotype on growth was assumed to be constant across genders, but boys and girls were allowed different birth lengths and growth rates in the multilevel model. The only other covariate included in models was a binary indicator of source of height measurement (questionnaire versus measured by ALSPAC clinic staff or health visitors). The genotypes and allelic score were modelled as additive factors. α = 0.01 (accounting for five time periods) was taken to be significant for the allelic score and α = 6 × 10−5 (accounting for five time periods and 180 SNPs) was taken to be significant for the individual SNPs. For each SNP (and allelic score), the heterogeneity of the coefficients between birth length and four growth periods (in SDs) was assessed using Cochran's Q-statistic. For the individual SNPs, α = 0.0003 was taken to be significant (accounting for the 180 SNPs).

Average growth trajectories were plotted for simulated individuals with the 10th and 90th percentile of the proportion of tall alleles. We predicted individual heights at exactly 1, 3 and 10 years of age for all children, to enable us to plot heights by genotype for these exact ages, from a multi-level model that did not include the genetic terms. These measures of height at age 10 years were also used to assess the aggregate associations with individual SNPs (and allelic score), by regressing against the genotype with sex as a covariate (carried out in Stata 11.1).

To investigate the hypothesis that the associations of the allelic score with growth rates would be stronger in those of smaller birth length, we divided the sample into thirds of birth length. We ran separate multilevel models for each third of birth length and examined the effect of the allelic score within each group. We tested for statistical evidence of differing effects of allelic score between thirds of birth length by carrying out a heterogeneity test on the resulting coefficients.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at HMG online.

FUNDING

L.P. and D.M.E. are supported by a Medical Research Council New Investigator Award (MRC G0800582 to D.M.E.). L.D.H. is supported by a grant from the UK Economic and Social Research Council (RES-060-23-0011). R.M.F. is funded by a Sir Henry Wellcome Postdoctoral Fellowship (Wellcome Trust grant 085541/Z/08/Z). The UK Medical Research Council (grant 74882), the Wellcome Trust (grant 076467) and the University of Bristol provide core support for ALSPAC. L.P., L.D.H., N.J.T., G.D.S., D.M.E. and D.A.L. work in a Centre that receives funds from the UK Medical Research Council (G0600705) and the University of Bristol. Funding to pay the Open Access publication charges for this article was provided by the Wellcome Trust.

Supplementary Material

Supplementary Data
supp_20_20_4069__index.html (946B, html)

ACKNOWLEDGEMENTS

We are extremely grateful to all the families who took part in this study, the midwives for their help in recruiting them and the whole ALSPAC team, which includes interviewers, computer and laboratory technicians, clerical workers, research scientists, volunteers, managers, receptionists and nurses. This publication is the work of the authors, and they will serve as guarantors for the contents of this paper.

Conflict of Interest statement. None declared.

REFERENCES

  • 1.Silventoinen K., Sammalisto S., Perola M., Boomsma D.I., Cornes B.K., Davis C., Dunkel L., De Lange M., Harris J.R., Hjelmborg J.V.B., et al. Heritability of adult body height: a comparative study of twin cohorts in eight countries. Twin Res. Hum. Genet. 2003;6:399–408. doi: 10.1375/136905203770326402. doi:10.1375/twin.6.5.399. [DOI] [PubMed] [Google Scholar]
  • 2.Perola M., Sammalisto S., Hiekkalinna T., Martin N.G., Visscher P., Montgomery G.W., Benyamin B., Harris J.R., Boomsma D., Willemsen G., et al. Combined genome scans for body stature in 6,602 European twins: evidence for common caucasian loci. PLoS Genet. 2007;3:1019–1028. doi: 10.1371/journal.pgen.0030097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Macgregor S., Cornes B.K., Martin N.G., Visscher P.M. Bias, precision and heritability of self-reported and clinically measured height in Australian twins. Hum. Genet. 2006;120:571–580. doi: 10.1007/s00439-006-0240-z. doi:10.1007/s00439-006-0240-z. [DOI] [PubMed] [Google Scholar]
  • 4.Silventoinen K., Pietilainen K.H., Tynelius P., Sørensen T.I.A., Kaprio J., Rasmussen F. Genetic regulation of growth from birth to 18 years of age: the Swedish young male twins study. Am. J. Hum. Biol. 2008;20:292–298. doi: 10.1002/ajhb.20717. doi:10.1002/ajhb.20717. [DOI] [PubMed] [Google Scholar]
  • 5.Weedon M.N., Lango H., Lindgren C.M., Wallace C., Evans D.M., Mangino M., Freathy R.M., Perry J.R.B., Stevens S., Hall A.S., et al. Genome-wide association analysis identifies 20 loci that influence adult height. Nat. Genet. 2008;40:575–583. doi: 10.1038/ng.121. doi:10.1038/ng.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Weedon M.N., Lettre G., Freathy R.M., Lindgren C.M., Voight B.F., Perry J.R.B., Elliott K.S., Hackett R., Guiducci C., Shields B., et al. A common variant of HMGA2 is associated with adult and childhood height in the general population. Nat. Genet. 2007;39:1245–1250. doi: 10.1038/ng2121. doi:10.1038/ng2121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Soranzo N., Rivadeneira F., Chinappen-Horsley U., Malkina I., Richards J.B., Hammond N., Stolk L., Nica A., Inouye M., Hofman A., et al. Meta-analysis of genome-wide scans for human adult stature identifies novel Loci and associations with measures of skeletal frame size. PLoS Genet. 2009;5:e1000445. doi: 10.1371/journal.pgen.1000445. doi:10.1371/journal.pgen.1000445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Sanna S., Jackson A.U., Nagaraja R., Willer C.J., Chen W.-M., Bonnycastle L.L., Shen H., Timpson N., Lettre G., Usala G., et al. Common variants in the GDF5-UQCC region are associated with variation in human height. Nat. Genet. 2008;40:198–203. doi: 10.1038/ng.74. doi:10.1038/ng.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Lettre G., Jackson A.U., Gieger C., Schumacher F.R., Berndt S.I., Sanna S., Eyheramendy S., Voight B.F., Butler J.L., Guiducci C., et al. Identification of ten loci associated with height highlights new biological pathways in human growth. Nat. Genet. 2008;40:584–591. doi: 10.1038/ng.125. doi:10.1038/ng.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Johansson A., Marroni F., Hayward C., Franklin C.S., Kirichenko A.V., Jonasson I., Hicks A., Vitart V., Isaacs A., Axenovich T., et al. Common variants in the JAZF1 gene associated with height identified by linkage and genome-wide association analysis. Hum. Mol. Genet. 2009;18:373–380. doi: 10.1093/hmg/ddn350. doi:10.1093/hmg/ddn350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Gudbjartsson D.F., Walters G.B., Thorleifsson G., Stefansson H., Halldorsson B.V., Zusmanovich P., Sulem P., Thorlacius S., Gylfason A., Steinberg S., et al. Many sequence variants affecting diversity of adult human height. Nat. Genet. 2008;40:609–615. doi: 10.1038/ng.122. doi:10.1038/ng.122. [DOI] [PubMed] [Google Scholar]
  • 12.Lango Allen H., Estrada K., Lettre G., Berndt S.I., Weedon M.N., Rivadeneira F., Willer C.J., Jackson A.U., Vedantam S., Raychaudhuri S., et al. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 2010;467:832–838. doi: 10.1038/nature09410. doi:10.1038/nature09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Knight B., Shields B.M., Turner M., Powell R.J., Yajnik C.S., Hattersley A.T. Evidence of genetic regulation of fetal longitudinal growth. Early Hum. Dev. 2005;81:823–831. doi: 10.1016/j.earlhumdev.2005.06.003. doi:10.1016/j.earlhumdev.2005.06.003. [DOI] [PubMed] [Google Scholar]
  • 14.Cameron N. Human Growth and Development. UK: Academic Press; 2002. pp. 1–20. [Google Scholar]
  • 15.Sovio U., Bennett A.J., Millwood I.Y., Molitor J., O'Reilly P.F., Timpson N.J., Kaakinen M., Laitinen J., Haukka J., Pillas D., et al. Genetic determinants of height growth assessed longitudinally from infancy to adulthood in the northern Finland birth cohort 1966. PLoS Genet. 2009;5:e1000409. doi: 10.1371/journal.pgen.1000409. doi:10.1371/journal.pgen.1000409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Zhao J., Li M., Bradfield J.P., Zhang H., Mentch F.D., Wang K., Sleiman P.M., Kim C.E., Glessner J.T., Hou C., Keating B.J., et al. The role of height-associated loci identified in genome wide association studies in the determination of pediatric stature. BMC Med. Genet. 2010;11:96. doi: 10.1186/1471-2350-11-96. doi:10.1186/1471-2350-11-96. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Howe L.D., Tilling K., Galobardes B., Smith G.D., Gunnell D., Lawlor D.A. Socioeconomic differences in childhood growth trajectories: at what age do height inequalities emerge? J. Epidemiol. Community Health. 2010 doi: 10.1136/jech.2010.113068. ePub ahead of print]. doi:10.1136/jech.2010.113068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Chuang P-T., McMahon A.P. Vertebrate Hedgehog signalling modulated by induction of a Hedgehog-binding protein. Nature. 1999;397:617–621. doi: 10.1038/17611. doi:10.1038/17611. [DOI] [PubMed] [Google Scholar]
  • 19.Tse W.Y., Hindmarsh P.C., Brook C.G.D. The infancy-childhood-puberty model of growth: clinical aspects. Acta Paediatr. Scand. 1989;356:38–43. doi: 10.1111/j.1651-2227.1989.tb11238.x. doi:10.1111/j.1651-2227.1989.tb11238.x. [DOI] [PubMed] [Google Scholar]
  • 20.Golding J., Pembrey M., Jones R. ALSPAC-the avon longitudinal study of parents and children. I. study methodology. Paediatr. Perinat. Epidemiol. 2001;15:74–87. doi: 10.1046/j.1365-3016.2001.00325.x. doi:10.1046/j.1365-3016.2001.00325.x. [DOI] [PubMed] [Google Scholar]
  • 21.Howe L.D., Tilling K., Lawlor D.A. Accuracy of height and weight data from child health records. Arch. Dis. Child. 2009;94:950–954. doi: 10.1136/adc.2009.162552. doi:10.1136/adc.2009.162552. [DOI] [PubMed] [Google Scholar]
  • 22.Dubois L., Manon G. Accuracy of maternal reports of pre-schoolers’ weights and heights as estimates of BMI values. Int. J. Epidemiol. 2007;36:132–138. doi: 10.1093/ije/dyl281. doi:10.1093/ije/dyl281. [DOI] [PubMed] [Google Scholar]
  • 23.Leckie G., Charlton C. Centre for Multilevel Modelling, University of Bristol; 2011. Runmlwin: Stata module for fitting multilevel models in the MLwiN software package. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_20_20_4069__index.html (946B, html)
supp_ddr309_ddr309supp.doc (634KB, doc)

Articles from Human Molecular Genetics are provided here courtesy of Oxford University Press

RESOURCES