Interpretation of transit compartments pharmacodynamic models as lifespan based indirect response models

Abstract

Transit compartments (TC) models are used to describe pharmacodynamic responses that involve drug action on cells undergoing differentiation and maturation. Such pharmacodynamic systems can also be described by lifespan based indirect response (LIDR) models. The purpose of this report is to investigate conditions under which the transit compartments models can be considered a special case of LIDR models. An integral representation of a solution to TC model has been used to determine the lifespan distribution for cell population described by this model. The distribution served as a basis for definition of new LIDRE (lifespan based indirect response with an effect on the lifespan distribution) models. Time courses of responses described by both types of models were simulated for a monoexponential pharmacokinetic function. The limit response was calculated as the number of transit compartments approached infinity. The difference between the limit response and TC responses were evaluated by computer simulations using MATLAB 7.7. TC models are a special case of LIDR models with the lifespan distribution described by the gamma function. If drug affects only the production of cells, then the cell lifespan distribution is time invariant. In this case an increase in the number of compartments results in a basic LIDR model with a point lifespan distribution. When the drug inhibits or stimulates cell aging, the cell lifespan distribution becomes time dependent revealing a new mechanism for drug effect on the gamma probability density function. The TC model with a large number of transit compartments converges to an LIDRE model. The limit LIDR models are approximated by the TC models when the number of compartments is at least 5. A moderate improvement in the approximation is observed if this number exceeds 20. The lifespan distribution for a cell population described by a TC model is described by the gamma probability density function. A drug affects this distribution only if it stimulates or inhibits the rate of cell maturation. If the number of transit compartments increases, then the TC model converges to a new type of LIDR model.

Introduction

A cellular response to chemotherapeutic agents is one of pharmacodynamic markers used for assessment of drug efficacy and toxicity. Kinetics of cell populations of hematopoietic lineages has been intensively modeled to provide quantitative measures of drug effects and cell turnover. One of most commonly used models consists of a series of compartments representing various stages of cell development that are meant to reflect the time course of the cell population count in tissues such as bone marrow and blood [1]. These compartments are connected via first-order cell transfer rates and represent the maturation process from progenitor cells in bone marrow to peripheral cells in blood. The reciprocal of each rate constant is the mean transit time of a cell, which is interpreted as an average age of cells in the compartment. Therefore, a sequence of the age compartments may also account for a cell development process starting from their production (birth) and ending with elimination (death or transfer to another tissue) [2]. Such a sequence of compartments is necessary to account for a delay between exposure of progenitor cells to a therapeutic agent and its effect which is typically determined from the blood cells count (maturation) or the time dependent change in the age of a particular cell type (senescence). A sequence of age compartments is the bone structure of more complex pharmacodynamic models of drugs affecting hematopietic cell populations such as neutrophils [3, 4], red blood cells [5], and platelets [2]. In these models drug stimulated or inhibited the production of cell precursors or the transfer rate between the age compartments.

Another approach has been proposed to describe the cell development kinetics that is based on the assumption of a priori knowledge of lifespan distribution in a cell population. In this concept a cell remains in the population until its assigned lifespan expires. Consequently, the cell removal rate is determined by the cell production rate and the lifespan distribution [6]. Pharmacodynamic models have been developed assuming a simplistic point cell lifespan distribution [6-8]. More realistic continuous distributions were also investigated [9]. The drug effect on the cell aging process was modeled by introducing time variant lifespan distributions where the time changes were controlled by drug effect [10-12]. Besides the senescence, the lifespan based indirect response model has been also used to model the maturation of neutrophils following chemotherapy treatment [13].

Therefore, both lifespan based indirect response models and transit (age) compartments models have been used to model the maturation and the senescence of different type of cells. Interestingly, the catenary structure of the transit (age) compartments models for cell populations is very similar to signal transduction models used in modeling a delay between drug effect at a site of action and measurable response [14]. The properties of the gamma function are central for understanding the behavior of transduction models [15]. This function has also been applied to account for the lifespan distribution of cell populations exposed to random destruction [16, 17]. A link between these two apparently separate applications of the gamma function is not coincidental. Under baseline conditions, the lifespan distribution of a cell population described by the age compartment model is identical with the gamma function. An objective for this report was to investigate if the transit (age) compartments model accounting for a drug effect can be described by the time variant lifespan distribution indirect response model. Mathematical derivations are provided to claim that this is indeed the case. Additionally, computer simulations were used to explore the convergence of the transit compartment models to the lifespan based indirect response models when the number of compartments increases to infinity and the mean lifespan is set constant.

Theoretical and results

Transit compartments model

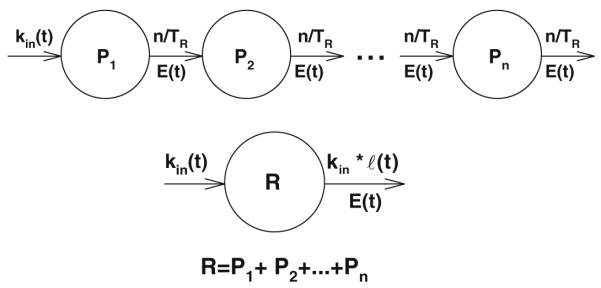
The transit compartments model consists of a series of compartments P₁, …P_n connected with each other by first-order processes in a catenary manner as shown in Fig. 1. A compartment P_i represents a subset of cells of the mean age i · T_R/n, since the mean transit time through each compartment is T_R/n, if T_R denotes the mean cell lifespan. We assume that cells are produced at a time dependent zero-order rate k_in(t), and the drug affects the transit rates between the compartments. The drug effect is described by a function E(t) that will be specified later. Then transit compartments model is described by the following system of differential equations:

$$\frac{{\text{dP}}_1}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-\frac{\text{n}}{{\text{T}}_{\text{R}}}E\left(\text{t}\right){\text{P}}_1,{\text{P}}_1\left(0\right)=\frac{{\text{R}}_0}{\text{n}}$$ (1)

$$\frac{{\text{dP}}_{\text{i}}}{\text{dt}}=\frac{\text{n}}{{\text{T}}_{\text{R}}}\text{E}\left(\text{t}\right)({\text{P}}_{\text{i}-1}-{\text{P}}_{\text{i}}),{\text{P}}_{\text{i}}\left(0\right)=\frac{{\text{R}}_0}{\text{n}},\text{i}=2,\dots \text{n}$$ (2)

where R₀ is the total number of cells in all compartments. It is additionally assumed that drug was administered at time t = 0, and prior to that the system was at steady state:

$${\text{k}}_{\text{in}}\left(\text{t}\right)={\text{k}}_{\text{in0}},\text{and}\text{E}\left(\text{t}\right)=1,\text{for}\text{t}\le 0$$ (3)

Consequently, the initial conditions can be determined from the baseline equation:

$${\text{R}}_0={\text{k}}_{\text{in0}}\cdot {\text{T}}_{\text{R}}$$ (4)

We limit our analysis to a pharmacodynamic response R that consists of the total cell count:

$$\text{R}={\text{P}}_1+\cdots +{\text{P}}_{\text{n}}$$ (5)

Although the transit compartments model can be applied to describe responses which are defined by one age group (usually the oldest R = P_n), or a subset of all cells. We show in Appendix 1 that the solution for each transit compartment is of the following form:

$${\text{P}}_{\text{i}}\left(\text{t}\right)=\frac{{\text{R}}_0}{\text{n}}+\frac{1}{(\text{i}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{i}-1}\underset{0}{\overset{\text{t}}{\int }}\left({\text{k}}_{\text{in}}\left(\tau \right)-\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}\text{E}\left(\tau \right)\right)\times {\left(\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (6)

for i = 1, …, n.

Fig. 1.

Schematic representation of the transit compartments model (upper) and basic lifespan based indirect response model (lower). In both models cells are produced at a zero-order rate that can be affected by drug k_in(t). The transfer rates between the transit compartments are first-order constants n/T_R where n is the number of compartments and T_R is the total mean transit time through all compartments. The cell elimination for the lifespan indirect response model is determined by their time dependent lifespan distribution ℓ(t,τ). Drug affects both n/T_R and ℓ(t,τ) via a mechanism described by the effect function E(t). The transit compartments P₁, P₂, …, P_n are described by Eqs. 1-2. The sum of the transit compartments can be described by a lifespan driven indirect response R. The convolution symbol is defined by Eq. 11

Drug effect

Typically a drug affect is determined by the plasma drug concentration C(t). According to the indirect paradigm of drug action [18], one can consider stimulation or inhibition of the transit rates that results in a decrease or increase of the cell maturation or the mean age of each cell in each compartment, and its lifespan overall. Then the effect can be described by the E_max model

$$\text{E}\left(\text{t}\right)=1+\frac{{\text{S}}_{\text{max}}\text{C}\left(\text{t}\right)}{{\text{SC}}_{50}+\text{C}\left(\text{t}\right)}(\text{stimulation}\text{of}\text{n}∕{\text{T}}_{\text{R}})$$ (7)

and

$$\text{E}\left(\text{t}\right)=1-\frac{{\text{I}}_{\text{max}}\text{C}\left(\text{t}\right)}{{\text{IC}}_{50}+\text{C}\left(\text{t}\right)}(\text{inhibition}\text{of}\text{n}∕{\text{T}}_{\text{R}})$$ (8)

where S_max (I_max) denotes the maximal drug effect, and SC₅₀ (IC₅₀) is the drug plasma concentration eliciting 50% of the maximum effect.

For drugs acting on the cell production, the E_max function multiplies the baseline production rate constant k_in0. Consequently, the cell lifespan is constant and does not depend on the drug effects and the cell production rate affected by drug is as follows:

$${\text{k}}_{\text{it}}\left(\text{t}\right)={\text{k}}_{\text{in0}}\left(1+\frac{{\text{S}}_{\text{max}}\text{C}\left(\text{t}\right)}{{\text{SC}}_{50}+\text{C}\left(\text{t}\right)}\right)\left(\text{stimulation}\text{of}{\text{k}}_{\text{in0}}\right)$$ (9)

and

$${\text{k}}_{\text{it}}\left(\text{t}\right)={\text{k}}_{\text{in0}}\left(1-\frac{{\text{I}}_{\text{max}}\text{C}\left(\text{t}\right)}{{\text{IC}}_{50}+\text{C}\left(\text{t}\right)}\right)\left(\text{inhibition}\text{of}{\text{k}}_{\text{in0}}\right)$$ (10)

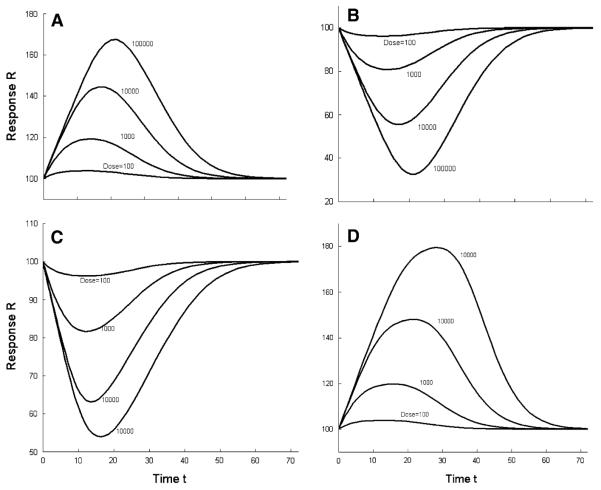
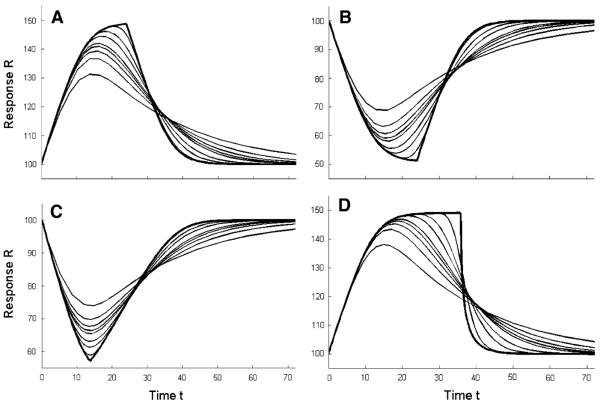
The responses for four types of transit compartments models corresponding to concentration time profiles generated for the monoexponential kinetic function for doses increasing in 10-fold increments are presented in Fig. 2.

Fig. 2.

Simulated response versus time profiles for transit compartments models corresponding to the monoexponential pharmacokinetic function at indicated doses. a Stimulation of k_in0 (Eqs. 9, 1, 2). b Inhibition of k_in0 (Eqs. 10, 1, 2). c Stimulation of n/T_R (Eqs. 7, 1, 2). d Inhibition of n/T_R (Eqs. 8, 1, 2). The parameter values used for simulations were n = 10, kin₀ = R₀/T_R, R₀ = 100, T_R = 24, I_max = S_max = 1, and IC₅₀ = SC₅₀ = 100

Lifespan distribution for a cell population described by the transit compartments model

If each cell is assigned at any moment of time t a lifespan, then one can describe the cell loss rate for the population due to expiration of lifespan of individual cells [12], which can be also understood as the finalization of the maturation process. If ℓ(t,τ) denotes the probability density function for the distribution of lifespans τ at time t, then the differential equation for describing the change of the cell number R due to a balance between the production rate k_in(t) and elimination rate due to the lifespan distribution is [12]

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau )\mathcal{l}(\text{t}-\tau ,\tau )\text{d}\tau$$ (11)

with the baseline initial condition

$$\text{R}\left(0\right)={\text{R}}_0={\text{k}}_{\text{in0}}\cdot {\text{T}}_{\text{R}}$$ (12)

where T_R is the mean lifespan for the baseline lifespan distribution ℓ₀(τ) = ℓ(∞,τ):

$${\text{T}}_{\text{R}}=\underset{0}{\overset{\infty }{\int }}\tau {\mathcal{l}}_0\left(\tau \right)\text{d}\tau$$ (13)

The objective of this section is to determine the lifespan distribution for the cell population described by the transit compartments model. If R is the sum of the cells in each of the aging compartments then adding the differential equations 1 and 2 side by side results in

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-\frac{\text{n}}{{\text{T}}_{\text{R}}}\text{E}\left(\text{t}\right){\text{P}}_n$$ (14)

with the initial condition

$$\text{R}\left(0\right)={\text{R}}_0$$ (15)

Using Eq. 6 we show in Appendix 2 that

$$\frac{\text{n}}{{\text{T}}_{\text{R}}}\text{E}\left(\text{t}\right){\text{P}}_{\text{n}}={\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}}\frac{\text{E}\left(\text{t}\right)}{(\text{n}-1)!}\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau ){\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (16)

Equations 11, 14 and 16 imply that the probability density function (p.d.f.) for the lifespan distribution for a cell population described by the transit compartments model is

$${\mathcal{l}}_{\text{n}}(\text{t},\tau )={\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}}\frac{\text{E}(\text{t}+\tau )}{(\text{n}-1)!}{\left(\underset{\text{t}}{\overset{\text{t}+\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}}{\overset{\text{t}+\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)$$ (17)

One can utilize the properties of the gamma function γ_n(τ) [15]

$${\gamma }_{\text{n}}\left(\tau \right)={\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}}\frac{{\tau }^{\text{n}-1}}{(\text{n}-1)!}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\tau \right)$$ (18)

and verify by a direct integration that for any moment of time t

$$\underset{0}{\overset{\infty }{\int }}{\mathcal{l}}_{\text{n}}(\text{t},\tau )\text{d}\tau =1$$ (19)

For derivations see Appendix 3. Equation 19 implies that ℓ_n(t, τ) is indeed a p.d.f. The plots of ℓ_n(t, τ) at several time points for drug stimulating and inhibiting n/T_R are shown in Fig. 3. Since for t → ∞, E(t) → 1, then ℓ_n(∞, τ) reduces to the p.d.f. for the gamma distribution, this implies that the mean lifespan is T_R. Consequently, the total cell number R described by the transit compartments model is a solution to the lifespan driven model Eqs. 11-12 if the lifespan distribution p.d.f. is given by Eq. 17. If the drug acts only on k_in (E(t) ≡ 1), then ℓ_n(t, τ) becomes time independent and reduces to the gamma function γ_n(τ). These types of lifespan distributions have been applied in the lifespan based indirect response models [9]. The case n = 1 can be interpreted as a cell population described by an indirect response model. Consequently, each of the basic indirect response models [18] can be considered as a lifespan driven indirect response model where

$${\mathcal{l}}_1(\text{t},\tau )=\frac{\text{E}(\text{t}+\tau )}{{\text{T}}_{\text{R}}}\text{exp}\left(-\frac{1}{{\text{T}}_{\text{R}}}\underset{\text{t}}{\overset{\text{t}+\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)$$ (20)

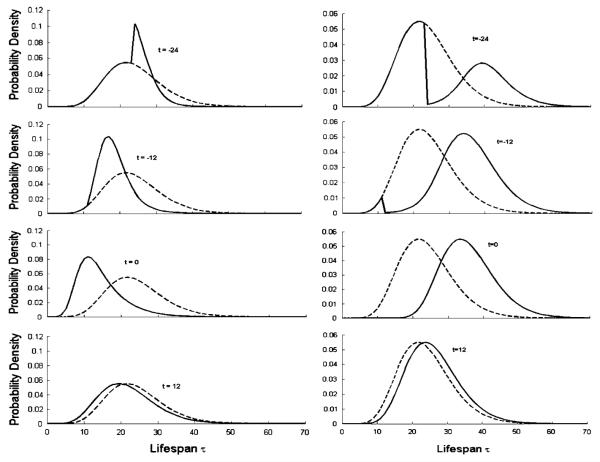
Fig. 3.

Effect of drug on the lifespan distribution at various times. Probability density functions ℓ_n(t,τ) corresponding to stimulation of n/T_R (Eqs. 7, 1, 2) (left) and inhibition of n/TR (Eqs. 8, 1, 2) (right). The parameter values used for simulations were Dose = 1000, k_el = 0.3 and V = 3, n = 10, kin₀ = R₀/T_R, R₀ = 100, T_R = 24, I_max = S_max = 1, and IC₅₀ = SC₅₀ = 100

Effect of drug on lifespan distribution

Equation 17 describes how the drug acting on the transit rates in the transit compartments model affects the distribution of lifespans at any moment of time t. This relationship suggests a generalization of a function describing a drug effect on any arbitrary lifespan distribution ℓ(t,τ). Prior to introducing a formal definition let us notice that for a time t the transformation

$${\widehat{E}}_{\text{t}}\left(\tau \right)=\underset{\text{t}}{\overset{\text{t}+\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}$$ (21)

satisfies the following conditions

$${\widehat{E}}_{\text{t}}\left(0\right)=0,{\widehat{E}}_{\text{t}}\left(\infty \right)=\infty ,\text{and}\frac{\text{d}{\widehat{E}}_{\text{t}}}{\text{d}\tau }>0$$ (22)

Equation 22 implies that ${\widehat{\mathrm{E}}}_{\mathrm{t}}$ is a smooth invertible transformation of the lifespan interval 0 < τ < ∞ onto itself. Let Φ_t(τ) be an arbitrary transformation of the lifespan interval satisfying conditions in Eq. 22, i.e.

$${\Phi }_{\text{t}}\left(0\right)=0,{\Phi }_{\text{t}}\left(\infty \right)=\infty ,\text{and}{\Phi }_{\text{t}}^{\prime }\left(\tau \right)>0$$ (23)

Then a transform of a p.d.f. for lifespan distribution that is time invariant ℓ₀(τ) can be defined as follows

$${{\mathcal{l}}_0}^{\stackrel{‒}{°}}{\Phi }_{\text{t}}\left(\tau \right)={\mathcal{l}}_0\left({\Phi }_{\text{t}}\left(\tau \right)\right){\Phi }_{\text{t}}^{\prime }\left(\tau \right)$$ (24)

One can use the change of variable s → Φ_t(τ) to show that ${{\ell }_0}^{\stackrel{‒}{°}}{\Phi }_t\left(\tau \right)$ is a p.d.f. for any time t. Its dependence on time is determined entirely by Φ_t(τ). In particular ℓ_n(t,τ) can be viewed as the effect of ${\widehat{\mathrm{E}}}_{\mathrm{t}}\left(\tau \right)$ on the time invariant gamma distribution γ_n(τ):

$${{\gamma }_{\text{n}}}^{\stackrel{‒}{°}}{\widehat{E}}_{\text{t}}\left(\tau \right)={\mathcal{l}}_{\text{n}}(\text{t},\tau )$$ (25)

Figure 3 shows the transformed gamma p.d.f. due the drug effect E(t). Using this notation the TC model Eq. 14 is identical with a lifespan based indirect response model with drug effect E(t) acting on the lifespan distribution γ_n(τ) according to Eq. 25:

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau ){\mathcal{l}}_{\text{n}}(\text{t}-\tau ,\tau )\text{d}\tau$$ (26)

Equation 26 serves as a rationale for a definition of a new lifespan based indirect response model for drugs affecting a time invariant lifespan distribution ℓ₀(τ):

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau )\mathcal{l}(\text{t}-\tau ,\tau )\text{d}\tau$$ (27)

where

$$\mathcal{l}(\text{t},\tau )={{\mathcal{l}}_0}^{\stackrel{‒}{°}}{\widehat{E}}_{\text{t}}\left(\tau \right)={\mathcal{l}}_0\left({\widehat{E}}_{\text{t}}\left(\tau \right)\right)\text{E}(\text{t}+\tau )$$ (28)

In this report we will limit ℓ₀(τ) to the simplest point lifespan distribution δ_τ0(τ) = δ(τ − τ₀). Then

$${{\delta }_{\tau 0}}^{\stackrel{‒}{°}}{\Phi }_{\text{t}}\left(\tau \right)={\delta }_{{\Phi }_{\text{t}}^{-1}\left(\tau 0\right)}\left(\tau \right)$$ (29)

where ${\Phi }_{\mathrm{t}}^{-1}\left(\tau \right)$ is the inverse of Φ_t(τ) (see Appendix 4 for derivations). For τ₀ = T_R Eq. 27 becomes (see Appendix 5 for derivations):

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-{\text{k}}_{\text{in}}\left({\text{T}}_{\text{E}}\left(\text{t}\right)\right)\frac{\text{E}\left(\text{t}\right)}{\text{E}\left({\text{T}}_{\text{E}}\left(\text{t}\right)\right)}$$ (30)

with the initial condition

$$\text{R}\left(0\right)={\text{k}}_{\text{in0}}{\text{T}}_{\text{R}}$$ (31)

where the variable T_E is a solution to the following differential equation:

$$\frac{{\text{dT}}_{\text{E}}}{\text{dt}}=\frac{\text{E}\left(\text{t}\right)}{\text{E}\left({\text{T}}_{\text{E}}\left(\text{t}\right)\right)}$$ (32)

with the initial condition

$${\text{T}}_{\text{E}}\left(0\right)=-{\text{T}}_{\text{R}}$$ (33)

In particular, when the drug affects only k_in0, E(t) ≡ 1, then the solution to Eqs. 32-33 is

$${\text{T}}_{\text{E}}\left(\text{t}\right)=\text{t}-{\text{T}}_{\text{R}}$$ (34)

In this case Eq. 30 simplifies to

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-{\text{k}}_{\text{in}}(\text{t}-{\text{T}}_{\text{R}})$$ (35)

which is identical with the basic lifespan based indirect response model introduced by Krzyzanski et al. [6]. The signature profiles for R(t) corresponding to the monoexponential pharmacokinetic function are shown in Fig. 4. Equations 30-33 constitute a definition of a new basic model of the lifespan based indirect response with an effect on the lifespan distribution (LIDRE).

Fig. 4.

Response time courses for basic lifespan indirect response models corresponding to the monoexponential pharmacokinetic function at indicated doses. a Stimulation of k_in0 (Eqs. 9 and 35). b Inhibition of k_in0 (Eqs. 10 and 35). c Stimulation of n/T_R (inhibition of T_R) (Eqs. 7 and 30). d Inhibition of n/T_R (stimulation of T_R) (Eqs. 8 and 30). The parameter values used for simulations were k_in0 = R₀/T_R, R₀ = 100, T_R = 24, I_max = S_max = 1, and IC₅₀ = SC₅₀ = 100

Convergence of the transit compartments model

If the number of transit compartments n increases and the mean lifespan T_R is constant, then the sequence of gamma p.d.f.s γ_n(τ) approaches the point life-span distribution δ(τ − T_R), where the convergence is defined by the following integrals:

$$\underset{0}{\overset{\infty }{\int }}\text{f}\left(\tau \right){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \to \underset{0}{\overset{\infty }{\int }}\text{f}\left(\tau \right)\delta (\tau -{\text{T}}_{\text{R}})\text{d}\tau =\text{f}\left({\text{T}}_{\text{R}}\right)\text{as}\text{n}\to \infty$$ (36)

for any arbitrary continuous and bound function f(τ). This convergence property of the gamma p.d.f. is called the approximate identity [19] and it is illustrated in Fig. 5. Equation 36 implies that the solution R_n(t) of Eq. 14 corresponding to n transit compartments approaches the solution R_∞(t) of the basic indirect response model described by Eq. 30 as n becomes very large:

$${\text{R}}_{\text{n}}\left(\text{t}\right)\to {\text{R}}_{\infty }\left(\text{t}\right)\text{as}\text{n}\to \infty$$ (37)

and the convergence is understood in the usual sense. The error between R_n(t) and R_∞(t) is equal to:

$${\text{R}}_{\text{n}}\left(\text{t}\right)-{\text{R}}_{\infty }\left(\text{t}\right)=\underset{0}{\overset{\text{t}}{\int }}\left(\underset{0}{\overset{\infty }{\int }}{\varphi }_{\text{s}}\left(\tau \right){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau -{\varphi }_{\text{s}}\left({\text{T}}_{\text{R}}\right)\right)\text{ds}$$ (38)

where

$${\varphi }_{\text{t}}\left(\tau \right)=\frac{{\text{k}}_{\text{in}}(\text{t}-{\Psi }_{\text{t}}^{-1}\left(\tau \right))\text{E}\left(\text{t}\right)}{\text{E}(\text{t}-{\Psi }_{\text{t}}^{-1}\left(\tau \right))}$$ (39)

and Ψ_t(τ) is defined in Appendix 5. For proofs see Appendix 6. Simulations of R_n(t) and R_∞(t) profiles are shown in Fig. 6. The percent errors of approximation of R_∞(t) by R_n(t) are presented in Table 1. Equation 38 simplifies when there is no drug effect on n/T_R. Then E(t) ≡ 1, and ${\Psi }_{\mathrm{t}}^{-1}\left(\tau \right)=\tau$, and consequently,

$${\varphi }_{\text{t}}\left(\tau \right)={\text{k}}_{\text{in}}(\text{t}-\tau )$$ (40)

Fig. 5.

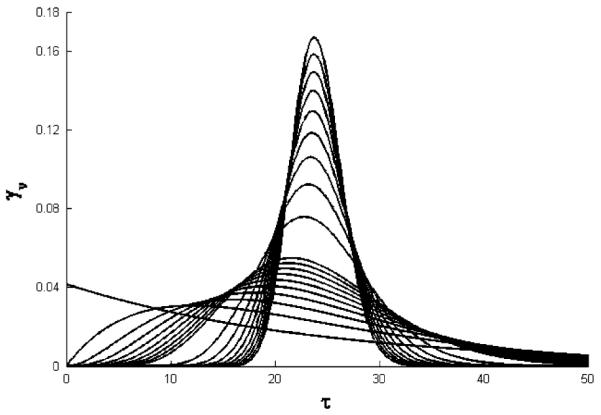
Simulated profiles of the p.d.f. γ_n(τ) for n = 1, 2, …, 10, 20, …, 100. The T_R = 24. Each curve has a unique peak at τ_n = (1 − 1/n)T_R. For n → ∞, γ_n(τ) approaches the delta function δ(τ − T_R). This property of the gamma p.d.f. is called the approximate identity

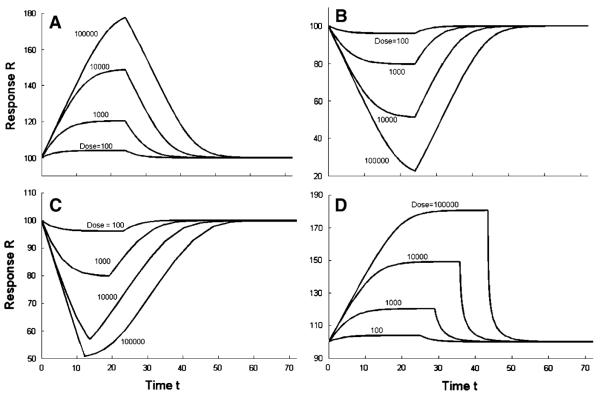
Fig. 6.

Response time courses for transit compartments models with an increasing number of compartments. a Stimulation of k_in0 (Eqs. 9, 1, 2). b Inhibition of k_in0 (Eqs. 10, 1, 2). c Stimulation of n/T_R (Eqs. 7, 1, 2). d Inhibition of n/T_R (Eqs. 8, 1, 2). The bold curves are solutions of the basic lifespan based indirect response model: a Stimulation of k_in0 (Eqs. 9 and 35). b Inhibition of k_in0 (Eqs. 10 and 35). c Stimulation of n/T_R (inhibition of T_R) (Eqs. 7 and 30). d Inhibition of n/T_R (stimulation of T_R) (Eqs. 8 and 30). The parameter values used for simulations are the same as for Fig. 2, except for Dose = 10,000, and n = 1, 2, 3, 4, 5, 10, 20, 100

Table 1.

Percent difference between the transit compartments model response R_n(t) and the limit lifespan based indirect model response R_∞(t) for four models

n	Stimulation of kin0	Inhibition of kin0	Stimulation of n/TR	Inhibition of n/TR
1	75.3	76.1	64.7	77.5
2	52.5	53.2	42.1	63.1
3	42.9	43.7	32.9	57.8
4	37.2	37.9	27.8	54.9
5	33.5	33.8	24.4	53.0
10	23.6	24.4	16.4	47.9
20	16.4	16.9	11.2	43.9
100	6.5	7.8	4.7	35.4

The difference was evaluated at as the maximum absolute difference between R_n(t) and R_∞(t) relative to the maximum absolute difference between R_∞(t) and ${\text{R}}_0:\underset{\text{t}\ge 0}{\text{max}}\mid {\text{R}}_{\text{n}}\left(\text{t}\right)-{\text{R}}_{\infty }\left(\text{t}\right)\mid ∕\underset{\text{t}\ge 0}{\text{max}}\mid {\text{R}}_{\infty }\left(\text{t}\right)-{\text{R}}_0\mid \times 100$.

The model parameters are as in Fig. 6

Methods

The simulations of drug effects were done assuming the monoexponential pharmacokinetic function:

$$\text{C}\left(\text{t}\right)=\frac{\text{Dose}}{\text{V}}{\text{e}}^{-{\text{k}}_{\text{el}}\text{t}}$$ (41)

where k_el = 0.3 and V = 3. Units were omitted for all variables not to imply a particular time, concentration, or response scale. Series of simulations was performed to demonstrate an effect of dose on response time profiles for TC and LIDRE models. The doses were selected to cover the whole range of responses from a close to baseline to a maximal response. They were Dose = 100, 1000, 10,000, and 100,000. The parameters for the E_max effect models were S_max = I_max = 1, SC₅₀ = IC₅₀ = 100. The baseline for the response was R₀ = 100, the lifespan T_R was set to 24, and the response production rate k_in0 was calculated from Eq. 4. Additional simulations were performed to evaluate the shape of the gamma p.d.f. as a function of the number of transit compartments n and assess the error of the approximation of the basic LIDRE model by TC models as n → ∞. MATLAB 7.7 (The MathWorks Inc., Natic, MA) was used for simulations. The PD responses generated for both transit compartments and lifespan based indirect response models were coded as MATLAB m-functions. The ODE solver ode15s capable of solving stiff differential equations was used to solve model equations. All plots were generated as MATLAB figures. The MATLAB m-functions for simulations of the LIDRE models are included as a supplementary material.

Discussion

The interpretation of the transit compartments as consecutive stages of aging pools is mechanistically sound and offers a very flexible modeling tool to describe drug effects on various cell populations. This model is especially robust when additional processes to cell maturation or senescence are considered such as cell loss due to random destruction [2], chemo-toxic effects, apoptosis, mobilization [4] or margination/demargination. Also the cell production rate might be different from a zero-order process. Alternatives account for a first-order mechanisms of cells proliferation [1] or a size-limited cell population growth [20]. These processes were not included into our analysis for sake of simplicity and are subjects for future studies.

Despite of numerous modeling advantages of the TC model that include simplicity, robustness, and easy numerical applications, there are few drawbacks that are often encountered during this model application. First, most common, is a selection of the number of transit compartments. A typical approach when the number of transit compartments cannot be determined as the number of cell development stages is to increase the number of compartments until a negligible improvement in the model performance is observed, or a limit for the number of differential equations in applied software has been reached. The lifespan based indirect response model offers a generalization of an integer parameter n to a real valued parameter p that can be estimated along with the mean lifespan parameter T_R. This can be simply achieved by replacing the gamma function γ_n(τ) described in Eq. 19 by a general equation for the gamma distribution [21]

$${\gamma }_{\text{p}}\left(\tau \right)={\left(\frac{\text{p}}{{\text{T}}_{\text{R}}}\right)}^{\text{p}}\frac{{\tau }^{\text{p}-1}}{\Gamma \left(\text{p}\right)}\text{exp}\left(-\frac{\text{p}}{{\text{T}}_{\text{R}}}\tau \right)$$ (42)

where Γ(p) is the Euler gamma function that extends evaluation of the factorial on the real numbers. This function can be easily coded using several lines of the code to achieve 7 digit accuracy [22].

A second drawback of the TC model is a problem with calculation of the mean lifespan for a cell population with the time variant transfer rates (e.g. affected by drug). The interpretation of T_R/n as a mean transit time of a cell residing in a transit compartment holds true only if the transfer rate is constant. For time variant transit rates the mean transit time is time dependent and its calculation requires a re-derivation of non-compartmental parameters [2, 5]. The derived equation for the lifespan distribution ℓ_n(t,τ) offers a calculation of the time dependent mean lifespan T_R(t) as defined by the elementary probability theory

$${\text{T}}_{\text{R}}\left(\text{t}\right)=\underset{0}{\overset{\infty }{\int }}\tau {\mathcal{l}}_{\text{n}}(\text{t},\tau )\text{d}\tau$$ (43)

Finally, the assumption of the transfer rate between the transit compartments as a first-order process that is proportional to the compartment size can be challenged. Although, the cell number in a particular aging stage is a factor, it is unrealistic to assume that the transfer rate between aging pools is solely controlled by the size of the cell population. For example, the age of reticulocytes is determined by their residual RNA content, and their maturation rate is a function of the RNA degradation half-life [23]. An application of p.d.f. other than ℓ_n(t,τ) in the lifespan based indirect response model can release that assumption.

The simulated profiles of p.d.f.s corresponding to stimulation or inhibition of the cell transfer rates between the transit compartments shown in Fig. 3 are in agreement with what is expected about the drug effect on the mean lifespan. Stimulation accelerates the aging process which results in a temporal shift of the p.d.f. to earlier lifespans followed by a return to the baseline lifespan distribution when the drug is cleared from the system. A similar pattern can be observed for drug inhibiting the aging process but with an opposite direction. There p.d.f.s shift toward longer lifespans. A somewhat paradoxical feature to be observed is that the drug effect on a p.d.f. takes place for times when the drug was not in the system (zero is a mark for the drug administration). This supposedly counterintuitive observation can be explained by the definition of the lifespan of a cell at a time t. The lifespan of cells prior to drug administration that will live long enough to be exposed to drug action should reflect this effect. Consequently, at time t = 0, the p.d.f. is different from the baseline p.d.f. because all cells in the population will be exposed to drug effect that will change their survival expectancy based on the baseline (drug free) lifespan distribution. The time variant p.d.f. converges to the baseline p.d.f. as the drug effect diminishes.

Consistently with the paradigm for basic indirect response models, four types of drug action result in four distinct response profiles also for the transit compartments model [18]. The inhibition and stimulation of the cell production rate results in no effect on the cell lifespan distribution. The inhibition and stimulation of the rate of the cell aging affects lifespan distribution. Responses will increase when aging is inhibited (mean lifespan increases) and decrease when aging is stimulated (mean lifespan decreases). These response time profiles are shown in Fig. 2 for varying doses. The basic feature of the presented profiles is a delayed peak that increases with doses. The peak times for all model types also increase with doses. When the mean lifespan parameter T_R is independent on the number of transit compartments n, increasing n to infinity results in a response profile R that is controlled by a point lifespan distribution centered at T_R. In the case of drug affecting k_in0, R is a basic lifespan based response that has been described previously [6]. Here the response elimination rate is the production rate delayed by T_R. The peaks increase with the doses but the peak times occur at the same time T_R. The lifespan based indirect response model obtained as n approaches infinity for TC models with drug affecting the aging process is different form a previously introduced model [12]. The latter assumed a bimodal lifespan distribution with drug changing temporarily the proportions between the modes. This resulted in a presence of a lag in the response profile. Also, the peak times did not depend on dose. As shown in Fig. 4 the basic LIDRE model does not have either of these characteristics. There is no lag in the response curve and the peak times are dose dependent. If drug increases T_R, then the peak times increase with doses. If drug decreases T_R, then response peak times decreases with increasing doses. Interestingly, the latter characteristic is opposite to the behavior of the peak times for an analogous transit compartments model if the number of compartments is relatively small. Contrary to all previously introduced LIDR, the LIDRE model does not exhibit a delay time, but requires an additional variable T_E to account for the drug effect.

The proposed basic LIDRE model assumes a point lifespan distribution for a cell population affected by a drug. As mentioned above such a model can be potentially applied to describe the cell responses for drugs known to accelerate cell maturation, increase proliferation, and inhibit cell death. Hematopoietic growth factors posses these characteristics. Recombinant human granulocyte colony stimulating factor (rHuG-CSF) is known to accelerate maturation of neutrophil precursors and stimulate mobilization of progenitor cells [26], recombinant human erythropoietin (rHuEPO) promotes release from the bone marrow to the circulation of young (stress) reticulocytes [27] that changes the lifespan distribution of these cells in the circulation. Similar effects on platelet release have been reported for agonists of the c-mpl receptor, a thrombopoietin receptor [2]. rHuEpo has been shown to act as a survival factor for red blood cells [28]. Pharmacodynamic TC models have been developed to account for cell responses to rHuG-CSFs [4, 29], c-mpl agonists [2, 30,31], and rHuEPO [5]. These TC models are LIDR models with the lifespan distribution described by the gamma function. Therefore more simplistic LIDRE models with point lifespan distribution may also adequately describe such data. Standard model selection techniques should be applied to yield the best model.

Analysis of the equation for a p.d.f. for the lifespan distribution obtained for the transit compartments model permitted a general mechanism by which a drug can affect an arbitrary lifespan distribution. This model is described by the operation ${{\ell }_0}^{\stackrel{‒}{°}}{\widehat{\mathrm{E}}}_{\mathrm{t}}\left(\tau \right)$ where the invariant (baseline) lifespan distribution ℓ₀(τ) becomes a time variant distribution ℓ(t,τ) due to the changes caused by a time dependent drug effect ${\widehat{\mathrm{E}}}_{\mathrm{t}}\left(\tau \right)$. A clear intuitive interpretation of this effect is difficult to offer, but one can interpret it as a time dependent change in the τ-axis for the lifespan distribution p.d.f. that shifts the distribution to the right or left. Freise et al. [10] introduced a pharmacodynamic model of drug affecting the distribution of cell lifespan that was further expanded to account for the changes in the environment [11]. The fundamental equation defining the p.d.f. for lifespan distribution was identical to Eq. 11. The mathematical derivations describing drug effect on the life distribution bare similarity to the operator ${{\ell }_0}^{\stackrel{‒}{°}}{\widehat{\mathrm{E}}}_{\mathrm{t}}\left(\tau \right)$ introduced in Eq. 28. Further analysis is necessary to determine if a new mechanism for drug effect on the cell lifespan distribution obtained from the generalization of the equation of the drug effect in the TC model is a special case of the models introduced by Freise and colleagues.

If T_R is fixed and n approaches infinity, the gamma p.d.f. for the lifespan distribution γ_n(τ) approaches the point distribution δ(τ − T_R). This property is called the approximate identity and results in a convergence of the TC models to a basic LIDR or LIDRE model. Figure 5 implies that even for n as large as 100 the approximation of δ(τ − T_R) is far from accurate. However, the resulting transit compartments response curves R_n(t) presented in Fig. 6 are very close to the LIDR model for n = 100. The maximum absolute difference between R_n(t) and R_∞(t) relative to the maximum absolute difference between R_∞(t) and R₀ is listed in Table 1 for an array of n values. The difference ranges between models 16.4–47.9% for n = 10, 11.2–43.9%, for n = 20, and 4.7–35.4% for n = 100. These ranges are calculated at a fixed dose of 10,000 across all four models reflecting four different mechanisms of drug action. The poorest approximation is observed for the inhibition of k_in0 PD model where even for n = 100 the error was greater than 35.4%. This approximation error assessment is meant to provide guidelines in selection of the number of transit compartments for a model that would mimic the lifespan based indirect response. It is clear if n is less than 5 then approximations are not satisfactory. Increasing n leads to a gradual improvement but there is no outstanding number that can be considered as a mark. In practice, this implies that a transit compartments model with n between 5 and 20 provides a relative good approxiation of the LIDR model. An addition of more transit compartments than n = 20 leads to a modest improvement of the error of the approximation. To explore which model parameters control the approximation error one can use Eq. 38.

In summary, the transit compartments models can be considered as lifespan based indirect response models with the gamma lifespan distribution. Stimulation and inhibition of the cell aging process in transit compartments model is interpreted as a temporal change in the lifespan distribution in the LIDR model. If the number of compartment increases and the mean lifespan is constant, then the transit compartments models approach a basic LIDR model with a point lifespan distribution. A modest improvement of this approximation can be observed if the number of the transit compartments exceeds 20. Finally, the mechanism by which drug affects the lifespan distribution for cells described by the transit compartments models can be generalized to arbitrary cell lifespan distributions, which leads to a new class of basic lifespan based indirect response models that will be explored in future studies.

Appendix 1

Derivation of Eq. 6

To simplify calculations we introduce the following variables

$$\text{k}\left(\text{t}\right)={\text{k}}_{\text{in}}\left(\text{t}\right)-\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}\text{E}\left(\text{t}\right)\text{and}{\text{Y}}_{\text{i}}={\text{P}}_{\text{i}}-\frac{{\text{R}}_0}{\text{n}}\text{for}\text{i}=1,\dots ,\text{n}.$$ (44)

Then the transit compartments model Eqs. 1-2 become

$$\frac{{\text{dY}}_{\text{1}}}{\text{dt}}=\text{k}\left(\text{t}\right)-\frac{\text{n}}{{\text{T}}_{\text{R}}}\text{E}\left(\text{t}\right){\text{Y}}_1,{\text{Y}}_1\left(0\right)=0$$ (45)

$$\frac{{\text{dY}}_{\text{i}}}{\text{dt}}=\frac{\text{n}}{{\text{T}}_{\text{R}}}\text{E}\left(\text{t}\right)({\text{Y}}_{\text{i}-1}-{\text{Y}}_{\text{i}}),{\text{Y}}_{\text{i}}\left(0\right)=0,\text{i}=2,\dots ,\text{n}$$ (46)

Equation 45 can be solved using the integrating factor technique [24]:

$${\text{Y}}_1\left(\text{t}\right)=\underset{0}{\overset{\text{t}}{\int }}\text{k}\left(\tau \right)\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (47)

We will show by mathematical induction that for i = 1, …, n

$${\text{Y}}_{\text{i}}\left(\text{t}\right)=\frac{1}{(\text{i}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{i}-1}\underset{0}{\overset{\text{t}}{\int }}\text{k}\left(\tau \right){\left(\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (48)

Since the case i = 1 reduces to Eq. 47, it remains to show that Eq. 48 is true for i + 1 assuming it holds for i. Using the same integrating factor as for Eq. 47 one can solve Eq. 46 with i + 1 to obtain the following representation of Y_i+1:

$${\text{Y}}_{\text{i}+1}\left(\text{t}\right)=\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{0}{\overset{\text{t}}{\int }}\text{E}\left(\tau \right){\text{Y}}_{\text{i}}\left(\tau \right)\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (49)

One can substitute the right hand side of Eq. 48 for Y_i(τ) in Eq. 49:

$${\text{Y}}_{\text{i}+1}\left(t\right)=\frac{1}{(\text{i}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{i}}\underset{0}{\overset{\text{t}}{\int }}\text{E}\left(\tau \right)\underset{0}{\overset{\tau }{\int }}\text{k}\left(\text{s}\right){\left(\underset{\text{s}}{\overset{\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{s}}{\overset{\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{ds}\times \text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (50)

Equation 50 can be further reduced to

$${\text{Y}}_{\text{i}+1}\left(\text{t}\right)=\frac{1}{(\text{i}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{i}}\underset{0}{\overset{\text{t}}{\int }}\underset{0}{\overset{\tau }{\int }}\text{E}\left(\tau \right)\text{k}\left(\text{s}\right){\left(\underset{\text{s}}{\overset{\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{s}{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{dsd}\tau$$ (51)

Changing the order of the first two integrals in Eq. 51 results in

$${\text{Y}}_{\text{i}+1}\left(\text{t}\right)=\frac{1}{(\text{i}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{i}}\underset{0}{\overset{\text{t}}{\int }}\underset{\text{s}}{\overset{\text{t}}{\int }}\text{E}\left(\tau \right)\text{k}\left(\text{s}\right){\left(\underset{\text{s}}{\overset{\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{s}}{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau \text{ds}$$ (52)

The only part of the integrant that depends on τ is equal to

$$\underset{\text{s}}{\overset{\text{t}}{\int }}\text{E}\left(\tau \right){\left(\underset{\text{s}}{\overset{\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}-1}\text{d}\tau =\frac{1}{\text{i}}\underset{\text{s}}{\overset{\text{t}}{\int }}{\left(\underset{\text{s}}{\overset{\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}}\text{d}\tau$$ (53)

Substituting Eq. 53 in the integrant of Eq. 52 gives

$${\text{Y}}_{\text{i}+1}\left(\text{t}\right)=\frac{1}{\text{i}!}{\left(\frac{\text{n}}{\text{T}}\right)}^{\text{i}}\underset{0}{\overset{\text{t}}{\int }}\text{k}\left(\text{s}\right){\left(\underset{\text{s}}{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{i}}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{s}}{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{ds}$$ (54)

Equation 11 is equal to Eq. 48 with i + 1, which completes the recursive proof that Eq. 48 holds true for i = 1, …, n. Finally, to derive Eq. 6 one needs to replace Y_i(t) and k(τ) in Eq. 48 with the original P_i and k_in(t) using Eq. 44.

Appendix 2

Derivation of Eq. 16

Equation 6 with i = n implies that the solution for the n-th compartment is

$${\text{P}}_{\text{n}}\left(\text{t}\right)=\frac{{\text{R}}_0}{\text{n}}+\frac{1}{(\text{n}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}-1}\underset{0}{\overset{\text{t}}{\int }}\left({\text{k}}_{\text{in}}\left(\tau \right)-\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}\text{E}\left(\tau \right)\right)\times {\left(\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (55)

Changing the variables τ → t − τ in the first integral results in

$${\text{P}}_{\text{n}}\left(\text{t}\right)=\frac{{\text{R}}_0}{\text{n}}+\frac{1}{(\text{n}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}-1}\underset{0}{\overset{\text{t}}{\int }}\left({\text{k}}_{\text{in}}(\text{t}-\tau )-\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}\text{E}(\text{t}-\tau )\right)\times {\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (56)

The difference in the integrand can be integrated separately as follows

$${\text{P}}_{\text{n}}\left(\text{t}\right)=\frac{{\text{R}}_0}{\text{n}}-\frac{1}{(\text{n}-1)!}\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}{\left(\frac{\text{n}}{\text{T}}\right)}^{\text{n}-1}\underset{0}{\overset{\text{t}}{\int }}\text{E}(\text{t}-\tau ){\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau +\frac{1}{(\text{n}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}-1}\underset{0}{\overset{\text{t}}{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau ){\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau$$ (57)

The change of the variable

$$\text{x}\to \underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}$$ (58)

reduces the integral in the second term of Eq. 57 to the following form

$$\begin{array}{cc}\hfill {\text{I}}_{\text{n}}& =\frac{1}{(\text{n}-1)!}\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}-1}\underset{0}{\overset{\text{t}}{\int }}\text{E}(\text{t}-\tau ){\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)\text{d}\tau \hfill \\ \hfill & =\frac{{\text{R}}_0}{\text{n}}\frac{1}{(\text{n}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}}\underset{0}{\overset{\underset{0}{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}}{\int }}{\text{x}}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}x\right)\text{dx}\hfill \end{array}$$ (59)

The properties of the gamma distribution imply that [21]

$$\frac{1}{(\text{n}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}}\underset{0}{\overset{\infty }{\int }}{\text{x}}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\text{x}\right)\text{dx}=1$$ (60)

Consequently,

$${\text{I}}_{\text{n}}=\frac{{\text{R}}_0}{\text{n}}-\frac{1}{(\text{n}-1)!}\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}-1}\underset{\text{t}}{\overset{\infty }{\int }}\text{E}(\text{t}-\tau ){\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\times \text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(z\right)\text{dz}\right)\text{d}\tau$$ (61)

where the original integration variable τ was restored in the integral in Eq. 60. The baseline conditions Eq. 3 imply that for τ > t

$$\frac{{\text{R}}_0}{{\text{T}}_{\text{R}}}={\text{k}}_{\text{in0}}={\text{k}}_{\text{in}}(\text{t}-\tau )\text{and}\text{E}(\text{t}-\tau )=1$$ (62)

Hence

$${\text{I}}_{\text{n}}=\frac{{\text{R}}_0}{\text{n}}-\frac{1}{(\text{n}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}-1}\underset{\text{t}}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau ){\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(z\right)\text{dz}\right)\text{d}\tau$$ (63)

One can insert I_n back in Eq. 57 resulting in

$${\text{P}}_{\text{n}}=\frac{1}{(\text{n}-1)!}{\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}-1}\underset{\text{t}}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau ){\left(\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}\right)}^{\text{n}-1}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(z\right)\text{dz}\right)\text{d}\tau$$ (64)

After multiplying both sides of Eq. 64 by nE(t)/T_R one arrives at Eq. 16.

Appendix 3

Derivation of Eq. 19

For given times t and τ let us define

$${\widehat{E}}_{\text{t}}\left(\tau \right)=\underset{\text{t}}{\overset{\text{t}+\tau }{\int }}\text{E}\left(\text{z}\right)\text{dz}$$ (65)

Since the derivative

$$\frac{\text{d}{\widehat{E}}_{\text{t}}\left(\tau \right)}{\text{d}\tau }=\text{E}(\text{t}+\tau )$$ (66)

Equation 17 can be simplified to the following form

$${\mathcal{l}}_{\text{n}}(\text{t},\tau )={\left(\frac{\text{n}}{{\text{T}}_{\text{R}}}\right)}^{\text{n}}\frac{{\widehat{E}}_{\text{t}}{\left(\tau \right)}^{\text{n}-1}}{(\text{n}-1)!}\text{exp}\left(-\frac{\text{n}}{{\text{T}}_{\text{R}}}{\widehat{E}}_{\text{t}}\left(\tau \right)\right)\frac{\text{d}{\widehat{E}}_{\text{t}}\left(\tau \right)}{\text{d}\tau }$$ (67)

Applying the change of variables $s\to {\widehat{\mathrm{E}}}_{\mathrm{t}}\left(\tau \right)$ in the following integral, one can further reduce it to the integral of the gamma function γ_n(s) defined in Eq. 18:

$$\underset{0}{\overset{\infty }{\int }}{\mathcal{l}}_{\text{n}}(\text{t},\tau )\text{d}\tau =\underset{0}{\overset{\infty }{\int }}{\gamma }_{\text{n}}\left(\text{s}\right)\text{ds}=1$$ (68)

The latter is a consequence of γ_n(s) as a probability density function. This proves Eq. 19.

Appendix 4

Derivation of Eq. 29

To prove Eq. 29 we use the definition of the Dirac delta function δ_τ0(τ) = δ(τ − τ₀) stating that for any test function φ(τ) (an indefinitely differentiable function with a compact support contained in the interval (0,∞)) the following relationship holds [19]:

$$\underset{0}{\overset{\infty }{\int }}\delta (\tau -{\tau }_0)\varphi \left(\tau \right)\text{d}\tau =\varphi \left({\tau }_0\right)$$ (69)

Let φ(τ) be a test function, then according to Eq. 24

$$\underset{0}{\overset{\infty }{\int }}{{\delta }_{\tau 0}}^{\stackrel{‒}{°}}{\Phi }_{\text{t}}\left(\tau \right)\varphi \left(\tau \right)\text{d}\tau =\underset{0}{\overset{\infty }{\int }}\delta ({\Phi }_{\text{t}}\left(\tau \right)-{\tau }_0){\Phi }_{\text{t}}^{\prime }\left(\tau \right)\varphi \left(\tau \right)\text{d}\tau$$ (70)

The substitution s → Φ_t(τ) transforms the last integral in Eq. 70 to the following

$$\underset{0}{\overset{\infty }{\int }}\delta (\text{s}-{\tau }_0)\varphi \left({\Phi }_{\text{t}}^{-1}\left(\text{s}\right)\right)\text{ds}=\varphi \left({\Phi }_{\text{t}}^{-1}\left({\tau }_0\right)\right)$$ (71)

where ${\Phi }_{\mathrm{t}}^{-1}\left(\mathrm{s}\right)$ is the inverse of Φ_t(τ). The integral in Eq. 71 is evaluated according to Eq. 69. Consequently, for any test function φ(τ)

$$\underset{0}{\overset{\infty }{\int }}{{\delta }_{\tau 0}}^{\stackrel{‒}{°}}{\Phi }_{\text{t}}\left(\tau \right)\varphi \left(\tau \right)\text{d}\tau =\varphi \left({\Phi }_{\text{t}}^{-1}\left({\tau }_0\right)\right)$$ (72)

This proves Eq. 29.

Appendix 5

Derivation of Eqs. 30, 32, and 33

A general form for the basic LIDRE model for drug affecting the point distribution according to Eqs. 27 and 28 will be described as follows

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau )\mathcal{l}(\text{t}-\tau ,\tau )\text{d}\tau$$ (73)

where after applying Eqs. 24, 65 and 66:

$$\mathcal{l}(\text{t},\tau )={{\delta }_{{\text{T}}_{\text{R}}}}^{\stackrel{‒}{°}}{\widehat{E}}_t\left(\tau \right)=\delta ({\widehat{E}}_{\text{t}}\left(\tau \right)-{\text{T}}_{\text{R}})\text{E}(\text{t}+\tau )$$ 74

Therefore Eq. 73 can be further simplified to

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-\tau )\delta ({\widehat{E}}_{\text{t}-\tau }\left(\tau \right)-{\text{T}}_{\text{R}})\text{E}\left(\text{t}\right)\text{d}\tau$$ (75)

To calculate the integral in Eq. 75 let us introduce a transformation Ψ_t(τ)

$${\Psi }_{\text{t}}\left(\tau \right)={\widehat{E}}_{\text{t}-\tau }\left(\tau \right)=\underset{\text{t}-\tau }{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}$$ (76)

One can verify that for any time t

$${\Psi }_{\text{t}}\left(0\right)=0,{\Psi }_{\text{t}}\left(\infty \right)=\infty ,\text{and}\frac{\text{d}{\Psi }_{\text{t}}}{\text{d}\tau }\left(\tau \right)=\text{E}(\text{t}-\tau )>0$$ (77)

The change of variables s → Ψ_t(τ) transforms the integral in Eq. 74 to

$$\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{t}-{\Psi }_{\text{t}}^{-1}\left(\text{s}\right))\delta (\text{s}-{\text{T}}_{\text{R}})\frac{\text{E}\left(\text{t}\right)}{\text{E}(\text{t}-{\Psi }_{\text{t}}^{-1}\left(\text{s}\right))}\text{ds}={\text{k}}_{\text{in}}(\text{t}-{\Psi }_{\text{t}}^{-1}\left({\text{T}}_{\text{R}}\right))\frac{\text{E}\left(\text{t}\right)}{\text{E}(\text{t}-{\Psi }_{\text{t}}^{-1}\left({\text{T}}_{\text{R}}\right))}$$ (78)

where the derivative of the inverse is

$$\frac{\text{d}{\Psi }_{\text{t}}^{-1}}{\text{ds}}=\frac{1}{\text{E}(\text{t}-{\Psi }_{\text{t}}^{-1}\left(\text{s}\right))}$$ (79)

and the definition of the delta function δ(τ − T_R) has been utilized. To abbreviate the right hand side of Eq. 78 the following function of time t is introduced:

$${\text{T}}_{\text{E}}\left(\text{t}\right)=\text{t}-{\Psi }_{\text{t}}^{-1}\left({\text{T}}_{\text{R}}\right)$$ (80)

Then Eq. 73 simplifies to Eq. 30

$$\frac{\text{dR}}{\text{dt}}={\text{k}}_{\text{in}}\left(\text{t}\right)-{\text{k}}_{\text{in}}\left({\text{T}}_{\text{E}}\left(\text{t}\right)\right)\frac{\text{E}\left(\text{t}\right)}{\text{E}\left({\text{T}}_{\text{E}}\left(\text{t}\right)\right)}$$ (81)

Notice that Eq. 81 was derived without an assumption of any specific form for k_in(t) like one specified by Eqs. 9 and 10. Equations 76 and 80 imply

$$\underset{{\text{T}}_{\text{E}}\left(\text{t}\right)}{\overset{\text{t}}{\int }}\text{E}\left(\text{z}\right)\text{dz}={\text{T}}_{\text{R}}$$ (82)

At t = 0, Eq. 82 becomes

$$\underset{{\text{T}}_{\text{E}}\left(0\right)}{\overset{0}{\int }}\text{E}\left(\text{z}\right)\text{dz}={\text{T}}_{\text{R}}$$ (83)

Since T_R > 0 and E(z) > 0, then T_E(0) < 0. For z < 0, E(z) = 1 (see Eq. 3), which implies

$${\text{T}}_{\text{E}}\left(0\right)=-{\text{T}}_{\text{R}}$$ (84)

This proves Eq. 33. To derive a differential equation for T_E(t), calculate the derivative with respect to t of both sides of Eq. 82. The derivative of the right-hand side is zero, and the derivative of the integral in the left-hand side results in the following equation:

$$\text{E}\left(\text{t}\right)-\frac{{\text{dT}}_{\text{E}}\left(\text{t}\right)}{\text{dt}}\text{E}\left({\text{T}}_{\text{E}}\left(\text{t}\right)\right)=0$$ (85)

That results in Eq. 32.

Appendix 6

Proof of Eqs. 37-39

Integration of both sides of Eq. 26 leads to

$${\text{R}}_{\text{n}}\left(\text{t}\right)={\text{R}}_0+\underset{0}{\overset{\text{t}}{\int }}{\text{k}}_{\text{in}}\left(\text{s}\right)\text{ds}-\underset{0}{\overset{\text{t}}{\int }}\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{s}-\tau ){\mathcal{l}}_{\text{n}}(\text{t}-\tau ,\tau )\text{d}\tau \text{ds}$$ (86)

Similarly, integration of Eq. 30 results in

$${\text{R}}_{\infty }\left(\text{t}\right)=R_0+\underset{0}{\overset{\text{t}}{\int }}{\text{k}}_{\text{in}}\left(\text{s}\right)\text{ds}-\underset{0}{\overset{\text{t}}{\int }}{\text{k}}_{\text{in}}\left({\text{T}}_{\text{E}}\left(\text{s}\right)\right)\frac{\text{E}\left(\text{s}\right)}{E\left({\text{T}}_{\text{E}}\left(s\right)\right)}\text{ds}$$ (87)

Upon subtraction of both sides of Eqs. 87 and 86:

$${\text{R}}_{\infty }\left(\text{t}\right)-{\text{R}}_{\text{n}}\left(\text{t}\right)=\underset{0}{\overset{\text{t}}{\int }}\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{s}-\tau ){\mathcal{l}}_n(\text{t}-\tau ,\tau )\text{d}\tau \text{ds}-\underset{0}{\overset{\text{t}}{\int }}{\text{k}}_{\text{in}}\left({\text{T}}_{\text{E}}\left(\text{s}\right)\right)\frac{\text{E}\left(\text{s}\right)}{\text{E}\left({\text{T}}_{\text{E}}\left(\text{s}\right)\right)}\text{ds}$$ (88)

Following the definition of Ψ_t(τ), Eq. 88 implies that

$$\begin{array}{cc}\hfill \underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{s}-\tau ){\mathcal{l}}_{\text{n}}(\text{t}-\tau ,\tau )\text{d}\tau & =\underset{0}{\overset{\infty }{\int }}{\text{k}}_{\text{in}}(\text{s}-{\Psi }_{\text{s}}^{-1}\left(\text{z}\right))\frac{\text{E}\left(\text{s}\right)}{\text{E}(\text{s}-{\Psi }_{\text{s}}^{-1}\left(\text{z}\right))}{\gamma }_{\text{n}}\left(\text{z}\right)\text{dz}\hfill \\ \hfill & =\underset{0}{\overset{\infty }{\int }}{\varphi }_{\text{s}}\left(\text{z}\right){\gamma }_{\text{n}}\left(\text{z}\right)\text{dz}\hfill \end{array}$$ (89)

Analogously, Eq. 80 implies

$${\text{k}}_{\text{in}}\left({\text{T}}_{\text{E}}\left(\text{s}\right)\right)\frac{\text{E}\left(\text{s}\right)}{\text{E}\left({\text{T}}_{\text{E}}\left(\text{s}\right)\right)}={\text{k}}_{\text{in}}(\text{t}-{\Psi }_{\text{s}}^{-1}\left({\text{T}}_{\text{R}}\right))\frac{\text{E}\left(\text{s}\right)}{\text{E}(\text{s}-{\Psi }_{\text{s}}^{-1}\left({\text{T}}_{\text{R}}\right))}={\varphi }_{\text{s}}\left({\text{T}}_{\text{R}}\right)$$ (90)

Hence

$${\text{R}}_{\infty }\left(\text{t}\right)-{\text{R}}_{\text{n}}\left(\text{t}\right)=\underset{0}{\overset{\text{t}}{\int }}\underset{0}{\overset{\infty }{\int }}{\varphi }_{\text{s}}\left(\text{z}\right){\gamma }_{\text{n}}\text{dzds}-\underset{0}{\overset{\text{t}}{\int }}{\varphi }_{\text{s}}\left({\text{T}}_{\text{R}}\right)\text{ds}$$ (91)

and Eq. 37 follows. To show that Eq. 37 holds true one can transform Eq. 91 further utilizing the fact that γ_n(τ) is a p.d.f.

$${\text{R}}_{\infty }\left(\text{t}\right)-{\text{R}}_{\text{n}}\left(\text{t}\right)=\underset{0}{\overset{\text{t}}{\int }}\underset{0}{\overset{\infty }{\int }}({\varphi }_{\text{s}}\left(\text{z}\right)-{\varphi }_{\text{s}}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\text{z}\right)\text{dzds}$$ (92)

Since Eqs. 7-10 imply that φ_s(τ) is a bound function of s and τ, i.e. there is a constant M > 0 such that for any s and τ

$${\varphi }_{\text{s}}\left(\tau \right)\le \text{M}$$ (93)

Hence

$$\mid \underset{0}{\overset{\infty }{\int }}({\varphi }_{\text{s}}\left(\text{z}\right)-{\varphi }_{\text{s}}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\text{z}\right)\text{dz}\mid \le 2\text{M}\underset{0}{\overset{\infty }{\int }}{\gamma }_n\left(\text{z}\right)\text{dz}=2\text{M}$$ (94)

The dominated convergence theorem [25] implies that for any t the right hand side of Eq. 92 approaches 0 as n → ∞, for any s

$$\underset{0}{\overset{\infty }{\int }}({\varphi }_{\text{s}}\left(\text{z}\right)-{\varphi }_{\text{s}}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\text{z}\right)\text{dz}\to 0\text{as}\text{n}\to \infty$$ (95)

Equation 95 is true due to the approximate identity property of the gamma distribution p.d.f. γ_n(τ) cited in Eq. 36, which we will prove for an arbitrary continuous and bound function f(τ). Let ε >0 be a small number and M > 0 be such |f(τ)| ≤ M for all τ. Then the continuity of f(τ) implies that there is a small ε > 0 such that for any T_R-ε < τ < T_R+ ε

$$\mid \text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)\mid \le ∊$$ (96)

The integral in Eq. 95 can be partitioned into a sum of three integrals:

$$\underset{0}{\overset{\infty }{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau =\underset{0}{\overset{{\text{T}}_{\text{R}}-∊}{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau +\underset{{\text{T}}_{\text{R}}-∊}{\overset{{\text{T}}_{\text{R}}+∊}{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau +\underset{{\text{T}}_{\text{R}}+∊}{\overset{\infty }{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau$$ (97)

The first and third integral in Eq. 97 can be bound as follows:

$$\mid \underset{0}{\overset{{\text{T}}_{\text{R}}-∊}{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \mid \le 2\text{M}\underset{0}{\overset{{\text{T}}_{\text{R}}-∊}{\int }}{\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau$$ (98)

and

$$\mid \underset{{\text{T}}_{\text{R}}-∊}{\overset{\infty }{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \mid \le 2\text{M}\underset{{\text{T}}_{\text{R}}-∊}{\overset{\infty }{\int }}{\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau$$ (99)

The bound for the second integral in Eq. 97 is

$$\mid \underset{{\text{T}}_{\text{R}}-∊}{\overset{{\text{T}}_{\text{R}}+∊}{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \mid \le ∊\underset{{\text{T}}_{\text{R}}-∊}{\overset{{\text{T}}_{\text{R}}+∊}{\int }}{\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \le ∊\underset{0}{\overset{\infty }{\int }}{\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau =∊$$ (100)

Since

$$\underset{0}{\overset{{\text{T}}_{\text{R}}-∊}{\int }}{\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \to 0\text{and}\underset{{\text{T}}_{\text{R}}-∊}{\overset{\infty }{\int }}{\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \to 0\text{as}\text{n}\to \infty$$ (101)

the first and third integral in Eq. 97 can be bound by ε for large enough n, and consequently

$$\mid \underset{0}{\overset{\infty }{\int }}(\text{f}\left(\tau \right)-\text{f}\left({\text{T}}_{\text{R}}\right)){\gamma }_{\text{n}}\left(\tau \right)\text{d}\tau \mid \le 3∊$$ (102)

This completes the derivations of Eqs. 36, 37 and 38.