Semiparametric Bayesian analysis of gene-environment interactions with error in measurement of environmental covariates and missing genetic data

Abstract

Case-control studies are widely used to detect gene-environment interactions in the etiology of complex diseases. Many variables that are of interest to biomedical researchers are difficult to measure on an individual level, e.g. nutrient intake, cigarette smoking exposure, long-term toxic exposure. Measurement error causes bias in parameter estimates, thus masking key features of data and leading to loss of power and spurious/masked associations. We develop a Bayesian methodology for analysis of case-control studies for the case when measurement error is present in an environmental covariate and the genetic variable has missing data. This approach offers several advantages. It allows prior information to enter the model to make estimation and inference more precise. The environmental covariates measured exactly are modeled completely nonparametrically. Further, information about the probability of disease can be incorporated in the estimation procedure to improve quality of parameter estimates, what cannot be done in conventional case-control studies. A unique feature of the procedure under investigation is that the analysis is based on a pseudo-likelihood function therefore conventional Bayesian techniques may not be technically correct. We propose an approach using Markov Chain Monte Carlo sampling as well as a computationally simple method based on an asymptotic posterior distribution. Simulation experiments demonstrated that our method produced parameter estimates that are nearly unbiased even for small sample sizes. An application of our method is illustrated using a population-based case-control study of the association between calcium intake with the risk of colorectal adenoma development.

1. INTRODUCTION

A key component to prevention and control of complex diseases, such as cancer, diabetes, hypertension, is to analyze genetic and environmental factors that lead to the development of these complex diseases. The analysis is complicated by the fact that the genetic and environmental factors interplay while causing complex diseases (Hunter, 2005). Such gene-environment interactions have the potential to (1) yield insight into the mechanism of action of the environment under various settings of the genetic background; (2) suggest disease prevention strategies; (3) obtain a better estimate of the population-attributable risk for genetic and environmental risk factors by accounting for their joint interaction; and (4) result in improved analysis of the association between environmental factors and complex disease by examining factors in genetically susceptible individuals. A challenge in statistical analyses is that a weak overall association may mask important genetic susceptibility to the effects of the environmental exposure in the population subgroups. Separate estimation of the contributions of genes and environment and ignoring their interaction will lead to an incorrect estimate of the proportion of the disease (the population attributable risk) that is explained by genes, environment, and their joint effect (Hunter, 2005). Restricting analysis of environmental exposure to individuals who are genetically susceptible to the exposure is likely to increase the magnitude of relative risk, thus improving the ability to detect association signal.

Further, many variables that are of interest to biomedical researchers, such as dietary intake and cigarette smoking exposure are very difficult to measure on individuals. Measurement error causes bias in gene-environment parameter estimates, thus masking key features of data and leading to loss of power and spurious/masked associations (Lobach, et al., 2008). Loss of power prevents the ability to detect important relationships among variables (Carroll, et al. 2006). For example, nutrition — defined broadly to indicate diet, body size, physical activity — is likely to be causally related to cancer (Schatzkin, et al., 2009). Nevertheless, nutritional epidemiology of cancer remains problematic, largely because of persistent concerns that standard instruments measure diet and physical activity with too much error. While it is recognized that information collected about dietary level contains error, considerable uncertainty remains about their qualitative and quantitative characteristics (Subar, et al. 2003). Understanding this error is critical to interpreting findings and surveillance research efforts.

In this paper, we develop a Bayesian methodology for analysis of case-control data in the situation when measurement error is present in an environmental covariate as well as the genetic variable contains missing data (unobserved genotype or haplotype-phase ambiguity). Conventionally, case-control data are analyzed using prospective logistic regression ignoring the fact that under this design subjects are sampled into the study conditionally on their disease status. The validity of this approach relies on the classic results by Cornfield (1956) who showed the equivalence of prospective- and retrospective odds-ratios. The efficiency of the approach was established in two other classic papers by Andersen (1970) and Prentice and Pyke (1979). Recently, Chatterjee and Carroll (2005), Spinka, et al. (2005), and Lobach, et al. (2008 and Lobach, et al. (2010) developed an efficient approach for analysis of case-control studies, the key idea of which is to treat retrospectively collected data as if they were coming from a random sample. Because the retrospectively collected data are analyzed as if they were coming from a random sample, the conventional Bayesian techniques are not valid. The pseudo-likelihood function employed in our analysis is not the same as the conventional prospective likelihood. Validity of the Bayesian analysis needs to be examined when the proposed likelihood function is not a proper likelihood (Monahan and Boos, 1992). Lazar (2003) has examined the validity of Bayesian empirical likelihood based methods. We followed Monahan and Boos (2003) to validate our Bayesian approach under this pseudo-likelihood function and exploit it to obtain posterior inferences about the unknown parameters. Due to the complexity of the pseudo-likelihood function, the posterior distribution of the parameters is not in explicit form, therefore Markov Chain Monte Carlo (MCMC) algorithms are required to sample from this posterior distribution to make necessary inference.

Our work is motivated by a case-control study of colorectal adenoma (Peters et al., 2004). Briefly, the available data consist of measures of dietary calcium intake obtained by a food frequency questionnaire (FFQ), genotype data for three SNPs in the calcium receptor gene CaSR, and various individual-level data such as age, sex and race. The main interest is in studying the interaction between CaSR haplotypes and dietary calcium intake.

The Colorectal Adenoma study thus has unique features, specifically the following.

• First, genetic information is missing. We wish to model the effect of CaSR haplotypes, but these are not observed, and instead we have unphased haplotype information in the form of the three SNPs.

• Second, one of the environmental variables (calcium intake) is subject to substantial measurement error because of the use of a FFQ. It is well known that the FFQ as a measure of long-term diet is subject both to biases and random errors, as illustrated in the OPEN study (Subar, et al., 2003).

FFQs as a measure of long-term diet result in massive amounts of measurement error. It is well known (Schafer and Purdy, 1996) that huge measurement error often results in skewed sampling distribution of parameter estimates and the skewness is more pronounced for small sample sizes. Hence possibly both estimation and inference are not precise (Carroll, et al., 2006). In our motivating example the situation is further complicated by the fact that not only massive amount of measurement error is present in the environmental covariate, furthermore the genotype contains missing values.

We develop a Bayesian approach utilizing the pseudo-likelihood function to quantify the uncertainty of the model parameters exactly. Our approach has the ability to shrink the parameter estimates towards prior using a proper prior distribution and hence reduce variability of these estimates. Moreover, Bayesian methods can incorporate available prior historical or biological information to make inferences more precise. For example, the proposed pseudo-likelihood function allows to incorporate prior information about the probability of disease, which cannot be done in a standard analysis. Typically a good estimate of a probability of disease is available a priori. This information can be used to improve estimation of parameters, especially the intercept.

Our approach is general enough to accommodate any complicated pseudo-likelihood function and use MCMC techniques to obtain the parameter estimates with uncertainty bounds. The method will be particularly useful when this pseudo-likelihood function is multimodal (since MCMC can search the modes) or when the solution lies on the boundary (since prior can constrain the solution space). When the sample size is small or measurement error is massive, the non-Gaussian behavior of an estimate is very common. In terms of the Bayesian model and MCMC based computation, we can perform exact analysis and capture these non-Gaussian behaviors. On the other hand, when the sample size is large enough, we can derive the asymptotic posterior distribution which will ease the computation burden.

Alternative semiparametric Bayesian approach will be to assign Dirichlet process or some other nonparametric prior processes to model the unknown joint distribution of the covariates without measurement error and perform full Bayesian analysis using MCMC (Müller and Roeder, 1997; Sinha et al., 2005). In this process we need to estimate potentially high dimensional nuisance parameters and the MCMC algorithms are computationally demanding. In addition, the analysis could be sensitive towards the specification of the hyper-parameters of these nonparametric processes. Our approach avoids the complete specification of this distribution, hence reduces the computational burden significantly. Furthermore, we can obtain the asymptotic posterior distribution of the parameters and can avoid MCMC in those situations. However it requires a validation step which could be computationally intensive.

An outline of this paper is as follows. In Section 2 we introduce notation and formally state the problem. Section 3 presents the proposed methodology for parameter estimation based on a pseudo-likelihood function. In Section 4 we describe the full Bayesian model under various scenarios. In Section 5 we derive an asymptotic posterior distribution. Section 6 gives the results of simulation studies, where we show that our methodology results in parameter estimates that are nearly unbiased and error rates close to the nominal. Section 7 analyzes the Colorectal Adenoma Data discussed above. Section 8 gives concluding remarks.

2. NOTATION AND PSEUDO-LIKELIHOOD FUNCTION

Suppose a sample consists of n₀ controls and n_d cases with disease stage d = 1, 2, …, K to accommodate different subtypes of disease. Let H = (H₁, H₂) denote the diplotype status, that is, the two haplotypes that a subject carries at the loci of interest on the pair of homologous chromosomes. Note that typically multilocus genotype data G = (G₁, …, G_M) are available. Due to lack of haplotype-phase information, multiple configurations of haplotypes can be consistent with the same genotype data. For example, if A/a and B/b denote the major/minor alleles in two bi-allelic loci (e.g. single nucleotide polymorphisms), then subjects with genotypes (Aa) and (Bb) at the first and the second locus, respectively, are considered phase ambiguous: their genotypes could arise from either the haplotype-pair (A-B, a-b), or the haplotype pair (A-b, a-B). Humans are diploid individuals and a pair of haplotypes that a person carries is called diplotype. Let 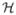denote the set of all possible diplotypes in the underlying population and 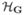denote the set of all possible diplotypes that are consistent with a particular genotype G. We impose a parametric structure on the genetic covariate of interest in the form pr(H) = Q(H, θ). In our example we used Hardy-Weinberg Equilibrium (HWE) of the following form.

$$\begin{array}{ll}Q(H,\theta )=\text{pr}\{H=(h_j,h_k)\mid \theta \}& ={\theta }_k^2,\text{if}{h}_j=h_k;\\ & =2{\theta }_k{\theta }_j,\text{if}{h}_j\ne h_k.\end{array}$$

However, the methodology is general enough to allow various parametric forms of Q(H, θ). For instance, it is possible to introduce a parameter that models departure from the HWE. Alternatively, one can specify a parametric distribution of H given (X, Z) that could account for gene-environment association (Chatterjee, et al. 2006).

Let (X, Z) denote all of the environmental (non-genetic) covariates of interest with X denoting the factors susceptible to measurement errors. We assume that H and (X, Z) are independently distributed in the underlying population. Only changes in notation are needed to model genotype and environment within strata thus relaxing gene-environment independence assumption. We suppose that the type of genetic covariate measured does not depend on the individual’s true genetic covariate, given disease status, environmental covariates and the measured genetic information. Further, we suppose that the observed genetic variable does not contain any additional information on disease status and true environmental covariate given the genetic variable of interest.

Recall that the environmental covariate X is measured with error. Let W denote the error-prone version of X. We assume a parametric model of the form f_mem(w|X, H, Z, D; ξ) for the conditional distribution of W given the true exposure X, additional environmental factors Z and disease-status D. This model is general enough to capture a differential on the disease status, genetic and other environmental variables f_mem(w|X, H, Z, D; ξ) can be estimated using replications or an external study. We assume that the joint distribution of the environmental factors in the underlying population can be specified according to a semi-parametric model of the form f_X,Z (x, z) = f_X (x|z, η)f_Z (z), where f_Z (z) is left completely unspecified, thus avoiding the need to estimate potentially high-dimensional nuisance parameters.

Given the environmental covariates X and Z and diplotype data H, the risk of the disease in the underlying population is given by the polytomous logistic regression model

$$\text{pr}(D=d\mid H,X,Z)=\frac{exp\{{\beta }_{0d}+m(H,X,Z,\beta )\}}{1+{\sum }_{j=1}^{K}exp\{{\beta }_{0j}+m(H,X,Z,\beta )\}},d\ge 1.$$

Here m(·) is a known function parameterizing the joint risk of the disease from H^dip, X and Z in terms of the odds-ratio parameters β. Define n_d be the number of subjects with disease status d. Let π_d = pr(D = d), κ_d = β_0d + log(n_d/n₀) − log(π_d/π₀), and κ̃ = (κ₁, …, κ_K)^T. Define κ₀ = β₀₀. Let β̃₀ = (β₀₁, …, β_0K)^T. Let 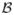$\mathrm{\Omega }={({\stackrel{\sim }{\beta }}_0^{\text{T}},{\beta }^{\text{T}},{\mathrm{\Theta }}^{\text{T}},{\stackrel{\sim }{\kappa }}^{\text{T}})}^{\text{T}}$, = (Ω^T, η^T)^T. Define I_(d≥1)(d) be the indicator function. Make the definition

$$S(d,h,x,z,\mathrm{\Omega })=\frac{exp[I_{(d\ge 1)}(d)\{{\kappa }_d+m(h,x,z,\beta )\}]}{1+{\sum }_{j=1}^{K}exp\{{\beta }_{0j}+m(h,x,z,\beta )\}}Q(h,\theta ).$$

Consider a sampling scenario where each subject from the underlying population is selected into the case-control study using a Bernoulli sampling scheme, where the selection probability for a subject given his/her disease status D = d is proportional to n_d/pr(D = d). Let R = 1 denote the indicator of whether a subject is selected in the case-control sample under the above Bernoulli sampling scheme.

Lobach, et al. (2008) proposed to use the following function in place of the likelihood function, that is to ignore the retrospective design and analyze the data as if it were coming from a random sample. The outlined above Bernoulli sampling connects the retrospective design employed to collect data and the pretend random sample scheme.

$$L_n(d,g,w,z,\mathcal{B},\xi )=\prod _{i=1}^n{L}_i(d,g,w,z,\mathcal{B},\xi );$$ (1)

where

$$L_i(d,g,w,z,\mathcal{B},\xi )=\text{pr}(D=d_i,W=w_i,\mathbf{G}=g_i\mid Z=z_i,R=1)=\frac{\int {\displaystyle \sum _{h^{\ast }\in {\mathscr{H}}_G}}S(d_i,h^{\ast },x,z_i,\mathrm{\Omega })f_{\text{mem}}(w_i\mid d_i,h^{\ast },x,z_i,\xi )f_X(x\mid z_i,\eta )dx}{\int {\displaystyle \sum _{d_{\ast }=0}^{K+1}}{\displaystyle \sum _{h_{\ast }\in \mathscr{H}}}S(d_{\ast },h_{\ast },x,z_i,\mathrm{\Omega })f_X(x\mid z_i,\eta )dx}.$$

Recall that S(d, h, x, z, Ω) is a product of the disease risk function and the density of a genetic variable; f_mem(w|d, h, x, z, ξ) defines the measurement error process; and f_X (x|z, η) is the density of environmental variables measured with error. Further, recall that 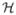is the set of all possible haplotypes, 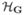- the set of all haplotypes consistent with the observed genotype G.

It was shown (Lobach, et al. 2008) that maximization of L_n, although not the actual retrospective-likelihood for case-control data, leads to consistent and asymptotically normal parameter estimates. Note that conditioning on Z in L_n allows it to be free of the nonparametric density function f_Z (z). In epidemiologic studies the vector of observations Z is likely to be multidimensional (e.g., age, bmi, race) hence this formulations allows gains of efficiency by not having to model parameters associated with these variables.

3. SEMIPARAMETRIC BAYESIAN ESTIMATION BASED ON PSEUDO-LIKELIHOOD

Since in our setting the retrospectively collected data is analyzed as if they were coming from a random sample, the function (1) is not a real likelihood function and hence the traditional Bayesian analysis is not technically correct. Conventional approaches to validity of posterior probability statements follow from the definition of the likelihood as the joint density of observations.

Monahan and Boos (1992) introduced a definition based on coverage of posterior sets that are constructed to contain the correct probability of including a parameter θ, if the underlying distribution of θ is the prior p(θ), and the model of data X f(X|θ) are correct. For example, in the one-dimensional case, the natural posterior coverage set functions are the one-sided intervals $I_{\alpha }^{\ast }=R_{\alpha }(X)=(-\infty ,{\theta }_{\alpha }^{\ast })$, where ${\theta }_{\alpha }^{\ast }$ is α-percentile of the posterior f(X|θ). Validity for such a posterior then means that all these intervals $I_{\alpha }^{\ast }$ have the correct coverage α. In practice it is often challenging to verify the required probability analytically. Monahan and Boos (1992) proposed a convenient numerical method. Briefly, define θ_k, k = 1, …, m to be a sample generated independently from a continuous prior p(θ) and for each θ_k let X^k denote a value generated from f(X|θ_k). Further, for each k define H_k to be a variable in the following form

$$H_k={\int }_{-\infty }^{{\theta }_k}f(\theta \mid X^k)d\theta .$$ (2)

This corresponds to posterior coverage set functions of the form (−∞, ${\theta }_{\alpha }^k$), where ${\theta }_{\alpha }^k$ is the αth percentile point of posterior density f(θ|X^k). Monahan and Boos (1996) argued that if the distribution of H_k fails to follow the uniform distribution for any prior, then the likelihood function cannot be a coverage proper Bayesian likelihood.

We propose to use the methodology described above to validate the likelihood function and apply conventional MCMC techniques to estimate parameters.

4. SEMIPARAMETRIC BAYESIAN ANALYSIS OF CASE-CONTROL DATA

The Bayesian modeling framework described above provides a conceptually elegant and general method to model gene-environment interactions. Practical implementation requires specification of a prior distribution and computations based on the corresponding posterior distribution. In this section we describe a Bayesian model including likelihood and prior distribution for two cases. The first scenario is based on a setting where all variables are binary. In the second case we model a continuous environmental covariate, e.g., calcium intake. Moreover, the genetic covariate is in the form of a haplotype. In both scenarios, we validate the likelihoods using ideas of Monahan and Boos (1992) as explained in the Section 3.

4.1 Genotype-based case-control studies

Within this setting we consider the case when the environmental covariates (X, W), genetic variant (G) and disease status (D) are binary. Let pr(G = 1) = θ, pr(X = 1) = η. This setting arises in the case when the genetic effect is recessive or dominant. Define the vector of risk parameters 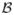= (β_x, β_g, β_xg)^T. Suppose that the genotype and environment are independent in the population but they do work together while causing a disease thus creating an interaction. Consider a multiplicative interaction and let m(x, g, 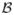) = β_g g + β_xx + β_xg xg. Make the following definition.

$$S(d,g,x,\mathcal{B},\theta )=\frac{exp[I_{(d\ge 1)}(d)\{{\kappa }_d+m(x,g,\mathcal{B})\}]}{1+exp\{{\beta }_0+m(x,g,\mathcal{B})\}}{\theta }^g{(1-\theta )}^{1-g}.$$

If W is an observed environmental covariate, denote the mis-classification probabilities as pr(W = 1|X = 0) = ξ₁ and pr(W = 0|X = 1) = ξ₀, hence the distribution of measurement error process f_mem(w|x, ξ₀, ξ₁) = {wξ₁ + (1 − w)(1 − ξ₁)}(1 − x)+ {w(1 − ξ₀) + (1 − w)ξ₀}x. In this situation W is, e.g. a smoking status reported by the study participant and X is the true long-term smoking exposure of interest. Note that, e.g., lung cancer patients who have the suspected risk factor (e.g., smoking) can blame this risk factor for causing the disease and therefore they are likely to over-report smoking, hence the misclassification probabilities can be differential in the disease status. In this case the measurement error process depends on disease status and misclassification probabilities need to be specified for cases and controls separately.

On the risk parameters we impose a Normal prior with mean 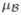and covariance matrix 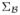. In the case when a massive amount of measurement error is present, the sampling distribution of risk parameter estimates is likely to be skewed (Shafer and Purdy (1996), Lobach, et al. (2008)).

But because the shape of the Normal distribution is symmetric, this prior is likely to bring the sampling distribution of the risk parameter estimates closer to Normal. For the frequency parameters η and θ we use noninformative Uniform(0, 1) priors. In this setting the prior information imposed on θ is non-informative. If a priori information is available about the genotype frequencies, it can be specified using a corresponding distribution or HWE.

Then the joint posterior distribution for the model unknowns is proportional to

$$\begin{array}{l}\prod _{i=1}^n\frac{{\displaystyle \sum _{x=0}^1}S(d_i,g_i,x,\mathcal{B},\theta )f_{\text{mem}}(w_i\mid x,{\xi }_0,{\xi }_1){\eta }^x{(1-\eta )}^{1-x}}{{\displaystyle \sum _{x=0}^1}{\displaystyle \sum _{d=0}^1}{\displaystyle \sum _{g=0}^1}S(d_i,g,x,\mathcal{B},\theta ){\eta }^x{(1-\eta )}^{1-x}}\\ \times {\mid {\mathrm{\sum }}_{\mathcal{B}}\mid }^{-1/2}exp\left\{-\frac{1}{2}{(\mathcal{B}-{\mu }_{\mathcal{B}})}^{\text{T}}{\mathrm{\sum }}_{\mathcal{B}}^{-1}(\mathcal{B}-{\mu }_{\mathcal{B}})\right\}\\ \times I_{(0,1)}(\eta )I_{(0,1)}(\theta ).\end{array}$$

4.2 Haplotype-based case-control studies

Within this setting we consider continuous environmental variables and assumed that the genetic risk depends on the number of copies of a putative haplotype. This setting is particularly useful in the situations when the available genetic information consists of a set of markers that are located closely to each other. The linkage disequilibrium (LD) is generally used to measure the degree of dependence between the genetic markers. When LD is high, the generic markers can be organized in the haplotype blocks according to the LD pattern. The continuous environmental variable can model dietary exposure, such as calcium intake, and X defines the true unobservable calcium intake, W - calcium intake measured using FFQ.

Suppose the true environmental exposure is distributed as Normal with mean μ_x and variance ${\sigma }_x^2$. On mean and variance of the environmental covariate we impose Normal(η₁, η₂) and IG(A, B) prior, respectively. Let θ_j be the frequency of haplotype j = 1, …, T, then the distribution of diplotypes in the population under consideration is specified using HWE. On all haplotype frequencies we impose a Uniform distribution. The true environmental covariate is not observable, instead W is subject to classic additive measurement error. The distribution of observed environmental covariate f_mem(w|x, ξ) is Normal with mean x and variance ξ. Note, however, that the methodology is general enough to model various types of measurement error including differential errors. Suppose h₁ is a reference haplotype, define 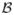= (β_x, β_h2, …, β_hk, β_xh2, …, β_xhk) to be vector of risk parameters. We use a Normal distribution with mean 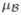and covariance matrix 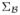as a prior distribution for 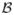. Denote N_j(H), j = 1, …, T to be the number of haplotypes h_j observed in a diplotype H. The function m(x, h, 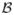) allows modeling various types of disease, such as additive, multiplicative, recessive, dominant, etc. Additionally, the risk of genotype, environment as well as their interaction are parameterized within this function. Consider a model of an additive disease status and multiplicative interaction defined as m(x, h, 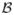) = β_xx + β_h2N₂(H) + ··· + β_hTN_T(H) + β_xh2xN₂(H) + ··· + β_xhTxN_T(H). Finally, define

$$S(d,h,x,\mathcal{B},\theta )=\frac{exp[I_{(d\ge 1)}(d)\{{\kappa }_d+m(x,h,\mathcal{B})\}]}{1+exp\{{\beta }_0+m(x,h,\mathcal{B})\}}Q(h,\theta ).$$

The joint posterior distribution becomes

$$\begin{array}{l}\propto \prod _{i=1}^n\frac{\int {\displaystyle \sum _{h^{\ast }\in {\mathscr{H}}_G}}S(d_i,h^{\ast },x,\mathcal{B},\theta )exp\{-\frac{{(w_i-x)}^2}{2\xi }-\frac{{(x-{\mu }_x)}^2}{2{\sigma }_x^2}\}\text{d}x}{\int {\displaystyle \sum _{d^{\ast }=0}^1}{\displaystyle \sum _{h^{\ast }\in \mathscr{H}}}S(d,h^{\ast },x,\mathcal{B},\theta )exp\{\frac{-{(x-{\mu }_x)}^2}{2{\sigma }_x^2}\}\text{d}x}\\ \times {\mid {\mathrm{\sum }}_{\mathcal{B}}\mid }^{-1/2}exp\left\{-\frac{1}{2}{(\mathcal{B}-{\mu }_{\mathcal{B}})}^{\text{T}}{\mathrm{\sum }}_{\mathcal{B}}^{-1}(\mathcal{B}-{\mu }_{\mathcal{B}})\right\}\\ \times {\eta }_2^{-1/2}exp\{-{({\mu }_x-{\eta }_1)}^2/(2{\eta }_2)\}{({\sigma }_x^2)}^{-A-1}exp(-B/{\sigma }_x^2)\\ \times \prod _{t=1}^T{I}_{(0,1)}({\theta }_t).\end{array}$$

We propose to validate the likelihood using ideas of Monahan and Boos (1992) and then apply conventional MCMC sampling techniques, such as Metropolis-Hastings algorithm to obtain the samples from the posterior for Bayesian inference.

5. ASYMPTOTIC POSTERIOR DISTRIBUTION

We now consider properties of an asymptotic posterior distribution based on the pseudo likelihood (1). MCMC techniques can be computationally challenging and knowing the form of an asymptotic posterior distribution would ease the computational burden.

Within this setting, for simplicity, we suppose that the parameter ξ that controls measurement error distribution is known, although this is not required. Denote Θ₀ and Θ̂_n to be values that maximize prior and pseudo-likelihood, respectively. Let Ψ(d, g, w, z, Θ, ξ) be the derivative of log{L_i(d, g, w, z, Θ, ξ)} with respect to Θ and

$$\mathrm{\Lambda }=\sum _d\frac{n_d}{n}\text{E}\{\mathrm{\Psi }(D,G,W,Z,\mathrm{\Omega },\eta ,\xi )\mid D=d\}\times \text{E}{\{\mathrm{\Psi }(D,G,W,Z,\mathrm{\Omega },\eta ,\xi )\mid D=d\}}^{\text{T}}.$$

Further, if p(Θ) is the prior distribution of the vector of parameters, define l(Θ) to be the derivative of log{p(Θ)} with respect to Θ. Then define ${\mathcal{L}}_n(\mathrm{\Theta },\xi )={\sum }_{i=1}^n\mathrm{\Psi }(D_i,G_i,W_i,Z_i,\mathrm{\Theta },\xi )$ and matrices $\mathcal{I}(\mathrm{\Theta })=-\text{E}[\frac{\partial \{{\mathcal{L}}_n(\mathrm{\Theta },\xi )\}}{\partial (\mathrm{\Theta })}]$ and $\mathcal{J}(\mathrm{\Theta })=-\text{E}[\frac{\partial \{l(\mathrm{\Theta })\}}{\partial (\mathrm{\Theta })}]$. The following theorem and its heuristic proof motivated by Bernardo and Smith (1994) concerns limiting properties of the posterior distribution.

Theorem 1

Under suitable regularity conditions the posterior distribution of vector of parameters Θ̂_n converges to a Normal distribution with covariance matrix consistently estimated by Σ̂_n = {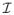(Θ̂_n) + J(Θ₀)}⁻¹ and mean vector ${\widehat{ℳ}}_n={\widehat{\mathrm{\sum }}}_n^{-1}\{\mathcal{I}({\widehat{\mathrm{\Theta }}}_n){\widehat{\mathrm{\Theta }}}_n+\mathcal{J}({\mathrm{\Theta }}_0){\mathrm{\Theta }}_0\}$.

Proof

Note that the posterior distribution of the vector of parameters Θ given data X can be written as

$$f(\mathrm{\Theta }\mid X)\propto p(\mathrm{\Theta })L_n(\mathrm{\Theta })=exp[log\{p(\mathrm{\Theta })\}+log\{L_n(\mathrm{\Theta })\}].$$

Let Θ₀ and Θ̂_n be maxima of the prior p(Θ) and pseudo-likelihood function L_n(Θ), respectively. They can be obtained by solving l(Θ) = 0 and 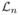(Θ) = 0. Under suitable regularity conditions which ensure that the remainder terms of the following expansion are small for large n, the logarithm of the prior and pseudo-likelihood function can be expanded around their maxima in the following manner.

$$\begin{array}{l}log\{p(\mathrm{\Theta })\}=log\{p({\mathrm{\Theta }}_0)\}-1/2{(\mathrm{\Theta }-{\mathrm{\Theta }}_0)}^{\text{T}}\mathcal{J}({\mathrm{\Theta }}_0)(\mathrm{\Theta }-{\mathrm{\Theta }}_0);\\ log\{L_n(\mathrm{\Theta })\}=log\{f(X\mid {\widehat{\mathrm{\Theta }}}_n)\}-1/2{(\mathrm{\Theta }-{\widehat{\mathrm{\Theta }}}_n)}^{\text{T}}\mathcal{I}({\widehat{\mathrm{\Theta }}}_n)(\mathrm{\Theta }-{\widehat{\mathrm{\Theta }}}_n).\end{array}$$

Hence

$$f(\mathrm{\Theta }\mid X)\propto exp\{-1/2{(\mathrm{\Theta }-{\mathrm{\Theta }}_0)}^{\text{T}}\mathcal{J}({\mathrm{\Theta }}_0)(\mathrm{\Theta }-{\mathrm{\Theta }}_0)\}\times exp\{-1/2{(\mathrm{\Theta }-{\widehat{\mathrm{\Theta }}}_n)}^{\text{T}}\mathcal{I}({\widehat{\mathrm{\Theta }}}_0)(\mathrm{\Theta }-{\widehat{\mathrm{\Theta }}}_n)\}.$$

Further, it can be easily seen that for large sample sizes

$$f(\mathrm{\Theta }\mid X)\propto exp\{-1/2{(\mathrm{\Theta }-ℳ)}^{\text{T}}{\mathrm{\sum }}^{-1}(\mathrm{\Theta }-ℳ)\}.$$

Remark 1

The development of Theorem 1 suggests that the posterior based on a pseudo-likelihood function has asymptotic distribution that is the same as Normal with mean that is equal to the weighted average of a maximum pseudo-likelihood estimate and a value that maximizes prior. The precision of this distribution is the sum of the observed information matrix and the prior precision matrix. These considerations suggest one approximation, namely if for large n the prior precision tends to be small compared to the precision provided by the data, it can be ignored.

Remark 2

It can be easily seen that n⁻¹∂{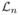(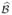, ξ)}/∂ 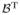is a consistent estimate of 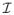(Θ). Alternatively, if Σ̂ is the sample covariance matrix of the terms Ψ(D_i, G_i, W_i, Z_i, 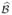, ξ), then Σ̂ + Λ̂ consistently estimates 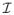(Θ).

Remark 3

When the sample size is large, we can use this asymptotic posterior distribution for validation purpose rather than using the MCMC based approach. That way, we can reduce the computation burden significantly.

Remark 4

If the parameter ξ controlling the measurement error distribution is unknown, additional data are necessary to estimate it. Consider the case of additive mean-zero measurement error with replications of W. Suppose that there are at most M replications of the W for any individual. Let W_i denote this ensemble of the M replicates, and let m_i be the number of replicates we actually observe. Let f_mem(w|d, h^dip, x, z, m, ξ) be the joint density of the first m replicates for m = 1, …, M; Ψ(D, G, W, Z, Ω, η, ξ, j), 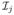, and Λ_j be matrices defined earlier for the case with exactly m = j replicates for each individual. Assume that m_i is independent of (D_i, W_i, Z_i, G_i, X_i, $H_i^{\text{dip}}$) and that pr(m_i = j) = p(j). Further, define $\mathcal{I}={\sum }_{j=1}^{M}p(j){\mathcal{I}}_j$. Then Lobach, et al. (2008) showed that the estimating function for 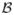= (Ω^T, η^T, ξ^T)^T can be written in the form

$$0=\sum _{i=1}^n\sum _{j=1}^M{I}_{(m_i=j)}(m_i)\mathrm{\Psi }(D_i,G_i,W_i,Z_i,\mathrm{\Omega },\eta ,\xi ,j).$$

and the corresponding consistent sequence of solutions is

$$n^{1/2}(\widehat{\mathcal{B}}-{\mathcal{B}}_0)\Rightarrow \text{Normal}\left[0,{\mathcal{I}}^{-1}\left\{\mathcal{I}-\sum _{j=1}^{M}p(j){\mathrm{\Lambda }}_j\right\}{\mathcal{I}}^{-1}\right].$$

The result of Theorem 1 can be readily applied to this situation when measurement error distribution is estimated using replications. Consistent estimates of 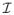and Λ_j can be obtained by applying formulas that are analogous to those outlined in the Remark 2.

6. SIMULATION EXPERIMENTS

To illustrate performance of the proposed methodology, we performed two simulation studies. First, we compared performance of the proposed Bayesian approach to the pseudo-MLE using genotype-based setting. In this setting all variables are categorical. Further, we investigated properties of estimation and inference based on the derived form of the Asymptotic Posterior distribution (Theorem 1) and its approximation discussed in Remark 1. This analysis does not require MCMC computations, instead it is uses a derived form of the Asymptotic Posterior Distribution.

6.1 Genotype-based case-control studies: Proposed Bayesian analysis vs. pseudo-MLE approach

We performed a series of simulation experiments to illustrate our approach in the setting of genotype-based case-control study.

We assumed that environmental variables (X, W), genetic variant (G), and disease status (D) are binary. Given the values of (G, X) we generated a binary disease outcome D from the logistic model logit{pr(D|G, X)} = β₀ + β_xX + β_gG + β_xg X * G, with parameters (β_x, β_g, β_xg) = (1.099, 0.693, 0.693). This setting arises in the presence of recessive or dominant effect. The misclassification probabilities were pr(W = 0|X = 1) = 0.10 and pr(W = 1|X = 0) = 0.15. The probability of disease in this setting is 0.016 and we assumed it is known in the population. We investigated the case of small (n₀ = n₁ = 200) and large (n₀ = n₁ = 1, 000) sample sizes.

First, it is necessary to validate the likelihood function. We validated coverage of the pseudo-likelihood function using ideas described in Monahan and Boos (1992) for numerous scenarios by setting different values of prior parameters, as well as varying sample size and misclassification probabilities. It was challenging to compute H_k using (2) since it requires calculations with multiple precision. We addressed this challenge by using the General Multiple Precision library in C. Further, the vector of parameters is 5-dimensional and since integration in (2) requires computations with high precision and high-dimensional integration is not feasible, we verified coverage probabilities of each parameter when all others are fixed at their posterior mean. For all cases we considered the Kolmogorov-Smirnov test failed to reject the null hypothesis that the sample H_k comes from the Uniform(0, 1) distribution at 0.05 significance level.

Since the likelihood function was validated, we proceeded to parameter estimation using the Metropolis-Hastings algorithm with the following settings. On the risk parameters 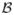we imposed a Normal(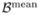, 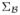) prior, where 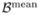= (0, 0, 0) and covariance matrix 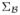= diag(3², 3², 3²). Note that in this setting reflects no a priori knowledge about the risk and mean of the prior distribution is conservatively set to be zero. The only prior information that we are imposing is that the shape of the distribution is symmetric to bring the sampling distribution of the parameter estimates closer to Normal. On both η and θ we imposed a Uniform(0, 1) prior. The a priori information specified on the frequency parameter θ is non-informative in this setting. If an estimate about genotype frequencies is available, it can be used while specifying the distribution. The proposal distribution of the new value 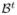given the current 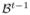was set to be Normal(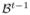, Σ^prop), where Σ^prop = diag(0.05², 0.05², 0.05²). Proposal distribution of a new value of θ^t given θ^t−1 was chosen to be Uniform(θ^t−1 − 0.05, θ^t−1 + 0.05). The proposal distribution for η has the same form as that for θ.

Proposed Bayesian approach and Pseudo-MLE

The simulation results presented in Table 1 illustrate that for a small sample size the proposed Bayesian approach produced parameter estimates that are less biased and less variable than the estimates obtained using pseudo-MLE approach. Moreover, distribution of the parameter estimates obtained using pseudo-MLE is skewed, while our simulations illustrated that the distribution of parameter estimates produced using our methodology is close to symmetric, when illustrating the ability of Bayesian methodology to shrink toward prior. In case of a large sample size, the proposed methodology resulted in parameter estimates that are nearly unbiased with RMSEs that are considerably smaller than the RMSEs of the pseudo-MLE approach.

Table 1.

Biases and Root Mean Squared Errors (RMSEs) for the proposed Bayesian and Pseudo-MLE approaches in a genotype-based case-control study. Genetic (G) and environmental (X) factors are binary with pr(G = 1) = 0.5 and pr(X = 1) = 0.5. pr(D = 1) = 0.016 is assumed to be known in the underlying population. Misclassification probabilities are pr(W = 1|X = 0) = 0.15 and pr(W = 0|X = 1) = 0.10. The results is based on 500 replications of n₁ cases and n₀ controls

			Proposed Bayesian Analysis		Pseudo-MLE
	Parameter	True Value	Bias	RMSE	Bias	RMSE
n0 = 200	βx	1.099	−0.007	0.229	0.023	0.339
n1 = 200	βg	0.693	−0.075	0.336	−0.195	1.023
	βxg	0.693	0.103	0.461	0.217	1.064
	θ	0.500	−0.002	0.002	−0.001	0.021
	η	0.500	−0.005	0.003	0.001	0.048
n0 = 1, 000	βx	1.099	−0.003	0.095	0.005	0.155
n1 = 1, 000	βg	0.693	−0.021	0.162	−0.004	0.305
	βxg	0.693	0.029	0.206	0.001	0.327
	θ	0.500	−0.001	0.001	0.000	0.008
	η	0.500	−0.001	0.001	0.002	0.022

In the case of massive measurement error, which is the case in our motivating example and simulation experiments, the finite sample distribution of parameter estimates can be skewed (Schafer and Purdy, 1996). We observed this phenomena in Lobach, et al. (2008) and our simulation studies. Hence one of the major advantages of the proposed Bayesian solution is that a symmetric prior can help to bring the finite sample distribution of the parameter estimates closer to Normal.

Rare genotype

To investigate performance of the proposed method in the rare genotype case, we performed the following simulation experiment. Genetic and environmental variables, disease status and measurement error were simulated using setup described above. However, the genotype frequency was set up to be θ = 5%, 2.5%. On the genotype frequencies we imposed Beta(A, B) distribution with parameters A = 5, B = 95 and A = 3, B = 97 for the case of genotype frequency 5% and 2.5%, respectively. These distributions have means that are equal to the true values and support indicating that the genotypes are rare. Table 2 presents simulation results. Pseudo-MLE estimation resulted in genotype frequency estimates that have elevated bias and larger variability. As a result, interaction parameter estimates and main effects of genotype are largely biased. The proposed Bayesian approach produced nearly unbiased estimates and have smaller variability. The sampling distribution of risk parameter estimates obtained using the pseudo-MLE method was heavily skewed, however that of our Bayesian estimates was closer to Normal. This demonstrates the ability of Bayesian approach with symmetric prior to bring posterior estimates closer to Normal.

Table 2.

Biases and Root Mean Squared Errors (RMSEs) of the proposed Bayesian and Pseudo-MLE approaches in a genotype-based case-control study when genotype is rare. Genetic (G) and environmental (X) factors are binary with pr(G = 1) = 0.05, 0.025 and pr(X = 1) = 0.5. pr(D = 1) = 0.0148, 0.0140 are assumed to be known. Misclassification probabilities are pr(W = 1|X = 0) = 0.15 and pr(W = 0|X = 1) = 0.10. The results is based on 500 replications of 1, 000 cases and 1, 000 controls

		Proposed Bayesian Analysis		Pseudo-MLE
Parameter	True Value	Bias	RMSE	Bias	RMSE
βx	1.099	0.011	0.257	0.003	0.311
βg	0.693	−0.010	0.318	−0.269	1.379
βxg	0.693	0.004	0.336	0.434	1.473
θ	0.050	−1.6 × 10−4	0.039	0.001	0.044
η	0.500	0.001	0.005	−0.007	0.011
βx	1.099	0.010	0.343	0.006	0.303
βg	0.693	−0.003	0.353	−0.470	1.853
βxg	0.693	0.010	0.039	0.607	1.907
θ	0.025	−1.9 × 10−4	0.026	0.001	0.044
η	0.500	−0.030	0.002	−0.025	0.028

6.2 Haplotype-based case-control studies: Analysis based on asymptotic posterior distribution

Following the simulation setup of Lobach, et al. (2008), we considered a continuous environmental variables and assumed that the genetic risk depends on the number of copies of a putative haplotype. We simulated the true environmental covariate (X) from a Normal distribution with zero mean and variance 0.1. To simulate observed environmental variables, we used an additive model of the form W = X + U, where U is generated from the Normal distribution with zero mean and variance ξ = 0.25. Note that we are simulating a case of large measurement error, such as would occur for dietary measurements. This gives a stern test for our methodology.

Given the haplotype frequencies (h₁, h₂, h₃, h₄, h₅, h₆) = (0.25, 0.15, 0.25, 0.1, 0.1, 0.15) we generated diplotypes for each subject under the assumption of Hardy-Weinberg Equilibrium. Then we coded haplotype h₃ as 1 and all the rest as 0. Given the diplotype information H^dip and environmental covariate X we generated binary disease status according to the following model

$$\text{pr}(D=d\mid H^{\text{dip}},X)=\frac{exp[d\{{\beta }_0+{\beta }_{x}X+{\beta }_g{N}_3(H^{\text{dip}})+{\beta }_{xg}X{N}_3(H^{\text{dip}})\}]}{1+exp\{{\beta }_0+{\beta }_{x}X+{\beta }_g{N}_3(H^{\text{dip}})+{\beta }_{xg}X{N}_3(H^{\text{dip}})\}]},$$

where N₃(H^dip) is the number of copies of h₃ in H^dip. In this setting we are interested in estimating the relative risk parameters and the frequency of haplotype h₃. For the sake of computational time we assumed that the probability of disease is known. Moreover, we assessed the effect of missing data by assuming that 50% of subjects were not genotyped and for those who were genotyped, the phase is unknown.

The pseudo-likelihood function validated in a similar way as has been described in the discrete situation. Results presented in the Table 3 are based on the estimates obtained using an approximation derived in the Theorem 1. Analysis of the simulation results presented in the Table 3 suggests that the proposed methodology resulted in parameter estimates that are nearly unbiased. Moreover, estimated variances of parameter estimates are very close to observed values, with one exception, namely β_x. This is due to the fact that when a large amount of measurement error is present in the data, parameter estimates can have skewed distributions even for large sample sizes.

Table 3.

Proposed Bayesian Analysis of a haplotype-based case-control study. Biases, Standard Errors (SE) of the estimates, and estimated SEs based on derived asymptotic posterior distribution (Theorem 1). The analysis is performed on the observed data combined with the prior information and the observed data only (see Remark 1). The results are based on a simulation study with 300 replications for 1,000 cases and 1,000 controls, where disease status (D) is binary, environmental variable (X) is Normal with variance 0.1 and the genetic variant h₃ is in the form of diplotype with a multiplicative interaction. The environmental variable is measured with error and the error variance is 0.25. Genotype is missing for 50% of the subjects and when it is observed, haplotype-phase ambiguity is present. The ^★ed value indicates 10%-trimmed estimate, ^†ed – 2%-trimmed estimates

		Observed Data and Prior Information			Observed Data Only
Parameter	True Value	Bias	SE	Estimated SE	Bias	SE	Estimated SE
βx	1.099	0.0215	0.0942★	0.0726	0.0201	0.0856	0.1108†
βg	0.693	−0.0058	0.0023	0.0025	−0.0003	0.0064	0.0026†
βxg	0.693	−0.0201	0.0528	0.0544	−0.0186	0.0972	0.0742†
θ	0.500	0.0006	0.0001	0.0001	0.0005	0.0004	0.0000†
η1	0.000	−0.0027	0.0010	0.0009	0.0016	0.0005	0.0003†
η2	0.100	0.0000	0.0001	0.0002	−0.0009	0.0002	0.0003†

Additionally we investigated an approximation discussed in the Remark 1. To recap, the Theorem 1 illustrates that the asymptotic precision is the sum of a precision provided by the observed data and prior precision matrix. Similarly, asymptotic mean is the weighted average of a maximum pseudo-likelihood estimate and a value that maximizes prior. The results presented in Table 3 are based on an approximation that ignores the prior precision and the covariance matrix is constructed using precision provided by the observed data only. Inspection of the results suggests that parameter estimates are unbiased and estimated standard errors are close to the observed standard errors. However, the SE of estimates are generally larger than the SE of estimates obtained with the use of prior information. Recall that in this case the only prior information induced in the model is on the shape of the parameter estimates distribution. And this information helped to bring sampling distribution of the parameter estimates closer to Normal thus reducing the variability and making the inferences more precise. Note, however, that absolute values of biases of parameter estimates in the case when prior information is used are generally slightly larger. The reason is that the the prior mean of the risk parameter estimates is zero, and hence it forces underestimation of risk parameters. In summary, we demonstrated that approximation derived in Theorem 1 can work well in practice and that a symmetric prior can improve inferences.

7. COLORECTAL ADENOMA STUDY

7.1 Modeling

Here we analyze the colorectal adenoma study data described above. To recap, there were 772 cases and 778 controls, the response D was colorectal adenoma status, the genetic data observed were three SNPs in the calcium receptor gene CaSR, the environmental variable X measured with error was log(1+calcium intake), which was measured by W, the result of a food frequency questionnaire. The variables Z measured without error were age, sex and race. The possible haplotypes in the data were ACG, ACT, AGG, GCG, AGT, GGG, and GCT. Since haplotypes AGT, GGG, GCT are rare, we pooled them with the next most common haplotype AGG. The distribution of haplotype frequencies is not significantly deviating from the HWE. A few subjects do not have measurements of calcium intake and we eliminated them from the analysis.

Given calcium intake (X) and diplotype information (H^dip) we considered the following risk model

$$\text{logit}\{\text{pr}(D=1\mid H^{\text{dip}},X)\}={\beta }_0+{\beta }_x\ast X+{\beta }_{h2}\ast N_2(H^{\text{dip}})+{\beta }_{h4}\ast N_4(H^{\text{dip}})+{\beta }_{h5}\ast N_5(H^{\text{dip}})+{\beta }_{xh2}\ast X\ast N_2(H^{\text{dip}})+{\beta }_{xh4}\ast X\ast N_4(H^{\text{dip}})+{\beta }_{xh5}\ast X\ast N_5(H^{\text{dip}}),$$

where N₂(H^dip) is the number of haplotypes ACT observed in a diplotype, N₄(H^dip) is the number of haplotypes GCG observed in a diplotype and N₅(H^dip) is number of haplotypes AGG, AGT, GGG, or GCT observed in a diplotype.

Using an external data set, Lobach et al. (2008) estimated the measurement error distribution and found that W = 0.22 + 0.75X + u, where ${\widehat{\sigma }}_u^2=\widehat{\xi }=0.65$. To assess sensitivity to the measurement error model specification, we considered several scenarios by imposing measurement error structure estimated using an external data and varying it through ${\sigma }_u^2$.

7.2 Estimation

To estimate parameters we employed Metropolis-Hastings algorithm with the following setting. Denote 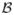to be the set of risk parameters, Θ to be the vector of haplotype frequencies and η to be parameters of the environmental covariate. Define 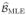, Θ̂_MLE, and η̂_MLE to be the set of estimates obtained using pseudo-MLE. We performed the analysis based on zero-mean priors for the risk parameters and obtained almost identical results. On the risk parameters we imposed Normal(0, 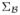) prior where 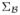is 8 × 8 diagonal matrix with elements 3². For the haplotype frequencies we used Uniform(Θ̂ − 0.5, Θ̂ + 0.5). Mean of the environmental covariate was chosen to follow $\text{Uniform}({\widehat{{\eta }_1}}_{\text{MLE}},{\sigma }_{{\eta }_1}^2)$ distribution, where ${\sigma }_{{\eta }_1}^2=1$. On the variance of the environmental covariate η₂ we imposed Inverse Gamma (IG) prior. Since we considered several scenarios by assuming various measurement error variances, we set the values of the IG distribution such that the mean of the IG distribution is equal to the pseudo-MLE estimate of the variance η₂. The proposal density of the new values 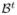given the current value 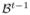is $\text{Normal}({\mathcal{B}}^{t-1},{\mathrm{\sum }}_{\mathcal{B}}^p)$, where ${\mathrm{\sum }}_{\mathcal{B}}^p$ is a 8 × 8 diagonal matrix with elements 0.5². The proposal distribution of a new value ${\eta }_1^t$ given the current ${\eta }_2^{t-1}$ is $\text{Normal}({\eta }_1^{t-1},1)$. The proposal value of the haplotype frequencies is simulated from the Uniform(Θ^t−1 − D_Θ, Θ^t−1 + D_Θ) distribution, where D_Θ is 0.01 for common and 0.001 for rare haplotypes. The proposal density for a new value ${\eta }_2^t$ given the current ${\eta }_2^{t-1}$ is IG distribution with parameters $5/{\eta }_2^{t-1}$ and 5 chosen so that the mean of the IG distribution is equal to the current value ${\eta }_2^{t-1}$.

7.3 Results

The four sets of parameter estimates presented in the Table 5 correspond to different values of measurement error variance. These results illustrate the importance of assessing the measurement error, since its incorrect specification results in substantial bias. Table 4 resents 95% posterior credible intervals obtained based on MCMC sampling. We also performed the analysis based on an asymptotic posterior distribution (not shown here). Both parameter estimates and credible intervals based on the asymptotic posterior are very close to those obtained using MCMC sampling.

Table 5.

Bayesian estimates of the Colorectal Adenoma Data risk parameters for various values of the measurement error variance (ξ). Results are based on the last 5,000 of 100,000 iterations of the Metropolis-Hastings algorithm. The estimated error variance is ξ̂ = 0.65

Parameter	ξ = 0.10	ξ = 0.60	ξ = 0.65	ξ = 0.70
κ	0.054	0.024	0.025	0.018
βx	−0.067	−0.141	−0.140	−0.179
βh2	−0.198	−0.182	−0.175	−0.144
βh4	−0.229	−0.361	−0.416	−0.522
βh5	−0.366	−0.652	−0.752	−0.932
βxh2	0.028	0.085	0.102	0.123
βxh4	−0.157	−0.467	−0.590	−0.756
βxh5	−0.239	−0.724	−0.887	−0.818

Table 4.

Proposed 95% Credible Intervals of the risk estimates in the Colorectal Adenoma Data. Results are based on the last 5,000 of 100,000 iterations of the Metropolis-Hastings algorithm. The estimated error variance is ξ̂ = 0.65

	ξ = 0.10	ξ = 0.60	ξ = 0.65	ξ = 0.70
κ	(−0.173, 0.280)	(−0.217, 0.215)	(−0.172, 0.244)	(−0.144, 0.233)
βx	(−0.269, 0.125)	(−0.324, 0.017)	(−0.367, 0.080)	(−0.360, 0.058)
βh2	(−0.410, 0.015)	(−0.365, −0.010)	(−0.365, 0.032)	(−0.337, 0.040)
βh4	(−0.451, −0.038)	(−0.612, −0.252)	(−0.622, −0.244)	(−0.642, −0.263)
βh5	(−0.544, −0.157)	(−0.938, −0.528)	(−0.946, −0.583)	(−0.933, −0.592)
βxh2	(−0.163, 0.211)	(−0.079, 0.294)	(−0.094, 0.290)	(−0.101, 0.274)
βxh4	(−0.334, 0.029)	(−0.731, −0.357)	(−0.806, −0.380)	(−0.789, −0.411)
βxh5	(−0.431, −0.019)	(−1.135, −0.692)	(−1.088, −0.662)	(−1.051, −0.711)

We examined the posterior distribution of risk parameter estimates, including the gene-environment interaction parameters. The distribution of the estimates was roughly Normal (data not shown), which illustrated the ability of prior information to bringing the sampling distribution of parameter estimates to symmetric.

Inspection of the credible intervals reveals that for all measurement error specifications presented in the Table 4 parameters β_xh4 and β_xh5 are significantly different from 0 at the 0.05 significance level. This indicates that there is sufficient evidence to conclude that among carriers of h₄ and h₅ increased calcium intake is associated with decreased risk of colorectal tumor development.

Comparison of results for small (ξ = 0.10) and large (ξ = 0.60, 0.65, 0.70) amounts of measurement error illustrates that ignoring measurement error leads to biased estimates and possibly incorrect inferences. For example, the interaction parameter β_xh4 is announced to be not significantly different from zero when error variance is set to be small. However when the measurement error is properly accounted for and the error variance is set to be the value that was estimated from an external dataset, the interaction parameter β_xh4 is announced to be significant. Further, sensitivity analysis illustrated that when the measurement error variance is close to what was estimated, the conclusion about the risk defined by β_xh4 did not change.

8. DISCUSSION

We proposed a Bayesian methodology for analysis of gene-environment interactions using interaction and using population based case-control data. A key aspect of our method is that retrospectively collected data is analyzed as a random sample allowing gains of efficiency in parameter estimates (Lobach, et al., 2008). Because the analysis is based on a pseudo-likelihood function, the conventional Bayesian machinery may not be applied directly.

The Bayesian approach allows prior information about risk parameter estimates to enter the estimation and inference procedures, which is particularly useful in the case of massive measurement error. In this case even for large samples the sampling distribution of risk parameter estimates can be skewed and hence inferences that use Normality assumption are not precise. A symmetric distribution helps shrink towards the prior and hence make the sampling distribution of the estimates be closer to Normal, thus improving inferences.