Abstract
CVSim is a lumped-parameter model of the human cardiovascular system that has been developed and used for research and for teaching quantitative physiology courses at MIT and Harvard Medical School since 1984. We present a brief historical background of lumped-parameter cardiovascular system models, followed by an overview of the development of the major versions of CVSim over a 25-year period in our laboratory. We describe the features and differences of four versions of CVSim that are freely available in open-source form via PhysioNet (http://physionet.org). These include a six-compartment cardiovascular model with an arterial baroreflex system, implemented in C for efficiency, with an X-based graphical user interface; a six-compartment model with a more extensive short-term regulatory system and incorporating resting physiologic perturbations, available as a stand-alone MATLAB application; and a pair of elaborated versions consisting of 6- and 21-compartment computational models implemented in C, with a separate and enhanced Java graphical user interface. We conclude with a discussion of the educational and research applications for which we have used CVSim.
Keywords: Cardiovascular, system model, teaching, research
INTRODUCTION
Computational models of the cardiovascular system have captured the interest of many over the past several decades [1]. As with any type of physiologic model, these in silico representations of cardiovascular physiology can serve a number of useful purposes. First and foremost, development of cardiovascular simulators can permit precise assessment of the level of understanding of system behavior. That is, the degree of correspondence between the simulator predictions and experimental observations reflects quantitatively how well the relevant aspects of system behavior are captured by the mathematical representation and thus understood. Cardiovascular simulators can also enhance teaching of the underlying physiology by providing students with the ability to manipulate the parameters of the system and thereby discover the functional relationships among the various physiologic components. One can argue that allowing students to explore physiology through simulation is not merely an advantage but a necessity for developing a deep understanding of the behavior of complex (closed-loop, non-linear, controlled, interacting) organ systems. The in silico systems are especially effective as pedagogical tools when coupled with intuitive graphical user interfaces. In addition to their value in teaching, cardiovascular simulators can facilitate research by yielding new hypotheses based on the numerical predictions that may be tested experimentally. Such a combined theoretical and experimental research approach has the potential to expedite the introduction of more effective cardiovascular diagnostics, patient-monitoring modalities, and therapies. Cardiovascular simulators based on open-source software in particular could obviously accelerate development and consequently the success of these various applications.
For 25 years, we – along with other colleagues – have put forth considerable effort in the development and application of a human cardiovascular simulator that we call “CVSim.” Initially, we constructed CVSim to represent six major circulatory compartments in terms of a lumped-parameter model. Thereafter, we extended CVSim in several different ways including incorporation of models of reflex arcs and system perturbations as well as coupling the models to user-friendly graphical interfaces. Today, four open-source versions of CVSim are readily available via the Internet. Our original intent for CVSim was to complement traditional classroom teaching of quantitative cardiovascular physiology. We have indeed used versions of CVSim extensively for this particular application both at MIT and at Harvard Medical School. More recently, we have applied versions of CVSim to address several different avenues of research.
In this paper, we present an overview of our longstanding work on CVSim. We specifically discuss its origins and history, outline the open-source versions that are available while highlighting their differences, and describe how we have used it in teaching as well as research. We conclude with summary remarks.
HISTORY
As early as 1959, Grodins [2] developed a cardiovascular system model based on electrical circuit components, beginning with the ventricles, then adding a pulmonary circuit, and finally a systemic circuit to obtain a closed-loop model with fourteen parameters. Defares, Osborne, and Hara [3] designed a simplified 6-compartment circulation model in which each compartment was a capacitor connected to ground, and also to the two adjacent nodes by impedances; current (flow) through the ventricular compartments was regulated by diodes representing valves. Defares and his colleagues implemented their model using discrete analog components to build an electric circuit analog computer for simulating hemodynamics, with real-time behavior grossly similar to that observed in vivo in humans.
Katz and colleagues [4] were able to achieve real-time digital simulation of a much simpler Windkessel model in 1978, using a FORTRAN program running on a PDP-12, with output via D/A converters to a polygraph recorder. The greater flexibility afforded by digital computer programs over analog circuit models allowed students to vary heart rate, stroke volume, total peripheral resistance, compliance, and valve competence. This hands-on experience, reported Katz, led to overwhelming student enthusiasm for the program.
In 1982, Campbell and colleagues [5] implemented a 5-compartment closed cardiovascular system model of canine hemodynamics, using a Hewlett-Packard 1000 computer equipped with an XY plotter. Campbell’s model was similar to that of Defares, but included time-varying capacitances as in earlier work by Suga and Sagawa [6]; because of its complexity, it ran considerably more slowly than real-time in the available hardware.
At MIT, interest in moving computing into the classroom led to the creation of Project Athena [7] in 1983. Athena was a hugely ambitious project to establish a first-class distributed computing system for undergraduate engineering students, at a time when no such systems existed. Athena still exists today as the primary computing environment at MIT; among its better-known products are the X Window System for networked graphics and the Kerberos security system.
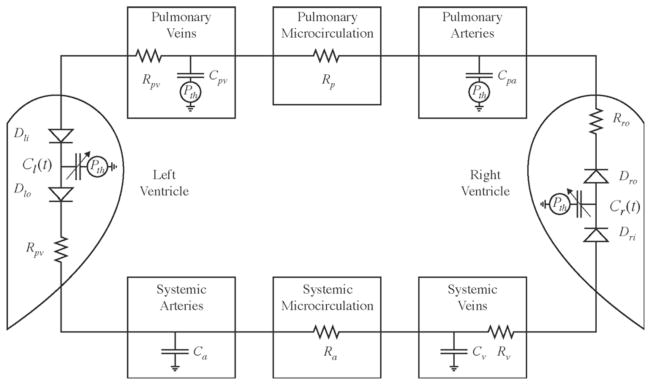
The first version of CVSim, based on the model of Defares and closely resembling the work of Campbell, was developed by Robert Sah in 1983 as an MIT UROP (Undergraduate Research Opportunities Program) project under the supervision of Roger Mark. Fig. (1) illustrates the six-compartment circuit model introduced by CVSim. Two compartments represent the left and right ventricles using time-varying capacitors connected via diodes representing heart valves. The other four compartments correspond to systemic and pulmonary arteries and veins, modeled using linear capacitors and resistors corresponding to the compliance and resistance of the vasculature segments. George Moody rewrote the simulation routines for numerical stability, and portions of the graphical user interface to support available graphics terminals, in the course of porting CVSim to Athena in 1984, predating the first version of the X Window System.
Fig. 1.
Circuit diagram of Sah’s lumped parameter hemodynamic model. Counterclockwise blood flow (electrical current) is driven by contraction of the ventricles (time-varying capacitors). Redrawn from Davis [Davis-1991].
Timothy Davis rewrote significant parts of CVSim in 1991 [8], adding a baroreceptor reflex model using a finite impulse response proportional controller, and a new graphical user interface using the X Window System; he also established solid experimental bases for the model parameters. George Moody made minor changes to this version while porting it to Linux in 1998, and renamed it XCVSim.
Initially, CVSim was conceived exclusively as a teaching tool. Starting in the late 1990s, Thomas Heldt and Eun Bo Shim – and independently Ramakrishna Mukkamala – adapted CVSim for research purposes. Much of their adaptations are outlined below. In 2005, Catherine Dunn rewrote the graphical user interface for two versions of CVSim in Java and made these versions available via the PhysioNet website ([9]; http://physionet.org/).
AVAILABLE VERSIONS
Up to now, we have made four versions of CVSim available via PhysioNet. Each version offers different extensions to the original lumped-parameter circulatory model and/or distinct user interfaces and generally includes commented source code, executables for multiple platforms, and user instructions (see Table 1).
Table 1.
Comparison of CVSim Versions Available from PhysioNet
| XCVSim | RCVSim | CVSim-6 | CVSim-21 | |
|---|---|---|---|---|
| Circulation model | Linear lumped-parameter | Nonlinear lumped-parameter | Linear lumped-parameter | Nonlinear venous pressure-volume relationships |
| Compartments | 6 | 6 | 6 | 17 vascular compartments, 4 cardiac compartments, 1 interstitial compartment |
| Control model | Arterial baroreflex | Short-term regulation | Arterial baroreflex | Short-term regulation |
| Other model features | Realistic parameters | Resting perturbations | Realistic parameters | Orthostatic stress test simulations |
| Progammable parameter changes | No | Yes | No | No |
| Library of simulated “patients” | Yes | No | Yes | No |
| User interface | X11 GUI | Command-line (text) interface; scripting | Java GUI | Java GUI |
| Plotting and printing | Integrated | External, via WAVE and gnuplot | Integrated | Integrated |
| Output can be stored | No | Yes | No | No |
| Software sources | C | MATLAB | Model in C GUI in Java | Model in C GUI in Java |
| Needed to create executables | ANSI/ISO C compiler, Xt library | MATLAB | ANSI/ISO C compiler, Sun Java SDK | ANSI/ISO C compiler, Sun Java SDK |
| Precompiled executables on PhysioNet | GNU/Linux | GNU/Linux | GNU/Linux, Mac OS X, Windows | None |
| URL | http://physionet.org/physiotools/cvsim | |||
XCVSim
XCVSim (available at http://physionet.org/physiotools/xcvsim/) is a didactic instrument for quantitative cardiovascular physiology courses. The cardiovascular system model is based on realistic parameter values representing normal human physiology and includes the important arterial baroreflex system for blood pressure homeostasis. The graphical user interface permits easy and intuitive interaction with the model. A full description of XCVSim is provided in [8].
The cardiovascular system model employs the original circulatory model of Fig. (1) but with model parameter values verified by solid experimental evidence1. More significantly, the model also includes an arterial baroreflex arc implemented in terms of a negative feedback system as shown in Fig. (2). This system attempts to maintain systemic arterial blood pressure near a pre-defined set-point pressure by dynamically controlling heart rate (which establishes the time of each cardiac contraction through an integrate-and-fire model of the sinoatrial node), minimum left and right ventricular compliances (cardiac contractility), systemic arterial resistance, and systemic venous unstressed volume. The control of each of these variables is achieved in parallel through a cascade combination of a static nonlinearity accounting for baroreflex saturation and a finite impulse response representing the dynamic properties of the afferent and efferent sympathetic and parasympathetic pathways of the nervous system with average systemic arterial blood pressure as the input. The degree of nonlinearity and the shape, gain value, and time delay of each impulse response originate from published experimental data. The model is able to simulate pulsatile blood pressures, volumes, and flow rates whose mean, systolic, and diastolic values are within the normal ranges of an adult human, as well as closed-loop regulatory responses to step perturbations to the model parameters. Similarly, the model is capable of simulating a range of pathological conditions, as shown in Figs. (3 and 4) for the case of severe aortic stenosis.
Fig. 2.
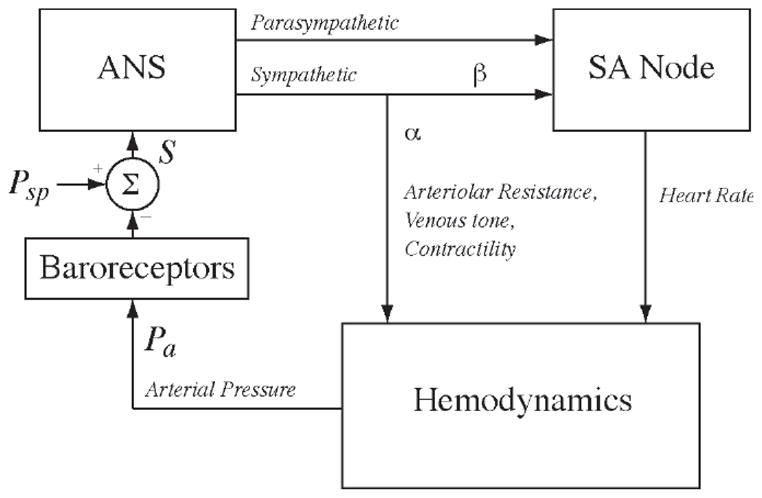
Block diagram of the arterial baroreflex implementation in terms of a set-point controller. Pa: arterial pressure; Psp: set-point pressure; S: error signal; ANS: autonomic nervous system; SA node: sinoatrial node; α, β: branches of the autonomic nervous system. Redrawn from Davis [Davis-1991].
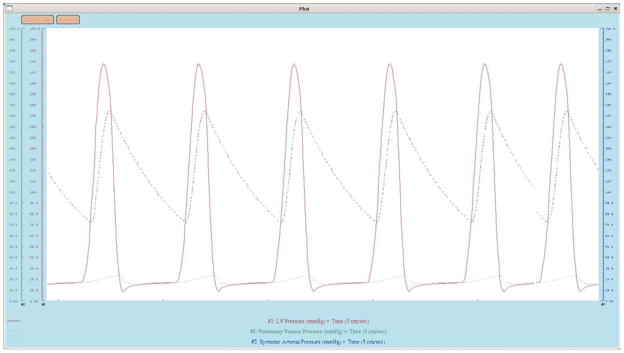
Fig. 3.
Screenshot of pressure tracings produced by XCVSim. Simulation of a patient with severe aortic stenosis. Left-ventricular pressure (red), arterial blood pressure (blue), and systemic venous pressure (green) waveforms.
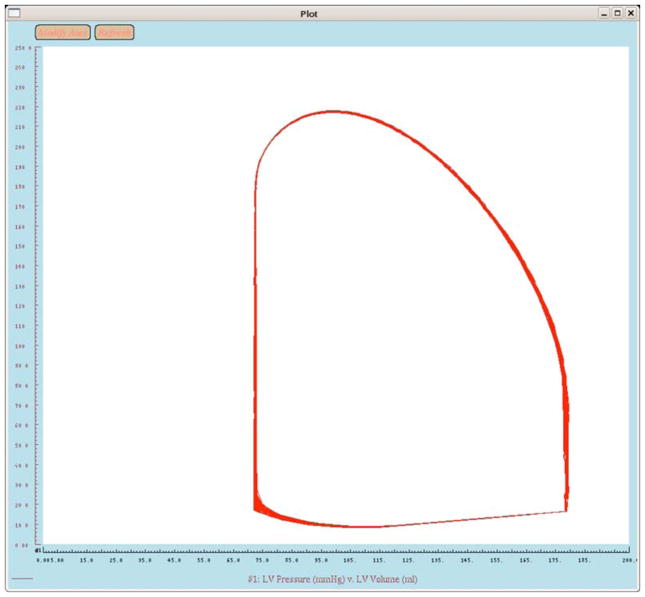
Fig. 4.
Screenshot of pressure-volume loop produced by XCVSim.
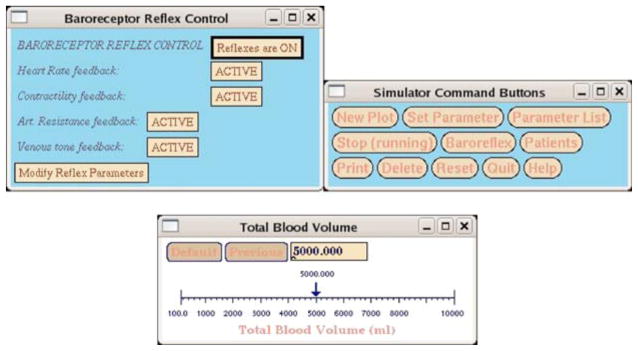
The user-friendly graphical interface is illustrated in Fig. (5). It allows the user to perform “physiologic experiments” on the model while being totally blind to the implementation details. The interface includes a circuit-diagram interaction window that intuitively relates the circulatory model to its parameters and hemodynamic variables. The interface allows for on-line, two-dimensional plotting and printing of the variables of interest in any combination and scale as well as dynamic graphical modification of the model parameters. In addition, a database of simulated patients accompanies the interface for student assignments (see below).
Fig. 5.
Graphical User Interface widgets of XCVSim. Three representative control panels are shown.
The open-source software is in the C programming language for the X Window System. The software includes executables for recent versions of Linux. The source code may be compiled on several other X11 Window platforms including Mac OS X and MS-Windows using Cygwin. Instructions for installing and compiling the software are included.
RCVSIM
RCVSIM (available at http://physionet.org/physiotools/rcvsim/) is a research tool that can complement investigations of experimental datasets available on PhysioNet. Most notably, the cardiovascular system model permits studies of subtle beat-to-beat hemodynamic variability in addition to cardiac pulsatility. The graphical interface and model outputs are fully compatible with other resources provided by PhysioNet. A complete description of RCVSIM is given in [10–12].
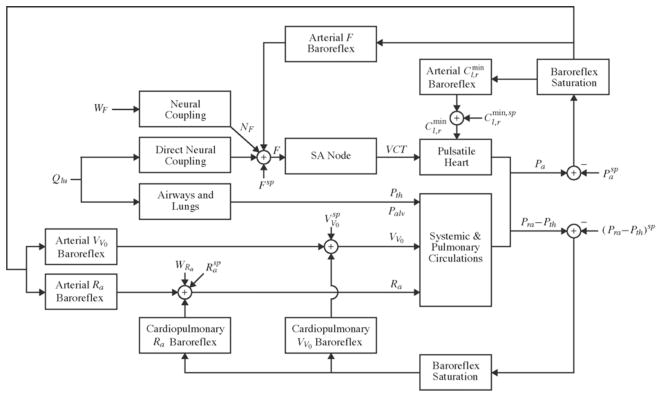
The cardiovascular system model is illustrated in Fig. (6) in terms of a block diagram and consists of three major components. The first component is a lumped-parameter model of the circulation. This model extends the original circulatory model of Fig. (1) through use of nonlinear elements that determine the performance of the circulation at its limits of operation. The nonlinear elements are systemic venous resistance characterized by a Starling resistor to account for venous collapse, pulmonary arterial resistance represented with parallel, vertically arranged Starling resistors to model the vascular waterfall effect, and right and left ventricular pressure-volume curves (rather than lines) to represent end-diastolic volume and end-systolic pressure maximums. The second component is a short-term regulatory system model. This model expands upon the arterial baroreflex system of XCVSim by inclusion of a cardiopulmonary baroreflex system that regulates right atrial transmural pressure and a direct neural coupling between respiration and heart rate likewise based on finite impulse response control. The third component is a model of resting physiologic perturbations. This model includes respiratory activity impinging on the circulatory model through intrathoracic pressure in addition to the direct neural coupling, the autoregulation of local vascular beds via a bandlimited exogenous disturbance to systemic arterial resistance, and higher brain-center activity modulating autonomic nervous system activity through a 1/f exogenous disturbance to heart rate. The aggregate model is therefore capable of simulating pulsatile waveforms, cardiac output and venous return curves, and spontaneous beat-to-beat hemodynamic variability as shown in Fig. (7).
Fig. 6.
Block diagram of the cardiovascular model of RCVSIM. The blocks in the diagram are mathematically characterized as follows: PULSATILE HEART and SYSTEMIC & PULMONARY CIRCULATIONS with a nonlinear lumped-parameter model; SA NODE with an integrate-and-fire model; each neural coupling and baroreflex block with finite impulse responses; BAROREFLEX SATURATION with arctan functions; and AIRWAYS AND LUNGS with a lumped parameter model. Cl,rmin is left and right ventricular minimum compliances; F, heart rate; NF, additive disturbance to heart rate; NRa, bandlimited disturbance to systemic arterial resistance; Pa, systemic arterial blood pressure; Palv, alveolar pressure; Pra-Pth, right atrial transmural pressure; Pth, intrathoracic pressure; Qlu, instantaneous lung volume; Ra, systemic arterial resistance; sp, set-point; VCT, ventricular contraction time; Vv0, systemic venous unstressed volume; and WF, 1/f noise. Adapted from [Mukkamala-2001].
Fig. 7.
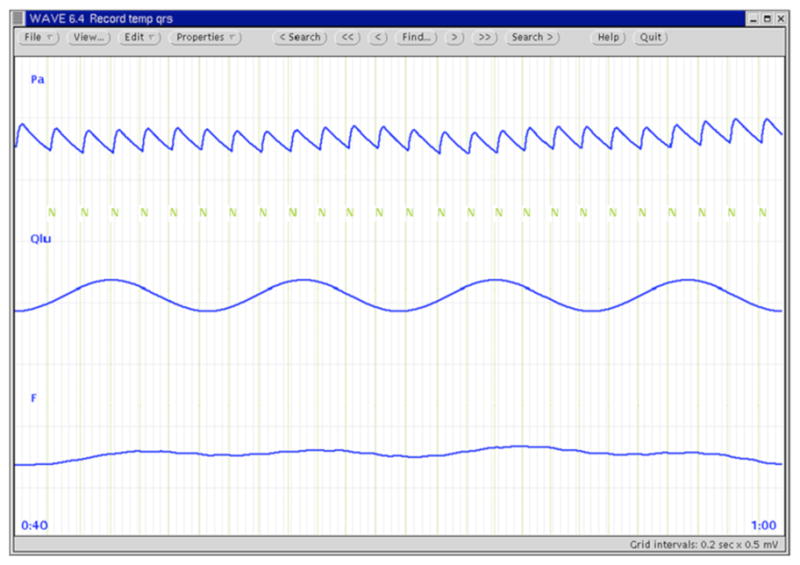
Example of systemic arterial blood pressure (Pa), instantaneous lung volume (Qlu), and heart rate (F) waveforms along with ventricular contraction times (N) simulated and displayed by RCVSIM. Reproduced from [Mukkamala/Moody-2001].
The simulated hemodynamic data are stored in a format that is identical to the experimental data sets available on PhysioNet. Thus, the simulated data are fully compatible with the open-source data analysis software provided by this resource. The simulated data may be viewed on-line as they are being generated or off-line after the completion of the simulation, using open-source visualization software available on PhysioNet. The model parameter values may be adjusted in batch mode or during a simulation.
The open-source software is written in the MATLAB programming language with heavy commenting. The software includes executables, which may be run at the Linux or MATLAB prompts. Furthermore, the source code may be compiled in MATLAB to create executables for other platforms. The software comes with an extensive user manual that describes how to install, compile, and use it with many examples and a detailed description of the source code.
CVSim-6 and CVSim-21
A second research version of CVSim was developed in parallel to RCVSIM in the late 1990s. The design of this version (available at http://physionet.org/physiotools/cvsim/cvsim/devel/C/21-comp-backend/) was largely dictated by its purpose of aiding in the understanding of post-spaceflight orthostatic intolerance, a critical impairment in maintaining arterial blood pressure homeostasis following spaceflight [13]. The hemodynamic model was designed to allow for regionally distributed blood flow to four major systemic peripheral vascular beds (upper body, kidneys, splanchnic circulation, and lower body) during a series of orthostatic challenge tests (head-up tilt, standing up, lower body negative pressure, and sudden onset exercise). Furthermore, the model contains two atria in addition to the left and right ventricles. In total, the hemodynamic portion of the simulator contains 21 vascular compartments, compared to the six compartments of XCVSim and RCVSIM. A substantial effort was spent on specifying the parameter values for each compartment to represent normal human physiology [14].
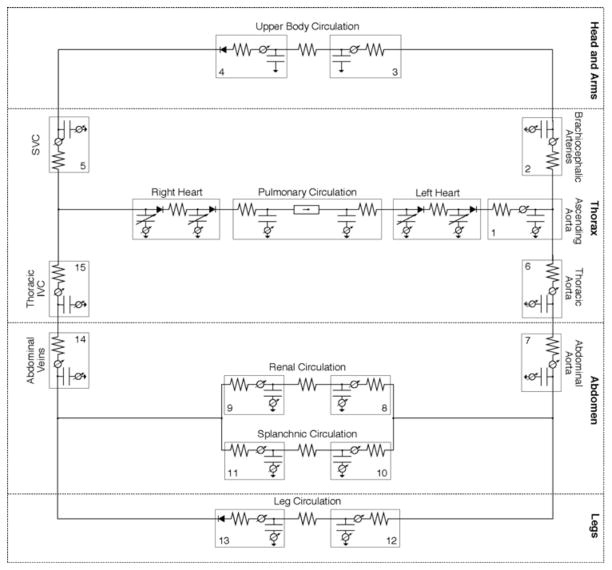
To allow for realistic simulations of blood pooling in the dependent vasculature during simulated orthostatic stress tests, the pressure-volume relationships of the lower body veins, the abdominal veins and the inferior vena cava were specified to exhibit marked non-linearities that limit the amount of volume stored at high transmural pressures. Furthermore, we introduced a phenomenological model of the interstitial fluid compartment to allow for fluid exchange between the vascular and interstitial fluid spaces during prolonged orthostatic stress. Finally, we introduced pressure sources within the vascular compartments to represent hydrostatic pressure components along the vascular tree. The full 21-compartment hemodynamic model is shown in Fig. (8).
Fig. 8.
Circuit model representation of CVSim-21. The hemodynamic model consists of seventeen vascular and four cardiac compartments.
This expanded research version of CVSim also incorporates the two major neurally mediated reflex arcs that maintain blood pressure homeostasis, namely the arterial baroreflex and the cardiopulmonary reflex. XCVSim and RCVSIM were largely designed to represent supine subjects. In the supine posture, the hydrostatic pressure difference between the level of the heart and the carotid sinus as well as the resistive pressure losses between these two locations are negligible, and therefore the exact location of the sensed pressure in the arterial tree is not critical. In this application, however, we were interested in simulating the dynamic cardiovascular response during transitions in posture and therefore had to take care in assigning the location of the pressure sensor of the arterial baroreflex, as the carotid sinus senses pressure some 30 cm above the level of the heart in the upright posture.
We validated this research version of CVSim against steady-state hemodynamic variables during head-up tilt and against the dynamic responses in arterial blood pressure and heart rate during slow and rapid head-up tilt and standing-up maneuvers. Furthermore, we simulated lower-body negative pressure, rapid-onset exercise, and a Valsalva maneuver and demonstrated good qualitative correspondence between simulations and experimental data [13, 14].
Initially, the program was implemented in the C programming language without a graphical user interface as computational efficiency for repeated simulations was the primary objective in this research program. Subsequent to model development, we used the model to estimate model parameters from experimental data for which we parallelized the code using the Message Passing Interface on an eleven-node Beowulf cluster [14].
Later, we decided to implement a platform-independent GUI in Java that can be used with either the expanded |21-compartment or the 6-compartment versions of our research model (in ANSI/ISO C for efficiency and portability). These recent teaching versions (CVSim-6 and CVSim-21, available at http://physionet.org/physiotools/cvsim/) represent all features of the prior incarnations of XCVSim. These models continue to be used in the teaching of quantitative physiology at MIT.
APPLICATIONS
Teaching
Since 1984, CVSim and XCVSim have been used for teaching the lumped-parameter cardiovascular model to engineering students at MIT and medical students in the Harvard Medical School’s Division of Health Sciences and Technology (London Society). Among their features, they include a small library of simulated “patients” that exhibit pathologies such as hypovolemia, hypertension, myocardial infarction, A-V fistula, and aortic stenosis. These were constructed by varying the model parameters, and each “patient” was accompanied by a narrative clinical history (see Fig. 9). The educational versions of CVSim allow students to observe the time-varying hemodynamic parameters such as pressure (voltage) and flow (current) at each node of the circuit model. Students develop an understanding of the model by experimentally determining how to perturb the normal model parameters in order to replicate the hemodynamics they observe in the “patients.” Students generally consider the cardiovascular simulator a useful learning experience and point out that the simulator is an effective tool in demonstrating how hemodynamic variables depend on component properties of the cardiovascular system. Students also credit the simulator for improved understanding of hemodynamics [8].
Fig. 9.

Patient history for patient simulation. Simulations for this case are shown in Figs. (3 and 4).
Research
Our research investigations with versions of CVSim are more recent and span several directions. They may be broadly categorized as either the development and evaluation of novel algorithms or the study of cardiovascular responses to physiologic perturbations.
We have used RCVSIM to successfully develop and assess system identification algorithms for estimating transfer functions and parameters that characterize important cardiovascular regulatory mechanisms (e.g., baroreflex control of heart rate and total peripheral resistance) and hemodynamic parameters (maximal ventricular elastance changes) from non-invasive measurements of beat-to-beat cardiorespiratory variability [15–19]. The advantage of using a cardiovascular simulator for this purpose is that the actual reference values of the quantities sought for estimation are precisely known. In contrast, obtaining reliable independent reference measurements in an experimental model may be difficult or even impossible in the case of a transfer function. In particular, our theoretical cardiovascular simulator-based investigation of system identification algorithms for quantifying the baroreflex control of total peripheral resistance led to conscious canine studies in which the algorithms proved capable of properly detecting changes in arterial and cardiopulmonary baroreflex functioning after chronic arterial baroreceptor denervation [15, 20]. These subsequent experimental studies are shining examples of how cardiovascular simulators can advance experimental research.
Furthermore, we have used CVSim as a point of departure for developing efficient cycle-averaging methods to track the dynamic inter-cycle behavior (rather than the intra-cycle behavior) of important cardiovascular variables [21–23]. Oftentimes, one is not interested in the instantaneous value of a particular physiological variable (pressure, flow, volumes, for example), but how the averages of such variables respond to perturbations in the system. Cycle-averaging allows for the isolation of the dynamic responses of such average variables. We have employed cycle-averaging, and its discrete-time analog, beat-by-beat averaging, to estimate cardiac output and total peripheral resistance from arterial blood pressure waveforms [23, 24].
We have used the extended 21-compartment model to investigate the normal hemodynamic response to passive and active changes in posture [14] as well as the conditions that might predispose astronauts to orthostatic intolerance upon return to Earth’s normal gravitational environment. The key insight derived from the latter investigation is that hypovolemia by itself might be the sole mechanism underlying post-spaceflight orthostatic intolerance if a sufficient amount of volume was shed in space. If, however, the contraction of vascular volume by itself is not sufficient to produce overt hypotension, then detrimental reductions in other parameters become very important, in particular those relating to the vascular feedback loops of the arterial and cardiopulmonary baroreflex arcs [25]. These findings are consistent with the realization of our colleagues that midodrine, a vascular α-adrenergic agonist, is an effective countermeasure against post-spaceflight orthostatic intolerance [26, 27].
Given the large cost associated with gathering data within the human life-science space program, it seems that using computational models to interpret such data rationally and to evaluate competing physiological hypotheses is not merely an advantage, but a necessity given the limited amount of data that can be collected before, during, and after each space mission.
We have also employed RCVSIM to study the cardiovascular responses to cardiac arrhythmias [28]. In particular, we replaced the lumped-parameter left and right ventricular models with detailed electromechanical ventricular models. We integrated the software using a simulation-reuse and interoperability architecture. We then induced ventricular tachycardia in the electromechanical models to elicit and assess hemodynamic and cardiovascular regulatory responses.
Finally, other investigators – especially our collaborators – have also used incarnations of CVSim in the context of their own research. These investigations have mainly involved the integration of versions of CVSim with other models [29–34].
CONCLUSIONS
We consider computational models of physiology to be powerful tools in both teaching and research.
With a view towards their utility in research, we stated elsewhere [13] that mathematical models often allow us to probe a system in much greater detail than is possible in experimental studies and can therefore help establish the cause of a particular observation. When fully integrated into an experimental protocol, mathematical models and experiments are highly synergistic in the sense that the existence of one greatly enhances the value of the other: models depend on experiments for specification and refinement of parameter values, but they also illuminate experimental results and allow for differentiation between competing scientific hypotheses [13]. Analyzing models rigorously, through sensitivity analyses, for example, also allow for identification of crucial gaps in our knowledge and therefore motivate the design of novel experiments. Finally, mathematical models serve as important test beds against which estimation and identification algorithms can be evaluated, as the true target values are precisely known and controllable.
In teaching physiology, mathematical models can play a similarly powerful role. Human physiology is quite complex, and it is therefore often difficult for students to develop an intuitive understanding of how a perturbation in one part of an organ system propagates and gives rise to a system-level response. Computational models allow for such thought experiments to be conducted; they also allow students to simply explore the system under consideration through simulation of “what-if ” scenarios. We have found such explorations by students to add tremendously to their understanding of the normal physiology and pathology of the cardiovascular system.
By making our models freely available through the PhysioNet web site, we hope that others might find our models to add equal value to their research and teaching endeavors.
Acknowledgments
The authors wish to acknowledge and thank their colleagues who have contributed to the development of CVSim over many years; these include Robert L. Sah, Timothy L. Davis, Eun Bo Shim, Roger Kamm, and Catherine Dunn.
Partial funding for CVSim development was provided by the National Aeronautics and Space Administration (NASA) through the NASA Cooperative Agreement NCC 9-58 with the National Space Biomedical Research Institute.
Footnotes
This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Some details of the figures may not be visible in printed copies of the paper. The figures in this paper are embedded at full resolution in the original (online) paper, and additional details can be viewed on-screen by using the zoom control of the reader’s pdf viewer.
References
- 1.Brunberg A, Heinke S, Spillner J, Autschbach R, Abel D, Leonhardt S. Modeling and simulation of the cardiovascular system: a review of applications, methods, and potentials. Biomed Tech (Berl) 2009;54:233–244. doi: 10.1515/BMT.2009.030. [DOI] [PubMed] [Google Scholar]
- 2.Grodins FS. Integrative cardiovascular physiology: A mathematical synthesis of cardiac and blood vessel hemodynamics. Q Rev Biol. 1959;34(2):93–116. doi: 10.1086/402631. [DOI] [PubMed] [Google Scholar]
- 3.Defares JG, Osborne JJ, Hara HH. Theoretical synthesis of the cardiovascular system. Study I: The controlled system. Acta Physiol Pharm Neerl. 1963;12:189–265. [PubMed] [Google Scholar]
- 4.Katz S, Hollingsworth RG, Blackburn JG, Carter HT. Computer simulation in the physiology student laboratory. Physiologist. 1978;21(6):41–4. [PubMed] [Google Scholar]
- 5.Campbell K, Zegien M, Kagehiro T, Rigas H. A pulsatile cardiovascular computer model for teaching heart-blood vessel interaction. Physiologist. 1982;25(3):155–62. [PubMed] [Google Scholar]
- 6.Sunagawa K, Sagawa K. Models of ventricular contraction based on time-varying elastance. Crit Rev Biomed Eng. 1982;7(3):193–228. [PubMed] [Google Scholar]
- 7.Champine GA. A Model for Distributed Campus Computing. Athena: Digital Press; 1991. MIT Project. [Google Scholar]
- 8.Davis TL. Master’s thesis. Massachusetts Institute of Technology; Cambridge, MA: Feb, 1991. Teaching Physiology through Interactive Simulation of Hemodynamics. [Google Scholar]
- 9.Goldberger AL, Amaral LAN, Glass L, Hausdorff JM, Ivanov PCh, Mark RG, Mietus JE, Moody GB, Peng CK, Stanley HE. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation. 2000;101(23):e215–e220. doi: 10.1161/01.cir.101.23.e215. [DOI] [PubMed] [Google Scholar]
- 10.Mukkamala R. Dissertation. Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology; Cambridge, MA: Jun, 2000. A Forward Model-Based Analysis of Cardiovascular System Identification Methods. [Google Scholar]
- 11.Mukkamala R, Moody GB, Mark RG. Introduction of computational models to PhysioNet. Comput Cardiol. 2001;28:77–80. [PubMed] [Google Scholar]
- 12.Mukkamala R. A Cardiovascular Simulator for Research: User’s Manual and Software Guide. 2004. [Google Scholar]
- 13.Heldt T, Shim EB, Kamm RD, Mark RG. Computational modeling of cardiovascular response to orthostatic stress. J Appl Physiol. 2002;92:1239–54. doi: 10.1152/japplphysiol.00241.2001. [DOI] [PubMed] [Google Scholar]
- 14.Heldt T. Dissertation. Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology; Cambridge, MA: Sep, 2004. Computational models of cardiovascular response to orthostatic stress. [Google Scholar]
- 15.Chen X, Kim JK, Sala-Mercardo JA, Hammond RL, Elahi RI, Scislo TJ, Swamy G, O’Leary DS, Mukkamala R. Estimation of the total peripheral resistance baroreflex impulse response from spontaneous hemodynamic variability. Am J Physiology. 2008;294(1):H293–H301. doi: 10.1152/ajpheart.00852.2007. [DOI] [PubMed] [Google Scholar]
- 16.Lu Z, Mukkamala R. Monitoring left ventricular contractility from respiratory-induced blood pressure variability. Comput Cardiol. 2004;31:705–8. [Google Scholar]
- 17.Lu Z, Mukkamala R. Non-invasive monitoring of left ventricular contractility and ventilatory mechanics. Proceedings of the 27th Annual Conference of the IEEE Engineering in Medicine and Biology Society. 2005;7:7636–9. doi: 10.1109/IEMBS.2005.1616280. [DOI] [PubMed] [Google Scholar]
- 18.Mukkamala R, Cohen RJ. A forward model-based validation of cardiovascular system identification. Am J Physiol. 2001;281(6):H2714–H2730. doi: 10.1152/ajpheart.2001.281.6.H2714. [DOI] [PubMed] [Google Scholar]
- 19.Mukkamala R, Toska K, Cohen RJ. Noninvasive identification of the total peripheral resistance baroreflex. Am J Physiol. 2003;284(3):H947–H959. doi: 10.1152/ajpheart.00532.2002. [DOI] [PubMed] [Google Scholar]
- 20.Mukkamala R, Kim J, Li Y, Sala-Mercado J, Hammond RL, Scislo T, O’Leary DS. Estimation of arterial and cardiopulmonary total peripheral resistance baroreflex gain values: validation by chronic arterial baroreceptor denervation. Am J Physiol. 2006;290(5):H1830–H1836. doi: 10.1152/ajpheart.00898.2005. [DOI] [PubMed] [Google Scholar]
- 21.Heldt T, Chang JL, Chen JJS, Mark RG, Verghese GC. Cycle-averaged dynamics of a periodically driven, closed loop circulation model. Control Eng Pract. 2005;13(9):1163–71. doi: 10.1016/j.conengprac.2004.10.012. [DOI] [PubMed] [Google Scholar]
- 22.Parlikar TA, Heldt T, Verghese GC. Cycle-averaged models of cardiovascular dynamics. IEEE Trans Circuits Syst. 2006;53(11):2459–68. [Google Scholar]
- 23.Parlikar TA. Dissertation. Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology; Cambridge, MA: Jun, 2007. Modeling and monitoring of cardiovascular dynamics for patients in critical care. [Google Scholar]
- 24.Parlikar TA, Heldt T, Ranade GV, Verghese GC. Model-based estimation of cardiac output and total peripheral resistance. Comput Cardiol. 2007;35:379–82. [Google Scholar]
- 25.Heldt T, Mark RG. Understanding post-flight orthostatic intolerance: a simulation study. Comput Cardiol. 2005;32:631–4. [Google Scholar]
- 26.Ramsdell CD, Mullen TJ, Sundby GH, Rostoff S, Sheynberg N, Aljuri N, Maa M, Mukkamala R, Sherman D, Toska K, Yelle J, Bloomfield D, Williams GH, Cohen RJ. Midodrine prevents orthostatic intolerance associated with simulated spaceflight. J Appl Physiol. 2001;90(6):2245–8. doi: 10.1152/jappl.2001.90.6.2245. [DOI] [PubMed] [Google Scholar]
- 27.Platts SH, Ziegler MG, Waters WW, Mitchell BM, Meck JV. Midodrine prescribed to improve recurrent post-spaceflight orthostatic hypotension. Aviat Space Environ Med. 2004;75(6):554–6. [PubMed] [Google Scholar]
- 28.Murphy S, Coolahan J, Lutz R, Saunders R, Feldman A, Mukkamala R. Integrating cardiac and cardiovascular simulations using the HLA. Spring Simulation Interoperability Workshop; 2002. pp. 1–16. 02S-SIW-012. [Google Scholar]
- 29.Coolahan JE, Feldman AB, Murphy SP. Simulation of integrated physiology based on an astronaut exercise protocol. Johns Hopkins APL Technical Digest. 2004;25(3):201–13. [Google Scholar]
- 30.Lim KM, Kim JH, Shim EB. Mathematical analysis of the long-term efficacy of daily hemodialysis therapy with a cold dialysate regeneration system. Blood Purif. 2009;29(1):27–34. doi: 10.1159/000245044. [DOI] [PubMed] [Google Scholar]
- 31.Shim EB, Kamm RD, Heldt T, Mark RG. Numerical analysis of blood flow through a stenosed artery using coupled multiscale simulation methods. Comput Cardiol. 2000;27:219–22. [PubMed] [Google Scholar]
- 32.Shim EB, Youn CH, Heldt T, Mark RG, Kamm RD. Computational modeling of the cardiovascular system after Fontan procedure. Lect Notes Comput Sci. 2002;2526:105–14. [Google Scholar]
- 33.Shim EB, Leem CH, Abe Y, Noma A. A new multi-scale simulation model of the circulation: from cells to systems. Philos Trans R Soc A. 2006;365:1483–1500. doi: 10.1098/rsta.2006.1782. [DOI] [PubMed] [Google Scholar]
- 34.Shim EB, Amano A, Takahata T, Shimayoshi T, Noma A. The cross-bridge dynamics during ventricular contraction predicted by coupling cardiac Cenn model with a circulation model. J Physiol Sci. 2007;57(5):275–85. doi: 10.2170/physiolsci.RP006007. [DOI] [PubMed] [Google Scholar]