The use of mathematical models to inform influenza pandemic preparedness and response

Summary

Influenza pandemics have occurred throughout history and were associated with substantial excess mortality and morbidity. Mathematical models of infectious diseases permit quantitative description of epidemic processes based on the underlying biological mechanisms. Mathematical models have been widely used in the past decade to aid pandemic planning by allowing detailed predictions of the speed of spread of an influenza pandemic and the likely effectiveness of alternative control strategies. During the initial waves of the 2009 influenza pandemic, mathematical models were used to track the spread of the virus, predict the time course of the pandemic and assess the likely impact of large-scale vaccination. While mathematical modeling has made substantial contributions to influenza pandemic preparedness, its use as a real-time tool for pandemic control is currently limited by the lack of essential surveillance information such as serologic data. Mathematical modeling provided a useful framework for analyzing and interpreting surveillance data during the 2009 influenza pandemic, for highlighting limitations in existing pandemic surveillance systems, and for guiding how these systems should be strengthened in order to cope with future epidemics of influenza or other emerging infectious diseases.

Background

Influenza pandemics have occurred throughout history. Three influenza pandemics in the 20^th century were associated with substantial excess mortality and morbidity.[1] The emergence of a highly pathogenic strain of avian influenza A/H5N1 in 1997[2] led to increasing concerns about the next pandemic. With limited empirical experience to guide planning decisions, mathematical modeling has been a key tool to facilitate planning for pandemic mitigation strategies. These simulation approaches, which explicitly take into account the ways in which the infection spreads between people,[3] were widely used in the “peace-time” between pandemics to characterize influenza dynamics and to explore the potential impact of alternative intervention strategies, and contribute to pandemic planning.

Through the first decade of the 21^st Century there was growing anticipation that a new pandemic would emerge from an avian virus in South-East Asia.[4] It was somewhat unexpected when in early 2009 a pandemic virus emerged from a swine influenza virus lineage in North America.[5] Mathematical modeling techniques were used in the ”war-time” as the 2009 influenza pandemic was unfolding to provide information on disease transmissibility and severity, and aid planning for vaccine allocation.

In this short review, we provide a general background on mathematical modeling, and highlight some of the contributions and limitations of mathematical modeling in the planning of influenza pandemic preparedness and response. We then proceed to discuss the predictive value of mathematical modeling in the context of the 2009 influenza pandemic. Our aim here is to give a broad overview of the various applications of mathematical modeling in pandemic planning rather than to review in detail every modeling study conducted on this topic.

Mathematical models

The application of mathematical models to describe infectious disease dynamics is a systematic way of translating assumptions and data regarding disease transmission into quantitative estimates of how an epidemic evolves through time and space. Similar approaches are used in classical physics to predict the movement of an object by translating inertia and gravity (assumptions regarding the laws of physics) and the force and angle at which an object is thrown (the data) into the trajectory of the object (the prediction). Epidemics of infectious diseases among humans are driven by transmission of the infectious agent among humans either directly, via fomites in the environment or via animal vectors. Disease transmission can also depend on biological characteristics of both the pathogen and the host, as well as social, behavioral and environmental factors. It is possible to express these dynamics in terms of mathematical equations.[3] While the dynamics of infectious diseases can be extremely complex, in many cases relatively parsimonious models can be used to describe the essential properties of epidemic dynamics.[6]

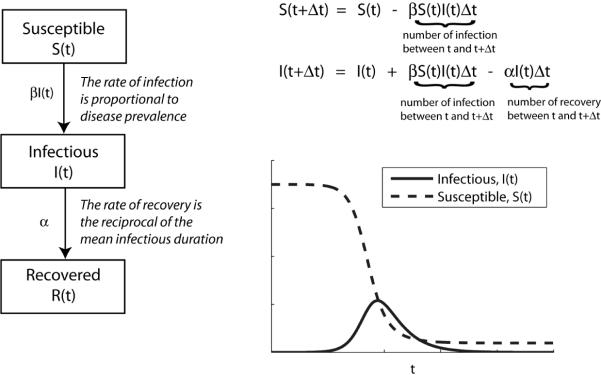
In the simplest epidemic model, a closed large population of size N is partitioned into three classes of individuals: Susceptible, Infectious, and Recovered (Figure 1). All individuals are assumed to be identical in terms of their susceptibility to infection, infectiousness if infected, as well as mixing behavior associated with disease transmission (the so-called homogenous mixing assumption). The assumption that all individuals are identical in terms of disease dynamics permits the grouping of individuals into aggregate “compartments”. The resulting SIR (Susceptible-Infectious-Recovered) model can be used to describe the number of individuals in each class at time t (S(t), I(t) and R(t)) based on two further assumptions. Firstly, the rate at which susceptible individuals become infected during any small time interval Δt is assumed to be proportional to the prevalence of infectious individuals. Secondly, infected individuals recover with long-lasting immunity after an average infectious duration of 1/α. These assumptions can be translated into the following equations describing the epidemic dynamics:

$$\begin{array}{cc}\hfill S(t+\Delta t)& =S\left(t\right)-\beta I\left(t\right)S\left(t\right)\Delta t\hfill \\ \hfill I(t+\Delta t)& =I\left(t\right)+\beta I\left(t\right)S\left(t\right)\Delta t-\alpha I\left(t\right)\Delta t\hfill \end{array}$$

The epidemic curve generated by this simple model captures the hallmarks of typical epidemics: (i) the number of infections increases exponentially during the early phase of a growing epidemic; and (ii) the epidemic curve is unimodal and peaks when the susceptible pool has been sufficiently depleted (Figure 1). Despite the apparent simplicity of the SIR model, many recent studies of pandemic influenza have been built from this basic model structure. The model can be extended to include variation in transmission dynamics by factors such as age and spatial location. The equations above describe a deterministic process, although it is straightforward to allow stochasticity (random variability) in the dynamics, and this can be particularly important when describing the early stages of an epidemic.[6]

Figure 1.

Schematic of the Susceptible-Infectious-Recovered model (left) and the typical epidemic curve that it generates (right).

Three epidemiologic parameters form the cornerstones of mathematical epidemiology: (i) the basic reproductive number R₀, which is defined as the average number of secondary cases generated by an index case when an epidemic begins in a completely susceptible population (the reproductive number R has the same definition but without requiring a completely susceptible population); (ii) the mean generation time T_g, which is defined as the average time it takes an index case to infect other individuals after he becomes infected; (iii) the growth rate of an epidemic r. The importance of these parameters stems from their intuitive implications on disease spread: If R₀ < 1, then an outbreak will die out without causing widespread infections. For a given R₀ > 1, the outbreak could lead to an epidemic and a shorter generation time would be associated with higher growth rate. The same results hold for the reproductive number R when considering a partially susceptible population. While the definitions of R₀, T_g and r are not model-dependent, model-based statistical inference of these parameters from epidemic data could be sensitive to the assumed structure of the model.[7] In the SIR model, the basic reproductive number is R₀ = βN/α, the mean generation time is T_g = 1/α, and the epidemic growth rate is r = (R₀−1)/T_g.

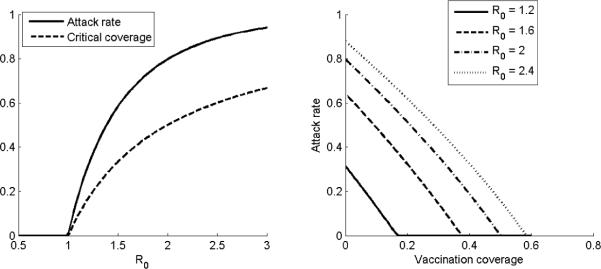
In addition to indicating the epidemic potential of an emerging pathogen, the basic reproductive number R₀ is an important parameter for estimating the proportion of a population infected throughout an epidemic (the final attack rate) and the degree to which interventions might be able to control or mitigate an epidemic. For example, the final attack rate typically increases sharply as R₀ increases beyond 1 (Figure 2). An important corollary of this relation is that it is not necessary to vaccinate the whole population in order to halt a growing epidemic. For example, under the SIR model, vaccinating a proportion 1–1/R₀ (known as the critical coverage) of the population is sufficient to push the reproductive number below 1 (Figure 2) and ensure that an epidemic will not take off.[3, 6] Furthermore, even if the critical coverage is not reached, vaccination could still substantially reduce the attack rate if R₀ is only moderately larger than 1 (Figure 2) because of increased herd immunity. Timely and accurate estimate of R₀ therefore allows a quick assessment of the potential impact and controllability of an emerging epidemic.

Figure 2. The nonlinear dependence of the final attack rate and critical coverage on R₀.

Knowing R₀, we can use the Susceptible-Infectious-Recovered model to estimate the final attack rate as well as the level of vaccination coverage required to prevent an epidemic (left). Similarly, the model can be used to estimate the potential reduction in attack rate provided by different levels of vaccination coverage (right).

Use of models to guide pandemic preparedness

Estimation of epidemiologic parameters

Combining historical epidemic data (e.g. pneumonia & influenza mortality) with mathematical modeling, several research groups have consistently estimated that R₀ was mostly in the range of 1.2 to 3 during the 1918, 1957, and 1968 pandemics.[8–10] Similarly, the mean generation time of pandemic influenza was estimated to be around 2 to 4 days.[11–14] These epidemiologic parameters provided a reference frame for planning influenza pandemic preparedness and response. Epidemic models parameterized with these estimates were built and used to assess the potential effectiveness of different pandemic mitigation strategies.[15]

Predicting the speed of global spread and the effectiveness of travel restrictions

Mathematical models have been used to study the global spread of infectious agents as early as the 1980s. Longini et al pioneered this method in which each population was represented as an SIR system and epidemic dynamics of different populations were linked together by international travel.[16] Recent modeling studies of global spread of infectious agents used essentially the same model structure but with more populations simulated in order to increase the realism of the models.[17–19] These modeling studies concluded that for plausible ranges of R₀ and T_g for pandemic influenza, the novel virus would spread around the world within a few months of emergence in the origin population. Furthermore, travel restrictions would have almost no effect in slowing international spread of pandemic influenza because only a small number of imported cases would be sufficient to spark an epidemic in seeded populations. Because the number of infections would grow exponentially in the origin population and non-symptomatic infected individuals could transmit the disease, the only way to stop international seeding would be to completely prohibit travel from and to the origin population, which is infeasible.

Assessing the effectiveness of containment and mitigation strategies

The need for influenza pandemic preparedness in the past decade has been a strong driving force for the development of large-scale agent-based epidemic simulations[11, 13–15, 20, 21] which represent a substantial advance in infectious disease modeling. Unlike compartmental models which partition a population based on demographics, disease status, etc., and track the number of individuals in these compartments over time, agent-based simulations model the population as a network in which each node represents a single person (“an agent”) and each edge represents a possible route of disease transmission between two persons (Figure 3). Agent-based simulations can easily take into account household demographics, individually targeted interventions (e.g. case isolation, antiviral prophylaxis of contacts) and spatial heterogeneity which are often difficult and cumbersome to simulate using compartmental models.

Figure 3. A schematic of transmission network for agent-based simulations.

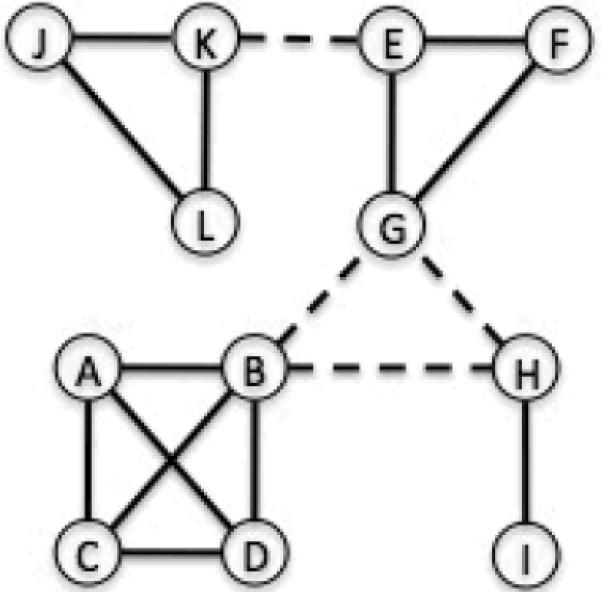
In general, a network is consisted of nodes (the circles) and edges (the links between circles). In agent-based simulations, each node represents a single person (“an agent”) and each edge represents a possible route of disease transmission between two persons. As such, there can be multiple types of edges and edges can form and disappear over time. In this example, solid edges represent family membership while dashed edges represent peer-group membership. In this hypothetical population of 12 individuals, there are 4 families (A-B-C-D, E-F-G, H-I, and K-L-J) and 2 peer-groups (B-G-H and K-E). The transmission network for homogeneous mixing models (e.g. the basic SIR model) would correspond to a network with one edge between every pair or nodes.

Using large-scale stochastic agent-based simulations parameterized with detailed demographic and spatial data, Ferguson et al and Longini et al concluded that early detection together with aggressive containment measures, including large-scale antiviral prophylaxis and quarantine, could in theory contain the pandemic virus at its origin of emergence (assumed to be a rural area) if R₀ is smaller than 1.6–1.8.[11, 14] However, given the high uncertainty associated with transmissibility of the pandemic virus and the risk of multiple introductions,[22] the probability of sustained containment is unlikely to be high and mitigation strategies would be necessary for all countries. These modeling studies have played an important role in advising countries to devise national influenza pandemic preparedness and response plans.[23]

Agent-based simulations of influenza pandemics have suggested that the most effective mitigation of an influenza pandemic would likely require combinations of influenza antiviral treatment and prophylaxis and non-pharmaceutical interventions of quarantine, isolation, school closure, community social distancing, and workplace social distancing.[15] Indeed, mathematical analyses of historical epidemic data from the 1918 influenza pandemic suggested that prolonged non-pharmaceutical interventions had a significant effect in reducing disease transmission.[24, 25] Among these interventions, school closure has received most attention and is present in pandemic influenza preparedness plans of many countries.[26, 27] To generate evidence on the effectiveness of school closure, several modeling studies assessed changes in transmission dynamics of seasonal influenza during scheduled school holidays or reactive school closure.[28–31] However, their findings were mixed, and even if school closure is indeed effective, simulations suggested that it would have to be implemented with high compliance for a prolonged period in order to have a significant reduction in attack rate. Consequently, there is still little consensus on the effectiveness and feasibility of school closure in reducing community transmission during an influenza pandemic.[30]

Optimizing antiviral strategies

Maintaining a stockpile of antiviral drugs is a major component of many influenza preparedness plans.[23] For example, before the 2009 influenza pandemic, the United States had stockpiled enough antivirals to treat 25% of its population.[32] Besides their use for treatment of ill individuals, antivirals can also be used for prophylaxis.[33] A series of mathematical modeling studies assessed the potential effectiveness and logistical requirement of different targeted antiviral prophylaxis strategies (e.g. household-based, school-based, spatially-targeted, risk-targeted, etc) in order to inform countries on the best use of their large antiviral stockpiles.[11–14, 17, 20, 21, 34, 35] These studies consistently showed that compared to treatment-only strategies, targeted prophylaxis, if implemented throughout the epidemic, would be an efficient use of antiviral stockpiles in terms of reducing the epidemic size. While demonstrating the potential effectiveness of large-scale antiviral intervention, mathematical modeling studies also provided quantitative assessments on the potential risk of drug-induced antiviral resistance.[19, 36–40] Specifically, these studies emphasized that if a drug-induced resistant strain with low fitness cost emerged during the early phase of a pandemic, this strain would subsequently replace the wild-type as the dominant pandemic strain. This could jeopardize effective treatment of severe cases. To try to reduce this risk of resistance, novel strategies have been proposed based on mathematical models, including the idea of stockpiling a secondary antiviral and using it as an adjunct to the primary antiviral in the early stages of a pandemic.[19, 37]

Optimizing vaccination strategies

Vaccine is the long-term solution for reducing morbidity and mortality associated with a novel influenza strain. However, in order for vaccines to provide protection against pandemic infections, the vaccine strain must be antigenically similar to the pandemic strain. Consequently, vaccine production cannot begin until the pandemic strain has been isolated. Because the lead-time for vaccine production is typically 4–6 months or more,[41] pandemic vaccines will likely be in severe shortage as the pandemic unfolds. This has motivated the proposal to stockpile pre-pandemic vaccines made before a pandemic and composed of potential pandemic strains; the antigenic match between these vaccines and the actual pandemic virus are expected to be moderate at best, although they may be able to confer some degree of protection.[42]

A series of modeling studies have emphasized that even low-efficacy or low-coverage targeted vaccination during the early stages of a pandemic could have a substantial impact on reducing disease transmission because R₀ is likely to be relatively low.[13, 15, 21, 43–46] To optimize the use of a limited amount of pandemic or pre-pandemic vaccines, several groups used mathematical modeling to assess the public health benefit of different vaccination strategies.[44, 45, 47–51] Because schoolchildren comprise the core group for influenza transmission, most studies concluded that vaccinating them would substantially reduce transmission because of the nonlinear effect of herd immunity. These studies have played an important role in influencing countries (including the US) to include schoolchildren in their recommendations for both seasonal and pandemic influenza vaccination.[52, 53]

Assessing the logistical requirement of interventions

Mathematical models of epidemics can be easily extended to take into account operational constraints in order to assess logistical feasibility of interventions. For example, earlier modeling studies of bioterrorist attack with smallpox and anthrax emphasized that the availability of manpower to perform contact tracing and antiviral dissemination was an important factor in limiting the effectiveness of response strategies [54, 55]. During the 2009 influenza pandemic, a study was conducted in Hong Kong to assess the efficacy of convalescent plasma (collected from lab-confirmed cases) in treating severe cases [56]. Motivated by the potential efficacy of this therapeutic approach, a mathematical modeling study illustrated that in a moderately severe pandemic and with blood transfusion capacity similar to that in Hong Kong, a population-wide program which collects plasma from a small percentage of recovered adults could harvest sufficient convalescent plasma to treat a substantial proportion of severe cases in real-time [57].

Use of models during the 2009 influenza pandemic

Some predictions made by mathematical modeling in “peace-time” are robust against uncertainties regarding strain-specific transmission dynamics and were applicable during the initial waves of pandemic (H1N1) 2009 (pdmH1N1). For example, travel restrictions and border screening were predicted to be ineffective in slowing down international spread of pdmH1N1 except for very isolated populations and were not recommended by the World Health Organization (WHO), and accordingly most countries did not aggressively attempt to prevent entry of the pandemic strain.[17, 58–61] Furthermore, most health authorities were well prepared for the likelihood of local epidemics within a few months of the WHO global pandemic alert in April 2009. These modeling predictions had likely influenced the WHO to not issue travel alerts during the 2009 pandemic (unlike during the 2003 epidemic of Severe Acute Respiratory Syndrome)[62] and were eventually consistent with the rate of international spread of the pdmH1N1 virus.

Rapid global dissemination of pdmH1N1 implied that containment strategies would not be sensible, and shortly after announcing the advent of the 2009 influenza pandemic, the WHO recommended that countries should focus on strategies for local mitigation but not containment.[63]. Several groups consistently concluded that large-scale vaccination targeted at schoolchildren during the early phase of a pandemic would be the most efficient use of vaccines across a wide range of plausible scenarios.[47, 50, 64, 65] However, given that vaccine production required at least 4–6 months, initial waves of the pandemic would be largely over in most countries by the time pandemic vaccines became available. Therefore, large-scale vaccination at that stage would probably have limited value in reducing morbidity and mortality and a more relevant question was the optimal use of vaccines following an initial wave. A recent modeling study suggested that the optimal vaccination strategy would in general depend on the stage of epidemic at which vaccination begins.[48]

Mathematical modeling was also used in the “war-time” during the 2009 influenza pandemic to inform situational awareness and public health decision making. In one example, a mathematical modeling approach was used to interpret surveillance data on influenza-like illness.[66] Although in the initial phase the model was unable to predict the course of the epidemic, once the epidemic peaked the model was able to accurately predict how long the epidemic would last, and the final attack rate. In the UK, an age-structured mathematical model fitted to influenza-like illness reports was able to track the course of the epidemic through time and provide timely predictions on the timing and size of the winter 2009–10 wave [65]. The results were subsequently validated on serologic data which showed substantial attack rates among children in certain areas of the UK in the spring 2009 wave [67].

Because influenza pandemic preparedness plans were formulated based on epidemiological understanding of past pandemics, estimation of R₀ and T_g was a top public health priority when the 2009 pandemic began in order to help policymakers quickly putting their preparedness plans into perspective. Shortly after the emergence and global spread of pdmH1N1, its R₀ and T_g were estimated to fall within the ranges of previous pandemic influenza viruses,[68–70] implying that this pandemic was not likely to be any more severe than its predecessors. The next but more formidable challenge was to estimate infection attack rate and severity (e.g. case-fatality) in order to assess the burden that the pandemic would pose on the healthcare and economic system. While existing influenza pandemic surveillance systems typically tracked the number of lab-confirmed pdmH1N1 cases or patients presenting to the local healthcare system with influenza-like illness,[71] this represented only the tip of the iceberg of the actual number of infections because not all infected cases would seek care.[72] Without an accurate count of the number of infections in different age groups, mathematical modeling studies conducted during the early stage of the 2009 pandemic failed to predict the age distribution of pdmH1N1 infections which skewed towards school-aged children to a greater extent than predicted based on typical modeling assumptions.[65, 73] Accurate estimates of attack rates, severity and other important epidemiologic characteristics of pdmH1N1 only became available months after the pandemic began.[67, 74–77]

Discussion

While influenza pandemics occur infrequently, the possibility of many millions of deaths worldwide in a severe pandemic means that they present a significant threat to public health. While the 2009 pandemic was only of mild to moderate severity, the next pandemic may be more serious and countries will continue to update their pandemic plans to insure against the impact of a low-probability but severe pandemic. Mathematical models provide a systematic framework that can be used to analyze and interpret infectious disease data, as well as to predict the course of epidemics and the impact of potential interventions.

The use of mathematical models in the interpandemic period provided valuable information on epidemiologic characteristics of past pandemic influenza viruses. Building on such understanding of past pandemics, mathematical modelers built simulation models to show that a pandemic virus would inevitably reach all countries within a few months once it spreads in a city linked to the international air travel network. These computer simulations have also provided a systematic platform to assess the effectiveness of different pandemic containment and mitigation strategies that would otherwise be difficult or impossible to evaluate in empirical settings. In particular, these modeling studies have provided well-documented guidelines on the plausible outcomes of large-scale antiviral intervention and vaccination which were and will remain major components of national influenza pandemic plans.

While mathematical models have demonstrated their value in “peace-time”, in general they were not able to facilitate accurate prediction of epidemic size and severity in real-time during the 2009 influenza pandemic. One critical limitation was the difficulty in interpreting available surveillance data in most settings, and in particular information on the proportion of infections leading to mild or severe illness, which were needed for accurate model formulation and parameterization.[43, 65] In particular, if serologic data had been available during the early stages of the pandemic, these would have been invaluable for estimating age-specific attack rates and severity as well as eliciting potential differences in susceptibility among different age groups against the pandemic virus.[43, 65, 67] Such data could have greatly reduced the uncertainties associated with the use of laboratory-confirmed case counts or influenza-like illness rates adjusting for symptomatic proportions and bias in healthcare seeking behavior.[67, 74]

In conclusion, although mathematical modeling has shown limitations as a “war-time” risk-assessment tool during the 2009 pandemic, it has nonetheless played an important role in pandemic response. Its use has provided a systematic framework for revealing the weaknesses of existing pandemic surveillance systems and guiding how these systems should be strengthened in order to cope with future epidemics of influenza or other emerging infectious diseases. Table 1 gives a brief overview of the contributions and limitations of mathematical modeling on informing influenza pandemic preparedness and response that we have discussed in this review, which cover only a subset of all mathematical modeling studies on this topic. We envision that mathematical modeling will remain an important tool for infectious disease control in the future.

Table 1.

Some contributions and limitations of mathematical modeling on influenza pandemic preparedness and response.

Contributions

Limitations

Transmissibility and mean generation time of influenza Rate of global spread and limited effectiveness of travel restrictions Potential effectiveness of containment and mitigation strategies Optimal use of antivirals and control strategies for drug-induced antiviral resistance Optimal pandemic and pre-pandemic vaccination strategies Logistical requirement of mitigation and treatment strategies Strategies for strengthening influenza surveillance

Accurate severity estimates early in the pandemic Accurate epidemic forecasts during the early pandemic stages Remaining uncertainty over the public health and economic burden posed by the pandemic Remaining uncertainty over the explanation for seasonality of annual influenza epidemics No consensus on the effectiveness and feasibility of school closure