Abstract
To study the strategy in responding to target displacements during fast goal-directed arm movements, we examined how quickly corrections are initiated and how vigorously they are executed. We perturbed the target position at various moments before and after movement initiation. Corrections to perturbations before the movement started were initiated with the same latency as corrections to perturbations during the movement. Subjects also responded as quickly to a second perturbation during the same reach, even if the perturbations were only separated by 60 ms. The magnitude of the correction was minimized with respect to the time remaining until the end of the movement. We conclude that despite being executed after a fixed latency, these fast corrections are not stereotyped responses but are suited to the circumstances.
Keywords: Online control, Reaction time, Movement adjustment, Visuomotor control, Double-step
Introduction
Hand movements towards a target are normally under continuous visual control (Carlton 1981; Keele 1968; Whiting and Sharp 1974). One important source of information for the control of movements is the visually perceived position of the target. Continuous visual control is particularly important when the initially perceived position of the target is incorrect, which is the case if mistakes are made when interpreting the sensory information (as occurs when looking through new corrective glasses) or if the actual target position is altered. The latter is frequently used to study corrections to errors in the perceived target position (Goodale et al. 1986; Pelisson et al. 1986; Georgopoulos et al. 1981). Previous studies have utilized this paradigm to determine which sources of information are involved in the correction of experimentally introduced errors (Bard et al. 1999; Magescas et al. 2009; Prablanc and Martin 1992; Gielen et al. 1984; Sarlegna et al. 2003), to determine which neural areas are involved in the corrections (Day and Brown 2001; Desmurget et al. 1999; Reichenbach et al. 2010) and to characterize the adjustments themselves (Brenner and Smeets 1997; Komilis et al. 1993; van Sonderen and Denier van der Gon 1991; Veerman et al. 2008; Soechting and Lacquaniti 1983). This study examines the properties of movement adjustments to perturbations at different times during or before the movement.
We suggest three different strategies for the control of movement adjustments. These control strategies are defined in terms of the latency of the correction (the time needed to initiate a correction) and the intensity of the correction (the acceleration of the hand to achieve the correction). To control the adjustment of an ongoing movement, the first and most elementary strategy (strategy 1) is to initiate and accomplish the correction as fast as possible, thus with a minimal latency and a maximal intensity (Fig. 1a). This strategy ensures that there is as much time as possible left to make other adjustments. However, it has frequently been suggested that this is not how corrections are performed. Research indicates that when perturbations occur later in time, either the response latency decreases (Reichenbach et al. 2009) or the response intensity increases (Gritsenko et al. 2009; Liu and Todorov 2007; Shabbott and Sainburg 2009). Following these results, we suggest two other extreme strategies.
Fig. 1.
Panel a shows three different strategies to end on a position-perturbed target and their predictions for responses to two different manipulations. The continuous lines indicate the three different target displacement sequences. The dashed lines represent the 12 corresponding predicted responses. Response latency (l) is the amount of time that passes before the finger starts deviating. Response intensity (β) is depicted as the slope of the finger movement; in the analysis of the experiment we use a measure based on the peak acceleration to quantify the intensity. Panel b is a schematic representation of the three strategies and all other combinations of latency and intensity that could lead to successful movement adjustments (grey area)
The second proposed control strategy (strategy 2) is to gather as much information as possible before the adjustment is initiated and therefore to make corrections as late as possible with a maximal intensity (Fig. 1a). This strategy ensures that one does not make surplus corrections. The third strategy (strategy 3) is to respond as soon as possible to the perturbation, thus with a minimal latency, and to adjust the speed of the response to the time left to make the correction (Fig. 1a). The advantage of this strategy is that the responses are not too vigorous and therefore probably also more accurate. These three strategies are the extremes of a set of possible successful strategies (Fig. 1b). The three strategies differ in the timing and intensity of the responses and are formulated independently of the sources of information that are used to achieve the corrections. To evaluate which strategy is used for controlling movement corrections, we subjected subjects to target perturbations of similar size early, late (Fig. 1a: Manipulation 1), or both early and late (Fig. 1a: Manipulation 2) in the movement and compared the latency and intensity of the responses to these perturbations with the predictions outlined in Fig. 1.
Method
Subjects
We executed the experiment in two sessions. Most of the experimental set-up and data analysis used was the same for both sessions; the exceptions are explicitly mentioned. Ten naïve subjects (5 women) aged 24–30 years participated in the first session. Seven other naïve subjects (4 women) aged 24–35 years participated in the second session. They were all right-handed and had normal or corrected-to-normal vision. All subjects gave their informed consent. This study is part of a programme that has been approved by the ethics committee of the faculty of Human Movement Sciences.
Experimental set-up
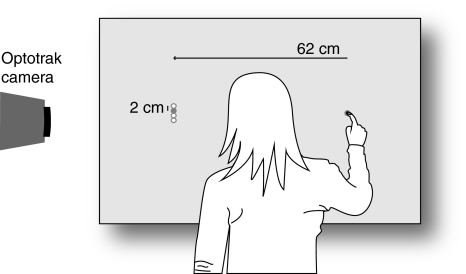
Subjects stood in front of a large back-projection screen (width: 124.5 cm; height: 99.5 cm; tilted backwards by 30°). The coloured stimuli and the white background were back-projected (InFocus DepthQ Stereoscopic Projector; resolution: 1,024 × 768 pixels; screen refresh rate: 100 Hz) on the projection screen (Techplex 150, acrylic rear projection screen). This set-up (see Fig. 2) provided the subjects with a clear view of the stimuli as well as of their arm, hand and finger. An Optotrak 3020 position sensor located to the left of the screen determined the position of a marker (500 Hz) attached to the left side of the tip of the right index finger.
Fig. 2.
Experimental set-up
The experiment was executed within Matlab. The stimuli were programmed with the Psychophysics Toolbox (Brainard 1997), and the Optotrak system was controlled with the Optotrak Toolbox (Franz 2004). In order to synchronize the appearance of the stimuli on the screen with the start of the trial, a flash in the upper left corner of the screen activated a photodiode connected to the parallel port of the computer at the same time as each stimulus. To ensure that subjects did not see the outline of the photodiode, the white background did not include the top 10 cm of the screen.
Experimental design
We used a single starting position for all trials (pink dot with radius of 1.5 cm) and four different target locations (pink dots with radius of 1 cm). The starting position was located 31 cm to the right of the screen centre. There were two initial target locations, both 62 cm to the left of the starting position but, respectively, 1 cm higher or lower than the starting position. The target perturbation was always 2 cm up or down with respect to the previous target location, resulting in four different final target locations.
In each session, there were four different conditions (Fig. 3). The only difference between the sessions was the timing of the perturbations. In the single-step condition, the target jumped from the starting position to one of the two target locations and stayed there throughout the trial. In the double-step conditions, the target jumped to one of the two target locations after which it jumped 2 cm up or down, 100 or 300 ms after the trial started (170 or 230 ms after the trial started in the second session). In the triple-step condition, the target jumped to one of the two target locations, jumped 2 cm up or down 100 ms after trial start (170 ms in the second session) and jumped back to the previous location 300 ms after trial start (230 ms in the second session). Thus, in the triple-step condition of the first session, the target was at the perturbed position for 200 ms. In the second session, this was the case for 60 ms. For all conditions, the first target jump could be either up or down, to one of the two target locations. For the double- and triple-step conditions, the next target jumps could also be either up or down. This leads to fourteen different configurations per session (Fig. 3) that were each repeated 15 times, resulting in 210 trials. The order of the configurations was randomized within blocks of fourteen different trials.
Fig. 3.
The 14 configurations grouped by the 4 conditions of each session. The vertical target location is shown as a function of time. The sessions only differ in the timing of the changes. During the initial step (t = 0), the target also moved 62 cm to the left
Procedure
Subjects were instructed to move their finger to the starting position and wait there for the target and a beep. The beep occurred at a random moment 2.5–3.5 s after the appearance of the starting position. The beep was the trigger to move as fast and as accurately as possible to the target that stepped at about the same moment to the other side of the screen (and 1 cm up or down). Subjects were free to lift their hand off the surface when moving to the target. Due to differences between the delays in generating images and beeps, the target appeared on average 23 ms after the beep.
Before the measurement started, subjects were given 20 practice trials to get familiar with the set-up and the speed with which they could move. Throughout the experiment, subjects received feedback about their performance. If the target was missed, it turned red. If it was hit, it exploded in one of nine colours (from red for slow movements to green for fast movements) and a score was presented. This score indicated the speed with which the trial was completed. A high score list was made to motivate the subjects. They were also encouraged verbally by the experimenter to move faster if they were slow. There was a 10-min break after 105 trials (halfway).
Data analysis
From the position information obtained with the Optotrak system, we determined the acceleration in vertical direction by numerical double differentiation. We low-pass-filtered these time series with a second-order recursive, bidirectional Butterworth filter at 50 Hz. The moment of movement initiation was defined as the last moment before the first peak in the speed (measured in three-dimensional space) at which the speed was lower than 0.02 m/s. The reaction time was defined as the time that elapsed between the beep and movement initiation.
Analysis of the reaction times showed that one subject of the second session had an average reaction time of 285 ms. Thus, on average, he initiated his movement after both the perturbations had occurred and after the time at which we would expect a reaction to the first perturbation. We therefore excluded this subject from further analysis. Of the remaining 3,360 trials (16 subjects; 210 trials each), 13 were excluded because the marker did not remain visible throughout the movement, 10 were excluded because the movement was initiated before the beep, and 11 were excluded because the movement was initiated more than 500 ms after the beep.
The method of Schot et al. (2010) was applied to determine the end of the movement. Four different characteristics of the movement were converted into a 0–1 probability of each data point being the end of the movement: the position in horizontal direction, the position perpendicular to the screen, the speed and the elapsed time. For the horizontal direction, we searched for an endpoint within a range that extends for 4 cm to either side of the target. Positions outside the range were considered to have zero probability of being the end of the movement. Within the range, the most leftward position was considered to have the highest probability and the most rightward position was considered to have the lowest probability of being the end of the movement. For intermediate points, the likelihood scaled linearly. For the position perpendicular to the screen, a binary function was constructed, whereby the probability of being the end position was 1 if the position was 1 cm or closer to the screen and 0 if the position was more than 1 cm away from the screen. The speed was converted into a linear 0–1 probability distribution, whereby the likelihood of the end of the movement was 0 when the velocity was highest and 1 when the velocity was zero. Finally, we defined a probability distribution that depended on the elapsed time. This was a linearly decreasing probability starting at trial start with value 1 and decreasing to 0 over 800 ms. This distribution was necessary to ensure that we took the first moment in time after the hand stopped, because some subjects sustained their end position. The four distributions were multiplied, which resulted in one overall probability distribution. The time of the peak of this distribution was considered to be the end of the movement. The movement time was the difference in time between movement initiation and movement end.
For each subject and each configuration, the average vertical positions and accelerations were computed over the 15 repetitions for each moment in time. These profiles were averaged over the two initial target locations, resulting in 7 average position and acceleration profiles for each subject. To determine the response latency and intensity, we computed the difference between average acceleration profiles for targets that jumped up and targets that jumped down (in the same condition). The intensity of the response was defined as the maximum in this difference in acceleration within 200 ms of the perturbation. To determine the response latency, we adapted the method described by Veerman et al. (2008). A line was drawn through the points at which the difference in acceleration reached 45 and 70% of the first peak difference that occurred more than 100 ms after the perturbation. Response latency was defined as the interval between the moment of the perturbation and the moment that this line crossed a difference value of zero. We were not able to define a latency for responses to the first step in the triple-step condition of session 2 (after 170 ms; Fig. 3) for one subject, because the difference in acceleration was very small.
For each subject and condition, we determined two measures of response accuracy. The first measure is the systematic difference in the vertical direction between the endpoints for targets that had jumped up and targets that had jumped down. For all double- and triple-step conditions, we first superimposed the distributions of the endpoints for the two different initial target locations and then computed the difference between the medians of the distributions for targets that jumped up and targets that jumped down. If subjects’ average endpoints had been perfectly on the target, the difference between the distributions of endpoint for the double-step conditions would be 4 cm, and there would be no difference for the triple-step condition. We analysed the deviation from this faultless difference for each subject. The second measure for the accuracy of the response is the standard deviation of each of the seven endpoint distributions, which we determined in both horizontal and vertical directions.
To check whether there were differences between the conditions in reaction time and movement time, we executed two Friedman’s ANOVAs. We performed paired-samples t tests to compare the response latencies to the double-step early perturbation with the response latencies to the double-step late perturbation. Furthermore, we compared the double-step late latency to the triple-step late latency with paired-samples t-tests to examine whether there was any influence of the previous perturbation during the trial on the response latency. We performed a Friedman’s ANOVA and post hoc Wilcoxon signed rank tests to compare the response intensities in the different conditions. We performed a Friedman’s ANOVA to determine whether the difference between up-and-down jumping targets’ endpoint distributions of the double-step early, double-step late and triple-step conditions were significantly different from each other and Wilcoxon signed rank tests to determine whether the difference for each condition was significantly different from 0. Another Friedman’s ANOVA was performed to check whether there were differences in standard deviation between the seven endpoint distributions. For all statistical tests, P < 0.05 was considered statistically significant.
Results
Reaction time and movement time
Average vertical displacements as a function of time since target appearance are displayed in Fig. 4. The moments of target perturbation are indicated with vertical lines. The figure shows that subjects make adjustments in response to the early and late perturbations, and that for the triple-step condition they first adjust in one direction and then back. It also shows that the vertical acceleration in response to the early target perturbation is smaller than that to the late perturbation.
Fig. 4.
Panels a and b show the average vertical hand position and acceleration for each kind of perturbation. The continuous lines are for perturbations up; dashed lines for perturbations down. The grey area around the single-step trace represents the standard error of the mean between the subjects. The vertical lines indicate the moments of the perturbations. For movements that ended before 600 ms, we used the position at the end of the movement for averaging from that moment. Panel c shows the difference in acceleration between movements to targets that jumped up and targets that jumped down
There were no significant differences in reaction time between the conditions; the median RT was 171 ms (IQR = 38 ms) in the first session and 177 ms (IQR = 38 ms) in the second session. Thus, the perturbations that occurred during the reaction time did not delay movement initiation. The perturbations did not affect the movement time either; the median MT was 367 ms (IQR = 52 ms) in the first session and 355 ms (IQR = 60 ms) in the second session. Beside the strategies described in Fig. 1, subjects could also have adapted their movement times to provide more time for making corrections. They did not do so.
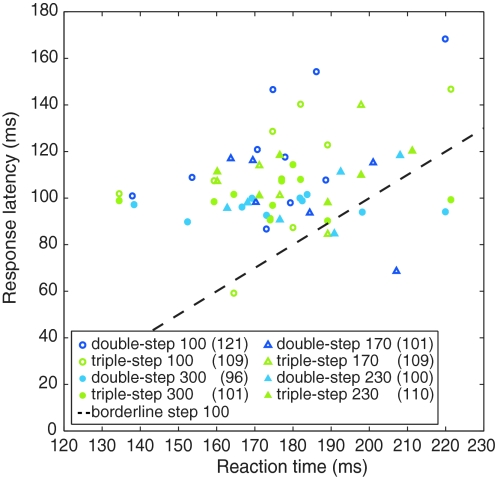
Response latency
Most subjects had response latencies of about 100 ms, but for the perturbation at 100 ms, several subjects had longer latencies (open circles in Fig. 5). A paired-samples t test between double-step 100 and double-step 300 ms revealed that the response latency to the early perturbation was significantly longer than the latency to the late perturbation (t(9) = 3.0, P = 0.016, 25-ms difference). Figure 5 shows that the subjects whose response latency was large for the early perturbation had long reaction times. As the 100-ms perturbation occurred before the onset of the movement of the hand, and our method to determine the latency only enabled us to detect a latency once the subject’s hand was moving, subjects who had long reaction times could not have short-latency reactions to the 100-ms perturbations because they had not initiated their movement yet when the response was expected. We therefore interpret the significant difference between the latencies to early and late perturbations as an artefact. The response latencies in the early and the late conditions of the second session were not significantly different (t(5) = 0.2, P = 0.88, 2-ms difference). Thus, the movement adjustments were initiated as fast as possible, independent of the timing of the perturbation, which is in accordance with strategies 1 and 3.
Fig. 5.
Each subject’s response latencies to the different perturbations in relation to their reaction times. The average latencies for the eight kinds of perturbations are displayed in the legend (in ms). The dashed line shows the region below which no latencies can be found for the 100-ms perturbation, because the movement has not started
Figure 4c shows that the responses in the triple-step conditions resemble a combination of the responses to the early perturbations and the responses to the late perturbations. In these averages, the responses to the last step in the triple-step conditions look as if they might occur a little bit later than the corresponding responses in the double-step conditions. We performed a paired-samples t-test between the response latencies to the late perturbations in the double-step and the triple-step conditions to determine whether the preceding jump in the triple-step condition influenced the response latency. The average latency to respond to the double-step 230 perturbations did not differ significantly from the latency to respond to the triple-step 230 perturbation (t(5) = 2.2, P = 0.08, 10-ms difference). Neither did the average latency for the double-step 300 perturbation differ significantly from that for the triple-step 300 perturbation (t(9) = 2.2, P = 0.052, 4-ms difference). Thus, the response latency is independent of previous perturbations during the trial.
Response intensity
The response intensities for each condition and each subject are plotted in Fig. 6. Friedman’s ANOVAs revealed a significant difference between the conditions both for session 1 (χ 2 = 24.2, P < 0.01) and session 2 (χ 2 = 15.2, P < 0.01). Post hoc comparisons between all combinations of the double-step early, triple-step early, double-step late and triple-step late conditions showed that for the four combinations in which an early perturbation was compared to a late perturbation, the response intensities to the early perturbations were significantly smaller than the intensities to the late perturbations (session 1, all four comparisons: Z = 2.8, P = 0.01; session 2, all four comparisons: Z = 2.2, P = 0.03), whereas for the combinations in which two early or two late perturbations were compared there were no significantly differences. An increased intensity for late perturbations (i.e. when there is less time left to correct) is consistent with strategy 3, according to which the duration of the response is maximized and the magnitude of the correction is minimized.
Fig. 6.
Relationship between the time left to correct the movement and the intensity of the response. Each symbol represents the average time and response intensity for the indicated condition for one subject
In order to determine whether the intensity of the responses is indeed minimized, we need to know how small the responses could have been. Small responses require the adjustments to be smooth, so we computed the intensity for maximally smooth movements (Flash and Hogan 1985). We computed 4-cm minimum jerk trajectories (4 cm is the difference between perturbations up and down) over a range of movement times. The acceleration profiles of these minimum jerk trajectories were calculated, and we took the peak of the acceleration as the intensity of the minimum jerk response (as was done for the data). Since measurement noise leads to an increase in the peak acceleration, we added noise to the minimal jerk trajectories. To get an indication of how much noise to add, we calculated (for each subject) the maximal difference in acceleration between the single-step and the double-step late conditions before the correction starts (from 200 to 300 ms after trial start, when any difference must be due to noise). We averaged the obtained differences in acceleration and added the resulting 2.9 m/s2 to the minimum jerk prediction. The resulting prediction gives a good description of the data (dashed line in Fig. 6). If we ignore the two cases in which the perturbations occurred when there was only about 170 ms left before the end of the movement, because the deviation of these points from the prediction is more likely to be due to variability in the time left than to variability in the response intensity, 66% of the variance in the data is accounted for by the prediction based on minimizing jerk. Apparently the changes in intensity are well adjusted to reach the target with a smooth movement within the remaining time, which is in accordance with strategy 3.
Response accuracy
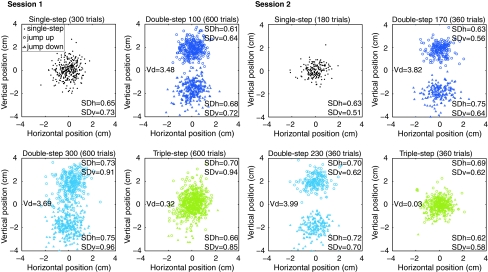
On average, subjects were able to hit the target on more than 60% of the trials. The end positions of the movements are shown in Fig. 7. Friedman’s ANOVAs revealed that the vertical differences between endpoint distributions for targets that had jumped up and down in the double-step early, double-step late and triple-step conditions were not significantly different from each other (in either session). We also tested whether the distance between the distributions was significantly different from the distance that would arise from complete adjustments. For the double-step perturbations, the distance between the final target positions was 4 cm, and for the triple-step condition, this was zero. Wilcoxon signed rank tests revealed that the distances between the double-step 300 distributions and between the double-step 100 distributions were significantly smaller than would arise from complete adjustments (resp. Z = 2.6, P = 0.02; Z = 2.6, P = 0.01). The endpoint distributions in the second session did not differ significantly from complete adjustments.
Fig. 7.
End positions of all trials for each condition and session. Vd indicates the vertical distance between the medians for jumps up and down. The standard deviations in horizontal (SDh) and vertical direction (SDv) are also given (average values across subjects)
For the standard deviations in the first session, Friedman’s ANOVAs revealed significant differences between the seven endpoint distributions in both the horizontal (χ 2 = 13.7, P = 0.03) and the vertical direction (χ 2 = 23.2, P < 0.01). Post hoc Wilcoxon signed rank tests revealed numerous significant differences in both directions, see Table 1 for Z-scores. All these differences were in the first session, and they all involved target position changes at 300 ms resulting in larger standard deviations. This is probably related to the high (required) response intensity in those conditions, because there was less time to make the correction (Fig. 6).
Table 1.
Z-scores and P values for the significant differences between the standard deviations in different conditions, both in horizontal and vertical direction
| Z | P | |
|---|---|---|
| Horizontal | ||
| D300 down > Single step | 2.09 | 0.04 |
| D300 down > D100 up | 2.80 | 0.01 |
| D300 down > D100 down | 2.09 | 0.04 |
| D300 down > Triple down | 2.29 | 0.02 |
| D300 up > D100 up | 2.99 | 0.05 |
| Triple up > D100 up | 1.99 | 0.05 |
| Vertical | ||
| D300 up > D100 up | 2.40 | 0.02 |
| D300 down > D100 up | 2.50 | 0.01 |
| Triple up > D100 up | 2.80 | 0.01 |
| Triple down > D100 up | 1.99 | 0.05 |
| D300 up > D100 down | 2.60 | 0.01 |
| D300 down > D100 down | 2.29 | 0.02 |
| Triple up > D100 down | 2.89 | 0.01 |
| Triple up > Single step | 2.80 | 0.01 |
The condition with the larger standard deviation is mentioned first
Discussion
We aimed at identifying the strategy that is used for controlling movement corrections. To discriminate between different strategies, we perturbed the target position at different phases of the movement and examined the characteristics of the response. We found that the timing of the perturbation did not influence the response latency (about 100 ms) but did affect the response intensity. When there is less time to adjust the movement, the correction is more vigorous. These results are congruent with strategy 3 and thus also with the results of Liu and Todorov (2007); Gritsenko et al. (2009) and Shabbott and Sainburg (2009), although the latencies in the last study were considerably longer (in the order of 300 ms). Our results are also consistent with studies that show responses with the same latencies to target perturbations of different sizes and response intensities that were adjusted to the size of the perturbation (Brenner and Smeets 1997; Gritsenko et al. 2009; Shabbott and Sainburg 2009; Veerman et al. 2008).
Our finding that the response latency is constant is not congruent with Reichenbach et al. (2009), who found a decrease in response latency when the perturbation occurred later during the movement. We propose that these seemingly contradicting findings are the result of the way in which the latency was analysed. Reichenbach et al. (2009) determined the response latency with a fixed threshold, which was a deviation away from the average trajectory that was larger than 25% of the amplitude of the displacement. The consequence of using such a method is that if responses are less vigorous, they will be considered to have occurred later in time. Other authors have also used a fixed threshold to analyse response latencies to perturbations in a grasping task with objects of different sizes and found a similar time-dependent latency (Hesse and Franz 2009; van de Kamp et al. 2009). A fixed threshold would not be a problem if corrections were performed in accordance with strategy 2, because then the strength of the correction would always be the same. However, we found an increase in the response intensity for later perturbations. The method of Veerman et al. (2008) allows us to compare the latencies of responses of different amplitudes.
Our finding that the latency of the response is constant also implies that movements are not controlled by strategy 2, according to which adjustments are postponed to a late stage of the movement, as suggested by many who assume that the initial part of the movement is under open-loop control, with online control emerging during the deceleration phase (Elliott et al. 2001; Komilis et al. 1993; Turrell et al. 1998; van der Meulen et al. 1990; Woodworth 1899). We found movement corrections near movement initiation. Van Sonderen and Denier van der Gon (1991) measured longer response latencies, but they also reported responses to target perturbations that took place before movement onset. These results strongly suggest that the online use of visual information is already operating before the movement actually begins.
The responses in the triple-step condition were also consistent with strategy 3. For this particular condition, it would have been more efficient to delay the response (as in strategy 2), because there was no need for a response at all. However, to do so, one would have to delay the response to the first target jump. This is not how the task was performed; subjects showed two opposing corrections with appropriate intensities. When saccadic eye movements are made between two targets, the duration of fixations is longer before return saccades than before other fixations (Hooge and Frens 2000). Thus, it takes more time to generate a return saccade compared to other saccades. Our results show that an equivalent delay in movement generation does not occur for corrections of hand movements, since even when the target was only at a perturbed position for 60 ms, the response latency to the second perturbation was 100 ms. These data provide a strong argument for online control with a constant (minimal) delay of 100 ms.
Studies in which the visual representation of the hand is perturbed, instead of the position of the target, reveal corresponding results. Franklin and Wolpert (2008) found no difference between response latencies to early and late perturbations, and Briere and Proteau (2011) reported no difference in response latency between back-and-forth perturbations in a paradigm similar to our triple-step condition. Although the response latencies to perturbations of the visual representation of the hand are somewhat longer than to target perturbations, the responses are very similar. This is an indication that the same controller is responsible for corrections to changes in the visual information of the target and the hand (Brenner and Smeets 2003).
Subjects had more variability and ended too far in the direction of the previous target when the perturbation occurred after 300 ms. Liu and Todorov (2007) also found that subjects made incomplete corrections in a late perturbation condition. They argue that this inadequacy is due to a change in the feedback gain during the movement, with the aim to stably end the movement, if necessary not on the target. Most of our findings are consistent with this, because despite the systematic shift in the median end position in the direction of the previous target position, the variability was also larger, thus, presumably a balance was found between variability and accuracy. However, the model of Liu and Todorov (2007) cannot explain the slight systematic undershoot that we found for the early perturbation condition, because the variance in this condition was not increased.
In conclusion, the mechanism responsible for online corrections has a minimal response latency of 100 ms and uses an optimal response intensity based on the most recent sensory information to find the most suitable adjustment at each moment, from before movement onset until just before reaching the target.
Acknowledgments
This work was supported by a grant from the Netherlands Organisation for Scientific Research (NWO), Vici grant 453-08-004.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Bard C, Turrell Y, Fleury M, Teasdale N, Lamarre Y, Martin O. Deafferentation and pointing with visual double-step perturbations. Exp Brain Res. 1999;125(4):410–416. doi: 10.1007/s002210050697. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10(4):433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Brenner E, Smeets JBJ. Fast responses of the human hand to changes in target position. J Mot Behav. 1997;29(4):297–310. doi: 10.1080/00222899709600017. [DOI] [PubMed] [Google Scholar]
- Brenner E, Smeets JBJ. Fast corrections of movements with a computer mouse. Spat Vis. 2003;16(3–4):365–376. doi: 10.1163/156856803322467581. [DOI] [PubMed] [Google Scholar]
- Briere J, Proteau L. Automatic movement error detection and correction processes in reaching movements. Exp Brain Res. 2011;208(1):39–50. doi: 10.1007/s00221-010-2458-1. [DOI] [PubMed] [Google Scholar]
- Carlton LG. Visual information: the control of aiming movements. Q J Exp Psychol-A. 1981;33:87–93. doi: 10.1080/14640748108400771. [DOI] [Google Scholar]
- Day BL, Brown P. Evidence for subcortical involvement in the visual control of human reaching. Brain. 2001;124(Pt 9):1832–1840. doi: 10.1093/brain/124.9.1832. [DOI] [PubMed] [Google Scholar]
- Desmurget M, Epstein CM, Turner RS, Prablanc C, Alexander GE, Grafton ST. Role of the posterior parietal cortex in updating reaching movements to a visual target. Nat Neurosci. 1999;2(6):563–567. doi: 10.1038/9219. [DOI] [PubMed] [Google Scholar]
- Elliott D, Helsen WF, Chua R. A century later: Woodworth’s (1899) two-component model of goal-directed aiming. Psychol Bull. 2001;127(3):342–357. doi: 10.1037/0033-2909.127.3.342. [DOI] [PubMed] [Google Scholar]
- Flash T, Hogan N. The coordination of arm movements: an experimentally confirmed mathematical model. J Neurosci. 1985;5(7):1688–1703. doi: 10.1523/JNEUROSCI.05-07-01688.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin DW, Wolpert DM. Specificity of reflex adaptation for task-relevant variability. J Neurosci. 2008;28(52):14165–14175. doi: 10.1523/JNEUROSCI.4406-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franz VH (2004) The optotrak toolbox, December 21, 2007 edn. Ontario, Northern Digital Inc
- Georgopoulos AP, Kalaska JF, Massey JT. Spatial trajectories and reaction times of aimed movements: effects of practice, uncertainty, and change in target location. J Neurophysiol. 1981;46(4):725–743. doi: 10.1152/jn.1981.46.4.725. [DOI] [PubMed] [Google Scholar]
- Gielen CCAM, van den Heuvel PJM, van Gisbergen JAM. Coordination of fast eye and arm movements in a tracking task. Exp Brain Res. 1984;56(1):154–161. doi: 10.1007/BF00237452. [DOI] [PubMed] [Google Scholar]
- Goodale MA, Pelisson D, Prablanc C. Large adjustments in visually guided reaching do not depend on vision of the hand or perception of target displacement. Nature. 1986;320(6064):748–750. doi: 10.1038/320748a0. [DOI] [PubMed] [Google Scholar]
- Gritsenko V, Yakovenko S, Kalaska JF. Integration of predictive feedforward and sensory feedback signals for online control of visually guided movement. J Neurophysiol. 2009;102(2):914–930. doi: 10.1152/jn.91324.2008. [DOI] [PubMed] [Google Scholar]
- Hesse C, Franz VH. Corrective processes in grasping after perturbations of object size. J Mot Behav. 2009;41(3):253–273. doi: 10.3200/JMBR.41.3.253-273. [DOI] [PubMed] [Google Scholar]
- Hooge ITC, Frens MA. Inhibition of saccade return (ISR): spatio-temporal properties of saccade programming. Vision Res. 2000;40(24):3415–3426. doi: 10.1016/S0042-6989(00)00184-X. [DOI] [PubMed] [Google Scholar]
- Keele SW. Movement control in skilled motor performance. Psychol Bull. 1968;70(6):387–403. doi: 10.1037/h0026739. [DOI] [Google Scholar]
- Komilis E, Pelisson D, Prablanc C. Error processing in pointing at randomly feedback-induced double-step stimuli. J Mot Behav. 1993;25(4):299–308. doi: 10.1080/00222895.1993.9941651. [DOI] [PubMed] [Google Scholar]
- Liu D, Todorov E. Evidence for the flexible sensorimotor strategies predicted by optimal feedback control. J Neurosci. 2007;27(35):9354–9368. doi: 10.1523/JNEUROSCI.1110-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magescas F, Urquizar C, Prablanc C. Two modes of error processing in reaching. Exp Brain Res. 2009;193(3):337–350. doi: 10.1007/s00221-008-1629-9. [DOI] [PubMed] [Google Scholar]
- Pelisson D, Prablanc C, Goodale MA, Jeannerod M. Visual control of reaching movements without vision of the limb. II. Evidence of fast unconscious processes correcting the trajectory of the hand to the final position of a double-step stimulus. Exp Brain Res. 1986;62(2):303–311. doi: 10.1007/BF00238849. [DOI] [PubMed] [Google Scholar]
- Prablanc C, Martin O. Automatic control during hand reaching at undetected two-dimensional target displacements. J Neurophysiol. 1992;67(2):455–469. doi: 10.1152/jn.1992.67.2.455. [DOI] [PubMed] [Google Scholar]
- Reichenbach A, Thielscher A, Peer A, Bulthoff HH, Bresciani JP. Seeing the hand while reaching speeds up on-line responses to a sudden change in target position. J Physiol. 2009;587(Pt 19):4605–4616. doi: 10.1113/jphysiol.2009.176362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reichenbach A, Bresciani JP, Peer A, Bulthoff HH, Thielscher A (2010) Contributions of the PPC to Online Control of Visually Guided Reaching Movements Assessed with fMRI-Guided TMS. Cereb Cortex. doi:10.1093/cercor/bhq225 [DOI] [PMC free article] [PubMed]
- Sarlegna F, Blouin J, Bresciani JP, Bourdin C, Vercher JL, Gauthier GM. Target and hand position information in the online control of goal-directed arm movements. Exp Brain Res. 2003;151(4):524–535. doi: 10.1007/s00221-003-1504-7. [DOI] [PubMed] [Google Scholar]
- Schot WD, Brenner E, Smeets JBJ. Robust movement segmentation by combining multiple sources of information. J Neurosci Methods. 2010;187(2):147–155. doi: 10.1016/j.jneumeth.2010.01.004. [DOI] [PubMed] [Google Scholar]
- Shabbott BA, Sainburg RL. On-line corrections for visuomotor errors. Exp Brain Res. 2009;195(1):59–72. doi: 10.1007/s00221-009-1749-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soechting JF, Lacquaniti F. Modification of trajectory of a pointing movement in response to a change in target location. J Neurophysiol. 1983;49(2):548–564. doi: 10.1152/jn.1983.49.2.548. [DOI] [PubMed] [Google Scholar]
- Turrell Y, Bard C, Fleury M, Teasdale N, Martin O. Corrective loops involved in fast aiming movements: effect of task and environment. Exp Brain Res. 1998;120(1):41–51. doi: 10.1007/s002210050376. [DOI] [PubMed] [Google Scholar]
- van de Kamp C, Bongers RM, Zaal FTJM. Effects of changing object size during prehension. J Mot Behav. 2009;41(5):427–435. doi: 10.3200/35-08-033. [DOI] [PubMed] [Google Scholar]
- van der Meulen JHP, Gooskens RHJM, Denier van der Gon JJ, Gielen CC, Wilhelm K. Mechanisms underlying accuracy in fast goal-directed arm movements in man. J Mot Behav. 1990;22(1):67–84. doi: 10.1080/00222895.1990.10735502. [DOI] [PubMed] [Google Scholar]
- van Sonderen JF, Denier van der Gon JJ. Reaction-time-dependent differences in the initial movement direction of fast goal-directed arm movements. Hum Mov Sci. 1991;10:713–726. doi: 10.1016/0167-9457(91)90024-R. [DOI] [Google Scholar]
- Veerman MM, Brenner E, Smeets JBJ. The latency for correcting a movement depends on the visual attribute that defines the target. Exp Brain Res. 2008;187(2):219–228. doi: 10.1007/s00221-008-1296-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whiting HTA, Sharp RH. Visual occlusion factors in a discrete ball-catching skill. J Mot Behav. 1974;6:11–16. doi: 10.1080/00222895.1974.10734974. [DOI] [PubMed] [Google Scholar]
- Woodworth RS (1899) The accuracy of voluntary movement. Psychol Rev 3 (Monograph Suppl 3 (Whole No. 13)): 1–114