Direct measurements of DNA-mediated colloidal interactions and their quantitative modeling

Abstract

DNA bridging can be used to induce specific attractions between small particles, providing a highly versatile approach to creating unique particle-based materials having a variety of periodic structures. Surprisingly, given the fact that the thermodynamics of DNA strands in solution are completely understood, existing models for DNA-induced particle interactions are typically in error by more than an order of magnitude in strength and a factor of two in their temperature dependence. This discrepancy has stymied efforts to design the complex temperature, sequence and time-dependent interactions needed for the most interesting applications, such as materials having highly complex or multicomponent microstructures or the ability to reconfigure or self-replicate. Here we report high-spatial resolution measurements of DNA-induced interactions between pairs of polystyrene microspheres at binding strengths comparable to those used in self-assembly experiments, up to 6 k_BT. We also describe a conceptually straightforward and numerically tractable model that quantitatively captures the separation dependence and temperature-dependent strength of these DNA-induced interactions, without empirical corrections. This model was equally successful when describing the more complex and practically relevant case of grafted DNA brushes with self-interactions that compete with interparticle bridge formation. Together, our findings motivate a nanomaterial design approach where unique functional structures can be found computationally and then reliably realized in experiment.

A promising route to forming unique nanoparticle-based materials is directed self-assembly—where the interactions among multiple species of suspended particles are intentionally designed to favor the self-assembly of a specific cluster arrangement or nanostructure. DNA provides a natural tool (1–3) for directed particle assembly because DNA double helix formation is chemically specific—particles with short single-stranded DNA-grafted on their surfaces will be bridged together if and only if those strands have complementary base sequences, allowing the two strands to spontaneously hybridize to form double-stranded DNA. Moreover, the temperature-dependent stability of such DNA bridges allows the resulting attraction to be modulated (1, 2) from negligibly weak to effectively irreversible over a convenient range of temperatures. Several groups have recently used such interactions to drive the assembly of three-dimensional (3D), crystalline structures from nanoscopic (4–8) and microscopic (9, 10) particles. Ultimately, we envision a highly versatile nanomaterial design protocol in which a user-designed matrix of specific interactions among multiple particle species leads to sequential or even hierarchical assembly of complex particle structures, controlled by a user-designed thermal program. Unlike this vision of designable, sequential, and hierarchical assembly among a significant number of different components, current experiments typically employ only one or two particle species, and only one or two pairs of interacting DNA strands.

We claim that the primary barrier to progress in creating more complex DNA-directed particle assemblies is the lack of a reliable, quantitative interaction model to both guide experiments and enable computational studies of structure nucleation, growth, or multistep material processing. Several groups have reported interaction models (9, 11–15), all based on capturing the entropic contributions and hybridization thermodynamics of individual grafted DNA molecules. While these models qualitatively describe the existing interaction measurements based on the temperature-dependent aggregation-disaggregation transition of DNA-labeled nanoparticles (16), microparticles (12, 14, 17–19), and polymers (20), or direct measurements with optical tweezers (9), they typically overpredict the interaction strength by roughly two orders of magnitude, corresponding to an unexpectedly large hybridization free energy difference of ∼5 k_BT per DNA bridge. Moreover, while the models predict that the interaction strength varies exponentially with temperature, they overestimate the steepness of the temperature dependence by roughly a factor of two. These disappointing findings are all the more surprising, given that DNA is so well understood—the hybridization free energy can typically be estimated a priori for any base sequence and its complement to better than 1 k_BT, and the entropic penalties associated with grafting and stretching polymer chains are well known.

Here we present high precision measurements of the DNA-induced interaction potentials between two microspheres, as a function of particle separation, temperature, and DNA composition. Unlike earlier modeling approaches that consider the interacting molecular degrees of freedom explicitly, we employ a mean-field approach based on chemical equilibration between two reactants having static, spatially varying concentration fields, whose form, in turn, is readily computed using a tethered freely jointed chain model. Our model successfully captures the separation and temperature dependence of the interaction quantitatively; it appears that earlier models overpredicted the interactions by not accounting for the spatially varying depletion of unreacted DNA strands in the gap between the particles. A simple generalization of this approach also quantitatively describes the interactions of a more complex but practically important system of spheres functionalized with mixed, interacting DNA strands. The ability to reliably model the interactions between particles with multiple, potentially interacting DNA strands will be key to the development of more complex nanomaterials using DNA-directed assembly.

Results and Discussion

Measurement of DNA-Induced Colloidal Interactions.

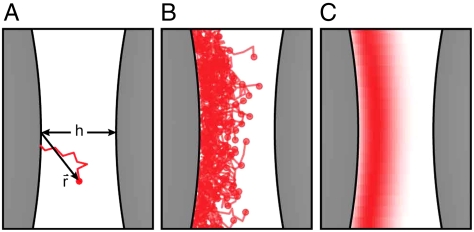
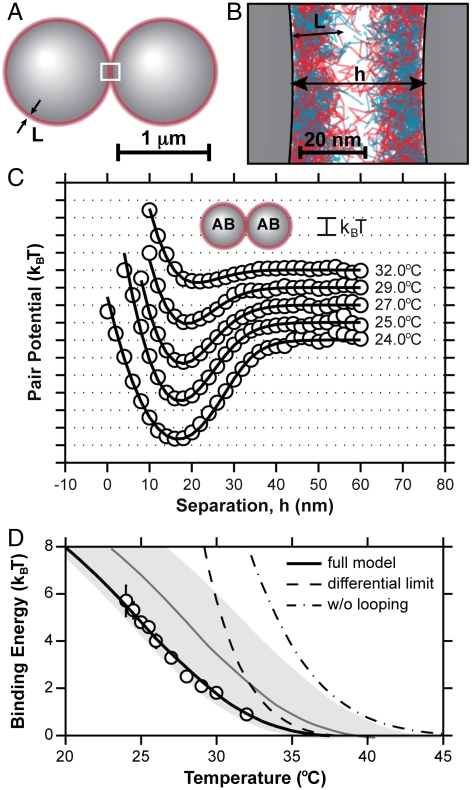
We synthesize DNA-functionalized colloids using a physical grafting technique described elsewhere (21). Briefly, a 5′-amine-modified, 65-oligonucleotide segment of single-stranded DNA (ssDNA) is covalently coupled to the terminal ends of a poly(ethylene oxide)-poly(propylene oxide)-poly(ethylene oxide) (PEO-PPO-PEO) triblock copolymer. Next, the DNA-labeled copolymer is adsorbed onto the surface of 1.1 μm diameter carboxyl-modified polystyrene colloids and firmly attached by swelling and deswelling the particles with toluene (see Materials and Methods). For a typical experiment, we prepare two different populations of DNA-labeled particles, A and B, which are functionalized with complementary sequences of DNA (Fig. 1A). Each particle is nominally labeled with 5,000 DNA strands and stabilized against nonspecific binding by the dense PEO brush. When two complementary particles come into close contact, h < 2L, where h is the relative separation between particles and L is the mean DNA brush thickness, their DNA clouds physically overlap and can hybridize together, inducing a short-range attraction between the spheres (Fig. 1B). Unlike previous studies that required a soluble linker strand to facilitate hybridization (9), our surface-tethered sequences (Fig. 1C) are complementary and can hybridize directly, improving the binding kinetics and allowing us to map the spatial dependence of much stronger interactions.

Fig. 1.

Measurement of DNA-mediated colloidal interactions. (A) Grafted ssDNA on two microspheres near contact can hybridize to form bridges (box). (B) Grafted DNA strands form a brush with a mean thickness, L ∼ 15 nm. (C) A and B oligonucleotides (red/blue) have a 7-basepair complementary section, 5′-GTCTACC-3′. (D) Experimental separation trajectories and histograms for A-A pairs show no binding, while A-B pairs show intermittent binding. (E) Equilibrium pair-interaction potentials for A-A and A-B interactions as a function of temperature. The circles are experimental data and the solid curves are model fits. A-B pairs show a temperature-dependent attraction, all pairs show a short-ranged repulsion.

To extract DNA-induced, pair-interaction potentials, we confine two DNA-functionalized particles in an extended optical potential and passively track and histogram their relative separation as they undergo Brownian motion (Fig. 1D) (see Materials and Methods). When the two particles are chemically identical (e.g., A-A or B-B interactions), we observe a very diffuse trajectory as the particles bump into one another and explore the underlying optical potential. When the particles are labeled with complementary sequences of DNA (A-B interactions), they follow a very different trajectory, transiently binding and unbinding as bridging DNA duplexes form and rupture between the particles. These results highlight the complete chemical specificity of the DNA-induced attraction.

The formation of transient bridges pulls the particles together and leads to the development of a sharp peak in the histogram of relative separation, P(h), near h ≈ L. The equilibrium pair free energy, F(h), can be computed from the experimental P(h), up to an additive constant, by inverting the Boltzmann relation, P(h) ∝ exp[-F(h)/k_BT], where k_BT is the thermal energy (22). Fig. 1E shows a representative set of measured pair-interaction potentials. All A-B pair potentials show a temperature-dependent, short-range attraction whose strength decreases monotonically with increasing temperature and a temperature-independent, soft repulsion near contact. The attractive interaction disappears completely at higher temperatures, but under those conditions, it is difficult to discriminate between A-A, A-B, and B-B interactions. As a control experiment, we verified that the A-A pair-interaction potential is purely repulsive, confirming the absence of any undesired attractive contributions to the pair potential (e.g., van der Waals, unintended hybridization, or unaccounted for optical forces).

Modeling DNA-Induced Interactions.

Computing the effective pair-interaction of DNA-grafted particles seems daunting at first blush: the confined region between the two microspheres contains scores of interacting random coil macromolecules packed together, that undergo complex, reversible conformational changes during hybridization, and are subjected to time varying forces from two microspheres undergoing coupled rotational and translational diffusion. Upon closer scrutiny, however, several simplifying assumptions break the problem down into conceptually clear and tractable parts. First, bridge formation due to DNA hybridization, while obviously a very complex molecular transformation, can be modeled as a “two-state” reaction of the type A + B↔AB, with a sequence-specific free energy change that can be readily computed from the nearest neighbor (NN) model (23). Second, the forces exerted by the spheres are small enough (< 0.5 pN) to not significantly destabilize double-stranded DNA (24) (see SI Text). Third, at typical DNA densities and ionic strengths, chain-chain (excluded volume) interactions are negligible, allowing the configuration of the grafted DNA polymers to be easily and reliably modeled as a static ensemble of tethered freely jointed chains. Lastly, the DNA density is high enough that each molecule can interact with several others, allowing a mean-field rather than explicitly stochastic description of the bridge formation process.

DNA-induced colloidal interactions arise from two dominant physical effects: (i) transiently forming and breaking DNA bridges act as entropic springs pulling the spheres together and (ii) the compression of unbridged DNA strands when particles come close together acts to push the spheres apart. The first, attractive interaction is the more involved to compute; the second, repulsive interaction can be evaluated from intermediate results derived while computing the first. A relation for the attractive interaction can be computed from the statistical mechanics of the combined two-sphere and reacting DNA system, ignoring for the moment the effects of DNA brush repulsion and assuming the DNA is in chemical and thermodynamic equilibrium. Multiple authors have shown (9, 13, 14) that, for the pair-interaction strengths considered here, the attractive interaction between the two spheres can be related to the average number of bridges, 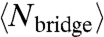, by

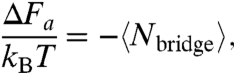[1]

assuming that the hybridization of different DNA strands is statistically independent (see SI Text for details). Note that both the attractive pair-interaction in Eq. 1 and are functions of the relative separation h. Because the that prevails at a given h is the result of a chemical reaction between nonuniformly distributed reactants, this problem consists of two parts: computing the total amount of bridge “product” in chemical equilibrium and computing the distribution of the DNA “reactants” themselves.

Because bridge formation is a reversible process, we can compute using conventional chemical equilibrium concepts generalized to the case of spatially nonuniform reactants, i.e., by solving the coupled equations

[2]

where C₀ = 1M is a reference concentration, is the equilibrium concentration of species i, and ΔG_hyb is the hybridization Gibbs free energy for the two-state reaction A + B↔AB. The second two formulae describe mole balances with initial concentrations 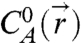and 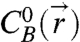, that are taken as static—they do not vary with the degree of reaction. In essence, we require that chemical equilibrium be satisfied separately at each point . The attractive free energy and equilibrium number of bridges between a pair of particles can then be calculated from

[3]

where N_Av is Avogadro’s number.

To compute the time-averaged concentration fields of reactants and 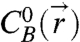in the gap between two microspheres, we model the grafted DNA strands as tethered flexible chains. The DNA strands we use have a contour length (l_c = 40 nm) that is ∼8 times the Kuhn length of single-stranded DNA, l_Kuhn = 5 nm (25). Specifically, we use Monte Carlo integration to generate unbiased, 3D random walk configurations consisting of N = l_c/(l_Kuhn) = 8 randomly oriented steps. Configurations that intercept either microsphere are rejected as unphysical. The terminal coordinate of the random walk is taken to be the coordinate of the DNA’s reactive “sticky end” (Fig. 2A). A large ensemble of such random walks (Fig. 2B) is partitioned to form a discrete approximation to the continuous concentration field 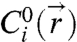(Fig. 2C). In practice, it is only necessary to generate configurations in the interaction region between the particles (i.e., between two spherical caps), as all other chains on the surface are sterically unavailable for bridge formation.

Fig. 2.

Construction of brush polymer ensemble. (A) Random walk configuration of a tethered Gaussian coil. The terminal node of the random walk is the coordinate of a point-like DNA sticky end. (B) An ensemble of coils, with uniformly distributed anchor points. (C) Computed time-averaged concentration field of reactive sticky ends on a discrete grid, two-dimensional (2D) slice along centerline.

A subtle but critically important case concerns those polymer configurations that do not intersect the sphere to which they are anchored, but intersect the facing sphere. Because these unphysical configurations must be omitted from the final ensemble, we oversample configurations in the narrow part of the gap, as necessary, until we obtain a uniform areal density of anchor points on the anchoring sphere. This approach allows us to construct an accurate numerical representation of the local concentration enhancement that occurs when a brush of uniformly distributed grafted strands is compressed. Without resorting to complicated numerical methods, this aspect of the calculation requires generating a new ensemble of brush polymers for each value of the separation h, rather than merely generating one ensemble and translating it as h is varied. Despite this minor complication, generating the necessary ensembles and computing the attractive interaction is readily tractable on a personal computer.

A second important aspect of computing the ensemble of compressed brushes relates to the repulsive part of the DNA-induced interaction. While constructing the ensemble at a given h, we count both the number of tethered coils (that do not intersect the anchor sphere), Ω(∞), as well as how many of those coils do not intersect the facing sphere, Ω(h). The entropic repulsion per coil (9) associated with brush compression can then be calculated directly from

[4]

The total repulsion between the spheres is then computed by multiplying Eq. 4 by the total number of grafted DNA polymers on both particles (to account for compressing two brushes). That is, Eq. 4 assumes that the ensemble of coils uniformly covers the entire anchoring sphere. If higher numerical efficiency is desired, a subensemble of chains on a spherical cap can be generated, and both Ω(∞) and Ω(h) can be incremented by the estimated number of coils on the rest of the sphere. Alternatively, approximate forms for the repulsive interaction (9) are available for the case where the particle radius is much larger than the coil. Our formalism presented here, however, is accurate when computing repulsions between nanoscale or nonspherical particles.

Comparing Model and Experiment.

The spatially resolved model predictions of the repulsive and attractive contributions to the DNA-induced pair-interaction potential for the conditions of our experiment are shown in Fig. 3A. As expected, the attraction becomes significant when the brushes begin to overlap, h ∼ 2L, and increases monotonically as the particles approach one another. Because we neglect chain-chain interactions, the repulsion has a much shorter range and does not appear until h < L. The repulsion is also much larger in magnitude than the attraction for h < L, which leads to a peak P(h) in around h ∼ L, as experimentally observed.

Fig. 3.

Interaction model. (A) Computed pair-interaction terms for a binding energy of 3 k_BT: repulsion (dashed curve), full attraction model (solid curve), and approximate attraction neglecting brush compression (dot-dashed curve). P(h) indicates the equilibrium distribution of separations. (B) Interaction strength or binding energy as a function of temperature. The circles are experimental measurements, each averaged over five pairs. Error bars are determined from the standard error among different pairs. The full interaction model is the solid curve, the dashed curve assumes a differential reaction approximation. The gray band is the full interaction model solution using the NN prediction for (gray curve) delimited by .

Solving Eqs. 2–4, blurred by our instrumental spatial resolution of ∼3 nm (see Materials and Methods), we compute and fit the experimentally measured pair-interaction potentials in Fig. 1E, taking ΔG_hyb as a fitting parameter while allowing particle diameter to fluctuate slightly about its mean value to account for particle polydispersity. The best-fit model predictions are overlaid on the measured pair potentials and capture the full spatial dependence of the pair-interactions at all temperatures. Moreover, when we compare the fitted hybridization Gibbs free energies to a priori predictions for ΔG_hyb for our sticky ends (5′-GTCTACC-3′ and 5′-GGTAGAC-3′) from the NN model (23), we find a constant deviation of only -0.03 kcal/mol at all temperatures, well within the uncertainty of the NN model predictions, estimated to have a standard deviation of ∼0.5 kcal/mol (23, 26). Fig. 3B shows the extracted pair-interaction well depths, or binding energies, for all A-B interactions measured, as well as our model predictions using the consensus hybridization Gibbs free energy. Our model quantitatively captures both the magnitude and the temperature dependence of the DNA-induced binding energy (up to 6 k_BT), without any free parameters or empirical corrections.

An interesting exercise is to compare the number of bridges that form to the number available to react, readily estimated to be > 50 molecules on each sphere. This estimate suggests that bridge formation could be considered highly unfavorable thermodynamically, and that the in Eq. 2 could be approximated by their initial values, 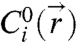. Such a “differential reaction” approximation, however, systematically overpredicts the binding energy in a temperature-dependent way (Fig. 3B). This error is the result of “lumping” the spatial variation of the degree of reaction—when h ∼ L, the maximum degree of reaction in the center of the gap is actually 30% at 3 k_BT binding strength. Such approximations implicit in earlier models (9, 27) likely account for their failure to capture the correct temperature dependence of the DNA-induced interactions. More sophisticated models (13–15, 17, 19), with explicit molecular degrees of freedom, can capture reactant depletion using binomial statistics, but their generalization to a nonuniform spatial distribution is not obvious. Our nonuniform continuum approach provides a conceptually clearer and systematically more reliable result.

Mixed-DNA Interactions: Experiments and Modeling.

In general, during a DNA-directed particle self-assembly experiment, an experimenter would like to specify the binding strengths between a number of different particle species, in essence a symmetric matrix of binding strengths, that will necessarily be temperature dependent. While such a matrix can be specified using soluble linking DNA strands, such approaches suffer from poor binding kinetics (9). An alternative approach is to attach mixtures of DNA strands having different sequences to each bead species. For example, particle A will bear DNA that is complementary to strands on particle B as well as other DNA strands that are complementary to those on particle C, etc. In this scheme, in order to induce binding between a particle and others of its own kind, the particle will necessarily have to contain DNA strands that can hybridize to other strands on its own surface. Such “self-binding” can lead to loop conformations of hybridized DNA strands that compete with bridging, and potentially complicate the interaction thermodynamics.

We now consider interactions where each particle contains mutually complementary DNA sequences. A single population of particles, AB, were functionalized with a mixture of two complementary sequences of DNA (sequences “A” and “B” from before) (Fig. 4A). Each particle is nominally labeled with ∼6,000 DNA molecules and has a mixing ratio, α_A/B = 0.4, i.e., 40% of the surface-bound strands have sequence “A” and the remaining 60% have sequence “B.” In this case, when two AB particles approach one another, h < 2L, their now chemically and structurally identical DNA brushes physically overlap and can hybridize together to induce a short-range attraction between the spheres (Fig. 4B). Fig. 4C shows a representative set of measured pair-interaction potentials between two mixed, DNA-functionalized colloids as a function of temperature. As was observed for the A-B interactions, all AB-AB pair potentials show a temperature-dependent attraction that decreases monotonically with increasing temperature and the same temperature-independent repulsion. Again, Fig. 4D shows the temperature dependence of the binding energy. Comparing Fig. 4D to Fig. 3B, we immediately see that the temperatures at which the AB-AB interactions are comparable in strength to the A-B interactions are systematically lower by ∼6 °C, even though the total DNA content has increased by ∼30%.

Fig. 4.

Models and experiments for mixed DNA brushes. (A) Each of the A-B type spheres is labeled with both oligonucleotides, forming a mixed brush, rendered in (B). Measured pair-interaction potentials (C) for two A-B type spheres (circles) with associated model (solid curve), both vs. temperature. (D) Binding energy as a function of temperature. The circles are experimental measurements, each averaged over five pairs. Error bars are determined from the standard error among different pairs. The full interaction model is the solid curve, the dashed curve assumes a differential reaction approximation, and the dot-dashed curve assumes all hybridized strands are bridges. The gray band is the full interaction model solution using the NN prediction for 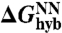(gray curve) delimited by .

The explanation for the knockdown in interaction strength at a given temperature is that some of the “A” and “B” strands on a given AB particle surface have hybridized together to form DNA loops (18, 19) rather than bridges. To correct for this effect on the attractive pair-interaction, we first solve for as described above, then assume that the “A” and “B” strands react to form an unbiased distribution of loops and bridges, which is determined solely by stoichiometry. 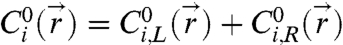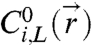That is, we estimate the fraction of hybridized strands that are bridges via , where and and 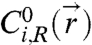are the contributions to the initial concentration of species i from the left and right particle, respectively. The time-averaged number of bridges is then

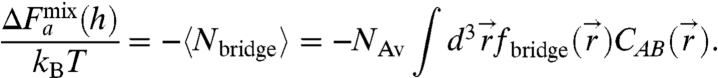[5]

We fit our AB-AB pair-interaction potentials in Fig. 4C as before, but replacing Eq. 3 with Eq. 5. Again, our model captures the spatial dependence of the DNA-mediated interaction for all experimental temperatures. Moreover, our model quantitatively captures the temperature dependence of the mixed-DNA binding energy (Fig. 4D), where the differential approximation and evaluation of Eq. 5 that neglects looping fail. This time, when we compare the fitted hybridization Gibbs free energy to predictions for ΔG_hyb from the NN model, we find a constant offset of 0.50 kcal/mol at all temperatures. Although this deviation in ΔG_hyb is within the a priori uncertainty for the NN model, the value is repeatedly different from that found above with unmixed A-B interactions. Because the total density of grafted DNA is higher in this case, we hypothesize that excluded volume effects and chain-chain interactions may cause a slight perturbation to the hybridization thermodynamics.

Conclusions

In this work, we have shown that the interaction between complementary DNA-labeled particles can be modeled in a mean-field manner as chemical equilibration between two continuous concentration fields, without explicit reference to polymer chain entropy or the necessity of costly many-body dynamical simulation. This approach, founded on basic concepts in polymer physics and statistical mechanics, is able to capture both the spatial and temperature dependence of DNA-induced pair-interactions, while being readily generalizable to particles that are small compared to the DNA strands or have nonspherical shapes, as well as cases where many-body interactions are possible. While we have relied on a numerical approach, we note that our general framework is also amenable to analytic evaluation of the interaction free energy.

The success of our modeling framework relies partially upon the design of our experimental system. We used long, flexible ssDNA spacers intentionally, to reduce entropic tension on the bridges and maximize the brush thickness. By using a density of grafted strands that was close to the polymers’ critical overlap concentration, we ensured that each strand would be able to sterically access several other polymers, despite being tethered to a solid surface, without introducing excluded volume effects. At a lower coverage of grafted DNA, we expect the actual interaction will be weaker than our continuum predictions, and will likely require an explicitly stochastic model. Beyond modeling convenience, however, our design choices also facilitate a maximally broad interaction well and a consistent mean-field interaction without significant static disorder (e.g., due to stochasticity) that, we conjecture, facilitates efficient self-assembly (3).

In the future, a quantitative understanding of the physical processes that govern DNA-mediated particle binding will be essential for control and design of DNA-directed particle assemblies and materials. The material design space for this versatile technology—particles labeled with DNA—is vast: an engineered matrix of specific interactions between a library of different sized (and shaped) particle species whose core chemistry is effectively decoupled from the final structure and assembly processes. The material processing design space is equally vast: the ability to modulate the interactions using thermal schedules (5), added soluble strands (28), enzymes (29), photochemistry (30, 31), and DNA actuators (6, 18) promise a wide variety of schemes for controlling nucleation (27), growth (10), structural transformations (6), and replication (30) to produce useful unique particle-based metamaterials in the form of clusters, bulk crystals, thin films, and heterojunctions. Navigating this complex space will rely on simulation now enabled by a framework for computing interparticle interaction matrices reliably, across a range of process conditions.

Materials and Methods

Particle Preparation.

We synthesize DNA-labeled colloids using a physical grafting technique described elsewhere (21). The PEO-PPO-PEO triblock copolymer (Pluronic® F108, BASF) and 1.1 μm diameter carboxyl-modified polystyrene (PS, Seradyn, Thermo Scientific) colloids are used as received. All ssDNA sequences are composed of a poly-T spacer followed by a unique 15-base handle and were designed to minimize secondary structure (Integrated DNA Technologies, Inc.) (see SI Text for details). The “A” and “B” sequences are 5′-(T)₅₀-TAATGCCTGTCTACC-3′ and 5′-(T)₅₀-TGAGTTGCGGTAGAC-3′, respectively. The underlined portions represent the sticky ends and can hybridize together to form a 7-basepair DNA duplex. The final DNA labeling densities are quantified using a BD FACScalibur flow cytometer (BD Sciences) and fluorescent calibration standards (Molecular Probes); A particles are labeled with 4,800 ± 480 “A” per particle, B particles are labeled with 4,200 ± 420 “B” per particle and AB particles are labeled with 2,400 ± 240 “A” and 3,500 ± 350 “B” per particle. All DNA-labeled particles are stored in aqueous buffer containing 10 mM Tris/1 mM EDTA/pH = 8.0 and are stable at 4 °C for ∼1 mo.

Pair Potential Measurements and Fitting.

We measure DNA-mediated colloidal interactions using a scanning-line optical tweezers instrument and video microscopy (see SI Text for details of the line optical tweezers). The imaging setup is described elsewhere (22). We achieve an elongated optical potential by rapidly scanning an ordinary optical trap back-and-forth in the focal plane of an inverted light microscope (Leica DM IRB, Leica Microsystems) with a 16-kHz resonant scanning mirror (Electro-Optical Products Corporation). While scanning, we modulate the laser intensity synchronously with a LabVIEW controlled acousto-optic modulator (AOM, Electro-Optical Products Corporation) to tailor the time-averaged intensity profile. By carefully tuning the trap potential along the scan direction, we are able to remove all optical contributions to the pair potential near particle-particle contact. Finally, the equilibrium pair-interaction between a pair of DNA-functionalized particles is computed from a histogram of their relative separation by inverting the Boltzmann relation (22) (see SI Text for details). All pair-interaction measurements were performed in aqueous buffer containing 125 mM NaCl/10 mM Tris/1 mM EDTA/pH = 8.0.

We fit the measured pair-interaction potentials to numerically blurred solutions of our model using procedures detailed elsewhere (22, 32) and in SI Text. Briefly, we convert our model solution of ΔF(h) into a probability distribution, P(h), using the Boltzmann relation. Next, we numerically convolve P(h) with a Gaussian kernel (with a standard deviation of 3 nm) to simulate the finite spatial resolution of our instrument and then convert the blurred P_blur(h) back to ΔF_blur(h), again using the Boltzmann relation. Finally, we fit the blurred model prediction, ΔF_blur(h), to our experimentally measured pair-interaction potentials by χ² minimization.