Tempo and mode of inhibitor–mutagen antiviral therapies: A multidisciplinary approach

Abstract

The continuous emergence of drug-resistant viruses is a major obstacle for the successful treatment of viral infections, thus representing a persistent spur to the search for new therapeutic strategies. Among them, multidrug treatments are currently at the forefront of pharmaceutical, clinical, and computational investigation. Still, there are many unknowns in the way that different drugs interact among themselves and with the pathogen that they aim to control. Inspired by experimental studies with picornavirus, here, we discuss the performance of sequential vs. combination therapies involving two dissimilar drugs: the mutagen ribavirin and an inhibitor of viral replication, guanidine. Because a systematic analysis of viral response to drug doses demands a precious amount of time and resources, we present and analyze an in silico model describing the dynamics of the viral population under the action of the two drugs. The model predicts the response of the viral population to any dose combination, the optimal therapy to be used in each case, and the way to minimize the probability of appearance of resistant mutants. In agreement with the theoretical predictions, in vitro experiments with foot-and-mouth disease virus confirm that the suitability of simultaneous or sequential administration depends on the drug doses. In addition, intrinsic replicative characteristics of the virus (e.g., replication through RNA only or a DNA intermediate) play a key role to determine the appropriateness of a sequential or combination therapy. Knowledge of several model parameters can be derived by means of few, simple experiments, such that the model and its predictions can be extended to other viral systems.

The ability of diverse and rapidly multiplying parasites to adapt to environmental changes is a major obstacle for the design of successful therapeutic strategies able to control their proliferation and propagation. RNA viruses count among the most plastic organisms on Earth and are an iconic example of populations persistently escaping the action of antiviral drugs (1, 2). Drugs exert constant selection pressures on viral populations, and as such, the question is not whether a resistant form of the virus will appear but when it will occur. Alternative therapies are continuously sought with the aim of impeding the appearance and fixation of resistance mutants (3–5). Among them, multidrug treatments have been established as an efficient way of delaying the appearance of resistant forms. However, to understand the mode of action of combined treatments, it is urgent to clarify the degree of interaction between the different drugs used (6) and the quantitative impact that they have on the virus that they are affecting. The joint action of two drugs can rarely be reduced to the simple addition of their independent effects (7), and the same drug might elicit different responses in different viral systems, including the appearance of compensatory mutations able to induce resistance (8). Thus, the complete characterization of a multidrug treatment applied to a particular viral system might require in the last term a systematic assay with a large number of drug doses delivered under different administration protocols. A full characterization of the response of the viral system in vitro is needed before any in vivo assay of the treatment. This procedure demands a costly amount of time and resources that can be significantly reduced through the guide offered by formal approaches to therapies.

Knowledge derived from in vitro studies of the response of pathogens to the action of one or a number of drugs might be combined with the information yielded by well-designed mathematical models involving the relevant mechanisms of action of and interaction among the drugs (9, 10), virus–host interactions (11), or role of the immune response (12). An important feature, rarely taken into account, is the intrinsic replicative ability of the pathogen. Many different ways to encode genomic information (ds- and ssRNA and different polarities) and a repertoire of replicating strategies have been selected by different RNA viruses. Hence, the knowledge gained for a particular virus may not be extrapolated to other systems, although suitable modifications of dynamical models can likely account for these different replication modes.

The dynamics of the picornavirus foot-and-mouth disease virus (FMDV) have been explored under different experimental regimens with the aim of disclosing protocols able to cause its extinction during replication in cell culture. It has been shown that a combination of mutagenic agents and antiviral inhibitors is an efficient way to drive FMDV to extinction (13, 14). The mutagen succeeds in raising the fraction of defective and lethal mutants in the population, thus decreasing its overall fitness. Defectors may also interfere with infectivity, as shown with specific mutants (15) and preextinction viral populations (16), and thus, accelerate extinction. For its part, the inhibitor contributes to extinction by reducing the viral load. However, the joint effect of a mutagen and an inhibitor cannot be reduced to the addition of their individual effects (9). Since the dawn of quasispecies theory (17), the use of mutagens has been proposed as a plausible strategy to induce viral extinction (18, 19). A significant increase in the mutation rate has been, indeed, successful to cause the extinction of infectivity in many different viral systems (20, 21), although the mechanisms through which extinction supervenes are diverse and related to a variety of molecular and population responses (22). In particular, increased mutagenesis can also bear beneficial effects for viral populations through an enhancement of their diversity, which promotes adaptation of low-fitness viruses (23) and facilitates the appearance of resistance mutants when an inhibitor of viral replication is present (24).

The increased likelihood of developing resistance to the inhibitor when dispensed simultaneously with a mutagen is what advocates the sequential administration of the two drugs, with the inhibitor followed by the mutagen. In a study with FMDV subjected to the action of the mutagen ribavirin (R) and the inhibitor of viral replication guanidinium hydrochloride (GU), it was shown that, under the experimental conditions assayed, the sequential therapy performs better than the simultaneous administration of both drugs (24). This finding is an interesting result that immediately queries the range of applicability and relative success of combined or sequential administration of those two dissimilar drugs. In this contribution, we face the characterization of the response of a general viral system to the action of an inhibitor of its replication and a mutagenic agent through a model for the dynamics of two different viral classes in the viral population. We obtain several exact results that predict the preferred therapy as a function of intrinsic viral characteristics and the administered drug doses. Our predictions are tested and confirmed by experiments with FMDV at different doses of inhibitor.

Results

Mathematical Model.

The present model is intended to reproduce the dynamics of a viral population after the addition of mutagens and/or replication inhibitors using the protocol represented in Fig. 1. Mutagens mostly promote the appearance of deleterious variants, although some particular mutations may, however, confer resistance to the inhibitor, thus favoring its survival. To capture this double role of the mutagen, the model considers that the dynamics are dominated by two types of individuals: viable individuals that are susceptible to the inhibitor (v) and viable individuals that are resistant to the inhibitor (V). Viable individuals are able to infect cells and replicate by themselves.

Fig. 1.

Schematic outline of the experimental protocol in cell culture. (A) Combined therapy. A dose d_GU of guanidine and a dose d_R of ribavirin are simultaneously added to the initial population. The viral titer 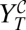is calculated after a single passage. (B) Sequential therapy. A dose d_GU is added to the initial population. After 24 h, the inhibitor is removed, and a dose d_R of ribavirin is added. The viral titer is obtained after this second passage. (C) Experimental results in a case example. The initial population has a titer of 3.7 × 10⁶ pfu/mL. The applied doses are d_GU = 18 mM and d_R = 5 mM. 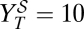With these drug doses, the viral titers after applying the protocols described in A and B are pfu/mL and pfu/mL, respectively. Passages are performed and quantified as described in Materials and Methods.

Let w₀ be the rate at which viable individuals produce, under replication, a nonviable class, including lethal variants, defective interfering forms, or any other mutant unable to complete an infection cycle on its own [(1 − w₀) is the intrinsic copying fidelity of the virus].^† Resistant forms appear at a rate of μ₀ = kw₀. Because mutations providing resistance to the inhibitor are rare compared with deleterious ones, k ≪ 1.^‡ Addition of a mutagen is implemented by increasing the mutation rate from its natural value w₀ to a higher w > w₀. As a consequence, the rate of appearance of resistant mutants, μ = kw, increases when the mutagen is added. Each time a viral genome replicates inside the cell, m copies are produced, and therefore, m is the replicative ability per genome and replication cycle. The effect of an inhibitor is to slow down replication of the susceptible type by multiplying parameter m by a factor 0 < i ≤ 1.

Let v(g) and V(g) denote the number of individuals of each type at replication cycle g. Populations after one replication cycle in the presence of a mutagen and an inhibitor will be (Eqs. 1 and 2)

To study the dynamics of the model and compare the sequential vs. the combined administration of the drugs, we will mimic the protocol described in Fig. 1. At cycle 0 (initial condition), we will assume that the population is formed by S₀ individuals of type v, which because of mutations, will populate the class or resistant mutants in successive replication cycles. A full solution of the model is given in Materials and Methods. The dynamics of the combined therapy correspond to applying Eqs. 1 and 2 iteratively for g = 1, … , G cycles with parameters i < 1 and w > w₀; the dynamics of the sequential therapy imply replication for G cycles in absence of the mutagen (i < 1 and w = w₀) and use of the generated population as initial condition to replicate for G additional cycles in absence of the inhibitor and presence of the mutagen (i = 1, w > w₀).

Model Analysis.

Viral particles are released from the cell after G replication cycles. This release finishes the process for the combined therapy, whereas there is a second passage to undergo in the sequential therapy. The size of the infective population [let us call it Y_T(G, w, i) to make explicit the experimental parameters involved] is obtained by adding the population of individuals in the two relevant classes after the first passage, Y_T(G, w, i) = v(G) + V(G) (Materials and Methods), and therefore (Eq. 3),

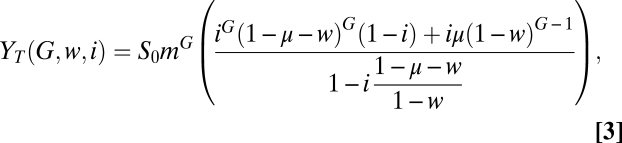which for i = 1 (absence of inhibition), yields Y_T(G, w, 1) = S₀m^G(1 − w)^G. The size of a viable viral population after one passage with a mutagen and/or a replication inhibitor is, thus, given by Eq. 3 with the corresponding parameters w and i. In the absence of drugs, the total population obtained is S₀m^G(1 − w₀)^G, such that the initial population is simply multiplied by m(1 − w₀) at each replication cycle, which is the basic reproductive ratio of the population.

Comparison between treatments: Viral titer.

Let us call the viral titer after the application for one passage of the combined treatment. According to the experimental protocol, the mutagen and the inhibitor have been simultaneously administered, and therefore, the viral yield is immediately given by Eq. 3: . Analogously, 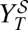is defined as the viral yield after the sequential administration of the drugs: first, the inhibitor for one passage and then, the mutagen for a second passage (Eq. 4),

where the initial condition for the second passage requires S₀ to be substituted by the yield obtained, Y_T(G, w₀, i). The comparison of the yields obtained using either treatment determines which of them is more efficient for each dose of mutagen and inhibitor. The curve C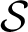, defined by , separates two regions in the space of parameters {i, w}, where one therapy or the other is better suited to obtain a low viral titer (Materials and Methods has an approximate expression of curve C and its asymptotic value at large values of the inhibitor). Fig. 2 A, C, and E shows the viral titer corresponding to the numerical solution of the equations above for the combined and sequential treatments.

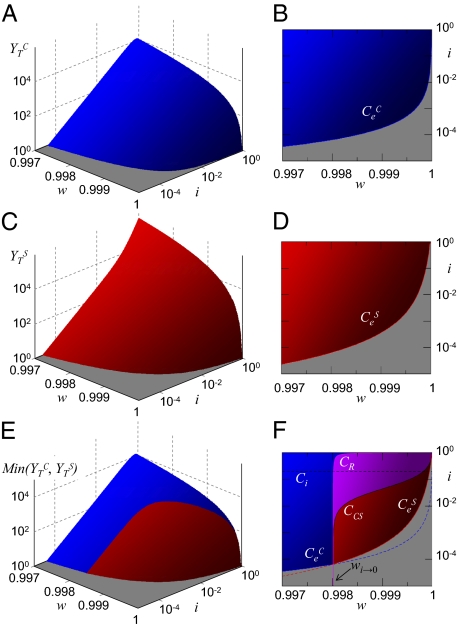
Fig. 2.

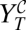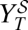Theoretical phase space representation of the model. (A) Viral titer after application of the combination treatment. (B) Doses that fall on the gray area cause viral extinction under application of the combination treatment. The frontier with the blue region corresponds to values {i, w} yielding , which defines curve . (C) Viral titer after application of the sequential treatment. (D) Doses that fall on the gray area cause viral extinction under application of the sequential treatment. The frontier with the red region corresponds to values {i, w} yielding , which defines curve . (E) Comparison of the titers produced by combination and sequential therapies. In the z axis, we represent the minimum value of the viral yield for each pair of {i, w} values. (F) In the gray area, extinction occurs if the appropriate therapy is used. Blue and red lines correspond to extinction with the combination or sequential treatment, respectively, and are as above. Black curve is C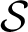. It signals the pairs of {i, w} values where both therapies produce the same titer. Violet curve C_R indicates when both treatments produce the same amount of resistants. In the violet region between C_R and C 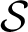curves, the combined treatment yields the lower titer, but the sequential treatment is less prone to produce resistance. In the limit of large amounts of inhibitor (i → 0), both therapies perform equally well in regard to titer and resistant production. The expression for the limit value of mutagen w_{i → 0}(Materials and Methods) is indicated with an arrow in the plot. Finally, the dotted line stands for curve C_i, which indicates the values of i (below the curve) that cause an efficient decrease of the population. Curve C_w, representing the values of the mutagen above which the population of viable individuals decreases from passage to passage, is out of the range shown in the plots. Parameters for all plots are m = 50, G = 2.5, w₀ = 0.9, and k = 0.01.

Comparison between treatments: Appearance of resistant mutants.

In addition to the viral titer produced after application of one or another therapy, it is important to know the fraction of resistant mutants that each treatment produces on average. This quantity corresponds to the final populations of type V(G) after one passage with both the mutagen and the inhibitor (combination therapy) or one passage with the inhibitor plus a second passage with the mutagen (sequential therapy). Let us call R and R the two final populations of resistants. The exact expressions for the two quantities are obtained as R = V(G, w, i) and , analogous to the way in which the titers were obtained. The amount of resistants produced with either treatment will be equal at values of w and i that fulfill R = R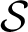. This finding defines curve C_R. A convenient way of calculating some of the properties of that curve is to express the difference in the number of resistants generated for a pair of values {w, i} as ΔR(w, i) = ΔY(w, i) − ΔS(w, i), where 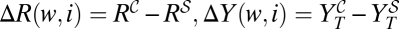; ΔS(w, i) = S₀(im(1 − μ − w))^G(1 − m^G(1 − μ₀ − w₀)^G) is defined as the difference in the amount of susceptible virus produced by the combined and sequential treatments, with v(G, w, i) as calculated in Materials and Methods.

The values of ΔR(w, i), when the yields of the two treatments are equal [that is, on curve C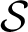, where ΔY(w, i) = 0], are always positive, because ΔS(w, i) < 0 because of the biological fact that the replication rate of the susceptible type is larger than one in the absence of drugs: m(1 − μ₀ − w₀) > 1 and 1 ≥ μ + w. The production of resistant mutants is, thus, lower through the sequential treatment when both therapies are equally efficient in terms of total titer. This finding also implies that curve C_R is always above curve C 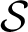(Fig. 2F). Hence, there is a region of doses of mutagen and inhibitor between curves C_R and C 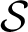where the combination treatment leads to lower titers but at the same time, the sequential treatment causes a lower population of resistants.

In the limit of high doses of the inhibitor, i → 0, and because lim_{i → 0}Δv(w, i) → 0 (the population of susceptibles is completely suppressed), the total population coincides with the population of resistants and ΔR(w, i) → ΔY(w, i). As a result, the limit value of w on curve C_R coincides with the limit value of w on curve C 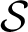(Materials and Methods).

Effect of treatment and virus parameters.

Not all possible drug doses are experimentally meaningful. First, there is a minimum amount of mutagen required for the therapy to be effective, and it corresponds to those values of w large enough to cause a decrease of viral yield in the absence of the inhibitor. This condition takes the formal expression m(1 − w) < 1. We, thus, define curve C_w as those points where m(1 − w) = 1, separating the regions of increase and decrease of the population size under the action of the mutagen. A similar reasoning leads to curve C_i, which marks the values of i below which the inhibitor is able to cause a decrease of the viable population before resistance appears, (im)^G(1 − w₀)^G = 1.

There is a limit under high enough values of the drug dose where either treatment may cause the extinction of the virus with the applied protocol. Curve is determined by those combinations of {i, w} where the population size of the combined treatment falls below one. The exact solution for curve can only be given in implicit form as those values solution of Y_T(G, w, i) = 1. To first order in μ, the curve fulfils the approximate expression m^GS₀(1 − w)^{G − 1}(i^G(1 − w) + kwγ) ≅ 1. Analogously, curve 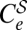is defined by those pairs {i, w} at which S₀⁻¹Y_T(G, w₀, i)Y_T(G, w, 1) = 1. Fig. 2 illustrates, in a representative case, the response of a viral population to the action of a combined or sequential treatment. All curves defined above (except for C_w, which occurs at values of w quite far from the domains shown) are represented in Fig. 2 B, D, and F.

Parameters m and G depend significantly on the mode of replication of the virus inside an infected cell. ssRNA viruses are characterized by large values of m and probably, quite low values of G. In double-stranded genomes with semiconservative replication, one would expect a value of m ∼ 2 and a larger value of G. In both cases, the accumulation of mutations proceeds differently, and therefore, w₀ would also vary accordingly. The model presented here cannot be directly applied to viruses that use other replication modes, such as retroviruses (with a DNA provirus phase) or DNA viruses such as the herpesviruses that include a latency step. Extension to such systems would require significant modifications of the dynamical rules.

Case of FMDV with R and GU.

The determination of viral productivity for a virus growing in excess of resources (P₀) in the presence of a given amount of mutagen (P_w) and inhibitor (P_i) bounds for the values of the model parameters (SI Text). Because FMDV is an ssRNA virus, we take m between 50 and 1,000. As for the intrinsic mutation rate w₀, data available put it in the range of 0.4–0.9. With a basal productivity of P₀ = 460 ± 35, G is bounded between 1 and 3.8. Estimation of P_w yields the range of possible values of w, which is bounded between 0.992 and 0.999. Similarly, estimation of the productivity in the presence of different doses of the inhibitor permits estimating parameter i as i = (P_i/P₀)^1/G (SI Text). More accurate measurements of the viral parameters by means of specific experiments directed to quantify m, G, and/or w₀ could significantly narrow the intervals compatible with the experimental results.

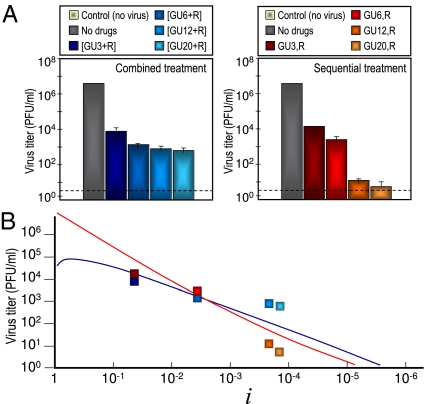
Results with FMDV subjected to the therapeutic protocols described under fixed doses of R and GU revealed that the sequential treatment could be better suited to cause viral extinction (24). However, in the light of the model described, the adequacy of sequential vs. combination treatment with a mutagen and an inhibitor of the viral replication depends on (i) the administered doses and (ii) the natural productivity of the virus when infecting a given host (i.e., parameters m, w₀, and G). In particular, the model predicts that, in most cases at a sufficiently low amount of inhibitor and for a fixed value of the amount of mutagen, the combination treatment should yield a lower titer, the same change holding for a fixed amount of inhibitor and a sufficiently low amount of mutagen. Increase of the doses d_GU or d_R above a threshold value changes the treatment that produces the lower amount of infectious virions. To test this prediction, we carried out several experiments at increasing doses of inhibitor and compared the viral yield after both therapeutic protocols (Fig. 3A). At low doses of inhibitor, the combined therapy causes lower viral yields than the sequential therapy. However, for a dose of the inhibitor between 6 and 12 mM, it is the sequential treatment that begins to yield lower viral titers. The effect of the therapies is, thus, exchanged as theoretically predicted (Fig. 3B).

Fig. 3.

Experimental protocol results using FMDV infection of cell cultures. Comparison with theoretical predictions. (A) Experimental results. Passages were carried out by infecting 2 × 10⁶ BHK-21 cells with pMT28 strain of FMDV (0.2 mL supernatant from the previous passage), and infectivity levels were determined as detailed in Materials and Methods. The combination or sequential protocol therapies were applied in the presence of a dose of mutagen d_R = 5 mM and increasingly high doses of viral inhibitor, d_GU = 3, 6, 12, or 20 mM, as indicated. The combination treatment is indicated in brackets (Left), whereas for the sequential treatment, the order of administration of GU and R is separated by a comma (Right). A control measure is shown for reference (first left bar in each panel), and other columns represent the mean ± SD (error bars) from triplicate determinations. The discontinuous lines in the virus titers indicate the limit of detection of infectivity. (B) Comparison of experimental results with the predictions of the model. Viral titers expected after applying the sequential or combination protocol in the mathematical model are shown as continuous lines (blue, combined treatment; red, sequential treatment; color code for data is the same as in A). Curves obtained with parameters that yield the least squares deviation to the logarithm of experimental data are shown as blue (combination) and red (sequential) curves. The obtained parameters are w₀ = 0.76, w = 0.998, k = 0.005, and m = 195. The values of the inhibitor i = 4.25 × 10⁻², 3.47 × 10⁻³, 2.10 × 10⁻⁴, and 1.41 × 10⁻⁴, corresponding to the four doses assayed, are shown in the x axis (SI Text).

Discussion

Ever since the quasispecies dynamics were revealed as general for pathogenic RNA viruses and retroviruses, the problem of treatment failure because of selection of drug-escape viral mutants was recognized (25). Several approaches have been used in medical practice to minimize selection of viral mutants resistant to antiviral agents. The most successful strategy was the implementation of combination therapy involving the simultaneous administration of two or more drugs directed to different viral targets. The advantages of combination therapy over monotherapy stem from basic statistical considerations on the frequency of generation of multidrug-resistant mutants (25). The advantage of combination vs. various regimens of sequential or treatment interruption (structured treatment interruptions or drug holidays) regimens has been supported by results of multiple clinical trials as well as theoretical models of viral dynamics (5, 11, 26–30). However, whenever residual viral replication is allowed, viral rebound and treatment failure often occur. For this reason, new proposals for the administration of drugs have been made. A recent one, yet to be tested in clinical trials, is the so-called proactive treatment in two steps: an induction regimen aimed at reducing the background of viral mutants followed by a maintenance regimen to control the viral load for extensive time periods (31). An alternative strategy is to target cellular factors needed for viral replication either alone or combined with drugs directed to viral functions (32). Provided no toxic effects on the cells intervene, resistance to inhibitors of cellular functions can also develop when the host factor interacts with viral nucleic acids or proteins.

Lethal mutagenesis introduces an important element in antiviral therapy in that a mutagenic agent is involved in treatment. When administered together with a nonmutagenic inhibitor, the mutagen can play a dual and opposite role: to deteriorate viral functions because of the excess mutations that it provokes, and increase the frequency of mutations that confer resistance to the partner, coadministered inhibitor. An advantage of a sequential over combination treatment during lethal mutagenesis protocols was suggested by a study of lethal mutagenesis of FMDV (33), and this advantage prompted the theoretical generalization reported in the present study and has been further supported by additional experiments also reported herein.

In this contribution, we have developed a theory that quantitatively describes the response of a viral population under two different protocols that involve the action of an inhibitor of viral replication and a mutagenic drug. A limited number of simple experiments allows us to estimate the parameters that describe the dominant processes, and knowledge of these few relevant parameters permits us to predict the behavior of the model for other combinations of drugs. Two important outcomes of the treatments have to be considered when choosing between a combined or sequential administration of the drugs: in a region of mutagen and inhibitor doses that can be calculated, the viral titer produced by one or another therapy is minimized. Furthermore, there is a domain of drug doses where combination treatment yields the lower titer, but the probability of appearance of mutants resistant to the inhibitor is lower with a sequential treatment. The use of analogous models can significantly reduce the number of in vitro assays to be performed in other viral systems as well, where different replication strategies should translate into dynamical equations similar to our Eqs. 1 and 2. The simulation of an in vivo situation entails additional difficulties, like development of a large viral population from an infecting seed, interaction with the immune system, or environmental and individual characteristics that may not lead to deterministic equations but should be included as noisy, fluctuating dynamical variables. The predictions of the model after being tested in vitro could be taken only as a rough guide to apply one or another administration protocol and infer minimum drug doses in in vivo assays.

Our predictions acquire more relevance in view of the evidence that lethal mutagenesis can indeed be effective in vivo (34) and that some clinical trials for AIDS patients that involve administration of a mutagenic nucleoside analog have been implemented (35). Our results will be particularly relevant when considering a lethal mutagenesis approach to combat viruses for which a repertoire of nonmutagenic inhibitory agents is already available. Detailed predictions of the viral response tailored to the particular system under study are now possible.

Materials and Methods

Cells and Viruses.

The origin of BHK-21 cells and procedures for cell growth in DMEM and plaque assays in semisolid agar have been previously described (36, 37). FMDV C-S8c1 is a plaque-purified derivative of serotype C isolate C1 Santa Pau-Sp70 (37). An infectious clone of FMDV C-S8c1, termed pMT28, was constructed by recombining into pGEM-1 plasmid subclones that represented the C-S8c1 genome as described (38, 39). Thus, FMDV pMT28 used in the experiments is the progeny of infectious transcripts that express the standard FMDV C-S8c1. To control for the absence of contamination, mock-infected cells were cultured, and their supernatants were titrated in parallel with the infected cultures; no signs of infectivity or cytopathology in the cultures or control plaque assays were observed in any of the experiments.

Treatment with R and GU.

A solution of GU in DMEM was prepared at a concentration of 50 mM, sterilized by filtration, and stored at 4 °C. A solution of R in PBS was prepared at a concentration of 100 mM, sterilized by filtration, and stored at −70 °C. Before use, the stock solutions were diluted in DMEM to reach the desired concentration. For infections of BHK-21 cells with FMDV in the presence of GU, no pretreatment of the cell monolayer with GU was performed. For infections in the presence of R, cell monolayers were pretreated during 7 h with 5 mM R before infection. After addition of FMDV and washing of the cell monolayers, infections were allowed to continue in the presence of a combination of GU + R or sequential passages consisting of a first passage in the presence of GU and a second passage in the presence of R. For the combination treatment, the infections were carried out at an MOI of 0.4 pfu/cell. For the sequential treatment, the initial infection in the presence of increasing concentrations of GU was carried out also at an MOI of 0.4 pfu/cell. The second infection in the presence of 5 mM R was carried out at MOIs of 1.1, 2.0 × 10⁻², 2.2 × 10⁻⁴, and 1.2 × 10⁻⁴ pfu/cell for GU 3, 6, 12, and 20 mM GU, respectively. Infections in the absence of GU, R, or a combination of GU + R and mock-infected cells were maintained in parallel, and no evidence of contamination of cells with virus was observed at any time.

Complete Solution of Eqs. 1 and 2.

The dynamics of the model system can be written in compact form through the vector n(g), whose components are the number of individuals in each of the classes v and V after g replication cycles (Eq. 5):

with A being the transition matrix of the system (Eq. 6),

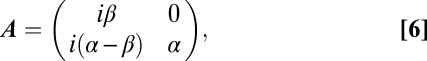and where we have defined α = 1 − w and β = 1 − μ − w. This dynamical system can be exactly solved for the initial condition n(0) = {S₀, 0} to yield the population of each viral class after g cycles (Eqs. 7 and 8),

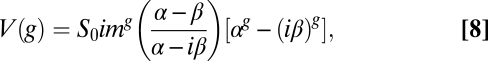from where the exact expression for the total number of viable elements is obtained (Eq. 3).

Approximate Analytic Expression for C.

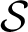The expression obtained from Eq. 4 yields the dependence between w and i in an essential nonalgebraic way, and therefore, it can be only numerically solved. However, if we assume that μ ≪ 1, an expansion in powers of μ yields the following approximate dependence for the points on curve C 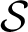(Eq. 9):

where γ = [i + i^G(iG − i − G)]/(1 − i). Given the amount of mutagen i, the sequential treatment causes a larger decrease in the viral titer for values of w > w_c, whereas the combined treatment is more efficient for w < w_c. The preferred therapy changes as well if the value of w is fixed and the amount of inhibitor increases. For values of i close to one, the combined treatment is better, whereas the sequential treatment will be preferred above a certain amount of inhibitor. Curve (Eq. 9) has two important limits, absence of inhibitor (i → 1) and large doses of inhibitor (i → 0). In the former case, both treatments become equivalent for values of w → 1 (Fig. 2F), a situation where all genomes produced under replication would be nonviable. Actually, w = 1 cannot be empirically tested, because the complete extinction of the population occurs at values of w below one, which will be shown. However, there is a saturation effect when the amount of inhibitor is very high in the sense that additional decreases in i diminish the viral titer but do not change the preference for one or another therapy (Eq. 10):

which is independent of i.