General hydrophobic interaction potential for surfactant/lipid bilayers from direct force measurements between light-modulated bilayers

Abstract

We establish and quantify correlations among the molecular structures, interaction forces, and physical processes associated with light-responsive self-assembled surfactant monolayers or bilayers at interfaces. Using the surface forces apparatus (SFA), the interaction forces between adsorbed monolayers and bilayers of an azobenzene-functionalized surfactant can be drastically and controllably altered by light-induced conversion of trans and cis molecular conformations. These reversible conformation changes affect significantly the shape of the molecules, especially in the hydrophobic region, which induces dramatic transformations of molecular packing in self-assembled structures, causing corresponding modulation of electrostatic double layer, steric hydration, and hydrophobic interactions. For bilayers, the isomerization from trans to cis exposes more hydrophobic groups, making the cis bilayers more hydrophobic, which lowers the activation energy barrier for (hemi)fusion. A quantitative and general model is derived for the interaction potential of charged bilayers that includes the electrostatic double-layer force of the Derjaguin–Landau–Verwey–Overbeek theory, attractive hydrophobic interactions, and repulsive steric-hydration forces. The model quantitatively accounts for the elastic strains, deformations, long-range forces, energy maxima, adhesion minima, as well as the instability (when it exists) as two bilayers breakthrough and (hemi)fuse. These results have several important implications, including quantitative and qualitative understanding of the hydrophobic interaction, which is furthermore shown to be a nonadditive interaction.

Self-assembled surfactant structures, such as micelles, vesicles, adsorbed surfactant monolayers, and bilayers, are utilized in many industrial and technological processes, including detergents and other cleaning products, coatings, separation processes, nano- and micromicellar reactors, dispersants, emulsifiers, and drug delivery vehicles. In all of these, precise control of morphologies and phases is crucial, properties that are largely governed by the interplay of the intramolecular interactions within individual aggregates (headgroup repulsions, steric and hydrophobic chain interactions, molecular packing) and the intermolecular interactions with other aggregates or surfaces [Derjaguin–Landau–Verwey–Overbeek (DLVO) forces, steric hydration forces, hydrophobic interactions, depletion forces]. Conventionally, one can modify these interactions by adjusting temperature, ionic strength, pH, or surfactant chain length, but only small changes occur in the resulting structures. New types of surfactants have been demonstrated to exhibit surfactant molecular structure and interactions that can be significantly and reversibly modified in situ by including active functional groups in the hydrophobic tail of the surfactant (1), thus causing dramatic corresponding transformations to surfactant morphologies and phases (i.e., micelles, vesicles, bilayers, etc.).

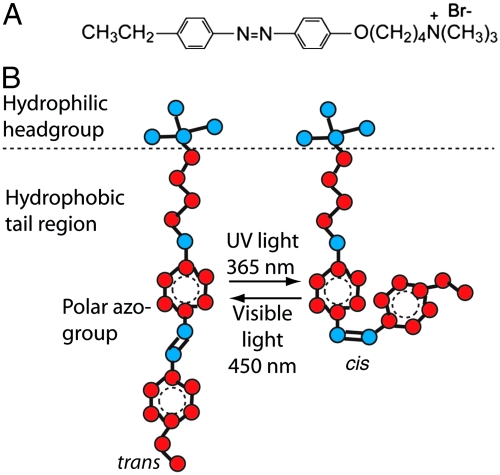
Recently, much attention has been directed toward systems that respond to external stimuli, such as light illumination or redox potentials that can be modified electrochemically. Redox-active groups, such as ferrocene, have been incorporated into surfactants in several studies and can induce a micelle-to-vesicle transition upon conversion from the reduced state to the oxidized state (2). Light-responsive moieties have also been used in a number of recent studies (3–6) to actively control surfactant architecture, utilizing functional groups such as azobenzene and stilbene, which reversibly isomerize from a straight trans conformation in visible light to a bent cis form upon UV illumination. Azobenzene-functionalized surfactants can reversibly modify surface tension at the air-water interface (3), form catanionic vesicles that can be reversibly disrupted and reformed for gene, DNA, and drug delivery applications (5–7), and reversibly control protein folding (4, 8). In this work, a photoresponsive azobenzene moiety has been incorporated into a conventional single-chain surfactant as a model light-responsive surfactant system. The surfactant azobenzene trimethylammonium bromide (azoTAB) has the chemical structure shown in Fig. 1A. This surfactant molecule adopts a planar trans conformation in 450 nm visible light conditions, which switches to the kinked cis isomer when exposed to 365 nm UV light, as depicted schematically in Fig. 1B.

Fig. 1.

Schematic diagrams of (A) the molecular structure of light-responsive cationic azoTAB and (B) the reversible photoisomerization processes that the azoTAB surfactant undergoes upon exposure to UV or visible light. The isomerization from trans to cis exposes the polar azo group and results in structural changes in the hydrophobic region of the molecule.

The light-induced modification of surfactant structures suggests that the surfactant packing parameter and the inherent thermodynamics—the energy potentials due to the separate intramolecular (packing) and interaggregate (colloidal) interactions—are changing, most likely in a correlated way. To our knowledge, no quantitative study of the light-responsive interactions has previously been undertaken. Here, light-dependent interaction forces between adsorbed self-assembled layers of photoresponsive surfactant on mica are measured by the surface forces apparatus (SFA) technique. The adsorbed surface (bilayer or monolayer) structure, interfacial and bilayer adhesion energies, and the electrostatic double layer and hydrophobic forces can be reversibly controlled by changing the wavelength of light illumination. Further, the energy potential due to each of the inter- and intramolecular interactions is calculated to derive a general quantitative mean-field theory for bilayer (hemi)fusion.

Results and Analyses

Light-Modulated Adsorption at the Air-Water Interface and on Solid Surfaces.

To examine first the effects of isomerization on the intramolecular interactions, the area-per-molecule, a, at the air-water interface is obtained from the Gibbs adsorption isotherm, as described in SI Text (9). In visible light, for trans azoTAB a ≈ 40 Å², which increases to 102 Å² in UV light (cis azoTAB). The reversible conformation changes are monitored by UV-visible spectroscopy, as described in SI Text. Trans azoTAB molecules pack more densely than cis azoTAB molecules and reversible adsorption and desorption at the air-water interface can be induced simply by tuning the wavelength of light illumination. This behavior is similar for all self-assembled (in solution and adsorbed) structures of azoTAB. The intramolecular headgroup and steric interactions can be modulated to confer structural changes to azoTAB molecules and aggregates. Such interactions depend on the bulk concentration of surfactant relative to the critical micelle concentration (CMC) and play critical roles in the behaviors of cationic surfactants in solution and their adsorption at solid anionic surfaces, such as mica or silica. Below the CMC, no self-assembled aggregates are present in solution, and individual molecules adsorb to form a submonolayer or monolayer on solid surfaces. Above the CMC, micelles adsorb and relax to form a full or partially depleted bilayer on the surface (10, 11). For azoTAB, the isomerization from trans to cis exposes the hydrophilic azo group (Fig. 1B), which causes the CMC to increase from 4 mM (trans, visible light) to 11 mM (cis, UV light) (12). Such light-modulated differences in aggregate structures arise directly from important and quantifiable differences in intermolecular interactions associated with the different light-dependent surfactant structures.

Direct Measurement of Light-Modulated Interactions.

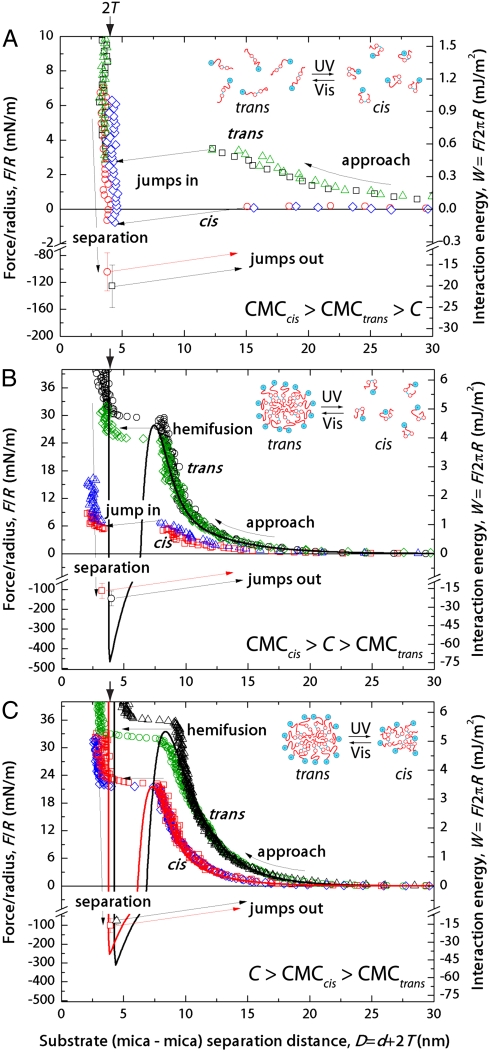
Light-responsive intermolecular forces and structural transformations of self-assembled monolayers and bilayers of azoTAB on mica were measured directly by SFA (Fig. 2). For concentrations below the CMC of both trans and cis azoTAB, monolayers (or patchy submonolayers) are expected in both UV and visible light. The interactions for monolayers adsorbed from 0.5 mM azoTAB are shown in Fig. 2A. In all force measurements a long-range electrostatic repulsion was followed by a jump-in to contact during approach, and strong adhesion due to the hydrophobic interaction was measured upon separation. This behavior is typical for surfactant monolayers. Reversible adsorption and desorption of azoTAB molecules at the mica surface occurred upon isomerization, as indicated by the fully reversible surface potentials and surface charge densities (determined by the magnitude of the electrostatic repulsion). The adhesion energy W₀ was correlated with the isomerization state as well; the adhesion energy is lower for cis azoTAB (W_0,cis = 17 ± 4 mJ/m² and W_0,trans = 20 ± 5 mJ/m²),* because the kinked cis form exposes the relatively hydrophilic azo group to the bulk solution more than the straight trans isomer. Monolayers of trans azoTAB can be reversibly converted to monolayers of cis azoTAB by UV illumination. Increasing the bulk concentration of azoTAB modifies the surface structure and interactions accordingly, as shown below.

Fig. 2.

Measured interaction forces for adsorbed layers from (A) 0.5 mM azoTAB, well below the CMC values of both the trans and cis isomers for which there is monolayer coverage of each; (B) 5.5 mM azoTAB, above the CMC of trans azoTAB but below the CMC of cis azoTAB, where there is monolayer coverage for the cis (UV illumination) and bilayer coverage for the trans (visible illumination) isomers; and (C) 12 mM azoTAB, above the CMC values of both trans and cis azoTAB and for bilayers of both. In each panel, the points shown in green and black were obtained in visible light (trans azoTAB), whereas the points in red and blue were obtained under UV illumination (cis azoTAB). The interaction forces are plotted versus mica-mica distance, D, where D = 0 corresponds to mica-mica contact in air.

As discussed above, surface coverage approaches a monolayer in sub-CMC solutions whereas bilayers form from solutions above their CMC. The surface forces for surfactant layers adsorbed from 5.5 mM azoTAB (above the trans CMC and below the cis CMC) are shown in Fig. 2B and indicate that the surface structure can reversibly alternate between trans azoTAB bilayers (visible light) and cis azoTAB monolayers (UV light). A strong electrostatic repulsion and jump-in measured during approach indicate a closely packed monolayer or a patchy bilayer in UV light. For visible light, the electrostatic repulsion was even larger and a strong short-range steric repulsion was measured, both of which stress the bilayer. The stress causes the bilayers to spread laterally, exposing the hydrophobic interior, until a critical point where the hydrophobic inner layers strongly attract and push the outer monolayers into the bulk. The two bilayers ultimately (hemi)fuse into one bilayer and the monolayers are strongly adhesive. This (hemi)fusion event is shown schematically in Fig. 3 and described in detail below. The adhesion energy measured upon separating the hydrophobic monolayers was again larger for trans azoTAB (W_0,cis = 17 ± 6 mJ/m² versus W_0,trans = 23 ± 5 mJ/m²). These results show that for an intermediate concentration between the CMCs of trans and cis azoTAB, the surface structure can reversibly switch from bilayer (trans, visible light) to monolayer (cis, UV light) coverage, with corresponding effects on electrostatic and hydrophobic interactions.

Fig. 3.

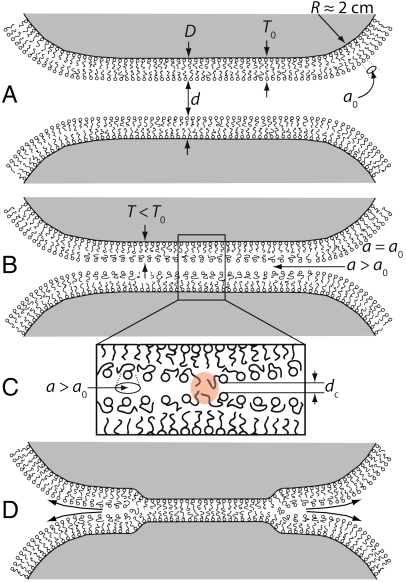
Schematic diagrams depicting the process by which two supported surfactant or lipid bilayers (hemi)fuse. (A) Initially two bilayers are separated by about 30 nm and begin to interact due to long-range electrostatic double-layer forces. (B) As the bilayers approach, they are forced together (2–3 nm), and the strong normal stresses associated with steric and electrostatic repulsions cause the outer layers to thin normally and spread laterally, exposing the hydrophobic interior of the bilayer. (C) A close-up of the instability that occurs near d_c≈1 nm: Stress opens a hydrophobic pore, causing the hydrophobic interiors to strongly attract each other, while the highly stressed outer monolayers begin to be pushed out of the contact area. (D) The instability grows, and the outer monolayers are expelled into the bulk, resulting in the inner monolayers on opposing surfaces to become in adhesive contact. [Vertical deformations of the substrates in (D) have been exaggerated.]

The interaction forces measured between bilayers adsorbed from 12 mM azoTAB in alternating UV and visible light conditions are shown in Fig. 2C. As expected, the surface potential was less for cis azoTAB bilayers, as they are less dense than trans azoTAB bilayers. Cis azoTAB bilayers break through at a smaller applied force due to depleted area density. In this case, the measured adhesion was actually higher for cis azoTAB layers (W_0,cis = 16 ± 6 mJ/m² versus W_0,trans = 12 ± 3 mJ/m²). The decreased adhesion is consistent with the solution concentration being much higher than the CMC of trans azoTAB, which favors the formation of bilayers. Increased hydrophobic interactions among the chains likely caused the molecules to assemble back into the contact area during separation, rendering those layers more hydrophilic and resulting in lower apparent adhesion energy in visible light. Increasing the bulk solution concentration above the CMC values of both cis and trans azoTAB results in adsorbed bilayers for both isomers, and surface properties, such as electrostatic interactions, breakthrough energies, and adhesion (surface) energy that can be adjusted by light.

Consequently, the structures of the azoTAB surfactant molecules undergo reversible light-mediated changes that affect their packing and self-assembly properties both in bulk solution and adsorbed at surfaces. The molecular packing is reflected by surface tension and area-per-molecule measurements at the air-water interface. These packing and molecular structural transformations result in corresponding modulation of long-range electrostatic and short-range hydrophobic interactions by light illumination, as shown in Fig. 2. The photoisomerization results in a direct modification of the surface forces and overall free energy, and thus surfactant CMC. Adsorbed structures are affected accordingly: below the CMC monolayer adsorption is observed, whereas above the CMC, bilayers form. Illumination with UV or visible light modifies the structures of adsorbed and solution-state surfactant molecules, leading to CMC values and adsorbed surface layers that are drastically altered by light.

Derivation of General Interbilayer Interaction Potential.

The separate intra- and intermolecular contributions can be quantified for interacting bilayers. As shown above, for self-assembled structures of azoTAB, the inter- and intraaggregate interactions can be reversibly modified in situ by light. By quantifying each interaction via a theoretical or empirical interaction potential, we derive and test a general theory for the bilayer (hemi)fusion process measured in Fig. 2 B and C. Bilayers are thought to fuse by a mechanism proposed by Helm et al. (13) in which bilayer stresses result in a localized spreading of molecules, causing exposure of the hydrophobic interior, shown schematically in Fig. 3 B and C. Such exposure leads to a breakthrough event in which the hydrocarbon interiors of the inner monolayers strongly attract and adhere to each other while pushing outer monolayer headgroups away and into the bulk (Fig. 3D). A quantitative description of bilayer hemifusion includes a contribution from the hydrophobic attraction that depends on the degree of lateral spreading of molecules within the outer monolayer. Electrostatic double-layer forces, steric-hydration forces, surface tension, and bilayer elasticity are explicitly calculated in the model as well. Van der Waals forces are not included here, because they are generally small compared to the others at all distances (14). The model is derived as shown below, beginning with a short description of each intermolecular interaction potential.

The interaction potential for the electrostatic double-layer force is well-known. The electrostatic interaction potential is given as E_ES = C_ESe^-κd, where 1/κ is the Debye length for a given bulk ion concentration, d is the distance between the surfaces, and the preexponential term C_ES depends on the surface geometry, surface potential, and solution conditions (15). The Grahame equation can then be used to calculate the surface charge density from the surface potential (14). Whereas the energy potential for the electrostatic force is known theoretically, an empirical potential is used for the steric-hydration force, a short-range repulsion which arises from water structuring near hydrophilic surfaces (16). As two hydrophilic surfaces approach each other, water molecules are strongly bound to surface hydrophilic groups. The repulsion arises because of the energy needed to confine and dehydrate these groups. Steric-type repulsions also originate from headgroup protrusions that might be more prevalent here because of the increased hydrophilicity near the azo group. Because both are short-range and repulsive, and there is no way to separate their effects in these measurements, the steric-hydration energy is modeled here as a short-range exponential repulsion, 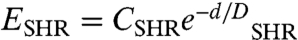, where the preexponential term on a per molecule basis C_SHR is 1–5 × 10^-20 J, and the decay length D_SHR is typically 2–10 Å (14).

There is no well-accepted theoretical energy potential for the hydrophobic interaction, so an empirically derived potential is used here. Hydrophobic surfaces strongly attract each other to eject the water into the bulk to minimize the free energy of the system. The short-range pure hydrophobic force that operates from 1–1.5 nm down to contact, appears in this regime as a short-range exponentially decaying attraction and is thought to be due to a depleted water density near hydrophobic surfaces (17). Here, the hydrophobic energy is proportional to the interfacial tension γ and the amount of exposed hydrophobicity within the bilayer, as shown on a per molecule basis in Eq. 1:

[1]

This term is nonzero and attractive when the molecules within the bilayers are stressed, exposing increased hydrophobic area in the bilayer. Typical values for γ range from 20–50 mJ/m², and the hydrophobic decay length D_hydro ≈ 1 nm (14, 17).

To quantify the intraaggregate energy, which includes contributions from the surface tension, headgroup repulsions, and bilayer elastic modulus, the first-order approximation for the free energy per molecule in any self-assembled aggregate is, as follows:

[2]

This equation has a minimum at the optimum area per molecule a₀, for which the total energy E is 2γa₀. The elastic energy is present in all self-assembled structures (14), which contributes to the bilayer thinning and eventual breakthrough.

To determine the overall interaction potential, it is assumed that at every equilibrium distance d the molecular area a will adjust to achieve the minimum energy configuration, i.e., (dE/da)_d = 0. This minimization leaves only terms that depend on the area per molecule, a, which is solved to obtain the area profile as a function of separation distance:

[3]

The individual contributions are summed on a per molecule basis. An additional factor of two is included for the hydrophobic and interfacial tension terms, because two unit areas are interacting, i.e., E_total = 2E_ST + 2E_hydro + E_SHR + E_ES. The total energy E is divided by the area profile a(d) to obtain the interaction energy per unit area, W. A Lennard–Jones hard-wall repulsive term acts only at short range when the surfactant molecules are in molecular contact with each other (monolayer-monolayer contact), yielding the following Eq. 4 for the overall interaction potential for bilayer hemifusion:

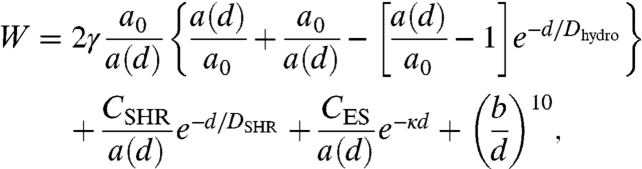[4]

where b is the Lennard–Jones hard-wall distance. By applying the Derjaguin approximation to the experimental forces measured by SFA, W_expt = F_expt/2πR, the force between crossed cylinders is converted to the energy between flat plates to compare to the theoretical calculation.

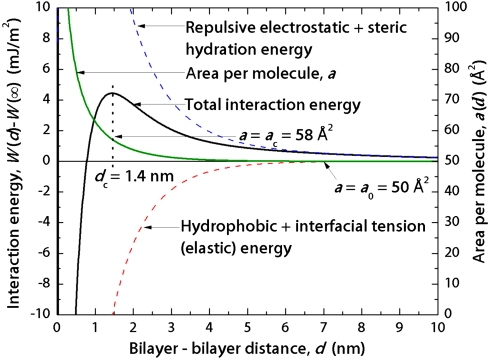
To directly compare the experiments with the model, the energy is referenced to the energy at d = ∞, i.e., W(d) - W(∞), and plotted against the mica-mica distance, D, which includes the thickness of the two (thinning) bilayers, D = d + 2T(d). This calculation is shown as the lines through the data points in Fig. 2 B and C, and the model predicts not only a breakthrough event but also a deep adhesive minimum due to the hydrophobic force, two characteristics that are defining events in the hemifusion process. The calculated energy and the separate contributions to the overall force law are shown in Fig. 4 as functions of bilayer-bilayer distance d. The hydrophobic force wins out at a bilayer-bilayer separation distance of d_c ≈ 1 nm.

Fig. 4.

Calculated interaction energies for trans azoTAB plotted against the bilayer-bilayer separation distance d and showing individual contributions to the overall force law. The hydrophobic contribution predominates over strong electrostatic and steric repulsions at about 1 nm of separation, as expected for the short-range pure hydrophobic force. The area per molecule (green curve) increases from 50 Å² to 58 Å² at the breakthrough point (energy maximum), indicating that the bilayer has compressed normally (thinned) or expanded laterally by about 16% before breakthrough.

The calculation for bilayer hemifusion includes contributions from the interfacial tension γ and the area per molecule in the bilayer, a₀. For azoTAB both of these parameters change depending on the wavelength of light illumination, so the theory is analyzed for two unique cases, trans and cis azoTAB. The parameters that are measured or calculated are fixed, with the value for a₀ approximated from film balance measurements described in SI Text, and κ^-1 calculated directly from the surfactant concentration; parameters for which we gain no direct knowledge from these experiments are assigned representative values. The main fitting parameters for the repulsive region are C_ES and C_SHR; the magnitude of the breakthrough and the attractive region are fitted by the interfacial tension γ. All parameters are summarized in Table 1. The electrostatic behavior is expected: The cis bilayer displays a lower surface potential due to decreased headgroup density, and the percent ionized does not change drastically. The interfacial tension γ is slightly lower than values expected for bilayers (14). The fitted value is reasonable for trans azoTAB bilayers, which should display a slightly smaller bilayer-water interfacial tension to begin with, because of the hydrophilic azo group in the middle of the hydrocarbon chain, and the fitted interfacial tension γ is 18 mJ/m². The isomerization to cis bilayers results in an even lower fitted value for interfacial tension (10 mJ/m²). This value is consistent with the cis layers being even more hydrophilic (the azo group is likely more exposed to both the interior and exterior of the bilayer).

Table 1.

Fitting parameters used for the calculation of bilayer hemifusion energy, Eq. 4

Isomer state	Measured and calculated		Assumed parameters			Fitted parameters			Calculated electrostatics
	a0 (± 3 Å2)	κ-1 (± 0.1 nm)	Dhydro (± 0.05 nm)	DSHR (± 0.2 Å)	b (Å)	CES (± 0.2 × 10-21 J)	CSHR (± 0.1 × 10-20 J)	γ (± 1 mJ/m2)	ψ0 (mV)	Dissociated (%)
trans	50	4.1*	1	9	0.2	1.4	3.8	18	145 ± 29†	80 ± 16‡
trans	50	2.8*	1	9	0.2	2.2	3.0	18	160 ± 25†	60 ± 15‡
cis	100	2.8*	1	9	0.2	2.9	4.4	10	105 ± 8†	75 ± 7‡

Calculated energy curves are shown as lines through the points in Fig. 2 B and C. Errors displayed indicate the range of values that result in satisfactory fits to the experimental data.

^*Calculated from κ^-1 = (ε₀εkT/2ρ_∞e²)^1/2 ≅ 0.304/[azoTAB]^1/2 nm.

^†Calculated from fit to: C_ES/a₀ = 64kTρ_∞ tanh²(eψ₀/4kT)/κ ≅ 0.0482[azoTAB]^1/2 tanh²[ψ₀(mV)/103] J/m².

^‡Calculated from 100(1-σa₀/e), where charge density σ is found from the Grahame equation σ = (8ε₀εkT)^1/2 sinh(eψ₀/2kT)[azoTAB]^1/2 ≅ 0.117[azoTAB]^1/2 sinh[ψ₀(mV)/51.4] C/m², and e is the elementary charge.

Discussion and Conclusions

A mean field, continuum approach is taken here, with the resulting model quantitatively capturing the major features of bilayer (hemi)fusion. These include the long- and short-range repulsive forces, hydrophobic forces, magnitude and separation of the critical breakthrough point, strongly adhesive minimum, and lateral bilayer stresses. Highly localized (molecular level) information is essentially smeared out, and the local dynamics, deformations, and rearrangements of the lowest-energy intermediate fusion structures are better captured by the calculations of authors like Chernomordik, Kozlov, Zimmerberg, and Safran, among others (18–20). These provide a representation of the local short-range effects of fusion, and specifically the local breakthrough mechanism of bilayers and the energetics involved in these processes. Indeed, many of the hemifusion models (19–21) and experiments (13, 22–24) indicate that bilayer thinning and lipid spreading or depletion of the outer leaflet is an important step in the process. However most models do not strictly invoke the hydrophobic interaction, which must predominate at small separations, because the lowest-energy state in the (hemi)fusion event is adhesive contact of the inner bilayer leaflets. Of course, the simple potentials used here allow for a nice fit to the experimental data, but the empirical potential for the hydrophobic interaction and inclusion of shorter range (lateral) effects due to surface tension and bilayer elasticity (which are indirectly due to the hydrophobic interaction) combine to accurately approximate the attractive regime.

The model is not limited to supported membranes and can likely be extended to more complicated systems, such as free bilayers, lipid vesicles, and biomembranes by adapting the model to these situations, for example, by including the undulation force. However, the energy barrier for (hemi)fusion could decrease because of the increased attraction from bending and exposed hydrophobicity (25). It is important to note that the model specifically applies to surfactant chains in a liquid-like state that can be easily deformed (depleted) by applying normal or lateral stresses. For bilayers in the gel or frozen state the area per molecule will be a much weaker function of separation, due to their larger elastic moduli. For these systems the energy potentials could be estimated by considering the DLVO forces together with established potentials for any steric and depletion forces that might be present, at constant a = a₀.

However, when the bilayers are in a fully fluid state, such as in systems with short surfactant chains, packing mismatches due to unsaturated chains, light-induced conformational changes, or less hydrophobic molecular structures, the bilayer is able to compress and spread, allowing the hydrophobic interaction to act. In the case of azoTAB, we have shown that the hydrophobic force dominates at short distances and can also be modulated to some degree by the light illumination, largely because the isomerization to cis results in a configuration such that the hydrophilic nitrogen atoms in the azo group are exposed. So-called hydrophobic surfaces generally have a contact angle greater than 90° and adhesion energy W₀ of up to 100 mJ/m² (17). For azoTAB surfaces the measured adhesion energies are ≈15 mJ/m² (cis) and ≈20 mJ/m² (trans). Because there is a reservoir of surfactant molecules in these experiments, upon separation azoTAB molecules will be diffusing back into the contact area to decrease the exposed hydrophobic area, resulting in a lower adhesion than 2γ_i. If there were no reservoir (or if the surfaces are separated quickly), it is likely that the adhesion would increase and approach the calculated value of 45–60 mJ/m².

One major finding is that the force measurements and theoretical model both show that the hydrophobic interaction (Eq. 1) is masked by hydrophilic groups until the hydrophobic area reaches a critical value in excess of the unstressed optimal area per molecule, at which point the strong exponential attraction becomes important (Fig. 3 C and D, Fig. 4). Delicate interplay of nearby ionic (hydrophilic) headgroups, hydrophilic moieties within the surfactant molecular structure itself, and local surface geometry appear to directly influence the hydrophobic interaction potential, indicating that the hydrophobic interaction is nonadditive. These effects are in qualitative agreement with recent simulations, which showed that a small number of hydroxyl groups surrounded by methyl groups effectively quench large local density fluctuations that are correlated with surface hydrophobicity (26). Thus, the empirical hydrophobic energy potential Eq. 1 can be generalized further, by using an effective hydrophobic area considering the fraction of hydrophobic area in a surfactant or polymer layer.

Although there is no theoretical evidence to this point for the exponential decay of the hydrophobic force, it has been measured by our group and others (17, 27). The decay could be biexponential, with a decay length that is not constant (27). An even steeper attraction likely exists in the final angstrom or two to reach the expected very deep adhesion minimum for pristine hydrophobic surfaces, due to water density depletion near hydrophobic surfaces (28). Regardless, the exponentially decaying attraction is a good first-order approximation for the attractive regime. Eq. 4 represents a significant step toward development of force-distance (or energy-distance) relationships that are valid at all distances and include the hydrophobic interaction for a full understanding of complex bilayer systems.

The light-responsive surface forces and structural transformations elucidated here can be interpreted generally for other stimuli-responsive surfactant systems. The interplay of surface forces and packing morphology will determine the degree to which the surface properties are modified by stimuli. For example, for a surfactant with an azobenzene spacer in the middle of a longer (hydrophobic) alkyl chain, photoisomerization would likely induce larger packing transformations and a larger difference in hydrophobicity. It is convenient to switch properties by light, but similar surface forces and packing transformations could be induced by electric fields, magnetic fields, mechanical or rheological stresses, bulk solution conditions, or ex situ synthesis steps. Engineered surfactant and lipid systems, such as consumer products, emulsifiers, dispersants, and drug delivery vehicles can take advantage of the ability to control the surface and solution state properties by light in situ, which can generally only be drastically altered by adjusting temperature, ionic strength, bulk surfactant concentration, pH, or surfactant chain length.

The conceptual understanding of the role of hydrophobic interactions in bilayer (hemi)fusion has implications for a broad class of biological and technological applications. Biological membranes undergo rupture and subsequent fusion in many processes, such as phagocytosis, protein trafficking, and signaling. Membrane fusion and hemifusion is also implicated in certain virus and disease propagation within the human body (29). As shown above, the (hemi)fusion process can only proceed spontaneously when enough hydrophobic area is exposed, such that the attractive interaction prevails over any repulsive forces. This behavior indicates that exposed hydrophobicity caused by packing mismatches of inserted proteins is one possible mechanism of biomembrane fusion. Furthermore, vesicle fusion must be prevented in consumer product and drug delivery suspensions so as to preserve phase stability. A theoretical and practical understanding of bilayer fusion and the effects of the strong hydrophobic force on the fusion process should aid in the rational design and engineering of advanced biomimetic and technological membrane systems.

Materials and Methods

The photoresponsive surfactant azoTAB (M_r = 420.4 g/mol) was synthesized as previously reported (12) and confirmed to have 99% purity by GC and NMR. Ultrapure water obtained from a Milli-Q (Elix 10 and Milli-Q Gradient A10) system was used to make aqueous solutions of azoTAB of given concentrations. The azobenzene bond undergoes a photoisomerization from the straight trans conformation to the bent cis isomer on exposure to 365 nm UV light (Fig. 1B). The trans isomer is thermodynamically stable; cis azoTAB converts back to trans in the dark in 24 h, or rapid isomerization from cis to trans azoTAB can be induced by 450 nm visible light. In these experiments, a 6 W 365 nm UV lamp (UVP LLC, Model UVL-56) was used to convert azoTAB to the predominantly cis state, whereas broadband white visible laboratory light was used to convert azoTAB to the predominantly trans form.

An SFA 2000 (30) was used to measure the forces between adsorbed layers of azoTAB in water. Briefly, the distance is measured interferometrically to angstrom resolution, whereas the force is measured dynamically by the spring deflection as the two mica surfaces are driven together at a constant rate. AzoTAB-adsorbed surfaces were prepared by injecting several droplets of azoTAB solutions (0.5, 5.5, or 12 mM) between the surfaces and waiting 1 h to allow equilibration of monolayer or bilayer self-assembly before performing the force measurements. Cis azoTAB was formed during force measurements by directing the 365 nm UV light through the front window of the SFA 2000. It was confirmed by UV-visible that the broadband white light used to observe fringes of equal chromatic order resulted in minimal reconversion of cis azoTAB to the trans isomer during the measurements (see SI Text). Force measurements were performed sequentially in alternating visible and UV light to observe trans and cis azoTAB, respectively, with at least 1 h to equilibrate between each light adjustment. UV-visible absorbance measurements indicated that photoisomerization was complete within 1 h, and repeated force measurements were performed under constant light conditions with consistent quantitative agreement, indicating that the bilayers can self-assemble quickly with healing times of ≤ 5 min. Results shown are representative for every contact position and approach/separation rate. Slower rates result in a smaller effective force/energy barrier (cf. Bell theory ref. 14), but the effect is slight (< 10% difference).