Ionic Strength Dependence of F-actin and Glycolytic Enzyme Associations: A Brownian Dynamics Simulations Approach

Abstract

The association of glycolytic enzymes with F-actin is proposed to be one mechanism by which these enzymes are compartmentalized, and, as a result, may possibly play important roles for: regulation of the glycolytic pathway, potential substrate channeling, and increasing glycolytic flux. Historically, in vitro experiments have shown that many enzyme/actin interactions are dependent upon ionic strength. Herein, Brownian dynamics (BD) examines how ionic strength impacts the energetics of the association of F-actin with the glycolytic enzymes: lactate dehydrogenase (LDH), glyceraldehyde-3-phosphate dehydrogenase (GAPDH), fructose-1,6-bisphosphate aldolase (aldolase), and triose phosphate isomerase (TPI). The BD simulations are steered by electrostatics calculated by Poisson-Boltzmann theory. The BD results confirm experimental observations that the degree of association diminishes as ionic strength increases but also suggest that these interactions are significant at physiological ionic strengths. Furthermore, BD agrees with experiments that muscle LDH, aldolase and GPADH interact significantly with F-actin whereas TPI does not. BD indicates similarities in binding regions for aldolase and LDH among the different species investigated. Furthermore, the residues responsible for salt bridge formation in stable complexes persist as ionic strength increases. This suggests the importance of the residues determined for these binary complexes and specificity of the interactions. That these interactions are conserved across species, and there appears to be a general trend among the enzymes, support the importance of these enzyme-F-actin interactions in creating initial complexes critical for compartmentation.

INTRODUCTION

The regulation of an enzyme system can be accomplished in a number of different ways, such as modulation of its substrate concentrations, ionic strength of the medium (counter ions in solution), or by subcellular compartmentation.^1–3 An example of regulation by subcellular compartmentation has been suggested in glycolysis.³ Fructose-1,6-bisphosphate aldolase (aldolase), glyceraldehyde-3-phosphate dehydrogenase (GAPDH), and lactate dehydrogenase (LDH) are key glycolytic enzymes that have been shown to concentrate around subcellular proteins (e.g., F-actin) in muscle tissue.^4–5 In vitro experiments show that the association between F-actin and the glycolytic enzymes is reversible and dependent upon the pH and ionic strength of the solvent media.^6–8 For example, glycolytic enzyme coprecipitation with F-actin shows that this interaction diminishes or is almost completely inhibited with increasing ionic strength.^5,7 Only F-actin/glycolytic enzyme pellets, however, were examined in these studies. Lakatos and Minton, using analytical centrifugation observed that appreciable interactions between aldolase and actin filaments still occur at physiological ionic strengths (0.1 – 0.15 M).⁶

Herein, Brownian dynamics (BD) simulations examine and quantify the effects of ionic strength on glycolytic enzyme association with F-actin. This is a systematic study to generalize the mechanism of compartmentation in glycolysis. The ionic strength of the solvent environment usually affects the thermodynamic properties of system, such as interaction affinity and complex formation. This is especially true at physiological ionic strengths where a large number of positive and negative ions are present. The ionic strength dependence on the binding energy and association between glycolytic enzymes and F-actin can therefore provide valuable information on the specificity and mechanism of such interactions. The choice of a 0.01–0.15 M ionic strength range is in accordance with a variety of experimental investigations.^7–9 The lower ionic strengths studied (0.01–0.05 M) are used to enhance potential interactions, making it easier to observe the important molecular determinants responsible for the interactions.¹⁰ In silico, at lower ionic strengths, there is an increased number of bimolecular complexes allowing for better visualization of the electrostatic potential effects and plausible mechanisms for binding, which can then be compared to the type of binding modes and complexes observed at physiological ionic strengths of 0.1–0.15 M. The similarities and differences in binding between four glycolytic enzymes and F-actin from three different species are examined to generalize the viability of compartmentation in glycolysis due to the dynamic interaction between glycolytic enzymes and the cytoskeletal protein F-actin. A possible explanation why each of these enzymes binds F-actin or not is explored along with molecular scale similarities and differences in the electrostatic interaction between protein pairs across different species. The simulations also compare the interactions between enzymes that have been shown by many experiments to interact with F-actin (aldolase, muscle LDH and GAPDH) and one that generally does not (triose phosphate isomerase (TPI).^11–12 The BD simulations provide a molecular and detailed account for such differences, and suggest important molecular determinants and requirements for F-actin/glycolytic enzyme interactions.

Typically, both experimental and theoretical studies suggest that the charge distribution in an enzyme or protein is a critical determinant of its properties and behavior in solution.^13–14 This charge distribution is strongly modulated by the ionic strength of the solvent medium. As a result, the extent to which a group is ionized depends on the electrostatic potential at that site. Many studies show that this electrostatic potential not only determines the orientation and initial docking of macromolecules, but also plays an important role in steering these molecules during their approach.¹⁵ Changing the ionic strength of the medium can significantly impact electrostatic interactions. This is because the ionic strength of the medium has the potential to limit the effects of long-range electrostatic forces experienced by proteins in solution.

Brownian dynamics simulations (BD) constitute one common theoretical method used to study electrostatically driven protein-protein interactions. BD has been used for over three decades to study the kinetics and energetics of rigid-body protein-protein association in complicated and realistic electrostatic fields. Much of the emphasis of BD has been on calculating the bimolecular rate constants for protein-protein association.^16–17 The quantitative values of the association rate constants obtained are in good agreement with experimental values.¹⁸ For example, BD has been employed to model the effect cytochrome f (cyt f) structure on its function by modeling electron transfer mechanisms and rates between the redox partners plastocyanin or cytochrome c₆ and seven different structures of cytochrome f (cyt f).¹⁹ The BD results indicate different electron transfer rates among the complexes formed in spite of the formation of similar binary complexes. The different rates are attributed to subtle variations in a small flexible loop of the small domain of cyt f.

BD is also capable of providing other information concerning macromolecular associations, including: the prediction of relative free energies of interaction and the dynamics of nonspecific binding for protein-protein or protein-DNA interactions²⁰ and the prediction of specific encounter complexes^21–22. BD has also been able to reproduce the ionic strength dependence of a variety of processes including the interaction of 464 Cro repressor and B-DNA.²³ The evaluation, interpretation and prediction of mutant effects involved in electrostatic interactions between proteins has also been achieved;²⁴ for example, when BD predicted mutants are made experimentally to increase the rate of electron transfer, a 200 fold increase in the electron transfer rate is observed.²⁴

The BD method simulates the relative translational and rotational diffusive motions of whole macromolecules under the influence of complex electrostatic and excluded volume interactions present in the solution. The electrostatic potentials are computed rigorously by iterating the solutions of the Poisson-Boltzmann equation (PB). The PB theory actually facilitates the explanation of salt effects by estimating the electrostatic potentials around the molecules as a function of ionic strength. The linearized PB has been extensively used to compute electrostatic forces between protein binary complexes. The LPB is considered less computationally expensive to compute, and for molecules with low charge densities, realistic results are maintained.²⁵ Proteins typically have a low charge density making the solution of the LPB sufficient for solving the electrostatic potential. The full Poisson-Boltzmann (FPB) (also known as the nonlinear Poisson Boltzmann) becomes critical when macromolecules exhibit large charge density (e.g., RNA or DNA).^26–27

The ultimate goals of simulations between glycolytic enzymes and F-actin are to make testable predictions,^11,21 including reproducing experiment, identifying initial binding modes and identifying important molecular determinants or residues responsible for significant interactions amongst glycolytic enzymes in three different species. Herein, BD examines the ionic strength dependence of the interactions of aldolase, GAPDH, LDH and TPI with F-actin. Three different species, rabbit (Oryctolagus cuniculus), zebrafish (Brachydanio rerio) and human (Homo sapiens) are examined. Rabbit and zebrafish were chosen for comparison with published experimental data, and human was chosen because of the availability of protein structural data. BD simulations answer the following questions: (1) Is there a general trend among glycolytic enzymes that bind compared to one that does not? (2) Are the interactions comparable across species? (3) How does the degree of association change over a range of ionic strengths (0.01 – 0.15 M)? (4) What is the effect of the ionic strength on the specificity of complex formation?

METHODS

Protein structures

The crystal structures of the enzymes were downloaded from the RCSB Protein Data Bank:²⁸ rabbit muscle aldolase (1ADO²⁹), rabbit muscle GAPDH (1JOX³⁰), rabbit muscle G-actin (1ATN³¹), human muscle aldolase (4ALD³²), human muscle GAPDH (3GPD³³), human muscle LDH (1I10³⁴), rabbit TPI (1R2R³⁵), and human TPI (1HTI³⁶). The coordinates of the helical structure of F-actin were generated using the parameters provided by Holmes and coworkers.³⁷ The tertiary structures of the other enzymes were built from their primary amino acid sequences obtained from the Uniprot Data Base.³⁸ These models were built using the Homology module of Insight®II molecular modeling package (Accelrys, San Diego, CA). The reference protein crystal structures employed, with their corresponding sequence similarities to the model proteins are shown in Table I. The glycolytic enzyme models built include: zebrafish muscle aldolase (Q8JH72),³⁹ zebrafish (embryonic tissue) GAPDH (Q5XJ10),⁴⁰ rabbit muscle LDH (P13491),⁴¹ zebrafish (embryonic tissue) LDH (Q9PVK5),⁴² and zebrafish triosephosphate isomerase (Q1MTI4)³⁹. The details for building zebrafish muscle aldolase are reported in Forlemu et al.,²¹ and a similar procedure was used for building zebrafish GAPDH, LDH and TPI models (See Supplement text and Figs. S1 and S2). The details for building the rabbit muscle LDH are found in Njabon (2005).⁴³

Table I.

Sequence Similarity Between Reference Proteins (Known Crystal Structures) and Desired Protein (Unknown Tertiary Structure).

Desired Protein	Reference Proteina	Sequence Identity (%)
Zebrafish Aldolase	Rabbit Aldolase (1ADO)	85
Zebrafish GAPDH	Rabbit GAPDH (1J0X)	76
Zebrafish LDH	Carp LDH (1V6A)	95
Rabbit LDH	Pig LDH (9LDT)	95
Zebrafish TPI	Rabbit TPI (1R2R)	80

^aThe PDB codes of the reference structures are given in parenthesis.

The primary sequence of zebrafish G-actin was also obtained from the UniProt database with primary accession number (Q7ZU23).⁴⁰ The rabbit crystal structure of G-actin in complex with gelsolin, accession code (1ATN), was used as reference protein to build the zebrafish G-actin model. Essentially, F-actin is extremely conserved with a sequence identity of about 99.6 % amongst zebrafish species. The zebrafish actin model was used for all simulations involving fish proteins. The helical model of this actin molecule, like the quaternary structure of the glycolytic enzymes, was obtained through superposition and transformation using the coordinate map of the Holmes model³⁷ F-actin structure. This was achieved using the Insight®II molecular modeling package.

The models obtained, were energy minimized using the Discover_3 module in Insight®II to obtain an atomic level structure with low energy and no atomic overlaps. In each case, the AMBER force field was used with a dielectric constant of 78.3 (water). A strategy of steepest descents followed by conjugate gradients was adopted for 5,000 iterations.

Charge assignments and electrostatic potentials

The program package MacroDox was used to calculate and assign charges to titratible sites on the proteins, determine the electrostatic potential around each molecule, and run the various BD simulations.⁴⁴ Based on the atomic coordinates of each protein, charges were calculated by applying the Tanford-Kirkwood⁴⁵ and Roxby⁴⁶ method with static accessibility modification. Charge assignment was done at a pH of 7.00 and a temperature of 298.15 K. The MacroDox charge set used the well established CHARMM force field, which has been successfully used in a variety of BD simulations of protein interactions as the partial charge library.⁴⁷

Following charge assignments, the electrostatic potential about each protein was computed by numerically solving the linearized Poisson-Boltzmann (PB) equation⁴⁸ for the molecules at four different ionic strengths: 0.01, 0.05, 0.1 and 0.15 M.

$$\nabla [\epsilon (r)\nabla \varphi (r)]-\epsilon (r){\kappa }^2(\varphi (r))+4\pi \rho (r)=0$$ (1)

Where ϕ(r) is the electrostatic potential, ε(r) is the continuum dielectric constant as function of position, and ρ(r) is the charge density. The parameter κ is the Debye screening constant, which is the inverse of the Coulomb Debye length. This constant describes the exponential decay of the potential in the solvent and thus takes into account mean properties mobile ions of such as the ionic strength, pH and temperature of the system as evident from.⁴⁹

$${\kappa }^2=\frac{8\pi e^{2}I}{\epsilon k_{B}T}$$ (2)

Where k_B is the Boltzmann constant, I is the ionic strength, T is the absolute temperature, and ε is the solvent medium dielectric constant. Each solution was iterated on a cubic lattice by the Warwicker and Watson method,⁵⁰ with the adaptation of Klapper et al.⁵¹. Further details of this calculation are given in Forlemu et al.²¹.

Brownian dynamics (BD) simulations

The BD algorithm for the program package MacroDox is based on the Ermak-McCammon algorithm⁵² and is detailed in Northrup et al.^22,44. BD simulations of the glycolytic enzymes with F-actin were performed to identify the formation of complexes, to determine the binding site, and to calculate the free energy of the interaction. In each simulation the enzymes were allowed to diffuse within a truncated cylinder around the F-actin filament.

A modified form of the BD algorithm was used to mimic the periodic property of the actin filaments as described by Ouporov et al.,¹⁰ Initially the center of mass (COM) of the enzyme was randomly positioned at a distance of about 135 Å from the helical axis of F-actin. During each trajectory, the enzyme was maintained close to the F-actin by relocating it to a position 135 Å from the F-actin molecule each time the distance between the center of mass atoms (COM) of both molecules exceeded 250 Å. Therefore, the simulations force the enzyme to spend more time in a region closer to F-actin to reduce the time spent out of this region where the electrostatic interaction energy is negligible. Each individual trajectory was terminated when the glycolytic enzymes performed 200,000 BD steps with a distance between the COM of both proteins less than 120 Å (separation at which complexes are formed) or when the distance became greater than 250 Å (the truncation radius at which point the electrostatic interactions between the molecules is negligible). During each trajectory a complex was saved for further analysis if the electrostatic interaction energy between the proteins was less than −4.00 kcal/mol and the most intimate complex with close contact distances between 2.00 Å and 6.0 Å. This range of distances is typical for salt bridges. The upper limit of 6 Å is somewhat arbitrary, but as the electrostatic interaction diminishes with distances it is a reasonable choice. The lower limit of 2 Å, however, is more important because of the excluded volume of the two proteins (atomic radii are typically 1–1.5 Å). 1,000 BD trajectories took 36 hours of CPU time on an SGI Fuel workstation.

BD simulations to follow the orientationally average free energy of the interaction of aldolase and F-actin consisted of single trajectories where the enzyme took 1.2 × 10⁷ diffusive steps within a cylinder of height 110 Å around the F-actin. The docking coordinate was defined as the distance between the aldolase COM and the F-actin helical axis. A distribution of residence times of the COM of aldolase in cylindrical concentric bins of 1 Å along the trajectory path was then tallied and converted to a potential of mean force (PMF) by a statistical mechanical formula as described previously by McCammon and Harvey (Equation 3).⁵³ The radial free energy of interactions was then calculated from the PMF (Equation 4). The potential of mean force constitutes the effective attractive force or radial free energy of enzyme-actin association, including Boltzmann statistical averaging over all orientational degrees of freedom.

$$\mathit{\text{PMF}}=-k_{B}T\text{ln}(\rho (R))+C$$ (3)

$$A=-k_{B}T\text{ln}(\rho (R))$$ (4)

Where k_B is the Boltzmann constant, T is the temperature, ρ(R) is the distribution of residence times at distance R, and C is the constant value of PMF when the electrostatic potential about protein is fully dissipated (zero) (116–120 Å). The radial free energy (A) was obtained by subtracting C, which set the PMF to zero since at this point the EP about F-actin is negligible or actually zero. This radial free energy is the actual driving force behind this interaction. To obtain good statistics, 10 different simulations, each of which took about 3 hours of CPU time on a SGI Fuel workstation, were performed and the results averaged to determine the free energy curves.

RESULTS

Effect of ionic strength on electrostatic potentials

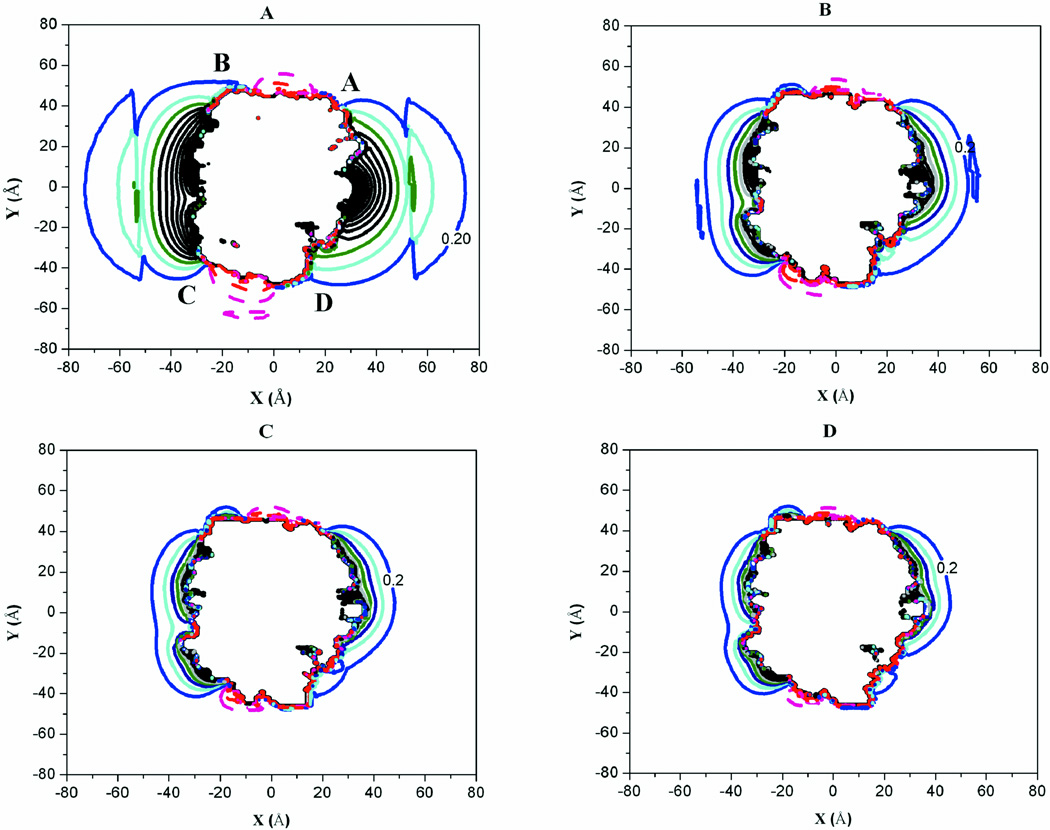
The electrostatic potential (EP) about each molecule is represented by two-dimensional contour maps (Fig. 1, and Supplement Figs. S3–S7). Each contour line represents the electrostatic potential about the molecule at a specific position from the molecular surface. This representation makes it easier to observe the effects of salt concentration or ionic strength on the interactions between the glycolytic enzymes and F-actin. Clusters of similar charges enhance and extend the electrostatic potential about the surface of the molecules facilitating long-range electrostatic interactions. Increasing the ionic strength screens the extension of the EP significantly. From an ionic strength of 0.01 to 0.15 M, the EP is reduced from approximately 80 Å to 40 Å from the center of mass of the enzymes (Fig. 1, Supplement Figs. S3–S4). For all ionic strengths, the EP is fully dissipated or reaches zero at a distance of about 90–100 Å in both directions (X- and Y- dimensions) from the center of mass of the molecule (not shown on maps). This suggests that for any meaningful interactions to occur, there must be an aggregation of highly exposed polar residues on the molecular surfaces of the proteins. Although each of the proteins do contain histidine residues that contribute to the overall charge and electrostatic potenital of the proteins, none of these histidine residues contributed to the electrostatic potential regions identified as important for the enzyme/actin interactions. An earlier examination of rabbit aldolase/rabbit actin interactions via computational mutants where only the histidines were mutated to alanine, the mutantations did not impact the binding of F-actin significantly.⁵⁴

Fig. 1.

Electrostatic Potential Contours about Rabbit LDH. (A) I = 0.01 M. (B) I = 0.05 M. (C) I = 0.1 M. (D) I = 0.15 M. In all cases, the contour levels are 0.3 kcal/mol apart. Red (−1 kcal/mol), Magenta (−0.71 kcal/mol), Purple (−0.43 kcal/mol), Dark red (−0.14 kcal/mol), Blue (0.2 kcal/mol), Cyan (0.5 kcal/mol), Navy blue (0.8 kcal/mol), Dark cyan (1.1 kcal/mol), Royal blue (1.4 kcal/mol), Violet (1.7 kcal/mol), Black (2–3 kcal/mol).

The aldolase contour maps (Supplement Fig. S3) show an extension of positive potential (solid lines) around the A/D and B/C groove regions that have been previously identified as important for complex formation with F-actin.^10,21 Positively charged residues involved in binding F-actin are located in this groove region explaining the long-range positive electrostatic potential. LDH also has a similar groove region between subunits A/D and B/C (Fig. 1) with a similar extension of the electrostatic potential. The figures presented here for rabbit are qualitatively similar for zebrafish and human proteins (Supplement Figs. S8–S11).

The potential actin binding regions (Supplement Fig. S4) on rabbit GAPDH (Supplement Fig. S12 for zebrafish GAPDH) show strong permeation of the electrostatic fields around the molecule at 0.01 M but contracts significantly (0.05–0.15M) as compared to aldolase and LDH enzymes. This region on rabbit GAPDH has also been identified as important for complex formation with F-actin. The residues responsible for complex formation, however, are not clustered in a deep groove, but located on the corners of the enzyme and are farther apart than similar surface residues in aldolase and LDH. The recognition patches are not well defined in human GAPDH (Supplement Fig. S5). The extension of the positive electrostatic field is attenuated by the presence of negatively charged residues. At all ionic strengths, the positive EP contour levels do not extend beyond 5 Å of the surface of human GAPDH.

The EP contours about TPI in all species does not show any considerable extension from the surface of the molecule as compared to other glycolytic enzymes (Supplement Fig. S6). This stark contrast is an indication of the absence of specific domains on the TPI molecule with clusters of similar charges. As a result the electrostatic potential contour lines do not extend beyond the protein surface into solution.

A representative contour map of the electrostatic potential about highly conserved F-actin also depicts a diminishing electrostatic potential as ionic strength increases (Supplement Fig. S7). Typically, at lower ionic strength, the EP extends between 85 and 90 Å into the solution indicating a potential strong attraction for positive patches of other molecules. As ionic strength increases the EP again becomes greatly reduced as observed with the glycolytic enzymes. This strong and extensive electrostatic field is a result of the aggregation of negatively charged residues around subdomain I of the actin monomer.

Ionic strength effects on complex formation

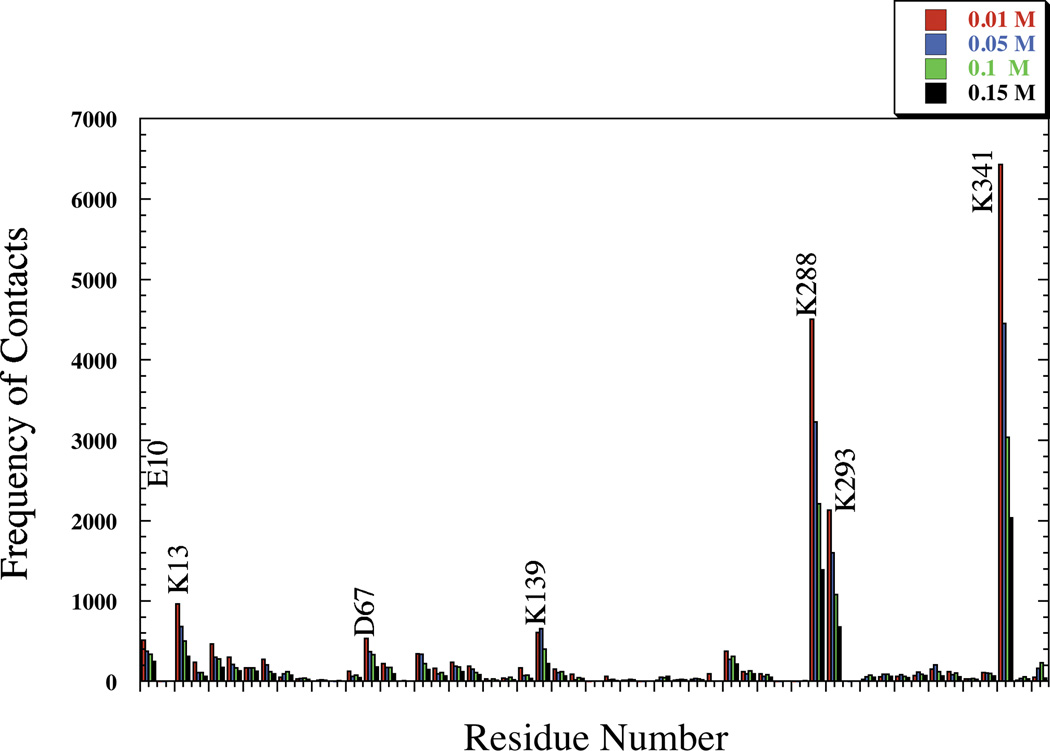
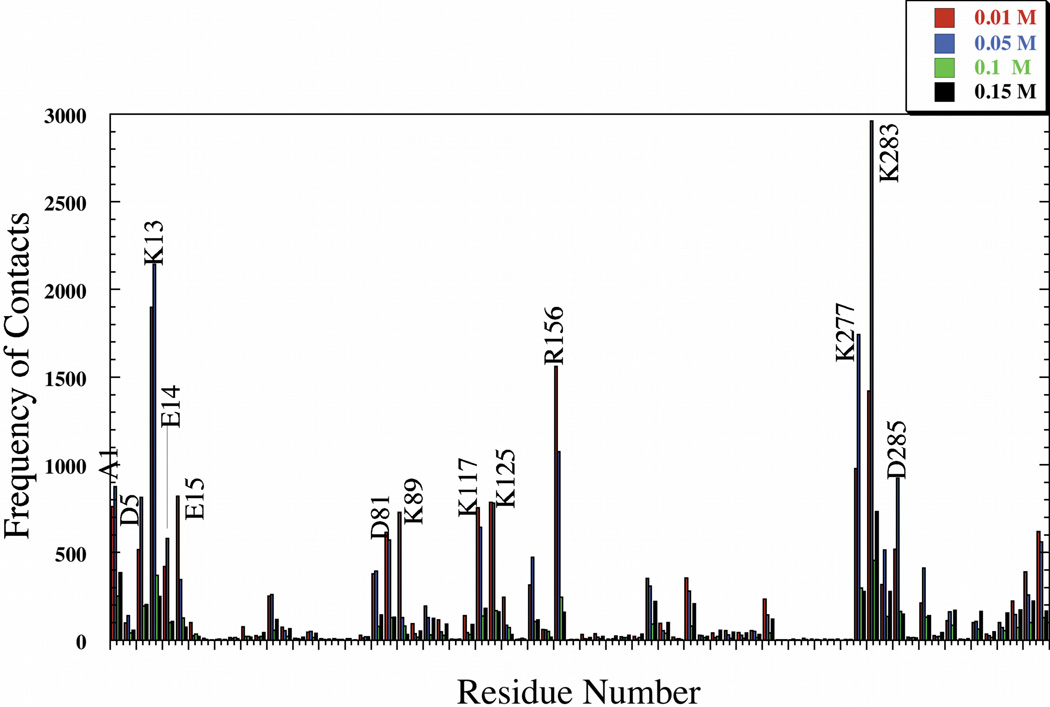
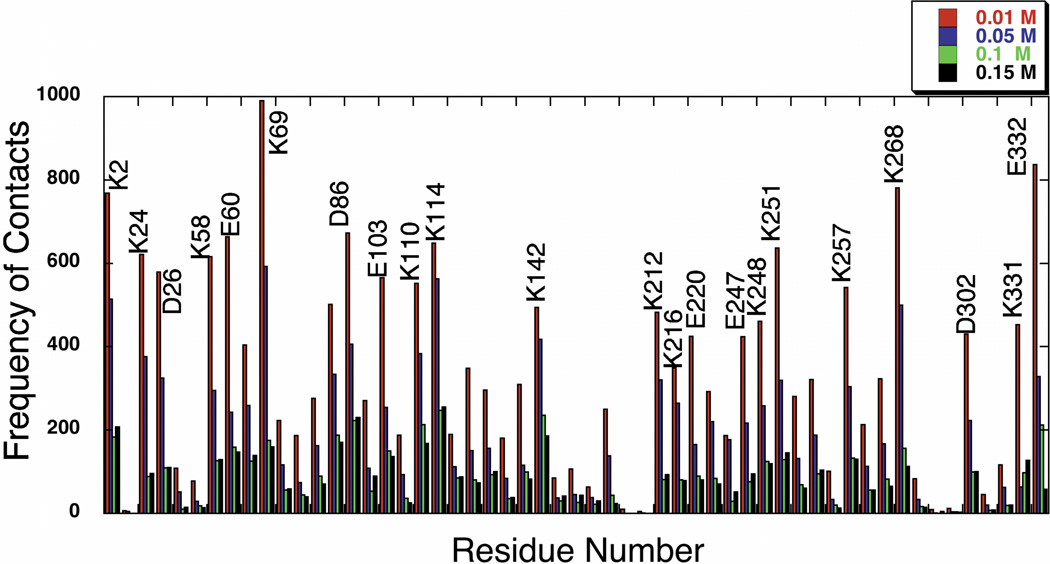
The complexes formed are stabilized by salt bridges. The residues involved in the formation of these binary complexes remain the same for the glycolytic enzymes (aldolase, LDH and GAPDH) as ionic strength increases (Figs. 2, 3 and 4 and Supplemental Figs. S13–S15). Typical complexes for each enzyme show that the residues identified are close to each other (Fig. 5) and form multiple salt bridges for each complex (Table II). The frequency at which each residue is involved in salt bridge formation, hence complex formation, however, decreases with increasing ionic strength. More complexes formed at lower ionic strength because a greater proportion of BD trajectories were successful at lower ionic strength.

Fig. 2.

Full Sequence Representation of Rabbit Aldolase Residues Participating in Complex Formation with F-actin as a Function of Ionic Strength.

Fig. 3.

Full Sequence Representation of Rabbit LDH Residues Participating in Complex Formation with F-actin as a Function of Ionic Strength.

Fig. 4.

Full Sequence Representation of Rabbit GAPDH Residues Participating in Complex Formation with F-actin as a Function of Ionic Strength.

Fig. 5.

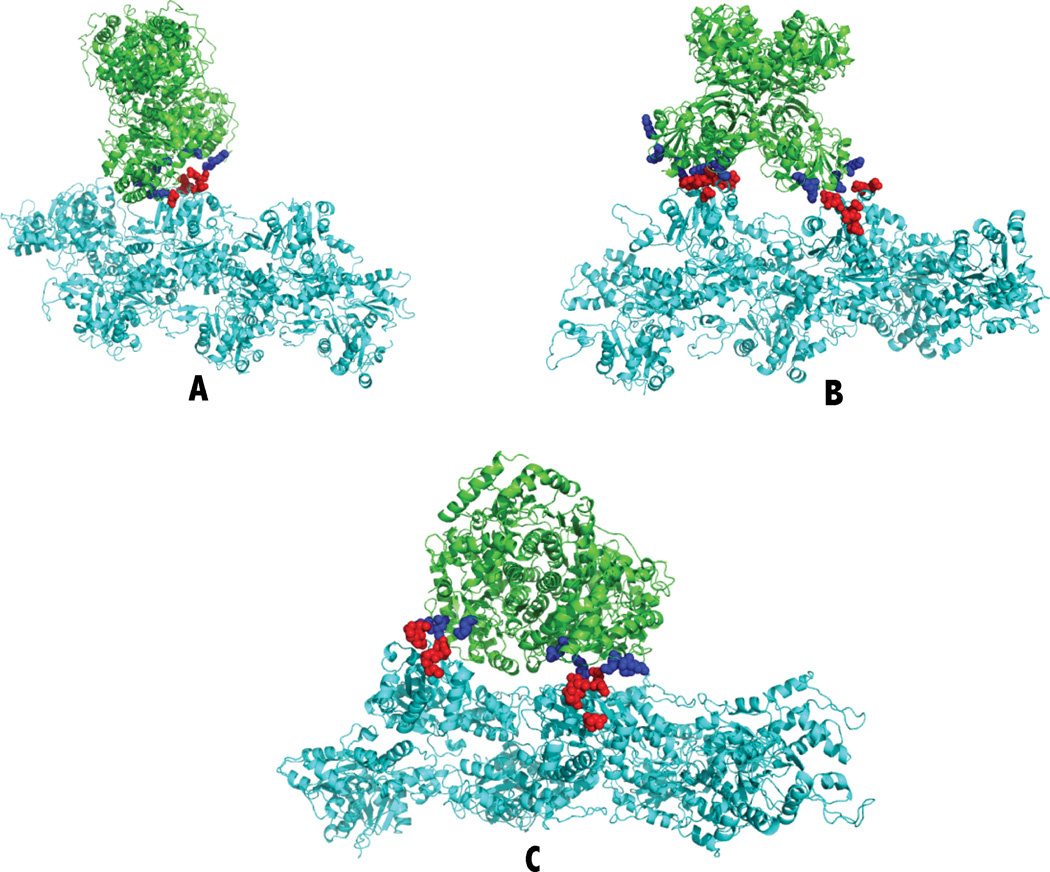
Typical Glycolytic Enzyme/F-actin Complexes. (A) Fish aldolase with F-actin. (B) Rabbit GAPDH with F-actin. (C) Rabbit LDH with F-actin. The green ribbons are the enzymes, and the cyan ribbons are F-actin. Blue spheres are the positively charged lysines and arginines identified in salt bridges (Table II). The red spheres are the negatively charges aspartates and glutamates identified in salt bridges (Table II).

Table II.

Salt Bridges Found in Typical Complexes of Glycolytic Enzymes with F-actin.

Complex type	Energy(kcal/mol)	Aldolase		F-actin
		Residues	Atom	Residues	Atom	Distance (Å)
Fish Aldolase	–11.3	Lys 341C	NZ	Asp 3D	OD2	3.63
		Arg 293C	NH2	Asp 2D	OD2	4.34
		Arg 293C	NH2	Asp 2D	OD1	4.38
		Lys 341B	NZ	Asp 25D	OD2	4.39
		Lys 341C	NZ	Asp 3D	OD1	5.12
		Lys 341B	NZ	Asp 25D	OD1	6.23
Rabbit LDH	–13.6	Lys 277B	NZ	Asp 25B	OD1	3.41
		Lys 277B	NZ	Asp 25B	OD2	3.85
		Lys 277C	NZ	Asp 25D	OD1	4.51
		Lys 13C	NZ	Asp 2D	OD1	4.57
		Lys 13B	NZ	Asp 1B	OD2	4.77
		Lys 283C	NZ	Asp 1D	OD2	4.97
		Lys 13C	NZ	Glu 4D	OE1	6.25
Rabbit GAPDH	–9.34	Lys 58Q	NZ	Glu 2C	OE2	4.23
		Lys 268O	NZ	Glu 99E	OE1	4.36
		Lys 110O	NZ	Glu 99C	OE2	4.96
		Lys 114Q	NZ	Glu 2C	OE1	5.40
		Lys 69O	NZ	Asp 3E	OD1	5.95
		Lys 2O	NZ	Glu 1E	OE2	5.94
		Lys 11OQ	NZ	Asp 1E	OD2	6.39

The energy describes the specific electrostatic interaction energy between the two proteins. Each residue is identified by the three-letter code for the amino acid followed by the residue number with subunit identification. The atom names are as defined in the Protein Data Bank crystal structure file. The distance is that between atoms involved in salt bridge formation; salt bridges are identified with distances of 6.4 Å or shorter. Each complex is pictured in Figure 5.

The center of mass (COM) profiles (Supplement Figs. S16–S18) indicate the degree of specificity of the interactions or complex formation. Aldolase and LDH (Supplement Figs. S16–S17) from all species show a strong and specific interaction with F-actin occurring at the positive grooves formed by the enzyme's quaternary structure especially at low (0.01 and 0.05 M) ionic strength. The interactions between GAPDH and actin, on the other hand, are less specific at all ionic strengths for all species (Supplement Fig. S18). There is still a preference in binding for the regions around the shallow groove of the GAPDH, as opposed to deeper substrate active grooves of the enzyme. Complexes are generally formed with the charged residues located on the corners of the GAPDH molecules. The TPI profile lacks any kind of binding mode either on the surface of binding simply appears random.⁵⁵ Aldolase, LDH and GAPDH do share the feature that they bind F-actin away from their active sites.

Free energy of interaction

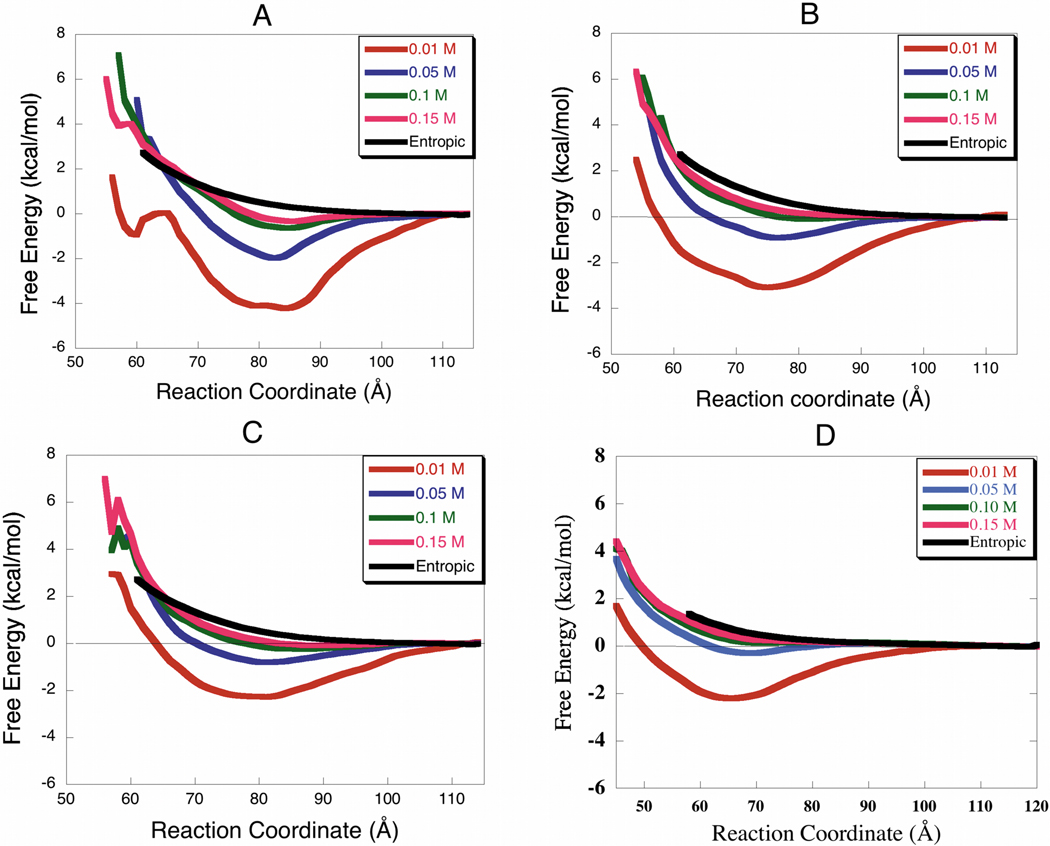
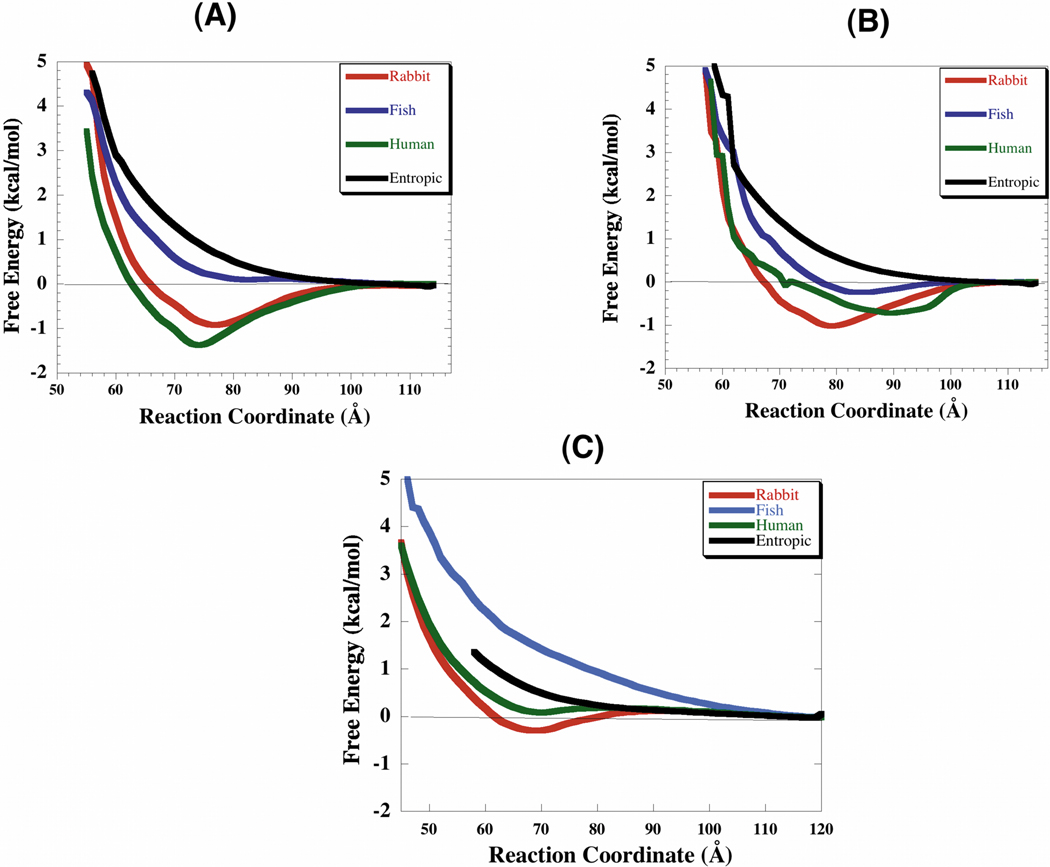
The free energy profiles (Fig. 6) describe the orientationally averaged interactions between the proteins. The curves provide a quantitative measure of the degree of interaction between glycolytic enzymes and F-actin. The deeper the well the greater the interaction and the more rapidly a pair of molecules will associate in solution. For all species investigated, aldolase, LDH, GAPDH and TPI show stronger interactions at lower ionic strength. The free energy minimum decreases as ionic strength increases, yielding shallower wells for all the proteins investigated at about physiological ionic strength (0.1–0.15 M). The enzymes (aldolase, LDH, and GAPDH) are still binding, but their interaction is weaker since the profiles at 0.1 and 0.15 M ionic strengths still have deeper free energy minima than the entropic curve (no electrostatic forces). The extent of the interaction, as indicated by the free energy profile minimum (Figs. 6–7) is species dependent. Rabbit and human enzymes (especially LDH and aldolase) interact more with F-actin than the zebrafish enzymes at all ionic strengths studied. In all the enzymes studied the positions of the free energy minimum describing the most stable complex conformation (binding mode) range between 60–90 Å (Table III).

Fig. 6.

Free Energy Profiles for the Association Between Glycolytic Enzymes and F-actin (Rabbit Proteins). The deeper the wells the greater the interaction. The strongest interactions are at 0.01 M and the weakest are at 0.15 M. (A) Aldolase, (B) LDH, (C) GAPDH, (D) TPI.

Fig. 7.

Species Dependence of Glycolytic Enzyme/F-actin Interactions at 0.05 M Ionic Strength. (A) Radial free energy between F-actin and LDH. (B) Radial free energy between F-actin and GAPDH. (C) Radial free energy between F-actin and TPI. The reaction coordinate is the distance between the aldolase COM and F-actin helical axis. The aldolase species dependence profiles can be seen in Forlemu et al.²¹.

Table III.

The Free Energy Well Depths for the Interactions Between F-actin and the Glycolytic Enzymes

Species	Rabbit		Human		Zebra Fish
Enzyme	Well Depth (kcal/mol)	Location (Å)	Well Depth (kcal/mol)	Location (Å)	Well Depth (kcal/mol)	Location (Å)
Aldolase	−2.00	83	−2.27	84	−1.50	83
LDH	−1.35	75–79	−1.50	75–79	0.12	75–79
GAPDH	−1.01	75–81	−0.73	87–93	−0.21	75–81
TPI	0.21	65	0.28	65	1.67	70

The standard deviations for each of the free energies reported are 0.01 kcal/mol.

DISCUSSION

The affinity of the glycolytic enzymes (aldolase, GAPDH, and LDH) for F-actin is supported by BD results. Furthermore, BD simulations indicate that the enzymes' affinity for F-actin diminishes with increasing ionic strength. The BD results also suggest that interactions are still occurring at ionic strengths as high as 0.15 M as observed by Lakatos and Menton,⁶ but that they are much weaker and less specific. TPI only shows a significant interaction at 0.01 M ionic strength for rabbit and human enzymes; these interactions, however, are random and not specific unlike LDH, aldolase and GAPDH. Zebrafish TPI shows repulsive interactions with F-actin at all the ionic strengths.⁵⁵

Is there a general binding trend among glycolytic enzymes that bind compared to one that does not?

In general, specific binding to F-actin requires a well-defined recognition patch on the glycolytic enzymes. This is the case for aldolase, LDH and GAPDH that bind to F-actin with higher affinity than TPI. This is because of specific residues and well-defined groove and domains on the surface of these proteins. Aldolase, LDH and GAPDH are also homotetrameric, with the residues identified for interaction with F-actin either facing each other on the surface (aldolase and LDH) or participating broadly across the surface between two subunits forming the recognition patches (GAPDH). The conserved nature of the positively charged residues in these recognition patches (especially aldolase and LDH) amongst the different species, and their location enhances the electrostatic potential of the region (Figs. 2, 3 and Supplement Figs. S19–S20). This enhancement is essential for the strong and specific binding observed with aldolase and LDH. GAPDH is also homotetrameric in nature, with positively charged residues in its groove region. There is little reinforcement of electrostatic potential, however, due to the diminished degree of exposure and location of these charged species in the groove region. In GAPDH the important binding residues identified by the simulations are further apart on each subunit and do not face each other as is the case with aldolase and LDH. This diminishes the interaction affinity between GAPDH and F-actin and binding affinity as compared with aldolase and LDH. The ionic strength variation with affinity (Fig. 6) and the center of mass profiles (Supplement Figs. S16–S18) suggest that GAPDH binds F-actin less specifically than aldolase and LDH. This can also be deciphered from the fact that the position of free energy minimum for the enzymes aldolase and LDH, does not vary across species, as opposed to GAPDH (Table III). TPI, on the other hand, is dimeric in nature and only randomly binds F-actin (in the case of rabbit TPI at 0.01 M). This is different from the homotetramers that have two potential binding sites (both grooves). Also, the TPI EP potential maps show little or no extension from the molecular surface. This implies that the pair of molecules must be much closer together for any meaningful interactions to occur. At distances less that 40 Å between the center of mass atoms of both proteins, repulsive forces become significant and reduce the extent of interaction. The broadness of the well indicates that binding is random with no specificity as has been seen for other glycolytic enzymes. When complexes are formed, they are only stabilized by one or two salt bridges.⁵⁵ This is in contrast with the other enzymes that have complexes stabilized by multiple salt bridges.^21,43 The smaller size of the TPI molecule implies it can bind in different areas of F-actin where the larger enzymes cannot reach, but such interactions are weak and nonspecific.

Are the interactions comparable across species?

BD results indicate that rabbit and human muscle enzymes bind F-actin more strongly than do zebrafish enzymes (Fig. 7). This can only be due to a more characteristic and well-defined actin binding regions or domains present in the mammalian enzymes as opposed to the zebrafish enzymes in general. Aldolase and LDH in all the species show stronger and more specific interactions than GAPDH. Despite the highly conserved nature of these enzymes across species, the variations in terms of binding affinity (Table III) observed in their interaction to F-actin can be explained by subtle differences in the recognition patches or grooves and residues responsible for binary complex formation. For example the replacement of lysine 293 present in rabbit and human aldolase, by an arginine 293 at the interaction groove in zebrafish aldolase, leads to a reduction in extension of the electrostatic potential (Supplement Figs. S1, S8–S9) as ionic strength increases. Even though arginine and lysines are positively charged, the side chains in lysine have a slightly more localized positive charge than arginine, which is delocalized amongst the three side chain nitrogen atoms. Furthermore, the groove regions in rabbit and human are much tighter than in fish. The fact that the lysine residues face each other in the groove and the tighter nature of the groove suggest a greater enhancement of the electrostatic potential in mammalian species as opposed to fish. Finally, in fish aldolase, there is the presence of more negatively charged residues that significantly impact the extension of electrostatic potential in fish.

How does the degree of association change over a range of ionic strengths (0.01 – 0.15 M)?

Electrostatics plays a major role in defining the mechanisms of association of some glycolytic enzymes with F-actin. Typically, using the farthest EP contour as a guide (Fig. 1, Supplement Figs. S3–S4), the glycolytic enzymes appear neutral to any charge particle about 40 Å away from its center of mass at higher ionic strength. This distance increases to about 80–85 Å at low ionic strength (0.01–0.05) (Fig. 1, Supplement Figs. S3–S4). The Coulomb Debye length (Equation 2) that describes the exponential decay of the electrostatic potential in the solvent medium is definitely shorter at higher ionic strength. This means the electrostatic potential decays to zero more rapidly at higher ionic strength (0.1–0.15 M) than at low ionic strength (0.01–0.05 M). Thus, the electrostatic contribution to the free energy of interaction at higher ionic strength is less negative because the salts screen the pair of molecules effectively. Many researchers have demonstrated an ionic strength dependence of the enzyme/F-actin interaction using electrophoretic, chromatographic and ultracentrifugation methods.^5,7,11 BD studies show similar patterns and in addition show that the residues responsible for the glycolytic enzyme/F-actin association persist as ionic strength increase especially for aldolase and LDH amongst the three species studied (Figs. 2–3, and Supplement Figs. S13–S14 and S19–S20). These findings suggest that the mode of binding between the protein pairs is not affected by salt concentration. Only the affinity is diminished due to ionic screening.

Additionally, zebrafish enzymes bind F-actin with a lower affinity than rabbit or human muscle enzymes. Zebrafish LDH and GAPDH do bind F-actin at lower ionic strengths (I = 0.01 M); however, weaker binding is observed at 0.05 M to 0.15 M ionic strength (Fig. 7). Nakagawa and Nagayama⁷ have shown using zebrafish myogen enzymes that about 60% of GAPDH binds actin at 0.05 M. Although BD simulations do show weak binding, the strength observed by experiments of Nakagawa and Nagayama⁷ were not obtained with purified enzyme preparations, but rather with suspensions of sarcoplasmic proteins containing glycolytic enzymes. This means that the high GAPDH activity in F-actin portions, interpreted as GAPDH binding to F-actin could also be a result of GAPDH binding to some other F-actin-binding enzyme such as aldolase.⁵ This phenomenon is referred to as “piggy backing”.^9,56

Sedimentation studies by Clark and Masters^57,58 suggest that aldolase and LDH from rabbit are found in higher bound proportions with F-actin than GAPDH, and LDH interactions become even stronger at lower ionic strength. The binding and ionic strength trends have also been observed by Walsh and Knull⁵⁹ and do agree with the BD results presented here. Herein, electrostatic analysis of the enzymes' surfaces reveals more specific binding regions (grooves) in aldolase and LDH as compared to GAPDH. These grooves benefit from a cooperative effect of charged residues from adjacent subunits. This cooperativity may explain why LDH and aldolase produce narrower and deeper wells compared to GAPDH at all ionic strengths and probably why aldolase and LDH bind F-actin with more specificity than GAPDH. The broadness of the GAPDH wells as opposed to aldolase and LDH also indicates a more flexible or less specific interaction due to the inability of the GAPDH molecule to rapidly find a specific orientation for a stable binding mode at the free energy minimum position. Thus, in addition to reproducing the patterns observed experimentally, the BD simulations provide an explanation for the degree and type of complexes for between the glycolytic enzymes (aldolase, LDH and GAPDH) with F-actin.

What is the effect of the ionic strength on the specificity of complex formation?

The affinity and specificity of the interaction depends on precise interactions between amino acids in specific domains of the molecules involved. BD simulation results provide detailed information on an atomic scale of the specific nature of the glycolytic enzyme F-actin interactions. For example, the F-actin binding domains on the surface of glycolytic enzymes are identified as a function of the electrostatic potential. BD also shows how these residues participate in complex formation as ionic strength changes (Figs. 2–4). There is conservation of a particular interaction site across species especially for interactions involving aldolase and LDH. Likewise some residues responsible for intermolecular contacts in complex formation are also common amongst the different species; human GAPDH, however, uses completely different residues to bind F-actin as opposed to rabbit and zebrafish GAPDH (Fig. 4 and Supplement Figs. S15, S21).

The variation in type of residues involved in complex formation as ionic strength increases serves as a good indication of which residues are important and are most exposed for binding with F-actin. The binding residues for aldolase (Supplement Fig. S13) and LDH (Supplement Fig. S14) persist at different ionic strength (Fig. 2–3). Electrostatic analysis reveals large grooves of positive potential (Supplement Fig. S3) created by a large patch of positively charged residues, including (lysines 341, 288, and 293 for rabbit and human enzymes; lysines 341, 348, and Arg 293 for zebrafish). Similarly, LDH residues (Lys 277, 13, and 283) are also found at the same site in both species, explaining the strong specificity in complex formation with F-actin at 0.01–0.05 M. Also, the contribution of the above mentioned residues in complex formation is more prominent at all ionic strength as opposed to any other residues in the molecule (Figs. 2–3). This reduction in frequency however at higher ionic strength is due to solvent media screening and formation of less energetically favorable charge-charge interactions.

The center of mass profile maps reveal that GAPDH from all species binds F-actin less specifically (Supplement Fig. S18). Electrostatic analysis also reveals regions of positive potential created by patch of positively charged residues, including (lysines 2, 24, 58, 63, 69, 110, 114,142, 251,257, and 268 for rabbit and zebrafish GAPDH) which are located on the corners of the molecules. The interaction to F-actin is attenuated by the presence of negatively charged residues interspersed and neutralizing the electrostatic field created by the positively charged residues (predominantly Glu 26, 56, 60, 103, 332, and Asp 26, 86). These residues compete with positively charged lysines for complex formation in interactions with F-actin and as a result diminish the affinity for GAPDH as compared to aldolase and LDH. A full sequence analysis for the molecule reveals an increase in the frequency of occurrence in complex formations for some of these residues (Lys 69, 114, 142, Asp 26, 86 and Glu 332) at higher ionic strengths (0.05 and 0.1) (Fig. 4). Human GAPDH residues include (Lys 4, 112, 116, 117, and 144, Glu 334 and Asp 28) all located on the corners of the quaternary structure. The electrostatic potentials field due to the positive lysines is much more neutralized (Supplement Fig. S5) by interspersed charged residues (Glu 334, Asp 28, 88, and 63). Rabbit GAPDH shows a deeper well in these species due to a combination of two factors: (1) fewer and minimal effect of negatively charged residues at the corners, and (2) the extension of the EP surface over the O/P and R/Q grooves of the molecule especially at 0.01 M. The results also suggest a better exposure of the rabbit residues, as opposed to zebrafish and human enzymes.

In all the simulations, the F-actin residues responsible for the interactions remain the same and only reduce in frequency as a consequence of the ionic strength. These F-actin residues are all present on subdomain I. These residues are conserved across species and are necessary for binding glycolytic enzymes. These residues include (Glu364, Glu4, Glu99, Glu100, Glu125, Asp2, Asp363, and Asp 25). The importance of some of these residues has been tested previously in Gustafson’s mutation studies.⁶⁰ Gustafson pointed out the importance of the N-termini of the various F-actin molecules in binding. She also showed that mutating Asp 24/25 or Glu 99/100 increased the dissociation constant of aldolase/F-actin complex by about 4.5 and 3.4 times respectively. BD simulations do suggest some other residues specifically at the C-termini including Asp363 and Glu 364. The nature of the interactions stays the same at all ionic strengths, but we observed that at higher ionic strength more statistics (larger number of complexes) are needed to obtain similar COM profiles obtained at lower ionic strengths. This is an indication of the screening power of solvent media at higher ionic strengths.

CONCLUSIONS

BD is capable of reproducing the ionic strength dependence observed experimentally for the binding of glycolytic enzymes to F-actin. Aldolase and LDH bind F-actin with specific recognition patches (grooves) at all ionic strength. Analysis of close contacts and of specific complexes indicates that the charged residues responsible for complex formation stay the same at all ionic strength studied. There is a reduction in specificity of the interactions, however, for both enzymes at higher ionic strength due to solvent media screening and minimized exposure of residues important for complex formation. The interaction between the glycolytic enzymes (aldolase and LDH) and F-actin are highly conserved in all the three species studied. This conservation is both in terms of binding domain and binding residues. GAPDH from all species, on the other hand, forms less specific complexes with F-actin with a less well-defined recognition patch as opposed to aldolase and LDH. F-actin binds all the glycolytic enzymes using the same residues, all located on subdomain I of the actin molecule. These enzymes still bind F-actin at 0.1–0.15 M suggesting that these interactions are of physiological significance. In general the BD results indicate minor variations for glycolytic enzyme/F-actin interactions amongst the species.