Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2011 Aug 30;5(3):241–251. doi: 10.1007/s11571-011-9169-6

Impact of gamma-oscillatory inhibition on the signal transmission of a cortical pyramidal neuron

Xiumin Li 1,2,✉, Kenji Morita 3, Hugh P C Robinson 4, Michael Small 2
PMCID: PMC3179542  PMID: 22942914

Abstract

Networks of synchronized fast-spiking interneurons are thought to be key elements in the generation of gamma (γ) oscillations (30–80 Hz) in the brain. We examined how such γ-oscillatory inhibition regulates the output of a cortical pyramidal cell. Specifically, we modeled a situation where a pyramidal cell receives inputs from γ-synchronized fast-spiking inhibitory interneurons. This model successfully reproduced several important aspects of a recent experimental result regarding the γ-inhibitory regulation of pyramidal cellular firing that is presumably associated with the sensation of whisker stimuli. Through an in-depth analysis of this model system, we show that there is an obvious rhythmic gating effect of the γ-oscillated interneuron networks on the pyramidal neuron’s signal transmission. This effect is further illustrated by the interactions of this interneuron network and the pyramidal neuron. Prominent power in the γ frequency range can emerge provided that there are appropriate delays on the excitatory connections and inhibitory synaptic conductance between interneurons. These results indicate that interactions between excitation and inhibition are critical for the modulation of coherence and oscillation frequency of network activities.

Keywords: Gamma oscillation, Fast-spiking interneurons, Pyramidal neuron, Inhibition, Neural network

Introduction

Cortical gamma (γ) frequency (30–80 Hz) oscillations have been suggested to underlie many aspects of cognitive function, including sensory binding, attentional selection, and consciousness (Fries 2009; Tiesinga et al. 2004). Both in vivo and in vitro recordings in the hippocampus indicate that fast-spiking interneurons (FS) are essential for the generation of γ oscillations (Bragin et al. 1995; Hajos et al. 2004; Cardin et al. 2009; Sohal et al. 2009). These FS cells are highly interconnected through GABA-type receptors, where the time course of inhibitory synaptic conductance change appears to be an important factor that determines the frequency of network oscillation (Whittington et al. 1995; Wang and Buzsaki 1996; Bartos et al. 2002; Brunel and Wang 2003). Also there is evidence that the intrinsic discontinuous type 2 threshold frequency of the FS neurons plays a pivotal role in organizing coherent γ oscillations in the local FS network (Tateno et al. 2004; Tateno and Robinson 2009). A modeling study of interactions between large populations of regular-spiking (RS) cells and FS cells in Traub et al. (1997, 2000) observed that the FS network can be obviously modified by the participation of pyramidal neurons. Phase shifting also occurs in the reciprocally-connected RS–FS network studied in a recent paper (Tiesinga and Sejnowski 2010).

In this work, we examined how the γ-oscillatory inhibition regulates the output of cortical pyramidal cell by using a biophysically detailed neuron model. We modeled a situation where a pyramidal cell receives inputs from γ-synchronized FS cells. In order to achieve this, first an isolated FS network is established by connections comprising both gap junctions (electrical synapses) and inhibitory synapses (chemical synapses). Besides the tonic excitatory drive, Poisson trains of subthreshold synaptic inputs are injected to all the FS cells, introducing high heterogeneity into the network. We found that gap junctions significantly improve the synchronization of the network. This result is consistent with the observations that both gap junctions and inhibition are important for synchronizing FS neurons (Gouwens et al. 2010). Using a network of interneurons oscillating synchronously at 40 Hz, we reproduce many aspects of Cardin et al.’s (2009) experiment results on the response regulation of RS neurons by γ oscillation in inhibitory neurons. This experiment addresses whisker sensation and indicates that the γ-frequency FS-induced inhibitory postsynaptic potentials (IPSPs) regulate signal propagation by restricting or permitting the generation of spikes at different phases within the γ cycle. We gave detailed analysis of the influence of γ-oscillatory inhibition on signal transmission. Similar result has also been observed in recent studies (Knoblich et al. 2010; Tiesinga and Sejnowski 2010). Next, we constructed a mutually-connected RS–FS network, and found that gamma oscillation can also emerge in such a network, even with parameter values with which no fast oscillation occurs if FS network is isolated. This indicates that the emergence of coherent oscillation in the mutually-connected RS–FS network results from both excitation from the RS cell and feedback inhibition from the FS network. Besides, delays on the connections have substantial effect on the regulation of feedback inhibition to the RS cell.

Methods

Simulations were performed using NEURON version 7.0 (Hines and Carnevale 1997). Each FS interneuron was modeled by a Hodgkin–Huxley type model obtained from the ModelDB section of the Senselab database (http://senselab.med.yale.edu) based on the work in Pospischil et al. (2008), which exhibited a steep initial segment in its firing frequency versus current relationship. The RS neuron was a layer II/III neocortical pyramidal cell model that was used in Morita et al. (2008). Synapses were set on the soma (not in dendrite) in this study. Each pre-synaptic input was modeled by using AMPA receptor conductance for excitation, and GABA receptor conductance for inhibition. The unitary AMPA conductance transient was implemented using the built-in function of NEURON (Exp2Syn), with 0.5 and 2 ms for the rise and decay time respectively, and a reversal potential of 0 mV. Each inhibitory stimulus was modeled as a GABA conductance, which was also implemented using the function of Exp2Syn(), with 0.5 and 7 ms for the rise and decay time respectively, and a reversal potential of −70 mV. The simulation time step was 50 μs. Power spectral density (shown in Figs. 11, 12) was estimated using the Discrete Fourier Transform function (fft) of Matlab.

Fig. 11.

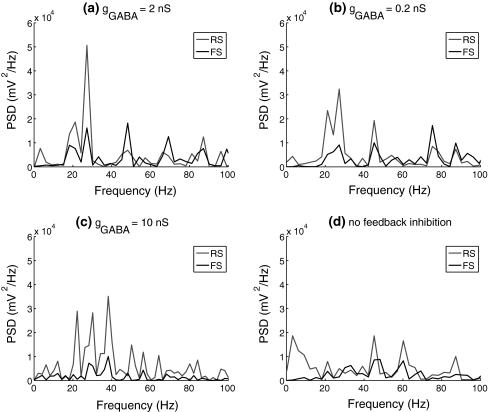
Fig. 11

Open in a new tab

Power spectrum density (PSD) of spike trains of the RS and FS cells with different conductance of the inhibitory connections between FS cells. PSD for FS cells is an averaged value calculated from the membrane potentials of the whole FS population. agGABA = 2 nS;  bgGABA = 0.2 nS; cgGABA = 10 nS; d no feedback inhibition

Results

Generation of gamma oscillations in a FS interneuron network

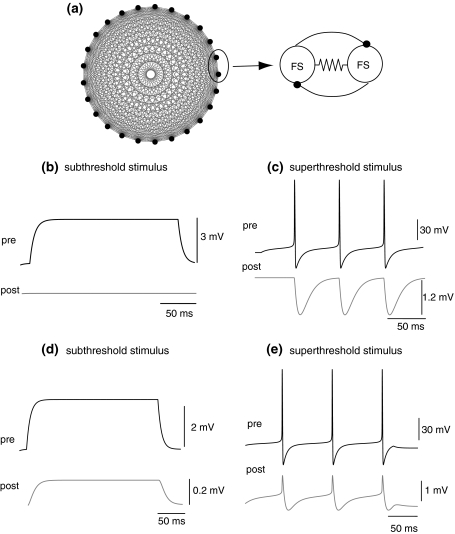
Here a network of 25 FS cells which are all-to-all connected is considered. Each pair of cells was coupled through both chemical and electrical synapses. Comparison between recordings from pairs of the chemically and electrically coupled cells is demonstrated in Fig. 1. The inhibitory post-synaptic potentials have large peak amplitudes, while the electrical post-synaptic potentials show minimal latency and bi-directionality.

Fig. 1.

Fig. 1

Open in a new tab

a All-to-all connections of the FS interneurons. Each pair of FS cells is coupled by both gap junction and synaptic inhibition; b, c Synaptic GABA inhibition in a pair of FS cells when one of the cells is stimulated with subthreshold and superthreshold stimulus respectively; d, e Gap junction in a pair of FS cells when one of the cell is applied with subthreshold and superthreshold stimulus, respectively

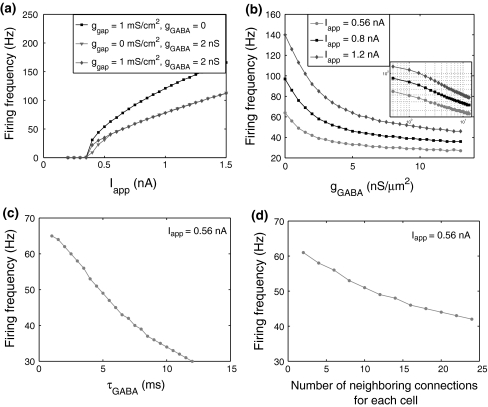
To introduce heterogeneity into the network, FS cells are subject to non-rhythmic and subthreshold excitatory synaptic inputs with a unitary conductance of 0.2 nS and mean frequency of 1,000 Hz. A common tonic excitatory drive is injected to initiate activity in the network. Figure 2 shows the different roles played by chemical synapses and electrical synapses. The existence of gap junctions among FS cells is essential for the network synchronization, which is consistent with the simulation results obtained in Traub et al. (2001). With only synaptic inhibition, but lacking gap junctions, the network can not reach synchronization no matter how much the inhibitory synaptic conductance is increased. The oscillation frequency of the network can not be obviously changed by gap junctions, while it can be significantly decreased when inhibitory synapses are involved. In order to investigate the major factors that determine the average firing frequency of the synchronized network, we plot the f–I curves of FS cells for a variety of parameter values, i.e., excitatory current, peak conductance and decay time constant of the unitary GABA synapse, and the number of neighboring connections for each cell. Note that the oscillation frequency of the network is equal to the average firing rate of the whole population when its activity reaches synchronization. Figure 3a shows that the slope of the f–I curve can be greatly affected by the inhibitory synapses. When the conductance of gap junctions (ggap) is 1 mS/cm2 and the unitary GABA conductance (gGABA) is 2 nS, the network generates synchronous oscillations in a wide range of frequencies (20–110 Hz) over a broad range of tonic excitatory drive (0.4–1.5 nA). Inhibitory conductance change makes the firing frequency change approximately exponentially (Fig. 3b). By tuning the unitary GABA conductance, the network firing frequency can be easily driven to the gamma-frequency range (30–80 Hz). This is robust to changes of external depolarization. Moreover, the decay time constant of inhibition and the number of neighboring connections for each neuron both exert a linear-like modulation of the firing rate (Fig. 3c, d). Note that inhibitory connections alone can synchronize the network only when the common excitatory current is large enough (here more than 0.6 nA see Fig. 3a).

Fig. 2.

Fig. 2

Open in a new tab

Effect of gap junctions and synaptic inhibition on the network activity of FS interneurons. ggap = 1 mS/cm2,  gGABA = 2 nS,  Iapp = 0.45 nA

Fig. 3.

Fig. 3

Open in a new tab

Firing frequency of the FS network for various parameter values: a excitatory current, b inhibitory synaptic conductance, c decay time constant of the unitary synaptic conductance and d the number of neighboring connections for each cell. Firing frequency is calculated as the average firing rate of all the FS cells

Gamma oscillation regulates signal processing of a pyramidal neuron

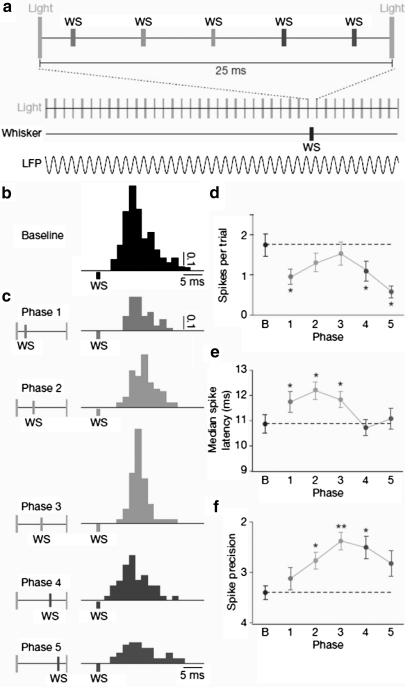
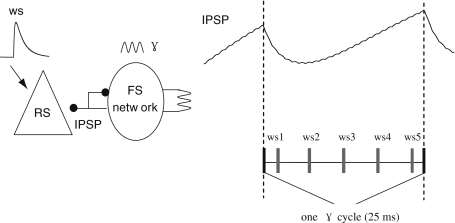
Based on the previous results, the FS network has a synchronous activity firing at 40 Hz when ggap = 1 mS/cm2, gGABA = 2 nS and Iapp = 0.56 nA. Using this FS network, we examined how the γ oscillations regulate the response of a pyramidal neuron to excitatory synaptic input, as has been characterized experimentally, using optogenetically-stimulated γ oscillations combined with single whisker stimulation in barrel cortex in vivo, by Cardin et al. (2009) (Fig. 6). In the following simulations, a subthreshold noisy background current (with unitary conductance of 0.7 nS and mean frequency of 1,000 Hz) is given to the soma of the target RS pyramidal neuron, which has connections with each FS cell by inhibitory synapses with unitary GABA conductance of 1 nS. Within one selected γ cycle, a single synaptic input which mimics the whisker stimulation (ws) is injected to the RS at five different phases (Fig. 4). This single synaptic stimulus has a unitary AMPA conductance of 20 nS, with the rise and decay time constant as 0.5 and 1 ms respectively. The corresponding EPSP is similar to the whisker-stimulus response recorded in Ferezou et al. (2006).

Fig. 6.

Fig. 6

Open in a new tab

Experimental results observed in Cardin et al.’s experiment (Cardin et al. 2009)

Fig. 4.

Fig. 4

Open in a new tab

Schematic diagram of the simulation. A RS neuron is inhibited by the synchronized FS cells firing at a γ frequency (ggap = 1 mS/cm2,  gGABA = 2 nS,   Iapp = 0.56 nA). The whisker stimulation (ws) at five different phases of unitary γ cycle together with noisy background current is also applied to the RS cell. In the γ cycle, the IPSP targeting the RS cell shows a peak of inhibition about 6 ms after the start of the cycle and then decays gradually. The spike train of the RS cell is recorded to examine how its responses is affected by the γ inhibition at different phases. For each particular phase, the simulation is conducted 200 times

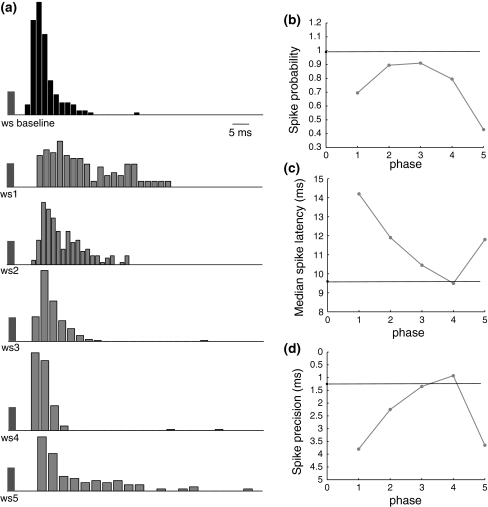
Since there exists several milliseconds delay between the whisker deflection used in the experiment and the RS’s response (Cardin et al. 2009), we incorporate a 6 ms delay to the action of ws stimulus. Figure 5a shows that responses to the stimulus at five different phases are prolonged by the synaptic inhibition and spike times are very sensitive to the recovery of inhibition, which makes the temporal spread larger than the response of the baseline stimulus. When inhibition within this γ cycle fully disappears at phases 3 and 4, spike probability reaches the highest level, spike latency and spike precision recover to the baseline value (Fig. 5b–d). Both spike latency and spike precision decrease with the increase of stimulus phases due to the recovery of the inhibition. As the response to phase the 5 stimulus is delayed to the next γ cycle, depolarization of membrane potentials is greatly suppressed by the peak inhibition, causing prolonged spike latency and large temporal spread of evoked spikes. These three indexes are basically consistent with Cardin et al.’s experiment results (Cardin et al. 2009). The relatively smaller value of the spike precision than that observed in the experiment may be caused by the differences between synaptic stimulus and the whisker deflection used in the experiment (Fig. 6).

Fig. 5.

Fig. 5

Open in a new tab

Simulation results for Cardin et al.’s experiment (2009). a Baseline response of the RS cell when there is no inhibition and responses when the stimulus is injected at each of the five phases within the γ cycle; b spike probability of the RS response for each case. Black line indicates baseline responses; c median spike latency of the RS response for each case; d spike precision of the RS response for each case, which is defined as the median inter-quartile range of all the spike times evoked by a pulse stimulus

Actually in some cases a doublet of spikes occurred in the whisker-evoked responses in Cardin et al.’s experiment, while in our simulation, there is only one single spike in response to the stimulus. If the stimulus strength is increased to be large enough to produce two spikes in the simulation, the interval of spike doublet is about 8 ms which leads to the histogram of spike times having two separate peaks. We have tried several other stimuli with different decay time and amplitude. It seems that with the RS cell it is difficult to generate spike doublet within less than 8 ms in response to a single synaptic input. Zhu and Connors (1999) observed that RS cells typically fired a single action potential in response to a brief whisker deflection. The behavior of our neuron model clearly differs in this respect from the firing shown in Cardin et al.’s experiment. However it is notable that the recording that they show is from a layer 4 RS neuron, potentially a spiny stellate cell rather than a pyramidal neuron, with slightly different firing properties. Nevertheless, although there are differences between this work and their experiment, the essential similarity of our results further verifies the idea that the FS-network-induced γ oscillation could lead to a temporal sharpening of neuronal responses by rhythmic gating synaptic inputs, leading to the synchrony of excitatory neurons (Engel and Singer 2001; Burchell et al. 1998).

Interactions between FS network and pyramidal neuron

Morita et al. (2008) suggested that recurrent excitation among RS pyramidal cells would occur with a wide variety of time delays. Although that study did not refer to the connection from pyramidal cell to FS cell, it can also entail delay of a similar nature. If a post-synaptic cell receives convergent inputs from a large number of pyramidal cells, the resulting total current would just resemble noisy tonic current even when pre-synaptic firing has a solid temporal structure such as γ-oscillation as suggested in that study. However, contrary to the case where the post-synaptic cell is a pyramidal cell, which usually receives inputs from a large number of other pyramidal cells, FS cells might receive inputs from a much smaller number of pyramidal cells, given the difference between these two cell types in size or shape. Considering at an extreme case, it is possible that a FS cell can be driven to generate a spike by input from only a single pyramidal cell. In such a case, a huge variety of delays on the connections from the pyramidal cell to FS cells does not result in similar noisy tonic currents in all the FS cells, but rather directly makes each individual FS cell fire at a different timing. Then, a question which arises is whether the electrical and chemical connections between FS cells can still synchronize their firings at a γ frequency, and also regulate the firing of the pyramidal cell with a certain phase lag.

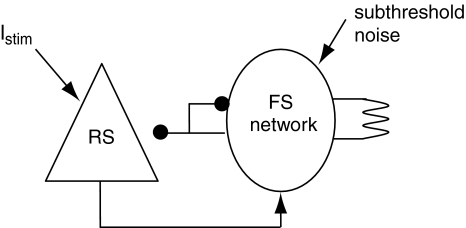
In order to address this issue, in this section we have incorporated widely distributed delays on the RS-to-FS excitatory connections in a microcircuit model with reciprocally connected RS and FS cells (Fig. 7). The inhibitory synapses from the FS cells to the RS cell have a unitary GABA conductance of 1 nS. Each FS cell receives excitation from the RS neuron with a unitary AMPA synaptic conductance of 15 nS. The delays from the RS cell to each FS cell follows the positive parts of a Gaussian distribution with a mean value of 9.6 ms and standard deviation of 12 ms as used in Morita et al. (2008). Two separate excitatory currents are applied to the RS neuron and the FS cells, with a superthreshold current (Istim) for the RS cell and a subthreshold noisy background current for the FS cells. Here the conductance of gap junctions among FS cells is increased to 2 mS/cm2 to counteract the high level of heterogeneity in the network due to the existence of noisy current and distributed delays in the RS-to-FS excitation.

Fig. 7.

Fig. 7

Open in a new tab

The RS cell is inhibited by a network of FS cells which are all-to-all connected by both gap junctions and synaptic inhibitions (ggap = 2 mS/cm2,  gGABA = 2 nS,  Iapp = 0.56 nA). The FS network also receives excitatory connections from the RS cell, which is stimulated by an excitatory current Istim. Noisy subthreshold currents are applied to each of the FS cell

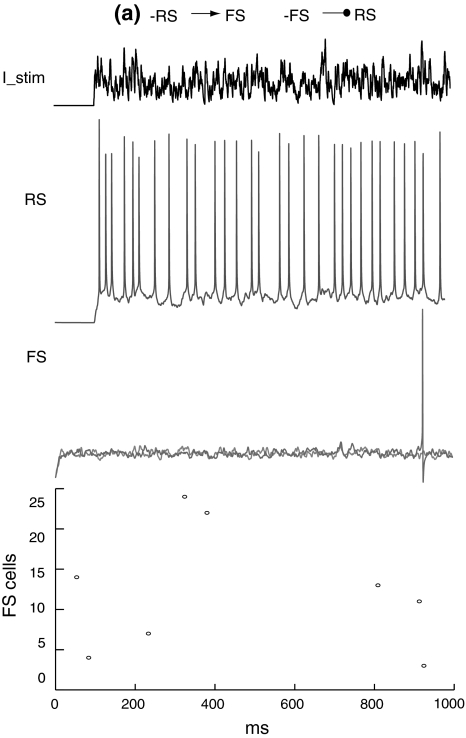
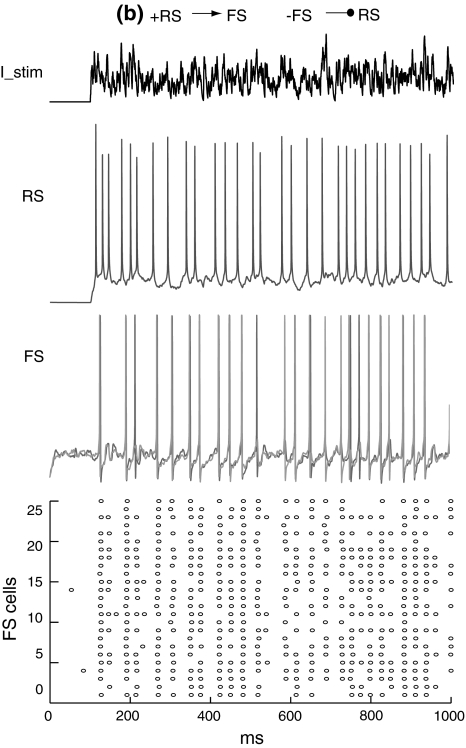
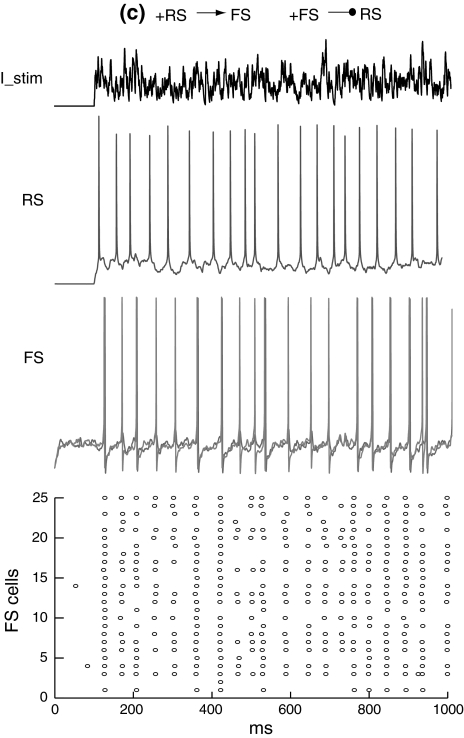
Figure 8 shows that when the RS cell and FS network are not mutually connected, the RS cell fires randomly with a mean firing rate of around 30 Hz and the FS network has a spontaneous activity at a very low frequency. If there is excitation from the RS cell to FS network, FS cells are excited and fire synchronously at a frequency close to the RS cell (Fig. 9). When feedback inhibition from the FS network to the RS cell is included, spikes are obviously depressed and have highly coherent inter-spike intervals (Fig. 10). Power spectral density estimate shows that there is a peak power at 20 Hz for the RS cell, while for the FS network, the dominant power occurs at around 40–60 Hz (Fig. 11a). If the unitary GABA conductance of inhibitory connections between FS cells is changed to be 0.2 and 10 nS separately, the corresponding dominant frequency power of FS cells is shifted to be 70–80 Hz and around 30–40 Hz respectively (Fig. 11b, c). Thereby, the emergence of γ-range oscillation of the FS network is mainly induced by the time course of inhibitory synaptic conductance. This result further indicates that the intrinsic synaptic inhibition within the FS network is a major factor that determines the oscillation frequency. Regular excitatory inputs from the RS cell are also responsible for the generation of FS oscillations. With the existence of a large variety of delays on the RS-to-FS connections, FS cells can still synchronize their firings, and also regulate the firing of the pyramidal cell. When there is no inhibitory feedback from the FS network, the RS cell fires randomly and this non-rhythmicity can transmit to the FS network and impair the coherent oscillation (Fig. 11d).

Fig. 8.

Fig. 8

Open in a new tab

Membrane potentials of the RS cell and two example FS cells when there are no excitatory and inhibitory connections between the RS and FS network. The black line (top) represents the external current Istim. Raster plots of the firing in the FS network are shown in the bottom figure

Fig. 9.

Fig. 9

Open in a new tab

Membrane potentials of the RS cell and example FS cells when there are excitatory connections from the RS cell to the FS network

Fig. 10.

Fig. 10

Open in a new tab

Membrane potentials of the RS cell and example FS cells when there are both excitatory and inhibitory connections between the RS and FS network. There is a mean time delay of 9.6 ms of excitation from the RS cell to the FS network

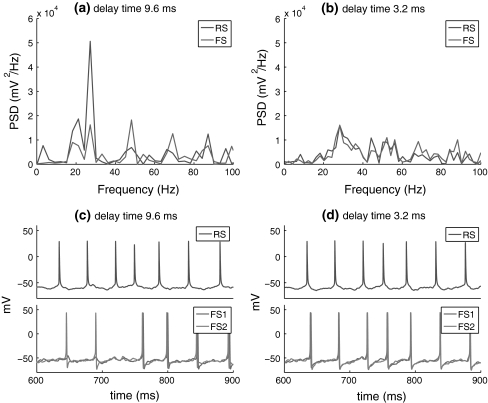
Hence, efficient inhibitory feedback is important for rhythmic oscillation of the RS–FS connected network. Since there are no fast oscillations in the isolated FS network, the emergence of coherent oscillations shown in Fig. 12a results from the interactions between the RS and FS network, where the temporal sharpening effect of the rhythmical inhibition on the responses of excitatory neuron plays an important role (as observed in Fig. 5). In the above simulations, there is a mean time delay of 9.6 ms of excitation from the RS cell to the FS network. We also examined another case of distributed delay with a mean value of 3.2 ms and mean standard deviation of 4 ms as used in Morita et al. (2008) (see Fig. 12). This figure shows that coherent oscillation of the network almost disappears. The small delay RS spiking and the resultant feedback inhibition mean that the inhibition falls within the refractory period of RS cells, making it ineffective. This suggests that appropriate delay in excitation from RS cells to FS cells plays an important role for efficient regulation of the inhibitory feedback.

Fig. 12.

Fig. 12

Open in a new tab

Effect of the delay time of RS-to-FS excitation on the firing frequency of RS and FS cells. a, b PSD of the spike trains of the RS and FS cells when the mean value of delay distribution is 9.6 and 3.2 ms, respectively (with the mean standard deviation of 12 and 4 ms; c, d Spike trains of the RS cell and the FS cells with these two different delay distributions

Discussion

In this paper, we studied γ oscillation of a FS interneuron network and the action of this network on the information processing of an excitatory neuron. The simulation result shows that γ oscillation can be robustly obtained in a FS interneuron network connected by both gap junctions and GABA inhibitory synapses. Using the network of interneurons oscillating synchronously at 40 Hz as input to a pyramidal cell, we reproduce the essential features of the experimentally observed regulation of γ inhibition on pyramidal neurons’ response. The rhythmic gating effect of the γ-oscillated interneuron networks on pyramidal neurons’ signal transmission is further illustrated by the interactions of this interneuron network and a single pyramidal neuron. Prominent power in the γ frequency range can emerge provided that there are appropriate delays and inhibitory synaptic conductances between interneurons. Our results suggest that highly-synchronized activity of inhibitory neurons is responsible for improving the spike coherence of excitatory neurons due to the temporal sharpening effect of inhibitory inputs on the responses of excitatory neurons. And the excitatory feedback in turn controls the oscillation frequency of inhibitory network. The interaction and balance of excitatory and inhibitory synapses are crucial for the information processing of neural networks.

Most of the previous network models that generate γ oscillations are driven by tonic depolarizing currents with amplitudes randomly chosen from a normal distribution (Whittington et al. 1995; Wang and Buzsaki 1996; Bartos et al. 2002). However, synchronization or coherence of γ oscillations is extremely sensitive to heterogeneity in the tonic excitatory drive (reviewed in Bartos et al. 2007). In the models of Wang and Buzsaki (1996), Bartos et al. (2002), synaptic inhibition alone could synchronize the network. This is because of the low heterogeneity which was realized by stimulating neurons with tonic depolarizing currents of different amplitudes varied in a very limited range. The uncoupled neurons fire at similar frequencies without noisy subthreshold oscillations. This makes the network much easier to be synchronized, but large heterogeneity will destroy synchrony. It has been shown that dendritic gap junctions of interneurons are significant for network synchrony when axonal conduction delays exist (Traub et al. 2001). There is also evidence that weak stochastic synchronization is much more robust than strong synchronization (Brunel and Hakim 1999; Tiesinga and José 2000). Robustness against heterogeneity of FS networks can also be improved by incorporating fast inhibitory synapses (Bartos et al. 2002) and shunting inhibition with the synaptic reversal potential between the rest potential and action-potential threshold (Vida et al. 2006). Moreover delays on the connections from the RS cell to the FS network are responsible for the coherent oscillations and even control the oscillation frequency of inhibitory networks (Bartos et al. 2002; Maex and De Schutter 2003).

In Sohal et al. (2009), γ frequency synchrony was observed experimentally from pyramidal cells with feedback inhibition of FS interneurons. In contrast to our results, they only recorded the γ oscillation from pyramidal cells instead of the FS cells, which are more prone to generate γ oscillations. In particular, we consider a relatively small number of FS cells, which should reasonably realistically represent the number of FS cells that receives influential input from the same single pyramidal cell. Further investigations on the complex interplay between RS and FS subnetworks are still needed to fully understand the functional roles of γ oscillations in cortical circuits.

Acknowledgments

This research was funded by a Hong Kong University Grants Council Grant Competitive Earmarked Research Grant (CERG) number PolyU 5279/08E. K. Morita is supported by KAKENHI 21700366 and 20246026 from MEXT. H. Robinson is supported by a grant from the EC Framework Programme 7 (No. 12788) and the Daiwa Anglo-Japanese Foundation.

References

  1. Bartos M, Vida I, Frotscher M, Meyer A, Monyer H, Geiger J, Jonas P. Fast synaptic inhibition promotes synchronized gamma oscillations in hippocampal interneuron networks. Proc Natl Acad Sci USA. 2002;99(20):13222. doi: 10.1073/pnas.192233099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nature Reviews Neuroscience. 2007;8(1):45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
  3. Bragin A, Jando G, Nadasdy Z, Hetke J, Wise K, Buzsaki G. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15(1):47. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brunel N, Hakim V. Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput. 1999;11(7):1621–1671. doi: 10.1162/089976699300016179. [DOI] [PubMed] [Google Scholar]
  5. Brunel N, Wang X. What determines the frequency of fast network oscillations with irregular neural discharges? I Synaptic dynamics and excitation-inhibition balance. J Neurophysiol. 2003;90(1):415. doi: 10.1152/jn.01095.2002. [DOI] [PubMed] [Google Scholar]
  6. Burchell T, Faulkner H, Whittington M. Gamma frequency oscillations gate temporally coded afferent inputs in the rat hippocampal slice. Neuroscience letters. 1998;255(3):151–154. doi: 10.1016/S0304-3940(98)00676-4. [DOI] [PubMed] [Google Scholar]
  7. Cardin J, Carlén K, Meletis K, Knoblich U, Zhang F, Deisseroth K, Tsai L, Moore C. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Engel A, Singer W. Temporal binding and the neural correlates of sensory awareness. Trends in cognitive Sciences. 2001;5(1):16–25. doi: 10.1016/S1364-6613(00)01568-0. [DOI] [PubMed] [Google Scholar]
  9. Ferezou I, Bolea S, Petersen C. Visualizing the cortical representation of whisker touch: voltage-sensitive dye imaging in freely moving mice. Neuron. 2006;50(4):617–629. doi: 10.1016/j.neuron.2006.03.043. [DOI] [PubMed] [Google Scholar]
  10. Fries P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Ann Rev Neurosci. 2009;32(1):209–224. doi: 10.1146/annurev.neuro.051508.135603. [DOI] [PubMed] [Google Scholar]
  11. Gouwens N, Zeberg H, Tsumoto K, Tateno T, Aihara K, Robinson H. Synchronization of firing in cortical fast-spiking interneurons at gamma frequencies: a phase-resetting analysis. PLoS Computational Biology. 2010;6(9):e1000951. doi: 10.1371/journal.pcbi.1000951. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hajos N, Palhalmi J, Mann E, Nemeth B, Paulsen O, Freund T. Spike timing of distinct types of GABAergic interneuron during hippocampal gamma oscillations in vitro. J Neurosci. 2004;24(41):9127. doi: 10.1523/JNEUROSCI.2113-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hines M, Carnevale N. The NEURON simulation environment. Neural computation. 1997;9(6):1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
  14. Knoblich U, Siegle J, Pritchett D, Moore C (2010) What do we gain from gamma? Local dynamic gain modulation drives enhanced efficacy and efficiency of signal transmission. Front Human Neurosci 4. Article 185 [DOI] [PMC free article] [PubMed]
  15. Maex R, Schutter E. Resonant synchronization in heterogeneous networks of inhibitory neurons. J Neurosci. 2003;23(33):10503. doi: 10.1523/JNEUROSCI.23-33-10503.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Morita K, Kalra R, Aihara K, Robinson H. Recurrent synaptic input and the timing of gamma-frequency-modulated firing of pyramidal cells during neocortical “UP” states. J of Neurosci. 2008;28(8):1871. doi: 10.1523/JNEUROSCI.3948-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Pospischil M, Toledo-Rodriguez M, Monier C, Piwkowska Z, Bal T, Frégnac Y, Markram H, Destexhe A. Minimal Hodgkin–Huxley type models for different classes of cortical and thalamic neurons. Biol Cybern. 2008;99(4):427–441. doi: 10.1007/s00422-008-0263-8. [DOI] [PubMed] [Google Scholar]
  18. Sohal V, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Tateno T, Robinson H. Integration of broadband conductance input in rat somatosensory cortical inhibitory interneurons: an inhibition-controlled switch between intrinsic and input-driven spiking in fast-spiking cells. Journal of neurophysiology. 2009;101(2):1056. doi: 10.1152/jn.91057.2008. [DOI] [PubMed] [Google Scholar]
  20. Tateno T, Harsch A, Robinson H. Threshold firing frequency-current relationships of neurons in rat somatosensory cortex: type 1 and type 2 dynamics. J of neurophysiol. 2004;92(4):2283–2294. doi: 10.1152/jn.00109.2004. [DOI] [PubMed] [Google Scholar]
  21. Tiesinga P, José J. Robust gamma oscillations in networks of inhibitory hippocampal interneurons. Network: Computation in Neural Systems. 2000;11(1):1–23. doi: 10.1088/0954-898X/11/1/301. [DOI] [PubMed] [Google Scholar]
  22. Tiesinga P, Sejnowski T (2010) Mechanisms for phase shifting in cortical networks and their role in communication through coherence. Front Human Neurosci 4. Article 196 [DOI] [PMC free article] [PubMed]
  23. Tiesinga P, Fellous J, Salinas E, José J, Sejnowski T. Inhibitory synchrony as a mechanism for attentional gain modulation. J of Physiology-Paris. 2004;98(4-6):296–314. doi: 10.1016/j.jphysparis.2005.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Traub R, Jefferys J, Whittington M. Simulation of gamma rhythms in networks of interneurons and pyramidal cells. J Comput Neurosci. 1997;4(2):141–150. doi: 10.1023/A:1008839312043. [DOI] [PubMed] [Google Scholar]
  25. Traub R, Bibbig A, Fisahn A, LeBeau F, Whittington M, Buhl E. A model of gamma-frequency network oscillations induced in the rat CA3 region by carbachol in vitro. Eur J Neurosci. 2000;12(11):4093–4106. doi: 10.1046/j.1460-9568.2000.00300.x. [DOI] [PubMed] [Google Scholar]
  26. Traub R, Kopell N, Bibbig A, Buhl E, LeBeau F, Whittington M. Gap junctions between interneuron dendrites can enhance synchrony of gamma oscillations in distributed networks. J Neurosci. 2001;21(23):9478. doi: 10.1523/JNEUROSCI.21-23-09478.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Vida I, Bartos M, Jonas P. Shunting inhibition improves robustness of gamma oscillations in hippocampal interneuron networks by homogenizing firing rates. Neuron. 2006;49(1):107–117. doi: 10.1016/j.neuron.2005.11.036. [DOI] [PubMed] [Google Scholar]
  28. Wang X, Buzsaki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16(20):6402. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Whittington M, Traub R, Jefferys J. Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature. 1995;373(6515):612–615. doi: 10.1038/373612a0. [DOI] [PubMed] [Google Scholar]
  30. Zhu J, Connors B. Intrinsic firing patterns and whisker-evoked synaptic responses of neurons in the rat barrel cortex. J Neurophysiol. 1999;81(3):1171. doi: 10.1152/jn.1999.81.3.1171. [DOI] [PubMed] [Google Scholar]

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES