Maternal MCG Interference Cancellation Using Splined Independent Component Subtraction

Abstract

Signal distortion is commonly observed when using independent component analysis (ICA) to remove maternal cardiac interference from the fetal magnetocardiogram. This can be seen even in the most conservative case where only the independent components dominated by maternal interference are subtracted from the raw signal, a procedure we refer to as independent component subtraction (ICS). Distortion occurs when the subspaces of the fetal and maternal signals have appreciable overlap. To overcome this problem, we employed splining to remove the fetal signal from the maternal source component. The maternal source components were downsampled and then interpolated to their original sampling rate using a cubic spline. A key aspect of the splining procedure is that the maternal QRS complexes are downsampled much less than the rest of the maternal signal so that they are not distorted, despite their higher bandwidth. The splined maternal source components were projected back onto the magnetic field measurement space and then subtracted from the raw signal. The method was evaluated using data from 24 subjects. We compared the results of conventional, i.e., unsplined, ICS with our method, splined ICS, using matched filtering as a reference. Correlation and subjective assessment of the P-wave and QRS complex were used to assess the performance. Using ICS, we found that the P-wave was adversely affected in 7 of 24 (29%) subjects, all having correlations less than 0.8. Splined ICS showed negligible distortion and improved the signal fidelity to some extent in all subjects. We also demonstrated that maternal T-wave interference could be problematic when the fetal and maternal heartbeats were synchronous. In these instances, splined ICS was more effective than matched filtering.

I. Introduction

Over the last decade, fetal magnetocardiography (fMCG) has emerged as a valuable new technology for fetal surveillance. It can simultaneously assess fetal heart rate (FHR), beat-to-beat FHR variability, fetal activity, and fetal rhythm [1]–[4]. In terms of clinical utility, the most important application of fMCG is assessment of fetal rhythm [5], [6]. No other technique is as direct or precise. In recent years, the efficacy of fMCG for diagnosis and prognosis of serious fetal arrhythmia has become more widely recognized [7].

The quality of the fMCG signal is very important because it determines the amount of information that can be extracted. Some of the information derived from the fMCG, such as FHR and actogram tracings, is relatively easy to obtain because it only requires detection of the fetal QRS complex. Fetal rhythm assessment, however, is much more complicated and difficult because it involves subjective evaluation of waveform morphology, including the fetal P-wave and T-wave, which are approximately ten times smaller than the fetal QRS complex. Resolution of these smaller waveform components imposes considerable demands on the signal acquisition and analysis procedures.

Signal processing is an essential aspect of fMCG and fetal ECG (fECG) analysis due to the large interference from the mother’s cardiac signal, as well as the low amplitude of the fetal signal. The removal of maternal interference from fMCG and fECG recordings is a classic problem in signal processing; however, many papers on fMCG and fECG signal processing focus on the fetal and maternal QRS complex, while ignoring the other components. The fetal P-wave is essential for making an accurate differential diagnosis of fetal arrhythmia, and the T-wave allows diagnosis of repolarization anomalies that are undetectable by ultrasound [8]–[10]. While interference from the maternal P-wave is usually small, the maternal T-wave is large enough to confound rhythm interpretation in some situations.

Matched filtering was one of the earliest techniques employed to remove maternal interference from fMCG and fECG recordings, and is still widely used. It works by correlating the signal against a template, comprised of a representative maternal QRS complex, in order to detect the occurrence of maternal beats. When a maternal beat is detected, a suitably scaled version of the template is subtracted from the signal to cancel the maternal interference. The main disadvantage of matched filtering is that it distorts the fetal signal when the fetal and maternal QRS complexes overlap because the template scaling becomes corrupted; however, methods have been developed to overcome this problem [11].

Spatial filtering methods are especially well suited for fMCG because the spatial characteristics of the fetal signal and the maternal interference are more distinct than their temporal characteristics, which are largely similar. Unlike matched filters, spatial filters do not distort the fetal signal when it temporally overlaps the maternal interference, and they are more effective than matched filtering in removing all components of the maternal interference, including the maternal T-wave. They can also be designed to remove noise and other interferences at the same time. Among the various spatial filtering methods that have been tried, independent component analysis (ICA) has received the most attention in recent years [12]–[14]. ICA is a method of blind source separation that identifies source components on the basis of mathematical definitions of statistic independence. It makes few assumptions and requires little user input; thus, it is perhaps the easiest of all methods to implement. Filtering is achieved by retaining ICA components containing signal and/or rejecting components dominated by interference and noise. A significant disadvantage of ICA, however, is that it generally distorts the signal to some extent. In particular, filter performance degrades if the subspaces of the fetal signal and the maternal interference have appreciable overlap. In this case, it is impossible to completely remove the maternal interference without also removing some of the fetal signal.

In this paper, we propose a new method for reducing the signal distortion that commonly occurs when using ICA. It can significantly increase the fidelity of the fetal P-wave and QRS complex, thereby improving the accuracy of PR interval measurement. We also show that maternal T-wave interference can be problematic when the fetal and maternal heartbeats are synchronous. In these instances, our method is more effective than matched filtering.

II. Methods

The impetus for the study was the observation that ICA occasionally results in obvious signal distortion, even when used in the most conservative fashion, in which only the ICA components dominated by maternal interference are removed. Fig. 2 shows such an example. Even though ICA appears to have separated the maternal and fetal source components, the averaged fMCG waveform from this subject (Fig. 3, left) obtained after removing just the maternal source components shows substantial attenuation of the fetal P-wave. This may be due to suboptimal performance of the ICA algorithm or, more likely, partial overlap of the fetal and maternal subspaces. Regardless of the cause, the solution is to completely remove the fetal signal before subtracting the maternal source component from the raw signal. The main difficulty is that the temporal characteristics of the fetal and maternal MCG are similar. The method we have devised to overcome this problem employs downsampling and splining of the maternal source component. After downsampling the recording lightly during the maternal QRS complexes and heavily during the rest of the recording, splining is able to remove the residual fetal signal and preserve the maternal signal more effectively than a typical time-domain filter. Below we first describe the conventional method of performing maternal interference cancellation using ICA, which we refer to as independent component subtraction (ICS). We then describe the modified procedure, which we refer to as splined ICS. These techniques were compared with matched filtering, and were evaluated using human data.

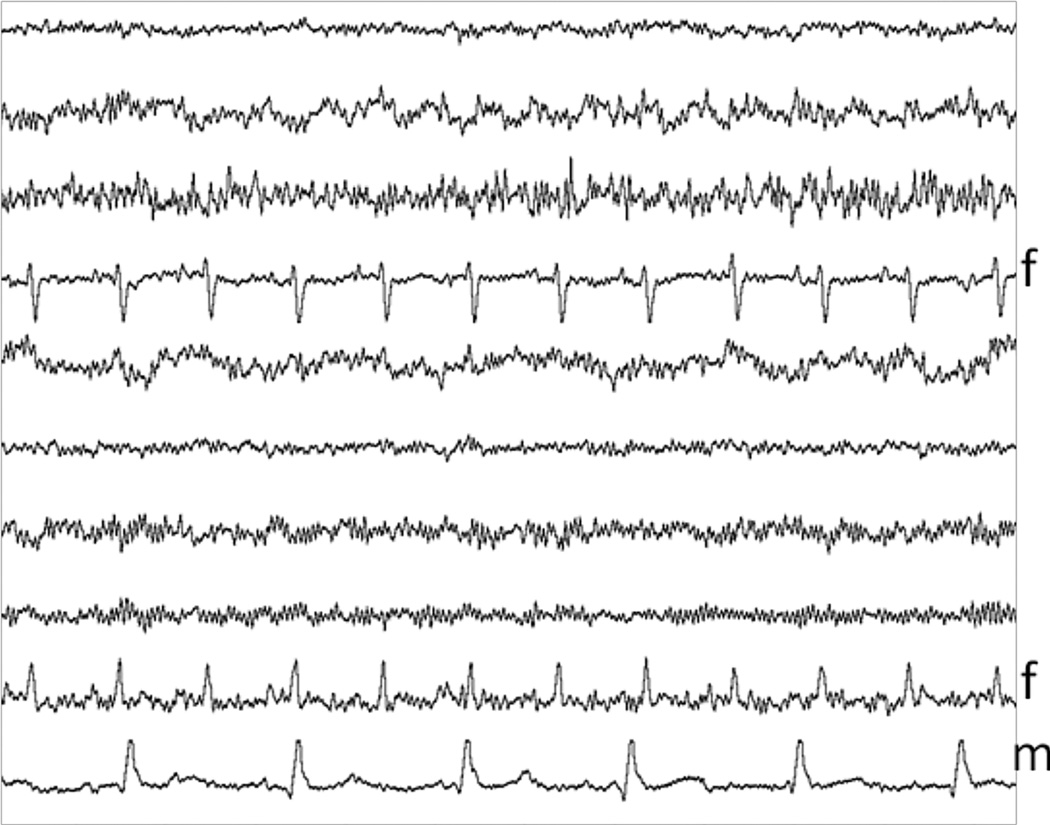
Fig. 2.

The ICA source components from subject 9 contain 2 fetal (f) and 1 maternal component (m).

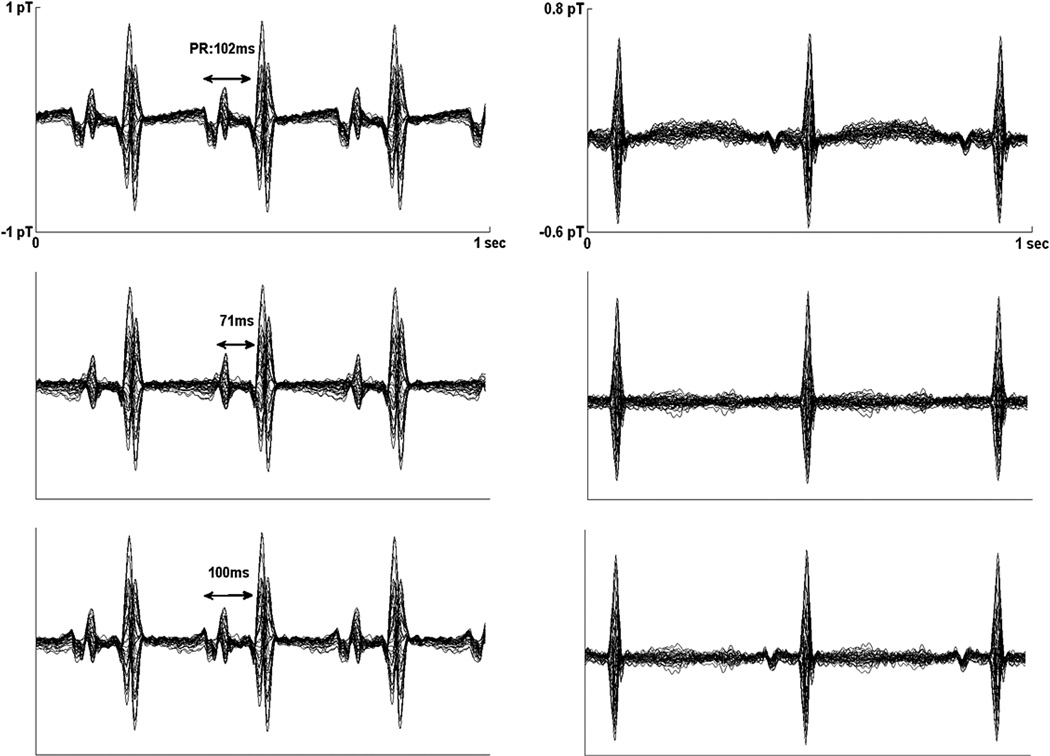
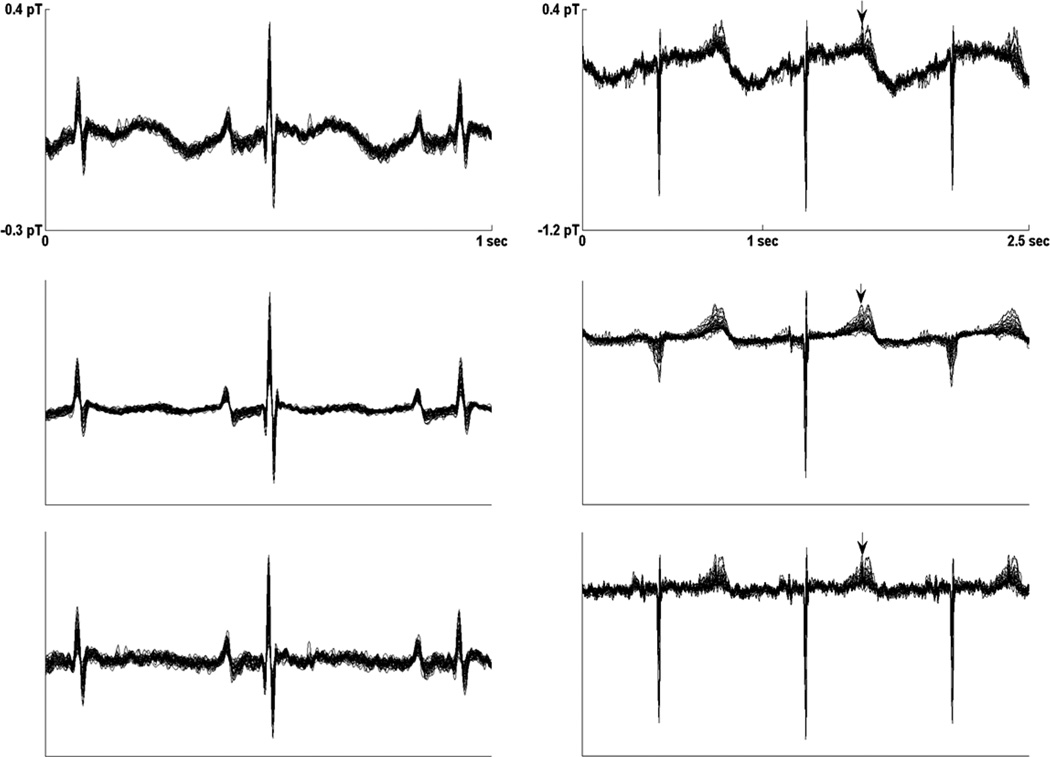
Fig. 3.

Averaged fMCG waveforms from subject 9 (left) and subject 3 (right), obtained using matched filtering (top), ICS (middle), and splined ICS (bottom). The splined ICS waveforms show good agreement with the matched filtered waveform, but the ICS waveforms show marked distortion of the P-wave. Subject 9 has supraventricular tachycardia. The large, broad P-wave may be a sign of cardiovascular compensation.

A. Subjects

We reviewed recordings from the last 38 consecutive subjects studied in our laboratory. In order to precisely assess the performance of ICS and splined ICS, it was necessary to obtain fMCG waveforms with high signal-to-noise ratio (SNR) for comparison. This was accomplished by excluding recordings with low amplitude and by averaging the signals for 200 s in order to remove the interference and noise. Five subjects were excluded because their P-waves had very low amplitude (< 50 fT). Seven were excluded because their signals could not be averaged for 200 s due to frequent ectopy and/or intermittent tachycardia. In addition, two were excluded because the fetal signal was much stronger than the maternal interference, which obviated with need for signal processing. The remaining 24 pregnancies were studied between 19 and 36 weeks’ gestation. Eight pregnancies were uncomplicated, as identified by clinical history and verified by fMCG. The others were referred to the study with suspicion of various forms of fetal arrhythmia; however, four showed only normal sinus rhythm (NSR) during the study. This could be due to natural resolution of the arrhythmia, an infrequent, intermittent arrhythmia, or incorrect referral diagnosis. Thus, 12 of the subjects had NSR and 12 had sustained arrhythmia during the study, as documented in Table I. The University of Wisconsin Institutional Review Board approved the protocol to study the patients and informed consents were obtained from each mother prior to the procedure.

TABLE I.

Subject Cohort Sorted in Order of Peak-to-Peak Signal Amplitude (Amp), Measured in the Channel With Largest Signal

#	GA (wks)	rhythm	heart rate (bpm)		amp (fT)	source components			p-wave correlation		QRS correlation		P/QRS ratio	T-wave power
			mom	fetus		F	M	X	sp-ICS	ICS	sp-ICS	ICS	ICS
1	20 2/7	NSR	75	130	580	3	2	1	0.988	0.840	0.998	0.781	1.123	0.545
2	19 4/7	NSR	70	140	590	2	1	1	0.984	0.753	0.935	0.731	1.109	0.037
3	26 4/7	NSR	65	137	700	2	3	0	0.950	0.366	0.927	0.910	0.535	0.422
4	24 6/7	NSR	70	130	860	3	2	1	0.977	0.914	0.995	0.962	0.937	0.276
5	22 1/7	SB	65	112	900	3	1	1	0.992	0.959	0.999	0.999	1.039	0.753
6	21 2/7	NSR	115	160	920	4	3	1	0.903	0.904	0.927	0.844	1.327	0.820
7	24	NSR	75	150	1000	1	1	0	0.992	0.985	1.000	0.962	0.797	0.046
8	21	2° AVB	80	75	1100	3	2	1	0.919	0.566	0.999	0.947	1.104	0.152
9	28 1/7	SVT	125	205	1110	2	1	0	0.959	0.538	0.998	0.950	0.484	0.793
10	23 2/7	NSR	90	150	1170	4	1	1	0.983	0.897	0.999	0.963	0.896	0.300
11	29 1/7	SVT	80	175	1230	2	1	0	0.919	0.725	0.944	0.926	0.731	0.624
12	23 6/7	SB	82	115	1310	2	2	0	0.980	0.911	0.998	0.881	0.986	0.534
13	21 6/7	NSR	90	135	1460	2	1	0	0.998	0.965	1.000	0.999	0.821	0.395
14	25 1/7	2° AVB	65	77	1520	4	1	1	0.907	0.766	0.981	0.766	0.936	0.548
15	23 5/7	NSR	85	140	1600	3	1	1	0.912	−0.523	0.991	0.468	0.331	0.160
16	19 5/7	NSR	80	144	1750	3	3	0	0.912	0.917	0.855	0.832	0.877	0.427
17	23 4/7	WPW	75	142	1790	2	1	0	0.996	0.970	1.000	0.999	1.051	0.782
18	29 5/7	NSR	95	143	1800	5	1	1	0.990	0.931	0.994	0.902	1.085	0.612
19	26 5/7	NSR	85	150	2370	6	2	2	0.991	0.981	0.973	0.375	0.103	0.223
20	35 4/7	SB	80	116	2900	3	3	1	0.985	0.968	0.987	0.946	0.899	0.064
21	26 3/7	LQTS	80	150	3110	3	1	1	0.962	0.911	0.995	0.898	1.099	0.385
22	31 5/7	SB	75	115	3300	5	3	2	0.923	0.538	1.000	0.929	0.946	0.355
23	32	LQTS	45	110	3900	4	3	1	0.941	0.403	0.880	0.879	0.576	0.789
24	25 4/7	LQTS	55	115	6400	5	2	1	0.994	0.823	1.000	0.992	1.202	0.864
ALL	25.24±4.16		79.25±16.86	134.00±27.96	1749±1289	3.17±1.24	1.75±0.85	0.75±0.61	0.961±0.03	0.750±0.33	0.974±0.04	0.868±0.16	0.875±0.29	0.454±0.26
NSR	23.46±3.14		82.92±13.73	142.42±8.99	1233±563	3.17±1.40	1.75±1.40	0.75±0.61	0.965±0.04	0.744±0.43	0.966±0.05	0.811±0.20	0.829±0.35	0.355±0.23
FA	27.02±4.40		75.58±19.41	125.58±37.40	2191±1573	3.17±1.12	1.75±0.87	0.75±0.62	0.956±0.03	0.756±0.20	0.982±0.04	0.926±0.07	0.921±0.22	0.554±0.27

Subjects 1,2,10,and 13 were referred with suspected diagnoses of bradycardia, atrioventricular block (AVB), supraventricular tachycardia (SVT), and AVB, respectively; however, they showed only normal sinus rhythm (NSR) during the study. The last three rows show the averages for all 24 subjects (ALL), the 12 NSR subjects, and the 12 fetal arrhythmia subjects (FA). SB= sinus bradycardia, WPW=Wolff-Parkinson-White Syndrome, LQTS= Long QT Syndrome, GA= gestational age, fT= 10⁻¹⁵ tesla, F= fetal, M= maternal, X= mixed (fetal+ maternal), sp-ICS= splined ICS. The sp-ICS and ICS correlations, respectively, are the correlations of sp-ICS with matched filtering and of ICS with matched filtering. The P/QRS ratio is the P/QRS ratio of ICS-filtered waveforms normalized to that of matched filtered waveforms. The T-wave power is the ratio of T-wave power in a 200 s average waveform to a 20 s average waveform.

B. fMCG Recordings

A brief ultrasound exam was performed to ascertain the position of the fetus. The fMCG recordings were made using a 37-channel superconducting quantum interference (SQUID) magnetometer (Magnes, 4-D Neuroimaging, Inc., San Diego, CA) in a magnetically shielded room. The signal was digitized at 520.8 Hz, and the analog filter passband was 0.1–200 Hz. A digital filter was applied to further band-limit the signals to 1.0–80 Hz. Three to five 37-channel recordings of duration 10 minutes were taken during each study. For the purpose of this study, we analyzed a single recording in which the SNR was high and the fetal heart rate was relatively constant.

C. Interference Cancellation Methods

1) Independent Component Subtraction

ICA was performed using the CubICA algorithm [15]. Prior to applying ICA, it is necessary to whiten and rank-reduce the data by applying singular value decomposition (SVD): X = UDV^T, where X is the n by t raw data matrix, U is the n by n matrix of left singular vectors, D is the n by n diagonal matrix of singular values, and V^T is the n by t transpose of the matrix of right singular vectors, V, where n is the number of channels and t is the number of time samples. Rank-reduction is accomplished by eliminating the SVD components corresponding to the smallest singular values. The rank r approximation of the raw data is ${\mathbf{X}}_{\mathbf{r}}={\mathbf{U}}_{\mathbf{r}}{\mathbf{D}}_{\mathbf{r}}{\mathbf{V}}_{\mathbf{r}}^{\mathbf{T}}$, where U_r is the n by r matrix formed from the first r left singular vectors, D_r is the r by r diagonal matrix formed from the first r singular values, and ${\mathbf{V}}_{\mathbf{r}}^{\mathbf{T}}$ is the r by t transpose of the matrix formed from the first r right singular vectors, V_r. The ICA algorithm operates on ${\mathbf{V}}_{\mathbf{r}}^{\mathbf{T}}$, and yields r ICA source components. The r by t matrix, Y^T, formed from the r ICA source components, is related to ${\mathbf{V}}_{\mathbf{r}}^{\mathbf{T}}$ through the r by r ICA mixing matrix, A, as follows: ${\mathbf{V}}_{\mathbf{r}}^{\mathbf{T}}={\mathbf{\text{AY}}}^{\mathbf{T}}$. In this study, we used a rank-10 approximation of the raw data because further rank-reduction sometimes resulted in distortion of the fetal signal. This could be seen by inspecting the fetal signal after projecting the data onto the r-dimensional subspace spanned by the singular vectors. The ICA components were inspected, and the number of fetal and maternal source components with SNR>2 were tabulated, where SNR is defined as the peak-to-peak amplitude of the QRS complex divided by the root-mean-square noise. Source components containing both fetal and maternal signal were deemed “mixed” components. ICS was performed by reconstructing the data from the ICA source components following deletion of the maternal source components. This was accomplished by projecting the signal back to the magnetic field measurement space according to:

$${\mathbf{X}}^{\mathbf{\text{ICS}}}={\mathbf{U}}_{\mathbf{r}}{\mathbf{D}}_{\mathbf{r}}\mathbf{A}{\overline{\mathbf{Y}}}^{\mathbf{T}}$$ (1)

where X^ICS is the ICS-filtered data and Ȳ^T is formed by zeroing the rows of Y^T corresponding to the maternal source components. Mixed components were excluded from the reconstructed signal if the maternal signal was larger than the fetal signal. Notice that the ICS-filtered data contains not only the fetal components but also the “noise” components, i.e., components in which the fetal signal is weak or absent. Retaining these components can help increase signal fidelity at the expense of reduced signal-to-noise ratio. Due to the importance of signal fidelity for rhythm assessment, the noise components were retained and, as described below, averaging was used to increase the signal-to-noise ratio.

2) Splined Independent Component Subtraction

In splined ICS, the maternal source component is downsampled and then interpolated to its original sampling rate using a cubic splining routine. The aim of this procedure is to selectively remove the residual fetal signal while preserving the maternal interference. A key to the effectiveness of our method is that the maternal QRS complexes are downsampled less than the rest of the signal. This is necessary to preserve the maternal QRS complex because it has much higher bandwidth than the T-wave. The fetal QRS complex has even higher bandwidth. It is removed because it cannot be resolved in the downsampled signal, except possibly when it overlaps the maternal QRS complex, but during those periods it is dominated by the much larger maternal signal. For the results presented below, the downsampling was performed by retaining one of every five samples of the maternal QRS complex, taking care to include the sample at the peak of the QRS complex, and one of every twenty samples in the remainder of the recording. This produced the best overall results. If the maternal source component is downsampled too much, then the splined maternal interference will be distorted and the subtraction of the maternal interference from the raw signal will be poor. If the component is downsampled too little, then the fetal signal will not be adequately rejected and the subtraction of the maternal interference from the raw signal will remove some of the fetal signal. The maternal QRS complexes are detected in the usual way by computing the correlation of the signal with a template consisting of a representative maternal QRS complex. The maternal QRS duration is assumed to be 100 ms or less.

Unlike ICS, where interference cancellation is accomplished by zeroing out the maternal source components during the signal reconstruction, here the splined maternal source components are reprojected back onto the 37-channel magnetic field measurement space and then subtracted from the raw signal; (Fig.1) i.e., the output of the splined ICS filter is X^spICS = X-M, where the projected maternal interference, M, is obtained from the transpose of the matrix formed from the splined maternal components, m, as follows:

$$\mathbf{M}={\mathbf{U}}_{\mathbf{r}}{\mathbf{D}}_{\mathbf{r}}{\mathbf{\text{Am}}}^{\mathbf{T}}.$$ (2)

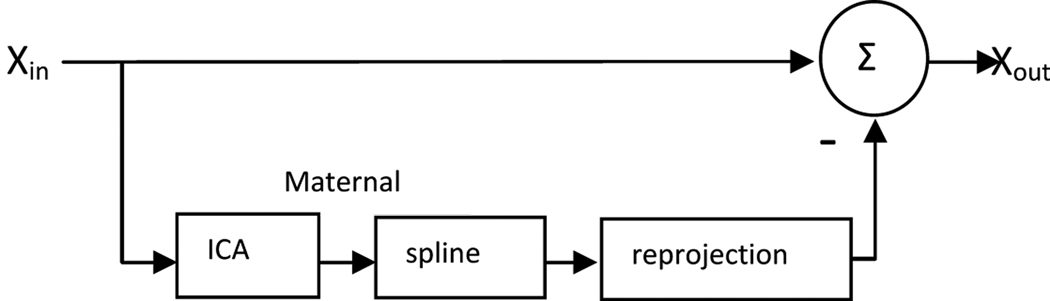
Fig. 1.

Schematic diagram of the splined ICS filter. ICA is used to isolate the maternal source component, which is splined to remove the fetal signal. The splined maternal source component is then projected back to the magnetic field measurement space and subtracted from the original signal.

3) Matched Filtering

Matched filtering is a temporal filtering technique, in which a template of the interference is subtracted from the recording whenever the interfering heartbeat is detected. In our implementation, the template consists of a representative maternal complex that is scaled by the correlation between the data and the template, so that the filter adapts to changes in the amplitude of the cardiac interference. Matched filters can distort the signal when there is temporal overlap of the fetal signal and maternal interference; however, we used a filter that largely mitigates the overlap problem [11]. Furthermore, the distortion usually does not affect the averaged fMCG waveform because it occurs sufficiently infrequently and randomly, provided that the fetal and maternal heartbeats are not synchronized. For this reason, matched filtered waveforms are commonly used as a reference when evaluating the effects of signal processing on averaged waveforms.

D. Signal Fidelity of Fetal P-Wave and QRS Complex

Correlation and subjective assessment of P-wave and QRS morphology were used to assess the performance of ICS and splined ICS, using matched filtering as a reference [16]. To increase the SNR, averaging was performed using autocorrelation to align all of the fetal complexes within a 20 s interval. Signal fidelity of the ICS and the splined ICS signals, X^ICA, was quantified by computing their correlations with the matched filtered output, X^MF, according to

$$C=\frac{|X^{\text{MF}}{X}^{\text{ICA}}|}{|X^{\text{MF}}||X^{\text{ICA}}|}$$ (3)

where <.,.> is the inner product and ‖ is the magnitude, or L2 norm. The correlations were computed separately for the P-wave and the QRS complex. X^ICA and X^MF are vectors of length 37 × n, where n is the number of time samples in the P-wave or the QRS complex. They were formed by concatenating the P or QRS segments of each channel. Prior to concatenation, the mean value of the signal was subtracted to eliminate the effects of dc offsets.

The ratio of the P-wave amplitude to the QRS amplitude (P/QRS ratio) was computed by measuring the peak-to-peak amplitude of the P-wave and the QRS complex. The measurement was performed in the channel with the largest P-wave. The P/QRS ratios were measured for the ICS-filtered and splined ICS-filtered waveforms, and the values were normalized by the P/QRS ratios of the matched filtered waveforms.

Subjective assessment of the P-wave and QRS complex was performed by manual inspection of the waveforms to determine whether ICS or splined ICS altered the PR interval, based on the onsets of the P-wave and the QRS complex relative to those of the matched filtered waveform.

E. Maternal T-Wave Interference

Occasionally, the matched filtered waveforms showed large interference from the maternal T-wave, even after averaging for 20 s. This is not that surprising because the maternal T-wave can be large and is not removed by the matched filter. In some cases the maternal T-wave interference is difficult to discern because it mimics the fetal T-wave. An easy way to verify the interference is to reduce it to a negligible level by averaging for a much longer period of time. Thus, to assess the interference in the 20 s averaged waveforms, we computed 200 s averaged waveforms and compared them by calculating the power during the interval from the end of the QRS complex to the beginning of the next P-wave. If we assume that the 20 s averaged waveforms are contaminated with noise and residual interference, arising primarily from maternal T-wave interference, and that the 200 s averaged waveforms are comparatively free of interference and noise, then the ratio of the T-wave power for the 200 s versus the 20 s averaged waveform is approximately P_f/P_f+P_int, where P_f is the power of the fetal T-wave and P_int is the power of the residual interference and noise. Thus, the ratio estimates the fraction of the power due to the fetal signal in the 20 s averaged waveforms.

III. Results

The numerical results of the study are tabulated in Table I. Below, we summarize the main findings, and describe the correspondences between the numerical data and the subjective assessments of the waveforms.

A. Fetal and Maternal Source Components

The number of fetal source components ranged from 1–6 with mean 3.17. The number of maternal source components ranged from 1–3 with mean 1.75. Mixed components were observed in 16 subjects. A positive correlation was found between signal amplitude and the number of fetal source components (p = 0.0072, r² = 0.2852, n = 24). This result suggests that some fetal signal components are obscured when the signal amplitude is low and that more can be resolved when the signal amplitude is high.

B. P-Wave Correlation, QRS Correlation, and P/QRS Ratio

Perhaps the most important result of the study was that the P-waves obtained by matched filtering showed a much higher correlation with the P-waves obtained by splined ICS (0.961 ± 0.034) than by ICS (0.750 ± 0.330). For splined ICS, none of the correlations were below 0.9. For ICS, 12 (50%) were below 0.9.

Similarly, the QRS complexes obtained by matched filtering showed a higher correlation with the QRS complexes obtained by splined ICS (0.974± 0.041) than by ICS (0.868 ± 0.157), although the difference was not as great. Compared to the P-wave, the QRS correlations were higher, most likely due to the higher SNR of the QRS complex.

For the ICS-filtered waveforms, six subjects showed normalized P/QRS ratios less than 0.6. Of these, three showed low P-wave correlation (<0.54), one showed low QRS correlation (0.375), and one showed negative P-wave correlation and low QRS correlation (0.468). For the splined ICS-filtered waveforms, only one subject showed a P/QRS ratio less than 0.6.

C. PR interval

For splined ICS, subjective evaluation showed that PR interval was unchanged to within 4 ms in comparison to the matched filtered waveforms.

For ICS, subjective evaluation showed that PR interval was adversely affected in seven subjects. In three subjects, the initial portion of the P-wave was removed, resulting in underestimation of PR interval (Fig. 3 left) by 30%, 19%, and 16%, respectively, in subject 9, 22, and 23. Thus, the PR changes were due to changes in P-wave onset; the QRS onsets were not affected, even when the QRS correlation was low and distortion was evident (Fig. 4). In four subjects (subjects 3, 8, 11, and 15), the P-wave was severely attenuated, such that the onset was ambiguous (Fig. 3 right). Significantly, in all of these subjects the P-wave correlations were less than 0.8.

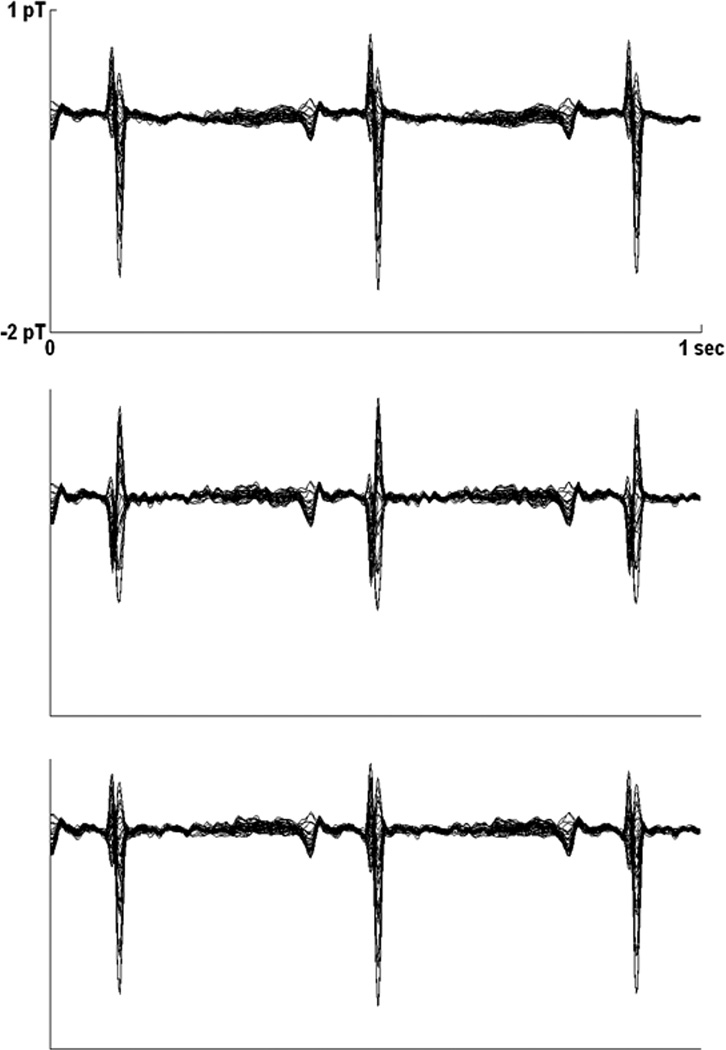
Fig. 4.

Averaged fMCG waveforms from subject 19, obtained using matched filtering (top), ICS (middle), and splined ICS (bottom). The splined ICS waveform shows good agreement with the matched filtered waveform, but the ICS waveform shows distortion of the QRS complex.

D. Maternal T-Wave Interference

On average, the ratio of the T-wave power for the 200 s- and 20 s-average matched filtered waveforms was 0.454, but in some subjects it was very low; in three (13%; subjects 2, 7, 20), it was less than 0.07 (Table I). This was due to a combination of large residual maternal T-wave interference in the 20 s waveform and small fetal signal in the 200 s waveform. The next smallest ratio, 0.152 (subject 8, Fig. 5 right), was also a case in which the residual maternal interference in the 20 s waveform was large, but the fetal signal in the 200 s waveform was relatively large, which moderated the ratio.

Fig. 5.

Averaged fMCG waveforms from subject 2(left) and subject 8(right). Subject 8 had 2:1 2° AV block, obtained using matched filtering and 20 s of averaging (top), matched filtering and 200 s of averaging, and splined ICS and 20 s of averaging (bottom). The splined ICS waveform is compatible with the 200 s-average matched filtered waveform, but the 20 s-average matched filtered waveform shows strong residual interference from the maternal T-wave. Although the 200 s-average waveform has higher SNR, notice that the nonconducted P-wave (arrow) overlapping the T-wave is broadened by the longer averaging time, while it remains narrow in the 20 s-average waveforms. Subject 2 had normal sinus rhythm with the fetal and maternal heart rates in a 2:1 ratio.

Subjective evaluation of the waveforms was compatible with the T-wave power ratios. The aforementioned subjects with the four smallest ratios were the subjects who showed large residual maternal interference. Normally, the maternal T-wave interference is adequately reduced by 20 s of averaging. The explanation for the large residual interference in these subjects is that the fetal and maternal rhythms were synchronized over the 20 s averaging time because the heart rates were in a simple ratio. For subjects 2 and 7, the fetal and maternal heart rates were in a 2:1 ratio. For subject 8, a fetus with second-degree heart block, the ratio was 1:1. Interestingly, subject 20 showed a 3:2 ratio (Fig. 6). It is worth noting that the residual maternal T-wave interference often mimics a fetal T-wave because their morphologies are similar (Figs. 5 and 7). The interference is apparent only upon comparison with the splined ICS and the 200 s averaged waveforms, which contain minimal interference.

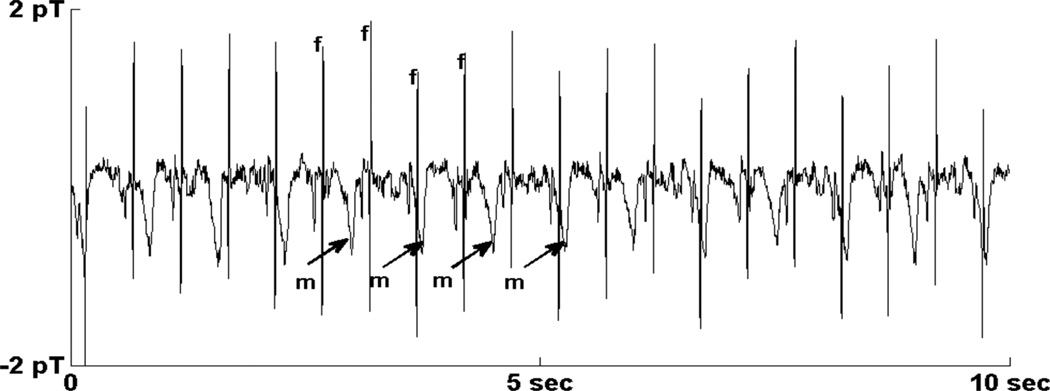
Fig. 6.

Rhythm strip from subject 20 showing 3:2 synchronization of the fetal and maternal heart rates. The maternal QRS complex was removed via matched filtering. Fetal QRS complexes and maternal T-waves are indicated by “f” and “m,” respectively.

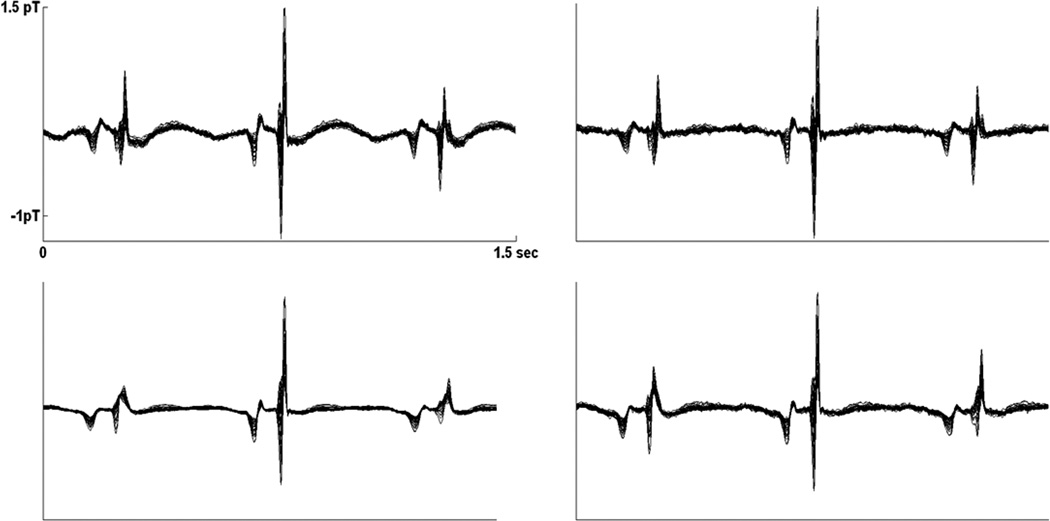
Fig. 7.

Averaged fMCG waveforms from subject 20, in which the fetal and maternal heart rates were in a 3:2 ratio, obtained using matched filtering and 20 s of averaging (top left), matched filtering and 200 s of averaging (bottom left), and splined ICS and 20 s of averaging (top right), and matched filtering and 20 s of averaging at a time within the same run when the fetal and maternal heart rates were not synchronous (bottom right). The splined ICS waveform shows good agreement with the 200 s-average matched filtered waveform, but the 20 s-average matched filtered waveform shows strong residual interference from the maternal T-wave when the fetal and maternal heart rates are synchronous.

E. Normal Sinus Rhythm Versus Fetal Arrhythmia Subjects

T-testing was used to compare normal and fetal arrhythmia subjects, but no significant differences in the means were found for any of the data in Table I.

IV. Discussion

In this study, we showed that splined ICS could mitigate the signal attenuation associated with ICS filtering of the fMCG. It provided a substantial improvement in signal fidelity, most notably for the fetal P-wave and to a lesser extent for the fetal QRS complex. ICS performed well most of the time, but in 7 of 24 subjects it adversely affected PR interval measurement by abolishing the P-wave or by removing the initial segment. Although this represents a minority of subjects, there is ample justification for applying the method routinely. First, it provides some degree of improvement in signal fidelity in virtually all subjects. Second, there is little drawback to using to the method in that the improvement does not appear to compromise its ability to reject maternal interference. Third, it is difficult to predict beforehand the degree to which ICS will distort the signal. The distortion, which was evidenced by low correlation and/or altered PR interval, did not correlate significantly with signal amplitude, gestational age, or rhythm. In addition to PR interval, the distortions associated with ICS can alter the P/QRS amplitude ratio. ICS usually attenuates the P-wave more than the QRS complex, resulting in underestimation of P/QRS ratio. We have shown previously that elevated P/QRS amplitude ratio is an indicator of atrial enlargement and cardiovascular compensation [17].

Splined ICS combines splining, a temporal filtering technique, with ICA, a spatial filtering technique, in a synergistic manner; i.e., it is much more effective than sequential application of the separate methods. In addition to its simplicity, a major advantage of splined ICS is that it readily adapts to beat-to-beat as well as longer-term variations in the amplitude and morphology of the maternal interference. The method implicitly assumes that in the maternal ICA components the maternal interference is much larger than the fetal signal. This was most often the case, but occasionally we observed mixed components, in which the fetal and maternal signals were similar in amplitude. In this study, we adopted the strategy that such ICA components would be subtracted if the maternal component was larger than the fetal component, but other criteria can be used, depending on the desired trade-off between interference attenuation and signal fidelity.

We showed that the interference from the maternal T-wave could be much larger than expected due to synchrony between the fetal and maternal heart rates. It is actually quite common for the fetal and maternal heart rates to exhibit a ratio of approximately 2:1. For example, in normal pregnancies this can occur if the fetal and maternal heart rates are 140 and 70 bpm, respectively. In addition to 2:1 synchrony, we observed 1:1 synchrony in a fetus with AV block, the most common type of fetal bradycardia, in which the fetal rate is typically half of its normal value. We even observed 3:2 synchrony in a fetus with sinus bradycardia, which underscores the need to be vigilant for this phenomenon. In all of these cases, the synchrony we observed was likely coincidental; however, some studies have shown that true phase locking is possible [18]. The main problem with maternal T-wave interference is that it is not always apparent after averaging because it can be easily mistaken for the fetal T-wave. A simple remedy is to average for a long period of time, but this may be limited by the stationarity of the signal if the fetus is active and/or the rhythm is irregular, as was the case for 7 of the 38 subjects considered for the study. Removal of the T-wave can be accomplished via matched filtering by extending the template to encompass the T-wave as well as the QRS complex; how-ever, this compromises removal of the QRS complex. Matched filtering can also be applied sequentially to remove the T-wave following removal of the QRS complex, but the performance is often unsatisfactory because accurate scaling of the template is difficult due to the lower amplitude and longer duration of the T-wave. ICA is particularly useful for removing maternal T-wave interference because the maternal source components usually contain the T-wave as well as the QRS complex; thus the T-wave is removed with no additional effort.

An unexpected finding was that the fetal signal was present in as many as six ICA components, and was present in at least four components in 8 of 24 subjects. Most prior studies have reported fewer fetal components. Thus, the rank of the fMCG signal may be higher than is generally believed. Many spatial filters, including ICA, implicitly assume that the fetal signal is confined to a small number of components. Such filters should be applied with caution due to potential signal distortion that can result when assumptions regarding the signal rank are violated. Our implementation of splined ICS was the most conservative. We removed only the maternal source components and retained all others. Our intent was to show that significant distortion of the fetal signal could occur even in this situation. ICA is usually applied more aggressively, retaining only components dominated by fetal signal and rejecting all others. This increases the signal-to-noise ratio, but may also increase signal distortion.

The effectiveness of ICA and other spatial filters depends to an appreciable extent on the sensor used to make the recordings. Ideally, the sensor should deploy a large number of channels, arranged such that the resulting spatial patterns of the signal and the various interferences are as distinct as possible. In this ideal scenario, conventional ICA should be able to separate the signal with minimal distortion. In practice, however, the sensor design is often dictated by technical and/or cost constraints, and the method proposed here can be of significant benefit. The method may also be useful for fECG, which typically uses a smaller number of channels.

In summary, we have demonstrated a useful refinement of ICA that overcomes the problem of signal distortion that has limited its utility for assessment of fetal rhythm. The method is very simple to implement and is suitable for routine processing of fMCG recordings.

Biographies

Suhong Yu was born in Sichuan, China. She received the B.S. degree in materials physics, in 2006, from Sichuan University, China, and the M.S. degree in physics from Northern Illinois University, DeKalb, Illinois, in 2009. Since then, she is working toward the Ph.D. degree in the Department of Medical Physics at the University of Wisconsin, Madison, Wisconsin.

She was in a one-year exchange program at the University of Washington-Seattle, in 2005. Her research interests include biomedical signal processing with an emphasis on fetal magnetocardiography.

Ronald T.Wakai’s (M’xx) photograph and biography not available at the time of publication.