Abstract
Case-ascertained household transmission studies, in which households including an ‘index case’ are recruited and followed up, are invaluable to understanding the epidemiology of influenza. We used a simulation approach parameterized with data from household transmission studies to evaluate alternative study designs. We compared studies that relied on self-reported illness among household contacts versus studies that used home visits to collect swab specimens for virologic confirmation of secondary infections, allowing for the trade-off between sample size versus intensity of follow-up given a fixed budget. For studies estimating the secondary attack proportion, 2–3 follow-up visits with specimens collected from all members regardless of illness were optimal. However, for studies comparing secondary attack proportions between two or more groups, such as controlled intervention studies, designs with reactive home visits following illness reports in contacts were most powerful, while a design with one home visit optimally timed also performed well.
INTRODUCTION
Influenza virus is associated with a substantial global burden of morbidity and mortality, yet many characteristics of the disease are poorly understood including transmissibility and its relations with viral shedding during infection, factors affecting infectiousness and immunity, and the effectiveness of interventions to reduce transmission. Households are important in influenza epidemiology (1), and it has been estimated that around a third of all influenza transmission occurs in households (2). Historically, household studies have provided invaluable insights into influenza epidemiology (3), while recent household studies have investigated the effectiveness of antiviral treatment and prophylaxis (4–8), hand hygiene (9–11), face masks (10–13), and transmissibility of seasonal influenza (14) and 2009 pandemic influenza A (H1N1) (15–22).
There are two main types of design for household studies. A cohort of initially uninfected households can be recruited and then followed up through periods of influenza activity (3,23). While this is regarded as a gold standard for influenza household studies, this design can be extremely resource intensive because the expected number of households in which an infection occurs is relatively small. Alternatively, households can be enrolled in a study once influenza infection is identified in one member (an ‘index’ case), and followed up to observe secondary infections. The latter design is termed a case-ascertained design (24), and is the focus of this paper. Case ascertained studies are believed to be the most efficient method of assessing secondary transmission of influenza because smaller sample sizes are required to observe an equivalent number of secondary infections as compared to a cohort study. In case-ascertained studies, influenza transmission is typically measured via the secondary attack proportion (SAP), defined as the proportion of household contacts that are infected with influenza virus from the index case (15).
While some case-ascertained studies rely entirely on self-reports of symptoms and signs associated with acute respiratory illnesses (12–17), repeated home-visits can be arranged to collect specimens and allow virologic confirmation of influenza virus infections (10,11,19–22). Since secondary cases shed detectable virus for 3–5 days after illness onset it is important to consider the number and timing of visits in order to maximize the number of secondary cases that can be virologically confirmed. However, home visits can be associated with significant costs and there is a resource trade-off between the number of home visits per household versus the total number of households that can be recruited given a fixed total budget for fieldwork.
Selecting an appropriate study design is part of Good Clinical Practice and use of suboptimal designs could squander research funding and put participants at unnecessary risk and inconvenience. In this manuscript we evaluate which study designs make most cost-effective use of resources for accurately and robustly estimating the SAP in a transmission study, and for maximising statistical power in a comparative study.
METHODS
As a basic scenario, we consider case-ascertained studies of household transmission of influenza virus where index cases are recruited after presentation at a study clinic. In this scenario, relatively inexpensive point-of-care rapid tests which can detect influenza virus infection with moderate sensitivity and high specificity (25) are used to identify index cases with influenza. For those index cases with a positive rapid test result, an initial home-visit would be conducted as soon as possible to collect laboratory specimens from all household contacts to determine whether there were any co-primary cases. If a co-primary case were found, the family would not be enrolled in the study (10,26). A series of additional home-visits might be conducted at later dates to collect further specimens for virologic confirmation of secondary cases. Symptom diaries would also be provided to household members to permit self-reporting of signs and symptoms associated with acute respiratory illness. We define acute respiratory illness (ARI) as presence of 2 of the following symptoms: fever (≥37.8 °C), cough, headache, sore throat, or myalgia, and influenza-like illness (ILI) as temperature (≥37.8 °C) plus cough or sore throat (10,21). ILI is a more specific but less sensitive indicator of acute influenza virus infection than ARI (10,21,27).
Transmission study
In a transmission study primary interest is in estimating the household SAP. If home visits are not logistically feasible, studies based on self-reported secondary cases can be conducted (14,15). However no clinical definition of influenza has high sensitivity and high specificity and therefore estimates of the SAP based on clinical definitions may not accurately or robustly measure the true SAP (10,21,27). If feasible, home visits are an important component of a design to allow virologic confirmation of secondary cases. It is also possible to restrict home visits to households where contacts report illness (5–7). Since sample size calculations without any home visits are straightforward using standard methods, here we focus on comparing transmission studies with one or more follow-up visits versus the use of ILI or ARI among contacts to trigger home visits, or clinical outcome definitions alone.
Comparative study
In a typical comparative study, one or more active intervention is compared with a control. In these studies primary interest is usually in comparing the effectiveness of interventions on household SAPs with a measure such as the incidence rate ratio, the relative risk, or the odds ratio, and studies would be designed to allow moderate to high power to detect intervention effects. In this scenario virologic confirmation of secondary cases might be less important since intervention effects might still be identifiable in comparisons of clinical outcomes between arms. We compare two-arm comparative studies with no follow-up visits, visits triggered by ARI or ILI, or one or more follow-up visits regardless of illness.
Sources of data
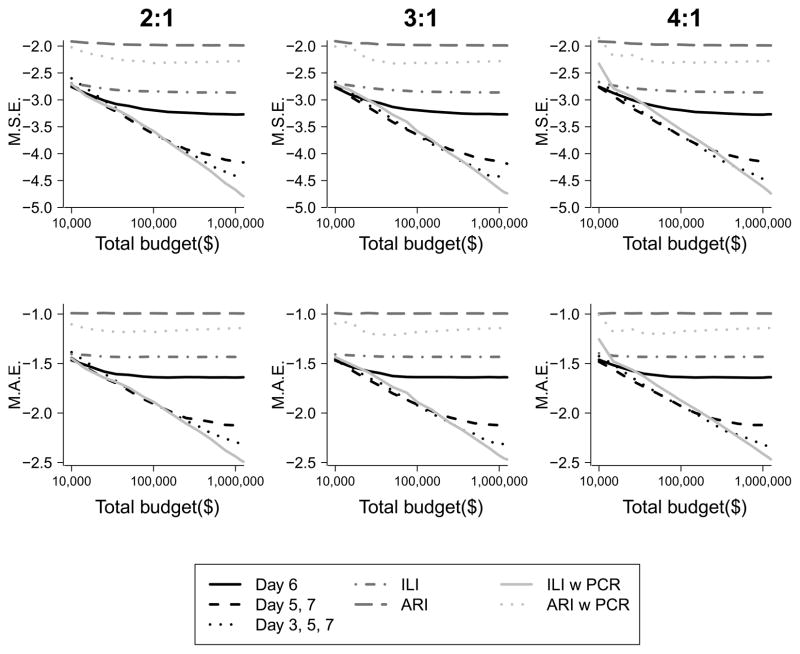
To permit simulation of alternative study designs, some basic parameters are required which characterise influenza transmission in households (Table 1). We assumed that in addition to the index case there are three additional household members. We assumed that an index case is seen in a clinic and a subsequent home-visit confirms that the remaining household members are negative within 24 hours of symptom onset of the index case. We also assumed that there is no within-household tertiary transmission because tertiary transmission is relatively rare and should have little effect on the estimation of the SAP. Costs are also required, since an optimal design must trade off the total sample size with the number of follow up visits. We specified the recruitment and enrollment costs per household as CE and the cost of a home visit as CV. In a previous study in Hong Kong, CE was three times as much as CV (Table 1). In sensitivity analyses we also considered ratios of 2:1 and 4:1. With a fixed fieldwork budget of C, the total number of households n that can be recruited depends on the number of follow-up home visits v and can be calculated via the formula n = C/(CE + vCV).
Table 1.
Epidemiological parameters.
| Parameter | Value | Source |
|---|---|---|
| Serial Interval for influenza | Weibull distribution with mean 3.2 days | (21) |
| SAP Control Group | 10% | Assumed |
| SAP Intervention Group | 5%, 7.5% | Assumed |
| Total Number of People per Household | 4 | Assumed |
| Specificity of RT-PCR | 100% | Assumed |
| Sensitivity of ARI compared to virologically-confirmed infection | 68% | (10) |
| Specificity of ARI compared to virologically-confirmed infection | 86% | (10) |
| Sensitivity of ILI compared to virologically-confirmed infection | 40% | (10) |
| Specificity of ILI compared to virologically-confirmed infection | 98% | (10) |
| Cost of recruiting an index case | US$360 | (personal communication, BJ Cowling) |
| Cost of a home visit | US$120 | (personal communication, BJ Cowling) |
Statistical analysis
We reanalyzed data on viral shedding during illness associated with natural influenza virus infection (10,28). The probability of virologic confirmation by RT-PCR was estimated using logistic regression with a cubic spline term for time since illness onset.
For transmission studies, accurately estimating the SAP is of primary importance. Consequently as a design with only one home visit will miss more infections than those with more home visits, studies with more home visits will be less biased than those with fewer home-visits. However, this should come at the cost of greater variance in parameter estimates due to the reduced sample size. Therefore the choice of more home visits relative to decreased overall sample size should represent a bias-variance tradeoff. We examined the overall efficiency of estimation by estimating the mean squared error (MSE) and mean absolute error (MAE) of the SAP under each design. The MSE and MAE are both measures of the expected difference between the estimate of a parameter and the actual parameter value, and a smaller MSE or MAE indicates greater precision and less bias.
For comparative studies, we estimated the power of each potential design to detect a specific treatment effect in terms of a reduction in the estimated SAP in the intervention versus the control group, expressed as an odds ratio. To calculate power, a logistic generalized estimating equation (29) accounting for within family correlations was fitted to the simulated data. The statistical power was estimated as the number of simulated datasets in which the intervention effect was identified at a significance level of p≤0.05.
Due to the non-linearities in transmission dynamics we used a simulation approach to compare alternative study design variants (30). For each study design variant we used a Monte Carlo approach to simulate a set of 2,500 datasets. The MSE and MAE or power of each variant were evaluated by statistical analysis of the set of 2,500 simulated datasets and compared across design variants. Further technical details are provided in the Appendix.
Sensitivity analyses
In addition to examining the sensitivity of our results to costs as described above, we also examined how a shorter serial interval of mean 2.6 days (15,31,32) or a longer serial interval of mean 3.6 days (33) would affect our results.
RESULTS
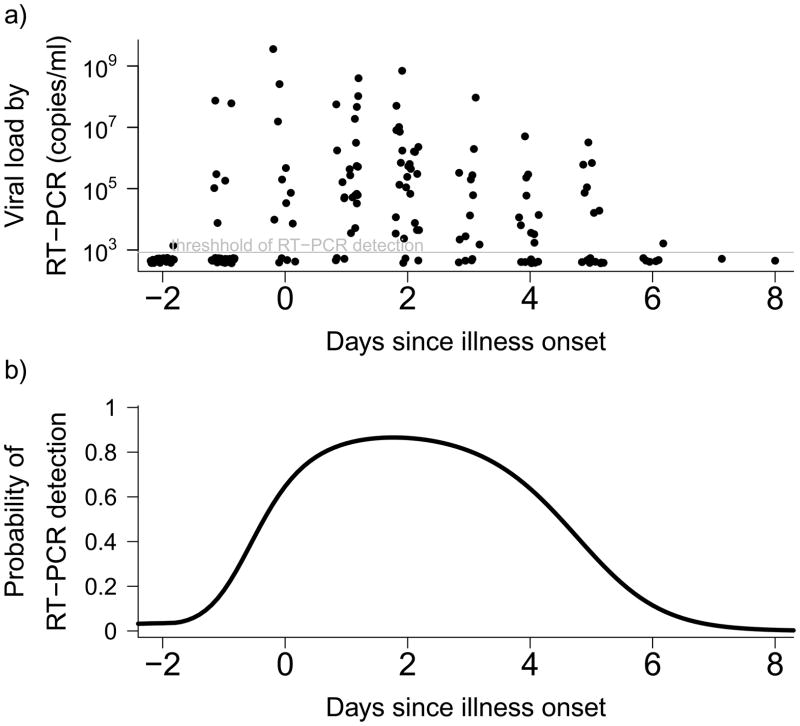
We parameterized our simulation model using results from the literature and analyses of data from a household study (Table 1) (10,28). In a secondary analysis of data from a field study, we estimated that the probability of virologic confirmation of infection was highest when specimens were collected within 1–3 days of illness onset (Figure 1).
Figure 1.
(a) Intensity of viral shedding associated with influenza A virus infections, and (b) probability of virologic confirmation of influenza A virus infection in a subject by day of collection of a nose and throat swab. Based on data from (28).
Transmission studies
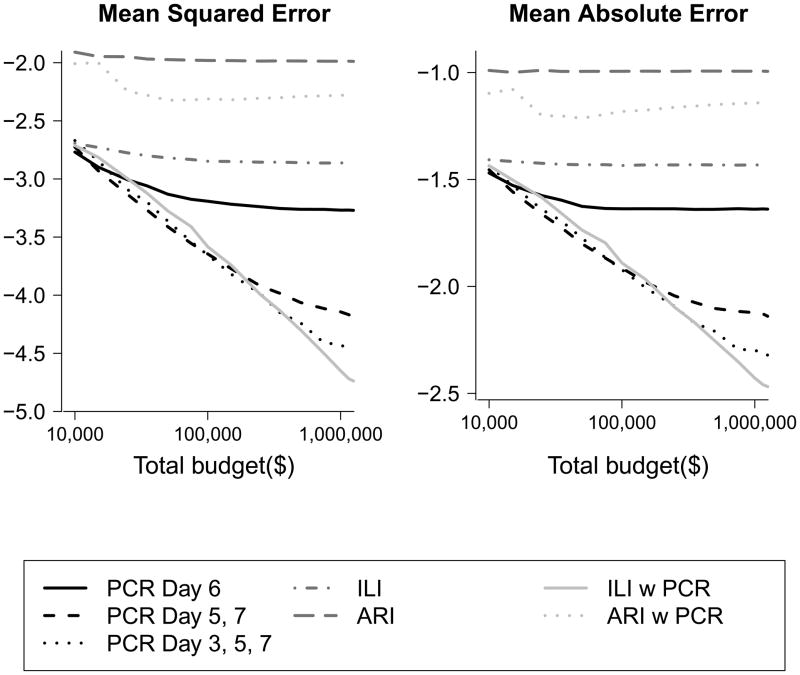
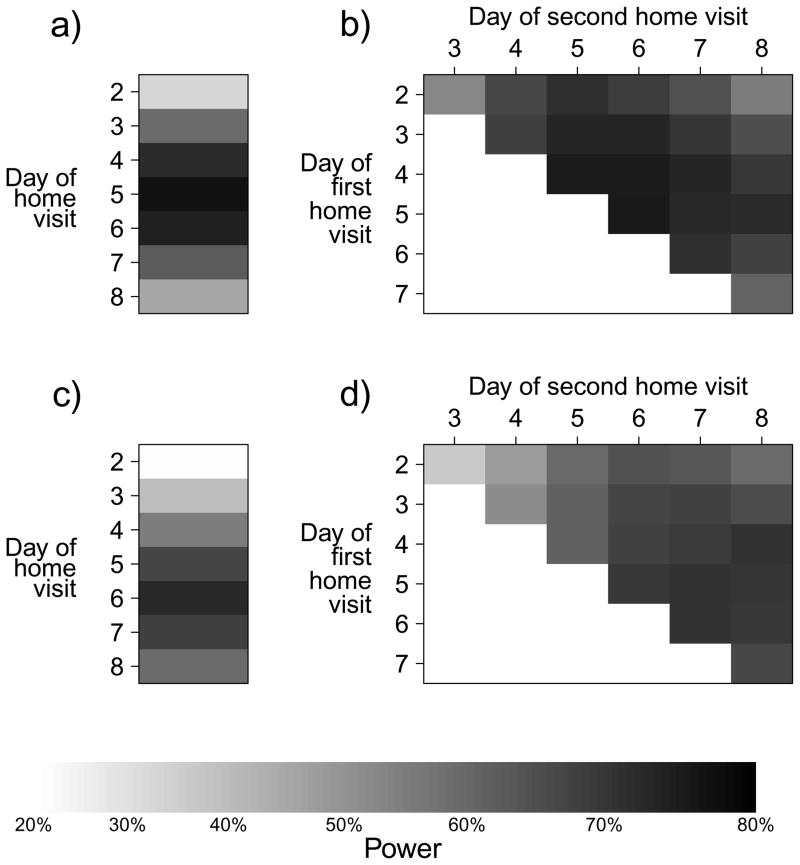
We examined the optimal timing of home-visits for a transmission study with one or with two home visits. We found that the optimal timing was 6 days from ARI onset in the index case for a one visit design, 5 and 7 days from ARI onset in the index case for a two home-visit design and 3, 5, and 7 days for three-home visit design. We found that as the study budget increased, designs with two and then three home visits led to the lowest MSE and MAE, and this was robust to differences in the CE:CV ratio (Figure 2). As total study budget increases, designs with four, five, and even more home visits would become optimal in terms of reducing the MSE (data not shown). We also found that studies with more home-visits performed substantially better in terms of MSE and MAE than those using only using the self-reported clinical outcomes of ILI and ARI. Using ILI to trigger home visits appeared to be as accurate as conducting home visits for all families regardless of illness.
Figure 2.
Estimated mean squared error (MSE) (left) and mean absolute error (MAE) (right) of the SAP for varying transmission studies. For a given budget, lower values of MSE and MAE indicate better designs. The black lines represent study designs involving home visits with subsequent virological confirmation for all families on the specified days, the medium grey lines represent self-report of ILI or ARI without virological confirmation, and the light gray lines represent home visit with subsequent virological confirmation when an ARI or ILI is reported within a family.
Comparative studies
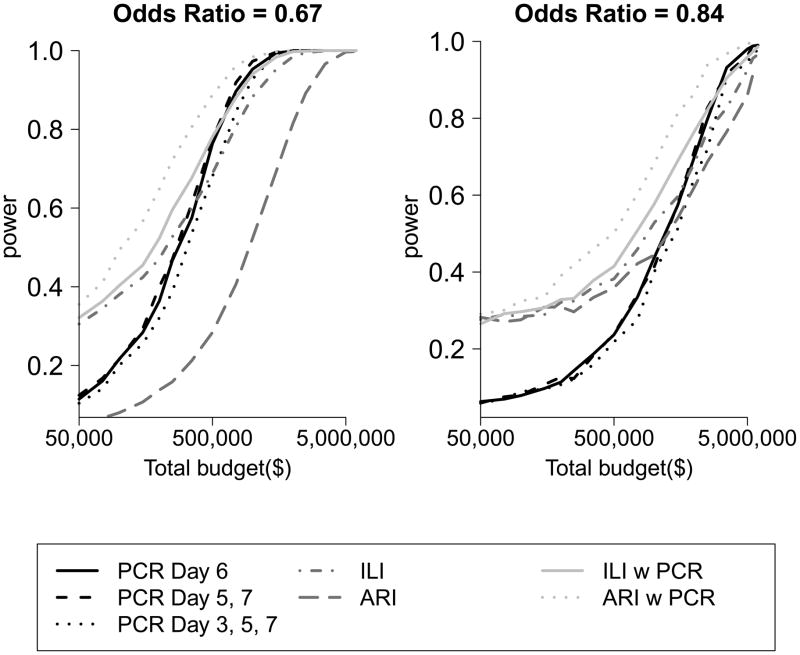
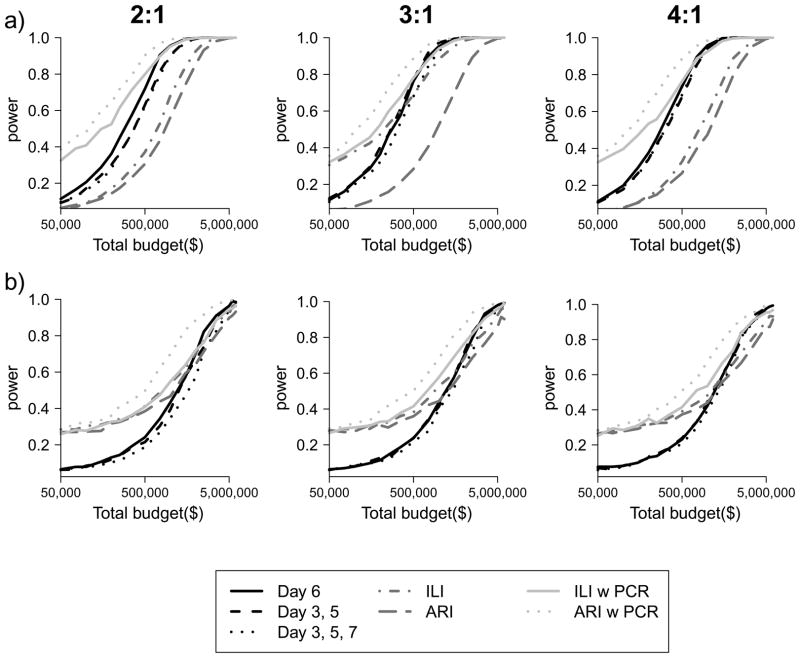
For a comparative study we found that the optimal visit timing was 6 days from ARI onset in the index case for a one visit design, 5 and 7 days from ARI onset in the index case for a two home-visit design (Figure 3) and 3, 5, and 7 days for three-home visit design. For the comparative study, a design in which a home-visit occurs after being triggered by ARI in a family member was most powerful. Among designs where visits were conducted to swab all participants regardless of illness, a design with one home visit on day 6 was most powerful to detect an overall difference in the SAP between the control and intervention groups (Figure 4). However, differences in power between designs with one home visit and multiple home visits were very small, particularly as the cost of home visits decreased relative to the cost of enrolment.
Figure 3.
Power of comparative study designs with alternative home visit schedules by days since ARI onset in the index case for (a) studies with one home visit and (b) studies with two home visits.
Figure 4.
Power of alternative designs for comparative studies with respect to (a) an odds ratio of 0.67 (true relative risk of 0.7) and (b) an odds ratio 0.84 (true relative risk of 0.85). The black lines represents home visits with subsequent virological confirmation for all families on the specified days, the medium grey lines represent self-report of ILI or ARI without virological confirmation and the light gray lines represent home visit with subsequent virological confirmation triggered by reports of ARI or ILI by a household contact.
Designs with home visits outperformed those relying solely on the self-reported clinical outcomes of ARI and ILI. Finally, studies based on the ILI outcome had higher power than those based on ARI.
Sensitivity analyses
Using a serial interval with mean 2.6 or 3.6 days resulted in the optimal timing of visits being shifted slightly earlier or later respectively but that the patterns in terms of the optimal strategy for visits remained similar. For example, for a comparative design the optimal timing with a serial interval with mean 2.6 days was day 5 for one visit and days 4 and 6 after illness onset for 2 visits, while for a serial interval with mean 3.6 days it was 6 days for one visit and 5 and 7 days after illness onset for 2 visits.
DISCUSSION
Careful consideration is necessary when planning case-ascertained studies of influenza transmission. If the aim of a study is to assess the household SAP, then conducting more than one home visit in most circumstances would be optimal (Figure 2). In the case of a study comparing SAPs between two or more groups, such as a controlled trial, the optimal design would be to have one home visit on day 6. However, the differences in power between designs with one visit or multiple visits were relatively small (Figure 4). Our results would suggest that given a reasonable cost per home visit, the use of home-visits is a cost-effective strategy as compared to relying solely on clinical diagnosis of influenza from self-report data. If resources for home visits were limited, ARI or preferably ILI could be used to trigger home visits (Figure 3) and this method performs well. In comparative studies based on clinical outcomes alone, ILI was associated with greater power than ARI because of the very high specificity of ILI case definition.
Despite the number of clinical and epidemiological studies using longitudinal (repeated measure) designs, there is little literature discussing the optimal choice of the number of repeated measurements (34). The majority of work considering the design of randomized controlled trials with repeated measurements treats the number of repeated measurements as a fixed and known aspect of design (35,36). Of the few studies which have treated the number of repeated measurements as a variable to be optimized, Winkens et al (37) consider the optimal number of repeated measurements when treatment outcomes are linearly divergent while Cook et al (38) considered the optimal choice of measurements in epidemic processes. Those approaches are not directly applicable to the scenarios described in this paper because the probability of influenza infection and subsequent detection is highly non-linear with regard to time since infection (Figure 1). While our work is specific to household transmission of influenza virus, the results may generally translate to similar studies of other respiratory viruses such as rhinovirus and respiratory syncytial virus, provided that corrections are made for their specific natural history (39).
Throughout all simulations the use of ARI or ILI to trigger home visits performed as well or better than the use of home visits for all families. One caveat is that in that scenario some illnesses might not be reported leading to missed infections, while symptom diaries might be completed more meticulously if household members knew that home visits would be conducted regardless of illness. One other possibility is to invite participants to swab themselves during follow-up to reduce the cost of a home visit but maintain a virologic outcome. We did not include self-swabs in our analyses as we could not find any data on the sensitivity of self-swabs compared to swabs collected by experts.
The optimal timing of home visits depends on the serial interval, which determines when infected secondary cases will on average have illness onset, and also depends on the probability of virologic confirmation of infection by day since illness onset. In a novel analysis of secondary data we showed that the probability of virologic confirmation of an infection is highest if swabs are taken on days 1–3 of illness (Figure 1). While we compared study designs in terms of time since index case illness onset, in some protocols timing is specified as time from enrollment of a family and if enrollment is completed on average 24 or 48 hours after symptom onset, then one or two days should be subtracted to calculate optimal timing of visits after enrollment. Figure 3 shows that home visit timings of around 4 to 7 days after symptom onset after work reasonably well. While the optimal timing may seem late compared to the mean serial interval, it should be noted that later follow-up visits allow the detection of secondary cases with earlier infection (who are still shedding detectable virus) as well as those with later infection.
Our study has practical limitations when considering its application to the planning of future studies. First, our results on the optimal timing of visits depend on estimates of the serial interval and the duration of detectable viral shedding. We have focused on studies of influenza A epidemiology. Studies including influenza B should consider how differences in viral shedding (28,40) and other epidemiologic characteristics might affect these conclusions. Second, future improvements in the cost or accuracy of laboratory methods could change the optimal number of home visits. Third, we would caution that although it appears diagnosis of influenza based on self-report provides less power than influenza detection through home-visits and subsequent RT-PCR, clinical influenza may be the only feasible outcome measure in some settings, and an important primary outcome in studies such as antiviral prophylaxis if the aim were to reduce illness among household contacts rather than prevent infection. We incorporated alternative assumptions about the relative costs of enrollment and follow-up, but other logistical considerations may play a role in study design. For example if only one clinic is available for recruitment then a study with many home visits and a smaller sample size might be preferred, but the reverse could be true if community nurses capable of conducting home visits were in short supply. If paired sera were available from baseline (pre-infection) and convalescence (21–28 days after infection), comparison of antibody titers could provide serologic confirmation of infection, although it can be challenging to obtain sera from participants in community studies. Finally, Yang et al. (24) noted that in simulation studies that direct randomization of family members rather than cluster randomization of families would be more powerful. However, this is not always possible, for example in studies where non-pharmaceutical interventions or antiviral treatments are given to the index case to try to reduce onwards transmission.
Despite these potential limitations, our results should serve as useful guidelines for researchers planning future case-ascertained studies of influenza transmission and control. Our findings illustrate that if feasible, collection of specimens for virologic testing can be a cost-effective use of resources.
Appendix Figure 1.
Estimated mean squared error (MSE) (above) and mean absolute error (MAE) (below) of the SAP for varying transmission studies for varying ratios of enrollment costs (CE) to visit costs (CV) 2:1, 3:1 and 4:1. For a given budget, lower MSE and MAE indicate better designs.
Appendix Figure 2.
Power of a comparative study design associated with alternative timing of home visits by days since ARI onset in the index case assuming a serial interval with mean 2.6 days for (a) designs with one home visit and (b) designs with two home visits; and assuming a serial interval with mean 3.6 days for (c) designs with one home visit and (d) designs with two home visits.
Appendix Figure 3.
Power of alternative designs for comparative studies with respect to (a) odds ratio of 0.67 (relative risk = 0.7) and (b) odds ratio of 0.84 (relative risk = 0.85) with ratios of enrollment costs (CE) to visit costs (CV) 2:1, 3:1, and 4:1.
Acknowledgments
We thank Lincoln Lau for technical assistance. This work received financial support from the Research Fund for the Control of Infectious Disease, Food and Health Bureau, Government of the Hong Kong SAR (grant no. HK-10-04-05), the Area of Excellence Scheme of the Hong Kong University Grants Committee (grant no. AoE/M-12/06) and the Harvard Center for Communicable Disease Dynamics from the National Institute of General Medical Sciences (grant number 1 U54 GM088558). BK is supported by a Hong Kong PhD Fellowship from the Research Grants Council, Hong Kong. The funding bodies were not involved in the collection, analysis and interpretation of data, the writing of the manuscript, or the decision to submit for publication. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.
Technical Appendix for: Optimal design of studies of influenza transmission in households I: case-ascertained studies
We used a simulation approach to evaluate alternative study designs for case-ascertained household influenza transmission studies, in which households including an ‘index case’ are recruited and followed up. In our simulations, we assumed that in each family one index case was indentified and that there were no co-primary infections. Furthermore, we assume all families had besides the index case 3 susceptible, initially uninfected family members. Once enrolled, we compared designs which used one of three alternative methods to identify subsequent secondary influenza infections: regular home visits with virological confirmation of secondary infections for all families, diagnosis based solely on certain self reported signs and symptoms, or home visits and virological confirmation only in the event of (i.e. triggered by) certain self reported signs and symptoms. We defined acute respiratory illness (ARI) as presence of 2 of the following symptoms: fever (≥37.8 °C), cough, headache, sore throat, or myalgia, and influenza-like illness (ILI) as temperature (≥37.8 °C) plus cough or sore throat. Our data and assumptions regarding the sensitivity and specificity of virological confirmation and ARI and ILI case definition are given in Table 1 and Figure 1 in the main text.
For both transmission and comparative studies, we ran simulations for studies with a wide range of total fieldwork budgets. For each fixed fieldwork budget C the sample size was determined based on the calculation n = C/(CE + vCV) where v is the number of home visits. For the CE:CV ratios of 2:1, 3:1, 4:1 CE was US$320, US$360, US$384 and CV was US$160, US$120, and US$96 respectively. The sum of CE and CV is US$480 in all cases and this is consistent with field budgets we have used in Hong Kong. In the case of planned, fixed home visits for all families v was known and fixed. For designs in which home visits are triggered v was considered to be the expected number of individuals per family reporting either ARI or ILI depending on the design (see Figure 2 and 4). For designs relying solely on self-report ARI and ILI without lab confirmation, we assume CV = 0 and therefore n = C/CE. Since each family has three uninfected individuals, there is a total study population of 3n individuals
Transmission study
For transmission we considered study budgets from US$10,000 to US$1,000,000. We adopted the following procedure to simulate infections within that study population.
Each uninfected individual had a probability of getting infected given by the secondary attack proportion = 0.1. Therefore in each simulation infection for each individual (3n in total) was simulated from a Bernoulli distribution with p = SAP.
If an individual was infected, we then take a stochastic realization from a Weibull distribution with parameters shape = 2.8 and scale = 3.6 (see Table 1). This realization was considered to be that individual’s symptom onset time.
The probability of detection given the particular method of detection was calculated via the probability of detection relative to time since symptom onset (Figure 1) for designs with home visits for all enrolled families or ARI and ILI sensitivity for those designs relying on ARI, ILI, ARI trigger, and ILI trigger (Table 1).
For designs, relying on ARI and ILI without virological confirmation, we also simulated the number of false positives. The probability of a false positive is 1–specificity. False positives were treated as true positive in the subsequent calculation the secondary attack proportion.
For designs which relied on home visits and virological confirmation for all families triggered by self report, the total number of home visits could vary stochastically based on the number of ILI or ARI episodes. If the number of home visits caused the study to be over budget, that is if n*Ce + total # home visits*Cv > C, we discarded this realization and repeated the simulation until the particular study budget given the number of home visits required was less than or equal to the allowed fieldwork budget.
Estimated secondary attack proportion was calculated as # tested positive (including false positives when it was possible)/3n.
This procedure was repeated 2500 times giving 2500 estimates of the secondary attack proportion. Using the 2500 individual estimates of the SAP, the mean squared error (MSE) was estimated based on the definition E[(true SAP - estimated SAP)2] and the mean absolute error (MAE) was estimated using its definition E[|true SAP -estimated SAP|]. These two measures were chosen because they both represent measures of the expected difference between true parameter value and the value of the parameters. The mean squared error is widely used and has the appealing property that it is also equivalent to the sum of the standard error plus the bias squared. While less widely used, various authors suggest that mean absolute error is appealing when considering non-convex loss functions. We show both metrics to illustrate the robustness of the results.
Comparative study
The total number of families enrolled, n, was calculated for a wide range of fixed field work budgets ranging from US$50,000 to US$5,000,000. The number of families per arm was n/2 and the total of number of individuals per arm was 3n/2. We adopt the following procedures to simulation infections within that study population.
The secondary attack proportion for the control group was 0.1
Relative risk between the intervention and control arms was defined as SAP in the intervention are divided by the SAP in the control arm. Therefore for a relative risk of 0.7 the SAP in the intervention arm was 0.07. Relative risks were converted into odds ratios using the following equation [(SAP intervention)/(1 - SAP intervention)]/[(SAP control)/(1 - SAP control)
Each uninfected individual had a probability of getting infected equal to the secondary attack proportion. Therefore in each simulation infection for each individual (3n) was simulated from a Bernoulli distribution with p = SAP.
If an individual was infected, we then take a stochastic realization from a Weibull distribution with parameters shape = 2.8 and scale = 3.6 (see Table 1). This realization was considered to be that individual’s symptom onset time.
The probability of detection given the particular method of detection was calculated via the probability of detection relative to time since symptom onset (Figure 1) for designs with home visits for all enrolled families or ARI and ILI sensitivity for those designs relying on ARI, ILI, ARI trigger, and ILI trigger (Table 1).
For designs, relying on ARI and ILI without virological confirmation, we also simulated the number of false positives. The probability of a false positive was 1–specificity. False positives were treated as true positive in subsequent calculation of the estimated odds ratio.
For designs which relied on home visits and virological confirmation for all families triggered by self report, the total number of home visits could vary stochastically based on the number of ILI or ARI episodes. If the number of home visits caused the study to be over budget, that is if n*Ce + total # home visits*Cv > C, we discarded this realization and repeated the simulation until the particular study budget given the number of home visits required was less than or equal to the allowed fieldwork budget.
A logistic general estimating equation model controlling for within household clustering was used to compare attack proportion between the control and treatment arm. The null hypothesis was that odds ratio corresponding to the intervention as compared to control was equal to 1. If a p-value of less than or equal to 0.05 was observed, the null hypothesis was rejected.
This procedure was repeated 2500 times. The statistical power was calculated as the number of times the null hypothesis was rejected at a significance level of 0.05, divided by 2500. All simulations were conducted in R version 2.10.1 (R Development Core Team, Vienna, Austria).
Footnotes
Disclaimer
BJC has received study funding from MedImmune Inc., a manufacturer of influenza vaccines. The authors report no other conflicts of interest. We declare that we have each participated in the conception, design, analysis and writing of the report and that we have read and approved the final version.
References
- 1.Carrat F, et al. Influenza burden of illness: estimates from a national prospective survey of household contacts in France. Archives of Internal Medicine. 2002;162:1842–8. doi: 10.1001/archinte.162.16.1842. [DOI] [PubMed] [Google Scholar]
- 2.Ferguson NM, et al. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448–52. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Monto AS, Koopman JS, Longini IM., Jr Tecumseh study of illness. XIII. Influenza infection and disease, 1976–1981. American Journal of Epidemiology. 1985;121:811–22. doi: 10.1093/oxfordjournals.aje.a114052. [DOI] [PubMed] [Google Scholar]
- 4.Hayden FG, et al. Inhaled zanamivir for the prevention of influenza in families. Zanamivir Family Study Group. New England Journal of Medicine. 2000;343:1282–9. doi: 10.1056/NEJM200011023431801. [DOI] [PubMed] [Google Scholar]
- 5.Monto AS, et al. Zanamivir prophylaxis: an effective strategy for the prevention of influenza types A and B within households. Journal of Infectious Diseases. 2002;186:1582–8. doi: 10.1086/345722. [DOI] [PubMed] [Google Scholar]
- 6.Hayden FG, et al. Management of influenza in households: a prospective, randomized comparison of oseltamivir treatment with or without postexposure prophylaxis. Journal of Infectious Diseases. 2004;189:440–9. doi: 10.1086/381128. [DOI] [PubMed] [Google Scholar]
- 7.Welliver R, et al. Effectiveness of oseltamivir in preventing influenza in household contacts: a randomized controlled trial. JAMA. 2001;285:748–54. doi: 10.1001/jama.285.6.748. [DOI] [PubMed] [Google Scholar]
- 8.van Boven M, et al. Transmission of novel influenza A(H1N1) in households with post-exposure antiviral prophylaxis. PLoS One. 2010;5:e11442. doi: 10.1371/journal.pone.0011442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cowling BJ, et al. Preliminary findings of a randomized trial of non-pharmaceutical interventions to prevent influenza transmission in households. PLoS One. 2008;3:e2101. doi: 10.1371/journal.pone.0002101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cowling BJ, et al. Facemasks and hand hygiene to prevent influenza transmission in households: a cluster randomized trial. Annals of Internal Medicine. 2009;151:437–46. doi: 10.7326/0003-4819-151-7-200910060-00142. [DOI] [PubMed] [Google Scholar]
- 11.Simmerman JM, et al. Findings from a household randomized controlled trial of hand washing and face masks to reduce in uenza transmission in Bangkok, Thailand. Influenza and Other Respiratory Viruses. 2011 doi: 10.1111/j.1750-2659.2011.00205.x. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.MacIntyre CR, et al. Face mask use and control of respiratory virus transmission in households. Emerging Infectious Diseases. 2009;15:233–41. doi: 10.3201/eid1502.081167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Canini L, et al. Surgical mask to prevent influenza transmission in households: a cluster randomized trial. PLoS One. 2010;5:e13998. doi: 10.1371/journal.pone.0013998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Viboud C, et al. Risk factors of influenza transmission in households. British Journal of General Practice. 2004;54:684–9. [PMC free article] [PubMed] [Google Scholar]
- 15.Cauchemez S, et al. Household transmission of 2009 pandemic influenza A (H1N1) virus in the United States. New England Journal of Medicine. 2009;361:2619–27. doi: 10.1056/NEJMoa0905498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.France AM, et al. Household transmission of 2009 influenza A (H1N1) virus after a school-based outbreak in New York City, April-May 2009. Journal of Infectious Diseases. 2010;201:984–92. doi: 10.1086/651145. [DOI] [PubMed] [Google Scholar]
- 17.Looker C, et al. Influenza A (H1N1) in Victoria, Australia: a community case series and analysis of household transmission. PLoS One. 2010;5:e13702. doi: 10.1371/journal.pone.0013702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Doyle TJ, Hopkins RS. Low secondary transmission of 2009 pandemic influenza A (H1N1) in households following an outbreak at a summer camp: relationship to timing of exposure. Epidemiology and Infection. 2010:1–7. doi: 10.1017/S095026881000141X. [DOI] [PubMed] [Google Scholar]
- 19.Papenburg J, et al. Household transmission of the 2009 pandemic A/H1N1 influenza virus: elevated laboratory-confirmed secondary attack rates and evidence of asymptomatic infections. Clinical Infectious Diseases. 2010;51:1033–41. doi: 10.1086/656582. [DOI] [PubMed] [Google Scholar]
- 20.Morgan OW, et al. Household transmission of pandemic (H1N1) 2009, San Antonio, Texas, USA, April-May 2009. Emerging Infectious Diseases. 2010;16:631–7. doi: 10.3201/eid1604.091658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cowling BJ, et al. Comparative epidemiology of pandemic and seasonal influenza A in households. New England Journal of Medicine. 2010;362:2175–84. doi: 10.1056/NEJMoa0911530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Suess T, et al. Shedding and transmission of novel influenza virus A/H1N1 infection in households--Germany, 2009. American Journal of Epidemiology. 2010;171:1157–64. doi: 10.1093/aje/kwq071. [DOI] [PubMed] [Google Scholar]
- 23.Monto AS, Koopman JS, Bryan ER. The Tecumseh Study of Illness. XIV. Occurrence of respiratory viruses, 1976–1981. American Journal of Epidemiology. 1986;124:359–67. doi: 10.1093/oxfordjournals.aje.a114406. [DOI] [PubMed] [Google Scholar]
- 24.Yang Y, Longini IM, Jr, Halloran ME. Design and Evaluation of Prophylactic Interventions Using Infectious Disease Incidence Data from Close Contact Groups. Journal of the Royal Statistical Society Series C (Applied Statistics) 2006;55:317–30. doi: 10.1111/j.1467-9876.2006.00539.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hurt AC, et al. Performance of six influenza rapid tests in detecting human influenza in clinical specimens. Journal of Clinical Virology. 2007;39:132–5. doi: 10.1016/j.jcv.2007.03.002. [DOI] [PubMed] [Google Scholar]
- 26.Sikora C, et al. Transmission of pandemic influenza A (H1N1) 2009 within households: Edmonton, Canada. Journal of Clinical Virology. 2010;49:90–3. doi: 10.1016/j.jcv.2010.06.015. [DOI] [PubMed] [Google Scholar]
- 27.Call SA, et al. Does this patient have influenza? JAMA. 2005;293:987–97. doi: 10.1001/jama.293.8.987. [DOI] [PubMed] [Google Scholar]
- 28.Lau LL, et al. Viral shedding and clinical illness in naturally acquired influenza virus infections. Journal of Infectious Diseases. 2010;201:1509–16. doi: 10.1086/652241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Diggle P. Analysis of longitudinal data. 2. xv. Oxford; New York: Oxford University Press; 2002. p. 379. [Google Scholar]
- 30.Moineddin R, Matheson FI, Glazier RH. A simulation study of sample size for multilevel logistic regression models. BMC Medical Research Methodology. 2007;7:34. doi: 10.1186/1471-2288-7-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ferguson NM, et al. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209–14. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]
- 32.White LF, et al. Estimation of the reproductive number and the serial interval in early phase of the 2009 influenza A/H1N1 pandemic in the USA. Influenza and Other Respiratory Viruses. 2009;3:267–76. doi: 10.1111/j.1750-2659.2009.00106.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cowling BJ, et al. Estimation of the serial interval of influenza. Epidemiology. 2009;20:344–7. doi: 10.1097/EDE.0b013e31819d1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vickers A. How many repeated measures in repeated measures designs? Statistical issues for comparative trials. BMC Medical Research Methodology. 2003;3:22. doi: 10.1186/1471-2288-3-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bloch DA. Sample size requirements and the cost of a randomized clinical trial with repeated measurements. Statistics in Medicine. 1986;5:663–7. doi: 10.1002/sim.4780050613. [DOI] [PubMed] [Google Scholar]
- 36.Lui KJ, Cumberland WG. Sample size requirement for repeated measurements in continuous data. Statistics in Medicine. 1992;11:633–41. doi: 10.1002/sim.4780110508. [DOI] [PubMed] [Google Scholar]
- 37.Winkens B, et al. Optimal number of repeated measures and group sizes in clinical trials with linearly divergent treatment effects. Contemporary Clininical Trials. 2006;27:57–69. doi: 10.1016/j.cct.2005.09.005. [DOI] [PubMed] [Google Scholar]
- 38.Cook AR, Gibson GJ, Gilligan CA. Optimal Observation Times in Experimental Epidemic Processes. Biometrics. 2008;64:860–8. doi: 10.1111/j.1541-0420.2007.00931.x. [DOI] [PubMed] [Google Scholar]
- 39.Okiro EA, et al. Duration of shedding of respiratory syncytial virus in a community study of Kenyan children. BMC Infectious Disease. 2010;10:15. doi: 10.1186/1471-2334-10-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Carrat F, et al. Time lines of infection and disease in human influenza: a reviewof volunteer challenge studies. American Journal of Epidemiology. 2008;167:775–85. doi: 10.1093/aje/kwm375. [DOI] [PubMed] [Google Scholar]