Counting RNA Pseudoknotted Structures

Abstract

In 2004, Condon and coauthors gave a hierarchical classification of exact RNA structure prediction algorithms according to the generality of structure classes that they handle. We complete this classification by adding two recent prediction algorithms. More importantly, we precisely quantify the hierarchy by giving closed or asymptotic formulas for the theoretical number of structures of given size n in all the classes but one. This allows us to assess the tradeoff between the expressiveness and the computational complexity of RNA structure prediction algorithms.

1. Introduction

The ab initio RNA structure prediction problem consists, given a RNA sequence, in finding a conformation that the molecule is likely to take in the cell. Condon et al. (2004) classified RNA structure prediction algorithms according to the inclusion relations between their classes of structures. The class of structures of a given algorithm is the set of structures that can, in theory, be returned by the algorithm. Condon et al. focused only on exact algorithms, that is, algorithms that guarantee to give an optimal solution to the structure prediction problem, stated as an optimization problem. They considered the class of pseudoknot-free structures (Nussinov et al., 1978; Zucker and Stiegler, 1981) (PKF) and the following classes for pseudoknotted structures: Lyngsø and Pedersen (2000) (L&P), Dirks and Pierce (2003) (D&P), Akutsu and Uemura (Akutsu, 2000; Uemura et al., 1999) (A&U), and Rivas and Eddy (1999) (R&E). They notably proved the following inclusion relations: P K F ⊂ L&P ⊂ D&P ⊂ A&U ⊂ R&E. Since then, two other exact prediction algorithms have been developed, involving new classes: Reeder and Giegerich (2004) (R&G) and Cao and Chen (2009) (C&C) algorithms.

In this article, we aim to quantify the tradeoff between the computational complexity and the expressiveness of all these algorithms. For this purpose, we compare them from the double point of view of their computational complexities and the cardinalities of their classes of structures, for a given size n. And we give closed or asymptotic formulas for the theoretical number of structures of given size n except for the class R&E. More precisely, we establish that, except for the L&P class whose asymptotic formula is simpler, the number of structures of size n is, asymptotically, 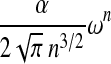, where α and ω are two constants which depend of the class. Table 1 summarizes our results.

Table 1.

Counting and Complexity Results

Class	Asymptotic	α	ω	Complexity	Remark
PKF		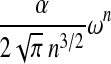2	4		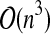Catalan numbers
L&P *		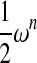—	4		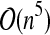Closed formula
C&C *		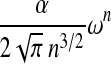1.6651	5.857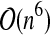
R&G *		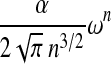0.1651	6.576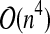
D&P *		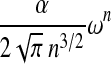0.7535	7.315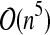
A&U *		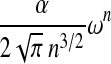0.6575	7.547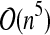
R&E	open	—	—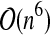
All		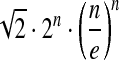—	—	NPC	Involutions with no fixed points

We indicate by “*” the classes that had not been counted before. The class “All” denotes the whole set of pseudoknotted structures. The row “Compl” gives the complexity of each algorithm.

Additionally, we place the two new classes, R&G and C&C, in Condon et al.'s hierarchy.

A number of works have been done on combinatorial enumeration of RNA structures without pseudoknots (Hofacker et al., 1998; Lorenz et al., 2008; Nebel, 2003; Vauchaussade de Chaumont and Viennot, 1985; Waterman, 1978) or, more recently, with pseudoknots (Huang and Reidys, 2008; Jin and Reidys, 2010; Rødland, 2006; Vernizzi et al., 2005), for instance. Our purpose is different, as our classes of structures are not defined per se, but correspond to given exact prediction algorithms.

The article is organized as follows. In Section 2, we give some notation and definitions. In Section 3, we present a bijection between the L&P class and a class of combinatorial planar maps, leading to a closed formula for the L&P class. In Section 4, we establish that each of the classes D&P, A&U, R&G, C&C, and L&P can be encoded by a context-free language. For each of them, we derive an equation for the generating function, leading to an asymptotic formula for the number of structures of size n. In Section 5, we conclude by giving some remarks on the expressiveness of the structure prediction algorithms compared to their complexity.

2. Definitions and Notation

An RNA secondary structure (possibly with pseudoknots) is given by a sequence of integers 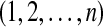and a list of pairs (i, j), called basepairs or arcs, where i < j and each number in 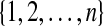appears exactly in one pair. Such a structure can be represented as in Figure 1, where each basepair (i, j) is represented by an edge between i and j. In real RNA structures there are unpaired bases, but we do not consider them.

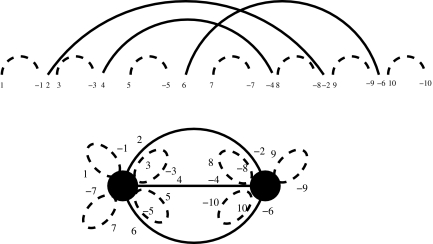
FIG. 1.

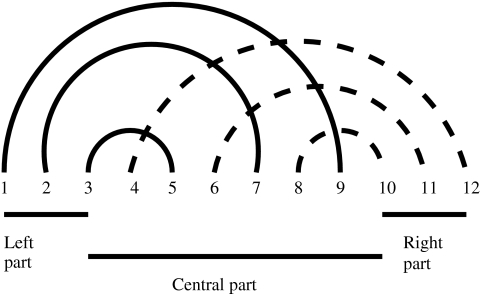
A pseudoknot given by the sequence 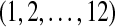and the arcs (1, 9), (2, 7), (3, 5), (4, 12), (6, 11), (8, 10). This pseudoknot is simple, with j₁ = 4 and j₂ = 9.

Definition 1 (Crossing arcs)

Let (i, j) and (k, l) two arcs such that i < k. We say that (i, j) and (k, l) are crossing if i < k < j < l.

Definition 2 (Crossing graph)

The crossing graph of an RNA structure is a graph G defined as follows: the vertices of G are the arcs of the structure, and two vertices are connected by an edge if and only if their two corresponding arcs are crossing.

Definition 3 (Pseudoknot)

A pseudoknot is a set of arcs that is not a singleton and that corresponds to a maximal connected component in the crossing graph.

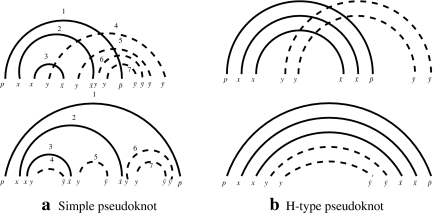
Definition 4 (Simple pseudoknot [Akutsu, 2000])

A pseudoknot P is simple if there exist two numbers j₁ and j₂, with j₁ < j₂, such that:

• • each arc (i, j) in P satisfies either i < j₁ < j ≤ j₂ or j₁ ≤ i < j₂ < j,

• • and if two arcs (i, j) and (i′, j′) satisfy i < i′ < j₁ or j₁ ≤ i < i′, then j > j′.

The first property ensures that, for each arc of P, one of its ends exactly is between j₁ and j₂. And the arcs are divided in two sets: those having their other end smaller than j₁, and those having their other end greater than j₂. We call these two sets, respectively, the left part and the right part of the pseudoknot. The second property of the definition ensures that two arcs in the same set cannot intersect each other. Figure 1 shows a simple pseudoknot.

Definition 5 (H-type Pseudoknot)

A H-type pseudoknot is a simple pseudoknot having the following additional property: each arc in one of the two above sets crosses all the arcs of the other set.

3. A Bijection Between the L&P Structures and a Class of Planar Maps

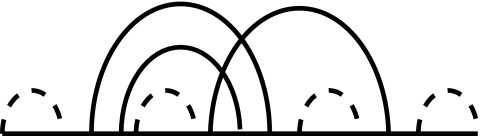
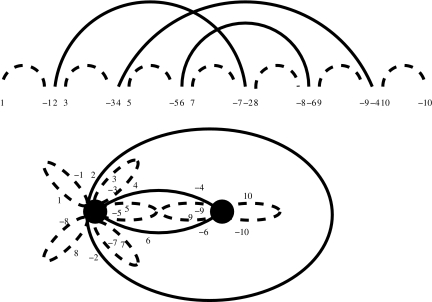
The Lyngsø-Pedersen (L&P) class is the simplest class of pseudoknotted structures. According to Condon et al. (2004) and Lyngsø and Pedersen (2000), a structure is in the L&P class if and only if it contains either no pseudoknot or a unique H-type pseudoknot, and this pseudoknot is not embedded under any arc (Fig. 2).

FIG. 2.

A structure from the L&P class.

Between any two consecutive ends of the arcs of the pseudoknots, there can be a nested structure. Theorem 1, and its straightforward Corollary 1, give the closed formula and the asymptotic formula for the number of such structures, respectively.

Theorem 1

The number of L&P structures with n arcs is:

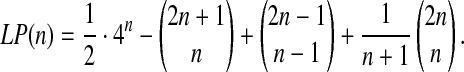Corollary 1

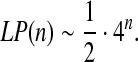Proof of Theorem 1

The proof is bijective: we establish a bijection between the set of L&P structures of any size n and the set of rooted isthmusless planar maps with n edges and one or two vertices. The first three terms of the formula count the number of such maps with two vertices (Sloane and Plouffe, 1995; Walsh and Lehman, 1975), while the last term, a Catalan number, counts the number of such maps with one vertex (Tutte, 1963). Hence the theorem.

A planar map is a proper embedding of a connected planar graph. It is said isthmusless if the deletion of any edge does not split the graph. A rooted planar map is a planar map where a vertex and an edge adjacent to it are distinguished.

A permutation of a given finite set of integer numbers is a bijection from this set to itself. A permutation σ can be represented by its set of cycles, that is the cycles of numbers 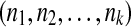such that σ(n_i) = n_i + 1 for any i between 1 and k − 1, and σ(n_k) = n₁.

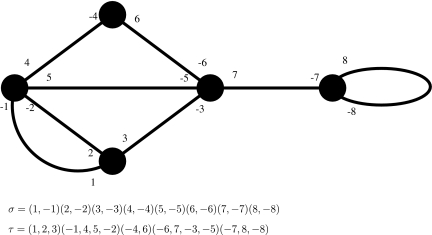
Any planar map with n edges can be represented by two permutations σ and τ on 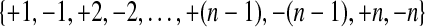, in the following way: the edges of the map are numbered from 1 to n. Then, for any edge i, one labels its extremities with +i and −i, respectively. By convention, the root edge is labelled with +1 and −1, in such a way that −1 labels the extremity adjacent to the root vertex. Now, the two permutations are as follows:

• • the permutation σ is an involution without fixed points that represents the edges of the map. Each cycle of σ is of size two and contains both ends of one edge:

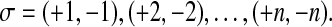
• • the permutation τ has as many cycles as vertices in the map. Each cycle is given by the sequence of labellings around the corresponding vertex, clockwise.

Figure 3 shows a planar map and two permutations that represent it. By convention, the drawing is such that the root edge separates the external face from an internal face.

FIG. 3.

A planar map and its two associated permutations σ and τ.

Let us consider a L&P structure S with n edges, and let us label the left extremities of its arcs with 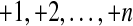from left to right, and give to each right foot the label −i if the corresponding left foot has label +i. Let 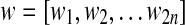be the sequence of labels of S, from left to right. From any w we can now construct two permutations σ and τ that represent an isthmussless rooted planar map with one or two vertices. Regarding σ, we just set .

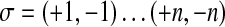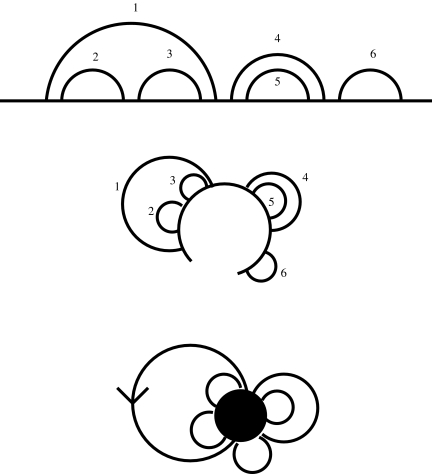
Let us first consider the simple case where there is no crossing in the structure. It is known for a long time that such nested structures are counted by Catalan numbers. This can be established, for example by a folkloric bijection with planar maps having one vertex, by setting σ as above, and τ = (w) (Fig. 4).

FIG. 4.

An illustration of the straightforward bijection between nested structures and planar maps with one vertex.

Now suppose that there is a pseudoknot in the structure, and let us present a bijection between the set of such structures and the set of rooted ithmusless planar maps with two vertices. Start from w. Since τ must have two cycles, we have to split w in two parts that will be the two cycles. Let us define the left set (resp. the right set) of arcs of the pseudoknot, respectively, as the set of arcs whose left (resp. right) extremities are in the left (resp. right) part of the pseudoknot, where left and right parts are defined as in Section 2. There are two cases:

Case 1

There is only one arc in the right set. In this case, let ℓ be the position of the first right extremity of an arc in the left set. We cut w between positions ℓ − 1 and ℓ. Each part corresponds to a cycle of 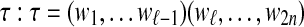(Fig. 5).

FIG. 5.

(Top) L&P structure corresponding to case 1. (Bottom) Corresponding planar map. Arcs not involved in the pseudoknot are drawn in dotted lines.

Case 2

There are at least two arcs in the right set. We cut w just before the first right extremity of an arc in the right set (Fig. 6).

FIG. 6.

(Top) L&P structure corresponding to case 2. (Bottom) Corresponding planar map. Arcs not involved in the pseudoknot are drawn in dotted lines.

Let us show that, in both cases, the resulting map is planar and isthmusless. At first, remark that if the map is not planar or has an isthmus, necessarily it comes from arcs that are involved in the pseudoknot. Indeed, by construction, non crossing arcs in the structure give non crossing loops in the map. So, without loss of generality, we can consider only structures where all the arcs are involved in the pseudoknot. Consider such a structure with n arcs. In the case 1, we have 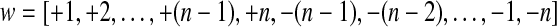, hence 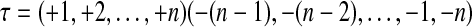. Clearly, this gives a planar map, since the two cycles of τ are in opposite order. And there is no isthmus because all edges go from one vertex to the other. In the case 2, we have 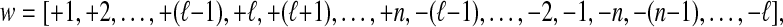, hence 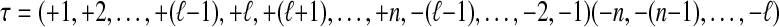. Again, this gives a planar map: edges 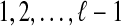are nested loops, and edges 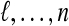go from one vertex to the other, without any crossing. And there is no isthmus because the number of edges going from one vertex to the other, n − ℓ + 1, is greater or equal to 2.

Now let us present the converse transformation. Consider an isthmusless rooted planar map with two vertices, given by 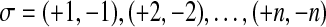and τ having two cycles. We aim to construct the sequence w that represents the corresponding pseudoknotted structure. Let us consider the cycle of τ which contains 1, and write it in such a way that it begins with 1. Let us call u this sequence of labels. This gives the first part of the sequence w. We are now searching for the second part of w, that is the sequence v such that uv = w. For that purpose, consider the set of isolated labels, that is the labels in u that have not their opposite label in u. We have the two following cases:

Case 1

There is no pair (+i, −i) in u such that the isolated labels are located between +i and −i. Let +j the penultimate isolated label in u. Write the second cycle of τ in such a way that it begins with −j. This gives v, and there is exactly one edge in the second part of the pseudoknot.

Case 2

There is a pair of labels (+i, −i) in u such that all isolated labels are located between +i and −i. Let +j the last isolated label in u. Write the second cycle of τ in such a way that it begins with −j. This gives v. In this case, there are at least two edges in the second part of the pseudoknot.  ▪

4. Asymptotic Enumeration of Pseudoknotted Structures

4.1. A context-free encoding for simple and H-type pseudoknots

As will be seen, all the classes that are involved in exact prediction algorithms but one involve either H-type pseudoknots or simple pseudoknots. The only exception is the R&E class. Here we define a transformation that allows to encode any class of pseudoknotted structures where all pseudoknots are simple by a context-free language.

Let us first recall some definitions. Let L be a language on a given alphabet A, and 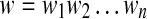a word of L, where the w_i's are the letters of w. A word v is a subword of w if 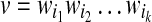, where 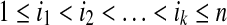. The projection of w onto an alphabet 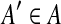is the subword w′ obtained by erasing in w all letters that do not belong to A′. The projection of L onto A′ is the set of projections of the words of L onto A′. Finally, let us recall that the Dyck language on any two-letter alphabet 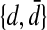is the language of balanced parentheses strings, where d and 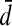stand, respectively, for opening and closing parentheses. Now we can state the two following straightforward lemmas:

Lemma 1

Any class of pseudoknotted structures where all pseudoknots are simple can be encoded by the words of a language L on the alphabet 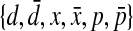where

• • d and 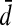encode, respectively, the left and right ends of arcs that are not involved in pseudoknots;

• • p and 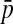encode, respectively, the left and right ends of the first arc involved in the left part of pseudoknots;

• • x and 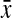encode, respectively, the left and right ends of arcs that are involved in the left parts of pseudoknots;

• • y and 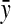encode, respectively, the left and right ends of arcs that are involved in the right parts of pseudoknots.

Additionally, the projection of the language to the alphabet 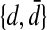(resp. 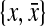, , 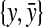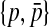) is a sublanguage of the Dyck language on the same alphabet.

Lemma 2

Let S be a pseudoknotted structure, and w be the word on 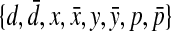that encodes S. Then every simple pseudoknot in S is encoded by a subword v of w, such that

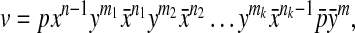where 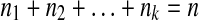and .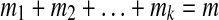

Remark that a H-type pseudoknot is a simple pseudoknot where k = 1. Thus every H-type pseudoknot in S is encoded by a subword 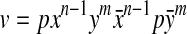. Finally, the following Proposition gives a way to encode any pseudoknotted structure where all pseudoknots are simple by a subset of the Dyck language with four kinds of pairs of parentheses, that is on the alphabet .

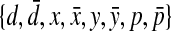Proposition 1

Let S be a pseudoknotted structure, and w be the word on 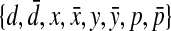that encodes S. Then w can be encoded by a word where every subword 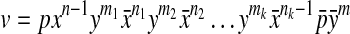, corresponding to a H-type pseudoknot is replaced with .

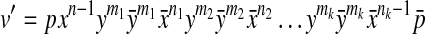In particular, every subword 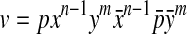corresponding to a simple pseudoknot is replaced with .

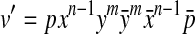Proof

The proof is straightforward, as there is an immediate one-to-one correspondance between the two kinds of words below. The transformation is illustrated in Figure 7 for simple pseudoknots and for the particular case of H-type pseudoknots.  ▪

FIG. 7.

(Top) Two pseudoknots and their encodings v. (Bottom) Corresponding nested structures and their encodings v′ given by Proposition 1. Full lines represent x and 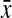, dotted lines represent y and .

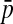4.2. Asymptotic results

For each of the D&P, A&U, R&G, and C&C classes, we give an asymptotic equivalent for the number of structures of size n. In each case, the proof is in three steps:

• 1. We design an unambiguous context-free grammar which generates the language that encodes the considered structures, according to Proposition 1.

• 2. From the grammar, we deduce an algebraic equation satisfied by the ordinary generating function (o.g.f.) of the language.

• 3. From this equation, we compute an asymptotic formula for the number of structures of size n.

For any class X&Y, we write X&Y(n) for its number of structures having n arcs.

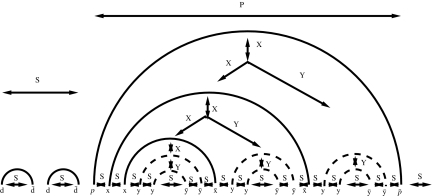
4.2.1. The Akutsu and Uemura class (A&U)

Following Akutsu (2000) and Condon et al. (2004), the A&U structures are composed of noncrossing edges and of any number of simple pseudoknots. As these pseudoknot can embed other substructures, which can be pseudoknotted in turn, they are said to be recursive (Akutsu, 2000).

Theorem 2

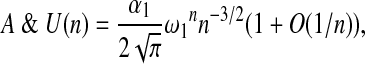where 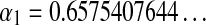, , 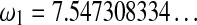are algebraic constants.

Proof

Let L_A&U be the language that encodes the A&U class, according to Proposition 1. The following unambiguous context-free grammar generates L_A&U:

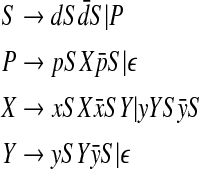The two rules in the first line allow to generate non crossing arcs and to place pseudoknots anywhere. The other rules generate words which correspond to the code for a simple pseudoknot as shown in Figure 8.

FIG. 8.

Building a structure with the grammar of L_A&U.

Given the grammar, we obtain the set of recursive equations for the o.g.f. of the various sets defined in the 1-to-1 encoding. Letting the formal symbol z denote an arc, we thus have through a straightforward translation:

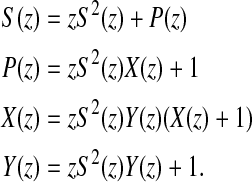By iterated bottom-up substitutions, we ultimately get that the o.g.f. S(z) is solution of the algebraic equation

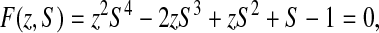(1)

from which we can derive the number of structures of size n.

For this proof, we present in some detail the main steps of the computations that have to be performed in order to get the asymptotics for an o.g.f. given by the algebraic implicit equation F(z, S) = 0 satisfied by the o.g.f. S(z). The foundations can be found in Flajolet and Sedgewick (2009).

Since ∂F/∂z∣_{z = 0,S = 1} = 1 is defined and ∂F/∂S∣_{z = 0,S = 1} = 1 is nonvanishing, z = 0 is not a singular point for S; by the implicit function theorem, S(z) exists as a regular function in a circular neighborhood of z = 0 where ∂F/∂S is non-zero. The degree in S of this bivariate equation being 4, and the coefficient a(z) of S⁴ satisfying a(0) = a′(0) = 0, this bivariate equation defines two folds z = ζ(S).

The radius of convergence ρ₁ of the o.g.f. S(z) is thus a solution of the system {F(z, S) = 0, ∂F/∂S(z, S) = 0}. At such a point, the local holomorphic solution z = ζ(S) is no longer invertible, which implies that this point is a singular point for the o.g.f. S(z).

Let (z = ρ₁, S = σ₁) be the point of the Riemann surface of the solution located on the fold issued from (z = 0, S = 1), that satisfies ∂F/∂S = 0 and that has the smallest modulus. This point is unique and located on the positive real axis, since the o.g.f. is indeed a function of z with all coefficients being positive. Since the first derivative, 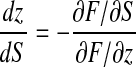vanishes at (z = ρ₁, S = σ₁) and the second derivative 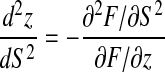is strictly positive, (z − ρ₁)^1/2 is well defined in a neighborhood of S = σ₁. At this point, the local expansion of z with respect to S writes:

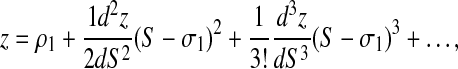(2)

and we get the Taylor expansion at S = σ₁:

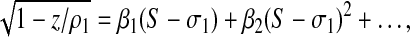(3)

with 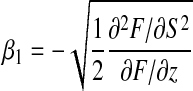. This equation can now be inverted locally, which yields:

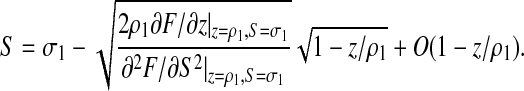(4)

This expansion can be calculated at any order, so that we obtain for the coefficients A&U(n) an infinite asymptotic development. The dominant term is given by the first square root in the previous expansion. Since it is well known that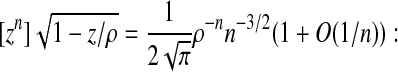

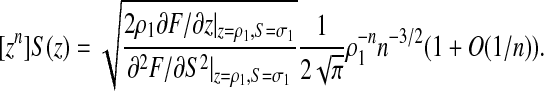(5)

We thus get the general form of the solution, as stated in the theorem, with 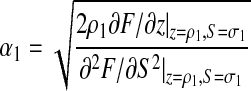and ω₁ = 1/ρ₁. In order to get the values for the constants in the expansions and for the radius of convergence, we used Maple. From Equation 1, we compute the partial derivatives ∂F/∂z = 2zS⁴ − 2S³ + S² and ∂F/∂S = 4 * z² * S³ − 6 * z * S² + 2 * z * S + 1. The system is too complex to be solved formally; so we lower the degree in S by considering the combination R = 4F − S∂F/∂S = −2zS³ + 2zS² + 3S − 4 which has to vanish at the points where F and ∂F/∂S do. Since R is of degree 1 in z, it is easy to get an expression for z that we substitute into ∂F/∂S, obtaining that 8S³ − 31S² +42S − 20 should equivalently be zero. Hence, we obtain 3 possible algebraic roots, one being real σ1 and the other two conjugate complex numbers. Only 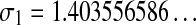and the associated real value of z for which 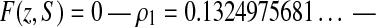are of interest. A direct approximate solution using the floating point solver of Maple confirms this situation, and a more involved study or the Riemann surface also yields 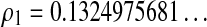to be the radius of convergence of the series. Further computations provide all the constants encountered in the proof and stated in the theorem.  ▪

4.2.2. The Dirks and Pierce class (D&P)

Structures of D&P class are characterized by the presence of noncrossing edges and any number of H-type pseudoknots (Condon et al., 2004; Dirks and Pierce, 2003).

Theorem 3

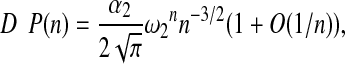where 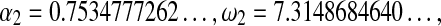, are algebraic constants.

Proof

The following unambiguous grammar generates the language that encodes the D&P structures, according to Proposition 1:

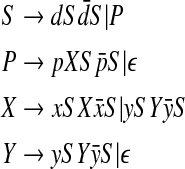The first line allows us to generate structures without pseudoknots and to place pseudoknots, by symbol P, anywhere in the sequence. The last three lines generate words which correspond to the code for H-Type pseudoknot. P generates the first arc of the left set. Other arcs in the left set can be generated by X. The symbol Y generates arcs of the right part.

From this grammar, we get the following algebraic equation:

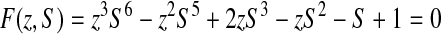(6)

which is very similar to the equation satisfied by the o.g.f. for the A&U family. We solve it in the same way, and find out the dominant singularity in 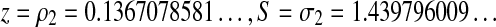, with the same local behaviour, implying similar asymptotics for the coefficients. The only problem encountered in finding this dominant singularity comes from the fact that there exists another singularity closer to the origin in 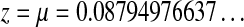, , 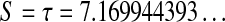but which is not on the same fold of the Riemann surface and which therefore does not have to be taken into consideration.  ▪

4.2.3. The Reeder and Giegerich class (R&G)

The R&G class which corresponds to the structures handled by Reeder and Giegerich's (2004) algorithms. It has a 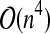time complexity.

Theorem 4

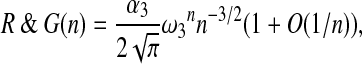where 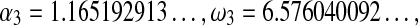, are algebraic constants.

Proof

In Reeder and Giegerich (2004), the following grammar is given (we removed the unpaired bases):

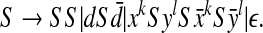This grammar is not context-free. However, we remark that the pseudoknot defined here is a particular case of a H-Type pseudoknot. So by applying Proposition 1 again, we define the following context-free grammar:

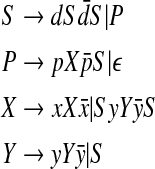The related algebraic equation

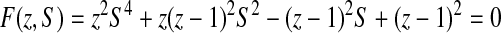(7)

is again very similar to the equation satisfied by the o.g.f. for the A&U family. We solve it in the same way, and find out the dominant singularity in 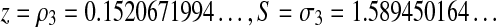, with the same local behavior, implying similar asymptotics for the coefficients.  ▪

Additionally, the following theorem places this new class into Condon et al.'s classification.

Theorem 5

R&G ⊂ D&P, L&P ∩ R&G = ∅ and R&G Ø L&P

Proof

The grammar that describes the pseudoknots in R&G is less general than the grammar for H-type pseudoknots. So R&G ⊂ D&P and L&P ∩ R&G ≠ ∅. As R&G structures can contain several pseudoknots, we have L&P ∩ R&G ≠ L&P.  ▪

4.2.4. The Cao and Chen class (C&C)

The C&C class corresponds to the structures handled by Cao and Chen's (2009) algorithm, whose complexity is .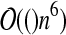

Theorem 6

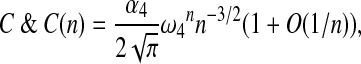where 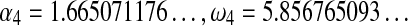, are algebraic constants.

Proof

The following non-context-free grammar generates the C&C structures:

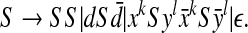It can be translated into a context-free grammar which is a restriction of the R&G grammar:

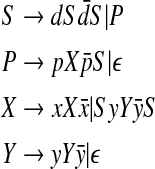Now the following algebraic holds for the o.g.f of C&C structures:

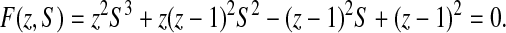(8)

Again, it is very similar to the equation satisfied by the o.g.f. for the A&U class. We solve it in the same way, and find out the dominant singularity in 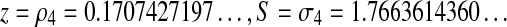, with the same local behaviour, implying similar asymptotics for the coefficients.  ▪

Additionally, we easily state that

Theorem 7

C&C ⊂ D&P, L&P ∩ C&C ≠ 0, C&C Ø L&P and C&C ⊂ R&G

4.2.5. The Lyngsø and Pedersen class (L&P)

We already gave a closed formula and an asymptotic equivalent for this class in Section 3. We briefly outline below another way to prove Theorem 1: we prove that any L&P structure can be encoded by a word of a nonambiguous context-free language.

Further standard computations lead to the generating function, then to the closed formula.

Theorem 8

The number of L&P structures of size n, L&P (n) satisfies the following asymptotics formula when n tends to infinity:

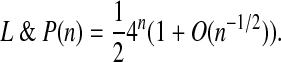Proof

Any L&P structure of size n can be encoded by a word of length n of the context-free language generated by the following nonambiguous grammar:

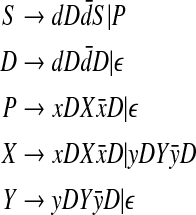The system of equations which the o.g.f. S(z) = Σ_nL&P(n)zⁿ satisfies, where n is the number of base pairs in contact deduces from the grammar:

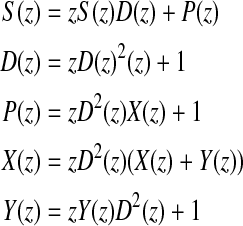The series D(z) is readily identified to be the o.g.f. for the Dyck language: 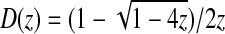. Contrarily to what we encountered previously, this system can now be solved explicitely, since all the other equations are linear and the system is clearly trigonal; so we get successively Y(z), X(z), P(z) and S(z), using repeatedly the fact that zD²(z) = D(z) − 1. Ultimately, we find:

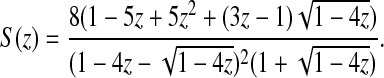The denominator vanishes for z = 0 and z = 1/4, but S(z) is not singular at the origin, since it has a Taylor development: S(z) = 1 + z + 3z² + 12z³ + 51z⁴ + 218z⁵ + 926z⁶ + 3902z⁷ + O(z⁸). Hence, S(z) has its dominant singularity in z = ρ₅ = 1/4 where it admits the following expansion in :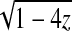

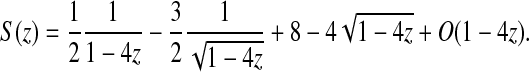Consequently, the coefficients of S(z) have the following asymptotic expansion:

  ▪

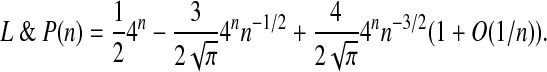5. Conclusion

We proved that most classes of pseudoknotted structures that can be predicted by exact algorithms (all but R&E for which the problem remains open) can be encoded by context-free languages. We extended Condon et al.'s (2004) hierarchy by adding two more classes, and we computed closed or asymptotic formulas for the cardinality of all classes but one.

These results, summarized in Table 1, allow us to quantify the relationship between the complexity of each algorithm and the generality of the class that it can handle.

Notably, from a strict quantitative point of view, the growth of complexity by a factor n² between the PKF and L&P classes seems not to be justified compared to the very small increase in cardinality.

At a first glance, the situation seems to be even worse for the C&C class, whose related algorithm has a stronger complexity than the R&G one, while C&C ⊂ R&G and the ratio of their cardinalities is exponential. However, the C&C algorithm computes the partition function with an elaborated thermodynamic model, and the R&G algorithm does not.

On the other hand, A&U and D&P have the same complexity, whereas the A&U class is exponentially larger than the D&P one. But D&P computes the partition function.

Finally, the linear increasing between PKF andR&G complexities seems very reasonable compared to the exponential increase of the cardinality.

Acknowledgments

This research was supported in part by the ANR project BRASERO ANR-06-BLAN-0045 and by the Digiteo project RNAomics.

Disclosure Statement

No competing financial interests exist.