Abstract
Motivation: A number of penalization and shrinkage approaches have been proposed for the analysis of microarray gene expression data. Similar techniques are now routinely applied to RNA sequence transcriptional count data, although the value of such shrinkage has not been conclusively established. If penalization is desired, the explicit modeling of mean–variance relationships provides a flexible testing regimen that ‘borrows’ information across genes, while easily incorporating design effects and additional covariates.
Results: We describe BBSeq, which incorporates two approaches: (i) a simple beta-binomial generalized linear model, which has not been extensively tested for RNA-Seq data and (ii) an extension of an expression mean–variance modeling approach to RNA-Seq data, involving modeling of the overdispersion as a function of the mean. Our approaches are flexible, allowing for general handling of discrete experimental factors and continuous covariates. We report comparisons with other alternate methods to handle RNA-Seq data. Although penalized methods have advantages for very small sample sizes, the beta-binomial generalized linear model, combined with simple outlier detection and testing approaches, appears to have favorable characteristics in power and flexibility.
Availability: An R package containing examples and sample datasets is available at http://www.bios.unc.edu/research/genomic_software/BBSeq
Contact: yzhou@bios.unc.edu; fwright@bios.unc.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Sequencing of RNA-based libraries (‘RNA-Seq’) can provide digital gene expression measurement, and is an attractive approach, potentially replacing microarrays for analyzing the transcriptome in an unbiased and comprehensive manner. For genes with very low or very high levels, microarrays often lack sensitivity, or can result in saturated signal. In contrast, RNA-Seq has been shown to have high accuracy across many orders of expression magnitude (Marioni et al., 2008), with clear advantages over microarray hybridization. At a basic level, simple counts of RNA sequences can be used for digital gene expression measurement, and are the subject of this article. Additional information derived from the sequences, such as de novo exon discovery, are beyond our scope, although many of the considerations here may be applied to the deeper study of sequence content.
RNA-Seq technology is currently more expensive than comparable array technologies, and thus the sample sizes are typically small. In addition, even as the cost of RNA-Seq profiling drops, the precision of the technology will enable sensitive investigation of small samples (for example, pairwise comparisons among many experimental conditions examined). Eventually, however, we expect that sequence-based transcriptional profiling will become the standard, with large datasets becoming affordable. Thus, there is a pressing need for sensitive statistical approaches that can accommodate large variation in the available sample sizes.
RNA-Seq count data consists of the number of instances that each transcript has been sequenced, arising from random sampling events for a large number of sequences (the library size). The simplest data model may be multinomial, with probability proportional to the true expression level. These probabilities are small and counts are accumulated over many reads, so Poisson approximations are commonly used. However, it has been repeatedly shown that RNA-Seq data are overdispersed (Robinson et al., 2010)—i.e. the variance of sequence counts tends to be greater than would be expected for multinomial or Poisson data. Thus, any careful analysis of the data, and in particular any differential expression analysis, must account for this overdispersion. Additional factors, such as the length of the transcript and potential sequencing bias, are important in performing inference on absolute expression levels, but here we are concerned primarily with comparison of expression values across different samples. Before proceeding to our testing framework, we briefly review the available methods for performing differential expression analysis for RNA-Seq data.
The package edgeR (Robinson et al., 2010) was initially designed as a penalized approach to identify differences between two sample groups. The current version has a variety of penalized overdispersion approaches, including ‘common’ penalized dispersion, a ‘tagwise’ approach that shrinks individual genes/tags and the tagwise procedure with a trend as a function of expression level. A negative binomial model is used, which essentially corresponds to an overdispersed Poisson model. The approach uses empirical Bayes methods to moderate the degree of overdispersion, with the aim of reducing error in a similar manner as penalized methods in microarray analysis (Smyth, 2004). The baySeq approach (Hardcastle and Kelly, 2010) is more explicitly Bayesian, also assuming negative binomially distributed count data, and can use the data to elicit a prior for the overdispersion parameters. BaySeq provides log posterior probability ratio for differential expression, rather than P-values, limiting its utility somewhat for standard multiple-testing approaches. The specification of multiple group comparisons is somewhat complicated, as all types of alternatives (in which some group subsets may be equivalently expressed) must be considered. The package DESeq (Anders and Huber, 2010) employs mean–variance estimation to produce moderated test statistics, which is similar to a model that we describe below. DEGseq does not accommodate overdispersion (Wang et al., 2010), and is not used here for our comparisons.
1.1 Are new methods necessary?
For RNA-Seq data, it is important to consider whether purpose-built procedures are necessary. Count data with overdispersion can be modeled using standard generalized linear models (GLMs) implemented in packages such as dispmod in R. The competing methods described here produce shrunken estimates of differential expression, which have been shown to be useful for microarray analysis. However, for RNA-Seq, we are not aware that the need for shrinkage or penalization has been carefully examined. An additional danger is posed by sample outliers, which are more likely to be encountered in large datasets, and for which the behavior of the existing approaches is unknown. Similarly, the presence of zero counts (e.g. all zeros in one of the compared experimental conditions) can produce missing values or spurious tests. The vast majority of publications have used purely simulated data, or small example datasets for which comparative conclusions are difficult. An exception is the Myrna package of Langmead et al. (2010), who apply it to real HapMap YRI data and can analyze multiple groups, but for which the count-based analysis is standard Poisson. Analysis of future, more complex datasets will require more flexible approaches.
In this article, we describe BBSeq, a comprehensive approach to the analysis of RNA-Seq transcriptional count data. BBSeq assumes a beta-binomial model for the count data, corresponding to the view that the observation of a sequence for a particular transcript is a Bernoulli random variable with an intrinsic probability for each sample. These probabilities are allowed to vary according to a beta distribution, thus allowing for overdispersion, with a mean that depends on the design variables/covariates. As the library size is large, the beta-binomial behaves similarly to an overdispersed Poisson. We thus expect that the beta-binomial provides similar fits as a negative binomial, which in the limit corresponds to a gamma-Poisson mixture (Lawless, 1987). The beta-binomial model directly describes unexplained variation in the sequence-read probabilities, simplifying choices of starting values in model fitting, and in this sense may provide a more direct interpretation of overdispersion in the data. However, intuitive descriptions of overdispersion for negative binomial data may be expressed in terms of coefficients of variation. We use a logistic regression framework to describe the dependence of expression on the experimental factors and covariates, using generic design matrices for flexibility. In this manner, any experimental factors or other covariates, such as age or sex, can be considered. Overdispersion is handled as either (i) a free parameter to be fit separately for each transcript or (ii) a term that arises from a mean overdispersion model fit to the data, with natural shrinkage properties and allowing information to be shared across genes. BBSeq is intended as easy-to-use software for handling RNA-Seq data, and our power/FDR results indicate that straightforward beta-binomial modeling has favorable characteristics. In contrast to the competing penalization approaches, we find only modest advantages for penalization, which is mainly useful for very small sample sizes.
2 METHODS
2.1 Mean–overdispersion modeling
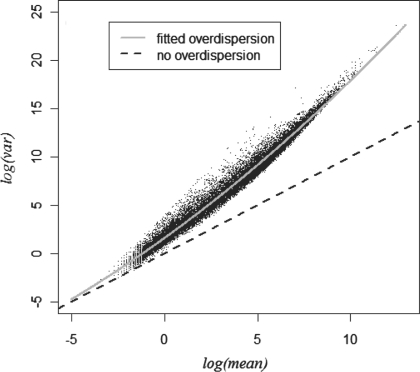
The 60 HapMap CEU RNA-Seq samples from Montgomery et al. (2010) (~20 000 genes, described in detail below) are used to illustrate the overdispersion typical of such datasets. Figure 1 shows the sample variance versus the sample mean on the log–log scale for the read counts across the samples. The relationship between the mean and variance is very strong, and the overdispersion increases with mean expression, as evidenced by the increasing gap between the data points and the unit line which corresponds to a Poisson assumption. The pattern remains essentially unchanged if the counts are standardized by the library size per sample (data not shown). A similar plot using a random subset of five samples shows the same pattern (Supplementary Fig. S1). The data illustrate that overdispersion is an important feature of the data, and can either be fit as a separate parameter or in a model for the dependence of the overdispersion on the average expression.
Fig. 1.
The mean–variance relationship in the CEU data suggests a mean–overdispersion relationship. A third-degree polynomial fit is also shown.
Discussions of RNA-Seq data often focus on the ‘length bias’, the phenomenon that longer transcripts are more likely to contain mapped reads. For example, Oshlack and Wakefield (2009) point out differing mean–variance relationships for shorter versus longer genes. Supplementary Figure S2 illustrates that, at least for datasets analyzed here, the mean is a stronger determinant of the variance (and overdispersion) than the length (also see Methods and Results in Supplementary Material). In addition, we are mainly interested in comparing expression levels within genes, across experimental conditions, and so the length bias is essentially a constant feature for these comparisons.
2.2 Data format and definitions
The data consist of an m × n matrix Y, with m genes and n samples. Each entry yij represents the transcriptional count for the i-th gene in the j-th sample. We will use θij to denote the probability that a single read in sample j maps to gene i, and θi. as the n-vector of these probabilities. The beta-binomial models θ as a random variable, which produces the overdispersion. Reads within the same sample are assumed independent. X will denote an n×p design matrix, consisting of indicator variables for experimental conditions and any desired covariates. The effect of X on gene i is modeled as
| (1) |
for the p×1 matrix of regression coefficients Bi=[β0,i,‥, βp−1, i]T. θij follows a Beta distribution, parameterized so that its variance is ϕiE(θij)(1−E(θij)). Values ϕ>0 correspond to overdispersion compared with the binomial, after considering design effects. We will use sj=∑iyij to represent the library size for the j-th sample. Marginally, the likelihood is
| (2) |
where B() is the Beta function, α1ij=E(θij)(1−ϕi)/ϕi, and α2ij=(1−ϕi) (1−E(θij))/ϕi.
Parameter estimation is performed by maximum likelihood, using either of two approaches:
the free model, in which ϕi is estimated as a ‘free’ parameter separately for each gene; and
- the constrained model, in which ϕi is estimated using an assumed mean–overdispersion relationship. For the constrained model, it might be reasonable for the overdispersion to also depend on the sample j, but for simplicity and comparability with the free model it is simpler to assume a single ϕ for each gene i. Each ϕi∈[0, 1], and so it is convenient to work with a logistic transformed parameter, and we adopt the polynomial relationship
where the mean is over the n-vector XBi. Note that the logit specification does not allow for underdispersion, which would be biologically implausible. In practice, a low degree polynomial, with K≤3, appears to provide an adequate fit, and we use simple plug-in estimates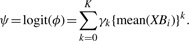
(3) 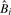 and
and 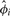 from the free model to obtain least squares estimates of the γ values. The γ values are assumed to be the same across the genes. This approach is similar to and generalizes a mean–variance modeling approach for expression microarrays (Hu and Wright, 2007),which had previously been performed only for two-sample experiments. The intent of the modeling is to increase power to detect differential expression for small sample sizes. Note that the estimation of the mean–overdispersion relationship does not reduce the degrees of freedom for individual genes, as all genes are used to estimate the few γ parameters.
from the free model to obtain least squares estimates of the γ values. The γ values are assumed to be the same across the genes. This approach is similar to and generalizes a mean–variance modeling approach for expression microarrays (Hu and Wright, 2007),which had previously been performed only for two-sample experiments. The intent of the modeling is to increase power to detect differential expression for small sample sizes. Note that the estimation of the mean–overdispersion relationship does not reduce the degrees of freedom for individual genes, as all genes are used to estimate the few γ parameters.
Supplementary Figure S3a shows the 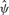 values obtained from the free model for 6 versus 6 samples from the CEU dataset, with equal number of males and females in each group, plotted against mean
values obtained from the free model for 6 versus 6 samples from the CEU dataset, with equal number of males and females in each group, plotted against mean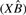 . The relationship is reasonably polynomial, inspiring the constrained model, with much of the variation in
. The relationship is reasonably polynomial, inspiring the constrained model, with much of the variation in 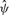 explained (multiple R2 = 0.60 for a cubic fit). Moreover, the variation in the
explained (multiple R2 = 0.60 for a cubic fit). Moreover, the variation in the 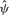 residuals can mostly be attributed to sampling variation consistent with the
residuals can mostly be attributed to sampling variation consistent with the 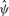 standard errors (Supplementary Fig. S3b).
standard errors (Supplementary Fig. S3b).
Optimization for both models is performed using the R optim function, with starting values for Bi obtained from linear regression and for 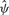 from marginal evidence of overdispersion (without considering design effects).
from marginal evidence of overdispersion (without considering design effects).
Finally, we note that real data can produce outlying estimates for a small percentage of genes, especially for the constrained model and large sample sizes. Thus, we have devised very simple outlier detection/correction approaches to avoid spurious results (Methods and Results in Supplementary Material).
2.3 Testing and design matrices
The free and constrained models both provide considerable flexibility, as the design matrix X is arbitrary and can be specified by the user. The statistical significance of any covariate can then be determined from the corresponding Wald statistic (the estimate of differential expression divided by its standard error). The vast majority of published RNA-Seq studies involve simple two-sample comparisons, so the primary testing is on β1i in each Bi, corresponding to the indicator column in X representing group assignment. Empirical investigation in small samples indicates that the Wald statistic 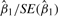 is distributed approximately tn−p for the free model under the null hypothesis (and standard normal for constrained), with adjustments for zero counts in the data (Methods and Results in Supplementary Material), and we employ this approximation for two-sample testing.
is distributed approximately tn−p for the free model under the null hypothesis (and standard normal for constrained), with adjustments for zero counts in the data (Methods and Results in Supplementary Material), and we employ this approximation for two-sample testing.
Many future studies are likely to focus on a few (perhaps multilevel) factors, as is performed in ANOVA analysis. Thus, BBSeq has been designed with a simple function to generate design matrices corresponding to multilevel factors. Moreover, BBSeq performs likelihood ratio comparisons for the overall statistical significance of each included factor. A more detailed description is provided in Methods and Results of Supplementary Material for the CEU HapMap samples, along with a real example for which etoposide IC50 cytotoxicity response scores (Huang et al., 2007) are used as a continuous predictor, along with sex and the sex × IC50 interaction.
In summary, BBSeq is designed to make it easy to perform testing for a variety of experimental designs, with modifications for small sample sizes to take advantage of the mean–overdispersion relationship.
2.4 HapMap RNA-Seq data sources
The CEU HapMap lymphoblastoid RNA-seq dataset of Montgomery et al. (2010) was obtained from their website (60 samples, http://jungle.unige.ch/rnaseq_CEU60/) as mapped tags (these and all other data downloaded in March 2010). RefSeq annotation for 21 498 genes (corresponding to 32 644 transcriptional isoforms) from the hg18 genome build was downloaded from the UCSC Genome Browser (http://genome.ucsc.edu/), with gene/exon boundaries used for a transcript database. Mismatches of up to two bases were allowed. Counts were obtained by summing RNA-Seq reads mapping to the exons of each RefSeq entry, and RefSeq IDs further annotated to the official gene symbol. An average of 9.8 million reads per sample were mapped. Mapping of reads to multiple transcript isoforms were kept in the dataset for completeness. Differential expression analyses using only the most-common isoforms for each gene versus retaining all isoforms as if they were separate genes resulted in nearly identical inference. Mapped reads from the Argonne HapMap YRI dataset (69 unique samples), (Pickrell et al., 2010) were downloaded from http://eqtl.uchicago.edu/RNA_Seq_data/mapped_reads/, extracted and applied to hg18 using the same procedures as performed for the CEU data (an average of 4.3 million mapped per sample). The total number of genes containing mapped reads in the CEU dataset was 20 904 (32 027 with redundant isoforms included), and in the YRI dataset was 20 488 (31 508).
2.5 Simulated data and subsampling from real datasets
For simulated datasets, as well as analysis of the HapMap data, the two BBSeq models were compared with other approaches, including the three edgeR models, DESeq, baySeq and a quasi-likelihood overdispersed binomial GLM (detailed descriptions of Methods in Supplementary Material).
Dataset 1: the first dataset consists of 100 independent simulations of 10 000 genes with 5 versus 5 samples for two-sample comparisons, reported in Hardcastle and Kelly (2010) (under ‘Random dispersion simulations’). A known 10% of the genes were differentially expressed with a ratio of average count levels of (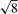 ) between two experimental groups. The data were obtained from the authors, who used edgeR parameter estimates from a SAGE dataset (Zhang et al., 1997). However, it is not clear whether the simulation setup mimics current RNA-Seq data.
) between two experimental groups. The data were obtained from the authors, who used edgeR parameter estimates from a SAGE dataset (Zhang et al., 1997). However, it is not clear whether the simulation setup mimics current RNA-Seq data.
Dataset 2: the second dataset consisted of our own simulations of two-sample comparisons of groups 1 and 2 (n1=5 versus n2=5 or n1=2 versus n2=2), with average expression levels matched to that of a real RNA-Seq dataset. For a two-sample experiment, the coefficient matrix is B=[β0, β1]T (suppressing the subscript i). We used the parameterization
| (4) |
to control the degree of differential expression, which is interpretable as the odds ratio for the expected read probabilities in group 2 versus group 1. Values r>1, r<1 and r=1 correspond to group 2 having greater, lower and equal average expression, respectively, as group 1. To obtain empirically driven parameter values, we first drew random subsamples of the CEU data (Montgomery, 2010), and for each subsample ran the free and constrained models to obtain β0, and γ estimates for each gene. Then for each value r, 20 simulations were performed following Equation (3), treating the estimated values as true parameters, with 10% of the genes chosen to be differentially expressed (i.e. with r at the alternate value), which together with β0 determined the corresponding β1. Then the data were simulated according to the corresponding beta-binomial distribution, with library sizes (total number of reads) obtained from the actual samples. Any simulated genes consisting entirely of zero counts across the samples were removed. For the receiver operator characteristic (ROC) curve comparisons, we attempted to make the results as realistic as possible by using, for null genes and each simulation, the actual read counts drawn from a random set of n1 versus n2 samples drawn from the full CEU dataset. Although both Datasets 1 and 2 consist of simulations, with Dataset 2 we attempted to closely follow features of a modern RNA-Seq dataset, to be as realistic as possible.
Dataset 3: it is difficult for simulations to capture the complexities of real data, but it is also difficult to obtain RNA-Seq datasets for which the ‘truth’ of differential expression is known. Moreover, results from any single small dataset can be highly variable, and possibly not reflect the overall behavior of a procedure. We reasoned that comparisons of differentially expressed genes between males and females in the HapMap RNA-Seq datasets would be an ideal testing ground for the ability to detect differential expression, and we used subsamples of the CEU and YRI HapMap data to form our third dataset. Genes on the sex chromosomes would be expected to predominate among those most differentially expressed. Despite chromosomal inactivation, a sizeable number of X-chromosome genes are differentially expressed, with modern estimates of this proportion ranging from ~15% (Carrel and Willard, 2005) to 5% (Johnston et al., 2008). Y chromosome genes should be expressed only in males, but the expression in transformed lymphocytes for many genes may be low. Nonetheless, using the genes on the autosomes as a control, the ability to efficiently detect differential expression on the sex chromosomes can be used to compare procedures, with the degree of differential expression varying widely across this set.
3 SIMULATIONS AND EXAMPLES
3.1 Comparisons with other approaches
3.1.1 Comparisons using Dataset 1
The original authors (Hardcastle and Kelly, 2010) used ROC curves to compare baySeq to a number of other methods, including edgeR. Focusing on the most significant genes and expressed as a false discovery rate produces the result in Supplementary Figure S5, which is directly comparable to the lower right panel of Figure 2 in Hardcastle and Kelly (2010). BaySeq has the best performance, while our two approaches perform similarly to edgeR and DESeq for the most significant genes, but perform more poorly for larger numbers of rejected genes. A careful comparison shows that the free model is similar to the unpenalized ‘log-linear’ model in the original baySeq figure, as expected, as is the overdispersed GLM.
Fig. 2.
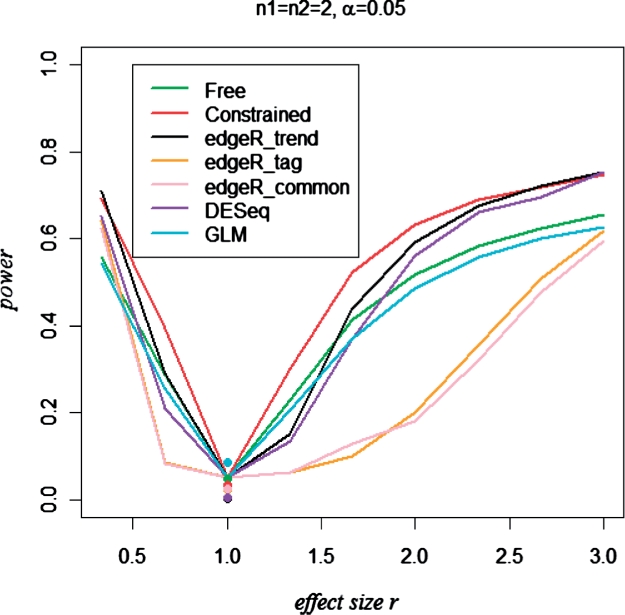
Power comparisons for one scenario, Dataset 2.
The results are perhaps to be expected, as the data follow the idealized simulation conditions for baySeq. Supplementary Figure S5 shows the relationship between log(variance) and log(mean) for the first group in the first simulation. Although there is an apparent mean–overdispersion relationship, note that the dispersion in sample variance is more extreme, especially for genes with low expression than encountered in the CEU data (Fig. 1 and Supplementary Fig. S1). Moreover, the average expression level in the real RNA-Seq datasets tends to be higher than for Dataset 1. This difference is strikingly illustrated in the number of zero counts. For either the CEU or YRI datasets, ~60% of the genes in a subsample of size 10 will show no zero counts across the samples, while for Dataset 1 the value is 17%. It is unclear how these differences affect the performance of these methods with current RNA-Seq data.
3.1.2 Comparisons using Dataset 2
As described earlier, Dataset 2 consists of simulations with n1=n2=2 and n1=n2=5, under the model using intercept β0 and mean–overdispersion relationships obtained from the CEU data, with parameter r controlling the degree of true differential expression. In each simulation, a random 10% of the genes were used as ‘alternative’. We were interested in power to declare differential expression at α=0.05 and the more stringent α=0.001. Such a comparison requires interpretable P-values, and so we do not show results for baySeq, which provides only posterior probabilities for differential expression. The remaining approaches exhibited reasonable control of type I error, but to make precise power comparisons we also determined the empirical threshold for each approach such that Pr=1(p<pthreshold)=α. An illustrative power curve for n1=n2=2 and α=0.05 is shown in Figure 2. The additional scenarios are shown in Supplementary Figure S6.
For these simulations, the constrained model performs best, as might be expected, as the approach is able to accurately estimate overdispersion using the model. The relative improvement in power for the constrained model over the other models is greatest for n1=n2=2 and α=0.001, and for modest effect sizes r. For n1=n2=5, the relative improvement of the constrained model over other penalized approaches is reduced.
For these simulations, the empirical type I error for the nominal P-values is shown in Supplementary Table S1. The BBSeq models show near-nominal type I error, while the other methods do not generally perform as well. Focusing on n1=n2=5 and a moderate effect size r=2.0 and using the resampled data counts to create ‘null’ genes as described above, we show ROC curves for the various methods in Figure 3. Examination of ROC curves reveal differing behavior for genes with low expression versus high expression (using the median β0 estimate as a splitting criterion). Here, the free model outperforms the other models, except for high expression genes, where it is similar to baySeq and to the overdispersed GLM. However, using all genes, the free model appears to be best. Note that these results differ somewhat from the ‘pure’ simulations for the power curves, because the sampling of null genes by random draws from the CEU induces correlations and dispersion behavior that may not be reflect in pure null simulation.
Fig. 3.
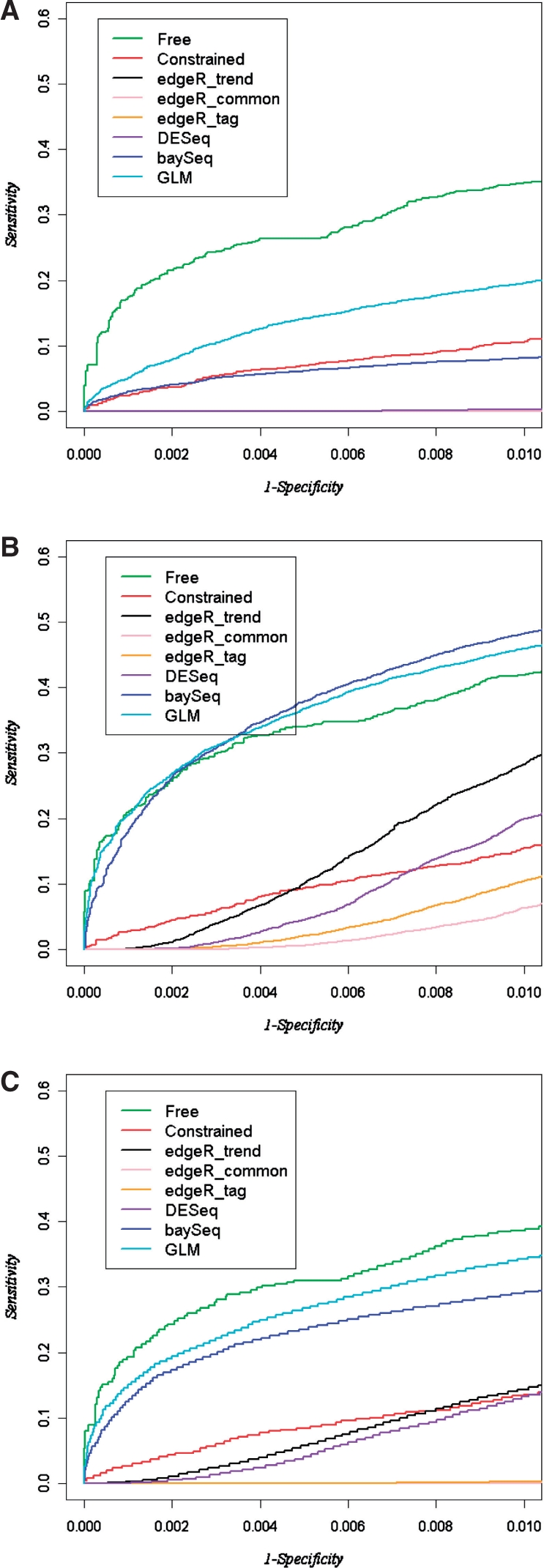
Portions of ROC curves for Dataset 2. (A) The curve for low-expression genes with the x-axis ranging 0–0.01 (see text); (B) a similar set of curves for high-expression genes; (c) all genes, but with a more stringent 1 − specificity.
Based on these simulations and potential sensitivity to the vagaries of real data, we propose that the constrained model has value mainly for very small sample sizes (such as n1=n2=2), with the theoretical advantages for larger sample sizes outweighed by potential model deviations. Thus, we recommend the constrained model only for very small sample sizes.
After consideration of the simulations, we were motivated to compare the free model to competing models for moderate sample sizes and real data. These comparisons are performed in Dataset 3 below.
3.1.3 Comparisons using Dataset 3
Using the sex information for the CEU HapMap and YRI samples, we applied the free model and the competing approaches to 10 random subsamples of n1=6 males versus n2=6 females for CEU and YRI separately. For the edgeR approach, we used only the trend penalization procedure, as this had performed generally the best in the power comparisons. For each subsample, we counted the number of sex chromosome genes among the top detected/rejected genes. The average across the 10 subsamples is shown in Figure 4. Here, the free model is best for the CEU data, and is similar to edgeR, DESeq and the GLM for the YRI data. For YRI, the baySeq approach is the most sensitive in detection.
Fig. 4.
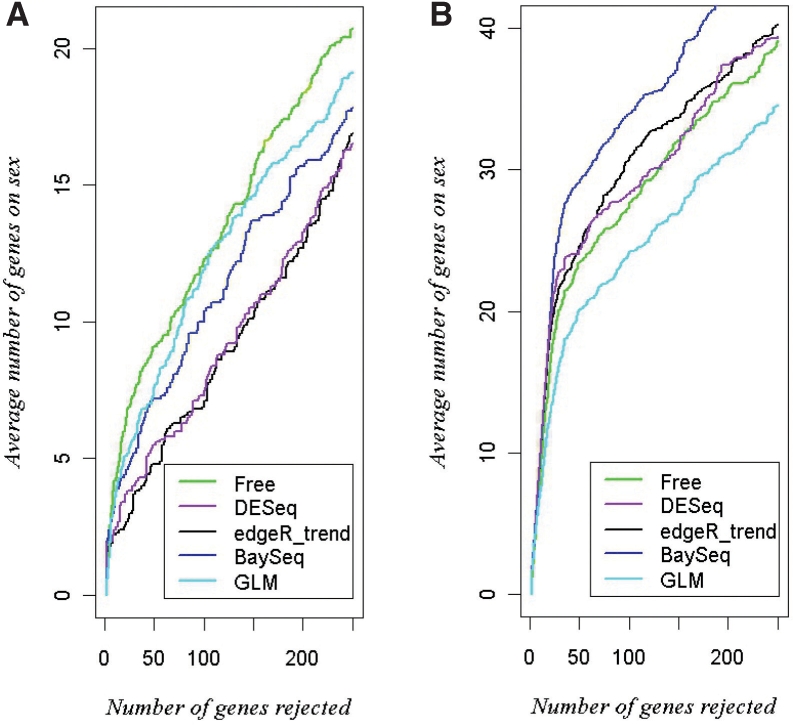
Number of detected genes on the sex chromosomes versus number of genes detected, using subsamples from Dataset 3 with n1=6 males versus n2=6 females. (A) The CEU dataset; (B) the YRI data.
These comparisons are among the most extensive such examinations performed with real data and for which we are able to explore the ‘truth’ of differential expression in the dataset. We emphasize that true differential expression between males and females may occur for some genes on the autosomes. The rationale of our analysis, following current understanding of sex chromosome expression, is merely that genes on the sex chromosomes should be over-represented if a detection procedure is sensitive.
As described in Section 2, for completeness of mapped reads, our analyses were performed using multiple common transcript isoforms (e.g. splicing variants) as if they were separate genes. Many reads map to several isoforms of a gene, technically violating independence assumptions for read counts. RNA-Seq analysis packages typically provide little guidance on this issue. However, the library sizes are typically so large that the inference for any one isoform is essentially the same whether or not the analysis is restricted to unique genes, as illustrated for a 12-sample CEU analysis, shown in Supplementary Figure S7.
3.1.4 Sex-specific expression and outlier sensitivity
We also used the five methods to perform differential expression analysis for males versus females for the entire set of 60 CEU samples. Knowledge of X-inactivation and dosage compensation remains surprisingly incomplete, and microarray analysis of HapMap cell lines (including CEU and YRI) by Johnston et al. (2008) has provided much of our recent understanding of genes that are inactivated (or effectively so) in females. Interestingly, among the top 10 genes identified by the free model (Table 1), 9 are on the X chromosome and all were described by Johnston et al. (2008) or Carrel and Willard (2005) as escaping inactivation. It is reassuring that the known X-inactivator XIST (Herzing et al., 1997) is the most differentially expressed gene [although technically with the cDNA-based technology, it cannot be distinguished from its antisense counterpart TSIX (Lee et al., 1999)]. Analysis of the entire gene list (data not shown) shows many Y chromosome genes ranking highly, but typically with lower read counts and correspondingly lower significance. The GLM approach similarly identifies 9 genes on X among the top 10, although XIST is ranked much lower (162nd). Unlike the free model, both edgeR with Trend and DESeq identify only XIST among the top 10 genes. For these methods, the XIST result is strikingly significant, which we attribute to differing variances within each of males and females (data not shown), to which these methods may be more sensitive. Bayseq identifies three genes from the X chromosome among the top 10. We were interested in the reasons for such strikingly different gene lists. For each approach, we examined the most significant autosomal genes, and some potentially spurious results emerged. Separate male/female histograms of normalized read counts are plotted in Supplementary Figure S8. The top autosomal gene from the free and GLM models, FAHD2A (free model P = 5.86E-11, GLM P = 1.78E-07, has not been widely described, and a literature search did not reveal compelling evidence for sex-specific expression. Nonetheless, the histogram shows a clear trend of higher expression in males. SULF1 does not appear differentially expressed (Supplementary Figure S8), but has P = 7.82E-42 according to edgeR Trend, and P = 8.14E-47 according to DESeq This result is largely driven by a single outlying high value in females. BaySeq identifies ACTG1 as the most differentially expressed of all genes, although the count distributions overlap almost entirely, with the two highest values occurring in females. We speculate that the high expression of the gene (fourth highest among all genes) may make it vulnerable to spurious baySeq findings, but further investigation is warranted. Beyond the potential sensitivity to outliers, most of the methods are in broad agreement—e.g. the top-ranked genes by the free model are also significant by the other methods, but appear further down on their respective lists. The entire list of genes and P-values for all methods are provided on the software website.
Table 1.
Top differentially expressed genes for 27 males versus 33 females, CEU dataset
| Free | edgeRtrend | baySeq | DESeq | GLM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| chrX | XIST | 1.73E-11 | chrX | XIST | 1.03E-213 | chr17 | ACTG1 | 94.4 | chrX | XIST | 8.82E-227 | chrX | EIF1AX | 1.34E-14 |
| chrX | PNPLA4 | 5.86E-11 | chr7 | ABP1 | 2.80E-42 | chrX | XIST | 44.58 | chr7 | ABP1 | 3.86E-53 | chrX | PNPLA4 | 5.27E-14 |
| chrX | EIF1AX | 2.36E-10 | chr8 | SULF1 | 7.82E-42 | chr11 | RPS3 | 37.49 | chr2 | RAPH1 | 3.90E-52 | chrX | HDHD1A | 1.30E-11 |
| chrX | NLGN4X | 2.09E-08 | chr2 | RAPH1 | 1.16E-40 | chr22 | RPL3 | 28.82 | chr22 | MIR650 | 9.95E-49 | chrX | RPS4X | 4.27E-11 |
| chrX | RPS4X | 4.22E-08 | chr22 | MIR650 | 1.72E-37 | chr12 | RPLP0 | 26 | chr8 | SULF1 | 8.14E-47 | chrX | KDM6A | 6.57E-09 |
| chrX | HDHD1A | 5.06E-08 | chr20 | EEF1A2 | 9.58E-27 | chr15 | PKM2 | 24.7 | chr11 | NEAT1 | 6.77E-31 | chrX | KDM5C | 3.03E-08 |
| chrX | PRKX | 5.62E-07 | chr12 | HMGA2 | 3.48E-22 | chrX | NLGN4X | 21.27 | chr20 | EEF1A2 | 2.30E-19 | chrX | NLGN4X | 6.60E-08 |
| chrX | KDM6A | 6.38E-07 | chr2 | SCN3A | 1.54E-19 | chr22 | MYH9 | 20.13 | chr12 | HMGA2 | 2.87E-19 | chrX | PRKX | 6.69E-08 |
| chr2 | FAHD2A | 1.19E-06 | chr1 | S100A8 | 6.42E-18 | chr13 | LCP1 | 19.71 | chr14 | IFI27 | 2.26E-18 | chr2 | FAHD2A | 1.78E-07 |
| chrX | CXorf15 | 1.43E-06 | chr18 | DSG1 | 7.40E-18 | chrX | EIF1AX | 18.35 | chr15 | GOLGA8B | 1.82E-17 | chrX | CXorf15 | 2.62E-07 |
BaySeq results are shown as log posterior odds for differential expression.
4 CONCLUSION AND DISCUSSION
We have described a procedure to implement beta-binomial modeling of RNA-Seq tag counts. For the free-ϕ model, our procedure is somewhat similar to other overdispersed generalized linear models. However, in our simulations and in the HapMap data, the direct parametric modeling of the overdispersion parameter appeared to be advantageous. Moreover, our BBSeq software simplifies the analysis for researchers less familiar with modeling and construction of design matrices, and issues such as outlier detection are handled automatically. The constrained-ϕ approach, while still very simple, has potential advantages in the analysis of very small datasets, which remain very common. We emphasize that both procedures offer much more flexible handling of design variables and other covariates than competing purpose-built procedures.
A surprising result from our investigation is that it is unclear for modest size samples (say 5 or more per sample group) that the careful attention to penalization procedures, which are implicit in both the competing procedures and in our constrained approach, are truly necessary for effective inference. A better understanding of the true nature of differential expression may be necessary in order to fully understand these issues. Much of the motivation behind penalized approaches lies in a notion that genes with low expression have an unfavorable ratio of signal to noise. As the accuracy of expression profiling further improves, this notion may be replaced by a deeper understanding of the degree of differential expression need to produce biologically important changes, which may depend on baseline expression level as well as other contextual information. Our analysis of male/female differential expression in the entire CEU dataset was intended only as a simple illustration, but highlights a possible sensitivity to outliers of shrinkage/penalization methods, and deserves further investigation.
Several investigators have pointed out that a relatively small number of genes can be responsible for large variations in total read counts (Robinson and Oshlack, 2010; Bullard et al., 2008), and thus it is conceivable that a gene at constant mRNA concentration might appear to vary. This phenomenon would be expected to be strongest in differential expression experiments involving widely divergent samples (e.g. liver and kidney samples, as in Robinson and Oshlack, 2010). For datasets of the same tissue type, as described here, we expect that total read counts will remain a sound basis for normalization. However, these considerations suggest that further extensions of BBSeq modeling might consider alternate terms which reflect the sources of such read count variation.
The procedures described here reflect only global gene expression changes, ignoring the rich mRNA sequence information. Extensions to BBSeq could potentially be used to summarize evidence of allele-specific expression and differential expression, and to investigate differential expression of various isoforms (Blekhman et al., 2010). Sequence reads that are otherwise uninformative about allele specificity or varying isoforms still provide evidence of overall expression level, which in turn may indirectly inform a deeper understanding of expression changes.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Drs Hardcastle and Kelly for kindly providing Dataset 1, which was among the datasets reported in their paper, and Dr Wei Sun for helpful discussions.
Funding: Support provided in part by the Gillings Innovation Laboratory in Statistical Genomics, the National Institute of Environmental Health Sciences (P30ES010126), and the National Institute of Mental Health (RC2MH089951), and the U.S. Environmental Protection Agency (RD83382501).
Conflict of Interest: none declared.
Note Added in Proof: The advance access version of this manuscript included an incorrect plot of the baySeq results in Figure 4. We regret the error. In addition, analysis of the full CEU dataset by an updated version of baySeq (version 1.6) is reported to identify fewer outliers (Dr. Thomas Hardcastle, personal communication).
REFERENCES
- Anders S., Huber W. Differential expression analysis for sequence count data. Genome Biol. 2010;11:R106. doi: 10.1186/gb-2010-11-10-r106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhasin J.M., et al. Sex specific gene regulation and expression QTLs in mouse macrophages from a strain intercross. PLoS One. 2008;3:e1435. doi: 10.1371/journal.pone.0001435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blekhman R. Sex- specific and lineage-specific alternative splicing in primates. Genome Res. 2010;20:180–189. doi: 10.1101/gr.099226.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullard J.H., et al. Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics. 2010;11:94. doi: 10.1186/1471-2105-11-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrel L., Willard H.F. X-inactivation profile reveals extensive variability in X-linked gene expression in females. Nature. 2005;434:400–404. doi: 10.1038/nature03479. [DOI] [PubMed] [Google Scholar]
- Hardcastle T.J., Kelly K.A. baySeq: empirical Bayesian methods for identifying differential expression in sequence count data. BMC Bioinformatics. 2010;11:422. doi: 10.1186/1471-2105-11-422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herzing L.B., et al. Xist has properties of the X-chromosome inactivation centre. Nature. 1997;386:272–275. doi: 10.1038/386272a0. [DOI] [PubMed] [Google Scholar]
- Hu J., Wright F.A. Assessing differential gene expression with small sample sizes in oligonucleotide arrays using a mean-variance model. Biometrics. 2007;63:41–49. doi: 10.1111/j.1541-0420.2006.00675.x. [DOI] [PubMed] [Google Scholar]
- Huang R.S., et al. A genome-wide approach to identify genetic variants that contribute to etoposide-induced cytotoxicity. Proc. Natl Acad. Sci. USA. 2007;104:9758–9763. doi: 10.1073/pnas.0703736104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston C.M., et al. Large-scale population study of human cell lines indicates that dosage compensation is virtually complete. PLoS Genet. 2007;4:e9. doi: 10.1371/journal.pgen.0040009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B., et al. Cloud-scale RNA-sequencing differential expression analysis with Myrna. Genome Biol. 2010;11:R83. doi: 10.1186/gb-2010-11-8-r83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawless J.F. Negative binomial and mixed Poisson regression. Canadian J. Stat. 1987;15:209–225. [Google Scholar]
- Lee JT, et al. Tsix, a gene antisense to Xist at the X-inactivation centre. Nat. Genet. 1999;21:400–404. doi: 10.1038/7734. [DOI] [PubMed] [Google Scholar]
- Marioni J.C., et al. RNA-seq: an assessment of technical reproducibility and comparison with gene expression arrays. Genome Res. 2008;18:1509–1517. doi: 10.1101/gr.079558.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montgomery S.B., et al. Transcriptome genetics using second generation sequencing in a Caucasian population. Nature. 2010;464:773–777. doi: 10.1038/nature08903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oshlack A., Wakefield M.J. Transcript length bias in RNA-seq data confounds systems biology. Biol. Direct. 2009;4:14. doi: 10.1186/1745-6150-4-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell J.K., et al. Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature. 2010:768–772. doi: 10.1038/nature08872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M.D., et al. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010;26:139–140. doi: 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M.D., Oshlack A. edgeR: a scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2010;11:R25. doi: 10.1186/gb-2010-11-3-r25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth G.K. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Genet. Mol. Biol. 2004;3 doi: 10.2202/1544-6115.1027. Article 3. [DOI] [PubMed] [Google Scholar]
- Wang L., et al. DEGseq: an R package for identifying differentially expressed genes from RNA-seq data. Bioinformatics. 2010;26:136–138. doi: 10.1093/bioinformatics/btp612. [DOI] [PubMed] [Google Scholar]
- Zhang L., et al. Gene expression profiles in normal and cancer cells. Science. 1997;276:1268–1272. doi: 10.1126/science.276.5316.1268. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.