A Quantitative Comparison of the Influence of Individual versus Population-Derived Vascular Input Functions on DCE-MRI in Small Animals

Abstract

For quantitative analysis of DCE-MRI data, the time course of the concentration of the contrast agent in the blood plasma, or vascular input function (VIF), is required. We compared pharmacokinetic parameters derived using individual and population-based VIFs in mice for two different contrast agents, Gd-DTPA and P846. Eleven mice with subcutaneous 4T1 breast cancer xenografts were imaged at 7T. A pre-contrast T₁ map was acquired along with dynamic T₁-weighted gradient echo images before, during, and after a bolus injection of contrast agent delivered via a syringe pump. Each animal's individual VIF (VIF_ind) and derived population-averaged VIF (VIF_pop) were used to extract parameters from the signal-time curves of tumor tissue at both the region of interest (ROI) and voxel level. The results indicate that for both contrast agents, K^trans values estimated using VIF_pop have a high correlation (CCC > 0.85) with K^trans values estimated using VIF_ind on both an ROI and voxel level. This work supports the validity of using of a population-based VIF with a stringent injection protocol in pre-clinical DCE-MRI studies.

Introduction

Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) uses fast imaging techniques to characterize the pharmacokinetics of an injected paramagnetic contrast agent (CA), which acts by changing the relaxation times of water in surrounding tissue (T₁ and T₂). By injecting a CA into the vasculature and imaging the changes in signal intensity over time as the CA extravasates into the tissue of interest, vascular and tissue properties can be evaluated. The signal intensity-time curves can be fit to appropriate pharmacokinetic models whose parameters can be related to physiological properties. Specifically, pharmacokinetic parameters returned from a DCE-MRI analysis have been shown to reflect vessel wall permeability, blood flow, and blood volume (1,2). DCE-MRI has the ability to non-invasively measure changes in these vascular properties and so it has been frequently employed in both preclinical and clinical studies to assess the efficacy of drugs that target vascular or angiogenic processes (3).

The most commonly used model incorporates the exchange of CA between the extracellular vascular space (plasma) and the tissue extracellular space (1). The movement of CA between the vascular space and the tissue space can be described with transfer rate constants. The rate of influx from the vascular space to the tissue space can be described by the transfer rate constant K^trans, while the efflux rate of the CA moving from the tissue space back to the vascular space is K^trans divided by the extravascular, extracellular volume fraction v_e (K^trans/v_e) (1,4). If we assume an instantaneous homogeneous distribution of CA in both compartments, then this system can be described by a first order, linear, ordinary differential equation

$$\frac{d}{\mathit{\text{dt}}}{C}_t(t)=K^{\mathit{\text{trans}}}·C_p(t)-(K^{\mathit{\text{trans}}}/v_e)·C_t(t),$$ [1]

where C_t(t) and C_p(t) are the concentrations of the CA in the tissue space and the plasma space, respectively. The solution to this equation is

$$C_t(t)=K^{\mathit{\text{trans}}}·{\displaystyle \underset{0}{\overset{t}{\int }}}{C}_p(u)·e^{-(K^{\mathit{\text{trans}}}/v_e)·(t-u)}\mathit{\text{du}}.$$ [2]

As has been noted by many other investigators, Eq. [2] neglects the vascular volume in the tissue itself. While this may be a reasonable assumption in healthy tissues with low vascular fractions (≤ 2%), it may not be valid in many pathologic tissues, including cancer (5,6). The model can be extended to include a vascular fraction component, v_p (5):

$$C_t(t)=K^{\mathit{\text{trans}}}·{\displaystyle \underset{0}{\overset{t}{\int }}}{C}_p(u)·e^{-(K^{\mathit{\text{trans}}}/v_e)·(t-u)}\mathit{\text{du}}+v_p·C_p(t).$$ [3]

During a DCE-MRI experiment, signal intensity-time courses can be collected and converted to CA concentrations; then, both C_t(t) and C_p(t) can be fit to extract K^trans, v_e, (Eq. [2]) or K^trans, v_e, and v_p (Eq. [3]).

In order to employ Eqs. [2] and [3], three data sets are required: 1) a pre-contrast T₁ map, 2) T₁-weighted images with reasonably high spatial and temporal resolution from which T₁ changes can be calculated, and 3) the rate of change of the concentration of contrast agent in the blood plasma (vascular input function, or VIF). Typical characteristics of the VIF from a bolus injection include a rapid wash-in of high CA concentration up to a sharp peak concentration and a bi-exponentially decaying wash-out period. Capturing the first pass of the bolus is critical but difficult in small animals due to the need for high temporal as well as spatial resolution.

Several techniques have been developed to obtain the VIF. A “gold standard” is blood sampling, as this is independent of any NMR assumptions. This requires drawing blood at multiple time points during and after the CA injection in order to measure the concentration of CA contained in the sample (7,8). While this provides accurate estimation of the CA concentration, it has obvious drawbacks. It is an invasive procedure that is difficult to perform while dynamic scans are being acquired. Furthermore, the small blood volume of a mouse limits the number of sampled time points that can be obtained before potentially changing the physiology of the animal.

To circumvent these issues, some investigators measure the VIF using the imaging data itself. By carefully selecting slices that contain a blood pool and calibrating the signal intensity to changes in CA concentration (the relaxivity in plasma), the signal from that region can be converted into a VIF (9,10). While this method is noninvasive, strategically including a blood pool in the field of view (FOV) can limit the location of the region of interest (ROI). Additionally, the spatial resolution must be high enough to avoid partial volume or flow effects, while the temporal resolution must be high enough to capture the peak of the VIF. Because of these requirements, signal to noise ratio (SNR), the number of slices, and spatial resolution over the tumor are typically compromised.

Because of the difficulties in obtaining a high-quality VIF from every subject at every time point, some investigators have used a population-averaged VIF for data analysis. Typically, a cohort of patients or animals is used to obtain multiple individual VIFs, which are then averaged together to form a high-SNR population VIF (11–13). Then, the DCE-MRI treatment study is performed using a separate cohort, and the population derived VIF is used for all subjects. Thus, the temporal resolution can be “traded” for higher spatial resolution and/or increased SNR, and the location of the imaging ROI becomes less important since a major vessel is not required in the FOV. This higher spatial resolution is particularly important when characterizing the heterogeneity of the tumor on a voxel by voxel basis.

Currently, there are few studies that discuss the relative merits and accuracy of using the population VIF versus an individual VIF in small animals (11,14). Pickup, et al., obtained the VIF from the left ventricle as seen in imaging data in mice. Temporal resolution for this study was approximately one image/s, but spatial resolution was severely restricted. Additionally, the injection was manually performed. The authors concluded that an individual-derived VIF is preferred to a population-derived VIF due to the variability in resulting pharmacokinetic parameters (11). More recently, another study by McGrath et al., compared the VIF in rats (using a manual injection) with frequently used VIF models and the population averaged VIF and reported the effects on pharmacokinetic modeling parameters. Interestingly, it was found that using a bi-exponential model of a population-averaged VIF provided optimum repeatability and sensitivity for K^trans and v_e parameters in the presence of low temporal resolution data (14).

The goal of this study is to assess the error in parameters extracted from DCE-MRI modeling of tumor tissue when using a VIF derived from a population average versus those extracted with an individually measured VIF in mice. These VIF measurements were obtained in a cohort of mice using two different contrast agents of varying molecular weight. The comparison between pharmacokinetic parameters was performed on both an ROI and voxel-based analyses. Voxel analysis allows characterization of tumor heterogeneity while the ROI-analysis may be more typically used in a treatment response study. Additionally, performing voxel analysis allows for performing intra-animal comparisons that are not possible when just an ROI value is computed. Error and agreement between these methods are reported, and the consequences for using either an individual or population VIF in DCE-MRI data analysis are discussed.

Methods

Tumor Model

Murine 4T1 breast cancer cells were cultured in Dulbecco’s modified Eagle’s medium supplemented with 10% fetal bovine serum and 0.2% Gentamicin. Cells were incubated at 37° C in a mixture of 5%/95% CO₂/air. Cells growing at 80% confluence were harvested, and a single cell suspension containing 5 × 10⁶ cells suspended in 100 µL of medium was injected subcutaneously near the shoulder. Tumors were allowed to grow for six to nine days before imaging; tumor size ranged from 100 mm³ to 400 mm³ thereby producing a range of kinetic parameters.

Animal Model

Eleven female Balb/c mice (approximately 20 g, 8–10 weeks of age) were purchased from Charles River Laboratories (Wilmington, MA), housed in pathogen-free facilities and provided with rodent chow and tap water ad libitum. A 26-gauge jugular catheter was surgically implanted to allow for delivery of the contrast agent. All animals were imaged twice: once using an injection of 120 µL of 0.05 mmol/kg gadopentetate dimeglumine, Gd-DTPA, (Magnevist, Wayne, NJ) (15) and once using an injection of 120 µL of 0.05 mmol/kg P846 (Guerbet Research, Aulnay-sous-Bois, France) on a later day (16). During all imaging procedures, the mice were anesthetized using a 2%/98% isoflurane/oxygen mixture. Temperature, respiratory rate, and electrocardiogram (ECG) signal were monitored throughout the entire experiment. All procedures in the experiment were reviewed and approved by our Institutional Animal Care and Use Committee.

MRI Contrast Agents

Gd-DTPA is a small (~0.5 kDa) hydrophilic, paramagnetic molecule that is not transported into cells. Gd-DTPA has rapid clearance and minimal toxicity (15). P846 has a molecular weight of approximately 3.5 kDa and consists of a single Gd ion in a macro-cyclic 3-armed chelate. This larger contrast agent has a lower extravasation rate allowing an elongated contrast enhancement period along with a higher relaxivity than Gd-DTPA (16–18). Relaxivities for Gd-DTPA and P846 at 7T were found using the T₁ mapping technique detailed below; the measured values of 4.71 s⁻¹mM⁻¹ and 10.62 s⁻¹mM⁻¹, respectively, were used in subsequent data analyses (data not shown) and reflect values found in the literature (19,20).

Data Acquisition

MR imaging was performed using a Varian 7.0T Inova scanner equipped with a 25-mm quadrature volume coil (both Varian, Inc. Palo Alto, CA). A respiratory- and ECG-gated gradient echo sequence was used to locate a 2 mm slice that both contained the tumor and cut across the short-axis of the left ventricle (LV) of the heart. Data for constructing a pre-contrast T₁ map were obtained by an inversion recovery snapshot FLASH (Fast Low Angle SHot) gradient echo sequence with an adiabatic inversion pulse over nine inversion times (TI) ranging logarithmically from 200 – 6000 ms with TR\TE \α= 10000 ms\ 3.44 ms\15° and NEX = 4, FOV = 25 mm², and matrix = 64². While a detailed derivation of this technique is described in references (21,22), we briefly provide the salient details. For each inversion pulse, eight lines of k space were acquired; these eight lines account for a single effective TI (TI_eff), with the TI_eff corresponding to the timing of the first collected line. A centric phase encode table was used to reconstruct the data, and no cardiac gating was used during the acquisition. Under the assumption that TR >> T₁ and a sufficiently low flip angle, the signal at each acquisition can be described in the following equation:

$$S=S_0·|(\mathit{1}-\mathit{2}·e^{-{\mathit{\text{TI}}}_{\mathit{\text{eff}}}/T_{\mathit{1}}})|,$$ [4]

where and S₀ and S are the signal intensities at equilibrium and at the effective inversion time, respectively. For each inversion pulse, eight lines of k-space were acquired and TI_eff is the time from the inversion pulse to the center of k space (22). During the data fit, S₀ was also a free parameter in order to account for incomplete longitudinal inversions.

The DCE-MRI protocol employed a T₁-weighted, spoiled gradient echo sequence to obtain serial images at a temporal resolution of 1.536 seconds for 20 minutes with TR\TE\α = 6 ms\2.41 ms\10°, NEX = 4, and the same acquisition matrix and FOV as for the T₁ map. A 120 µL bolus of 0.05 mmol/kg Gd-DTPA or P846 was delivered via a jugular catheter using an automated syringe pump (Harvard Apparatus, Holliston, MA, USA) at a rate of 2.4 mL/min after 100 baseline images were acquired.

Data Analysis

Data collected for the T₁ map were fit using a nonlinear least squares method in Matlab 2008a (The Mathworks, Natick, MA, USA) to Eq. [4]. Once pre-contrast T₁ maps were calculated for the interrogated slice, regions of interest were drawn to include the entire left ventricle of the mouse. Each voxel was then converted to an R₁ (= 1/T₁) time course by the method of Landis, et al. (23)

$$R_{\mathit{1}}(t)=-\frac{\mathit{1}}{\mathit{\text{TR}}}·\mathit{\text{ln}}\left[\frac{(S_0·\text{sin}\alpha ·e^{-\mathit{\text{TE}}/T_{\mathit{2}}^{*}})-S(t)·\text{cos}\alpha }{S_{\mathit{0}}·\text{sin}\alpha ·e^{-\mathit{\text{TE}}/T_{\mathit{2}}^{*}}-S(t)}\right],$$ [5]

where R₁, TR, TE, T₂^*, and α are described previously, S(t) is the signal intensity time course, and

$$S_0=S_{\mathit{\text{ss}}}·\frac{(\mathit{1}-e^{-\mathit{\text{TR}}/T_{\mathit{1}}}·\text{cos}\alpha )}{(\mathit{1}-e^{-\mathit{\text{TR}}/T_{\mathit{1}}})·\text{sin}\alpha ·e^{-\mathit{\text{TE}}/T_{\mathit{2}}^{*}}},$$ [6]

where S_ss is the steady state averaged signal intensity before contrast agent administration (pre-CA). At a short TE, T₂* contribution to the signal was assumed to be neglible. Using the R₁ time course for the LV, the concentration of contrast agent in the plasma [C_p] was then determined using the fast exchange limit (FXL) assumption

$$R_{\mathit{1}}=r_{\mathit{1}}·(\mathit{1}-h)·C_p+R_{\mathit{10}},$$ [7]

where r₁ is the relaxivity for Gd-DTPA and P846, (values reported above), h is the hematocrit of a mouse (h = 0.45 was used in this study based on literature values (24)) and R₁₀ is the pre-contrast R₁ value.

Due to potential flow and motion artifacts, a simple filter was employed to examine every voxel within the LV blood pool for specific characteristics; in particular, voxels were included in the VIF calculation if the SNR ≥ 30 at all time points and if the peak concentration was ≥ 0.15 mM and VIF characteristics found in the literature (11). Each voxel returned was also visually inspected for appropriate wash-out activity to prevent potential myocardial wall contamination. An ROI in the left ventricle was drawn and all voxel time courses were graphically displayed. If the time course had elongated washout (characteristic of tissue), it was excluded from analysis (typically only 2–3 voxels per animal). These appropriate voxels were then averaged together to represent the individual VIF for that animal. Once the individual VIFs were collected (N = 11 for Gd-DTPA and N = 9 for P846), they were aligned to the same initial uptake time. Briefly, the peaks (maximum value) of the individual VIFs were used to align the data to form the population VIF. Alignment typically varied 1–3 time points and interpolation (if needed) was either added to the baseline acquisition or at the tail end of the washout period. For each animal, an individual VIF (VIF_ind) and a population VIF (VIF_pop), which was determined by taking the mean of the individual VIFs (excluding its own individual VIF), were used to fit that animal’s ROI signal curves to both the standard and extended model represented in Eqs. [2] and [3] to extract K^trans, v_e, and v_p.

Statistical Analysis

By fitting the tissue signals to the standard (ST) and extended (EX) models with both VIF_ind and VIF_pop, two sets of five parameters were produced: 1) using VIF_ind: K^trans,ind (ST), v_e,ind(ST), K^trans,ind(EX), v_e,ind(EX), and v_p,ind (EX) and 2) using VIF_pop: K^trans,pop (ST), v_e,pop(ST), K^trans,pop(EX), v_e,pop(EX), and v_p,pop(EX). Each parameter was paired for comparison (e.g., K^trans,ind (ST) and K^trans,pop (ST)); these so-called “parametric pairs” were compared on two levels.

First, a ROI was drawn around the tumor for each animal. The signal from the ROI was averaged to produce one R₁ time course, which was then analyzed by both the standard and extended models. The absolute agreements between the resulting parametric pairs were then assessed using the concordance correlation coefficient (CCC) (25). Specifically, the CCC evaluates the degree to which these pairs fall on the 45 degree line through the origin when they are plotted against each other. Like standard correlation, a perfect correlation of the pairs produce a CCC value of 1, while completely independent pairs produce a CCC equal to 0. The Pearson correlation coefficient, was also calculated. In addition to the correlation indices, each parametric pair was analyzed using linear regression.

The second level of comparison was based on individual voxel data for each animal. Voxels within the whole tumor ROIs were fit individually to produce two sets of five parametric maps for all animals (as described above). To ensure that only properly fit data was employed for further comparison, the data and respective model fit were compared and an r² describing the quality of the fit was obtained for each voxel. Then, the voxel fits were filtered based on the returned r² (r²> 0.6); that is, if the r² value was less than 0.6, the voxel data was excluded from further analyses. Additionally, voxel data were filtered to ensure the resulting parameters fell within a physiologically relevant parametric range (0 < K^trans < 1 min⁻¹, 0 < v_e < 1, and 0 < v_p < 1). Voxels that could be fit using the VIF_ind but not the VIF_pop were tabulated and reported in Table 6. For each animal, the CCC and Pearson correlation coefficient were determined on a voxel by voxel basis between the parametric pairs described previously; additionally these paired data were compared using linear regression. A t-test was used in the linear regression framework to determine whether the fitted slope and intercept were significantly different (p < 0.05) than 1.0 and 0, respectively.

Table 6.

Ill-fit voxel data for Gd-DTPA and P846

Mouse ID	Gd-DTPA	P846
	Percentage of voxels fit only by VIFind but not VIFpop	Percentage of voxels fit only by VIFind but not VIFpop
1	0	0
2	3	0
3	0	0
4	0	0
5	0	0
6	0	11
7	0	5
8	0	8
9	0	2
10	52	na
11	42	na

Gd-DTPA (n = 11) and P846 (n = 9)

Modeling and Temporal Resolution Analysis

Both raw VIF_ind and VIF_pop data were fit to a bi-exponential decay model (13). Kinetic parameters produced using the fitted VIF_ind and fitted VIF_pop data were compared using the similar statistics as above in order to assess the accuracy of using a fitted VIF_pop versus using a fitted VIF_ind. Additionally, ROI signal data were downsampled by selecting every 20^th point (simulating a temporal resolution of approximately 30 seconds). Data were then interpolated using a linear interpolation scheme in Matlab (the ‘interp1’ function) and fit to extract kinetic parameters using the VIF_ind and VIF_pop as an input to the model. Kinetic parameters were compared with similar statistics as described above.

Results

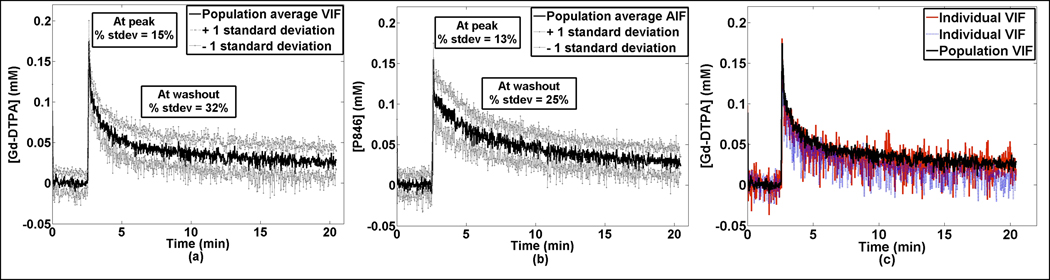
Initial T₁₀ estimates were comparable to literature values; T₁ values for paravertebral muscle ranged from 1.61 s to 1.80 s while the T₁ of the left ventricular blood pool was approximately 1.49 ± 0.06 s. Tumor T₁ values ranges from 1.88 to 3.57 s (26). Using a standard injection protocol, the resulting population averaged VIF for both Gd-DTPA (n=11) and P846 (n=9) are presented in Figure 1a and 1b (black line); the grey lines represent one standard deviation from each population VIF. Figure 1c illustrates two VIF_ind from two separate mice using Gd-DTPA (blue dashed and red lines) compared to the VIF_pop (black solid line). Note that while the red VIF_ind seems to fall along the VIF_pop, the VIF_ind indicated by the blue dashed line has a slightly different washout period. Since P846 is a larger contrast agent, the P846 VIF has a longer wash-out period than those obtained using Gd-DTPA. The peak values for both agents were very similar across all subjects, yielding a standard deviation of approximately 15% while the wash-out was different for both Gd-DTPA and P846 with a standard deviation of 32% and 25%, respectively.

Figure 1.

Population derived VIFs using Gd-DTPA (N = 11) (a) and P846 (N = 9) (b). P846 had a longer wash-out period than Gd-DTPA due to its larger size. Both Gd-DTPA and P846 have a relatively small standard deviation at the peak (13% and 15%, respectively). However, both have a larger standard deviation at ~5–10 minutes during wash-out equal to 32% and 25%, respectively. Panel (c) illustrates two example VIF_ind (blue dashed and red solid lines) obtained using Gd-DTPA compared to the VIF_pop (solid black line).

ROI Analysis

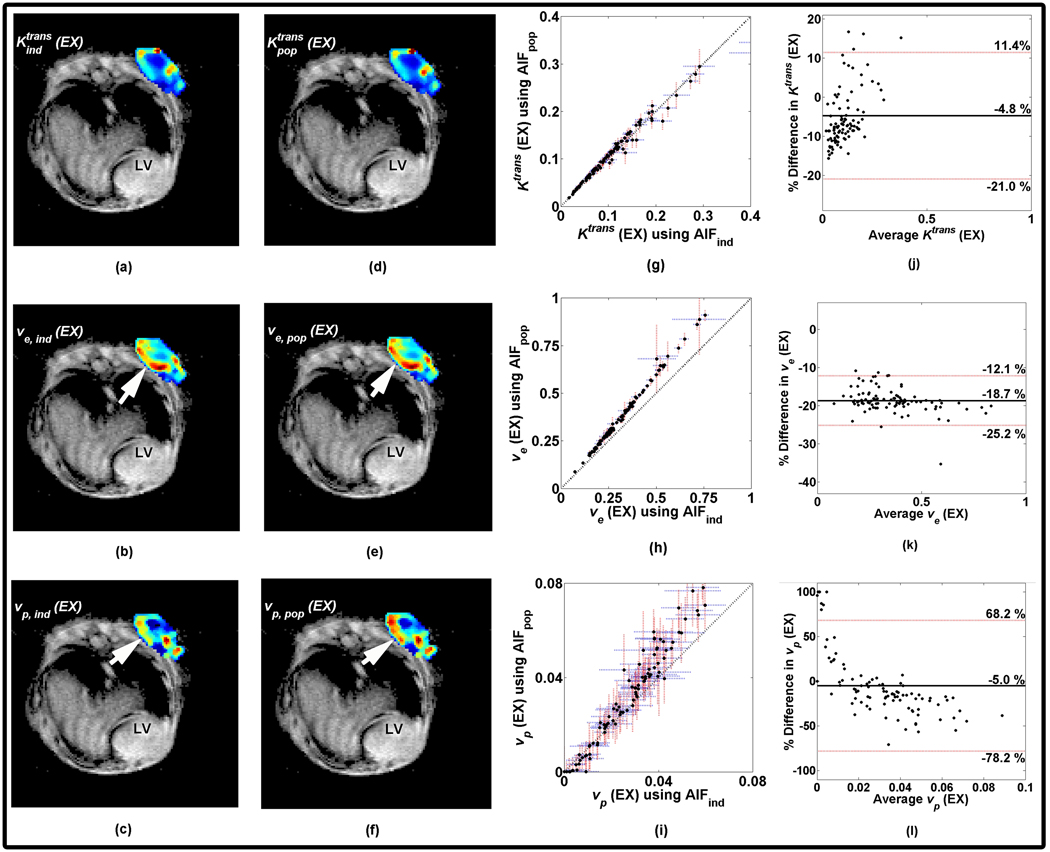
The first set of analyses examined the ROI averaged signal time course from the tumor of each mouse. Each averaged time course was then fit to Eqs. [2] and [3] to extract the pharmacokinetic parameters. By modeling each time-intensity course using both the VIF_ind and VIF_pop, two sets of five parameters (K^trans(ST), v_e(ST), K^trans (EX), v_e (EX), and v_p(EX)) were produced and the subsequent parametric pairs (i.e., K^trans,ind(ST) and K^trans,pop(ST)) were compared. Figure 2 shows the results of this study for Gd-DTPA (a–e) and P846 (f–j). Upon visual inspection, these parameters appear to fall close to the line of identity for both agents; also in both agents, the parametric pairs for v_e(ST) and v_e(EX) tend to deviate from unity more than K^trans(ST), K^trans(EX), and v_p(EX). The CCC, reported in Table 1, represents a quantitative measure of parameter proximity to the line of unity. The CCC values for K^trans (both ST and EX) are > 0.90 for Gd-DTPA and > 0.85 for P846 indicating a strong correlation between the pairs. However, the CCC values for v_e (both ST and EX) are lower for both contrast agents (0.79 to 0.83 for Gd-DTPA and P846, respectively). Interestingly, while both the CCC for K^trans and v_e were similar between the contrast agents, v_p (EX) was very different. v_p (EX) produced using Gd-DTPA had a stronger correlation than the data produced using P846. In addition to the CCC, the Pearson correlation coefficients show a strong significant linear relationship between each paired set of parameters (ranging from 0.80 to 0.97). The results of the linear regression analysis agrees with the interpretation of the CCC in that K^trans (both ST and EX) have slopes that are not statistically different from 1.0 (p > 0.05). Additionally, with the exception of the v_p (EX) fit (p < 0.01), the slopes were not significantly different from 1.0 (p > 0.05) for the ROI parameter comparisons. The intercepts were also not significantly different from 0.0 (p > 0.05) for either contrast agents.

Figure 2.

Parametric plots for both Gd-DTPA (a–e) and P846 (f–j) resulting from the ROI analysis. Each parameter found from using the VIF_ind (x-axis) and VIF_pop (y-axis) are plotted and the solid black line indicates the line of identity. The units of K^trans is min⁻¹ while both v_e and v_p are unitless volume fractions.

Table 1.

Results from the ROI-based comparison.

	CCC (95% CI)		Pearson		Slope		Intercept
	Gd- DTPA	P846	Gd- DTPA	Gd- DTPA	Gd- DTPA	P846	Gd- DTPA	P846
Ktrans (ST)	0.93 (0.81,0.98)	0.93 (0.73,0.98)	0.95	−0.02	1.20	1.10	−0.02	0.00
ve (ST)	0.82 (0.48,0.95)	0.84 (0.62,0.94)	0.83	0.08	0.74	1.48	0.08	−0.08
Ktrans (EX)	0.96 (0.85,0.99)	0.85 (0.47,0.96)	0.96	−0.01	1.06	0.82	−0.01	0.01
ve (EX)	0.80 (0.42,0.94)	0.82 (0.58,0.93)	0.81	0.09	0.69	1.45	0.09	−0.07
vp (EX)	0.88 (0.76,0.97)	0.45 (0.02,0.74)	0.98	0.00	1.54*	1.61	0.00	0.00

^*slope significantly different from 1 (p < 0.05)

Voxel Analysis

As described above, voxels for each animal were fit to Eqs. [2] and [3] to yield paired parametric maps using both the VIF_ind and VIF_pop. Since both the standard and extended models followed similar trends, an example mouse fit to the extended model is demonstrated in Figure 3. Panels a–c demonstrate the parametric maps overlaid on a (gated) T₁-weighted anatomical image obtained using the VIF_ind during modeling, while panels d–f depict parametric maps obtained using the VIF_pop. When plotted against each other, as in panels g–i the voxel level data are linearly related (black line represents unity). Panels j–l illustrate Bland-Altman plots for each kinetic parameter with the x-axis representing the average parametric value between those obtained using the VIF_ind and VIF_pop while the y-axis is the percent difference between VIF_ind and VIF_pop parametric estimations with respect to the VIF_ind parameter. The solid black line is the mean difference while the dotted red lines represent ± 2*standard deviation. The slopes of the fit lines for K^trans pairs for the subject shown in Figure 3 differ from unity by 5–7% while the slopes of the fit lines for v_e and v_p deviate from the identity line by as much as 24–31%. Upon closer inspection of the maps of this particular mouse, the overestimation of v_e and v_p by the VIF_pop (panels e and f) compared to their respective pairs (b and c) are shown by the arrows in panels b, c, e, and f. The differences between these estimations are quantified in panels j–l. For this animal, confidence intervals (CI), shown as the vertical red and horizontal blue dotted lines for K^trans are very tight (g) while CI boundaries for v_e tend to be tighter for lower values and increase as the value of v_e increases (h). CI values for v_p are quite large but are similar for both the VIF_ind and VIF_pop (i).

Figure 3.

Parametric maps determined using the extended model overlaid on a T₁-weighted anatomical image (gated) for one mouse. Panels a–c depict the parametric maps using the VIF_ind while d–f show the maps resulting from using the VIF_pop. Each parameter for each voxel is plotted with respect to its pair in g–i where the solid black line indicates the line of unity. Each data point has a set of dotted vertical red and horizontal blue lines that represent the 95% CI for the respective axes. A Bland-Altman plot is presented in j–l for each parameter. The x-axis represents the average parametric value between those obtained using the VIF_ind and VIF_pop while the y-axis is the percent difference between VIF_ind and VIF_pop parametric estimations with respect to the VIF_ind parameter. The solid black line is the mean difference while the dotted red lines represent ± 2*standard deviation. The maps are very similar, particularly for K^trans. However, overestimations in v_e and v_p are evident using the VIF_pop versus the VIF_ind. The arrows in panels b and e emphasize the areas within the maps where v_e found using VIF_pop is overestimated relative to v_e found using VIF_ind. In panels c and f, the overestimations are also noted for the v_p parameter as well.

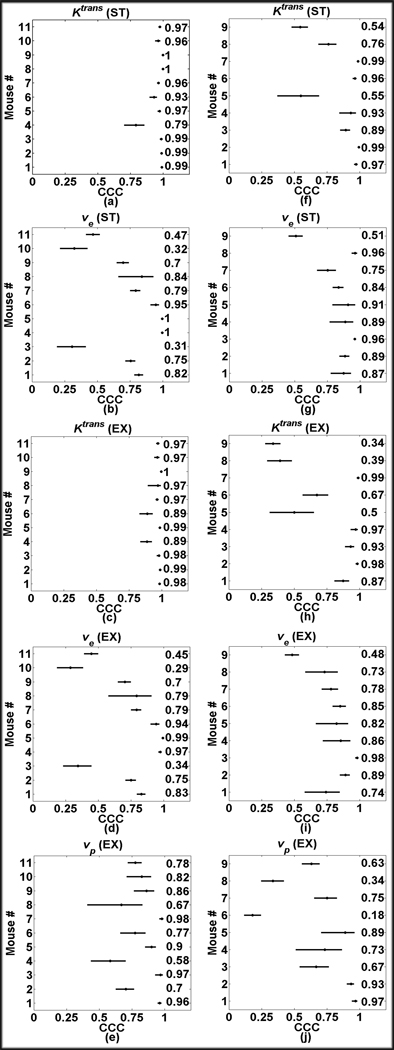
The CCC was computed for each animal for each parameter and results are presented in Figure 4. Panels a–e in Figure 4 display the plots of the CCC (x axis) for each animal (y axis) with the solid lines showing the 95% CI boundaries for each value while the number on the far right is the nominal CCC. While the voxel-based analysis echoes the results of the ROI-based analysis, the difference between the parameter pairs is magnified for some animals. K^trans (both ST and EX) still reflects very high correlation with unity (panels a and c) with the exception of one mouse in the ST analysis and two mice in the EX analysis that used Gd-DTPA, yielded a CCC > 0.90. For P846, seven mice had CCC > 0.75 for K^trans (ST) (panel f). K^trans correlation for P846 is reduced in the extended model, yielding five mice with CCC > 0.85. Three mice using Gd-DTPA had CCC < 0.70 for v_e (both ST and EX), (panels b and d). For mice that were imaged using P846, eight had CCC > 0.70 for v_e (panels g and i); again, modeling with the standard model provided higher correlations than the extended model for P846 data. Additionally, v_p had nine mice with CCCs higher than 0.75 for Gd-DTPA data while only four had CCC > 0.75 using P846.

Figure 4.

Panels a–e show the CCC plots for the respective kinetic parameter in the voxel based analysis found using Gd-DTPA; the P846 data is shown in panels f–j. Each plot displays the CCC values (y-axis) and 95% CI for voxels obtained from each animal (x-axis). The nominal values are listed in the column on the right side of the plot.

Additional quantitative results from the voxel-by-voxel study are shown in Tables 2–5. Tables 2 and 3 show the Pearson correlation coefficient and linear regression results for Gd-DTPA for the standard and extended models, respectively. Tables 4 and 5 present results for P846 using the standard and extended models, respectively. The Pearson correlation coefficients reflect a high degree of linearity between parameter pairs in both Gd-DTPA and P846 data. For the P846 data, 10 of 11 mice have regression slopes for K^trans(as estimated by the two VIFs in either ST or EX modeling) that are statistically different from 1.0, while 7 of 11 mice receiving Gd-DTPA have slopes that are significantly different than 1.0. For both contrast agents, 7 of 11 animals yielded slopes from the v_e and v_p linear regression that are significantly differently from 1.0 (p < 0.05). In general, more animals had significantly different intercepts (p < 0.05) in the P846 data set then the Gd-DTPA as indicated in Tables 2–5; for example, five animals had significantly different intercepts (p < 0.05) for the K^trans (EX) parameter in the Gd-DTPA data set while eight of the nine animals in the P846 data set had significantly different intercepts from 0.0 (p < 0.05).

Table 2.

Voxel-based results for Gd-DTPA data using ST model.

Mouse	Pearson Corr. Coefficient		Slope		Intercept
	Ktrans (ST)	ve (ST)	Ktrans (ST)	ve (ST)	Ktrans(ST)	ve (ST)
1	1.000	0.992	0.927*	0.796*	−0.006†	0.005
2	0.999	0.996	1.090*	1.340*	0.010†	−0.005
3	0.998	0.882	0.983	0.457*	−0.011†	0.084†
4	0.998	0.998	1.441*	1.011	−0.031†	−0.017†
5	0.999	1.000	1.144*	0.957*	−0.008†	0.008
6	0.999	0.981	0.826*	0.975	−0.011†	−0.023
7	1.000	1.000	0.921*	0.836*	−0.002†	0.008†
8	0.999	1.000	1.011	0.695*	−0.004	−0.001
9	0.999	0.989	0.998	0.829*	−0.011†	−0.033†
10	0.998	0.888	1.146*	1.631*	0.007†	0.081
11	0.993	0.975	1.047*	1.565*	0.011†	0.037†

^*slope significantly different from 1 (p < 0.05),

^†intercept significantly different from 0 (p ≤ 0.05)

Table 5.

Voxel-based results for P846 data using EX model.

Mouse	Pearson Corr. Coefficient			Slope			Intercept
	Ktrans (EX)	ve (EX)	vp (EX)	Ktrans (EX)	ve (EX)	vp (EX)	Ktrans (EX)	ve (EX)	vp (EX)
1	0.982	0.846	0.987	1.469*	0.597*	0.869*	−0.005†	0.058†	−0.001
2	0.989	0.997	0.983	0.925*	1.251*	1.313*	0.010†	−0.013†	−0.004†
3	0.995	0.994	0.983	1.301*	1.010	1.735*	−0.011†	0.002	−0.002†
4	0.993	0.998	0.989	1.217*	0.734*	1.612*	−0.023†	0.004	0.003
5	0.993	0.976	0.921	2.056*	0.695*	0.918	−0.029†	0.047†	0.004†
6	0.904	0.975	0.789	0.484*	1.214*	3.318*	0.037†	0.032†	0.008†
7	0.993	0.993	0.990	1.028	1.328*	1.784*	0.007	0.006	−0.002
8	0.935	0.739	0.940	0.343*	0.828	2.824*	0.013†	0.069	0.005†
9	0.960	0.986	0.935	0.301*	0.517*	1.824*	0.007†	0.002	0.002†

^*indicates a slope significantly different from 1 or intercept significantly different from 0 (p ≤ 0.05)

Table 3.

Voxel-based results for Gd-DTPA data using EX model.

Mouse	Pearson Corr. Coefficient			Slope			Intercept
	Ktrans (EX)	ve (EX)	vp (EX)	Ktrans (EX)	ve (EX)	vp (EX)	Ktrans (EX)	ve (EX)	vp (EX)
1	0.998	0.993	0.978	0.922*	0.793*	1.129*	−0.010†	0.004	−0.001
2	0.991	0.992	0.888	0.968*	1.319*	1.638*	0.021†	−0.001	−0.001
3	0.997	0.924	0.976	0.909*	0.488*	0.957	−0.003	0.065†	−0.002
4	0.998	0.998	0.949	1.248*	0.939*	1.725*	−0.001	0.004	−0.008
5	0.997	1.000	0.991	1.072*	0.956*	1.371*	−0.003	0.005†	0.001†
6	0.986	0.980	0.868	0.784*	0.958	1.401*	−0.006	−0.018	−0.003
7	1.000	0.999	0.990	0.921*	0.833*	0.979	−0.002	0.009†	−0.002
8	0.987	0.999	0.999	0.890	0.647*	2.186*	−0.001	0.006	0.000
9	0.998	0.987	0.881	1.027*	0.826*	0.953	−0.015†	−0.029†	−0.003
10	0.995	0.863	0.957	1.096*	1.609*	1.454*	0.009†	0.106	0.002
11	0.989	0.973	0.965	1.005	1.613*	1.725*	0.014†	0.027	−0.003†

^*slope significantly different from 1 (p < 0.05),

^†intercept significantly different from 0 (p ≤ 0.05)

Table 4.

Voxel-based results for P846 data using ST model.

Mouse	Pearson Corr. Coefficient		Slope		Intercept
	Ktrans (ST)	ve (ST)	Ktrans (ST)	ve (ST)	Ktrans (ST)	ve (ST)
1	1.000	0.922	1.211*	0.745*	−0.002†	0.034†
2	0.997	0.996	0.951*	1.244*	0.009†	−0.013†
3	0.999	1.000	1.232*	1.038*	−0.005†	0.001†
4	0.998	0.999	1.327*	0.750*	−0.018†	0.010†
5	0.998	0.972	1.865*	0.770*	−0.024†	0.043†
6	0.990	0.999	0.811*	1.309*	0.025†	0.012†
7	1.000	0.987	1.091*	1.356*	0.006†	0.003
8	0.997	0.964	0.597*	0.903*	0.005†	0.027†
9	1.000	0.996	0.451*	0.528*	0.001†	−0.001

^*slope significantly different from 1 (p < 0.05),

^†intercept significantly different from 0 (p ≤ 0.05)

Modeling and Temporal Resolution Analysis

Upon fitting both the Gd-DTPA VIF_ind and VIF_pop, absolute kinetic parameter values changed somewhat with respect to that of the raw data analysis; however, no significant difference (p-values ranging from 0.897 to 0.904) was found between these absolute values produced. Additionally, the range of CCC values found in the statistical comparison between values produced using the fitted VIF_ind and the fitted VIF_pop and the comparison between values produced using the raw VIF_ind and the raw VIF_pop data changed little as well compared to CCC values reported in Table 1; for the fitted VIF analysis, the CCC values for each parameter were as follows: K^trans (ST) = 0.96, v_e (ST) = 0.85, K^trans (EX) = 0.97, v_e (EX) = 0.83, and v_p (EX) = 0.69. The parameters resulting from the bi-exponential decay analysis resulted in the following parameters for the population VIF data: for Gd-DTPA, a₁ = 0.0516 kg/L, m₁ = 0.0450 sec⁻¹, a₂ = 0.0820 kg/L, and m₂ = 1.3045 sec⁻¹; for P846, a₁ = 0.0602 kg/L, m₁ = 0.0452 sec⁻¹, a₂ = 0.0516 kg/L, and m₂ = 0.4920 sec⁻¹.

Parameters determined using the original sampled (1.5 sec) tissue signal and the parameters obtained by downsampling the data (30 sec) displayed an insignificant difference in absolute parametric values (p-values ranging from 0.792 to 0.933); additionally, the effect of using the population vs. the individual VIF to fit the data still follows a similar trend as presented for the Gd-DTPA ROI analysis using the original temporal resolution. Similar to those reported in Table 1, CCC values for the downsampled data were as follows: K^trans (ST) = 0.94, v_e (ST) = 0.85, K^trans (EX) = 0.95, v_e (EX) = 0.75, and v_p (EX) = 0.95.

Discussion

Measuring the vascular input function is one of the more challenging aspects of DCE-MRI measurement and quantification, particularly in small animals. In Pickup, et al., only four mice were used in the study, and spatial resolution was sacrificed in order to obtain an adequate temporal resolution for VIF acquisition (11). A very comprehensive study by McGrath et al., compared the VIF in rats with frequently used VIF models and the population averaged VIF and reported the downstream effects on pharmacokinetic modeling parameters (14). As mentioned previously, these two studies came to different conclusions on the use of a population derived VIF. To the best of our knowledge, no study has extensively examined population and individual VIFs in mice and the effects on pharmacokinetic modeling parameters. Additionally, this study has eliminated injection variability in that an automated syringe pump was used with identical settings for all animals.

The temporal resolution requirements for measuring an accurate VIF typically are not compatible with the spatial resolution requirements of imaging a large heterogeneous tumor. In order to alleviate these technical demands, the use of a population VIF has been proposed, and this work has focused on assessing the feasibility and resultant error when using a population VIF instead of acquiring individual VIFs in mice. In order to construct an accurate population VIF, a consistent injection protocol must be established. The rapid injection protocol in this study was used for a two main reasons. Firstly, the shorter injection time has been shown to more closely relate K^trans to the initial uptake of the contrast agent within a given voxel as well as more closely relate v_e to the accumulation of the agent extravascularly using this specific model (1). Additionally, a rapid injection protocol yields a rapidly rising, short-lived peak concentration which is typically the most difficult to capture and characterize; thus, the “worst-case” VIF was used in this work to compare the downstream effects on the kinetic parameters. We would anticipate translation of the kinetic parameter comparison using a longer, slower injection protocol to be similar. Other injection protocols can be found in the literature with a couple of examples provided here (27,28).

Care was also taken to minimize the error associated with a VIF. A low dose of Gd-DTPA (0.05 mmol/kg) was used to reduce T₂^* effects. Additionally, cardiac and respiratory gated scouts allowed placement in the left ventricle such that 1) the number of voxels in the center of chamber was maximized to reduce partial volume effects from the ventricle walls, and 2) the slice was the farthest away from the mitral valve to reduce flow effects, but sufficiently distant from the cardiac apex to avoid contamination from the myocardium; thus cardiac motion artifacts were minimized. While an inversion recovery sequence with an adiabatic inversion pulse was incorporated to reduce T₁₀ measurement errors, the authors acknowledge that the accuracy of the T₁ measurements during the dynamic acquisition would be improved by incorporating a saturation pulse to reduce partial saturation of the blood. Incorporating a saturation pulse, however, would have required an increase in temporal resolution and/or a decrease in spatial resolution. By foregoing the saturation pulse and obtaining a rapidly-sampled VIF and an in-plane spatial resolution of 230 µm², comparisons between the VIF_ind and VIF_pop at both a ROI- and voxel-based level were achievable. Finally, an automated syringe pump was used to ensure reproducible delivery of the contrast agent to all mice. These details are critical to measure reproducible individual VIFs that will ultimately produce a population VIF.

In Figure 1, the population VIFs for Gd-DTPA and P846 have a relatively low standard deviation at the peak of the curve which suggests these individual VIFs are reaching very similar peak concentration in the LV. In the Gd-DTPA and P846 data, the higher variability in the wash-out manifests itself primarily in the v_e parameter while the smaller variability at the peak and wash-in phase seem to be reflected in the high correlations between K^trans measures.

In the ROI analysis, correlations and trends for K^trans and v_e are similar for the standard and extended models as well as the different contrast agents. K^trans (both ST and EX) displays a high correlation, indicating that parameters produced using the VIF_pop are very similar to those that are produced using the VIF_ind. For v_e, however, the CCCs are lower, which is most likely an indirect manifestation of the larger wash-out variability seen in Figure 1. However, the ROI-based analysis did not appear to be as sensitive to this variability as the voxel-based comparison. The ROI-based analyses suggest that using a population VIF produced statistically similar parameters, especially for K^trans(ST and EX) indicated by a correlation with unity > 0.90. For v_e and v_p parameters, the results did not follow a similar trend as they tended to drift from unity. However, these parameters show a large degree of linearity, which indicates that an overall shift in the wash-out period of the VIF_ind compared to that of the VIF_pop would produce parameters that were linearly shifted as well (either over- or underestimated). While this is not ideal, the strong linearity of these parameters suggests that the VIF shape is similar. Thus, if the VIF_pop was used in a treatment study, for example, the pre- and post-treatment values for v_e would both be potentially over- or underestimated but the relative change in the parameter may remain the same.

One of the goals of using larger contrast agents such as P846 is to differentiate flow and permeability characteristics in the tissue. Gd-DTPA is small (~ 0.5 kDa); thus, clearance and extravasation to the tissue may be more flow-limited when compared to a larger agent. However, by inspection of the VIFs in Figure 1, it is evident that the larger contrast agent provides a longer peak and wash-out period. The permeability of tissue and the ability to clear a contrast agent are characteristics that are unique to each animal; thus, for smaller agents such as Gd-DTPA the differences in permeability and clearance do not have as great an impact on the VIF_ind or VIF_pop. However, with P846 the permeability and clearance rate become a more important factor in both the VIF_ind and tissue curves; hence, the greater disparity between parameter pairs such as v_e and v_p, indicate that the variability in permeability and clearance for P846 between animals may lead to greater differences between the VIF_ind and VIF_pop.

The voxel-based data follows a similar trend as the ROI-based analysis; however, the sensitivity to the differences between parameter pairs is magnified, as illustrated in Figures 3 and 4. The parametric maps show that, in this particular mouse, the wash-in and peak phase of the VIF are similar, thus producing K^trans (both ST and EX) data points that fall along the line of identity. In this mouse, the v_e and v_p parameters obtained from the VIF_pop are always overestimated from the parameters produced from the VIF_ind. The plots show this linear increase, which is an indirect demonstration of the VIF_ind curve being overestimated by the VIF_pop. It is also worth noting that, as mentioned in the Methods section, some voxel signal data were fit using the VIF_ind but could not be fit with VIF_pop (i.e., the parameters returned using VIF_pop were outside a physiologically relevant range). These data were not included in the above analysis as these “outlier” data tended to severely skew linear regression analysis. Instead, these occurrences were tallied to show the frequency of the occurrences within each mouse and shown in Table 6.

Additional results comparing a fitted VIF_ind and a fitted VIF_pop showed similar statistical trends to that of comparing the raw VIF_ind and a raw VIF_pop suggesting than if bi-exponentially fit data is used for the VIF, the conclusions discussed here remain valid. By examining a temporal resolution that better reflects a more realistic application of obtaining high resolution, high signal to noise scans, it was concluded that while the downsampled data may produce differing absolute parametric values, the comparison to using a VIF_ind or a VIF_pop remains the same. As noted in the results examining the effects of temporal resolution, the comparison of kinetic parameters using a VIF_pop relative to the VIF_ind is of interest and is independent of T₁-mapping and DCE-MRI protocol as long a stringent protocol guidelines are in place.

The results of this study indicate that for animals imaged with Gd-DTPA, K^trans (obtained by both the standard and extended models) estimated using a population based VIF have a very high correlation with K^trans parameters estimated using an individual VIF on both a global (ROI) and local (voxel) level. Since K^trans is typically the primary metric for the majority of DCE-MRI studies, this work supports the use of a population derived VIF with a stringent injection protocol.