Monetary Incentives in Speeded Perceptual Decision: Effects of Penalizing Errors Versus Slow Responses

Abstract

The influence of monetary incentives on performance has been widely investigated among various disciplines. While the results reveal positive incentive effects only under specific conditions, the exact nature, and the contribution of mediating factors are largely unexplored. The present study examined influences of payoff schemes as one of these factors. In particular, we manipulated penalties for errors and slow responses in a speeded categorization task. The data show improved performance for monetary over symbolic incentives when (a) penalties are higher for slow responses than for errors, and (b) neither slow responses nor errors are punished. Conversely, payoff schemes with stronger punishment for errors than for slow responses resulted in worse performance under monetary incentives. The findings suggest that an emphasis of speed is favorable for positive influences of monetary incentives, whereas an emphasis of accuracy under time pressure has the opposite effect.

Introduction

The assumption that incentives – and in particular monetary rewards – have beneficial effects on performance is widely accepted and frequently determines human decisions and behavior. Empirical data, however, support this intuition at best partly, and reviews of the corresponding literature reveal a rather inconclusive mixture of results (Jenkins et al., 1998; Camerer and Hogarth, 1999; Bonner et al., 2000; Bonner and Sprinkle, 2002). Bonner et al. (2000), for instance, found in their meta study that monetary rewards improve performance in no more than half of the cases. In the other half, incentives had no effect or even impaired performance. Apparently, incentive effects depend on the interplay with other moderating variables that have to be taken into account for a comprehensive understanding of the relation between reward and behavior. Accordingly, Bonner and Sprinkle (2002) specified a number of mediating factors, such as person variables, task difficulty, environmental conditions, and incentive schemes. Despite the identification of these factors, however, their particular contribution to reward effects has rarely been studied systematically. The present study therefore aimed at further exploring one of these links and investigated influences of different incentive schemes on perceptual decision making under time pressure.

Our starting point was a recent study by Hübner and Schlösser (2010) that revealed a positive relation between monetary incentives and performance in a flanker task (Eriksen and Eriksen, 1974). In this experiment, participants received a positive payoff of 10 points for correct responses that were faster than a given deadline. Erroneous responses before deadline expiration resulted in a loss of 10 points, whereas responses exceeding the deadline entailed a 20 point penalty, irrespective of correctness. Thus, under this payoff scheme, response speed would ideally be adjusted in a way that avoids deadline misses without sacrificing too much accuracy. The result shows that participants receiving performance-contingent monetary reward (earned points were converted to money) were able to follow this strategy more successfully than participants getting a fixed amount of money (earned points were only symbolic). Yet, it remained unclear to what extent this finding translates to other payoff schemes.

Given the sensitivity of incentive effects to mediating factors, it is possible that this pattern of results is specific for payoff schemes comprising relatively small rewards for rapid decisions in combination with high penalties for slow responses. That penalties play a special role for behavior is indicated by the phenomenon of loss aversion (Kahneman and Tversky, 1979; Tversky and Kahneman, 1991). In their seminal work, Kahneman and Tversky demonstrated that loss and disadvantage have a greater impact on decisions than gain or benefits. Thus, payoff schemes relying on high penalties rather than on bonuses may effectively influence performance. In fact, there is some evidence indicating an increase of effort under impending penalties (Hannan et al., 2005). Accordingly, especially the risk of losing money (compared to only symbolic points) may encourage the mobilization of additional resources and motivate an increase of attentional effort to achieve optimal performance (Sarter et al., 2006).

Despite these considerations, though, the exact role of penalties in payoff schemes remains unclear. With respect to Hübner and Schlösser (2010), for instance, it is an open question whether positive incentive effects rely on punishment especially of slow responses or whether monetary penalties for incorrect responses per se trigger enhanced performance. Different behavior for these two variants of payoff schemes is possible because they presumably involve different response strategies. In particular, with high penalties for slow responses, an advantageous strategy is a general increase of reaction speed, such that deadline criteria are met even if this comes at the cost of accuracy. A wealth of studies examining the speed–accuracy tradeoff have shown that participants are remarkably good in adjusting their response latencies even to very brief time limits by accepting higher error rates (e.g., Link and Tindall, 1971; McElree and Carrasco, 1999; Miller et al., 2008). In fact, formal models are able to simulate this behavior accurately and to predict response time and error distributions via shifts of corresponding decision criteria (Ratcliff and Rouder, 1998; Usher and McClelland, 2001; Ratcliff and Smith, 2004; Hübner et al., 2010). Thus, it is conceivable that participants can easily identify and apply a strategy of speeding up responses if required, especially when monetary loss is higher for slow responses than for errors.

In comparison, a payoff scheme with higher punishment for errors than for slow responses may cause a different behavior because the relevance of accuracy augments relative to that of speed. In this case slow responses are profitable because they grant higher accuracy while the cost of missing time requirements is comparably low. At the same time, however, the presence of deadlines induces time pressure, resulting in a competition between subjective accuracy and objective speed demands. The necessity of high accuracy without an overmuch reduction of speed potentially increases task complexity and the involvement of corresponding cognitive strategies, a situation that has proven to be detrimental for positive effects of monetary incentives (Bonner et al., 2000). It is therefore possible that positive incentive effects decline or even vanish under payoff schemes that emphasize accuracy in speeded response tasks. The present study examined this issue by manipulating the relative height of penalties for errors and slow responses.

To grant comparability to previous findings, we adopted the experimental setup and procedure from Hübner and Schlösser (2010). In particular, we used a flanker task (Eriksen and Eriksen, 1974) that requires the classification of a target stimulus in presence of response-incompatible or neutral flankers. As a standard finding, responses are slower and less accurate to targets accompanied by incongruent compared to neutral flankers. This flanker effect is often considered as an index for the efficiency of selective spatial attention. That is, a small effect indicates that attention is narrowly focused on the target stimulus, which largely prevents co-processing of flankers. Conversely, a large flanker effect signals a wide attentional span, such that flankers substantially contribute to stimulus processing and response selection. In this case, incongruent flankers co-activate the incorrect response and therefore evoke a response conflict (e.g., Eriksen and St. James, 1986; LaBerge et al., 1991; Gratton et al., 1992; Hübner et al., 2010). Although Hübner and Schlösser (2010) found a general improvement of performance under monetary incentives there was no strong evidence for an increase of selective spatial attention; however, a trend toward a smaller flanker effect for short deadlines pointed to slightly enhanced selective attention in the monetary condition. Yet, there is also evidence that incentives may enhance distractor effects (Seifert et al., 2006). In a flanker task, Seifert and colleagues reported generally faster response times for trials holding out rewards or penalties as compared to non-incentivized trials. Error rates, however, revealed a larger flanker effect for the rewarded condition. Given these reverse patterns, the present study also tested again whether monetary incentives improve or impair selective attention.

Experiment 1

Experiment 1 examined whether monetary incentives have a positive effect on performance when deadline misses are not punished (DLnP scheme). Correct and erroneous responses faster than the deadline were rewarded with a 10-point gain and loss, respectively. For comparison, we also included a condition in which deadline misses were additionally punished by a loss of 20 points (DLP scheme), a payoff scheme that has previously yielded positive incentive effects (Hübner and Schlösser, 2010).

We expected improved performance for monetary compared to symbolic incentives for both the DLP and the DLnP payoff scheme if incentive effects are independent from penalties for deadline misses. Alternatively, if punishment of slow responses is crucial for positive effects in these schemes, the influence of monetary incentives should be stronger under the DLP than under the DLnP scheme.

Materials and methods

Participants

A total of 104 voluntary participants recruited at the University of Konstanz were randomly assigned either to the Deadline-Punished (DLP, N = 50) or to the Deadline-not-Punished (DLnP, N = 54) payoff scheme¹. Within each payoff group, an equal number of subjects was randomly allotted to the monetary (DLP: 22.7 years, 19 female; DLnP: 21.5 years, 21 female) and to the symbolic incentive condition (DLP: 22.8 years, 18 female; DLnP: 23.6 years, 18 female). Payoff and incentive conditions are described in detail below.

Apparatus and stimuli

Stimuli were presented on an 18″ color-monitor with a resolution of 1280 × 1024 pixels and a refresh rate of 60 Hz. A computer mouse served as response device. Stimulus presentation and response registration were controlled by the same computer.

Numerals from two to nine served as target items in a parity-judgment task. Stimulus congruency was manipulated by two identical flankers on either horizontal side of the target. For incongruent stimuli, flankers consisted of response-incompatible numerals, i.e., flankers and targets differed in parity. For neutral stimuli the characters $, &, ?, or # were used as flankers. The target was always presented at screen center. Each character extended a visual angle of approximately 0.9° horizontally and 1.27° degrees vertically, the spacing between characters (center to center) was 1.27° of visual angle. Stimuli were presented in white on a black background.

Payoff and incentives

Participants were assigned to one of two payoff schemes. In the Deadline-Punished scheme (DLP or [10, −10; −20]), they received 10 points for correct responses that were faster than the deadline. For incorrect responses that were faster than the deadline, they lost 10 points. If the deadline was missed they lost 20 points irrespective of response correctness. Similarly, in the Deadline-not-Punished scheme (DLnP or [10, −10; 0]), responses faster than the deadline resulted in a 10-point gain for correct and in a 10-point loss for incorrect answers. However, there was neither a gain nor a penalty for responses missing the deadline.

Incentives were either symbolic or monetary in both payoff schemes. Participants in the symbolic condition were informed that the points they earned throughout the experiment are indicative for their performance but that payment (8 EUR) is independent from their balance. In the monetary condition, the earned points were converted to money after the experiment. Participants were told that they would receive a base payment of 6 EUR and could earn an additional amount of up to 5 EUR, depending on their final balance. Information about payoff scheme and incentive condition was given prior to the experiment. In all conditions, a start-up balance was set to a value of 1000 points.

Procedure

Participants were seated at a distance of approximately 50 cm from the monitor. Their task was to indicate the parity of the target numeral by pressing the corresponding mouse button with the index or middle finger of their right hand. A trial started with a central fixation cross for 400 ms. After a cue–stimulus interval of 600 ms, the stimulus array appeared for 165 ms. The screen remained blank until response. A feedback screen (see below) appeared then for 1300 ms and was followed by a blank screen for another 1000 ms before the next trial started. Categorization errors were signaled by a brief sound. A total of nine blocks à 64 trials with three blocks of each of the long (650 ms), medium (525 ms), and short (450 ms) deadlines were presented in decreasing order. Note that this is different to the study of Hübner and Schlösser (2010) who counterbalanced deadline sequences across participants to account for specific effects of fatigue and learning in speed–accuracy tradeoff functions (SATFs). We chose only decreasing orders because deadline counterbalancing was not crucial for the present objective, and because a reanalysis of Hübner and Schlösser’s data revealed the most reliable incentive effects for decreasing deadlines. The experimental session took 1 h.

Feedback

After each response, a feedback screen informed participants about their performance. Feedback showed the current response time in green color if the response was correct and faster than the deadline, in red if the response was an error but faster than the deadline, and in yellow if the deadline was missed, irrespective of response correctness. In addition, the current deadline and the total sum of points were displayed. After each block, participants took a short break (maximally 60 s) while an additional feedback screen informed about the overall performance, i.e., mean response time, error rate, and percentage of missed deadlines in the last block as well as the current point balance (accumulated over all blocks).

Data analyses

Response times shorter than 100 ms and longer than 2500 ms were discarded. Mean response latencies (deadline misses and errors not excluded) and accuracies (proportion of correct answers) are shown in Table 1. Data are illustrated as SATFs in Figure 1.

Table 1.

Mean response times and proportion of correct responses (accuracy).

Payoff–incentives	450 ms deadline				525 ms deadline				650 ms deadline
	RT		Accuracy		RT		Accuracy		RT		Accuracy
DLP-monetary (Experiment 1)
Incongruent	384	(5.34)	0.825	(0.020)	419	(5.16)	0.904	(0.013)	459	(7.15)	0.955	(0.007)
Neutral	375	(4.34)	0.874	(0.015)	405	(4.13)	0.935	(0.010)	443	(6.83)	0.972	(0.006)
DLP-symbolic (Experiment 1)
Incongruent	402	(7.76)	0.825	(0.020)	433	(6.27)	0.883	(0.013)	463	(9.74)	0.934	(0.009)
Neutral	386	(7.66)	0.871	(0.017)	417	(7.01)	0.931	(0.009)	442	(10.59)	0.955	(0.005)
DLnP-monetary (Experiment 1)
Incongruent	425	(8.41)	0.834	(0.014)	462	(6.94)	0.897	(0.011)	518	(9.21)	0.916	(0.007)
Neutral	415	(7.45)	0.882	(0.014)	446	(6.16)	0.928	(0.008)	498	(8.79)	0.943	(0.008)
DLnP-symbolic (Experiment 1)
Incongruent	419	(9.42)	0.842	(0.016)	445	(9.54)	0.900	(0.010)	482	(15.00)	0.913	(0.009)
Neutral	406	(8.55)	0.890	(0.011)	430	(10.04)	0.935	(0.009)	463	(13.56)	0.962	(0.005)
ErrP-monetary (Experiment 2)
Incongruent	415	(5.49)	0.825	(0.018)	454	(5.99)	0.886	(0.012)	500	(9.02)	0.909	(0.009)
Neutral	401	(4.63)	0.884	(0.012)	435	(5.45)	0.927	(0.009)	486	(9.09)	0.939	(0.008)
ErrP-symbolic (Experiment 2)
Incongruent	416	(6.31)	0.860	(0.013)	448	(7.09)	0.910	(0.009)	482	(8.21)	0.940	(0.008)
Neutral	404	(5.31)	0.898	(0.012)	430	(6.34)	0.942	(0.006)	465	(8.40)	0.967	(0.005)
ErrDLnP-monetary (Experiment 3)
Incongruent	383	(4.92)	0.823	(0.023)	416	(5.36)	0.881	(0.017)	448	(8.96)	0.932	(0.011)
Neutral	374	(3.68)	0.866	(0.020)	403	(5.40)	0.932	(0.015)	431	(7.90)	0.951	(0.011)
ErrDLnP-symbolic (Experiment 3)
Incongruent	406	(9.33)	0.820	(0.020)	438	(10.33)	0.855	(0.018)	469	(12.60)	0.914	(0.013)
Neutral	395	(7.98)	0.861	(0.022)	422	(8.94)	0.908	(0.014)	454	(12.32)	0.938	(0.013)

Standard errors of means are given in parentheses.

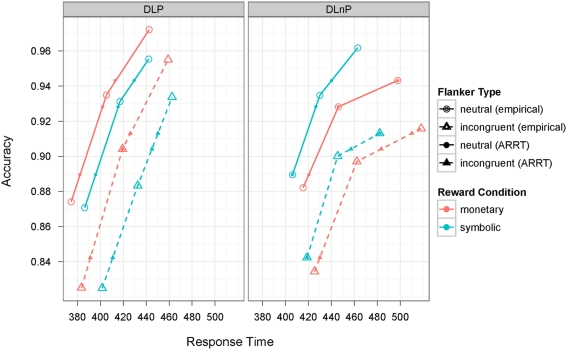
Figure 1.

Speed–accuracy tradeoff functions for incentive conditions (monetary, symbolic) and flanker types (neutral, incongruent) under the payoff schemes DLP [10, −10; −20] and DLnP [10, −10; 0] of Experiment 1. Open symbols in each function reflect empirical data points across three deadline conditions (450, 525, 650 ms). Small filled symbols show corresponding accuracy-referenced response times (ARRTs).

Because performance is reflected in response times as well as in accuracy, the consideration of both dependent variables is crucial for a comprehensive data description. As a pitfall, however, the two measures are naturally correlated, that is, longer response latencies come along with a larger proportion of correct answers (Figure 1). Consequently, independent analyses of response times and accuracy are often difficult to interpret and may even lead to inaccurate conclusions (Wickelgren, 1977). For instance, it is hard to decide whether performance is superior in an experimental condition that yields higher accuracy but also longer response times than a second condition. As another example, an overall increase in performance might show up partly in response times and partly in accuracies (cf, Figure 1), so that effects in both measures are merely indicated by non-significant trends. Such results may then be interpreted in favor of the null hypothesis, although the data suggest an overall improved performance in one condition.

Fortunately, SATFs provide a solution for this dilemma because these functions allow the transformation of one performance measure into another. In other words, SATFs relate each response time to a unique value of accuracy. They therefore permit the estimation of effects in response times at equalized accuracy levels (and vice versa) across experimental conditions. As an example, consider our data for neutral flankers at the longest deadline in the DLnP scheme (Figure 1). Here, monetary incentives yielded a mean response time of 498 ms and an accuracy level of 94.3%. In the symbolic condition, mean response time and accuracy amounted to 463 ms and 96.2%, respectively. SATFs can now be used to adjust both data points to the same accuracy level, so that performance is purely reflected in response times. In particular, we use the monetary incentive condition as reference and interpolate the data point of the symbolic group along its SATF to the corresponding accuracy level of 94.3% (see the corresponding filled small circle in Figure 1). As a result we obtain an accuracy-referenced response time (ARRT) of 440 ms for the symbolic incentive condition. That is, the 1.9% drop in accuracy translates into a decrease of 23 ms in response times. In order to compare performance between payoff schemes, ARRTs in the DLP scheme (650 ms deadline, neutral flankers; see left panel of Figure 1) are computed for the same accuracy level. Notably, choosing the data point closest to the overall mean of accuracies as reference permits the interpolation (in contrast to extrapolation) of values in the other conditions; that is, ARRTs are only estimated within the ranges of their empirical SATFs. Thus, ARRTs provide a novel and largely unbiased approach to estimate performance in speeded decisions as they account for the correlation between response latencies and error rates (for similar approaches see Kliegl et al., 1995; Oberauer and Kliegl, 2001).

In Experiment 1, ARRTs on averaged data were computed separately for flanker types across payoff schemes and incentive conditions (see Figure 1). For each deadline, response times were linearly interpolated² to the accuracy level of the empirical data point that was closest to the grand mean of accuracies (i.e., least squared error). Individual subject data were then corrected accordingly, such that the overall range of accuracies shrunk, but that empirical and referenced data points were situated on the same SATF. Individual ARRTs were submitted to four-way ANOVAs on between-subjects factors payoff scheme (DLP, DLnP) and incentives (monetary, symbolic), and within-subjects factors deadline (long, medium, short), and flanker type (neutral, incongruent). Mean ARRTs together with corresponding accuracies are listed in Table 2. Results of the ANOVAs on unreferenced response times and accuracies are shown in “Experiment 1” in the Appendix. Analyses were conducted in R, a language and environment for statistical computing (R Development Core Team, 2011). Data were visualized with the R-package ggplot2 (Wickham, 2009).

Table 2.

Means of accuracy-referenced response times and corresponding accuracies for the payoff schemes DLP and DLnP (Experiment 1) as well as DLP and ErrP (Experiment 2) across three deadlines (450, 525, 650 ms).

	DLP			DLnP//ErrP			Accuracy
Incentives/deadline	450	525	650	450	525	650	450	525	650
EXPERIMENT 1
Monetary
Incongruent	391	419	426	430	484	510	0.842	0.904	0.913
Neutral	382	402	413	420	446	498	0.890	0.928	0.943
Symbolic
Incongruent	411	445	450	419	457	482	0.842	0.904	0.913
Neutral	396	416	430	406	427	440	0.890	0.928	0.943
EXPERIMENT 2
Monetary
Incongruent	399	419	423	437	490	500	0.860	0.904	0.909
Neutral	386	402	408	412	435	486	0.898	0.927	0.939
Symbolic
Incongruent	420	445	448	416	444	448	0.860	0.904	0.909
Neutral	400	415	425	404	422	428	0.898	0.927	0.939

Results

A significant main effect of payoff scheme in the four-way ANOVA revealed faster ARRTs (p < 0.001) for the DLP (i.e., 20 point penalty for missed deadlines) than for the DLnP scheme (i.e., no penalty for deadline misses). Further, an interaction of payoff scheme × incentives (p = 0.005) pointed to faster ARRTs for monetary than for symbolic condition under the DLP scheme; in contrast ARRTs under the DLnP scheme were slower for monetary than for symbolic incentives (see below). Since the four-way interaction of payoff scheme × incentives × deadline × flanker type was significant (p < 0.001), we scrutinized further effects in separate three-way ANOVAs on the factors incentives × deadline × flanker type for each payoff scheme. Table 3 presents a full list of the four-way ANOVA results.

Table 3.

Results of four-way ANOVAs on accuracy-referenced response times in Experiment 1 and 2.

	Experiment 1: DLP–DLnP			Experiment 2: DLP–ErrP
	df	F	Pr(>F)	df	F	Pr(>F)
Payoff scheme	1	21.60	<0.001	1	19.79	<0.001
Incentives	1	0.33	0.567	1	1.45	0.231
Payoff × incentives	1	8.24	0.005	1	18.01	<0.001
Residuals	100			98
Deadline	2	153.09	<0.001	2	101.79	<0.001
Deadline × payoff	2	13.50	<0.001	2	10.11	<0.001
Deadline × incentives	2	3.12	0.046	2	6.85	0.001
Deadline × payoff × incentives	2	4.39	0.014	2	8.77	<0.001
Residuals	200			196
Flanker type	1	526.62	<0.001	1	626.96	<0.001
Flanker × payoff	1	13.51	<0.001	1	7.62	0.007
Flanker × incentives	1	22.02	<0.001	1	1.41	0.238
Flanker × payoff × incentives	1	<0.01	0.966	1	39.11	<0.001
Residuals	100			98
Deadline × flanker	2	48.97	<0.001	2	35.55	<0.001
Deadline × flanker × payoff	2	6.67	0.001	2	11.28	<0.001
Deadline × flanker × incentives	2	13.37	<0.001	2	11.28	<0.001
Deadline × flanker × payoff × incentives	2	17.04	<0.001	2	16.04	<0.001
Residuals	200			196

Between-subjects factors are payoff scheme (DLP, DLnP in Experiment 1; DLP, ErrP in Experiment 2) and incentives (monetary, symbolic). Within-subjects factors are deadline (long, medium, short) and flanker type (neutral, incongruent).

DLP payoff scheme

Under the DLP scheme, ARRTs increased with deadline, F(2,96) = 41.28, p < 0.001, and were faster for neutral than for incongruent flankers, F(1,48) = 217.58, p < 0.001. Critically, as indicated in the above analysis, a main effect of incentives, F(1,48) = 4.67, p = 0.036, revealed faster ARRTs for the monetary than for the symbolic condition. Further, an interaction of incentives × flanker type, F(1,48) = 12.85, p < 0.001, indicated a larger incentive effect for incongruent than for neutral stimuli. Finally, there was an interaction of deadline × flanker type, F(2,96) = 11.58, p < 0.001.

Performance differences between incentive conditions were also reflected in the total amount of points gained throughout the experiment. Scores were significantly higher in the monetary (mean: 1168; SD: 67) compared to the symbolic condition (mean: 931; SE: 91), F(1,148) = 4.44, p = 0.037.

DLnP payoff scheme

Main effects of deadline, F(2,104) = 119.36, p < 0.001, and flanker type, F(1,52) = 309.51, p < 0.001, were significant in the DLnP scheme. Moreover, the influence of incentives was reliable, F(1,52) = 4.21, p = 0.045; however, different from the DLP scheme, ARRTs were slower for monetary than for symbolic incentives. The two-way interactions of deadline × incentives, F(2,104) = 6.86, p = 0.002, flanker type × incentives, F(1,52) = 9.89, p = 0.002, and deadline × flanker type, F(2,104) = 40.75, p < 0.001, were further qualified by a reliable three-way interaction of deadline × flanker type × incentives, F(1,104) = 26.51, p < 0.001, indicating that the incentive effect increased with deadline, and that this increase was stronger for neutral than for incongruent stimuli at the longest deadline, whereas the pattern was reversed for the shorter deadlines.

Analogously to ARRTs, the pattern of earned points was reversed compared to the DLP scheme. Under DLnP, participants yielded numerically higher scores in the symbolic (mean: 1299; SD: 42) than in the monetary incentive group (mean: 1204; SD: 40); the difference revealed a statistical trend, F(1,160) = 2.70, p = 0.102.

Discussion

The results demonstrate that payoff schemes critically influence incentive effects. Besides the finding that responses were generally faster with (DLP) than without (DLnP) penalties for deadline misses, the two schemes resulted in opposite effects of monetary incentives.

In the DLP scheme, ARRTs as well as the number of attained points attested better performance for monetary than for symbolic incentives; this pattern replicated the previous finding of Hübner and Schlösser (2010). Moreover, a stronger incentive effect for incongruent than for neutral stimuli pointed to improved spatial selectivity in the monetary condition. That is, the negative effect of incongruent flankers was larger for symbolic incentives, suggesting a broader attentional focus than in the monetary condition. This result extends Hübner and Schlösser’s report of a similar trend and indicates that monetary incentives can enhance attentional spatial selection. Yet, Seifert et al. (2006) found a larger flanker effect in rewarded compared to non-incentivized trials. As one possible reason, payoffs (monetary rewards, penalties, or neutral) in that study varied between trials, whereas constant incentives (monetary or symbolic) and payoff schemes in our experiment facilitated optimal adjustment of selective attention. Yet, this account is speculative since there are other differences that might have contributed to the diverse patterns.

In contrast to improved performance under the DLP scheme, responses were slower for monetary than for symbolic incentives in the DLnP scheme. Compatible with the prediction of payoff-specific response strategies, it seems that participants receiving monetary incentives tried to respond slower in order to increase accuracy, i.e., to avoid costly errors (cf, Kahneman and Tversky, 1979). Indeed an increasing incentive effect with deadline pointed to some effort of adjusting response times to the maximal time limit, irrespective of the risk of missing the deadline. Yet, while this strategy appears reasonable, its realization turned out to be suboptimal because performance was in fact worse in the monetary condition. That is, although responses were successfully retarded, the additional processing time did not translate into an equivalent increase in accuracy. Accordingly, SATFs reveal a right-shift of data points in the monetary relative to the symbolic condition: Subjects receiving monetary incentives needed more time to achieve the same accuracy level as the symbolic group (see Figure 1). Likewise, the response strategy failed in terms of profit maximization since the monetary group earned (numerically) less points than the symbolic group. Obviously, participants ignored the fact that fast responses are generally advantageous as long as accuracy is above 50%. Hence, it seems that the response strategy was not solely determined by the aim of profit maximization but also by the tendency to avoid errors (Maddox and Bohil, 1998).

Although we only expected a reduced rather than a negative incentive effect in the DLnP scheme, the outcome is compatible with the assumption of suboptimal performance due to competition between accuracy and speed requirements. Higher penalties for errors than for slow responses emphasize accuracy over speed, while at the same time imposing deadlines induce time pressure. Arguably, this dilemma is especially relevant in the monetary condition, where the actual profit depends on performance. Thus, compared to the speed-prioritizing DLP scheme, the necessity of balancing accuracy against speed increases task complexity and complicates the identification of an optimal response strategy. This may create an imbalance of task requirements and available solutions, a situation that is known to counteract positive incentive effects (Bonner et al., 2000). Similarly, high subjective pressure and the involvement of cognitive strategies in the presence of incentives often result in a drop of performance below participants’ skill levels (Baumeister, 1984; Beilock, 2008; Chu et al., 2010; DeCaro et al., 2011).

In summary, Experiment 1 suggests that penalties for errors and slow responses play different roles for monetary incentive effects. When missed deadlines are punished participants have a strong motivation to respond fast, and they do so without sacrificing much accuracy. Conversely, when there are penalties for errors but not for missed deadlines participants succeed in slowing down response speed, but they fail to improve performance.

Yet, besides deadline penalties, another and potentially confounding difference between the payoff schemes was a generally lower level of punishment in the DLnP than in the DLP condition. Participants in the DLP scheme faced the risk of losing 10 or 20 points for errors or deadline misses, respectively, while the maximum gain per trial was 10 points. In contrast, participants in the DLnP scheme could maximally lose 10 points per trial. Hence, it is unclear whether improved performance for monetary incentives in the DLP condition resulted from the high penalty for deadline misses, or from the overall ratio of loss and gain opportunities. Experiment 2 examined this issue.

Experiment 2

In this experiment we tested potential influences of the proportion of benefits and losses. Like in Experiment 1, we used a payoff scheme entailing a 10-point gain for correct responses faster than the deadline. However, this time errors before the deadline were punished with a loss of 20 points, whereas deadline misses resulted in a 10-point penalty. Thus, in this Error-Punished scheme (ErrP or [10, −20; −10]), penalty was higher for errors than for missed deadlines, while the overall ratio of gains to losses was the same as in the DLP scheme of Experiment 1 [10, −10; −20].

We expected that the ErrP scheme yields a similarly positive influence of monetary incentives as the DLP scheme, if incentive effects depend on the overall gain-to-loss ratio. Alternatively, if the effect is particularly driven by an emphasis of speed due to high penalties of slow responses, the ErrP scheme should not yield a positive effect. Rather, the pattern of results may be similar to that of the DLnP scheme in Experiment 1.

Materials and methods

Participants

A total of 52 participants recruited at the University of Konstanz were randomly assigned to the monetary (N = 26, 22.1 years, 16 female) and the symbolic incentive group (N = 26, 24.5 years, 17 female; see text footnote 1).

Stimuli, procedure, and analyses

Stimuli, task, and procedure were the same as in Experiment 1, but a different payoff scheme was used in Experiment 2: Participants received 10 points for correct responses that were faster than the deadline. Erroneous responses faster than the deadline resulted in a 20 point loss and deadline misses entailed a penalty of 10 points in the Error-Punished scheme (ErrP or [10, −20; −10]).

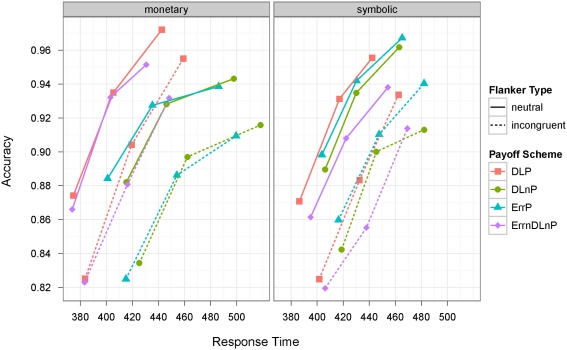
Response times shorter than 100 ms and longer than 2500 ms were excluded. Mean response latencies (deadline misses and errors not excluded) and accuracies (proportion of correct answers) are shown in Table 1. Figure 2 illustrates SATFs of the ErrP scheme together with the DLP and the DLnP schemes of Experiment 1 and the data of Experiment 3 (ErrDLnP scheme).

Figure 2.

Speed–accuracy tradeoff functions for monetary and symbolic incentives in the payoff schemes DLP [10, −10; −20] and DLnP [10, −10; 0] of Experiment 1, in the ErrP scheme [10, −20; −10] of Experiment 2, as well as in the ErrDLnP scheme [10, 0; 0] of Experiment 3. Data points in each function reflect three deadline conditions (450, 525, 650 ms).

For analyses, ARRTs were jointly computed for the ErrP payoff scheme of Experiment 2 and the DLP scheme of Experiment 1 (see Materials and Methods of Experiment 1 and Table 2). ARRTs were first compared in a four-way ANOVA on between-subjects factors payoff scheme (DLP, ErrP) and incentives (monetary, symbolic), and within-subjects factors deadline (long, medium, short), and flanker type (neutral, incongruent). Data of the ErrP scheme were then scrutinized in a three-way ANOVA. Results of ANOVAs on unreferenced response times and accuracies are depicted in “Experiment 2” in the Appendix.

Results

A significant main effect of payoff scheme in the four-way ANOVA revealed faster ARRTs for the DLP than for the ErrP scheme (p < 0.001). In addition, an interaction of payoff scheme × incentives (p < 0.001) yielded slower ARRTs for the monetary than for the symbolic condition in the ErrP scheme (see below), while the opposite held for the DLP scheme (cf, Experiment 1). The effects of the four-way ANOVA were qualified by a four-way interaction of payoff scheme × incentives × deadline × flanker type (p < 0.001; see Table 3 for a full list of results).

ErrP payoff scheme

Like in Experiment 1, the ErrP scheme revealed increasing ARRTs with deadline, F(2,100) = 99.58, p < 0.001, as well as faster ARRTs for neutral than for incongruent flankers, F(1,50) = 350.02, p < 0.001. A main effect of incentives, F(1,50) = 14.44, p < 0.001 confirmed slower ARRTs for the monetary than for the symbolic condition. Further, the effect increased with deadline, as indicated by the incentive × deadline interaction, F(2,100) = 17.53, p < 0.001. An interaction of incentives × flanker type, F(1,50) = 24.36, p < 0.001, together with an interaction of deadline × flanker type, F(2,100) = 35.81, p < 0.001 was qualified by the three-way interaction of incentives × deadline × flanker type, F(2,100) = 22.61, p < 0.001, indicating that the incentive effect was substantially smaller for neutral than for incongruent stimuli at the two fastest deadlines, whereas it was of similar size at the longest deadline.

Concerning performance-dependent points, absolute scores were significantly higher in the symbolic (mean: 974; SD: 68) than in the monetary group (mean: 756; SD: 67), F(1,154) = 5.22, p = 0.024. This pattern is similar to the DLnP data and opposite to the DLP scheme of Experiment 1.

Discussion

Experiment 2 tested whether positive effects of monetary incentives depend on the overall ratio of benefits to losses in payoff schemes. The results do not support this hypothesis, but confirmed the conclusions derived from the findings in Experiment 1. Under the ErrP scheme, where penalty was smaller for deadline misses than for errors, responses were slower than in the DLP payoff scheme. Moreover, slower ARRTs and a smaller amount of earned points in the ErrP scheme indicated worse performance for the monetary than for the symbolic condition, an effect that increased with deadline in ARRTs. Thus, the data suggest that the ratio of gains to losses in a payoff scheme plays a subordinate role for positive incentive effects.

Instead, the results line up with the data of the DLnP scheme in Experiment 1 that also yielded suboptimal performance for monetary incentives, and they are in stark contrast to the positive effects in the DLP scheme (see Figure 2). Apparently, response strategies are substantially modulated by the relative height of penalties for errors and deadline misses, a finding that is compatible with the notion that impending losses have a major impact on behavior (Kahneman and Tversky, 1979). However, in the present experiments performance was improved only when high penalties for deadline misses encouraged speeded responses. This result indicates that loss aversion does not generally produce a positive relation between monetary incentives and performance and raises the question whether explicit penalties are necessary for positive incentive effects. It seems that a general emphasis of speed over accuracy is sufficient in this respect. In Experiment 3 we addressed this issue.

Experiment 3

Data of Experiments 1 and 2 suggested that compulsion of speed rather than of accuracy improves performance in prospect of monetary incentives. We established this finding using payoff schemes in which deadline misses received higher (DLP) or lower punishment than errors (DLnP, ErrP), and entailed either explicit penalties (DLP, ErrP) or just the absence of rewards (DLnP). These schemes leave open, though, whether penalties are in fact imperative for positive incentive effects. Alternatively, similar results may be obtained when neither errors nor deadline misses are punished, and therefore have the same financial consequences³.

Given our previous considerations, the latter option appears indeed possible because – similar to the DLP scheme – payoff involving rewards for fast correct responses but no penalties or rewards for errors and deadline misses should emphasize speed over accuracy. The reason is that such a scheme comes with a 0% chance to gain profit for any response missing the deadline, irrespective of correctness. In contrast, odds for responses meeting time demands amount to at least 50%, i.e., when subjects are simply guessing. Thus, a strategy of speeding up responses to avoid deadline misses is generally more profitable than attempting to maximize accuracy by accepting slow responses. Similar to the DLP scheme in Experiment 1, zero-penalties for errors and deadlines therefore prioritize speed and potentially engage positive incentive effects.

We tested this possibility in Experiment 3 with an Error-and-Deadline-not-Punished (ErrDLnP or [10, 0; 0]) scheme that involved 10-point benefits for fast and correct responses, but neither gains nor losses for errors or deadline misses. We expected that monetary incentives improve performance if positive effects depend on an emphasis of speed over accuracy. In contrast, if incentive effects depend on explicit punishment of slow responses, monetary, and symbolic conditions may reveal similar results.

Materials and methods

Participants

A total of 36 participants from the University of Konstanz were randomly assigned to the monetary (N = 18, 23.8 years, 8 female) and the symbolic incentive group (N = 18, 24.3 years, 14 female; see text footnote 1).

Stimuli, procedure, and analyses

Stimuli, task, and procedure were adopted from the previous experiments, except for the payoff scheme. In the Error-and-Deadline-not-Punished scheme of Experiment 3 (ErrDLnP or [10, 0; 0]), participants received 10 points for correct responses before the deadline, whereas errors and deadline misses entailed neither gains nor losses.

As before, response times shorter than 100 ms and longer than 2500 ms were discarded. Mean response latencies (deadline misses and errors not excluded) and accuracies (proportion of correct answers) are shown in Table 1. Figure 2 illustrates SATFs of the ErrDLnP scheme together with data from Experiments 1 and 2.

ARRTs for incentive conditions in the ErrDLnP scheme were calculated separately for neutral and incongruent stimuli (see Materials and Methods of Experiment 1 and Table 4) and were submitted to a three-way ANOVA with the between-subjects factor incentives (monetary, symbolic) and within-subjects factors deadline (long, medium, short), and flanker type (neutral, incongruent). Results of ANOVAs on unreferenced response times and accuracies are listed in “Experiment 3” in the Appendix.

Table 4.

Means of accuracy-referenced response times and corresponding accuracies for the payoff scheme ErrDLnP (Experiment 3) across three deadlines (450, 525, 650 ms).

Incentives/deadline	ARRT			Accuracy
	450	525	650	450	525	650
EXPERIMENT 3
Monetary
Incongruent	383	401	437	0.823	0.855	0.914
Neutral	374	393	411	0.866	0.908	0.938
Symbolic
Incongruent	409	438	469	0.823	0.855	0.914
Neutral	397	422	454	0.866	0.908	0.938

Results

In the ErrDLnP scheme, ARRTs increased with deadline, F(2,68) = 76.14, p < 0.001, and were longer for incongruent than for neutral flankers, F(1,34) = 109.65, p < 0.001. Importantly, a reliable incentive effect, F(1,34) = 8.58, p = 0.006, revealed shorter ARRTs for the monetary than for the symbolic group, a pattern that corresponds to the DLP scheme of Experiment 1. Further, the interaction of deadline × flanker type, F(2,68) = 6.17, p = 0.003, was qualified by a three-way interaction of incentives × deadline × flanker type, indicating a smaller incentive effect for neutral than for incongruent stimuli at short deadlines, whereas the reverse pattern held for the longest deadline (cf, Table 4).

Similar to the pattern of performance-contingent scores in the DLP scheme (Experiment 1), subjects earned more points in the monetary (mean: 1592; SD: 35) than in the symbolic group (mean: 1479; SD: 43), F(1,106) = 4.23, p = 0.042.

Discussion

Experiment 3 attested improved performance for monetary over symbolic incentives when neither errors nor deadline misses were punished. This pattern is in accordance with results from the DLP scheme of Experiment 1, that involved higher penalties for slow than for erroneous responses (see also Hübner and Schlösser, 2010). In fact, SATFs in the monetary condition revealed a considerable similarity between ErrDLnP and DLP data (Figure 2, left panel); accordingly, ARRT differences between the two schemes were far from being significant (F < 1). Concerning the symbolic condition, there was a small and not reliable trend [F(1,41) = 2.30, p = 0.13] toward slower responses for the ErrDLnP scheme.

Importantly, the analogous effects in the ErrDLnP and the DLP scheme are compatible with the notion of improved performance in prospect of monetary incentives, when payoff schemes prioritize response speed rather than accuracy. Moreover, the data show that explicit penalties are not imperative for positive incentive effects, but that equal payoffs for errors and deadline misses evoke a similar pattern. Thus monetary incentives appear to enhance performance when penalties for errors do not exceed those of deadline misses.

General Discussion

The present study examined the role of payoff schemes for the relation between monetary incentives and performance in speeded perceptual decision making. The issue is of great interest because – against common belief – positive influences of monetary incentives are not warranted. Rather, many studies report no or even negative effects (Jenkins et al., 1998; Camerer and Hogarth, 1999; Bonner et al., 2000; Bonner and Sprinkle, 2002). This suggests that the impact of incentives depends on specific conditions and mediating factors, such as payoff schemes. The exact nature of these relations, however, is not well established. For instance, while a payoff scheme with high penalties for missed deadlines yielded improved performance for monetary compared to symbolic incentives in a previous flanker task (Hübner and Schlösser, 2010) it was unclear whether monetary incentives are generally advantageous for this task, or whether the positive effect depends on the specific payoff scheme. Here, we addressed this question by manipulating the magnitude of penalties for slow responses and errors.

Experiment 1 compared incentive effects under conditions of relatively high (DLP) versus no (DLnP) penalties for deadline misses. While improved performance for the monetary compared to the symbolic condition in the DLP scheme replicated the previous finding (Hübner and Schlösser, 2010), the effect was reversed for the DLnP scheme: Monetary incentives led to a reduced performance. The latter result was confirmed in Experiment 2 (ErrP scheme), where slow responses entailed penalties, but where punishment for errors was higher, so that the overall ratio of gains to losses was identical to the DLP scheme. Thus, while the adjustment of response strategies in these payoff schemes point to marked behavioral variation in order to avoid punishment (e.g., Kahneman and Tversky, 1979), the data demonstrate that a positive relation between monetary incentives and performance can only be obtained when there is a relatively high penalty for slow responses. Yet, the results of Experiment 3 show that explicit punishment is not necessary. A similar positive effect of monetary incentives on performance was found when neither errors nor deadline misses entailed penalties (ErrDLnP scheme). It was sufficient to apply a payoff scheme that induced priority of speed over accuracy.

Presumably, an emphasis of speed encouraged participants to meet time demands by accepting reduced accuracy of rapid responses. That is, high penalties for slow responses in the DLP scheme rendered fast reactions more profitable than deadline misses. Likewise, the ErrDLnP scheme implied a 0% chance of profit when deadlines were missed, but at least a 50% chance (in case of guessing) for faster responses. Apparently, participants were able to translate these odds into appropriate strategies: With monetary incentives, they speeded up their responses while sacrificing relatively little accuracy. A plausible account for this positive effect is that performance-contingent payment motivated the engagement of additional resources, such as an increase of attentional effort (Sarter et al., 2006). As suggested by Hübner and Schlösser (2010), this extra effort may then have caused a general improvement of sensory encoding quality. Yet, the smaller flanker effect under the DLP scheme also points to a specific enhancement of selective spatial attention in the monetary compared to the symbolic condition. This finding augments the previous report of a trend in this direction for short deadlines only (Hübner and Schlösser, 2010), whereas the incentive effect in the DLP scheme was relatively constant across deadlines (see Figure 1). Overall, the data provide strong evidence that monetary incentives enhanced the efficiency of stimulus processing when payoff schemes stressed the relevance of speed.

In contrast to the DLP and the ErrDLnP schemes, higher penalties for errors than for deadline misses (i.e., DLnP and ErrP schemes) emphasized accuracy rather than speed. That is, the avoidance of errors received priority in order to maximize profit. At the same time, however, deadline-induced time pressure resulted in a competition between responding quickly and responding correctly; hence, the choice of an optimal response strategy may have been more difficult. Especially with the prospect of monetary incentives, such an increase of task demands enhances subjective pressure and presumably the involvement of various cognitive strategies, a situation that has been shown to impair performance (e.g., Camerer and Hogarth, 1999; Beilock, 2008). Our observation of negative incentive effects for payoff schemes with highly punished errors is compatible with this interpretation. Presumably, participants in the monetary group reduced response speed in order to avoid loss, but failed to improve performance.

As one of the reviewers pointed out, it is also possible that under the DLnP and ErrP schemes participants falsely assumed that they were expected to take longer to get it right and even more so when there were monetary incentives. Although we think that this is unlikely, we cannot definitively exclude it. Objectively, at least, there was no such requirement. Rather, it was expected that participants maximize their profit, especially under monetary incentives. To do so, they could have performed in the same way as the participants under the DLP scheme. But this is not what they did. Instead, they merely reduced their speed without using the extra time to increase accuracy, which is suboptimal in terms of earned points and money. In particular under the DLnP scheme the equal payoff for correct and erroneous responses rendered reactions before the deadline generally favorable as long as accuracy stays above 50%. However, participants chose the opposite strategy. They reduced response speed even though they missed the opportunity to gain points.

Together, our results suggest that payoff schemes critically mediate the relation between monetary incentives and performance. This interaction is also evident in Figure 2 that illustrates data of the four schemes separately for symbolic and monetary conditions. Concerning the symbolic group (Figure 2, right panel) it seems that payoff schemes had only moderate effects. While responses in the ErrDLnP scheme tend to be somewhat slower, almost all data points from the other schemes appear to originate from a common SATF. This indicates that participants largely adapted to individual conditions by simply adjusting their response criteria (e.g., Ratcliff and Rouder, 1998; McElree and Carrasco, 1999; Usher and McClelland, 2001; Ratcliff and Smith, 2004; Miller et al., 2008; Hübner et al., 2010). In contrast, the data for monetary incentives clearly show that the DLP and the ErrDLnP schemes stick out (Figure 2, left panel). Compared to the other two payoff schemes, the substantial increase of performance signifies the mobilization of additional effort when fast responses entail higher benefits.

The consideration of our data from different perspectives consistently indicates that enhanced performance under monetary incentives is confined to payoff schemes emphasizing response speed over accuracy, at least in speeded perceptual decision tasks. In other words, successful strategies to optimize profit are more easily exerted in settings that require control of speed rather than of accuracy. This notion appears to be compatible with the proposal of two systems that are involved in decision making: A fast pathway that makes rapid binary choices and a slow but more accurate cognitive system (Trimmer et al., 2008). Accordingly, an emphasis of speed would lead to an increased weight of the fast system whereas a focus on accuracy requires stronger involvement of slow cognitive processes (see also Hübner et al., 2010). Yet, further studies are needed to test the validity of this interpretation; at the moment this account remains speculative.

In conclusion, the present study fits into existing literature indicating that a multitude of factors mediates the influence of monetary incentives. The data demonstrate that payoff schemes, and in particular penalties for errors versus slow responses, can trigger qualitatively different behavior. Specifically, our findings suggest that payoff schemes support positive monetary effects when penalties for errors do not exceed those for slow responses. The present study may therefore contribute to the clarification of the yet mixed picture of incentive effects on performance.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

Experiment 1

Results of four-way ANOVAs on unreferenced response times and accuracies with between-subjects factors payoff scheme (DLP, DLnP) and incentives (monetary, symbolic), and within-subjects factors deadline (long, medium, short), and flanker type (neutral, incongruent).

	df	Response time		Accuracy
		F	Pr(>F)	F	Pr(>F)
Payoff scheme	1	16.96	<0.001	0.04	0.840
Incentives	1	0.51	0.476	0.04	0.849
Payoff × incentives	1	3.71	0.057	0.93	0.337
Residuals	100
Deadline	2	295.90	<0.001	165.07	<0.001
Deadline × payoff	2	2.55	0.081	6.15	0.003
Deadline × incentives	2	7.65	<0.001	0.38	0.681
Deadline × payoff × incentives	2	0.85	0.430	0.39	0.675
Residuals	200
Flanker type	1	298.81	<0.001	146.36	<0.001
Flanker × payoff	1	0.04	0.837	0.44	0.510
Flanker × incentives	1	1.62	0.206	1.34	0.250
Flanker × payoff × incentives	1	0.53	0.468	0.02	0.882
Residuals	100
Deadline × Flanker	2	7.63	<0.001	5.57	0.004
Deadline × Flanker × payoff	2	0.28	0.758	2.72	0.069
Deadline × Flanker × incentives	2	0.73	0.485	1.02	0.363
Deadline × Flanker × payoff × incentives	2	0.13	0.877	0.93	0.397
Residuals	200

Experiment 2

Results of four-way ANOVAs on unreferenced response times and accuracies with between-subjects factors payoff scheme (DLP, ErrP) and incentives (monetary, symbolic), and within-subjects factors deadline (long, medium, short), and flanker type (neutral, incongruent).

	df	Response time		Accuracy
		F	Pr(>F)	F	Pr(>F)
Payoff scheme	1	17.68	<0.001	0.04	0.836
Incentives	1	0.01	0.940	0.57	0.454
Payoff × incentives	1	2.29	0.133	3.57	0.061
Residuals	98
Deadline	2	345.66	<0.001	180.22	<0.001
Deadline × payoff	2	2.10	0.125	6.21	0.002
Deadline × incentives	2	6.13	0.003	0.36	0.696
Deadline × payoff × incentives	2	0.30	0.743	0.78	0.461
Residuals	196
Flanker type	1	336.67	<0.001	142.81	<0.001
Flanker × payoff	1	0.14	0.709	0.15	0.699
Flanker × incentives	1	0.57	0.451	0.17	0.685
Flanker × payoff × incentives	1	1.84	0.179	1.95	0.166
Residuals	98
Deadline × flanker	2	2.82	0.062	8.61	<0.001
Deadline × flanker × payoff	2	0.87	0.421	0.49	0.613
Deadline × flanker × incentives	2	0.24	0.785	1.02	0.362
Deadline × flanker × payoff × incentives	2	0.31	0.733	0.35	0.702
Residuals	196

Experiment 3

Results of three-way ANOVAs on unreferenced response times and accuracies with the between-subjects factor incentives (monetary, symbolic), and within-subjects factors deadline (long, medium, short), and flanker type (neutral, incongruent).

	df	Response time		Accuracy
		F	Pr(>F)	F	Pr(>F)
Incentives	1	3.93	0.056	0.51	0.482
Residuals	34
Deadline	2	103.34	<0.001	94.60	<0.001
Deadline × incentives	2	0.03	0.968	1.24	0.297
Residuals	68
Flanker type	1	102.17	<0.001	42.12	<0.001
Flanker × incentives	1	0.03	0.854	0.02	0.893
Residuals	34
Deadline × flanker	2	2.07	0.134	4.34	0.017
Deadline × flanker × incentives	2	0.43	0.650	0.04	0.963
Residuals	68