Skip to main content
PMC home page
Journal of Digital Imaging logoLink to Journal of Digital Imaging
. 2010 Sep 21;24(5):787–793. doi: 10.1007/s10278-010-9339-9

Accuracy of CBCT Measurements of a Human Skull

Kıvanç Kamburoğlu 1,✉, Eray Kolsuz 1, Hakan Kurt 1, Cenk Kılıç 2, Tuncer Özen 3, Candan Semra Paksoy 1
PMCID: PMC3180546  PMID: 20857166

Abstract

The purpose of this study is to assess the accuracy and reproducibility of cone-beam computed tomography (CBCT) measurements of a human dry skull by comparing them to direct digital caliper measurements. Heated gutta-percha was used to mark 13 specific distances on a human skull, and the distances were directly measured using a digital caliper and on CBCT images obtained with Iluma (3M Imtec, OK, USA) and 3D Accuitomo 170 (3D Accuitomo; J Morita Mfg. Corp., Kyoto, Japan) CBCT imaging systems. Iluma images were obtained at 120 kVp and 3.8 mA and reconstructed using voxel sizes of 0.2 and 0.3 mm3. Accuitomo images were obtained at 60 kVp and 2 mA and a voxel size of 0.250 mm3. In addition, 3-D reconstructions were produced from images obtained from both systems. All measurements were made independently by three trained observers and were repeated after an interval of 1 week. Agreement between observers and image type was assessed by calculating Pearson correlation coefficients, with a level of significance set at p < 0.05. Pearson correlation coefficients between readings ranged from 0.995 to 1 for all image types. Correlations among observers were also very high, ranging from 0.992 to 1 for the first reading and from 0.992 to 1 for the second reading for the different image types. All CBCT image measurements were identical and highly correlated with digital caliper measurements. Accuracy of measurements of various distances on a human skull obtained from different CBCT units and image types is comparable to that of digital caliper measurements.

Keywords: CBCT; Direct measurement; Radiography; 3-D imaging (imaging, three-dimensional); 3-D reconstruction; Automated measurement; Computed tomography

Introduction

Since the initial introduction of cone-beam computed tomography (CBCT) dedicated to dentomaxillofacial imaging, several novel systems offering different technical specifications and settings have become commercially available. CBCT is now commonly used for a variety of purposes in implantology, dentomaxillofacial surgery, image-guided surgical procedures, orthodontics, periodontics, and endodontics [1, 2]. Recently, the use of digital CBCT models has come to replace traditional dental casts in diagnosis, treatment planning, and simulation [3]. With CBCT, multiple single-frame images are acquired by a process of rotational scanning of an X-ray source and a reciprocating 2-D planar X-ray detector—either an amorphous silicon flat panel or an image intensifier/CCD detector. Images can be acquired with only one pass or less around the patient’s head and are recorded in a cylindrical or spherical volume of data with a field of view (FOV) ranging from 4 to 30 cm. Voxels are isotropic and typically range in size from 0.08 to 0.4 mm3. Images can be generated in orientations other than the conventional axial plane through the use of special algorithms that can produce multi-planar, reformatted two-dimensional (2-D), three-dimensional (3-D), and panoramic reconstructions on a personal computer [4–7]. In comparison to traditional medical computed tomography (CT) systems, dental CBCT units offer reduced effective radiation doses, shorter acquisition scan times, easier imaging, and lower costs [8–10]. Disadvantages associated with dental CBCT include scatter radiation, a limited dynamic range, minimal soft tissue detail, and beam hardening artifacts caused by dental care material and implants [11–14]. CBCT image quality is influenced by detector quality, imaging setting, voxel size, and hardware/software characteristics [15]. The present study assessed the accuracy and reproducibility of CBCT measurements obtained from specific distances on a human dry skull using 2-D tomographic slices and 3-D images and compared these with direct caliper measurements in order to provide clinically relevant data.

Materials and Methods

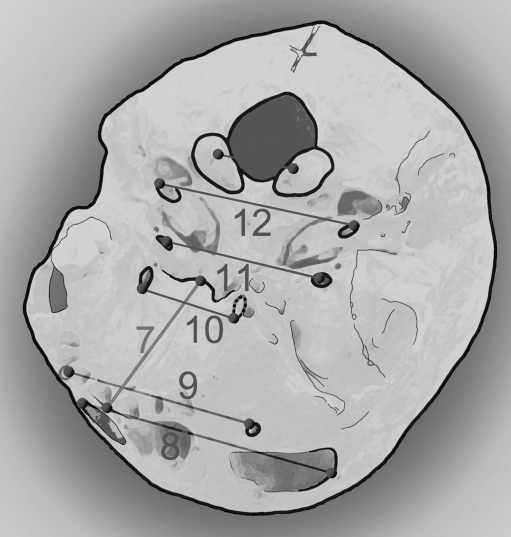
Gutta-percha was heated and glued to mark 13 points on a dry human skull in order to measure the following specific mandibular, maxillary, and skull-base distances: (1) distance between left and right foramen mentales, (2) distance between left and right distal tubercules of mandibular second molars, (3) distance between left and right angulus mandibulae, (4) distance between left and right coronoid process, (5) distance between left and right incisura mandibulae, (6) distance between left and right fovea pterygoidea, (7) distance between spina nasalis anterior and spina nasalis posterior, (8) distance between left and right foramen infraorbitalis, (9) distance between left and right infraorbital suture, (10) distance between left and right foramen palatinum majus, (11) distance between left and right foramen ovale, (12) distance between left and right canalis caroticus, and (13) distance between left and right occipital condyle. Figures 1 and 2 show schematic drawing of mandible and human skull along with specific distances measured, respectively.

Fig. 1.

Fig. 1

Open in a new tab

Schematic drawing of the mandible and specific distances measured

Fig. 2.

Fig. 2

Open in a new tab

Schematic drawing of the human skull and specific distances measured

The Frankfurt line (a line from the center of the ear through the lowest point of the eye socket) was held parallel to the horizontal plane. The skull was imaged using two different CBCT units: the Iluma CBCT (3M Imtec, OK, USA) and the 3D Accuitomo 170 CBCT (3D Accuitomo; J Morita Mfg. Corp., Kyoto, Japan). The Iluma CBCT has a 24.4 × 19.5 cm amorphous silicon flat-panel image detector and offers a cylindrical volume of reconstruction up to 21.1 × 14.2 cm. The 3D Accuitomo 170 CBCT has a flat-panel detector offering five different FOVs—40 × 40, 60 × 60, 80 × 80, 100 × 100, and 170 × 120 mm. With the Iluma system, images were obtained at 120 kVp and 3.8 mA with an exposure time of 40 s and were reconstructed using voxel sizes of 0.2 mm3 (high resolution) and 0.3 mm3 (low resolution). With the Morita system, images were obtained at 65 kVp, 2 mA with an exposure time of 30.8 s using a 170 × 170 × 120 mm FOV (0.250 mm3 voxel size). With both CBCT systems, axial scans and multi-planar reconstructions were obtained, and dedicated software was used to produce volumetric data and create 3-D reconstructions. A total of six image sets were obtained, as follows: (1) Accuitomo, 170 × 120 mm FOV 2-D (0.250 mm3); (2) Accuitomo, 170 × 120 mm FOV 3-D (0.250 mm3); (3) Iluma, high-resolution 2-D (0.2 mm3); (4) Iluma, high-resolution 3-D (0.2 mm3); (5) Iluma, low-resolution 2-D (0.3 mm3); (6) Iluma, low-resolution 3-D (0.3 mm3). Figure 3 shows 3-D reconstruction digital tomographic image obtained by Iluma CBCT.

Fig. 3.

Fig. 3

Open in a new tab

3-D reconstructed image obtained by Iluma CBCT

An Absolute Digimatic (Mitutoyo Corp., Kawasaki, Japan) digital caliper accurate to 0.01 mm was used to directly measure the mandibular, maxillary, and skull-base distances described above, and the same distances were measured on the CBCT images using the built-in measurement tools provided. One Data Viewer is a unique Morita software feature which is a stand-alone, executable application. It allows 3-D images to be viewed on any computer without installing special software. One Data Viewer is made by exporting the data files with the execution file of One Data Viewer, from i-Dixel. Data files can be taken from anywhere and viewed on all computers within the clinic network, including 3-D images and patient data. Functions to measure distances and angles, zoom, invert the gray scale, adjust brightness, contrast, and gamma are also available options. ILUMA Vision is a software application used for the display and 3-D visualization of medical image files from scanning devices, such as the ILUMA scanner. Additionally, ILUMA Vision is a preoperative software application used for the simulation and evaluation of dental implants, orthodontic planning, and surgical treatments. The ILUMA software suite provides all the capabilities needed for thorough image analysis and treatment planning. An image from one scan can be reconstructed at different levels of resolution, as many times as needed, without rescanning the patient. With a wide array of preset formats, a variety of full, multi-sectional and cross-sectional views can be accessed. The digital caliper measurements were considered the “gold standard” to which all CBCT measurements were compared. Figure 4 shows the caliper utilized for direct measurements.

Fig. 4.

Fig. 4

Open in a new tab

Photography of the digital caliper used for direct measurements. An Absolute Digimatic (Mitutoyo Corp., Kawasaki, Japan)

All caliper and CBCT measurements (millimeter) were separately recorded in a random order by three independent trained observers. Reproducibility of measurements was assessed by having each observer separately repeat both caliper and CBCT measurements after a 1-week interval to eliminate memory bias. No time restriction was placed on the observers. Images were viewed in a dimly lit room on a 22-in. LG Flatron monitor (LG, Seoul, Korea) with a screen resolution of 1,440 × 900 pixels and 32-bit color depth.

Agreement between observers and image type was assessed by calculating Pearson correlation coefficients with a level of significance set at p < 0.05.

Results

Pearson correlation coefficients for each observer and correlations between observers for the first and second readings are given in Tables 1, 2, and 3, respectively. Almost perfect intra- and inter-observer correlation coefficients were found (p < 0.001). Pearson correlation coefficients ranged from 0.995 to 1 for the first and second measurements of each observer and from 0.992 to 1 for the first reading and from 0.992 to 1 for the second reading for different image types. In addition, correlation coefficients for all image types were identical and highly correlated with the gold standard direct digital caliper measurements (p < 0.01). Given the near perfect intra-observer correlation coefficients, only the correlations for the first readings of observers 1, 2, and 3 are given in Tables 4, 5, and 6, respectively.

Table 1.

Intra-observer correlations

Pearson correlation
Observer 1 Observer 2 Observer 3
Caliper 1.000* 0.999* 0.999*
Iluma 0.3 0.997* 0.999* 0.999*
Iluma 0.3 3-D 1.000* 0.999* 0.999*
Iluma 0.2 0.999* 1.000* 0.999*
Iluma 0.2 3-D 0.998* 0.998* 0.998*
Morita 1.000* 0.995* 0.999*
Morita 3-D 0.999* 0.999* 0.999*
Open in a new tab

*p < 0.001

Table 2.

Inter-observer correlations for first reading

Pearson correlation
Observer 1–observer 2 Observer 1–observer 3 Observer 2–observer 3
Caliper 0.996* 0.996* 0.995*
Iluma 0.3 0.993* 0.999* 0.995*
Iluma 0.3 3-D 0.997* 1.000* 0.998*
Iluma 0.2 0.998* 0.998* 0.999*
Iluma 0.2 3-D 0.999* 0.998* 0.998*
Morita 0.992* 0.998* 0.995*
Morita 3-D 0.998* 0.998* 0.999*
Open in a new tab

*p < 0.001

Table 3.

Inter-observer correlations for second reading

Pearson correlation
Observer 1–observer 2 Observer 1–observer 3 Observer 2–observer 3
Caliper 0.994* 0.998* 0.993*
Iluma 0.3 0.992* 0.997* 0.994*
Iluma 0.3 3-D 0.996* 0.998* 0.998*
Iluma 0.2 0.998* 0.999* 0.997*
Iluma 0.2 3-D 0.994* 0.994* 0.995*
Morita 0.998* 0.998* 0.999*
Morita 3-D 0.997* 0.998* 0.999*
Open in a new tab

*p < 0.001

Table 4.

Observer 1: first reading

Correlations
Caliper Iluma 0.3 mm3 Iluma 0.3 mm3 3-D Iluma 0.2 mm3 Iluma 0.2 mm3 Accuitomo Accuitomo 3-D
Caliper Pearson correlation 1 0.999a 1.000a 1.000a 1.000a 0.999a 1.000a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.3 mm3 Pearson correlation 0.999a 1 0.999a 0.999a 0.999a 0.998a 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.3 mm3 3-D Pearson correlation 1.000a 0.999a 1 0.999a 1.000a 0.999a 1.000a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.2 mm3 Pearson correlation 1.000a 0.999a 0.999a 1 1.000a 0.999a 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 ,000
N 13 13 13 13 13 13 13
Iluma 0.2 mm3 3-D Pearson correlation 1.000a 0.999a 1.000a 1.000a 1 0.999a 1.000a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Accuitomo Pearson correlation 0.999a 0.998a 0.999a 0.999a 0.999a 1 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Accuitomo 3-D Pearson correlation 1.000a 0.999a 1.000a 0.999a 1.000a 0.999a 1
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Open in a new tab

aCorrelation is significant at the 0.01 level (two-tailed)

Table 5.

Observer 2: first reading

Correlations
Caliper Iluma 0.3 mm3 Iluma 0.3 mm3 3-D Iluma 0.2 mm3 Iluma 0.2 mm3 3-D Accuitomo Accuitomo 3-D
Caliper Pearson correlation 1 0.994a 0.996a 0.997a 0.997a 0.992a 0.998a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.3 mm3 Pearson correlation 0.994a 1 0.998a 0.998a 0.996a 0.990a 0.996a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.3 mm3 3-D Pearson correlation 0.996a 0.998a 1 0.999a 0.999a 0.993a 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.2 mm3 Pearson correlation 0.997a 0.998a 0.999a 1 0.999a 0.992a 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.2 mm3 3-D Pearson correlation 0.997a 0.996a 0.999a 0.999a 1 0.994a 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Accuitomo Pearson correlation 0.992a 0.990a 0.993a 0.992a 0.994a 1 0.995a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Accuitomo 3-D Pearson correlation 0.998a 0.996a 0.999a 0.999a 0.999a 0.995a 1
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Open in a new tab

aCorrelation is significant at the 0.01 level (two-tailed)

Table 6.

Observer 3: first reading

Correlations
Caliper Iluma 0.3 mm3 Iluma 0.3 mm3 3-D Iluma 0.2 mm3 Iluma 0.2 mm3 3-D Accuitomo Accuitomo 3-D
Caliper Pearson correlation 1 0.998a 0.999a 0.998a 0.996a 0.998a 0.998a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.3 mm3 Pearson correlation 0.998a 1 1.000a 0.999a 0.999a 0.999a 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.3 mm3 3-D Pearson correlation 0.999a 1.000a 1 0.998a 0.998a 0.999a 0.999a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.2 mm3 Pearson correlation 0.998a 0.999a 0.998a 1 0.998a 0.997a 0.998a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Iluma 0.2 mm3 3-D Pearson correlation 0.996a 0.999a 0.998a 0.998a 1 0.997a 0.998a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Accuitomo Pearson correlation 0.998a 0.999a 0.999a 0.997a 0.997a 1 1.000a
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Accuitomo 3-D Pearson correlation 0.998a 0.999a 0.999a 0.998a 0.998a 1.000a 1
Sig. (two-tailed) 0.000 0.000 0.000 0.000 0.000 0.000
N 13 13 13 13 13 13 13
Open in a new tab

aCorrelation is significant at the 0.01 level (two-tailed)

Discussion

The present study showed CBCT measurements of specific distances on a human dry skull to be highly accurate and reproducible. The similarities in measurements among imaging units, image types, and observers indicate the effectiveness of both the 2-D and 3-D reconstructions obtained from the Iluma and Accuitomo systems studied. One limitation of the present study is that no soft tissue or soft tissue equivalent was utilized since the main focus of the study was to assess the versatility of the measurement tools of both CBCT systems tested in measuring anatomical bone structures in the dentomaxillofacial region.

Our findings regarding accuracy are in line with those of a previous study that found two different CBCT systems, the NewTom QR DVT 9000 (Aperio Inc., Sarasota, FL) and the Hitachi MercuRay (Hitachi Medico Technology, Tokyo, Japan), to provide similar, highly accurate data with <1% error when compared to physical measurements [16]. Our results are also in line with another study that showed increasing voxel resolution did not affect the accuracy of surface model measurements [17].

While our study found both CBCT units tested yielded highly accurate and reproducible results for mandibular, maxillary, and skull-base measurements, a similarly designed previous study in which 13 sites on human dry skulls were measured using a NewTom 9000 CBCT (Quantitative Radiology, Verona, Italy) found CBCT images underestimated the real distances between skull sites; however, the differences between CBCT and direct measurements were only statistically significant for measurements of the skull base [18]. The differences in study findings may be related to observer performance and calibration or hardware/software capabilities of the different systems tested. It is also possible that in the previous study, the 2-mm diameter metal spheres affixed to the skull to mark the distances to be measured caused scatter and beam hardening that adversely affected observer performance.

The present study did not compare CBCT to 2-D systems; however, CBCT has already been shown to be superior to 2-D cephalometric radiography in providing linear measurements [19, 20]. Both intra-observer and inter-observer reliability in the identification of anatomical structures and landmarks have been shown to be significantly higher with CBCT when compared to 2-D measurements [21]. A study comparing linear measurement of the temporomandibular joint using CBCT and digital cephalometric radiography obtained similar results [22]. Moreover, skull orientation during CBCT scanning has not been found to affect accuracy or reliability of measurements [23–25].

Studies comparing CBCT with multi-slice CT found both 3-D methods yielded similarly accurate results in terms of measurements, but with a considerably lower effective radiation dose with CBCT when compared to CT [26, 27]. Our results are, in general, similar to the previous findings [28–30] in terms of measurement accuracy and reproducibility thereby suggesting the use of CBCT units in dentomaxillofacial diagnosis, treatment planning and follow-up.

Conclusion

All 2-D and 3-D images obtained with the Iluma and 3D Accuitomo 170 CBCT units tested in the present study performed similarly in terms of accuracy and reproducibility of measurements of predetermined mandibular, maxillary, and skull-base distances, with no differences in intra-observer or inter-observer agreement. Therefore, we recommend the use of CBCT in the measurement of the dentomaxillofacial region.

References

  • 1.Kau CH, Bozic M, English J, Lee R, Bussa H, Ellis RK. Cone-beam computed tomography of the maxillofacial region—an update. Int J Med Robot. 2009;5(4):366–380. doi: 10.1002/rcs.279. [DOI] [PubMed] [Google Scholar]
  • 2.Mischkowski RA, Pulsfort R, Ritter L, Neugebauer J, Brochhagen HG, Keeve E, Zöller JE. Geometric accuracy of a newly developed cone-beam device for maxillofacial imaging. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2007;104(4):551–559. doi: 10.1016/j.tripleo.2007.02.021. [DOI] [PubMed] [Google Scholar]
  • 3.Al-Rawi B, Hassan B, Vandenberge B, Jacobs R. Accuracy assessment of three-dimensional surface reconstructions of teeth from cone beam computed tomography scans. J Oral Rehabil. 2010;37(5):352–358. doi: 10.1111/j.1365-2842.2010.02065.x. [DOI] [PubMed] [Google Scholar]
  • 4.Scarfe WC, Farman AG. What is cone-beam CT and how does it work? Dent Clin North Am. 2008;52(4):707–730. doi: 10.1016/j.cden.2008.05.005. [DOI] [PubMed] [Google Scholar]
  • 5.White SC. Cone-beam imaging in dentistry. Health Phys. 2008;95(5):628–637. doi: 10.1097/01.HP.0000326340.81581.1a. [DOI] [PubMed] [Google Scholar]
  • 6.Patel S. New dimensions in endodontic imaging: Part 2. Cone beam computed tomography. Int Endod J. 2009;42(6):463–475. doi: 10.1111/j.1365-2591.2008.01531.x. [DOI] [PubMed] [Google Scholar]
  • 7.Watanabe H, Honda E, Kurabayashi T. Modulation transfer function evaluation of cone beam computed tomography for dental use with the oversampling method. Dentomaxillofac Radiol. 2010;39(1):28–32. doi: 10.1259/dmfr/27069629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Scarfe WC, Farman AG, Sukovic P. Clinical applications of cone-beam computed tomography in dental practice. J Can Dent Assoc. 2006;72(1):75–80. [PubMed] [Google Scholar]
  • 9.Ludlow JB, Ludlow LED, Brooks SL, Howerton WB. Dosimetry of 3 CBCT devices for oral and maxillofacial radiology: CB Mercuray, NewTom 3G and i-CAT. Dentomaxillofac Radiol. 2006;35(4):219–226. doi: 10.1259/dmfr/14340323. [DOI] [PubMed] [Google Scholar]
  • 10.Hirsch E, Wolf U, Heinicke F, Silva MA. Dosimetry of the cone beam computed tomography Veraviewepocs 3D compared with the 3D Accuitomo in different field of views. Dentomaxillofac Radiol. 2008;37(5):268–273. doi: 10.1259/dmfr/23424132. [DOI] [PubMed] [Google Scholar]
  • 11.Ritter L, Mischkowski RA, Neugebauer J, Dreiseidler T, Scheer M, Keeve E, Zöller JE. The influence of body mass index, age, implants, and dental restorations on image quality of cone beam computed tomography. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2009;108(3):e108–e116. doi: 10.1016/j.tripleo.2009.05.011. [DOI] [PubMed] [Google Scholar]
  • 12.Draenert FG, Coppenrath E, Herzog P, Müller S, Mueller-Lisse UG. Beam hardening artefacts occur in dental implant scans with the NewTom cone beam CT but not with the dental 4-row multidetector CT. Dentomaxillofac Radiol. 2007;36(4):198–203. doi: 10.1259/dmfr/32579161. [DOI] [PubMed] [Google Scholar]
  • 13.Hsieh J, Molthen RC, Dawson CA, Johnson RH. An iterative approach to the beam hardening correction in cone beam CT. Med Phys. 2000;27(1):23–29. doi: 10.1118/1.598853. [DOI] [PubMed] [Google Scholar]
  • 14.Carrafiello G, Dizonno M, Colli V, et al. Comparative study of jaws with multislice computed tomography and cone-beam computed tomography. Radiol Med. 2010;115(4):600–611. doi: 10.1007/s11547-010-0520-5. [DOI] [PubMed] [Google Scholar]
  • 15.Scarfe WC, Farman AG. Cone beam computed tomography. In: White SC, Pharoah MJ, editors. Oral Radiology. Principles and Interpretation. 6. St. Louis: Elsevier; 2009. pp. 225–243. [Google Scholar]
  • 16.Stratemann SA, Huang JC, Maki K, Miller AJ, Hatcher DC. Comparison of cone beam computed tomography imaging with physical measures. Dentomaxillofac Radiol. 2008;37(2):80–93. doi: 10.1259/dmfr/31349994. [DOI] [PubMed] [Google Scholar]
  • 17.Damstra J, Fourie Z, Huddleston Slater JJ, Ren Y. Accuracy of linear measurements from cone-beam computed tomography-derived surface models of different voxel sizes. Am J Orthod Dentofac Orthop. 2010;137(1):16.e1–16.e6. doi: 10.1016/j.ajodo.2009.06.016. [DOI] [PubMed] [Google Scholar]
  • 18.Lascala CA, Panella J, Marques MM. Analysis of the accuracy of linear measurements obtained by cone beam computed tomography (CBCT-NewTom) Dentomaxillofac Radiol. 2004;33(5):291–294. doi: 10.1259/dmfr/25500850. [DOI] [PubMed] [Google Scholar]
  • 19.Moshiri M, Scarfe WC, Hilgers ML, Scheetz JP, Silveira AM, Farman AG. Accuracy of linear measurements from imaging plate and lateral cephalometric images derived from cone-beam computed tomography. Am J Orthod Dentofacial Orthop. 2007;132(4):550–560. doi: 10.1016/j.ajodo.2006.09.046. [DOI] [PubMed] [Google Scholar]
  • 20.Vlijmen OJC, Maal TJJ, Berge SJ, Bronkhorst EM, Katsaros C, Kuijpers-Jagtman AM. A comparison between two-dimensional and three-dimensional cephalometry on frontal radiographs and on cone beam computed tomography scans of human skulls. Eur J Oral Sci. 2009;117(3):300–305. doi: 10.1111/j.1600-0722.2009.00633.x. [DOI] [PubMed] [Google Scholar]
  • 21.Chien PC, Parks ET, Eraso F, Hartsfield JK, Jr, Roberts WE, Ofner S. Comparison of reliability in anatomical landmark identification using two-dimensional digital cephalometrics and three-dimensional cone beam computed tomography in vivo. Dentomaxillofac Radiol. 2009;38(5):262–273. doi: 10.1259/dmfr/81889955. [DOI] [PubMed] [Google Scholar]
  • 22.Hilgers ML, Scarfe WC, Scheetz JP, Farman AG. Accuracy of linear temporomandibular joint measurements with cone beam computed tomography and digital cephalometric radiography. Am J Orthod Dentofacial Orthop. 2005;128(6):803–811. doi: 10.1016/j.ajodo.2005.08.034. [DOI] [PubMed] [Google Scholar]
  • 23.Ludlow JB, Laster WS, See M, Bailey LJ, Hershey HG. Accuracy of measurements of mandibular anatomy in cone beam computed tomography images. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2007;103(4):534–542. doi: 10.1016/j.tripleo.2006.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Berco M, Rigali PH, Miner M, DeLuca S, Anderson NK, Will LA. Accuracy and reliability of linear cephalometric measurements from cone-beam computed tomography scans of a dry human skull. Am J Orthod Dentofacial Orthop. 2009;136(1):171–179. doi: 10.1016/j.ajodo.2008.08.021. [DOI] [PubMed] [Google Scholar]
  • 25.Hassan B, Stelt P, Sanderink G. Accuracy of three-dimensional measurements obtained from cone beam computed tomography surface-rendered images for cephalometric analysis: influence of patient scanning position. Eur J Orthod. 2009;31(2):129–134. doi: 10.1093/ejo/cjn088. [DOI] [PubMed] [Google Scholar]
  • 26.Loubele M, Assche N, Carpentier K, Maes F, Jacobs R, Steenberghe D, Suetens P. Comparative localized linear accuracy of small-field cone-beam CT and multislice CT for alveolar bone measurements. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2008;105(4):512–518. doi: 10.1016/j.tripleo.2007.05.004. [DOI] [PubMed] [Google Scholar]
  • 27.Suomalainen A, Vehmas T, Kortesniemi M, Robinson S, Peltola J. Accuracy of linear measurements using dental cone beam and conventional multislice computed tomography. Dentomaxillofac Radiol. 2008;37(1):10–17. doi: 10.1259/dmfr/14140281. [DOI] [PubMed] [Google Scholar]
  • 28.Kobayashi K, Shimoda S, Nakagawa Y, Yamamoto A. Accuracy in measurement of distance using limited cone-beam computerized tomography. Int J Oral Maxillofac Implants. 2004;19(2):228–231. [PubMed] [Google Scholar]
  • 29.Periago DR, Scarfe WC, Moshiri M, Scheetz JP, Silveira AM, Farman AG. Linear accuracy and reliability of cone-beam CT derived 3-dimensional images constructed using an orthodontic volumetric rendering program. Angle Orthod. 2008;78(3):387–395. doi: 10.2319/122106-52.1. [DOI] [PubMed] [Google Scholar]
  • 30.Brown AA, Scarfe WC, Scheetz JP, Silveira AM, Farman AG. Linear accuracy of cone-beam CT derived 3D images. Angle Orthod. 2009;79(1):150–157. doi: 10.2319/122407-599.1. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Digital Imaging are provided here courtesy of Springer

RESOURCES