Abstract
Although originally designed for broadband inversion and decoupling in NMR spectroscopy, recent methodological developments have introduced adiabatic fast passage (AFP) pulses into the field of protein dynamics. AFP pulses employ a frequency sweep, and have not only superior inversion properties with respect to offset effects, but they are also easily implemented into a pulse sequence. As magnetization is dragged from the +z to the −z direction, Larmor precession is impeded since magnetization becomes spin-locked, which is a potentially useful feature for the investigation of microsecond to millisecond dynamics. A major drawback of these pulses as theoretical prediction is concerned, however, results from their time-dependent offset: simulations of spin density matrices under the influence of a time-dependent Hamiltonian with non-commuting elements are costly in terms of computational time, rendering data analysis impracticable. In this paper we suggest several ways to reduce the computational time without compromising accuracy with respect to effects such as cross-correlated relaxation and modulation of the chemical shift.
Electronic supplementary material
The online version of this article (doi:10.1007/s10858-011-9539-8) contains supplementary material, which is available to authorized users.
Keywords: NMR, Adiabatic fast passage, Microsecond–millisecond dynamics
Introduction
The functionality of proteins relies on their three-dimensional structure as well as on their dynamic properties. In proteins tumbling in solution, global dynamics are superimposed on local mobility, properties that can be dissected and quantified by NMR relaxation methods. Due to the causal relation between molecular motion and nuclear spin relaxation it is possible to determine protein motional parameters from relaxation measurements at atomic resolution. Possible targets of relaxation measurements are heteronuclei in the protein backbone, such as 15N or 13C, which are relaxed mainly by dipolar interactions with their covalently bound protons and their chemical shift anisotropies. A number of time-scales can be addressed by various NMR methods. Most prominently, nanosecond (global) to picosecond (local bond vector) motions can be characterized through longitudinal relaxation, transverse relaxation and cross-relaxation (Kay et al. 1989). Various other heteronuclear relaxation pathways have been exploited to study bond vector motions in great detail (Dayie et al. 1996; Peng and Wagner 1994). Conformational dynamics on the microsecond to millisecond time-regime encompass vital processes such as folding, ligand binding, allostery and catalysis (Kay 2005; Mittermaier and Kay 2006; Palmer 2004; Boehr et al. 2006; Frederick et al. 2007; Henzler-Wildman and Kern 2007; Kay et al. 1998; Popovych et al. 2006; Sugase et al. 2007; Tollinger et al. 2001, 2006) and are therefore the focus of many NMR studies. In particular, two methods have found widespread application, i.e., the Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion (Tollinger et al. 2001; Palmer et al. 2001) and spin-lock T 1ρ relaxation dispersion experiments (Trott and Palmer 2002; Palmer and Massi 2006). These experiments measure the transverse relaxation rate (R 2) of a signal of interest in dependence either of the repetition rate of a train of 180° pulses (CPMG) (Allerhand et al. 1966; Tollinger et al. 2001; Palmer 2004) or of the effective spin-lock amplitude (T 1ρ) applied during a relaxation period of constant time. Using these methods, the exchange contribution (R ex) to the transverse relaxation rate can be separated from the ‘exchange-free’ relaxation rate. Furthermore, it is possible (in favorable cases) to extract information about the motional parameters of the process that governs the relaxation dispersion. Both methodologies are well-established and have provided unprecedented insight into fundamental biological processes (Mittermaier and Kay 2006), in particular because otherwise ‘invisible’ states can be characterized. The CPMG technique responds strongly to processes with exchange rates between 102 and 104 per second as it monitors transverse relaxation exclusively. Hardware limitations concerning the repetition rates of refocusing pulses in the CPMG train restrict the upper limit of detectable time scales to exchange rate constants on the order of a few thousand per second (Loria et al. 1999; Palmer 2004; Tollinger et al. 2001). Conversely, although larger effective spin lock fields are used in off-resonance T 1ρ-dispersion experiments (and thus potentially faster time scale motions can be assessed), their sensitivity is compromised by the reduction of the contribution of transverse relaxation to the effective spin lock relaxation rate. Both methods are also limited with respect to the population of the minor state, which, if too large, may severely compromise signal to noise ratios. Thus the excellent sensitivity of these methods to very small populations of excited states turns into a disadvantage as soon as these states are populated to a substantial (>15%) degree.
More than a decade ago, the adiabatic fast passage (AFP) approach was used for generating optimal initial conditions in R 1ρ measurements (Mulder et al. 1998) and also for determining heteronuclear relaxation rates for a system in the absence of μs–ms motion (Konrat and Tollinger 1999). The AFP pulse is operative over an entire relaxation period, and it achieves effective spin locking simultaneously over a range of offsets determined by its sweep width (see below). The apparent spin-lock relaxation rate, R 1ρ, depends crucially on the amplitude of the AFP pulse. From this field dependence of R 1ρ the transverse relaxation rate R 2 can be extracted. Recently, Mangia et al. determined exchange parameters for a system with μs–ms dynamics by measuring R 1ρ and R 2ρ dispersions (Mangia et al. 2010) using trains of AFP pulses of different shape during a relaxation delay (R 2ρ is the relaxation rate of magnetization perpendicular to the effective field). They obtained the exchange contribution to the natural line-width by subtraction of relaxation rates of non-exchanging residues, assuming effects such as cross-relaxation, relaxation interference, or chemical shift anisotropy to cancel out to a large extent as long as these parameters are similar across the protein sequence. Thereby the authors avoided the time-consuming process of computing the entire trajectory of magnetization during the AFP pulses.
In this paper we show how spin dynamics during adiabatic fast passage can be treated mathematically in an exhaustive but efficient way. We explicitly consider the effects of CSA-DD cross-correlated relaxation and the modulation of the isotropic chemical shift in response to chemical/conformational exchange on the μs–ms time-scale and demonstrate the agreement between theory and experiment for a protein that accesses its excited state on a time-scale of several hundreds per second. We give an analytical as well as a numerical solution, and we show how to reduce computational time. In addition, we compare these exact results to an approximation that can be used for the computation of T 1ρ in systems with skewed populations. We show that CSA-DD cross-correlation, which is not explicitly included in the approximation, can be accounted for in a straightforward way, and we show the potential utility of this approximation for fitting AFP profiles using synthetic data sets.
Adiabatic fast passage
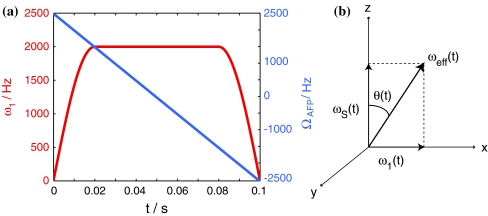
Over the years adiabatic fast passage (AFP) pulses have become an important tool in pulse sequence programming mostly in order to deal with radiofrequency (rf) inhomogeneity (Abragam 1962; Boehlen and Bodenhausen 1993; Kupce and Freeman 1995). Their most outstanding feature is their perfect inversion profile, which is nearly independent of offset and exact rf calibration. It was this property that triggered the development of early applications, i.e., broadband heteronuclear decoupling and broadband inversion. An AFP pulse is typically a relatively long rf pulse with both amplitude and (typically parabolic) phase modulation. The latter results in a linear frequency sweep over a defined spectral region (νsweep). The amplitude (ω 1 = γB 1) is constant throughout most of the pulse with the exception of the beginning and the end (approx. 10–20% of the total pulse length), where it is increased from 0 to ω max1 and decreased from ω max1 to 0 using a sinusoidal or cosinusoidal ramp, respectively. A typical pulse shape is depicted in Fig. 1a.
Fig. 1.
a Typical shape of an AFP pulse. The offset of the AFP-pulse with respect to the transmitter is shown in blue (right y-axis), and the field strength ω 1 (ramped at the beginning and end of the pulse in order to ensure magnetization gets aligned with the effective field) is depicted in red (left y-axis). b Snap-shot of the effective field ω eff(t) and its components. A spin experiences an instantaneous field that depends on its current offset ω S(t) with respect to the AFP pulse and on the strength of the AFP pulse, ω 1(t). Its response is to rotate around this field. Magnetization that is collinear with ω eff(t) remains aligned to it even as ω S(t) and ω 1(t) are modulated, as long as the adiabaticity condition is not violated
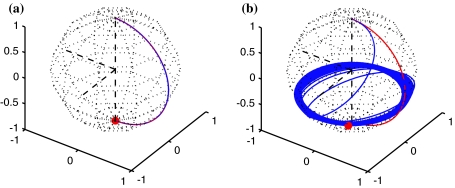
The inversion properties of an AFP pulse can be qualitatively understood on the basis of a coordinate frame shown in Fig. 1b. The time-dependence of offset ωS (depicted along the z-axis) and field strength ω 1 (depicted along x) results in a time-dependent effective magnetic field ω eff(t) characterized by an angle θ(t) with respect to the z-axis. During AFP inversion, the effective field starts out from the +z direction, sweeps through the transverse plane and ends up along −z. As long as the adiabaticity condition (dθ/dt « ω eff) is fulfilled (Abragam 1962; Boehlen and Bodenhausen 1993; Kupce and Freeman 1996), the magnetization vector rotates in very small circles around the effective field, appearing aligned with it, and remains so throughout the pulse (Fig. 2a). Ramping of the spin-lock amplitude ensures complete inversion by the end of the pulse, while the frequency sweep defines the spectral region where inversion occurs. The magnetization vector is effectively spin-locked since its Larmor precession is impeded by the alignment with the effective magnetic field. In the case where the adiabaticity condition is not fulfilled, the magnetization vector is not spin-locked and dephasing occurs (Fig. 2b).
Fig. 2.
a Trajectory of magnetization during an ideal AFP pulse, fulfilling the adiabaticity condition. The time dependence of the effective magnetic field is shown in red. The magnetization vector (blue) follows it and perfect inversion occurs. b Path of magnetization in case where the adiabaticity condition is not fulfilled. The magnetization vectors oscillates around the effective field, and the pulse does not lead to inversion. Attenuation due to relaxation has been neglected
Relaxation in the spinlock frame is composed of a longitudinal and a transverse component:
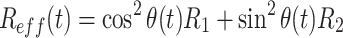 |
1 |
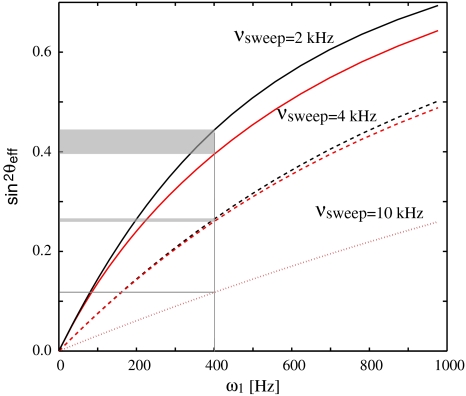
The overall effect of an AFP pulse on the spin-lock relaxation rate is quantitatively described by the parameter sin2
θ
eff, which is the time integral over 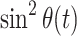 and, as such, a function of the spin-lock amplitude. It depends on the offset of the resonance, but also on the sweep width: Fig. 3 shows that in AFP pulses that employ a larger sweep range, the same spin-lock field strength leads to a smaller sin2
θ
eff.
and, as such, a function of the spin-lock amplitude. It depends on the offset of the resonance, but also on the sweep width: Fig. 3 shows that in AFP pulses that employ a larger sweep range, the same spin-lock field strength leads to a smaller sin2
θ
eff.
Fig. 3.
Dependence of sin2 θ eff on the spin-lock amplitude ω1 for different sweep ranges ν sweep (solid lines: 2 kHz, dashed lines: 4 kHz, dotted lines: 10 kHz). The black lines result from a resonance with a chemical shift in the middle of the sweep, and the red lines have a relative shift of 10 ppm with respect to the middle of the sweep. The effect of the offset of the resonance vanishes at larger sweep widths (10 kHz). The difference in sin2 θ eff between the resonances with the different chemical shifts is indicated as a grey shaded area
Equation 2 shows that in the absence of chemical or conformational exchange the spin-lock relaxation rate depends linearly on sin2 θ eff.
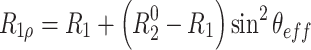 |
2 |
In the presence of chemical exchange, the transverse relaxation rate is 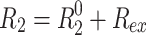 , where R
ex is the exchange contribution that affects the spin-lock relaxation rate to an extent that depends on sin2
θ
eff. Therefore R
1ρ is no longer a linear function of sin2
θ
eff. The deviation from linearity is characteristic for a set of exchange parameters, which are—in the simple case of a system undergoing two-site exchange between the states A and B—the exchange rate, k
ex, the population of the excited state, p
B, and the difference between the Larmor precession frequencies, Δω = Ω
S,B − Ω
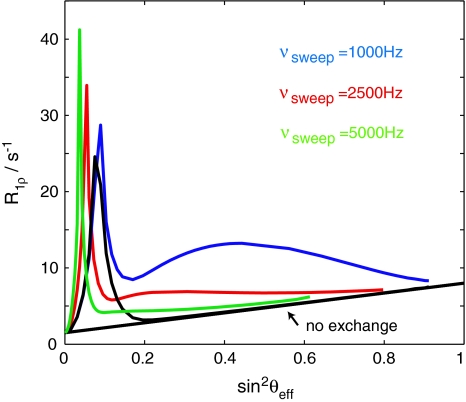
S,A. In addition, the deviation is dependent on the frequency sweep width of the AFP pulse (see below; Fig. 4).
, where R
ex is the exchange contribution that affects the spin-lock relaxation rate to an extent that depends on sin2
θ
eff. Therefore R
1ρ is no longer a linear function of sin2
θ
eff. The deviation from linearity is characteristic for a set of exchange parameters, which are—in the simple case of a system undergoing two-site exchange between the states A and B—the exchange rate, k
ex, the population of the excited state, p
B, and the difference between the Larmor precession frequencies, Δω = Ω
S,B − Ω
S,A. In addition, the deviation is dependent on the frequency sweep width of the AFP pulse (see below; Fig. 4).
Fig. 4.
Dependence of R 1ρ on sin2 θ eff in the presence of conformational exchange on the ms time-scale. As the exchange contribution to the natural line width is dependent on the spin lock field strength, exchange results in a deviation from linearity (the dependence of R 1ρ on sin2 θ eff in the absence of additional line-broadening effects is depicted as a thin black line). The sweep width νsweep influences sin2 θ eff as a function of spin-lock amplitude, but also the size of the deviation from linearity for exchanging spins. The spike on the left hand side is a consequence of the violation of the adiabaticity condition (e.g., imperfect inversion). Exchange parameters were k ex = 1,000 s−1, p B = 4%, Δω/2π = 240 Hz. The AFP pulse duration was 100 ms. Spin lock amplitudes ranged up to 2 kHz with 20% ramping at the beginning and the end of the pulse
In what follows, a more detailed description of the evolution of magnetization during adiabatic fast passage is given that accounts also for scalar coupling and cross-correlated relaxation.
Numerical description of AFP
Every spin system can be described in terms of its density operator σ(t). The numerical simulation of magnetization amounts to solving the differential equation (Ernst et al. 2003)
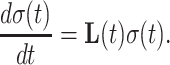 |
3 |
The Liouvillian contains all coherent and non-coherent mechanisms for the evolution of spin density. For a time-independent Liouvillian matrix L, as encountered in conventional spin-lock experiments, calculating the relaxation rate corresponds to finding the largest real eigenvalue of L (Trott and Palmer 2002). In the case of an AFP pulse the Liouvillian matrix L is time-dependent due to the offset sweep and the ramped amplitude. However, continuous behavior can be assumed for a sufficiently small time step τ, and integration of Eq. 3 can be performed iteratively resulting in a multi-step calculation. For each time step τ = t i − t i−1 the density matrix is computed according to
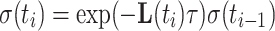 |
4 |
For an isolated spin S system with only Larmor precession and auto-relaxation, σ(t) and L(t) are given by
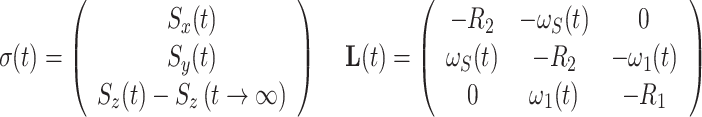 |
where ω 1(t) is the field strength of an AFP pulse applied from the x direction and ω S(t) is the offset of the spin-lock field at a given time t with respect to the precession frequency of spin S. R 1 and R 2 are the longitudinal and transverse autorelaxation rates, respectively, and S i(t) are the magnetization components of spin S at time t. 1
In a realistic spin system, however, it is necessary to include weak scalar coupling and cross-correlated relaxation channels. This can be accomplished by extending the basis to include the magnetization components that are created by these mechanisms. Here we assume an AX spin system (A = S, X = H), such that by scalar coupling the size of the base is doubled (there is no need to include magnetization modes where the scalar coupled spin is transverse). Furthermore we consider A(CSA)-AX(DD) cross-correlated relaxation (no extension of the basis is necessary). In addition, the size of the basis doubles in the presence of chemical or conformational exchange between two states, modulating the Larmor precession frequency (and other parameters) of the spins.
The following matrices show the Liouvillian and spin density matrices in the presence of scalar coupling, CSA-DD cross-correlated cross-relaxation,2 and modulation of the isotropic chemical shift. Here, J is the scalar coupling constant and G x/z are the transverse and longitudinal CSA-DD cross-correlated relaxation rates.3 The microscopic rate constants k ab and k ba describe conformational exchange, indices A and B refer to the two conformations that are interconverted by the exchange process. Note that, for simplicity, we set ω 1 = ω 1(t) and ω S = ω S(t).
 |
k AB and k BA are related to the exchange-rate constant k ex by
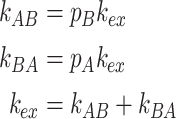 |
where p A and p B are the populations of species A and B, respectively.
The effective spin-lock relaxation rate R 1ρ can be calculated as
 |
5 |
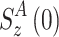 and
and 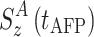 are the z-components of the magnetization at t = 0 and at the end of the AFP pulse (t = t
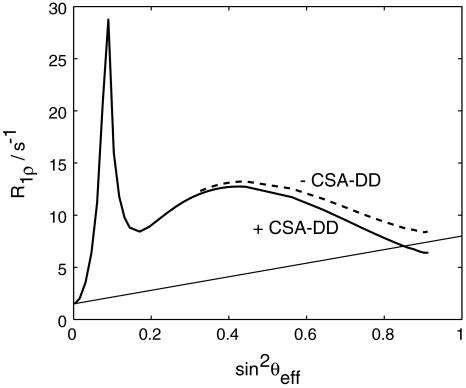
AFP). Whereas the effect of weak scalar coupling is negligible even if in- and anti-phase relaxation are very different (data not shown), cross-correlated relaxation has indeed a pronounced effect on the AFP profile (Fig. 5).
are the z-components of the magnetization at t = 0 and at the end of the AFP pulse (t = t
AFP). Whereas the effect of weak scalar coupling is negligible even if in- and anti-phase relaxation are very different (data not shown), cross-correlated relaxation has indeed a pronounced effect on the AFP profile (Fig. 5).
Fig. 5.
Numerical simulation of R 1ρ(sin2 θ eff) of a 15N spin undergoing chemical exchange (k ex = 1,000 s−1, p B = 4%, Δω/2π = 240 Hz) during an AFP pulse with the parameters ν sweep = 1 kHz, t AFP = 100 ms and 20% ramp with (solid line) and without (dashed line) CSA-DD cross correlation (G x = 5 s−1, G z = 0.5 s−1)
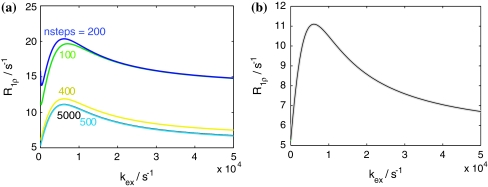
Since a typical AFP pulse consists of several thousand time steps τ, an iterative calculation of density matrices is quite time consuming.4 A reduction of the number of time steps is possible to a certain degree, but can lead to sizable errors (see Fig. 6a). However, another option to reduce computational time is to apply Baker-Campbell-Hausdorff theory (Ernst et al. 2003). This theory states that a product of matrix exponentials with non-commuting exponents can be approximated by one exponential (that is a function of the two exponents) in the following way:
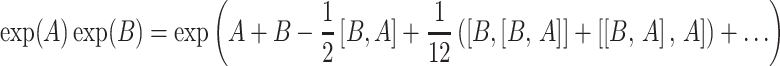 |
6 |
Fig. 6.
a Simulated dependence of R 1ρ on the step size for an AFP pulse with ω max1 = 1 kHz, ν sweep = 1 kHz, t AFP = 100 ms, 20% ramp (sin2 θ eff = 0.83). We simulated the rate as a function of k ex, with p B = 4%, and Δω/2π = 240 Hz. As a reference, the results for a step size of 0.02 ms (number of steps: 5,000) are given (black line). The required number of steps to obtain accurate results with the given parameters is about 500 steps (blue line). b Numerical simulation with (grey) and without (black) BCH approximation. (p B = 4%, Δω = 240 Hz, ω max1 = 1 kHz, ν sweep = 1 kHz, t AFP = 100 ms and 20% ramp, sin2 θ eff = 0.83)
The evaluation of the right-hand side of the equation can be computationally less expensive than the calculation of the product of two matrix exponentials depending on the required number of members of the expansion. In our case, where the expression
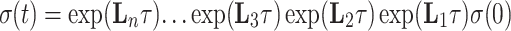 |
7 |
has to be evaluated, it proved optimal to combine four time steps to a first-order average Liouvillian
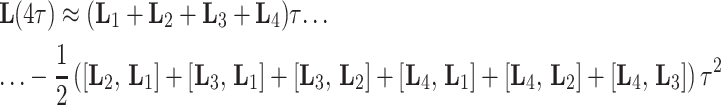 |
8 |
Simulations show no observable deviations between the density matrices obtained using BCH and the exact solution (see Fig. 6b) while computational speed is increased fivefold.
Analytical treatment
As numerical evaluations of large matrices are generally slower than the evaluation of analytical expressions, we opted to split the computation into two parts: (I) First we address coherent evolution, i.e., Larmor precession and scalar coupling, and derive an analytical expression for the effect of these mechanisms. Subsequently (II), the stochastic part is addressed where auto- and cross-relaxation mechanisms are introduced, as well as conformational exchange between two sites A and B. This is also performed in an analytical way. Due to the small time increments, the two parts can be performed sequentially without introducing noticeable deviations from the numerical approach.
-
(I)
Coherent evolution
This approach starts with the Hamiltonian for a heteronuclear, J-coupled IS spin system where the AFP pulse acts as a (time-dependent) spin-lock on S (Zwahlen et al. 1997, 1998)
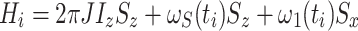 |
9 |
This constitutes an instantaneous Hamiltonian defined by the current offset 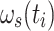 , the current spin-lock amplitude
, the current spin-lock amplitude 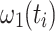 , and the scalar coupling interaction. In this first step, relaxation and conformational exchange are disregarded. The Hamiltonian can be diagonalized by rotation into a coordinate system that is tilted with respect to the z-axis by an angle
, and the scalar coupling interaction. In this first step, relaxation and conformational exchange are disregarded. The Hamiltonian can be diagonalized by rotation into a coordinate system that is tilted with respect to the z-axis by an angle 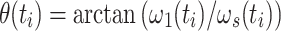 :
:
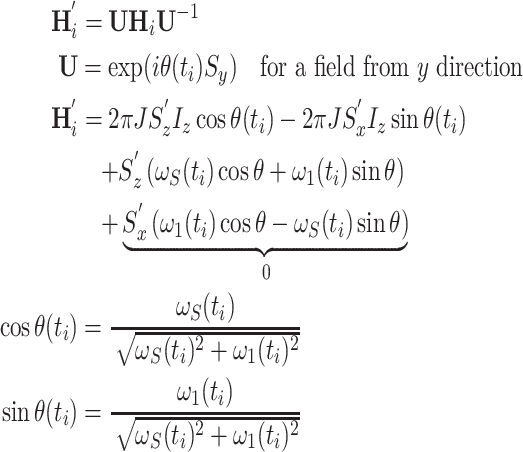 |
10 |
The prime indicates a product operator in the tilted frame. In contrast to Zwahlen’s et al. treatment of adiabatic pulses during INEPT steps (Zwahlen et al. 1997), simulations have shown that in our application the non-secular part of the Hamiltonian in the tilted frame (corresponding to 2S x′I z) cannot be generally neglected. Figure 7a shows that deviations resulting from omission of the term depend critically on the sweep width of the AFP pulse. This can be explained by considering the relative duration of the inversion with respect to the AFP pulse: if sweep widths are narrow, then the process of inversion covers a larger fraction of the AFP pulse, resulting in the above mentioned deviations. On the other hand, large sweep ranges lead to almost instantaneous inversion, resembling conventional 180 degree pulses, and non-secular terms have little to no effect. In particular, we have found substantial deviations for nuclei with small gyromagnetic ratio such as 15N. For 1H nuclei where generally larger sweep widths are employed due to the larger frequency range, the 2S x′I z-term can be safely neglected.
Fig. 7.
a Analytical simulation of the spin-lock relaxation properties of a 15N spin during an AFP pulse. Black All terms are considered. Red 2S x′I z is neglected. Deviations are dependent on the sweep width. b Comparison of the numerical (2,500 steps, grey line), analytical (25,000 steps, black line) and analytical simulations (2,500 steps, red dashed line) as a function of k ex employing an AFP pulse of duration 100 ms, sweep width 1,000 Hz, amplitude 1,000 Hz (sin2 θ eff = 0.83). Exchange parameters were p B = 4% and Δω = 240 Hz. The deviations become more pronounced as k ex increases
The trigonometric functions of θ that determine coherent evolution of the density matrix are calculated in three steps incorporating all terms of Eq. 10.
Rotation of the density matrix into the tilted frame by the equation
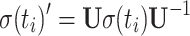 |
-
(2)
Calculation of the next time step using the tilted-frame Hamiltonian
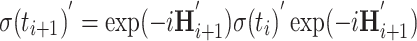 |
-
(3)
Rotation back into the rotating frame
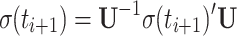 |
The density matrix for t = 0 consists of S z magnetization only. During the first time increment, S x, S y, 2S x I z, 2S y I z, and 2S z I z are generated; this set serves as initial magnetization for the subsequent steps. Details of the calculation are illustrated in supplementary material.
-
(II)
Non-coherent evolution (relaxation)
In order to include auto- and cross-correlated relaxation mechanisms as well as the modulation of the isotropic chemical shift by chemical/conformational exchange, their effects are introduced after step (I) for every time increment in a consecutive manner by solving the common mathematical problem 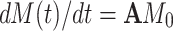 . The following matrices were solved analytically by determining the Eigenvectors and Eigenvalues of A.
. The following matrices were solved analytically by determining the Eigenvectors and Eigenvalues of A.
Longitudinal components of the density matrix are affected by
longitudinal relaxation and exchange between S z-terms
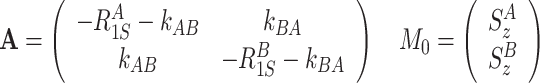 |
-
(b)
longitudinal relaxation and exchange between 2S z I z terms
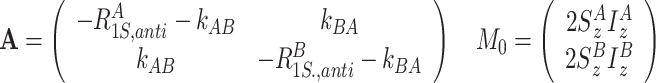 |
-
(c)
CSA-DD cross-correlation between S z and 2S z I z for both states A and B
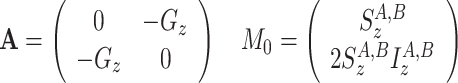 |
Equivalently, transverse components are treated using
Transverse relaxation and exchange between S x or S y terms
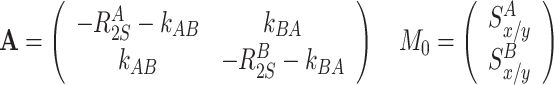 |
-
(b)
Transverse relaxation and exchange between 2S x I z or 2S y I z terms
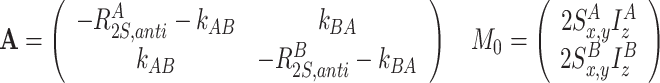 |
-
(c)
CSA-DD cross correlation between S x and 2S x I z (for both sites A and B) as well as S y and 2S y I z
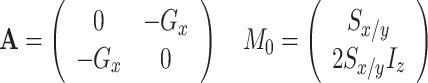 |
This approach is marginally faster than the numerical simulation with BCH for the same number of time steps. However, for large exchange rates the number of time steps in the analytical calculation has to be increased significantly in order to avoid substantial deviations (see Fig. 7b). The reason for this is the non-simultaneous treatment of exchange with respect to coherent evolution and relaxation.
Trott-Palmer equation
A few years ago Palmer and co-workers derived an expression (Eq. 11) for the rotating frame relaxation rate of the major species in an exchanging two-state system for all time regimes (Trott and Palmer 2002, 2003). Here, the time-consuming stepwise evaluation of the Liouville-van Neumann equation is circumvented and replaced by the computation of a closed form equation of R 1ρ(t) as a function of sin2 θ(t) and ΔΩ(t). For our purpose, R 1ρ(t) is computed in a stepwise manner, its time-average being the effective rotating frame relaxation rate.
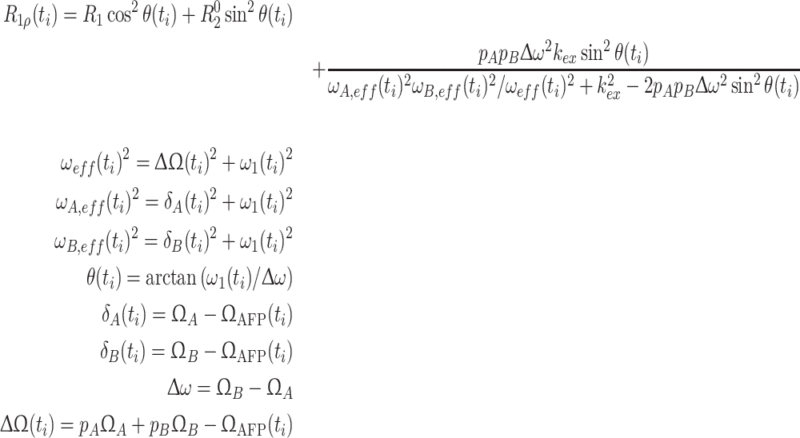 |
11 |
Ω A and Ω B are the resonance frequencies of species A and B, respectively. Ω AFP(t) is the frequency of the applied AFP pulse at a given time t i and ω 1(t) is the corresponding field strength. This expression does not account for CSA-DD cross-correlated relaxation. Our simulations, however, have shown that a correction term to R 1ρ can be obtained from a comparison of AFP profiles computed with and without cross-correlated relaxation (the cross-correlated relaxation rates have to be determined separately). This difference depends only on sin2 θ eff and not on the parameters of the exchange process, wherefore the correction can be applied without prior knowledge of the motional properties of the spin system.
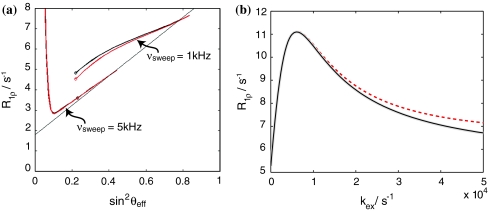
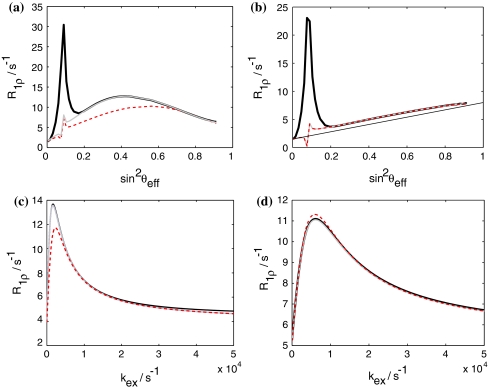
The stepwise calculation can in some cases (large field strengths) be substituted by a one step calculation (see Fig. 8). Here, the time-dependence of the Liouvillian is so small that little error is introduced by assuming a constant R 1ρ. It suffices in such cases to compute the spin lock relaxation rate for an angle sin2θeff. Overall, using the Trott-Palmer equation tremendously reduces computational time (by at least two orders of magnitude), which is particularly important for data analysis.
Fig. 8.
Comparison of the Trott-Palmer equation with numerical results. Black numerical. Grey Trott-Palmer equation with 2,500 steps. Red dashed Trott-Palmer equation with one step. a k ex = 1,000 s−1, p B = 4%, Δω/2π = 240 Hz, νsweep = 1 kHz, t AFP = 100 ms, 20% ramping. b k ex = 30,000 s−1, all other parameters as in (a). c ω max1 = 160 Hz (corresponding to a sin2θeff of 0.38). k ex is varied between 10 and 5,000 s−1, all other parameters as in (a). d ω max1 = 1 kHz (corresponding to a sin2 θ eff of 0.83), all other parameters as in (c). Panels (a) and (b) demonstrate that the accuracy of the one-step Trott-Palmer equation decreases with increasing exchange contribution. Panels (c) and (d) illustrate the dependence of the deviations on the spin-lock field strength. In all cases, employing the Trott-Palmer equation in an iterative calculation reproduces the numerical results
Experimental results
Data obtained on the protein KIX
We have conducted 15N AFP experiments on the protein KIX (1 mM, pH = 5.5, 50 mM phosphate buffer, 25 mM NaCl), which exhibits exchange in the intermediate regime on the chemical shift time-scale. NMR data were acquired on a Varian Inova spectrometer operating at 18.8 T at 27 degrees. We recorded AFP experiments with a 100 ms AFP pulse (with parabolic phase modulation and ramping of 20% at each end) for arrays of spinlock amplitudes given in Table 1. Sweep widths were 1, 1.4, and 5 kHz (see supplementary material). The measuring time was about 24 h per AFP array. Due to the uncertainty in the direct determination of R 1 from the AFP experiment we decided to record a separate experiment (for details see Table 1). In addition we recorded transverse 15N(CSA)-15N-1H-(DD) cross-correlated relaxation rates (Pelupessy et al. 2003), experimental parameters are given in Table 2. (Note that the exchange-free transverse relaxation rate can be obtained from these experiments, offering an additional constraint for the analysis). The effect of longitudinal 15N(CSA)-15N-1H-(DD) cross-correlated relaxation was neglected since its effect is very small (data not shown).
Table 1.
Experimental parameters for AFP and R 1 experiments on 15N for the protein KIX
| 15N AFP spin lock amplitude (Hz) | 15N AFP measuring time | 15N R 1 relaxation delays (ms) | 15N R 1 measuring time |
|---|---|---|---|
| 0, 37.7, 59.0, 73.4, 92.4, 115.7, 144.9, 181.3, 227.0, 284.1, 355.6, 445.2, 498.0, 557.2, 623.4, 697.5, 780.4, 873.1, 976.9, 557.2, 780.4 | 24 h | 0, 50, 100, 150, 200, 300, 400, 600, 900, 300 | 11 h |
Table 2.
Experimental parameters for transverse 15N(CSA)-15N1H-(DD) cross-correlated relaxation rate measurements (Pelupessy et al. 2003)
| 15N(CSA)-15N1H-(DD) relaxation delays (ms) | 15N(CSA)-15N1H-(DD) measuring time transfer experiment | 15N(CSA)-15N1H-(DD) measuring time reference experiment |
|---|---|---|
| 10, 20, 30, 40, 20 | 2 × 33 h | 2 × 5.5 h |
We compared our experimental results with theoretical curves calculated using parameters obtained from CPMG experiments (Tollinger et al. 2006). The results are in excellent agreement with the simulations, as demonstrated in Fig. 9 and supplementary material.
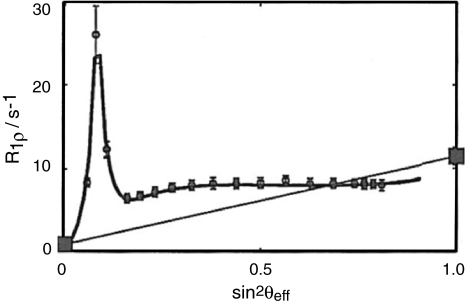
Fig. 9.
Comparison of experimental results (grey circles with error bars) and the theoretical curve (black solid line) computed from the exchange parameters obtained from CPMG experiments (KIX residue D638: k ex = 876 s−1, p B = 3.8%, Δω/2π = 1.80 ppm at 18.8T, νsweep = 1 kHz, t AFP = 100 ms, 20% ramping). Experimental R 1 and R 02 values are indicated as large grey squares at sin2 θ eff = 0 and 1, respectively. Further results are shown in Supplementary material
Synthetic data sets
The process encountered in KIX involves a rather small population of excited state (about 3%), and the AFP dispersion curves are not very pronounced, compared to the CPMG dispersion curves (see previous section). Fitting these data does not give reliable results, wherefore we have decided to demonstrate the applicability of the method using synthetic data sets that assume higher populations of excited states and various time-scales. Furthermore we assumed that we have determined R 1 and the cross-correlated relaxation rates from independent measurements. We used five fitting parameters only (k ex, p b, ∆ω, R 02(11.7T) and R 02(18.8T)); the antiphase relaxation rates do not exert significant influence on the AFP dispersion curves, as scalar coupling is suppressed to a large extent due to the spin lock). Also, to reduce the amount of computational time (of the numerical procedure), we decided to use 11 × 2 data points only (number of spinlock amplitudes time number of field strengths). We compared the numerical fitting procedure to the script that employs the Trott-Palmer equation using an equal number of steps, and we found a 150-fold decrease in computational time using the Trott-Palmer equation (150 Monte Carlo runs took about 15 h for the numerical fit and 6 min with the Trott-Palmer equation). Fitting was performed using Matlab (The MathWorks, www.mathworks.com). Details of the Monte Carlo fitting procedure are given in supplementary material. We tested the fit using the Trott-Palmer equation on several time-scales log(k ex/∆ω) = −0.07, 0.50, 1.02 at 11.7T) and several error levels using p b = 0.2 and ∆ω corresponding to 3 ppm. Results proved to be robust, an example is given in Fig. 10 and several others in supplementary material.
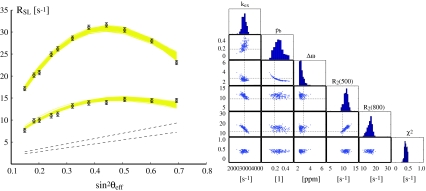
Fig. 10.
Fit of simulated data. Exchange parameters were k ex = 3,000 s−1, p b = 0.2, Δω = 3 ppm. Spinlock relaxation rates were generated for a 15N nucleus at 11.7 and 18.8T, with a 100 ms AFP pulse sweeping over a frequency range of 2,000 Hz in 2,500 steps (ramping 20% at the start and at the end of the pulse). The experimental error in measured rates was set to 0.5 s−1. The left panel shows the (simulated) ‘experimental’ AFP profile (black circles and error bars), superimposed with the individual fits of a Monte Carlo simulation (200 runs) using the Trott-Palmer equation, shown as yellow solid lines. The exchange free profiles for the two field strengths are depicted as dashed black lines. The right panel shows scatter plots of the resulting fit parameters, with the input values at the intersections of the dashed lines. We assumed that cross-correlated relaxation has been corrected for. Further examples (different k ex and errors) are shown in supplementary material
Discussion
Adiabatic fast passage, although widely used for the purpose of broadband decoupling, has not often been applied to the investigation of dynamic properties on the millisecond to microsecond time-scale of biological macromolecules. The reason for this is primarily the long computational times required to predict the behavior of a spin system under the influence of a time-dependent Hamiltonian with non-commuting elements. We believe, however, that AFP pulses present a valuable complement to existing strategies, such as CPMG relaxation dispersion measurements and R 1ρ experiments. The AFP technique, just as static R 1ρ experiments, is in principle less responsive to dynamic effects than CPMG as the relevant magnetization has a significant longitudinal component. This means that large exchange contributions due to pronounced excited state populations are quenched more efficiently, such that an AFP analysis may present an alternative to the CPMG method at excited state populations of 10–20%.5 At the same time, it entails the benefits of static R 1ρ experiments, i.e., the possibility to access faster time-scale motions. Of note, AFP pulses have an important advantage with respect to static R 1ρ experiments, as they allow to analyze spins that spread out over a large range of offsets while at the same time maintaining a large transverse magnetization component.6
Bearing in mind the potential of AFP pulses in this field, we have investigated different approaches for reducing the calculation time for the simulation and analysis of AFP pulse sequences. The methods have been described and discussed with respect to accuracy, computational speed and limitations. A stepwise calculation is generally necessary in all cases, and all methods proved to be robust. With regard to computational speed the Trott-Palmer equation is the method of choice if populations are sufficiently skewed. If the Trott-Palmer equation is used, a numerical or an analytical calculation has to be performed once for every spin in order to account for CSA-DD cross correlation. We have demonstrated the potential utility of the method for determining μs–ms dynamics by fitting synthetic data sets as a function of time-scale and experimental error. With the efficient computation of relaxation rates during the adiabatic fast passage pulses we hope to provide a basis for a spread in applications of this tool in the field of biomolecular NMR spectroscopy.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
RA was a recipient of a Doc fForte fellowship of the Austrian Academy of Sciences. This work was supported by the FWF (P20549) (to RK). MT is supported by the FWF (project number P22735). KK was a recipient of an APART fellowship of the Austrian Academy of Sciences and is currently holding an Elise Richter grant (FWF project V173). We are deeply indebted to Lewis for his seminal contributions to the field of NMR spectroscopy, for his generous support and—last but not least—for the continuous inspiration we have received during our stays in his lab and ever since.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Footnotes
In the absence of a spin-lock field, thermal equilibrium is represented by a polarization of Z magnetization, and S
z(t) relaxes towards 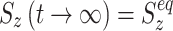 . During on-resonance spin-lock
. During on-resonance spin-lock 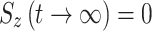 (as for the transverse components), and in the off-resonance case the value is between 0 and 1. Of note, we have found in our simulations that in the AFP experiment little or no error is introduced to the calculated AFP profiles if it is assumed that
(as for the transverse components), and in the off-resonance case the value is between 0 and 1. Of note, we have found in our simulations that in the AFP experiment little or no error is introduced to the calculated AFP profiles if it is assumed that 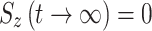 .
.
In AX spin systems where A is the nucleus of interest and X is scalar coupled to A, A(CSA)-AX(DD) is the most important of the cross-correlated relaxation mechanisms and has a significant effect on the outcome of quantitative relaxation studies (e.g. 15N(CSA)-15N-1H(DD) cross-correlation in 15N labeled proteins). Note, however, that in the presence of other dipole vectors or in more complicated spin systems such as methyl groups (AX 3), cross-correlated relaxation mechanisms are much more abundant and it is extremely demanding to account for them in calculations.
Note that the cross-correlation rate has been assumed equal for both exchanging species. Here we used mostly rates that are in accordance with a rigid bond vector tumbling at the rate of a small spherical protein. There is no significant influence of G x and G z of species B on the AFP profile (data not shown) given the limited range of CSA-DD cross-correlated relaxation rates for this system.
Using Matlab (The MathWorks, www.mathworks.com), one simulation of an array of 11 data points (spin-lock amplitude) at one field strength takes about 5 s, and one fit takes about 2–3 min. A Monte Carlo simulation of 100 runs takes about 4 h. Doubling the number of field strengths doubles the minimization time, and increasing the number of residues in a global fit increases the computational time accordingly.
This is true as long as line-broadening effects do not compromise the analysis. Note that CPMG experiments can, in principle, be recorded for short relaxation periods as well, but γB 1 sampling may not be as exhaustive as for longer periods.
On-resonance T 1ρ experiments can be conducted for one offset at a time only, and resonances at different offsets are prone to severe offset effects—their magnetization is efficiently scrambled due to oscillations in the xy plane. Therefore, a spin by spin measurement is required, which, however, is time-consuming and thus impractical. In order to simultaneously measure all spins within a large spectral range in one shot, R 1ρ experiments are usually performed at large offsets, with the spin-lock frequency so far away from all signals that the angle θ is approximately equal for all spins and dephasing due to offset effects can be safely neglected. The disadvantage of this approach is that, due to hardware limitations, only small deviations of the spinlock field from the z-axis can be realized. As a consequence, the magnetization component in the transverse plane is small, decreasing the sensitivity of the method. A solution to this problem has recently been suggested by Hansen and Kay (2007 J Biomol NMR, 37, 4, 245–255). AFP experiments present an alternative way to simultaneously measure many offsets at a time, since all spins in the sweep range are dragged along with the effective field. Also, larger tilt angles can be reached employing the same (maximum) field strength and narrowing the sweep range.
Contributor Information
Robert Konrat, Phone: +43-1-4277-52202, Email: Robert.konrat@univie.ac.at.
Karin Kloiber, Phone: +43-512-5075230, Email: karin.kloiber@uibk.ac.at.
References
- Abragam A. The principles of nuclear magnetism. Oxford: Clarendon Press; 1962. [Google Scholar]
- Allerhand A, Gutowsky HS, Jonas J, Meinzer RA. Nuclear magnetic resonance methods for determining chemical-exchange rates. J Am Chem Soc. 1966;88(14):3185–3193. doi: 10.1021/ja00966a001. [DOI] [PubMed] [Google Scholar]
- Boehlen JM, Bodenhausen G. Experimental aspects of Chirp NMR spectoscopy. J Magn Reson Ser A. 1993;102:293–301. doi: 10.1006/jmra.1993.1107. [DOI] [Google Scholar]
- Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313(5793):1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- Dayie KT, Wagner G, Lefevre JF. Theory and practice of nuclear spin relaxation in proteins. Annu Rev Phys Chem. 1996;47:243–282. doi: 10.1146/annurev.physchem.47.1.243. [DOI] [PubMed] [Google Scholar]
- Ernst RR, Bodenhausen G, Wokaun A (2003) Principles of nuclear magnetic resonance in one and two dimensions. International series of monographs on chemistry; 14, Repr. with further corrections. edn. Clarendon Press; Oxford University Press, Oxford [Oxfordshire], New York
- Frederick KK, Marlow MS, Valentine KG, Wand AJ. Conformational entropy in molecular recognition by proteins. Nature. 2007;448(7151):325–329. doi: 10.1038/nature05959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen DF, Kay LE. Improved magnetization alignment schemes for spin-lock relaxation experiments. J Biomol NMR. 2007;37(4):245–255. doi: 10.1007/s10858-006-9126-6. [DOI] [PubMed] [Google Scholar]
- Henzler-Wildman K, Kern D. Dynamic personalities of proteins. Nature. 2007;450(7172):964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- Kay LE. NMR studies of protein structure and dynamics. J Magn Reson. 2005;173(2):193–207. doi: 10.1016/j.jmr.2004.11.021. [DOI] [PubMed] [Google Scholar]
- Kay LE, Muhandiram DR, Wolf G, Shoelson SE, Forman-Kay JD. Correlation between binding and dynamics at SH2 domain interfaces. Nat Struct Biol. 1998;5(2):156–163. doi: 10.1038/nsb0298-156. [DOI] [PubMed] [Google Scholar]
- Kay LE, Torchia DA, Bax A. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry. 1989;28(23):8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- Konrat R, Tollinger M. Heteronuclear relaxation in time-dependent spin systems: (15)N-T1 (rho) dispersion during adiabatic fast passage. J Biomol NMR. 1999;13(3):213–221. doi: 10.1023/A:1008324721356. [DOI] [PubMed] [Google Scholar]
- Kupce E, Freeman R. Adiabatic pulses for wideband inversion and broadband decoupling. J Magn Reson Ser A. 1995;115:273–276. doi: 10.1006/jmra.1995.1179. [DOI] [Google Scholar]
- Kupce E, Freeman R (1996) Optimized adiabatic pulses for wideband spin inversion. J Magn Reson Ser A 118:299–303
- Loria JP, Rance M, Palmer AG., III A relaxation-compensated Carr–Purcell–Meiboom–Gill sequence for characterizing chemical exchange by NMR spectroscopy. J Am Chem Soc. 1999;121:2331–2332. doi: 10.1021/ja983961a. [DOI] [Google Scholar]
- Mangia S, Traaseth NJ, Veglia G, Garwood M, Michaeli S. Probing slow protein dynamics by adiabatic R(1rho) and R(2rho) NMR experiments. J Am Chem Soc. 2010;132(29):9979–9981. doi: 10.1021/ja1038787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittermaier A, Kay LE. New tools provide new insights in NMR studies of protein dynamics. Science. 2006;312(5771):224–228. doi: 10.1126/science.1124964. [DOI] [PubMed] [Google Scholar]
- Mulder FAA, de Graaf RA, Kaptein R, Boelens R. An off-resonance rotating frame relaxation experiment for the investigation of macromolecular dynamics using adiabatic rotations. J Magn Reson. 1998;131(2):351–357. doi: 10.1006/jmre.1998.1380. [DOI] [PubMed] [Google Scholar]
- Palmer AG., III NMR characterization of the dynamics of biomacromolecules. Chem Rev. 2004;104(8):3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- Palmer AG, III, Kroenke CD, Loria JP. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol. 2001;339:204–238. doi: 10.1016/S0076-6879(01)39315-1. [DOI] [PubMed] [Google Scholar]
- Palmer AG, III, Massi F. Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem Rev. 2006;106(5):1700–1719. doi: 10.1021/cr0404287. [DOI] [PubMed] [Google Scholar]
- Pelupessy P, Espallargas GM, Bodenhausen G. Symmetrical reconversion: measuring cross-correlation rates with enhanced accuracy. J Magn Reson. 2003;161(2):258–264. doi: 10.1016/S1090-7807(02)00190-8. [DOI] [PubMed] [Google Scholar]
- Peng JW, Wagner G. Investigation of protein motions via relaxation measurements. Methods Enzymol. 1994;239:563–596. doi: 10.1016/S0076-6879(94)39022-3. [DOI] [PubMed] [Google Scholar]
- Popovych N, Sun S, Ebright RH, Kalodimos CG. Dynamically driven protein allostery. Nat Struct Mol Biol. 2006;13(9):831–838. doi: 10.1038/nsmb1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugase K, Dyson HJ, Wright PE. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature. 2007;447(7147):1021–1025. doi: 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
- Tollinger M, Kloiber K, Agoston B, Dorigoni C, Lichtenecker R, Schmid W, Konrat R. An isolated helix persists in a sparsely populated form of KIX under native conditions. Biochemistry. 2006;45(29):8885–8893. doi: 10.1021/bi0607305. [DOI] [PubMed] [Google Scholar]
- Tollinger M, Skrynnikov NR, Mulder FA, Forman-Kay JD, Kay LE. Slow dynamics in folded and unfolded states of an SH3 domain. J Am Chem Soc. 2001;123(46):11341–11352. doi: 10.1021/ja011300z. [DOI] [PubMed] [Google Scholar]
- Trott O, Palmer AG., III R1rho relaxation outside of the fast-exchange limit. J Magn Reson. 2002;154(1):157–160. doi: 10.1006/jmre.2001.2466. [DOI] [PubMed] [Google Scholar]
- Trott O, Palmer AG., III An average-magnetization analysis of R1rho relaxation outside of the fast exchange limit. Mol Phys. 2003;101:753–763. doi: 10.1080/0026897021000054826. [DOI] [Google Scholar]
- Zwahlen C, Legault P, Vincent SJ, Greenblatt J, Konrat R, Kay LE. Methods of measurement of intermolecular NOEs by multinuclear NMR spectroscopy: application to a bacteriophage 1 N-Peptide/boxB RNA complex. J Am Chem Soc. 1997;119:6711–6721. doi: 10.1021/ja970224q. [DOI] [Google Scholar]
- Zwahlen C, Vincent SJ, Kay LE. Analytical description of the effect of adiabatic pulses on IS, I2S, and I3S spin systems. J Magn Reson. 1998;130(2):169–175. doi: 10.1006/jmre.1997.1289. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.