Effective drift and diffusion of a particle jumping between mobile and immobile states

Abstract

We study propagation of a particle that jumps between two states, in which it moves with different velocities and diffusion coefficients. To simplify analysis, in the main part of the paper we derive formulas assuming that in one of the states the particle is immobile. A generalization to the case when the particle is mobile in both states is given at the end of the paper. The formulas show how the effective drift velocity and effective diffusion coefficient depend on jump rates between the two states as well as on the particle velocities and diffusion coefficients in these states. Specifically, we find that the effective diffusion coefficient can exhibit a non-monotonic behavior as a function of the ratio of the jump rates.

1. Introduction

In many situations particle transport occurs intermittently and the particle motion consists of phases wherein the particle has different drift velocities and diffusion coefficients. Examples range from particle motion in the chromatographic column [1–3] to motion of proteins, vesicles, and viruses in the cytoplasm [4–11]. Although motions of this type are very different in details, they all have a common feature: after the particle changes its state sufficiently many times, the distribution of its position at time t is given by a coarse-grained propagator, which is Gaussian. For a particle that starts from the origin, x = 0, at t = 0 the one-dimensional propagator in the x-direction has the form

$$G(x,t)=\frac{1}{\sqrt{4\pi D_{\mathit{eff}}t}}exp\left[-\frac{{(x-v_{\mathit{eff}}t)}^2}{4D_{\mathit{eff}}t}\right],$$ (1.1)

where v_eff and D_eff are the effective drift velocity and diffusion coefficient.

This coarse-grained propagator is completely defined by v_eff and D_eff. In this paper we discuss how to find these quantities for a simple model of a particle that jumps between mobile (m) and immobile (im) states

$$m\underset{k_{im}}{\overset{k_m}{\rightleftarrows }}im,$$ (1.2)

where k_m and k_im are the rates constants, so that $k_m^{-1}={\tau }_m$ and $k_{im}^{-1}={\tau }_{im}$ are the particle mean lifetimes in the two states, respectively. When the particle is in the mobile state, its motion is characterized by the drift velocity, v, and diffusion coefficient, D.

Consider a particle that starts from the origin, x = 0, being in one of the two states. The fate of this particle is described by the exact propagator, g_αβ (x,t), which is the probability density of finding the particle in state α at point x at time t on condition that the particle was in state β at t = 0, α,β= m, im. On times that are much larger than the relaxation time, τ_rel = (k_m + k_im)⁻¹, the propagator becomes independent of the initial state of the particle and takes the form

$$g_{\alpha \beta }(x,t)=G(x,t)P_{\alpha }^{eq},t\gg {\tau }_{\mathit{rel}},$$ (1.3)

where $P_{\alpha }^{eq}$ is the equilibrium probability of finding the particle in state α:

$$P_m^{eq}=\frac{k_{im}}{k_m+k_{im}},P_{im}^{eq}=\frac{k_m}{k_m+k_{im}}.$$ (1.4)

The probability density of finding the particle at point x at t ≫τ_rel is given by the sum of the two propagators,

$$g_{m\beta }(x,t)+g_{im\beta }(x,t)=G(x,t),$$ (1.5)

since the sum of the equilibrium probabilities is equal to unity, $P_m^{eq}+P_{im}^{eq}=1$.

The fact that the propagator, Eq. (1.1), is Gaussian implies that it is completely determined by the first two moments of the particle displacement. We exploit this fact. To be more specific, we derive long time asymptotic behaviors of the moments and use them to find v_eff and D_eff. The formulas for v_eff and D_eff, Eq. (2.12) and (2.22), show how these quantities depend on v, D, and the rate constants k_m and k_im. Generalizations of these formulas to the case when the particle jumps between two states, in both of which it moves with different velocities and diffusion coefficients, are given at the very end of the paper, Eqs. (3.3) and (3.4). These formulas are the main results of the present paper. Another result is the approach we use to derive the formulas, which is straightforward and allows one to find the moments with relative ease.

2. Theory

The propagator g_αβ(x,t)satisfies

$$\begin{array}{l}\frac{\partial g_{m\beta }}{\partial t}=D\frac{{\partial }^2{g}_{m\beta }}{\partial x^2}-v\frac{\partial g_{m\beta }}{\partial x}-k_m{g}_{m\beta }+k_{im}{g}_{im\beta }\\ \frac{\partial g_{im\beta }}{\partial t}=k_m{g}_{m\beta }-k_{im}{g}_{im\beta }\end{array}$$ (2.1)

with the initial conditions

$$g_{\alpha \beta }(x,0)={\delta }_{\alpha \beta }\delta (x),\alpha ,\beta =m,im.$$ (2.2)

Both the asymptotic behavior of the moments and the effective parameters, v_eff and D_eff, are independent of the initial state of the particle. To shorten the derivation, it is convenient to consider the probability density of finding the particle in state α at point x at time t on condition that initially (at t = 0) it was in state β with the equilibrium probability $P_{\beta }^{eq}$. The new probability density, denoted by p_α(x,t), is the equilibrium average of the two propagators,

$$p_{\alpha }(x,t)=g_{\alpha m}(x,t)P_m^{eq}+g_{\alpha im}(x,t)P_{im}^{eq}.$$ (2.3)

Functions p_α(x,t)satisfy

$$\begin{array}{l}\frac{\partial p_m}{\partial t}=D\frac{{\partial }^2{p}_m}{\partial x^2}-v\frac{\partial p_m}{\partial x}-k_m{p}_m+k_{im}{p}_{im}\\ \frac{\partial p_{im}}{\partial t}=k_m{p}_m-k_{im}{p}_{im},\end{array}$$ (2.4)

with the initial conditions

$$p_m(x,0)=P_m^{eq}\delta (x),p_{im}(x,0)=P_{im}^{eq}\delta (x).$$ (2.5)

We use the probability densities p_α(x,t)to define the moments $\langle x_{\alpha }^n(t)\rangle$ by

$$\langle x_{\alpha }^n(t)\rangle =\underset{-\infty }{\overset{\infty }{\int }}{x}^n{p}_{\alpha }(x,t)dx.$$ (2.6)

The n = 0 moments are the probabilities of finding the particle in mobile and immobile states at time t, P_m(t) and P_im(t). Integrating the equations in Eq. (2.4) with respect to x from minus to plus infinity, we find that the probabilities P_α(t)satisfy the rate equations:

$$\frac{{dP}_m(t)}{dt}=-\frac{{dP}_{im}(t)}{dt}=-k_m{P}_m(t)+k_{im}{P}_{im}(t).$$ (2.7)

Solving these equations with the initial conditions $P_{\alpha }(0)=P_{\alpha }^{eq}$ we obtain

$$P_{\alpha }(t)=P_{\alpha }^{eq}.$$ (2.8)

This must be expected since the equilibrium initial distribution does not change with time.

Equations for the first moments 〈x_α(t)〉 can be obtained by multiplying the equations in Eq. (2.4) by x and then integrating with respect to x from minus to plus infinity. This leads to

$$\begin{array}{l}\frac{d\langle x_m(t)\rangle }{dt}=-{vP}_m^{eq}-k_m\langle x_m(t)\rangle +k_{im}\langle x_{im}(t)\rangle \\ \frac{d\langle x_{im}(t)\rangle }{dt}=k_m\langle x_m(t)\rangle -k_{im}\langle x_{im}(t)\rangle .\end{array}$$ (2.9)

The initial conditions that should be added to these equations are

$$\langle x_m(0)\rangle =\langle x_{im}(0)\rangle =0.$$ (2.10)

The mean displacement of the particle for time t, 〈x(t)〉, is the sum of the two moments,

$$\langle x(t)\rangle =\langle x_m(t)\rangle +\langle x_{im}(t)\rangle .$$ (2.11)

Summing up the two equations in Eq. (2.9) we arrive at

$$\frac{d\langle x(t)\rangle }{dt}={vP}_m^{eq}=v_{\mathit{eff}},$$ (2.12)

where we have used the definition of the effective drift velocity

$$v_{\mathit{eff}}=\underset{t\to \infty }{lim}\frac{d\langle x(t)\rangle }{dt}.$$ (2.13)

The advantage of the equilibrium initial distribution, $P_{\beta }(0)=P_{\beta }^{eq}$, is that it leads to the time-independent velocity, d 〈x(t)〉/dt, which is equal to v_eff from the very beginning of the process.

Multiplying the equations in Eq. (2.4) by x² and then integrating with respect to x from minus to plus infinity, we obtain the equations for the second moments, $\langle x_{\alpha }^2(t)\rangle$,

$$\begin{array}{l}\frac{d\langle x_m^2(t)\rangle }{dt}=2{DP}_m^{eq}-2v\langle x_m(t)\rangle -k_m\langle x_m^2(t)\rangle +k_{im}\langle x_{im}^2(t)\rangle \\ \frac{d\langle x_{im}^2(t)\rangle }{dt}=k_m\langle x_m^2(t)\rangle -k_{im}\langle x_{im}^2(t)\rangle .\end{array}$$ (2.14)

The initial conditions imposed on the solution are

$$\langle x_m^2(0)\rangle =\langle x_{im}^2(0)\rangle =0.$$ (2.15)

The mean squared displacement of the particle, 〈x²(t)〉, is given by the sum of the second moments,

$$\langle x^2(t)\rangle =\langle x_m^2(t)\rangle +\langle x_{im}^2(t)\rangle .$$ (2.16)

Summing up the equations in Eq. (2.14), we find that 〈x²(t)〉 satisfies

$$\frac{d\langle x^2(t)\rangle }{dt}=2{DP}_m^{eq}+2v\langle x_m(t)\rangle$$ (2.17)

with the initial condition 〈x² (0)〉= 0. Function 〈x_m(t)〉 can be found by solving the equations in Eq. (2.9). The result is

$$\langle x_m(t)\rangle =\left[P_m^{eq}t+{\tau }_{im}(1-e^{-t/{\tau }_{\mathit{rel}}})\right]v_{\mathit{eff}}.$$ (2.18)

Substituting this into Eq. (2.17) and integrating the resultant equation with the initial condition 〈x²(0)〉= 0, we obtain

$$\langle x^2(t)\rangle =2{DP}_m^{eq}t+v_{\mathit{eff}}^2\left\{t^2+2\frac{k_m}{k_{im}}{\tau }_{\mathit{rel}}\left[t-{\tau }_{\mathit{rel}}(1-e^{-t/{\tau }_{\mathit{rel}}})\right]\right\}.$$ (2.19)

Effective diffusion coefficient, D_eff, is defined as

$$D_{\mathit{eff}}=\frac{1}{2}\underset{t\to \infty }{lim}\frac{1}{t}\left(\langle x^2(t)\rangle -{\langle x(t)\rangle }^2\right).$$ (2.20)

According to Eq. (2.12) the mean displacement of the particle is

$$\langle x(t)\rangle =v_{\mathit{eff}}t.$$ (2.21)

Substituting this and the expression for 〈x²(t)〉 in Eq. (2.19) into Eq. (2.20) we find that D_eff is given by

$$D_{\mathit{eff}}=(D+v^2{k}_m{\tau }_{\mathit{rel}}^2)P_m^{eq}={DP}_m^{eq}+v^2\frac{{\tau }_{\mathit{rel}}^3}{{\tau }_m{\tau }_{im}}.$$ (2.22)

The approach we have used in our analysis, the formulas for v_eff and D_eff, Eqs. (2.12) and (2.22), as well as their generalizations, Eqs. (3.4) and (3.5), are the main results of the present paper.

3. Discussion and concluding remarks

Expression for the effective drift velocity, Eq. (2.12), has a transparent physical interpretation. According to Eq. (2.21) the mean displacement of the particle is given by $\langle x(t)\rangle =v_{\mathit{eff}}t={vP}_m^{eq}t$. This formula, as might be expected, gives the mean displacement in time t as a product of the particle velocity v in the mobile state and the mean time that the particle spends in this state. The latter is given by $P_m^{eq}t$ leading to $v_{\mathit{eff}}={vP}_m^{eq}$.

Expression in Eq. (2.22) presents D_eff as a sum of two terms: the first gives D_eff at v= 0, $D_{\mathit{eff}}{\mid }_{v=0}={DP}_m^{eq}$, while the second gives D_eff at D= 0, D_eff|_D=0 = v²τ_rel/(τ_m τ_im). The first term has the same interpretation as the effective velocity: it takes into account the fact that the random force acts on the particle only when the particle is in the mobile state. The second term is due to fluctuations of the time spent by the particle in the mobile state: realizations with larger or smaller times than the average time, $P_m^{eq}t$, are responsible for the displacements that are, correspondingly, larger or smaller than 〈x(t)〉. While the first term determines D_eff at small v, the second term determines D_eff at large v when the inequality $v^2{k}_m{\tau }_{\mathit{rel}}^2\gg D$ is fulfilled. The fractions of the total time spent by the particle in each of the two states have been analyzed in Ref. 12 devoted to the single-molecule fluorescence spectroscopy of two-state systems. As shown there, at large times, the cumulative residence times in the two states fluctuate around their average values, and the fluctuations are Gaussian. This results in the Gaussian form of the propagator in Eq. (1.1).

If the drift velocity is large enough, the dependence of D_eff on the equilibrium binding constant defined as the ratio of the rate constants, K = k_m/k_im, exhibits non-monotonic behavior. To make this point clear we rewrite Eq. (2.22) in the form

$$D_{\mathit{eff}}=D\left[\frac{1}{1+K}+V^2\frac{K^2}{{(1+K)}^3}\right],$$ (3.1)

where V is dimensionless velocity,

$$V^2=\frac{v^2}{{Dk}_m}.$$ (3.2)

Figure 1 illustrates this non-monotonic behavior of the normalized effective diffusion coefficient D_eff/D. At large V the second term in Eq. (3.1) dominates at most K values. This term is non-monotonic in K with the maximum located at K = 2. It is seen that, indeed, the effective diffusion coefficient exhibits a maximum in the vicinity of K = 2.

Figure 1.

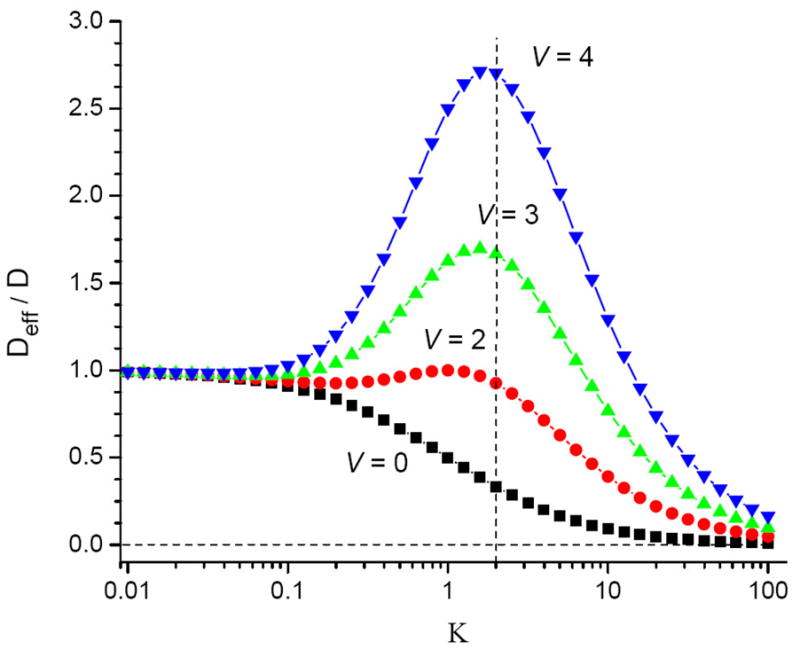
Effective diffusion coefficient, Eqs. (2.22) and (3.1), normalized to the particle diffusion coefficient in the mobile state, as a function of the equilibrium binding constant, K = k_m/k_im, shows a non-monotonic behavior if the dimensionless velocity V defined in Eq. (3.2) is large enough.

The non-monotonic behavior of the effective diffusion coefficient discussed above should not be confused with similar behavior of D_eff analyzed recently in Refs. 13–17, devoted to driven transport in periodic systems. Though there could be some similarities in the physics involved, it is important to indicate that Refs. 13–17 demonstrate non-monotonic dependence of D_eff on the strength of the applied driving force, while we consider the effective diffusion coefficient as a function of equilibrium binding constant, K = k_m/k_im.

Finally, we note that the approach we have used to derive the formulas for v_eff and D_eff, Eqs. (2.12) and (2.22), is equally applicable in a more general case when the particle jumps between two states in which it moves with different velocities and different diffusion coefficients. Although the derivation becomes more cumbersome, it eventually leads to simple formulas for v_eff and D_eff. Denoting the mean lifetimes of the particle in the two states by ${\tau }_1=k_1^{-1}$ and ${\tau }_2=k_2^{-1}$, where k₁and k₂are the rate constants, we can write v_eff and D_eff as

$$v_{\mathit{eff}}=v_1{P}_1^{eq}+v_2{P}_2^{eq},$$ (3.3)

$$D_{\mathit{eff}}=D_1{P}_1^{eq}+D_2{P}_2^{eq}+{(v_1-v_2)}^2\frac{{\tau }_1^2{\tau }_2^2}{{({\tau }_1+{\tau }_2)}^3}.$$ (3.4)

Here $P_1^{eq}$ and $P_2^{eq}$ are equilibrium probabilities of finding the particle in states 1 and 2,

$$P_1^{eq}=\frac{{\tau }_1}{{\tau }_1+{\tau }_2};P_2^{eq}=\frac{{\tau }_2}{{\tau }_1+{\tau }_2},$$ (3.5)

in which the particle motion is characterized by velocities v₁ and v₂ and diffusion coefficients D₁ and D₂, respectively.

To summarize, the paper is focused on the coarse-grained propagator of a particle that randomly jumps between two states of different drift velocities and diffusion coefficients. Since the propagator is Gaussian, Eq. (1.1), it is completely determined by two parameters, the effective velocity and diffusion coefficient. These quantities can be readily found using the definitions, Eqs. (2.13) and (2.20), and the solutions for the first two moments of the particle displacement, Eqs. (2.19) and (2.21). Note that a similar approach based on finding the moments has been used to determine the effective diffusion coefficient of a particle that moves in a medium with fluctuating viscosity [18].